ML and Statistics-Driven Route Planning: Effective Solutions Without Maps

Abstract

Background: Accurate route planning is a core challenge in logistics, particularly for small- and medium-sized enterprises that lack access to costly geospatial tools. This study explores whether usable distance matrices and routing outputs can be generated solely from geographic coordinates without relying on full map-based infrastructure. Methods: A dataset of over 5000 Hungarian postal locations was used to evaluate five models: Haversine-based scaling with circuity, linear regression, second- and third-degree polynomial regressions, and a trained artificial neural network. Models were tested on the full dataset, and three example routes representing short, medium, and long distances. Both statistical accuracy and route-level performance were assessed, including a practical optimization task. Results: Statistical models maintained internal consistency, but systematically overestimated longer distances. The ANN model provided significantly better accuracy across all scales and produced routes more consistent with map-based paths. A new evaluation method was introduced to directly compare routing outputs. Conclusions: Practical route planning can be achieved without GIS services. ML-based estimators offer a cost-effective alternative, with potential for further improvement using larger datasets, additional input features, and the integration of travel time prediction. This approach bridges the gap between simplified approximations and commercial routing systems.

1. Introduction

In the modern world, route planning plays a key role both for companies managing complex logistics and for everyday people navigating their daily lives. While many individuals rely on routing technologies unknowingly through mobile applications, large companies often establish dedicated departments or outsource route-related operations to specialized service providers. These entities are responsible for managing deliveries, returns, packaging workflows, and other logistical processes that require precise, efficient coordination.

Such professional environments typically rely on advanced route planning software, composed of several interconnected modules, such as scheduling components, load-balancing engines, traffic prediction units, and vehicle capacity optimizers. Among these, one of the most critical and most expensive parts is the geospatial mapping module. This layer provides essential map data, including road networks, nodes, and spatial relationships, which form the foundation for accurate route computation. The continuous updating of this data with real-time traffic conditions, new infrastructure, and closures is often maintained through subscription-based services that charge significant monthly or annual fees.

Small- and medium-sized enterprises (SMEs) frequently cannot afford such solutions. As a result, they tend to fall back on manual methods or free-to-use online maps, such as Google Maps [1]. However, these platforms are not designed for large-scale optimization and often fail to deliver cost-efficient routing, especially when the number of stops and delivery constraints increases. Furthermore, even “free” platforms typically impose daily usage quotas or start charging once a threshold is crossed.

A core requirement for optimal routing is the availability of a full distance matrix—that is, a dataset containing all pairwise distances between route points [2]. In most cases, obtaining such a matrix directly from map services is infeasible due to both cost and query limitations. This study explores an alternative approach, aiming to infer the complete distance matrix without relying on expensive map-based queries.

This study explores how route planning can be achieved without relying on costly or limited-access geospatial data. It begins with an (1) overview of existing methods proposed in the literature for estimating complete distance matrices. Building on this foundation, (2) statistical techniques are presented, including ones the author commonly uses. To improve these traditional methods, (3–4) a machine learning approach using artificial neural networks (ANNs) is introduced, aiming to enhance accuracy while maintaining simplicity and low cost. The practical potential of the method is demonstrated through a (5) layered case study involving real-world routing tasks between locations in Hungary. The (6) results are then validated against actual distances, and the findings are critically evaluated to assess the reliability, scalability, and practical value of the proposed approach.

2. Literature Review

The task of approximating real-world distances for logistical planning has received significant attention in both academic and industrial domains, driven by the demand for scalable, efficient, and cost-effective routing solutions. Applications such as last-mile delivery, on-demand mobility, and supply chain optimization often rely on reliable distance estimations—even in settings where detailed geospatial data is unavailable or prohibitively expensive [3]. Across transportation science, operations research, and computational geography, various techniques have been developed, ranging from heuristic models to advanced data-driven methods. A key area of focus involves generating or approximating distance matrices—critical inputs for routing algorithms—without full dependence on commercial GIS platforms or costly APIs.

Traditional routing methods, including Dijkstra’s algorithm [4], A* and its variants [5], and Rapidly-exploring Random Trees [6], typically depend on comprehensive geospatial data and detailed road network information. However, such data is not always accessible, especially for small- and medium-sized enterprises. To address this, lightweight alternatives have emerged, notably the Haversine formula, which calculates great-circle (straight-line) distances using latitude and longitude coordinates. For instance, in the study “Determine the Shortest Path Problem Using Haversine Algorithm” [7], the authors used the formula to match students in Depok, Indonesia, to nearby schools based on proximity within zoning policies. The Haversine method also proves useful in contexts such as maritime asset tracking [8] and indoor industrial positioning systems [9].

In some implementations, the Haversine formula is combined with other algorithms to improve path selection, as in the GIS-based navigation system developed by Indra Surya Permana et al. [10]. They integrated the formula with a Greedy algorithm to locate the nearest art gallery from the user’s location. However, in this study, no such combination or modification was necessary; the Haversine algorithm was used purely as a data generation tool. This is similar to its role in the work of Baumbach et al. [11], where it was employed for graph construction in spatial-temporal modeling for graph neural networks (GNNs), though their focus was on network optimization rather than classical distance estimation.

Several other studies also treat Haversine as a supporting utility rather than a primary subject of evaluation. In “Optimized Bus Route Finder for Educational Institutes Using Haversine Formula” [12], the method is used to enhance the geospatial functionality of a transportation system by identifying the nearest bus stops from a user’s coordinates—again, not as a benchmarked algorithm, but as a backend calculation mechanism.

To bridge the known gap between straight-line and real-world road distances, various regression-based methods have been introduced. One notable example is the large-scale study by Boscoe et al. [13], which compared hospital accessibility in the U.S. using straight-line and driving distances. They reported strong correlations (R² > 0.9), with linear scaling coefficients between 1.1 and 1.417, demonstrating the practical viability of approximate methods when detailed data is unavailable. It is also referred to as the circuity factor, and several other studies have provided empirical estimates of its value.

The circularity factor (also known as detour index or route factor) is a simple metric used in route planning to compare the actual traveled distance (e.g., road or path) with the straight-line (as-the-crow-flies) or Haversine distance between two points. It is calculated as:

$$Circularity Factor={\displaystyle \frac{Actual route distance}{Straight-line distance}}$$

(1)

A circularity factor of 1 indicates a perfectly straight route, while values greater than 1 reflect increasing inefficiency due to detours or indirect paths. This method is widely used by researchers and practitioners alike who aim to estimate the real-world travel distance between two geographic points.

For example, in “Selected Country Circuity Factors for Road Travel Distance Estimation” [14], the reported average values range from as low as 1.12 to as high as 2.10, with standard deviations between 0.05 and 1.96. Variations between countries or regions are attributed to multiple factors, including city-pair sample size, road network density and connectivity, natural barriers such as mountains, lakes, and seas, the presence of restricted areas like military bases or reservations, terrain slope, the accuracy of road mapping, and the precision of location coordinate data. Also, Giacomin & Levinson [15] analyzed circuity in 51 major U.S. metropolitan areas from 1990 to 2010 and found a general increase, with 35 MSAs showing significant growth. Short trips were more circuitous than long ones, and a distance-decay function was introduced to describe this relationship, with parameters changing over time. While Kweon in 2019 [16] calculated circuity factors for 27 forest roads in South Korea, classifying them as ridge, mid-slope, or valley. Weighted averages were 2.09 for mid-slope, 1.36 for ridge, and 1.09 for valley roads, with unweighted values showing similar patterns. Mountain terrain had the greatest impact, and mid-slope circuity increased with distance, unlike ridges or valleys.

Stigell and Schantz [17] conducted a composite study in Stockholm comparing four commuting distance estimation methods—self-estimation, straight-line, GIS shortest route, and GPS—against map-drawn criterion routes. All methods exhibited systematic biases: self-estimation generally overestimated, straight-line underestimated, GIS results varied, and GPS slightly overestimated. While average errors could be corrected, individual deviations persisted. Compared to criterion distances, self-estimated distances averaged 114 ± 63%, straight-line 79.1 ± 10.5%, GIS 112–121 ± 22%, and GPS 105 ± 4%, demonstrating consistent systematic bias across all methods.

More recently, machine learning—especially artificial neural networks—has been applied to route prediction and travel time estimation tasks [18,19]. These methods are particularly useful in domains such as robot navigation, traffic forecasting, and delivery routing, where complete map data may be inaccessible or unnecessary.

Rui Si et al. [20] investigated how environmental factors shape intra-urban travel distance patterns using ride-hailing data divided into 1 × 1 km grid cells. Applying Extreme Gradient Boosting with SHAP analysis, they found that travel distances follow a log-normal distribution with strong spatial heterogeneity, influenced by variables such as proximity to the city center, bus station density, land use entropy, and company density. Many of these factors showed nonlinear and threshold effects, providing new insights into urban mobility dynamics.

Jeonghyeon and Seungku [21] developed a self-learning travel distance estimation method for robots using wheel encoder data and GNSS-based distance labels. Their deep self-learning approach reduces the impact of road surface noise, which is a major limitation of traditional wheel odometry, and allows for efficient, on-demand model generation for different environments. Experiments with a custom-built vehicle showed about a 30% improvement in accuracy compared to conventional methods.

Overall, related work on distance estimation and routing can be grouped into two main categories. The first category, stand-alone distance estimation methods, focuses on predicting travel distances independently from routing. These include geometric and heuristic formulas such as the Haversine calculation [7,8,9,10,11,12], statistical or regression-based scaling methods, and circuity factor–based approaches, where straight-line distances are adjusted using empirically derived coefficients; values for these factors, collected from various studies, are summarized in

Table 1. Summary of circuity factor estimates by region and/or trip type from prior research.

Author(s)	Estimated Subject	Estimated Circuity Factor
Boscoe et al. [13]	European counties	1.1–1.417
Ballou et al. [14]	United States	1.22–1.25
Ballou et al. [14]	Western Europe	1.25
Ballou et al. [14]	Japan	1.09
Ballou et al. [14]	Brazil	1.33
Giacomin et al. [15]	Typical short trips (~1 km)	1.5
Giacomin et al. [15]	Medium trips (~10 km)	1.27
Giacomin et al. [15]	Long trips (~50 km)	1.2
Kweon [16]	South Korea mid-slope roads	2.09
Kweon [16]	South Korea ridge roads	1.36
Kweon [16]	South Korea valley roads	1.09
Stigell et al. [17]	World average self estimation	1.14
Stigell et al. [17]	World average GPS estimation	1.05
Stigell et al. [17]	World average GIS estimation	1.12–1.21
This study	Hungary	1.3613

[13,14,15,16,17]. The second category, integrated distance estimation and routing, combines estimation with practical route optimization to evaluate both statistical accuracy and operational usability. This includes machine learning–based applications [18,19], environmental factor–driven travel pattern modeling [20], and self-learning robotic distance estimation methods [21].

Based on the above considerations, the study seeks to address the following research questions:

• Can accurate distance matrices be created using only geographic coordinates, without expensive mapping services?
• Can an artificial neural network outperform traditional statistical models in estimating real-road distances, even on unknown road networks?
• Can this AI-based distance estimation approach be effectively used for real route planning in small- and medium-sized businesses without full map infrastructure?
• Do SMEs incur losses when using estimates for route planning, and how large are these losses across different methods?

Unlike prior works that validate approximations only statistically, this paper tests whether such estimates can drive route optimization decisions reliably. The models are embedded into routing frameworks and compared with actual map-based outcomes, offering a new perspective on how predictive methods perform when deployed in constrained environments. This provides a practical benchmark for evaluating lightweight alternatives to full GIS-based planning systems.

3. Basics of Problems, Data Collection and Processing

In this research, two fundamental problems are addressed: the generation of a reliable distance matrix and the subsequent optimization of routing based on that matrix. To evaluate distance matrix generation methods, three approaches—Haversine-based scaling, polynomial regression, and the proposed Artificial Neural Network (ANN)—were compared against Google Maps reference distances using both overall dataset performance and range-specific subsets (short, medium, and long distances). Accuracy was quantified using the error metric: root mean square error (RMSE). A real-world case study validated the practical applicability of each method in operational routing scenarios. The results show that while traditional statistical approaches perform adequately, the ANN provides a strong balance of accuracy and computational efficiency, positioning it as a competitive alternative to state-of-the-art estimation techniques reported in the literature.

3.1. Problem Definition: Distance Matrix Generation

The first fundamental problem addressed in this research is the generation of an N × N distance matrix D, which represents the estimated road travel distances between N given locations. In practical terms, this matrix is the foundation for any routing optimization task, as it defines the “cost” of traveling between each pair of points. In the context of this study, the only available input for distance estimation is the set of geographic coordinates (lat_i, lon_i) for each location, without direct access to complete GIS data or precomputed road network information.

Three different approaches are considered for filling the matrix:

• Statistical formulas, such as variations of the Haversine method, which provide quick, low-cost approximations of great-circle distances.
• Artificial Neural Network (ANN) models, trained on a sample of road distances obtained from a reliable source, with the goal of learning a mapping between coordinate pairs and real travel distances.
• Reference distances directly retrieved from the Google Maps Distance Matrix API, which serves as the ground truth benchmark for evaluation.

The output of this process is a symmetric matrix where each element D_ij contains the estimated travel distance from location i to location j. This matrix is then used as the primary input for the routing procedure described in Section 3.2.

3.2. Problem Definition: Routing Procedure

The second fundamental problem is the determination of an optimal visiting sequence for a set of N locations, using the generated distance matrix as the cost function. In this case, the input is the N × N matrix D along with any problem-specific constraints, such as fixed start and end points or required order constraints between certain locations.

For solving this problem in a simple yet effective way, the evolutionary optimization method of the Solver add-in in Microsoft Excel is employed. This method is well suited for the study’s goals because it requires minimal additional infrastructure and can be run on standard office software, making it accessible for small- and medium-sized enterprises without dedicated routing software. The Solver aims to minimize the total route length, as defined by the sum of the distances for the chosen visiting order.

The output of the routing procedure consists of the following:

• An ordered list of locations that represents the computed optimal visiting sequence.
• The total estimated route length associated with that sequence.

This procedure is applied using distance matrices generated by all three estimation methods described in Section 3.1.

3.3. Data Collection and Processing

Accurate distance estimation and efficient routing cannot be addressed in isolation; both depend on the quality of the underlying geospatial data. Every statistical or machine learning-based method relies fundamentally on the availability of structured, reliable data. In the context of route planning, this requirement translates into the need for accurate geospatial information: the geographic coordinates of locations and the actual distances between them. Fortunately, today’s mapping platforms offer highly developed tools and APIs that make it possible to collect such data, even at a large scale.

For this study, geospatial data was gathered via Google’s internal platform, the Google Cloud Console, specifically using the Distance Matrix API. Although this service provides highly detailed and accurate route data, the data collection process proved to be more complex than expected. Initially, randomly generated GPS coordinates were used as test points. The Google Maps engine often fails to calculate routes between coordinates that do not match identifiable locations or valid addresses. Instead of serving as an exact geolocation tool, it behaves more like a search engine: trying to interpret the user’s intent based on textual inputs like place names or address fragments. While it is technically possible to work with randomly generated coordinates by using an additional API to identify nearby valid locations and then selecting the closest address, this approach was found to be highly inefficient, requiring a large number of API queries to obtain even a single usable data point. For this reason, real addresses were ultimately used in the study to ensure data quality and reduce the overhead of excessive API calls.

As a more effective approach, it required precise addresses including ZIP code, city, street, and house number. These addresses had to be geographically varied and consistently mappable. After evaluating several public datasets, the most complete and convenient source was found on GitHub [22], where a community-maintained dataset based on Hungarian postal service locations is available. This dataset includes detailed information about post offices, drop-off points, parcel lockers, local branches, and other related service locations, with the direct link provided in the Data Availability Statement of this article. In total, the database included 6237 distinct points across the country—which is more than all the municipalities in Hungary—including more than 800 in Budapest alone.

From this source, a representative sample of 5000 location points was selected. These were randomly paired, and for each pair, the travel distance was retrieved using the Google Maps Distance Matrix API. The travel distances returned by the API are inherently accurate; if a computation is not possible, the API returns a NaN value. Minor inaccuracies can, however, arise from mismatches between coordinates and valid addresses, typically due to human error in the source data. These imperfections are common across databases and cannot be eliminated. In this study, such inconsistencies were intentionally retained in the training dataset, as they generally do not interfere with the model’s learning process and may even enhance generalization by reducing the risk of overfitting. The acquired dataset now serves as the basis for comparison between actual road distances and approximate distances calculated using simpler methods.

One such method is the Haversine formula, which estimates the straight-line (“as-the-crow-flies”) distance between two points on the Earth’s surface using their GPS coordinates. Although it assumes a perfect sphere (and the Earth is more accurately modeled as an oblate spheroid), it offers a solid approximation for many practical purposes.

The Haversine formula is as follows:

$$d_{hav}=2\times 6371 \mathrm{k}\mathrm{m}\times \mathrm{a}\mathrm{r}\mathrm{c}\mathrm{s}\mathrm{i}\mathrm{n}\left(\sqrt{{\displaystyle \frac{1-\mathit{cos}\left(∆\phi \right)+cos{\phi }_1\times cos{\phi }_2\times \left(1 - cos(∆\theta )\right)}{2}}}\right)$$

(2)

where ${\phi }_1$ and ${\phi }_2$ are the latitudes of point 1 and point 2, respectively (in radians), and their difference is $∆\phi$. Also $∆\theta$ is the difference between the longitudes of the two points, also in radians. This formula provides an efficient way to compute approximate distances without relying on map queries.

While the study focuses on estimating physical distance between points, it is acknowledged that real-world route optimization is also influenced by variables such as traffic conditions, road quality, and time-dependent factors. These additional factors can, of course, be superimposed on the baseline distance estimation; however, it is maintained that obtaining a reliable and scalable distance metric is a prerequisite—without it, there is no foundation on which such variables can be overlaid. For this reason, the simplest and most widely available data source—geographic coordinates—has been deliberately prioritized, since traffic or road condition data are not always readily accessible in a cost-effective and scalable manner.

A subset of the collected data, including sample coordinate pairs and corresponding distances, is shown in

Table 2. (a) Sample distance records with addresses. (b) Sample distance records with coordinates and haversine estimates.

(a)
Orig	Dest	Location Origin			Location Destination
2272	2326	Balmazújvárosi út 7, 4027 Debrecen, H.			Derék utca 31, 4031 Debrecen, Hungary
1204	83	Tétényi út 2, 1115 Budapest, Hungary			Etele tér aluljáró, 1871 Budapest, Hun.
525	140	Váci út 201, 1138 Budapest, Hungary			Fő út 190, 2120 Dunakeszi, Hungary
1535	131	Fő út 104–106, 2220 Vecsés, Hungary			Sibrik Miklós út 30/B, 1103 Budapest
3141	2627	Fő út hrsz 7967, 2120 Dunakeszi, Hungary			Dunaföldvári út 2, 6000 Kecskemét, H.
1630	3307	Gyári út 3237, 2310 Szigetszentmiklós, H.			Vak Bottyán 54., 8600 Siófok, Hungary
242	1702	Földi János utca 55, 4242 Hajdúhadház, H.			Rákóczi út 20/A, 1871 Budapest, Hun.
4667	2167	Kodály Zoltán tér 7, 6000 Kecskemét, H.			Bajcsy-Zsilinszky út., 3530 Miskolc, H.
(b)
Origin	Destination	Latitude Origin	Longitude Origin	Latitude Dest.	Longitude Dest.	Map Distance (km)	Havers. Est. (km)
2272	2326	47.542960	21.596080	47.524920	21.597760	2.50	2.01
1204	83	47.472220	19.034110	47.464173	19.021581	2.50	1.30
525	140	47.559310	19.077270	47.655991	19.130066	12.50	11.46
1535	131	47.409750	19.275720	47.469300	19.154710	12.60	11.25
3141	2627	47.643420	19.129810	46.887530	19.636490	113.00	92.34
1630	3307	47.337480	19.028730	46.901610	18.048540	113.00	88.60
242	1702	47.690540	21.672320	47.406883	19.006548	255.00	202.53
4667	2167	46.914930	19.698840	48.103020	20.792230	255.00	155.55

. Each row in the table contains, following its index number, the origin and destination point identifiers, their full query address, latitude and longitude coordinates, the actual road distance retrieved from the map service (in kilometers), and the straight-line distance calculated using the Haversine formula.

As shown in Table 2b, the measured distances appear in identical pairs, since the data was extracted in a sorted and symmetrical manner. In contrast, the Haversine-based estimates display noticeable asymmetry—particularly over shorter distances—due to rounding effects and the directional sensitivity of the formula when applied to closely spaced coordinate pairs. Nevertheless, a clear visual correlation is evident between the estimated and the actual distances. To quantify this relationship, Pearson correlation analysis was conducted on the 5000 sample, yielding a coefficient of r = 0.9581, which indicates a very strong positive correlation. This confirms that, despite its approximate nature, the Haversine formula effectively captures the overall pattern of real-world distances retrieved from the map service.

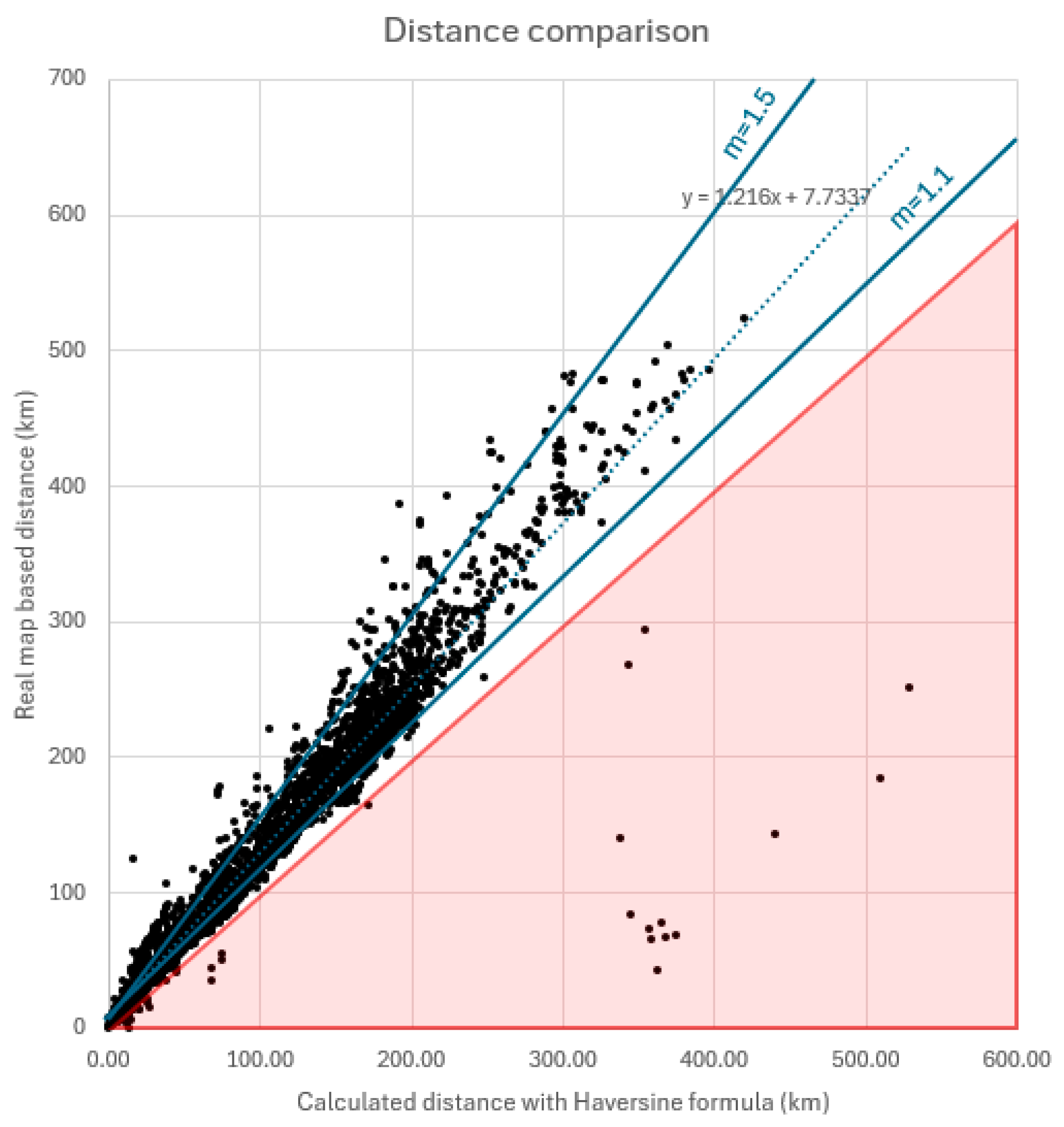
This strong correlation is also clearly illustrated in Figure 1, where the x-axis represents the distances calculated using the Haversine formula, and the y-axis shows the corresponding values retrieved from the geospatial map data. Most of the data points fall tightly between two bounding lines with slopes of approximately 1.1 and 1.5, indicating consistent proportionality. When calculating the average slope across the full sample, the result is approximately 1.3613. Based on prior experience from both research and teaching, it is often recommended that when precise measurements are unavailable, multiplying the straight-line distance by this factor provides a reasonably good estimate. However, just how reliable this heuristic truly is will be examined in more detail in the following section.

Further insight from Figure 1 confirms that real-world data was used, as the distribution includes a small number of points with significant deviations. Notably, any data point falling below the y = x line (that is, with a slope less than 1, showed by the red rectangle) should theoretically not exist, since no real-world route (excluding tunnels or underground shortcuts) can be shorter than the straight-line (Haversine) distance. Such anomalies likely indicate errors in the coordinate data, possibly due to incorrect or mismatched location entries, or due to improperly recorded coordinates during data collection.

These anomalous records were removed during the statistical analysis, as their presence could distort the calculated relationships and bias the results. However, they were deliberately retained in the machine learning phase, in the training of the artificial neural network (ANN) model. This decision assumed that such outliers might contribute useful variance to the learning process, potentially improving the model’s generalization capabilities and robustness in real-world applications.

4. Distance Estimation with Different Methods

In this chapter, four statistical estimation methods and one machine learning approach will be presented. The analysis is conducted on both the complete dataset and three segmented subsets, in order to examine patterns and assess consistency across different data partitions.

As outlined in the previous chapter, the statistical estimations are based on formulas derived from the Haversine calculation. This method is widely applied due to its straightforward implementation and the ease of acquiring geographic coordinates from online geospatial data sources. In contrast to computing a full distance matrix—which scales almost quadratically: $n\times (n-1)$ datapoint for n locations. Haversine-based estimations can be calculated rapidly and independently. This makes them a highly practical and resource-efficient alternative, particularly when working with large datasets.

4.1. Statistical Estimation of Distances

Of the four statistical estimation methods presented in this chapter, one has already been introduced as a practical rule of thumb used as the circularity factor: multiplying the straight-line (Haversine) distance by the average observed slope factor, approximately 1.3613, this represented by Equation (3). A second method is based on the linear trendline clearly visible in Figure 1, which models the relationship between estimated and actual distances using least-squares linear regression, which is Equation (4). The remaining two methods are also derived from the same dataset but apply second (5)- and third-degree (6) polynomial trendlines, respectively. These polynomial regressions were generated using Excel’s built-in curve-fitting tools, allowing for quick and convenient approximation based on the overall shape of the data distribution.

$$d_{avg}=1.3613\times d_{hav}$$

(3)

$$d_{lin}=1.216\times d_{hav}+7.7337$$

(4)

$$d_{poli2}=-0.0011\times d_{hav}^2+1.5119\times d_{hav}-3.5908$$

(5)

$$d_{poli3}=-8.12\times {10}^{-6}\times d_{hav}^3{+0.0033\times d}_{hav}^2+0.9373\times d_{hav}+9.0148$$

(6)

Using the samples from Table 2, the corresponding distance values were calculated and are presented in

Table 3. Sample distances with different methods.

Origin	Dest.	Real Dis.	Havers. Dis.	Avg. Dis.	Lin. Dis.	Poli2. Dis.	Poli3. Dis.	ML Dis.
2272	2326	2.50	2.01	2.74	10.18	−0.56	10.91	4.08
1204	83	2.50	1.30	1.77	9.31	−1.63	10.24	5.19
525	140	12.50	11.46	15.59	21.66	13.59	20.17	15.71
1535	131	12.60	11.25	15.32	21.42	13.29	19.97	14.53
3141	2627	113.00	92.34	125.70	120.02	126.64	117.40	116.98
1630	3307	113.00	88.60	120.61	115.47	121.73	112.40	112.88
242	1702	255.00	202.53	275.71	254.01	257.50	267.75	259.27
4667	2167	255.00	155.55	211.75	196.88	204.97	204.55	200.12

. The last column of the table displays the output of the best-performing machine learning model, based on the trained artificial neural network, which yielded the most accurate estimations among all tested methods.

As shown in Table 3, the average-based distance estimation may initially appear reasonable for shorter distances. However, this method tends to distort the overall results. At low values, fractional differences are less perceptible, leading to underestimated variance, while at higher distances (even within this limited sample) the method significantly overestimates actual values. In fact, this overestimation is consistent across nearly all ranges.

The distance estimation based on a simple linear equation provides more acceptable results—particularly for longer distances—where it closely aligns with the actual values. The second- and third-degree polynomial estimations exhibit similar trends: they perform reasonably well for medium and high distances but introduce considerable error at short ranges. In some cases, the second-degree polynomial even produces negative values, which are clearly invalid in this context. Among all tested methods, the machine learning model delivered the most accurate overall performance. Although it tended to overpredict short distances by nearly doubling them, it approximated medium and long distances with more precision than any of the statistical models.

In addition to the overall analysis performed on the full dataset, the statistical behavior of the models was also examined across three distance-based subsets: under 10 km, between 10 and 40 km, and above 40 km. The choice of these thresholds was inspired in part by the approach of Giacomin et al. [15], but adapted to the specific geographical context of Hungary. Distances under 10 km generally correspond to intra-city travel within larger urban areas; the 10–40 km range represents suburban or regional (intra-county) movement; and distances above 40 km are considered intercity or national-level travel. This segmentation enables a clearer understanding of how the estimation models perform across short-, medium-, and long-distance scenarios.

To characterize the distributions within each group, the ratio of actual road distance to the calculated distance was computed. For each subset, the mean and standard deviation of this ratio were calculated, offering insight into how consistently each model approximates real-world travel distances at different scales.

The trends in Table 3 are also evident in

Table 4. Average and SD. of Hungarian distance estimations by method and distance range.

	Avg. Distance		Lin. Distance		Poli2. Dis.		Poli3. Dis.		ML Distance
	Avg.	SD.	Avg.	SD.	Avg.	SD.	Avg.	SD.	Avg.	SD.
Full set	1.06	0.64	1.17	0.93	0.99	0.58	1.14	0.91	0.98	0.43
Below 10 km	1.22	2.23	2.75	3.28	0.71	2.07	2.80	3.23	1.12	1.20
10…40 km	1.07	1.21	1.78	1.87	0.84	1.13	1.72	1.86	1.01	0.66
Above 40 km	1.06	0.39	1.02	0.35	1.02	0.32	1.01	0.31	0.98	0.36

, which presents the mean values and standard deviations of the actual-to-Haversine distance ratios across the entire dataset, as well as within the short-, medium-, and long-distance subsets. This breakdown further illustrates how estimation accuracy and variability differ depending on the distance range.

The results presented in Table 4 reveal distinct patterns in how the five estimation techniques behave across different distance ranges. Ideally, the best estimation method would produce an average ratio close to 1, indicating unbiased predictions, and a standard deviation as low as possible, reflecting consistent and stable performance across all samples.

The average-based method tends to slightly be overestimated in all cases, with a full-set average of 1.06. However, its reliability is poor at short distances (below 10 km), where both the mean (1.22) and the standard deviation (2.23) indicate significant variability. This method performs more consistently in the long-distance range, where its average (1.06) and standard deviation (0.39) become more stable.

The linear regression estimation model shows a clear improvement as the distance increases. While it strongly overestimates short distances (Avg. = 2.75, SD = 3.28), it provides accurate and consistent estimates for distances above 40 km (Avg. = 1.02, SD = 0.35), suggesting that the linear model captures long-range trends better than local variations.

Second- and third-degree polynomial regressions follow a similar pattern. Both perform poorly at short distances, with the second-degree model showing particularly unreliable results. For medium and long distances, these models become more stable, with averages approaching 1 and lower standard deviations, although they never fully outperform the linear method.

In contrast, the machine learning-based approach using artificial neural networks provides the most balanced and robust performance across all ranges. While it modestly overestimates short distances (Avg. = 1.12), it maintains a relatively low standard deviation (1.20), and its accuracy improves significantly in the medium (SD = 0.66) and long (SD = 0.36) distance segments. These results indicate that the ML model adapts better to a wide variety of cases, offering consistent estimations regardless of scale.

The same procedure was applied to a dataset containing addresses and geographic coordinates from Denmark, in order to examine the solutions produced without retraining the ANN. The outputs, presented in

Table 5. Average and SD. of Danish distance estimations by method and distance range.

	Avg. Distance		Lin. Distance		Poli2. Dis.		Poli3. Dis.		ML Distance
	Avg.	SD.	Avg.	SD.	Avg.	SD.	Avg.	SD.	Avg.	SD.
Full set	1.04	0.35	1.08	0.35	0.99	0.34	1.05	0.36	0.92	0.52
Below 10 km	0.99	0.17	1.59	0.44	0.76	0.31	1.54	0.51	0.47	0.87
10…40 km	1.06	0.82	1.32	0.74	0.92	0.78	1.35	0.79	1.27	0.54
Above 40 km	1.02	0.27	1.02	0.25	1.03	0.27	1.02	0.27	1.12	0.23

, reflect the model’s ability to generalize to a geographical context different from that of the training data.

In Table 5, more consistent estimations were observed across all distance ranges compared to the Hungarian results in Table 4. It appears that Denmark possesses a much more efficient road network, as standard statistical estimation methods performed better, with significantly lower standard deviations. Short distances were estimated more accurately, particularly by the average-based method, which showed greater stability than in the Hungarian case. While the machine learning method was not fine-tuned for the Danish dataset and therefore performed slightly worse, its accuracy was not significantly affected. Overall, long-distance estimations were handled reliably in both countries, but greater consistency and balance were achieved in the Danish results.

4.2. Machine Learning Model-Based Approach for Destination Approximation

For this study, a machine learning framework was developed to perform regression using an artificial neural network model, implemented entirely within the MATLAB (ver. R2024a) environment. The goal was to predict a normalized target variable based on geospatial input features related to movement or location-based events. The system was executed on a standard consumer-grade computer, highlighting the feasibility of developing and training deep learning models without access to specialized hardware or software libraries: AMD Ryzen 7 5700X (8-core, 4.65 GHz) CPU, 32 GB of DDR4 RAM, and an NVIDIA Ge-Force RTX 4060 Ti GPU (8 GB VRAM).

The dataset used for training consisted of five input features per sample, all of which were normalized. These features included one value calculated using the haversine formula—representing the geographic distance between two locations—and four coordinate values corresponding to the latitude and longitude of both the departure and destination points. This combination allowed the neural network to learn latent spatial relationships and model complex transitions between locations, making the setup suitable for applications such as travel time prediction, routing, or location-based behavior analysis.

Initial experiments used sigmoid activation functions in all layers of the neural network. While the model exhibited partial learning, its performance was limited to a narrow range of output values. Specifically, improvements were observed only for small or large target values, but not across the entire output domain. This behavior indicated the presence of vanishing gradients, a common limitation of sigmoid activations in deeper architectures, which can result in the optimizer failing to effectively update weights in earlier layers.

To address these limitations, the internal structure of the network was modified to employ the Rectified Linear Unit (ReLU) activation function in all hidden layers, while retaining sigmoid activation exclusively in the output layer to preserve the [0,1] range of the predicted values. ReLU is widely known for its non-saturating gradient behavior and computational efficiency, which lead to faster convergence and improved performance in deep networks. After introducing ReLU, significant improvements were observed in both convergence rate and overall generalization accuracy across the full spectrum of target values.

The training process relied on a custom implementation of the AdamW optimizer, which combines the adaptive step size of the Adam algorithm with decoupled L2 regularization (weight decay). This optimizer was selected to enhance generalization performance while maintaining fast convergence during training. The optimizer was configured with a learning rate of 0.001, a weight decay factor of 0.01, momentum coefficients β₁ = 0.9 and β₂ = 0.999, and an epsilon value of 1 × 10⁻⁸ to ensure numerical stability during updates.

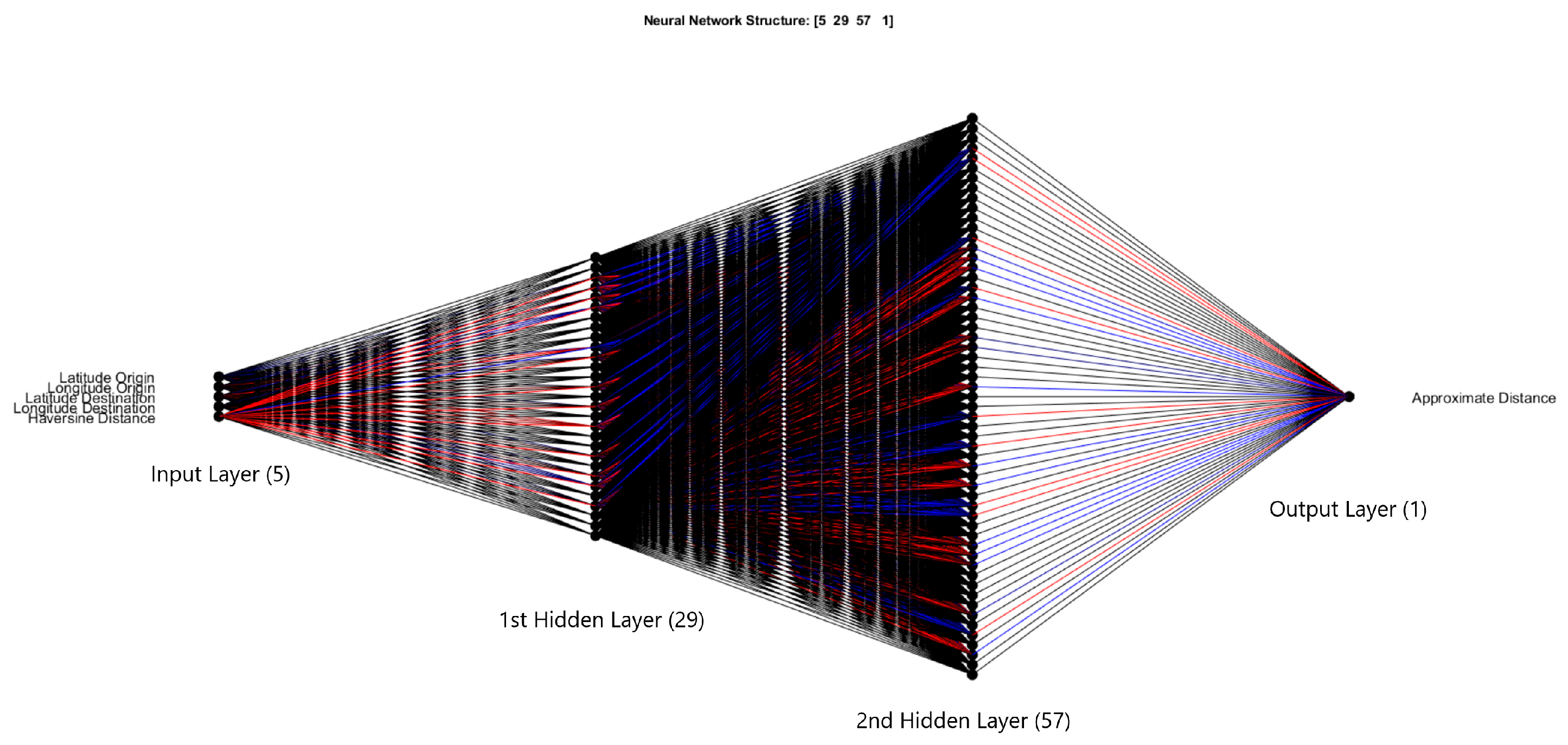
The final network architecture was selected using an automated evolutionary search procedure that evaluated candidate configurations based on their RMSE performance over short training runs. Through this process, the selected architecture comprised five input neurons (for distance and coordinates), two hidden layers with 29 and 57 neurons, respectively, and a single output neuron. 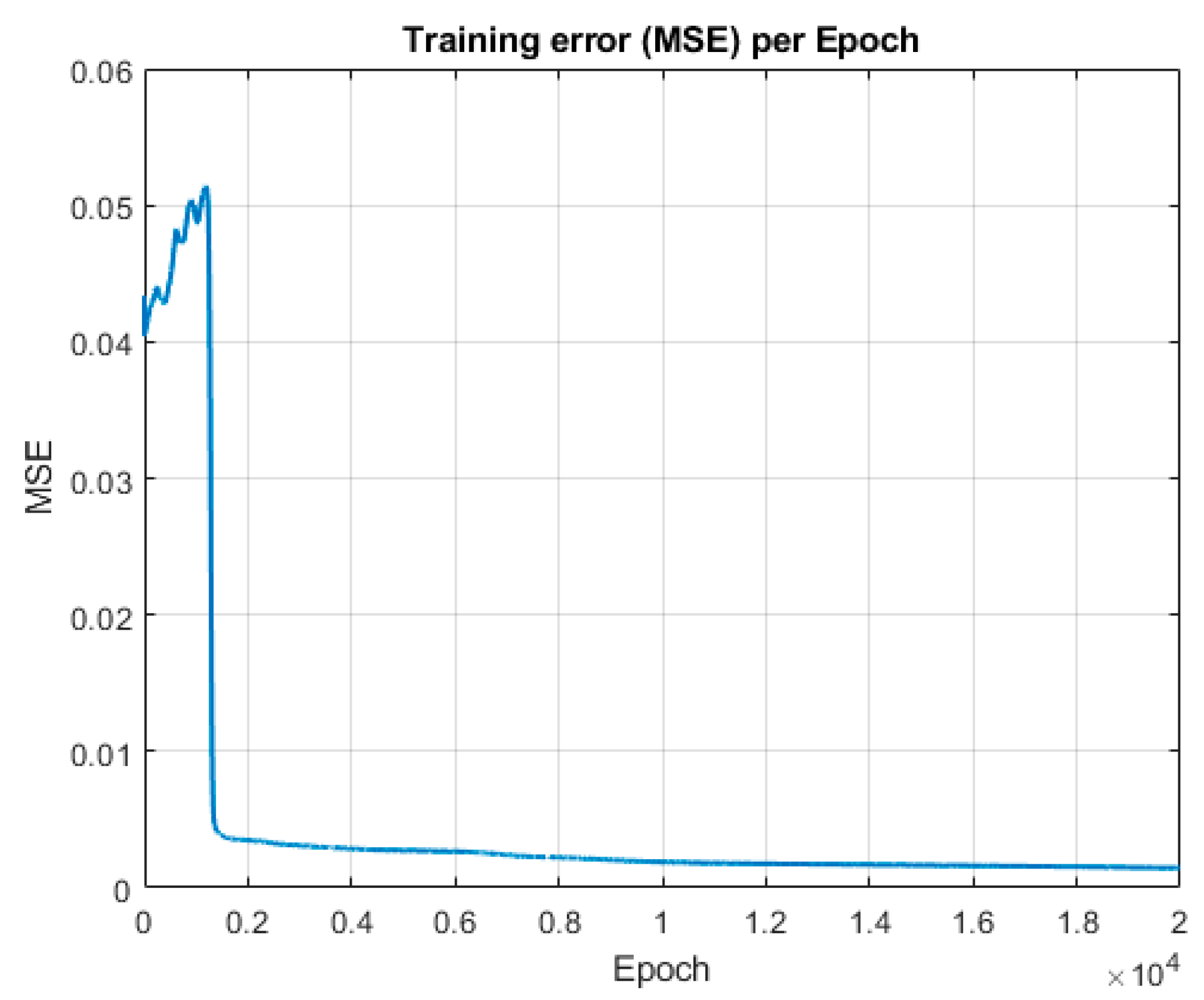This structure can be seen in Figure 2. While the numerical structure 5-29-57-1 refers to the number of neurons in each layer, the visual representation includes additional layers such as the normalization input pre-processing and final activation step, which may visually appear as distinct layers. This model was subsequently trained for 20,000 epochs, which took around 2 h ensuring deep convergence and the ability to generalize across a diverse set of input patterns. This training process can be seen in Figure 3.

The performance of the model was found to be most sensitive to the number of neurons in the first hidden layer and the learning rate. These parameters significantly affected convergence stability and final accuracy during training. Dropout rate and batch size had minor effects in this particular problem domain due to the relatively small dataset size. As can be observed from the architecture, the final input node—representing the Haversine distance—appears to be the most active and, unsurprisingly, the most influential. This is reflected in the color coding: the closer a value is to 1 or −1, the more it shifts toward blue or red, respectively, indicating stronger activation at those extremes.

Although small- and medium-sized enterprises may lack in-house expertise in neural networks, it is emphasized that real-world deployment of the trained model is straightforward. Once trained, inference reduces to a few matrix multiplications with fixed weights and biases, operations that can be reproduced in common tools (e.g., a simple Excel/VBA macro) or any lightweight runtime.

As shown in Figure 4, both the training procedure and the inference process for retrieving distance estimates from the trained ANN are presented in pseudocode. The settings reflect the current configuration; however, the code can naturally be adapted to use additional or larger hidden layers, or alternative training schemes.

5. Case Studies of Route Planning with Different Distance Estimations

In this chapter, we investigate practical route planning strategies through three distinct case studies, each based on a different spatial scale. The first scenario involves a localized delivery problem within a district of Budapest; the second expands the scope to routes within a single county; and the third addresses national-level transportation across regions of Hungary. For each case, we define a set of delivery points and construct a transportation loop that must be optimized.

To assess the robustness and consistency of the proposed methodologies, all five routing methods under consideration are applied to each location set. To provide a benchmark for comparison, reference distances were derived from real-world geospatial and routing datasets, covering every possible pairwise route in the location sets. This allows for a direct comparison between model-based route suggestions and real-world optimal paths.

The central question is whether these computational methods—despite producing differing distance estimates—can still produce route plans that align structurally with those derived from real-world geographic data. This evaluation provides insight into each method’s reliability across different spatial contexts.

In the following table set, real-world distances from a map service are shown between eight cities for three distance categories: short, medium, and long. Within each group, the goal is to determine the optimal route that visits all cities. The route optimization was intentionally carried out using the simplest possible approach: the corresponding distance matrices were used as input data, and the optimal sequence was computed using the evolutionary method of Solver add-in in Microsoft Excel. This method proved successful in producing valid route arrangements.

To simplify interpretation and avoid manually reviewing all permutations for each method, the first location in each group was designated as the fixed starting point. As a result, in most cases, only one or two optimal solutions exist; two when the matrix is symmetric, since mirror directions yield identical distances.

In the distance matrices presented in

Table 6. (a) Real-world distance matrices for short inner-city locations and optimal routes. (b) Real-world distance matrices for medium intra city locations and optimal route. (c) Real-world distance matrices for whole country locations and optimal route.

(a)
Real Dist. (km)	1	2	3	4	5	6	7	8	Best Route (90.5 km)
1	0.00	5.40	14.90	27.50	15.70	6.10	6.90	10.80	1
2	4.40	0.00	13.40	33.40	21.60	12.30	12.90	16.20	7
3	13.10	11.70	0.00	44.50	36.20	15.20	15.10	20.90	5
4	27.50	32.80	44.50	0.00	13.30	24.10	21.40	22.00	4
5	15.80	21.10	35.90	13.20	0.00	12.40	9.70	11.10	8
6	5.10	8.80	15.90	22.70	10.90	0.00	2.70	9.00	6
7	7.00	12.80	17.20	21.10	9.30	2.20	0.00	6.10	3
8	12.00	15.40	23.20	22.50	11.60	7.10	5.70	0.00	2
(b)
Real Dist. (km)	1	2	3	4	5	6	7	8	Best Route (309.9 km)
1	0.00	26.10	83.00	52.60	64.10	77.10	109.00	135.00	1
2	26.60	0.00	56.60	62.80	54.50	50.70	82.80	109.00	4
3	85.80	58.90	0.00	7.00	4.00	32.50	32.70	115.00	5
4	73.60	65.50	6.80	0.00	9.30	39.10	39.30	122.00	3
5	65.00	56.10	4.00	9.10	0.00	29.70	37.00	112.00	7
6	79.20	52.20	31.10	37.40	29.00	0.00	34.50	74.30	8
7	111.00	83.70	32.60	39.40	36.60	34.60	0.00	56.70	6
8	137.00	110.00	116.00	122.00	114.00	75.80	56.90	0.00	2
(c)
Real Dist. (km)	1	2	3	4	5	6	7	8	Best Route (757.2 km)
1	0.00	16.50	10.20	82.30	180.00	201.00	189.00	117.00	1
2	15.90	0.00	15.60	80.20	192.00	214.00	194.00	122.00	3
3	10.10	15.80	0.00	86.50	178.00	199.00	181.00	109.00	8
4	80.50	81.40	86.20	0.00	136.00	158.00	258.00	186.00	7
5	180.00	193.00	178.00	136.00	0.00	28.70	228.00	278.00	5
6	202.00	214.00	199.00	158.00	28.90	0.00	371.00	299.00	6
7	191.00	196.00	184.00	262.00	228.00	375.00	0.00	129.00	4
8	116.00	121.00	109.00	187.00	278.00	300.00	126.00	0.00	2

, the values were retrieved directly from the Google Distance Matrix API. For simplicity, each location within the 8-city groups is represented by a numeric label from 1 to 8, rather than full geographic names. A separate summary figure later in the document will illustrate the actual city locations corresponding to each numbered location.

The final column of each matrix contains the optimal route and its total distance based on total travel distance, calculated using Solver. In the case of real-world data, where the matrices are not fully symmetric, reverse routes do not necessarily yield the same result and are therefore treated as direction-dependent.

In the following section, the distance matrices computed using the Haversine formula are presented for the same set of locations. These matrices serve as the basis for the four statistical models introduced earlier. The individual matrices derived from each model are not shown separately, as they can be easily calculated using the provided equations. Unlike the real-world distances retrieved from the map service, the Haversine-based matrices are symmetric by nature, since they are purely geometrical and do not account for route-specific factors such as road networks or one-way constraints.

As demonstrated in the set of

Table 7. (a) Haversine distance matrices for medium intra city locations and optimal route. (b) Haversine distance matrices for short inner-city locations and optimal route. (c) Haversine distance matrices for whole country locations and optimal routes.

(a)
Real Dist. (km)	1	2	3	4	5	6	7	8	Best Route (46.8 km)
1	0.00	8.68	7.95	6.75	18.15	11.42	12.66	11.87	1
2	8.68	0.00	8.85	2.62	9.52	3.49	5.38	3.39	4
3	7.95	8.85	0.00	9.25	16.90	12.31	14.23	11.90	6
4	6.75	2.62	9.25	0.00	11.54	4.67	6.00	5.23	7
5	18.15	9.52	16.90	11.54	0.00	7.06	6.91	6.32	5
6	11.42	3.49	12.31	4.67	7.06	0.00	1.99	1.28	8
7	12.66	5.38	14.23	6.00	6.91	1.99	0.00	2.96	2
8	11.87	3.39	11.90	5.23	6.32	1.28	2.96	0.00	3
(b)
Real Dist. (km)	1	2	3	4	5	6	7	8	Best Route (287.2 km)
1	0.00	37.63	38.18	34.57	33.40	35.05	40.54	99.13	1
2	37.63	0.00	70.25	65.32	65.91	65.35	77.23	107.40	7
3	38.18	70.25	0.00	5.40	4.79	5.87	18.12	76.19	3
4	34.57	65.32	5.40	0.00	4.11	1.01	21.92	74.63	5
5	33.40	65.91	4.79	4.11	0.00	5.11	18.07	78.58	4
6	35.05	65.35	5.87	1.01	5.11	0.00	22.83	73.63	6
7	40.54	77.23	18.12	21.92	18.07	22.83	0.00	93.40	8
8	99.13	107.40	76.19	74.63	78.58	73.63	93.40	0.00	2
(c)
Real Dist. (km)	1	2	3	4	5	6	7	8	Best Route (641.3 km)
1	0.00	37.63	38.18	34.57	33.40	35.05	40.54	99.13	1
2	37.63	0.00	70.25	65.32	65.91	65.35	77.23	107.40	3
3	38.18	70.25	0.00	5.40	4.79	5.87	18.12	76.19	2
4	34.57	65.32	5.40	0.00	4.11	1.01	21.92	74.63	4
5	33.40	65.91	4.79	4.11	0.00	5.11	18.07	78.58	5
6	35.05	65.35	5.87	1.01	5.11	0.00	22.83	73.63	6
7	40.54	77.23	18.12	21.92	18.07	22.83	0.00	93.40	7
8	99.13	107.40	76.19	74.63	78.58	73.63	93.40	0.00	8

the Haversine-based approximation is functional; however, it often fails to reproduce the actual routing derived from real-world distance data. In cases involving short distances, the resulting route deviates significantly from the true one. For medium and long distances, some city pairs do align with the original optimal route, but the consistency remains limited. This limitation will be similar in the average-based approach, which relies solely on scaling the straight-line distances using a fixed factor, without accounting for spatial context or local road geometry.

In the final part of the matrix demonstration, the results obtained through neural network training are presented. These estimations cannot be generated from raw input data alone; instead, they must be produced by a trained artificial neural network. Unlike the previous statistical methods, where approximate results could be directly calculated, this approach requires the model to be fitted in advance using representative data. The outputs for the three route planning scenarios were generated by the trained network and are shown in

Table 8. (a) ML distance matrices for short inner-city locations and optimal route. (b) ML distance matrices for medium intra city locations and optimal route. (c) ML distance matrices for whole country locations and optimal route.

(a)
Real Dist. (km)	1	2	3	4	5	6	7	8	Best Route (105.1 km)
1	1.08	8.33	17.68	25.66	17.41	7.09	11.97	11.78	1
2	8.88	2.77	13.77	37.78	21.45	16.61	16.29	16.66	6
3	20.13	14.83	2.47	33.33	34.14	17.29	20.33	17.01	4
4	28.81	40.08	33.70	0.76	18.32	21.21	23.75	26.53	5
5	17.16	23.55	34.51	16.91	1.25	18.38	11.67	13.79	7
6	26.40	18.11	17.13	19.13	18.27	2.70	4.74	11.39	8
7	11.59	16.74	20.74	23.02	11.60	4.84	0.86	7.73	3
8	11.26	18.56	17.51	26.66	13.34	10.83	7.11	3.34	2
(b)
Real Dist. (km)	1	2	3	4	5	6	7	8	Best Route (304.1 km)
1	0.00	26.10	83.00	52.60	64.10	77.10	109.00	135.00	1
2	26.60	0.00	56.60	62.80	54.50	50.70	82.80	109.00	2
3	85.80	58.90	0.00	7.00	4.00	32.50	32.70	115.00	6
4	73.60	65.50	6.80	0.00	9.30	39.10	39.30	122.00	8
5	65.00	56.10	4.00	9.10	0.00	29.70	37.00	112.00	7
6	79.20	52.20	31.10	37.40	29.00	0.00	34.50	74.30	5
7	111.00	83.70	32.60	39.40	36.60	34.60	0.00	56.70	3
8	137.00	110.00	116.00	122.00	114.00	75.80	56.90	0.00	4
(c)
Real Dist. (km)	1	2	3	4	5	6	7	8	Best Route (766.3 km)
1	2.44	20.24	22.07	87.98	142.56	236.18	218.48	130.34	1
2	19.67	3.40	17.84	73.78	184.13	245.03	184.88	96.38	2
3	24.72	19.61	1.72	95.15	153.26	152.04	200.19	87.64	4
4	84.37	74.96	93.91	2.69	155.45	185.81	223.69	229.34	6
5	156.82	169.21	144.68	164.62	3.66	36.09	195.85	278.00	5
6	165.15	263.41	167.54	205.13	39.59	2.52	288.27	372.26	7
7	235.09	197.64	185.97	204.45	223.47	291.15	4.60	139.06	8
8	126.95	98.98	87.29	226.82	299.13	373.74	144.49	1.87	3

. These values reflect the network’s internalized understanding of spatial relationships, rather than explicit distance calculations.

As previously observed in the statistical analysis, the machine learning–based distance approximation yields promising—though not flawless—results. A comparison between Table 6 and Table 8 reveals that in several cases, not only are entire city pairs preserved, but full route segments remain unchanged, with only minor substitutions, such as swapping one or two cities. This phenomenon is particularly evident in the two corresponding Table C route plans, where the only noticeable difference is that the ML-based solution produces the reversed traversal of the original route.

An important observation in Table 8 is that, unlike the statistical methods, the machine learning model does not produce zero distance between identical locations. Instead, it consistently predicts a small nonzero value, even when the origin and destination are the same. This behavior can be attributed to two main factors: first, the nature of neural networks, which always produce a numerical output rather than a true null; and second, the absence of identical-location examples in the training data, which prevented the model from learning to associate such cases with zero distance. Importantly, this limitation is not unique to the ANN: apart from applying a fixed scaling factor to Haversine distances, none of the tested approaches, including the statistical models, would return a true zero for identical locations. Even if identical pairs had been included, there is no guarantee that the model—or other methods—would have achieved an exact zero, as perfect accuracy was never the goal. As a result, the model generalizes these inputs and returns an estimated value rather than a hard-coded zero.

In the subsequent table, the different estimation methods are evaluated in terms of their route structures and total distances, segmented across short-, medium-, and long-distance scenarios.

In

Table 9. Summary of routes and distances of multiple estimations for different tasks.

Task Size	Method	Route	Distance by Method (km)	Distance on Map (km)
Inner city task	Map data	1-7-5-4-8-6-3-2-1	90.5	90.5
	Haversine est.	1-4-6-7-5-8-2-3-1	46.8	116.6
	Average est.	1-4-6-7-5-8-2-3-1	63.71	116.6
	Linear method	1-4-6-7-5-8-2-3-1	118.8	116.6
	Polinimial 2 est.	1-4-6-7-5-8-2-3-1	41.7	116.6
	Polinimial 3 est.	1-4-6-7-5-8-2-3-1	117.0	116.6
	Neural training	1-6-4-5-7-8-3-2-1	105.1	97.5
Inter county task	Map data	1-4-5-3-7-8-6-2-1	309.9	309.9
	Haversine est.	1-7-3-5-4-6-8-2-1	287.2	352.1
	Average est.	1-7-3-5-4-6-8-2-1	390.9	352.1
	Linear method	1-7-3-5-4-6-8-2-1	383.1	352.1
	Polinimial 2 est.	1-7-3-5-4-6-8-2-1	411.1	352.1
	Polinimial 3 est.	1-7-3-5-4-6-8-2-1	394.5	352.1
	Neural training	1-4-6-8-7-5-3-2-1	304.1	324.6
Full country task	Map data	1-3-8-7-5-6-4-2-1	757.2	757.2
	Haversine est.	1-3-2-4-5-6-7-8-1	641.3	886.9
	Average est.	1-3-2-4-5-6-7-8-1	873.1	886.9
	Linear method	1-3-2-4-5-6-7-8-1	841.7	886.9
	Polinimial 2 est.	1-3-2-4-5-6-7-8-1	842.8	886.9
	Polinimial 3 est.	1-3-2-4-5-6-7-8-1	850.1	886.9
	Neural training	1-2-4-6-5-7-8-3-1	766.3	759.7

, the optimal routes generated by each of the methods discussed so far are presented. An interesting phenomenon emerges: all approaches based purely on statistical estimation—namely the Haversine formula, average-scaling, linear regression, and both polynomial models—produced the exact same route as the optimal solution. While these solutions are not entirely inaccurate, as previously discussed, they do not align closely with the real-world optimal paths derived from actual map data.

The fact that all five statistical methods converged on the same route, despite using different formulas to estimate distances, suggests a likely explanation: the relative ordering of pairwise distances remains mostly consistent across these methods. Although the absolute values differ by model, the rank or comparative magnitude of each distance tends to be preserved. As a result, even though the scales vary, the optimization process identifies the same path because the relative structure of the distance matrix remains unchanged.

In addition to the earlier observations, it can also be seen here that the trained ML-ANN model provides a significantly closer approximation to the map-based ground truth. Both in terms of route structure and individual distances, the predictions generated by the neural network alien more closely with the real-world values than those produced by the purely statistical models. In contrast, the latter often overestimate total distances, particularly for longer routes, leading to greater deviations from realistic expectations. This reinforces the practical advantage of using trained machine learning models in route planning when map queries are unavailable or restricted.

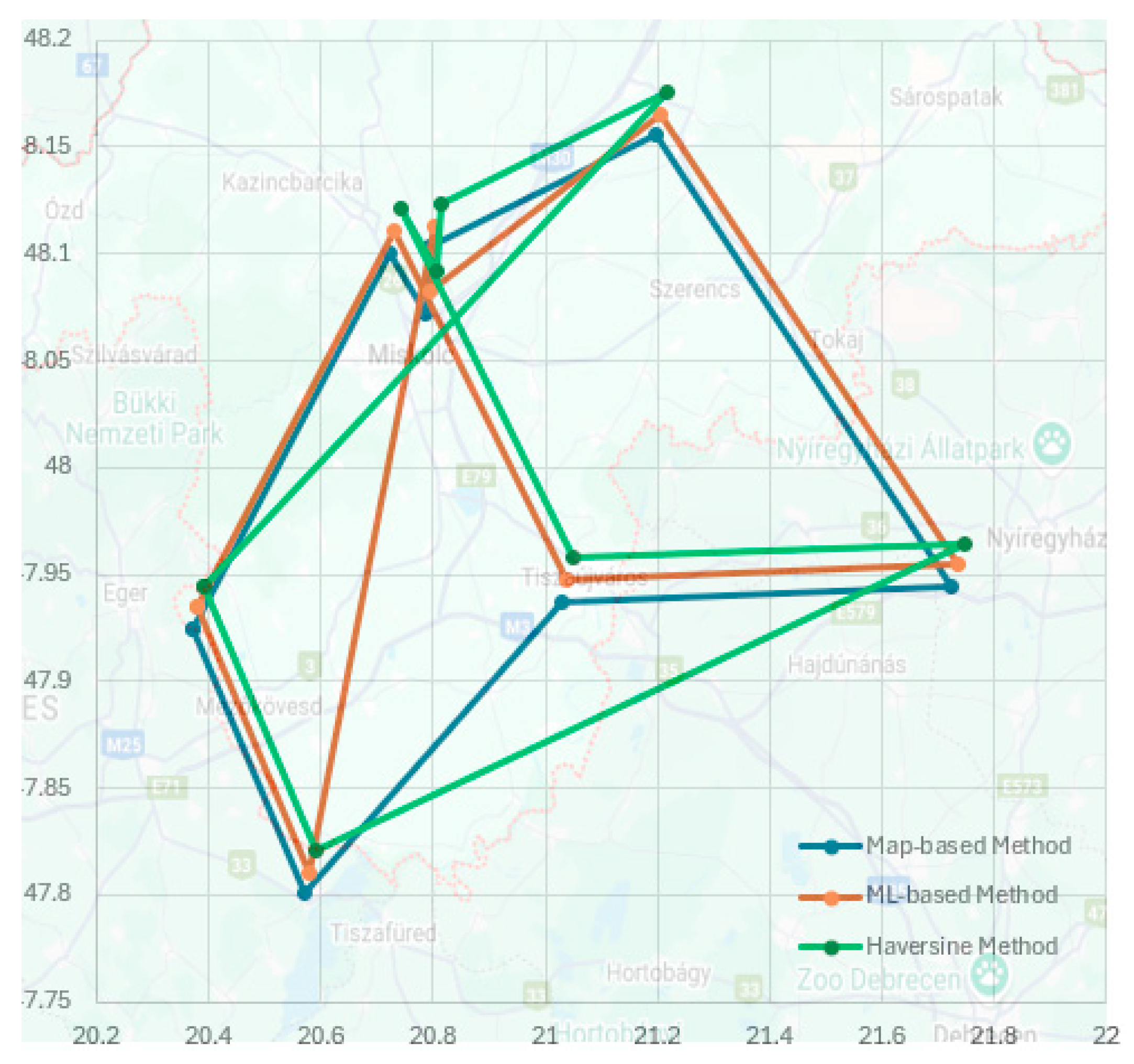
For visualization purposes, the medium-distance scenario has been illustrated using a scatter plot, placed above a segment of the Hungarian map to provide geographical context on Figure 5. This allows for a clearer understanding of how the different models would construct a route across actual locations. Since all four Haversine-based and statistical models (including average, linear, and polynomial estimations) resulted in the exact same routing solution, they are represented collectively as a single unified method (haversine method) in this figure. This visual comparison highlights both the structural similarities and the differences between model-generated and map-based routes.

What can also be observed in Table 9. is that when we project the resulting path back onto the precise cartographic data, the differences become clearly visible. This is shown in the last column of Table 9: we can see that, regardless of whether the estimates are good or poor, in the case of simple statistical models the projected and aggregated data result in roughly 10–30% redundant travel distance (116.6/90.5; 352.1/309.9; and 886.9/757.2). In contrast, with the machine learning–based models the increase in distance remains below 10% (97.5/90.5; 324.6/309.9; and 759.7/757.2). Moreover, in the full-country task we obtained an alternative route with ML that was only about 2 km longer than the ideal one.

While the primary focus of the validation was on distance estimation accuracy, the study also incorporated a practical evaluation within a real route optimization system. As detailed in the case study section, the estimated distance matrices—particularly those generated by the ANN model—were applied in an operational routing scenario. The resulting routes were compared with those generated using map-based distances, demonstrating that the ANN-based approach produced route structures more closely aligned with real-world travel patterns. This finding provides indirect evidence of the method’s compatibility with routing systems. Nevertheless, it is acknowledged that a more extensive quantitative assessment of potential time savings, operational efficiency gains, or computational advantages would further strengthen the validation. Such analyses represent a valuable direction for future research.

6. Discussion and Conclusions

The findings of this study confirm that reliable distance approximations can be achieved without full reliance on costly geospatial services (Hypothesis 1). Through the comparison of multiple statistical estimators and a trained artificial neural network, it has been demonstrated that route planning tasks—particularly at medium and long distances—can be reasonably approximated using limited data and lightweight computational models.

Among the statistical methods, all models that rely solely on variations of the Haversine calculation yielded similar results, both in terms of route structure and estimated distances. This consistency stems from the preserved relative order of inter-point distances across models, despite their differing mathematical formulations. However, while computationally efficient, these models consistently overestimated actual road distances, particularly at longer ranges, limiting their effectiveness in real-world scenarios. In addition, they inherently assume a static road network; in practice, network changes can occur and should be accounted for. In principle, such models could be adapted for real-time updates, where “real-time” is defined by the computational time required to recalculate affected distances after changes, while balancing responsiveness with efficiency.

In contrast, the ANN-based approach—although imperfect—proved more capable of approximating both the actual distances and the resulting optimal routes (Hypothesis 2). Notably, this method was able to capture segment-level patterns and route logic that purely statistical models could not. Still, the model demonstrated some instability at short distances and lacked the capacity to assign zero distance to identical locations, highlighting a key limitation related to training data representation. These higher errors in the under-10 km category reflect the inherent difficulty of short-range estimation: small route deviations in urban contexts represent proportionally larger changes than equivalent deviations over long distances. While the point-pair generation process was biased toward selecting closer locations to mitigate this, the amount of short-range data was still insufficient to fully resolve the issue. Moreover, short-range accuracy is influenced not only by physical distance, but also by factors such as traffic, travel time, and city layout—variables deliberately excluded to maintain the method’s simplicity and general applicability.

Importantly, it is expected that further improvements can be achieved through the use of larger and more diverse datasets, longer and more extensive training phases, and the inclusion of additional input features. Parameters such as estimated travel time, road classification (e.g., highway vs. local), elevation changes, traffic intensity, or population density of surrounding areas could enrich the input space and enhance the model’s ability to differentiate between similar geometric distances that lead to different real-world travel conditions. Many of these attributes are publicly available in open datasets or can be queried in batch from limited geospatial sources.

These results suggest that neural network–based models may serve as a viable middle ground between simplistic statistical estimators and high-cost routing APIs. Their predictive power, when properly trained, enables scalable, near-realistic routing without continuous geospatial querying, making them especially valuable for small- and medium-sized enterprises operating under resource constraints.

It is acknowledged that concerns may arise regarding the complexity of machine-learning-based solutions for SMEs. However, after training, the model can be executed with negligible computational overhead using standard linear-algebra operations; moreover, the training process itself is increasingly accessible due to widely available frameworks and cloud notebooks, allowing for models to be retrained or fine-tuned without specialized infrastructure (Hypothesis 3).

SMEs can incur losses when relying on estimates for route planning: with simple statistical models, the redundant travel distance is around 10–30%; with machine learning–based methods, it remains below 10%; and in full-country transport routes, it could be basically zero (Hypothesis 4).

Future work will focus on enhancing model generalization by expanding the training dataset with synthetic and real-world examples, particularly including self-reference pairs to correct the zero-distance estimation issue. Additionally, hybrid approaches combining fast statistical approximations for pre-filtering and ML-based refinement for critical segments could be explored. Estimating travel times for different vehicle types, such as cars and trucks, will also be investigated, as this adds an important temporal dimension to routing and logistics applications, enabling more realistic and context-aware planning. Further benchmarking against state-of-the-art route optimization frameworks will also be prioritized to situate this method within the broader research landscape and validate its practical applicability.