A Simulated Annealing Solution Approach for the Urban Rail Transit Rolling Stock Rotation Planning Problem with Deadhead Routing and Maintenance Scheduling

Abstract

Background: Urban rail transit ensures efficient mobility in densely populated metropolitan areas. This study focuses on the Cairo Metro Network and addresses the Rolling Stock Rotation Planning Problem (RSRPP), aiming to improve operational efficiency and service quality. Methods: A Mixed-Integer Linear Programming (MILP) model is developed to integrate rolling stock rotation, deadhead routing, and maintenance scheduling. Two single-objective formulations are introduced to separately minimize denied passengers and the number of Electric Multiple Units (EMUs) used. To address scalability for larger instances, a Simulated Annealing (SA) metaheuristic is designed using a list-based solution representation and customized neighborhood operators that preserve feasibility. Results: Computational experiments based on real-world data validate the practical relevance of the model. The MILP achieves optimal solutions for small and medium-sized instances but becomes computationally infeasible for larger ones. In contrast, the SA algorithm consistently produces high-quality solutions with significantly reduced solve times. Conclusions: To the best of the authors’ knowledge, this is the first study to apply SA to the urban rail RSRPP while jointly integrating deadhead routing and maintenance scheduling. The proposed approach proves to be robust and scalable for large metro systems such as Cairo’s.

1. Introduction

Efficient transportation systems are the lifeblood of modern urban centers, providing essential connectivity and mobility for millions of people daily. As one of the oldest and most cost-effective forms of land transportation, railway travel systems present a particularly suitable alternative for passenger transport [1]. Among these systems, metro networks are a cornerstone of sustainable urban transportation, offering a fast, reliable, and environmentally friendly means of moving people within densely populated cities and sprawling metropolises [2]. A key component in the successful operation of a metro network is the management and planning of rolling stock, which involves the allocation of vehicles, maintenance scheduling, and deadhead routing strategies.

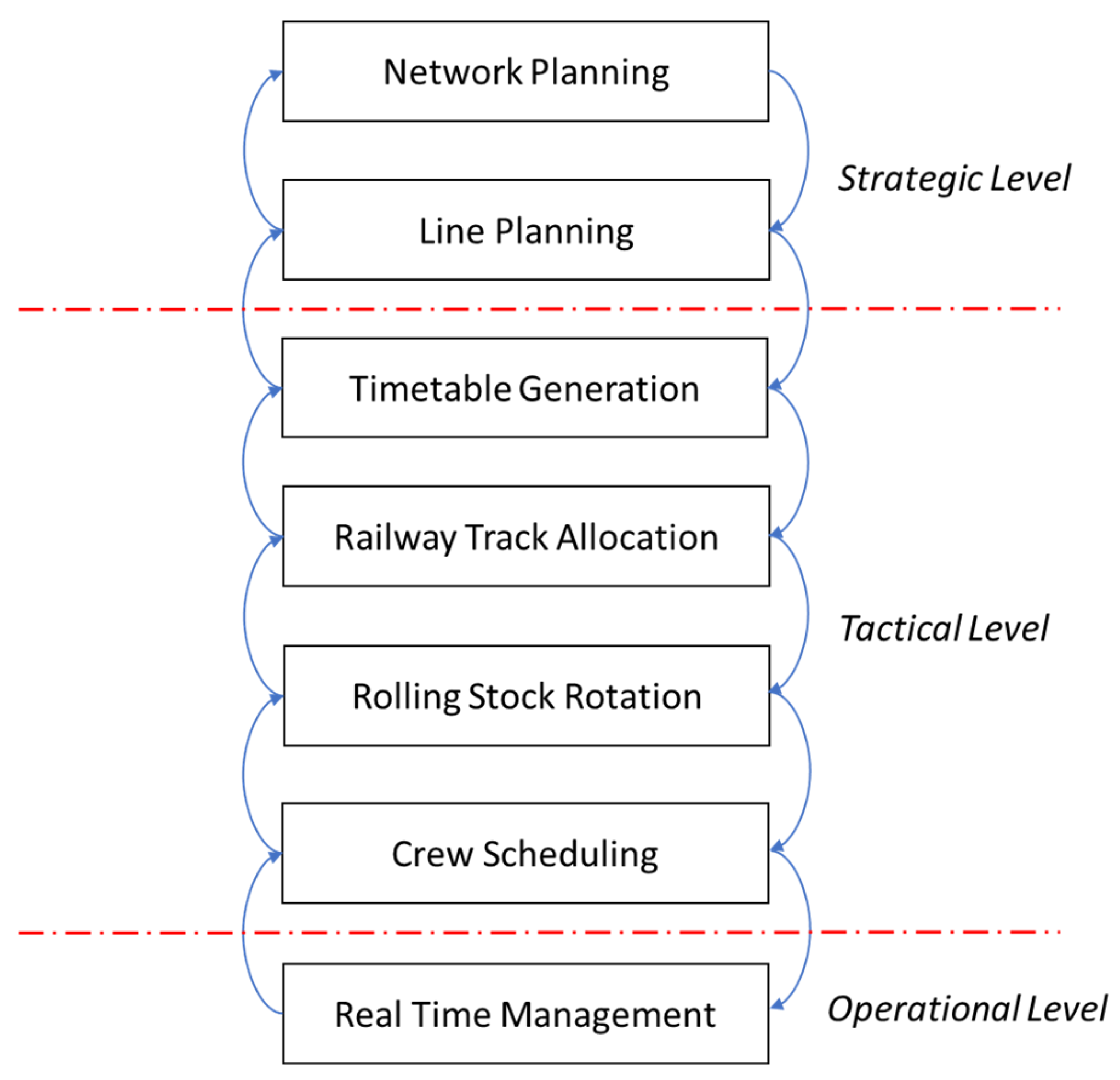
In general, the planning of railway operations consists of several interconnected planning problems. Due to the complexity, the problems are often seen as independent stages that can be solved individually. The most prominent planning problems in railway optimization are line planning, train timetabling, train platforming, rolling stock scheduling, and crew scheduling [3]. Figure 1 presents the different railway optimization planning problems while showing their planning level and the order at which these planning problems are carried out.

This study is motivated by the operational challenges faced by the Cairo Metro Network, Egypt’s largest urban rail system and one of the most heavily utilized networks in Africa and the Middle East. With over 84 stations across three lines and a daily ridership exceeding 3.6 million passengers, the Cairo Metro plays a central role in the city’s mobility ecosystem. The network is expected to serve more than 38 million people by 2050, intensifying the demand for efficient rolling stock management [4]. The high ridership value (about 17% of total population) and the dependency on the metro network as a means of public transport, highlights the importance of properly managing the involved assets and maintaining balance between satisfying the passengers’ demand, reducing costs, and maintaining the available assets.

Given these pressures, this paper addresses the Urban Rail Transit RSRPP, focusing on optimizing the utilization of EMUs over a multi-day planning horizon. The study explicitly incorporates deadhead movements, preventive maintenance, and passenger demand constraints into a unified model. Two optimization objectives are considered independently: minimizing the number of denied passengers and minimizing the number of used EMUs. The model is designed to capture real operational complexities while remaining computationally tractable.

To solve the problem, a MILP model is developed and tested on realistic scenarios derived from the Cairo Metro timetable and infrastructure. However, due to the limitations of MILP in large-scale instances, we propose a complementary SA algorithm tailored to preserve feasibility while navigating the solution space efficiently. Unlike traditional applications of SA in related domains, the proposed heuristic is equipped with a structured list-based solution representation and customized neighborhood operators designed to enforce mileage and maintenance constraints.

The contributions of this work are threefold:

• It develops a MILP formulation for the RSRPP that integrates routing and maintenance scheduling.
• It introduces a customized SA algorithm capable of scaling to large, real-world metro instances.
• It applies the framework to a multi-line case study of the Cairo Metro, offering insights into operational planning and resource trade-offs.

The outcomes of this study offer practical insights for urban transit agencies, particularly in improving EMU utilization, reducing passenger denial, and supporting informed scheduling decisions under operational constraints.

The remainder of this paper is organized as follows. Section 2 reviews the literature on rolling stock scheduling and urban rail optimization. Section 3 presents the problem description and illustrative example. Section 4 provides the mathematical model. Section 5 outlines the SA algorithm. Section 6 discusses computational results. Section 7 concludes with practical insights and directions for future research.

2. Relevant Literature

The optimization of Urban Rail Transit (URT) operations poses significant challenges, particularly in the efficient rotation of rolling stock, the coordination of deadhead movements, and the planning of maintenance activities. These interconnected problems require sophisticated mathematical and computational models to ensure that resources are utilized effectively while maintaining high service reliability. This review is structured into four parts. Section 2.1 discusses the joint timetable and rolling stock scheduling problem. Section 2.2 presents key contributions related specifically to the RSRPP. Section 2.3 highlights the differences between High-Speed Rail (HSR) and URT in the context of RSRP. Section 2.4 summarizes the research contributions and gaps addressed in this study.

2.1. The Joint Timetabling and Rolling Stock Scheduling Problem

As depicted in Figure 1, timetabling—or train timetable generation—is a fundamental and preliminary phase in the rolling stock scheduling process. In URT systems, especially metro networks, there is a high frequency of trips and considerable variation in passenger demand across different time periods (e.g., peak hours, holidays). Integrating Train Timetabling (TT) with Rolling Stock Scheduling (RSS) can lead to better-coordinated and more efficient plans. However, this integration significantly increases problem complexity due to the interdependence of time and resource constraints.

In the train timetabling problem, the objective is to determine precise arrival and departure times of trains across a given network of stations connected by tracks. This process must comply with several constraints. These include minimum travel and stop durations, headway constraints to maintain safe time intervals between consecutive trains, and track usage limitations to avoid overtaking and crossing conflicts, particularly in single-track sections or terminals [5]. On the other hand, the RSRPP comprises two main aspects:

• Rolling stock routing, which identifies the sequence of trips assigned to each train unit while considering mileage accumulation and maintenance thresholds [6];
• Rolling stock assignment, where train units are allocated to the identified routes based on their capacity, availability, and operational readiness [7].

Recent studies have increasingly focused on the joint optimization of timetabling and rolling stock scheduling, especially under disruption scenarios. Disruptions—such as unexpected delays, maintenance overruns, or infrastructure failures—require real-time adaptation of plans to prevent cascading delays and preserve service quality. To handle such cases, researchers have proposed robust and reactive strategies. For instance, Su et al. [8] proposed a hybrid deep reinforcement learning (DRL) framework combined with adaptive large neighborhood search (ALNS) to optimize train timetables and rolling stock circulation under disruptions. Their model demonstrated superior performance compared to traditional rule-based heuristics, producing near-optimal results in complex, dynamic metro environments. Similarly, Wang et al. [9] introduced a two-stage optimization framework. First, a simplified version of the problem is solved at key turnaround stations to produce a feasible initial plan. Then, a full-scale MILP model is executed, incorporating the results of the first stage to improve solution quality and computational efficiency. These studies underscore the value of integrated approaches that treat timetabling and rolling stock scheduling as a unified problem, particularly in metro systems where passenger demand is dense and frequent service is critical.

2.2. The Rolling Stock Rotation Planning Problem

The RSRPP addresses the comprehensive scheduling of train units across multiple trips, incorporating routing, availability, and operational constraints. Several critical aspects influence the complexity of the RSRP, notably train compositions, deadhead movements, and maintenance requirements. An essential consideration is the train composition and coupling compatibility. Rolling stock units must conform to regulatory standards governing their configuration. For instance, not all rolling stock types are interoperable; some require a locomotive, while others, like EMUs, operate as fixed, indivisible configurations of multiple carriages. To ensure operational feasibility and regulatory compliance, coupling and decoupling procedures must be incorporated into the RSRP model. Several researchers have addressed train composition rules within the RSRP framework. Notably, Yang et al. [10], Pan et al. [11], and Wang et al. [12] proposed models that incorporate detailed composition constraints. Yang et al. [10] solved a joint timetabling and rolling stock scheduling problem using adaptive large neighborhood search (ALNS) and validated their approach on real-world metro instances, achieving high computational efficiency, while Pan et al. [11] applied a Benders decomposition technique to the same integrated problem. Their work on both small- and large-scale instances from the Shanghai Metro Line 17 demonstrated significant improvements when stochastic demand was accounted for. In contrast, Wang et al. [12] focused solely on the RSRP and employed branch-and-bound and branch-and-cut methods. Their experiments, including real-life datasets, reported enhanced operational efficiency and service quality.

Another crucial aspect of RSRP is deadhead routing, which refers to empty train movements between scheduled trips or to/from depots. Minimizing unnecessary deadhead mileage is vital for cost and energy efficiency. Several studies have incorporated deadhead routing into their models, including Zhong et al. [13], Wang et al. [14], Gao et al. [15], and Zhong et al. [16], all of whom focused on the rolling stock scheduling problem. Additionally, Wang et al. [17] addressed the combined timetabling and RSS problem and explicitly included deadhead mileage minimization in the objective function.

2.3. Difference Between High-Speed Railway and Urban Rail Transit in the Rolling Stock Rotation Problem

While both High-Speed Rail (HSR) and Urban Rail Transit (URT) systems require efficient rolling stock planning, their operational contexts and constraints differ significantly. High-Speed Railways are designed for long-distance travel between major cities. They operate on dedicated infrastructure with advanced signaling systems and maintain high operational speeds. Their scheduling typically prioritizes long headway and strict punctuality. In contrast, Urban Rail Transit systems—which include metros, trams, and light rail—serve shorter intra-city routes with frequent stops and high-frequency operations. These systems often share corridors with city traffic and operate in more congested and dynamic urban environments [18].

Due to these differences, the RSRP for HSR has generally received more attention in the literature concerning maintenance scheduling. Maintenance plays a critical role in extending the operational life and ensuring the safety of rolling stock, which represents a major capital investment. Studies by Zhong et al. [13], Gao et al. [15], and Lin and Zhao [19] incorporate detailed preventive maintenance planning in HSR rolling stock rotation models. On the other hand, research related to URT systems has largely focused on integrated timetabling and rolling stock scheduling, with limited inclusion of maintenance aspects. For example, Yang et al. [10], Pan et al. [11], Yin et al. [20], and Yuan et al. [21] propose comprehensive models for metro networks but generally omit maintenance considerations, likely due to the shorter operating cycles and decentralized maintenance procedures in urban contexts. This gap highlights an opportunity to bridge RSRP with maintenance scheduling in urban rail systems, particularly given the growing demand for smart, sustainable, and efficient metro operations.

2.4. Rolling Stock Rotation Planning Solution Approaches

Solving the RSRPP problem in urban rail transit systems presents significant computational and operational challenges. Over the years, a wide array of modeling and solution techniques have been proposed to address the complexity arising from integrating vehicle assignment, deadhead routing, maintenance scheduling, and passenger demand. These approaches can be broadly categorized into exact methods, heuristic/metaheuristic algorithms, and hybrid frameworks.

2.4.1. Exact Optimization Methods

Early and foundational contributions to the RSRP domain primarily employed MILP and Mixed Integer Non-linear Programming (MINLP) formulations. These models offer high precision and interpretability and are often solved using commercial solvers such as CPLEX or GUROBI. For example, Wang et al. [12] and Zhong et al. [16] developed MILP-based models to solve the RSRP with explicit deadhead routing. On the other hand, Pan et al. [22] introduced a column-generation-based formulation to handle demand-oriented timetabling and rolling stock circulation with flexible train compositions.

While exact methods are suitable for small- to medium-scale networks, their computational burden grows exponentially with network size and operational constraints, limiting their practicality for large real-world systems.

2.4.2. Metaheuristic and Heuristic Algorithms

To overcome scalability issues, many researchers have turned to metaheuristics, which offer more computational flexibility and adaptability for large-scale, real-world systems. For example, Yang et al. [10] and Gong et al. [23], who applied ALNS to solve joint timetabling and rolling stock scheduling problems, demonstrating superior performance on dense urban networks. Also, Ying et al. [24] proposed a DRL strategy to manage rolling stock circulation under stochastic demand.

Despite the loss of guaranteed optimality, metaheuristics offer a robust balance between solution quality and runtime performance, making them well-suited for dynamic and constraint-rich environments.

2.4.3. Hybrid Approaches

More recent works have explored hybrid models that integrate the strengths of different optimization paradigms. These include combining metaheuristics with machine learning, decomposition techniques, or rule-based preprocessing. In the reviewed literature, Su et al. [8] developed a hybrid deep reinforcement learning and ALNS algorithm for train rescheduling under disruption scenarios. A Benders decomposition framework was adopted by Yin et al. [20] to address timetable and rolling stock integration in large-scale metro networks. Another example is Pan et al. [11] who incorporated stochastic programming and decomposition in their robust routing models.

These hybrid approaches aim to reduce computational complexity while still accommodating real-world constraints like maintenance needs, passenger variability, and rolling stock compatibility.

2.5. Paper Contributions

Some of the most relevant studies which focused on solving the RSRP problem for passengers in urban rail transit were summarized.

Table 1. Summary of relevant studies on rolling stock rotation planning for passengers in an urban rail transit.

Paper	Planning Horizon	Deadhead Routing	Multiple Depots	Maintenance	Train Composition	Objective (min)	Solution Method
Zhang et al., 2019 [25]	2 days		✓	✓	✓	OC + penalties	CPLEX
Zhong et al., 2020 [16]	1 day	✓				DM + OC	CPLEX
Ying et al., 2020 [24]	4 h			✓		PWC + OC	ADRL
Wang et al., 2021 [17]	1 day	✓	✓			Headway deviation + EC	Iterative Searching approach
Yuan et al., 2022 [21]	1 day		✓			DT	Genetic algorithm
Zhou et al., 2022 [26]	5 h		✓			OC + PWT	Tabu search + CPLEX
Pan et al., 2023 [22]	4 h				✓	OC + PWT + CA	Column generation
Zhao et al., 2023 [27]	1 day		✓	✓	✓	PWT + NoR + number of formations + CA	Linearization, BARON, CPLEX
Yin et al., 2023 [20]	1 day		✓			OC + QoS	Benders Decomposition
Wang et al., 2023 [14]	1 day	✓	✓		✓	OC + penalties	Column generation
Huang et al., 2023 [28]	1 day					EC + PTT + OC	VNS + CPLEX
Yang et al., 2024 [10]	4 h		✓		✓	PWT + NoR	ALNS
Pan et al., 2024 [11]	4 h		✓		✓	OC + PWT + CA	Benders Decomposition
Gong et al., 2024 [23]	2 h		✓			PWT + EC	ALNS
Wang et al., 2024 [12]	1 day		✓		✓	OC + PWT	Branch & Price
Huang et al., 2025 [29]	1 day	✓	✓			EC + OC + PWT	VNS + CPLEX
Yang et al., 2025 [30]	1 day		✓		✓	NoR	CPLEX + AC
Bao et al., 2025 [31]	6 h	✓	✓		✓	OC + PWT	ASA
This paper	7 days	✓	✓	✓	✓	Denied Passengers/number of EMUs	GUROBI + SA

Symbol description for Table 1: High speed railway (HSR), Urban rail transit (URT), Rolling stock scheduling (RSS), Operating cost (OC), Passenger waiting time/cost (PWT/C), Number of rolling stock (NoR), Coupling activities (CA), Energy consumption (EC), Deadhead Mileage (DM), Dwell time (DT), Running distance (RD), Number of trains performed by type-L rolling stock (NTL), Mixed integer program (MIP), Adaptive large neighborhood search (ALNS), Adaptive simulated annealing (ASA), Variable neighborhood search (VNS).

presents the most relevant details for each one in terms of their planning horizon, mathematical formulations (such as constraints and objectives), and solution algorithms.

Table 1 illustrates the progressive shift from pure MILP-based approaches to heuristic and hybrid techniques in addressing RSRP. However, SA—a powerful metaheuristic known for escaping local optima and offering high-quality results for combinatorial problems [32,33]—has seen limited application in metro-based RSRP research. This gap underscores the need for further exploration of SA-based methods, particularly when integrated with structured repair mechanisms or domain-specific knowledge. Maintenance and deadhead routing also have seen limited application in metro-based RSRP research.

The present work addresses this gap by proposing a SA-based solution tailored to the urban rail transit RSRP with maintenance and deadhead routing. The proposed approach balances the solution quality, runtime feasibility, and model adaptability, making it a viable strategy for large-scale networks such as the Cairo Metro Network. This study also takes into consideration both the railway operator and passenger perspective and best interest. The developed optimization models take into consideration both the minimization of denied passengers and the number of utilized rolling stock. First a MILP model is introduced with the aim of minimizing each objective separately. Then, the model is solved using SA. The SA algorithm developed in this study differs from traditional SA applications in railway optimization in several keyways. It incorporates a list-based solution representation tailored for EMU sequences, along with custom neighborhood generation mechanisms that preserve trip feasibility, prevent over-mileage violations, and respect maintenance thresholds. To the best of the authors’ knowledge, this is the first SA implementation applied to the Urban Rail Transit Rolling Stock Rotation Planning Problem (RSRPP) that jointly optimizes EMU routing, deadheading, and maintenance on a real multi-line metro system. The model is formulated to accommodate for the urban rail transit in Egypt and in specific, the Cairo Metro Network. To the best of our knowledge, this was not attempted before in the literature. The instances used were all based on available public transport data for the Cairo Metro Network. Each of the suggested models, while solving the problem of rolling stock allocation, take into consideration the maintenance scheduling, deadhead routing, multiple depots, and different rolling stock types. In addition, the models allow for maintenance actions to be scheduled during the day and night shift.

3. Problem Description

This study addresses the Urban Rail Transit RSRPP by constructing a directed, weighted, and acyclic graph that integrates scheduled trips, deadhead routing, and maintenance scheduling. The following section describes the representation of the network routes and scheduled trips. The problem’s aim is to assign the available rolling stock to satisfy the urban rail transit timetable, determine the routes and maintenance schedule for each rolling stock while also satisfying the passenger demand.

3.1. Problem Statement and Modeling Approach

The proposed model assumes that the train timetable for the entire planning horizon is available, along with a detailed description of the URT network, including station-level arrival and departure times. The data used is based on the available data for Cairo Metro Network, which provides real-world relevance to the study. Each EMU k $\in$ K, where K is the set of available EMUs, is defined by EMU type, passenger capacity, mileage since last maintenance, start time, and location availability.

All rolling stock in the study are EMUs, which operate as indivisible multi-carriage trains. Each EMU has a maximum mileage threshold $r_k^{\max }$, beyond which maintenance is mandatory, and a minimum threshold $r_k^{\min }$ to avoid unnecessary maintenance. Maintenance costs are not modeled, nor are penalties imposed for premature maintenance; thus, the model emphasizes efficient utilization rather than cost optimization. The maintenance duration required for each EMU is known, as is the list of stations equipped with maintenance facilities. To solve the RSRPP, we define a graph with four types of nodes and three types of arcs, as follows:

Node Types

• $V^s$: EMU Starting Nodes—initial location of each EMU at the beginning of the planning period.
• $V^d$: Departure Nodes—represent the departure station and time of each scheduled trip.
• $V^a$: Arrival Nodes—represent the arrival station and time of each scheduled trip.
• $v_f$: Virtual Final Node—indicates the end of an EMU’s route.

In this model, each scheduled trip consists of a departure node and an arrival node, with known passenger demand and start/end times. Each trip represents an uninterrupted run from a line’s starting station to its terminus, reflecting Cairo Metro’s design where EMUs do not reverse direction mid-line. Passenger demand for each trip is assumed to be known and constant; estimating or forecasting demand is outside the scope of this study.

Arc Types

• $A_1$: Scheduled Trip Arcs—connect each departure node to its corresponding arrival node.
• $A_2$: Deadhead Arcs—represent empty vehicle movements between trips or to/from depots.
• $A_3$: Maintenance Arcs—a subset of deadhead arcs, representing movements that include a maintenance activity.

A deadhead arc (i, j) ∈ $A_2$ is added only if the following applies:

• It connects an EMU starting node i ∈ Vs. to a departure node j ∈ $V^d$, and a path exists between their associated stations;
• It connects an arrival node i ∈ $V^a$ to a departure node j ∈ $V^d$, where departure time at j > arrival time at i, and sufficient time exists to travel the distance between the two stations;
• It connects any arrival node i ∈ $V^a$ to the virtual final node $v_f$, allowing the EMU to terminate its operation.

Each deadhead arc is weighed by the distance $d_{i,j}$ between the connected stations. If nodes are trip nodes, the corresponding departure or arrival station is used to determine distance. A maintenance arc (i, j, k) ∈ $A_3$ is only added if all the following conditions are satisfied:

• The arc (i, j) ∈ $A_2$ already exists;
• Either node i or j is associated with a maintenance facility;
• The time difference between nodes i and j is sufficient to both travel the required distance and perform the maintenance activity for EMU k.

Maintenance arcs are EMU-specific and weighed the same distance measure $d_{i,j}$ used for deadhead arcs. As noted by Frisch et al. [34], this graph-based formulation implicitly encodes time into the structure of nodes and arcs, avoiding the need for explicit time decision variables in the MILP model. This significantly reduces problem dimensionality while maintaining temporal feasibility.

3.2. Illustrative Example

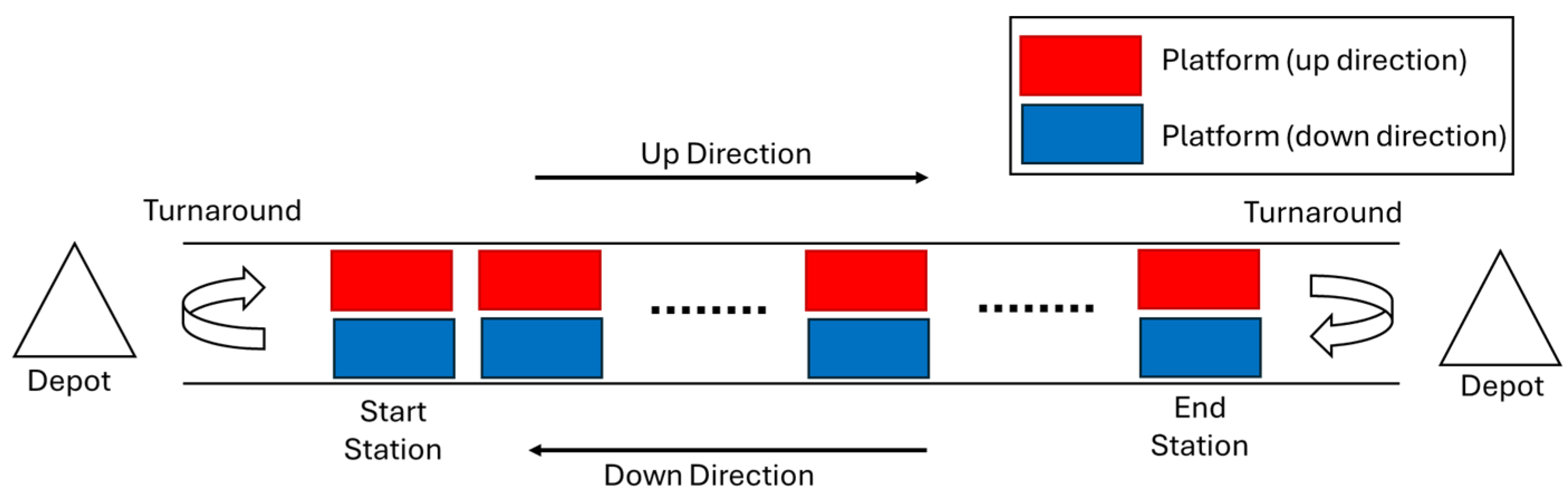
To demonstrate the proposed graph-based formulation, a simplified example of a bidirectional urban rail transit (URT) line is considered, which begins at Start Station and ends at End Station. Although the actual metro line comprises multiple intermediate stations, this representation abstracts the network by modeling each scheduled trip as a direct route from start to end station, without direction changes during the trip. The simplified two-station line presented in this example is intended to illustrate the structure of the graph-based formulation, including node and arc definitions, vehicle assignments, and maintenance arcs. In the proposed model, each scheduled trip is represented by a direct movement from the start to the end station of a metro line, with no directional changes or intermediate stops modeled explicitly. This abstraction is feasible for metro systems, where trains traverse the entire line without reversing direction, and intermediate station dwell times are already accounted for in the total trip time. Thus, abstracting the full line as a start-to-end trip offers a tractable yet operationally realistic representation of URT service patterns. Given that an EMU cannot reverse direction or return midway, this simplification is valid for rotation and routing purposes (see Figure 2).

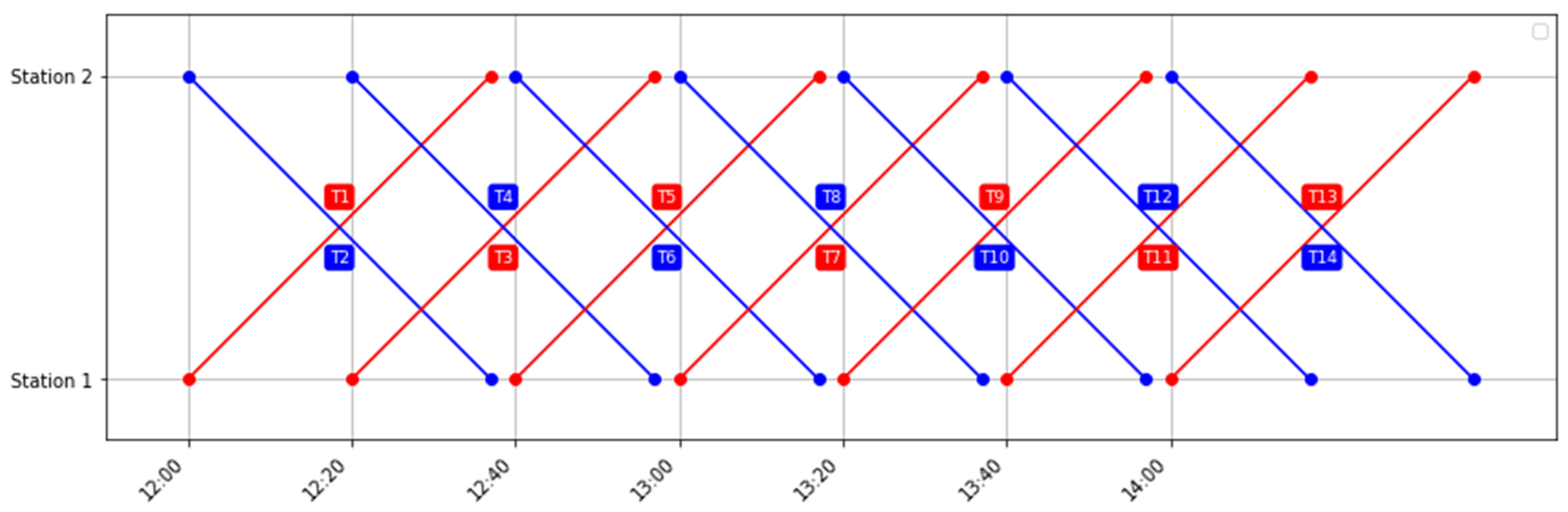
A corresponding train schedule for 14 trips is presented in Figure 3. These trips are scheduled in both up and down directions, beginning at 12:00 p.m. with a consistent headway of 20 min. Blue lines represent scheduled trips in the down direction, while red lines represent the up direction. The last scheduled trip departs at 2:00 p.m. Of the two terminal stations, both are equipped with depots, but only Station 2 includes a maintenance facility. A total of four EMUs are available for assignment during this planning horizon.

Figure 4 shows the resulting circulation plan, i.e., the sequence of trips assigned to each EMU. For instance, EMU 1 begins at Station 2 and starts service with Trip 4 at 12:20 p.m. in the down direction. It proceeds to operate Trip 7 and finally Trip 12, which concludes at 2:15 p.m. The EMU’s trajectory ensures timely service and adherence to routing constraints.

In Figure 5, the complete path of EMU 1 is highlighted, including deadhead arcs (empty movements) and a maintenance arc. Prior to initiating Trip 4, EMU 1 underwent maintenance at Station 2, enabled by its early availability before the start of the planning horizon. Due to the short duration of the planning period, no other EMU required maintenance during this window.

3.3. Assumptions

• In the considered URT network, intersections allow for the change of course.
• The overtaking or multi-train conflict scenarios are not common in normal operations of urban rail transit lines, due to high service frequency and signal control systems enforcing strict first-in first-out (FIFO) order from start station to end station or vice versa.
• Each scheduled trip in the model corresponds to a full traversal of a URT line, from the designated start station to the end station, with the time taken at all intermediate stations embedded in the total travel time. Since URT trains operate on fixed lines and follow consistent, non-reversible trajectories, there is no need to model individual intermediate stops explicitly.
• The rolling stocks used in urban rail transit lines are EMUs, which consist of motor cars and trailer cars. No separate locomotives are needed for the operations of EMUs.
• The EMUs are treated as a single complete unit with no need for coupling or decoupling actions or any changes in composition.
• Stop-skipping (skipping certain stations) or short-turning services (turnaround at an intermediate station instead of the end station) are not an available option.
• The passenger demand is given and is an estimated average on the entire trip without consideration of the origin and destination of each individual passenger.
• There are no specified limits on the maintenance yard capacity.

The modeling framework remains general enough to accommodate more complex interactions in future extensions, if overtaking or express services are introduced. The model currently assumes a fixed passenger demand for each scheduled trip, derived from average historical data. However, the formulation supports extensions to time-dependent demand profiles, such as differentiating between morning peak, mid-day, and evening peak hours. By assigning demand values based on the departure time of each trip, the model can easily incorporate realistic fluctuations in ridership without requiring structural changes.

4. MILP Formulation

Based on the problem statement explained in Section 3, the following MILP is formulated for solving the rolling stock rotation problem with deadhead routing and maintenance scheduling. This model is designed to optimize the scheduling of EMUs by considering passenger demand, maintenance requirements, and fleet utilization. It balances the need to meet service demand while minimizing the number of EMUs used and ensuring timely maintenance interventions. The model formulation was based on the model introduced by [34] with necessary modifications to fit the RSRP for URT.

Table 2. Overview of sets and parameters.

Sets:

${\mathit{V}}^{\mathit{d}}$: set of departure nodes ${\mathit{V}}^{\mathit{a}}$: set of arrival nodes ${\mathit{V}}^{\mathit{s}}$: set of EMU starting nodes $\left\{{\mathit{v}}_{\mathit{f}}\right\}$: virtual final node $$\begin{gathered} \mathit{V}:={\mathit{V}}^{\mathit{d}}\cup {\mathit{V}}^{\mathit{a}}\cup {\mathit{V}}^{\mathit{s}}\cup \left\{{\mathit{v}}_{\mathit{f}}\right\} \\ {\mathit{A}}_1:\mathrm{set}\mathrm{of}\mathrm{scheduled}\mathrm{arcs}, \\ {\mathit{A}}_2:\mathrm{set}\mathrm{of}\mathrm{deadhead}\mathrm{arcs}, \\ {\mathit{A}}_3:\mathrm{set}\mathrm{of}\mathrm{maintenance}\mathrm{arcs} \\ \mathit{A}:={\mathit{A}}_1\cup {\mathit{A}}_2\cup {\mathit{A}}_3 \end{gathered}$$ N: set of EMU types K: set of available EMUs M: set of maintenance locations

Parameters:

$$\begin{gathered} {\mathit{C}}_{\mathit{k}}:\mathit{P}\mathit{a}\mathit{s}\mathit{s}\mathit{e}\mathit{n}\mathit{e}\mathit{g}\mathit{e}\mathit{r}\mathit{c}\mathit{a}\mathit{p}\mathit{a}\mathit{c}\mathit{i}\mathit{t}\mathit{y}\mathit{o}\mathit{f}\mathit{E}\mathit{M}\mathit{U}\mathit{k} \\ {\mathit{N}}_{\mathit{k}}:\mathit{T}\mathit{y}\mathit{p}\mathit{e}\mathit{o}\mathit{f}\mathit{E}\mathit{M}\mathit{U}\mathit{k} \\ {\mathit{Q}}_{\mathit{i},\mathit{j}}:\mathit{N}\mathit{u}\mathit{m}\mathit{b}\mathit{e}\mathit{r}\mathit{o}\mathit{f}\mathit{p}\mathit{a}\mathit{s}\mathit{s}\mathit{e}\mathit{n}\mathit{g}\mathit{e}\mathit{r}\mathit{s}\mathit{d}\mathit{e}\mathit{m}\mathit{a}\mathit{n}\mathit{d}\mathit{f}\mathit{o}\mathit{r}\mathit{s}\mathit{c}\mathit{h}\mathit{e}\mathit{d}\mathit{u}\mathit{l}\mathit{e}\mathit{d}\mathit{a}\mathit{r}\mathit{c}\mathit{i},\mathit{j} \\ \mathit{\beta }:\mathit{M}\mathit{a}\mathit{i}\mathit{n}\mathit{t}\mathit{e}\mathit{n}\mathit{a}\mathit{n}\mathit{c}\mathit{e}\mathit{d}\mathit{u}\mathit{r}\mathit{a}\mathit{t}\mathit{i}\mathit{o}\mathit{n} \end{gathered}$$ T: number of available EMUs $$\begin{gathered} {\mathit{i}}_{\mathit{k}}:\mathit{s}\mathit{t}\mathit{a}\mathit{r}\mathit{t}\mathit{i}\mathit{n}\mathit{g}\mathit{n}\mathit{o}\mathit{d}\mathit{e}\mathit{f}\mathit{o}\mathit{r}\mathit{E}\mathit{M}\mathit{U}\mathit{k}\in \mathit{K} \\ {\mathit{r}}_{\mathit{k}}^{\mathrm{start}}:\mathrm{EMU}\mathrm{mileage}\mathrm{at}\mathrm{start}\mathrm{of}\mathrm{planning}\mathrm{horizon} \end{gathered}$$ $$\begin{gathered} {\mathit{r}}_{\mathit{k}}^{\max }:\mathit{M}\mathit{a}\mathit{x}\mathit{i}\mathit{m}\mathit{u}\mathit{m}\mathit{m}\mathit{i}\mathit{l}\mathit{e}\mathit{a}\mathit{g}\mathit{e}\mathit{t}\mathit{h}\mathit{r}\mathit{e}\mathit{s}\mathit{h}\mathit{o}\mathit{l}\mathit{d}\mathit{a}\mathit{f}\mathit{t}\mathit{e}\mathit{r}\mathit{w}\mathit{h}\mathit{i}\mathit{c}\mathit{h}\mathit{t}\mathit{r}\mathit{a}\mathit{i}\mathit{n}\mathit{u}\mathit{n}\mathit{i}\mathit{t}\mathit{m}\mathit{u}\mathit{s}\mathit{t}\mathit{u}\mathit{n}\mathit{d}\mathit{e}\mathit{r}\mathit{g}\mathit{o}\mathit{m}\mathit{a}\mathit{i}\mathit{n}\mathit{t}\mathit{e}\mathit{n}\mathit{a}\mathit{n}\mathit{c}\mathit{e} \\ {\mathit{r}}_{\mathit{k}}^{\min }:\mathit{M}\mathit{i}\mathit{n}\mathit{i}\mathit{m}\mathit{u}\mathit{m}\mathit{m}\mathit{i}\mathit{l}\mathit{e}\mathit{a}\mathit{g}\mathit{e}\mathit{t}\mathit{h}\mathit{r}\mathit{e}\mathit{s}\mathit{h}\mathit{o}\mathit{l}\mathit{d}\mathit{b}\mathit{e}\mathit{f}\mathit{o}\mathit{r}\mathit{e}\mathit{w}\mathit{h}\mathit{i}\mathit{c}\mathit{h}\mathit{t}\mathit{r}\mathit{a}\mathit{i}\mathit{n}\mathit{u}\mathit{n}\mathit{i}\mathit{t}\mathit{c}\mathit{a}\mathit{n}\mathit{n}\mathit{o}\mathit{t}\mathit{u}\mathit{n}\mathit{d}\mathit{e}\mathit{r}\mathit{g}\mathit{o}\mathit{m}\mathit{a}\mathit{i}\mathit{n}\mathit{t}\mathit{e}\mathit{n}\mathit{a}\mathit{n}\mathit{c}\mathit{e} \end{gathered}$$ M1, M2, M3: Big M terms $$\begin{gathered} {\mathit{E}}_{\mathit{s}}:\mathit{p}\mathit{e}\mathit{n}\mathit{a}\mathit{l}\mathit{t}\mathit{y}\mathit{f}\mathit{o}\mathit{r}\mathit{l}\mathit{o}\mathit{s}\mathit{i}\mathit{n}\mathit{g}\mathit{a}\mathit{s}\mathit{i}\mathit{n}\mathit{g}\mathit{l}\mathit{e}\mathit{p}\mathit{a}\mathit{s}\mathit{s}\mathit{e}\mathit{n}\mathit{g}\mathit{e}\mathit{r}\mathit{d}\mathit{u}\mathit{e}\mathit{t}\mathit{o}\mathit{s}\mathit{h}\mathit{o}\mathit{r}\mathit{t}\mathit{a}\mathit{g}\mathit{e} \\ {\mathit{E}}_{\mathit{k}}:\mathit{c}\mathit{o}\mathit{s}\mathit{t}\mathit{f}\mathit{o}\mathit{r}\mathit{u}\mathit{s}\mathit{i}\mathit{n}\mathit{g}\mathit{E}\mathit{M}\mathit{U}\mathit{k}\in \mathit{K} \\ {\mathit{d}}_{\mathit{i},\mathit{j}}:\mathit{d}\mathit{i}\mathit{s}\mathit{t}\mathit{a}\mathit{n}\mathit{c}\mathit{e}\mathrm{from}\mathrm{node}\mathrm{i}\mathrm{to}\mathrm{j} \end{gathered}$$ ${\mathit{c}}_{\mathit{i},\mathit{j}}:\mathit{c}\mathit{o}\mathit{s}\mathit{t}\mathit{a}\mathit{s}\mathit{s}\mathit{i}\mathit{g}\mathit{n}\mathit{e}\mathit{d}\mathit{t}\mathit{o}\mathit{a}\mathit{r}\mathit{c}(\mathit{i},\mathit{j}$)

provides a list for the sets and parameters used in this MILP model.

Decision Variables are introduced for deadhead arcs, maintenance arcs, visited nodes, used EMUs, denied passengers, and mileages.

$$x_{i,j}=\left\{\begin{array}{c}1ifarc\left(i,j\right)isused\\ 0otherwise\end{array}\right.x_{i,j}\in \left\{\mathrm{0,1}\right\},(i,j)\in A_2$$

$$y_{i,j,k}=\left\{\begin{array}{c}1ifarc\left(i,j,k\right)isused\\ 0otherwise\end{array}\right.y_{ijk}\in \left\{\mathrm{0,1}\right\},(i,j,k)\in A_3,$$

$$q_{i,k}=\left\{\begin{array}{c}1ifnodeiisvisitedbyEMUk\\ 0otherwise\end{array}\right.q_{ik}\in \left\{\mathrm{0,1}\right\},i\in V\setminus \left\{v_f\right\}$$

$$p_k=\left\{\begin{array}{c}1,\mathrm{i}\mathrm{f}\mathrm{E}\mathrm{M}\mathrm{U}k\mathrm{i}\mathrm{s}\mathrm{u}\mathrm{s}\mathrm{e}\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{t}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{e}\\ 0otherwise\end{array}\right.$$

$$S_{i,j}:Deniedpassengersforscheduledarci,j\in A_1$$

$$r_i:denotesthemileageinnodei{r}_i\in {\mathbb{R}}^{+},i\in V$$

The MILP has two separate objective functions. Objective function (1) aims to minimize the number of denied passengers, while (2) minimizes the number of EMUs used.

Objective function

$$\min \sum _{i,j\in A_1}{E}_s.({\displaystyle \raisebox{1ex}{$s_{i,j}$}\!\left/ \!\raisebox{-1ex}{$Q_{i,j}$}\right.})$$

(1)

$$\min \sum _{k\in K}{E_k.p}_k$$

(2)

Subject to:

$$\sum _{(i,j)\in A_2} x_{i,j}+\sum _{(i,j,k)\in A_3} y_{i,j,k}=1,j\in V^d$$

(3)

$$\sum _{(i,j)\in A_2} x_{i,j}+\sum _{(i,j,k)\in A_3} y_{i,j,k}=1,i\in V^a\cup V^s$$

(4)

$$\sum _{(i,j)\in A_2} x_{i,j}=T,j=v_f,$$

(5)

$$s_{i,j}\ge Q_{i,j}-\sum _k C_k{q}_{i,k}\forall \left(i,j\right)\in A_1,i\in V^d$$

(6)

$$s_{i,j}\ge 0\forall (i,j)\in A_1$$

(7)

$$p_k+x_{i{,v}_f}=1,i\in V^s,k\in K,i=i_k$$

(8)

$$q_{i,k}=1,i\in V^s,k\in K,i=i_k$$

(9)

$$\sum _{k\in K} q_{i,k}=1,i\in V\setminus \left\{v_f\right\}$$

(10)

$$q_{i,k}=q_{j,k},\left(i,j\right)\in A_1,k\in K$$

(11)

$$q_{j,k}\ge {q,}_{ik}-\left(1-x_{i,j}\right),(i,j)\in A_2,j\ne v_f$$

(12)

$$y_{i,j,k}\le q_{\mathcal{l},k},(i,j,k)\in A_3,\mathcal{l}\in \{i,j\}$$

(13)

$$r_i=r_k^{\mathrm{start}},i=i_k\in V^s$$

(14)

$$r_j=r_i+d_{i,j},\left(i,j\right)\in A_1$$

(15)

$$r_j\ge r_i+d_{i,j}-M_1\left(1-x_{i,j}\right),(i,j)\in A_2$$

(16)

$$r_j\le M_1\left(1-y_{i,j,k}\right),(i,j,k)\in A_3$$

(17)

$$r_i\le r_k^{max}+M_2\left(1-q_{i,k}\right),i\in V\setminus \left\{v_f\right\},k\in K$$

(18)

$$r_i+d_{i,j}\le r_k^{max}+M_2\left(1-y_{i,j,k}\right),(i,j,k)\in A_3$$

(19)

$$r_i\ge {\mathrm{r}}_k^{min}-M_3\left(1-y_{i,j,k}\right),(i,j,k)\in A_3$$

(20)

$$x_{i,j}\in \left\{\mathrm{0,1}\right\},(i,j)\in A_2$$

(21)

$$y_{i,j,k}\in \left\{\mathrm{0,1}\right\},(i,j,k)\in A_3$$

(22)

$$q_{i,k}\in \left\{\mathrm{0,1}\right\},i\in V\setminus \left\{v_f\right\},k\in K$$

(23)

$$r_i\ge 0,i\in V$$

(24)

$$p_k\in \left\{\mathrm{0,1}\right\},k\in K$$

(25)

Constraint (3) ensures that each departure node is visited by exactly one EMU via one incoming arc. Constraints (4) ascertain that each arrival node and each start node is left by exactly one EMU via one outgoing arc. Equations. (5) ensure that all EMUs enter the virtual final node. Constraint (6) specifies that the shortages on a certain train are not less than the difference between the required and the allocated capacity. Constraints (7) are required in order to exclude the possibility that shortages on a certain train are compensated by an excess of capacity on another train. Constraint (8) guarantees that the number of EMUs used is counted correctly and bounded by the number of EMU starting nodes in $V^s$. Constraints (9) link each EMU with its assigned starting node. Constraints (10) ensure that every node, except the final node, is visited by exactly one EMU. Constraints (11) ensures that if an EMU k is assigned to arc (i, j) ∈ $A_1$, it visits either both or none of the two nodes i and j. Inequalities (12) ascertain that if an arc (i, j) ∈ $A_2$ was used, nodes i and j are visited by the same EMU. Constraints (13) ensure that maintenance arcs can be used for an EMU only if it has visited the corresponding departure and arrival nodes. For each EMU, the mileage in the starting node is initialized in Constraints (14). The mileage in departure node j is updated in Constraint (15) for scheduled arc (i, j) ∈ A1. If a deadhead trip (an arc (i, j) ∈ $A_2$) is taken, the mileage is revised by Inequalities (16). In Constraints (17), the mileage of an EMU is reset to zero if it was serviced, i.e., if a maintenance arc (i, j, k) ∈ $A_3$ was used. Inequalities (18) and (19) avoid exceeding the maximally permitted mileage of an EMU until the next maintenance operation is performed. Constraints (20) sets a lower threshold for permitted mileage before maintenance. Constraints (21) to (25) define the decision variables domains.

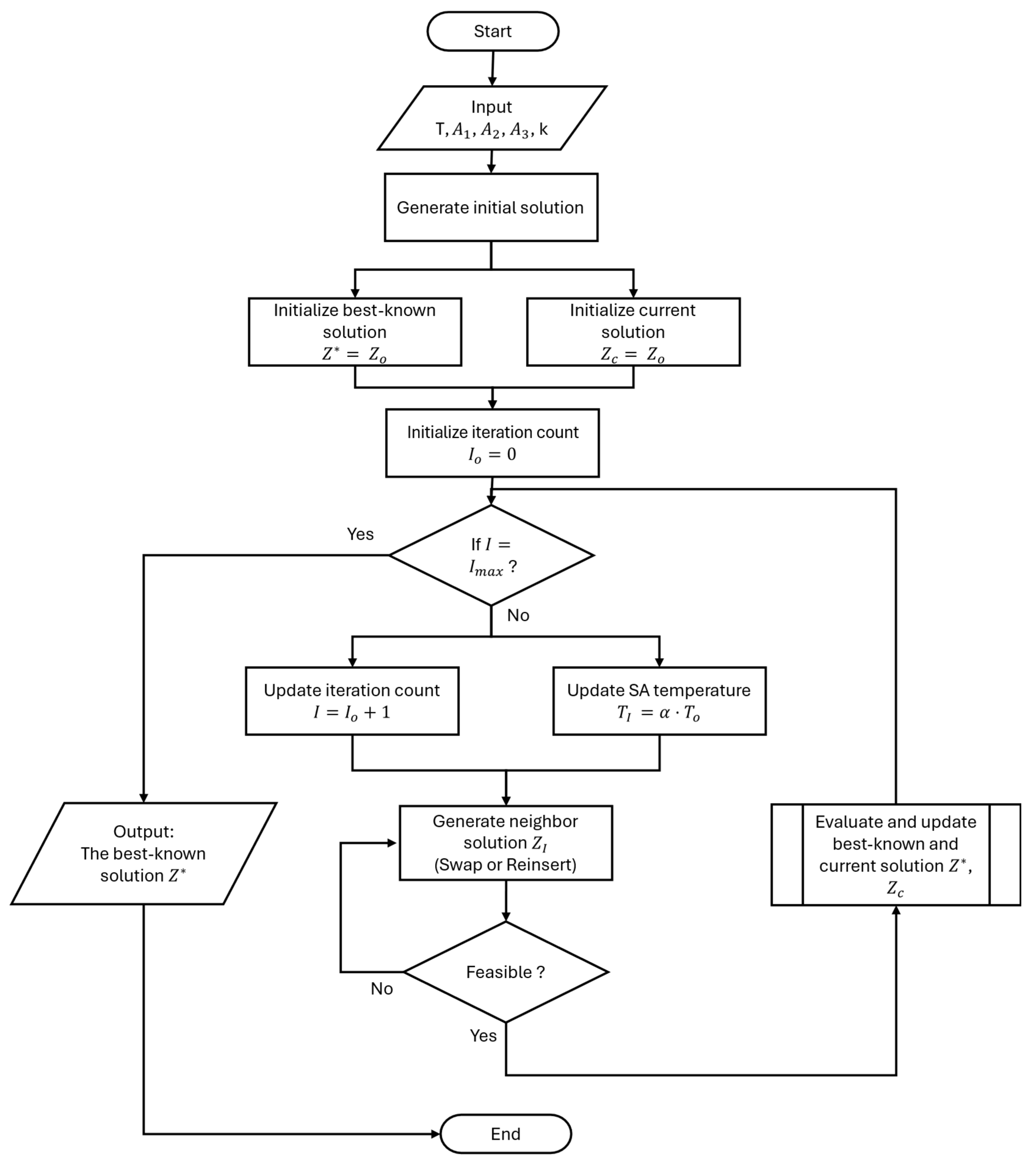
5. Simulated Annealing Algorithm

SA is a single-solution metaheuristic inspired by the physical process of annealing in metallurgy. The algorithm explores the solution space by probabilistically accepting not only improvements, but also worse solutions based on a temperature-controlled acceptance probability. This mechanism allows the search to escape local optima and converge toward a near-global optimum over time. It is well-suited for complex combinatorial problems, like RSRPP, as it can efficiently explore large search spaces and escape local optima [32,33].

5.1. Simulated Annealing Overview

The algorithm begins with an initial feasible solution and explores its neighborhood iteratively. If a neighboring solution improves the objective function, it is accepted. If the solution is worse, it may still be accepted with a probability defined by the Metropolis criterion:

$$P=\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\displaystyle \frac{\mathsf{\Delta }Z}{T}}\right)$$

(26)

where $\mathsf{\Delta }Z$ is the increase in the objective function value and $T$ is the current temperature.

The temperature decreases progressively throughout the process following a cooling schedule:

$$T_{I+1}=\alpha \cdot T_I$$

(27)

where $\alpha \in (0,1)$ is the cooling rate which controls the balance between exploration and exploitation, and I is the iteration. To summarize, the algorithm begins with an initial solution, which is iteratively refined through local modifications. Each iteration includes generating a neighbor solution, checking feasibility, and applying the Metropolis acceptance criterion. The process continues until the stopping criteria is reached. The framework for the SA algorithm is shown in Figure 6.

5.2. Solution Representation

In the SA framework, the solution of the RSRPP is defined as a mapping between available EMUs and sequences of scheduled trips. Each EMU is assigned a feasible sequence that may comprise scheduled arcs, supplemented by deadhead and maintenance arcs when needed to ensure continuity and compliance with mileage thresholds.

The solution is encoded using a list-based structure, where each list corresponds to a single EMU and contains the trip IDs it is scheduled to perform. This representation is memory-efficient and allows straightforward application of neighborhood operations (e.g., swap or reinsert), as well as rapid feasibility checks such as mileage tracking, temporal ordering, and arc connectivity.

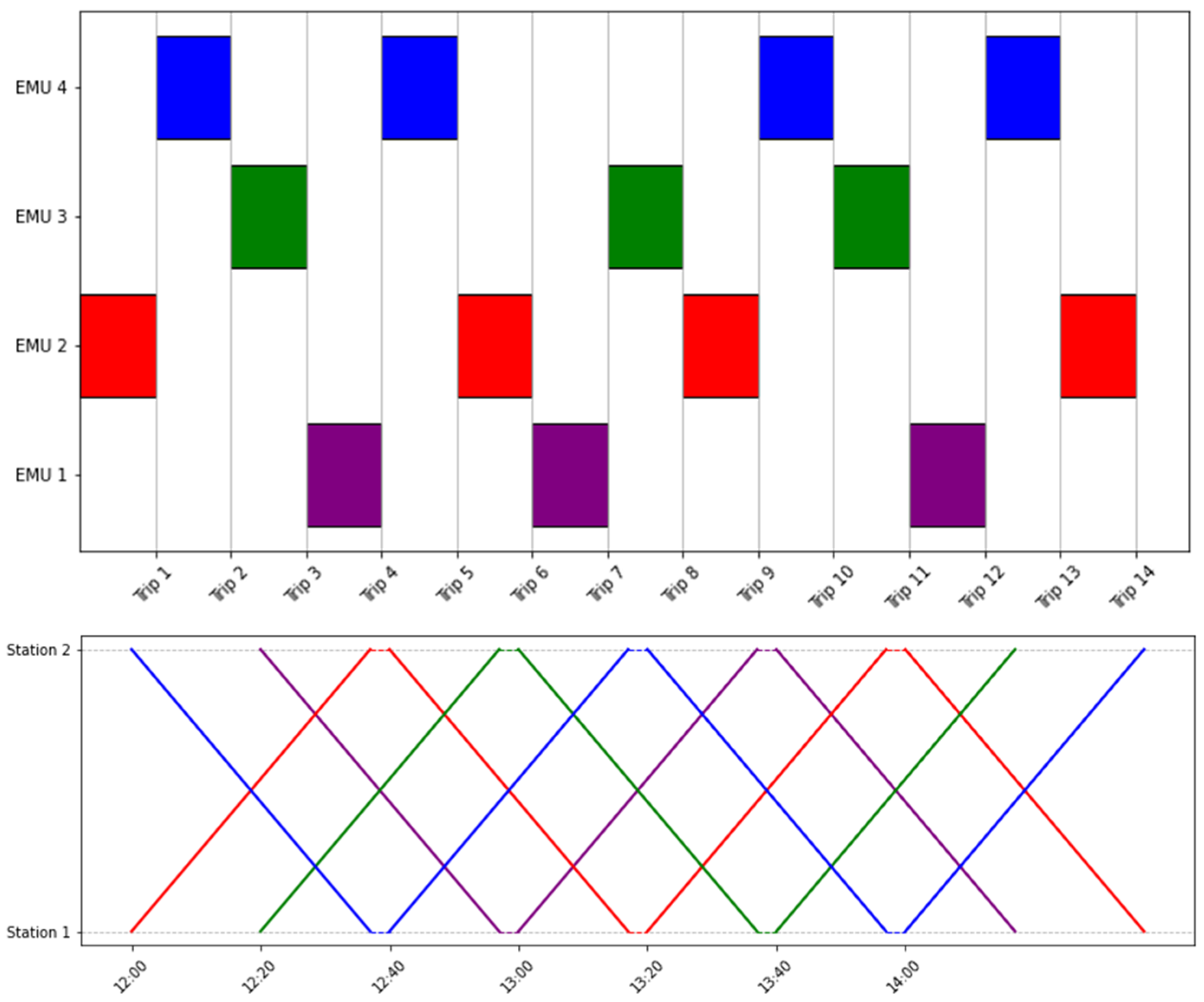
An example solution representation for a small instance with a one-day timetable and a single bidirectional line is illustrated in Figure 7. Each EMU (labeled E) is linked to a list of trip IDs it performs within the planning horizon. EMUs with no assigned trips are excluded from the figure for clarity. It is important to note that the trip IDs shown are not arranged chronologically; they denote only the trip identifiers, not departure time order.

5.3. Initial Solution Generation Using a Greedy Heuristic

The performance of metaheuristics, such as SA, is heavily affected by the quality of the initial solution. To ensure a feasible and reasonably good starting point, an Initial Solution Algorithm (ISA) was designed to construct an assignment of EMUs to scheduled trips while respecting mileage and maintenance constraints.

The ISA proceeds by iteratively assigning trips to EMUs based on earliest departure times and minimal deadhead distances. Each EMU’s rotation is extended by greedily appending trips that are reachable via either deadhead arcs or maintenance arcs, depending on the current mileage. The algorithm ensures feasibility by verifying connectivity and mileage thresholds at each assignment step.

Each EMU begins with its initial mileage value $r_k^{\mathrm{start}}$, and is assigned a sequence of trips starting from the earliest unassigned trip $T_i$. The algorithm then explores future trips that can be connected to T_i through deadhead or maintenance arcs. If the accumulated mileage does not exceed the maximum allowable threshold $r_k^{\max }$, a deadhead connection is used. Otherwise, a maintenance arc is considered. Upon successful assignment, the mileage is updated, and the shortage for that trip is computed as the difference between demand and EMU capacity. The process continues until no further assignments are feasible for the selected EMU, after which the next unassigned trip is handled.

The final output consists of the following:

• Solution mapping of EMUs to their assigned trip sequences;
• Arc type labels indicating whether arcs used are deadhead or maintenance;
• Number of denied passengers for each scheduled trip;
• Objective functions’ values capturing the total denied passengers and the number of EMUs used.

The pseudocode for the ISA is presented in

Table 3. Pseudocode for the initial solution generation algorithm.

	Input: Set of unassigned scheduled trips ($T$), set of scheduled arcs ($A_1$), set of deadhead arcs ($A_2$), set of maintenance arcs ($A_3$), set of available EMUs (K), maximum mileage threshold ($r_k^{\max }$)
1	$r_k=r_k^{\mathrm{start}}$                  // Initialize mileage for each EMU
2	$Z_o$ = {}, total denied passengers(s) = 0        //Initialize solution
3	while$T\ne \varnothing$:
4		Select earliest unassigned trip $T_i\in T$
5		Identify EMUs where the arc from $i_k$ to $T_i$ $\in$ $A_2$ or $A_3$
6		Select subset $K^{\ast }\subseteq \mathrm{K}$ with minimum distance
7		Choose $E_k\in K^{\ast }$ randomly
8		Assign $T_i$ to $E_k$, update ($T$, mileage, total denied passengers (s))
9		while $T$ $\ne \varnothing$:
10		Select the next trip $T_{i+1}$ in $E_k$ trip sequence where $\left(i,i+1\right)ϵA_2$
11		if $r_k+d_{\left(i,i+1\right)}\le r_k^{\max }$
12			Assign via deadhead arc, update mileage           Remove $T_{i+1}$ from $T$
13		elif $\left(i,i+1\right)ϵA_3$:
14			Assign via maintenance arc; reset mileage to 0           Remove $T_{i+1}$ from $T$
15		update total denied passengers (s), $Z_o$, and record arc type
16		Set current trip to $T_{i+1}$
17		Remove $T_{i+1}$ form $T$
18		end while
19		Remove $E_k$ from K
20	end while
21	Compute objective values [total denied passengers, number of used EMUs]
22	Return $Z_o$, arc type, objective values

. This constructive algorithm forms the foundation upon which the SA metaheuristic operates.

5.4. Neighbor Generation and Acceptance Criteria

In the proposed SA framework, neighborhood generation plays a critical role in exploring the solution space and guiding the search toward improved solutions. Two neighborhood operators are employed: Swap and Reinsert.

• Swap Operator: Randomly selects two trips assigned to different EMUs and exchanges their positions. This allows a global reshuffling of trips and encourages diversification in the search.
• Reinsert Operator: Selects a trip from the EMU with the least assigned trips and reinserts it into the sequence of another EMU that is currently utilized. This operator facilitates localized improvements by shifting workload.

The operator is selected randomly at each iteration with equal probability. After generating a neighbor solution, a feasibility check is applied. This involves first reordering the trip sequence by departure times, then, ensuring the existence of valid arcs (deadhead, or maintenance) between successive trips, and finally, verifying that cumulative mileage respects maintenance thresholds.

At the start, the best solution $Z^{\ast }$ is set to the initial solution $Z_o$. The iteration count starts at zero and for each iteration; both the iteration count and the temperature are updated. The temperature is updated by applying Equation (27). At each iteration of the SA algorithm, a neighbor solution is generated using either a swap or reinsert local search operator. A feasibility check is then carried out and another neighbor is produced in case of infeasibility. The solutions are evaluated according to the value of a fitness function, which in this study, is the same as the objective function value (same as Equations (1) and (2) from Section 4 used for the MILP). If the score (value of fitness function) for the obtained feasible neighbor solution $Z_I$ is better than $Z^{\ast }$, then the neighbor solution is accepted and both the current and best solutions $Z^{\ast }$, $Z_c$ are updated. Note that in the considered case, better means that $Z_I$ is lower than $Z^{\ast }$ since this is a minimization problem. If $Z_I$ is not better, then it can either be accepted with a probability P calculated by using Equation (26) or rejected. In case of acceptance, only $Z_c$ is updated, and in case of rejection, both $Z^{\ast }$, $Z_c$ remain unchanged. The stopping criteria for the SA algorithm was set to the max number of iterations $I_{max}$.

6. Results and Discussion

The MILP model was solved using GUROBI 11.0.0, and the SA algorithm was coded in Python 3.11. The computational study was executed on a Windows 64-bit workstation equipped with Intel(R) Xeon(R) Gold 6230R CPU 2.10GHz, 2.10 GHz (2 processors) with 128 GB RAM.

To the best of the authors’ knowledge, no standard instances exist for the RSRP problem with deadhead routing and maintenance scheduling in the literature. Section 6.1 details the instances adopted for the RSRP problem with deadhead routing and maintenance scheduling. The results for the MILP are presented in Section 6.2. Section 6.3 includes the performance results for the SA algorithm. The comparison between the MILP and SA algorithm is displayed in Section 6.4. Finally, Section 6.5 outlines concrete strategies that can be derived from the model’s findings.

6.1. Instances of the RSRP

All used benchmark instances were generated according to available public transport data from the Cairo Metro Network. Randomized instances were generated with fixed seeds to test the performance of the proposed approaches. Note that all maintenance locations were assumed to be at the start or the end of the metro line to fit with the modeling approach adopted. The passenger demand used in the instances was randomly estimated within a specific range (1500:2100) based on the available data. The values for the starting mileage for each of the available EMUs were also randomized within a certain range (1000:3500 km) based on the maintenance threshold and available data. The working hours for all scenarios start from 6 a.m. and the last train leaving is before 12 a.m. The timetable for each instance was set in two different settings. A trip is scheduled every 30 min for the first setting and every 15 min for the second. The planning horizon for the randomized instances is set at 1, 2, or 7 days. The number of available EMUs is varied based on the number of lines and scheduled trips. For each of the 12 randomized instances, the number of deadhead arcs, and maintenance arcs in the problem network are presented in

Table 4. Details for the 12 randomized instances.

Instance	Number of Lines	Number of Trips per Hour	Planning Horizon (Days)	Total Passenger Demand	Number of Available EMUs	Deadhead Arcs	Maintenance Arcs
1	1	2	1	124,951	15	3313	18,725
2			2	248,345		11,511	88,893
3			7	841,514		12,2017	1,171,551
4		4	1	245,166	20	11,372	94,420
5			2	485,237		41,768	460,207
6			7	1,683,604		475,500	6,306,176
7	2	2	1	243,388	30	7411	66,054
8			2	483,350		25,682	321,579
9			7	1,589,471		270,995	4,285,990
10		4	1	475,554	40	25,352	331,676
11			2	947,859		92,914	1,651,982
12			7	3,305,917		1,055,268	22,876,364

.

6.2. MILP Model Results

The MILP model was first solved with the first objective, which is minimizing total ratio of denied passengers to passenger demand and by extension the number of denied passengers. The time limit for solving each experiment was set to six hours. The solution time is reported in seconds. Gap % refers to the optimality gap reported by GUROBI at termination. The results for the 12 instances are displayed in

Table 5. Deterministic solution for single objective model with objective function (1).

Instance	Problem Size		Objective Value	Number of Denied Passengers	Gap (%)	Solution Time(s)
	Rows	Columns
1	137,182	22,266	0.304	631	0	13
2	609,670	100,604	0.476	986	0	538
3	7744888	1,293,700	2.266	4624	35	21,600
4	654186	99,741	0.497	1028	0	3009
5	3,064,620	489,432	0.884	1828	0	12,565
6	41,120,878	6,736,957	---	---	---	21,600
7	522,259	73,752	0.25	511	0	478
8	3,316,647	645,338	---	---	---	2584
9	41,708,510	8,401,618	---	---	---	21,600
10	3,737,325	685,503	1.32	2644	63.7	9389
11	16,851,859	3,273,665	---	---	---	21,600
12	221,244,113	44,403,495	---	---	---	21,600

, where the model was able to reach the optimum solution for less than half of the 12 instances with a maximum solution time of 12,565 s. For a single bidirectional line, the solver was able to solve instances with up to a two-day planning horizon. However, the solver was not able to reach a solution for any of the instances with a full week planning horizon and only obtained a solution for instance 3 with a gap of 35%. As for the instances with two bidirectional lines, an optimum solution was only obtained for instance 7 while for instance 10, the model was only able to reach a solution with a gap of 63.7% within the specified time limit. This also includes the scheduling of all maintenance activities for all used EMUs while minimizing the number of denied passengers. The absence of entries on the table is attributed to the lack of solutions within the time limit of 6 h.

As for the second objective of minimizing the number of EMUs used, out of the 12 instances, the solver was able to solve eight instances to optimality within a maximum of 1723 s;

Table 6. Deterministic solution for single objective model with objective function (2).

Instance	Problem Size		Objective Value	Gap (%)	Solution Time(s)
	Rows	Columns
1	137,182	22,266	4	0	9
2	609,670	100,604	4	0	62
3	7,744,888	1,293,700	5	0	1723
4	654,186	99,741	6	0	57
5	3,064,620	489,432	6	0	727
6	41,120,878	6,736,957	---	---	21,600
7	522,259	73,752	8	0	75
8	3,316,647	645,338	8	0	1034
9	41,708,510	8,401,618	---	---	21,600
10	3,737,325	685,503	12	0	727
11	16,851,859	3,273,665	---	---	21,600
12	221,244,113	44,403,495	---	---	21,600

. For the other four instances, the solver was not able to obtain a solution within the time limit of 6 h.

6.3. Simulated Annealing Algorithm Results

Although the MILP model formulated in Section 4 offers an exact solution to the RSRPP, it becomes computationally demanding for large-scale instances. As the number of trips, EMUs, and arcs increases, solving the MILP to optimality using commercial solvers may not be practical within reasonable time limits. In such a case, SA algorithm offers a potential alternative.

A set of experiments were conducted to explore the performance of the SA algorithm using different values for the algorithm parameters, T (initial temperature), $I_{max}$ (maximum number of iterations), and α (Equation (27)). A full factorial design was adopted with two levels for α, and three levels for both $I_{max}$ and

Table 7. The values for the SA algorithm parameters used at each experiment order.

Experiment Order	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
α	0.99									0.95
Imax	5000			10,000			20,000			5000			10,000			20,000
T of O1	0.2	0.6	1	0.2	0.6	1	0.2	0.6	1	0.2	0.6	1	0.2	0.6	1	0.2	0.6	1
T of O2	1	2	4	1	2	4	1	2	4	1	2	4	1	2	4	1	2	4

shows the values for the SA parameters used in this study. Note that O1 and O2 are objective 1 and objective 2 from the MILP, respectively. The SA algorithm was solved for the 18 different parameter combinations from the full factorial design for each of the 12 randomized instances. This was applied to both objectives and all the results from the 432 runs were recorded and analyzed.

6.3.1. Results When Minimizing Objective 1 (Total Ratio of Denied Passengers to Passenger Demand)

When minimizing Objective 1, as defined in Equation (1) in Section 4, which corresponds to minimizing the total ratio of denied passengers to passenger demand and by extension, the number of denied passengers, the best results obtained for each of the 12 test instances across all SA parameter configurations are presented in

Table 8. Results for the best objective obtained for each of the 12 instances when minimizing objective 1.

Instance	Number of Denied Passengers	Percentage of Denied Passengers	Number of Used EMUs	Solution Time (s)	α	Imax	T
1	631	0.50	7	8	-	-	-
2	986	0.40	7	13	-	-	-
3	3046	0.36	7	86	-	-	-
4	1028	0.42	11	14	-	-	-
5	1828	0.38	12	25	-	-	-
6	6620	0.39	12	98	-	-	-
7	511	0.21	11	27	0.99	10,000	0.6
8	970	0.20	11	89	0.99	20,000	1
9	10,913	0.69	13	329	0.99	20,000	0.2
10	1158	0.24	16	64	0.95	10,000	1
11	2063	0.22	19	228	0.99	20,000	0.2
12	15,263	0.46	23	855	0.95	20,000	1

. This table includes the minimum number of denied passengers observed for each instance, the corresponding percentage of denied passengers relative to the total passenger demand, and the parameter configuration at which these values were achieved. A complete breakdown of the results, including the number of denied passengers and solution time for all 18 configurations per instance, is provided in Appendix A, specifically in

Table A1. Total denied passengers value when minimizing objective 1.

α	Imax	T	I1	I2	I3	I4	I5	I6	I7	I8	I9	I10	I11	I12
0.99	5000	0.2	631	986	3046	1028	1828	6620	913	1307	18,510	1870	3096	21,178
		0.6	631	986	3046	1028	1828	6620	687	1542	25,494	2847	4253	21,341
		1	631	986	3046	1028	1828	6620	731	1239	17,278	1518	2930	20,551
	10,000	0.2	631	986	3046	1028	1828	6620	735	1139	35,464	1873	3788	17,679
		0.6	631	986	3046	1028	1828	6620	511	1179	22,256	2478	4235	17,746
		1	631	986	3046	1028	1828	6620	775	1423	26,831	2216	3682	18,346
	20,000	0.2	631	986	3046	1028	1828	6620	603	981	19,486	1206	2063	15,320
		0.6	631	986	3046	1028	1828	6620	708	990	23,768	1224	3116	17,111
		1	631	986	3046	1028	1828	6620	1312	970	21,573	1572	4273	17,744
0.95	5000	0.2	631	986	3046	1028	1828	6620	711	1608	31,004	1543	4151	18,363
		0.6	631	986	3046	1028	1828	6620	964	1699	22,225	1660	3519	20,546
		1	631	986	3046	1028	1828	6620	777	1361	14,220	1603	2813	22,424
	10,000	0.2	631	986	3046	1028	1828	6620	511	1337	24,575	1742	4785	18,957
		0.6	631	986	3046	1028	1828	6620	675	1474	28,460	1284	3013	18,284
		1	631	986	3046	1028	1828	6620	616	1380	22,666	1158	2314	19226
	20,000	0.2	631	986	3046	1028	1828	6620	552	1139	17,588	1518	2190	15,580
		0.6	631	986	3046	1028	1828	6620	669	1064	22,729	1269	2408	15,547
		1	631	986	3046	1028	1828	6620	884	1226	21,378	1526	2668	15,263
Mean			631	986	3046	1028	1828	6620	741	1281	23,084	1673	3294	18,400
Standard deviation			0	0	0	0	0	0	191	217	5149	454	824	2186

and

Table A2. Solve time (s) when minimizing objective 1.

α	Imax	T	I1	I2	I3	I4	I5	I6	I7	I8	I9	I10	I11	I12
0.99	5000	0.2	8	14	256	14	25	99	14	23	150	32	58	199
		0.6	8	14	425	14	26	101	14	22	132	32	59	186
		1	9	13	735	14	26	99	14	22	127	31	59	227
	10,000	0.2	17	29	147	28	52	190	28	45	274	65	111	595
		0.6	17	28	534	28	50	191	27	45	262	62	114	543
		1	17	26	146	27	50	224	27	45	263	65	107	455
	20,000	0.2	33	55	227	54	100	378	53	88	513	123	228	1210
		0.6	34	50	201	52	96	380	54	89	525	126	223	781
		1	30	52	256	57	94	384	53	89	477	126	223	1024
0.95	5000	0.2	8	13	186	15	27	98	14	23	127	33	49	225
		0.6	8	13	86	14	25	98	14	22	132	35	49	203
		1	9	13	132	17	26	105	15	23	116	31	47	194
	10,000	0.2	17	25	121	29	50	192	28	45	256	67	93	369
		0.6	17	26	126	29	51	214	28	45	261	66	87	381
		1	17	26	183	31	51	208	29	47	261	64	88	428
	20,000	0.2	631	986	3046	1028	1828	6620	552	1139	27,254	1518	2190	15,580
		0.6	631	986	3046	1028	1828	6620	669	1064	25,609	1269	2408	15,547
		1	631	986	3046	1028	1828	6620	884	1226	25,211	1526	2668	15,263

.

The SA algorithm was able to solve all instances within a reasonable computation time, which ranged from 8 s to 855 s. For the first six instances, all parameter configurations yielded the same objective value, which coincided with the optimal solutions obtained by the MILP model. The consistency in results for these instances can be attributed to their relatively small size and the simplicity of the objective structure, which limits the number of local optima. In these cases, the variation in SA parameters affected only the runtime, not the final solution quality. However, for the remaining instances—namely, Instances 7 to 12—both the solution time and the number of denied passengers varied depending on the parameter configuration. These instances involved more trips and EMUs, which increased the complexity of the solution space and made the algorithm more sensitive to changes in the cooling schedule and the number of iterations. This sensitivity is evident in the distribution of results.

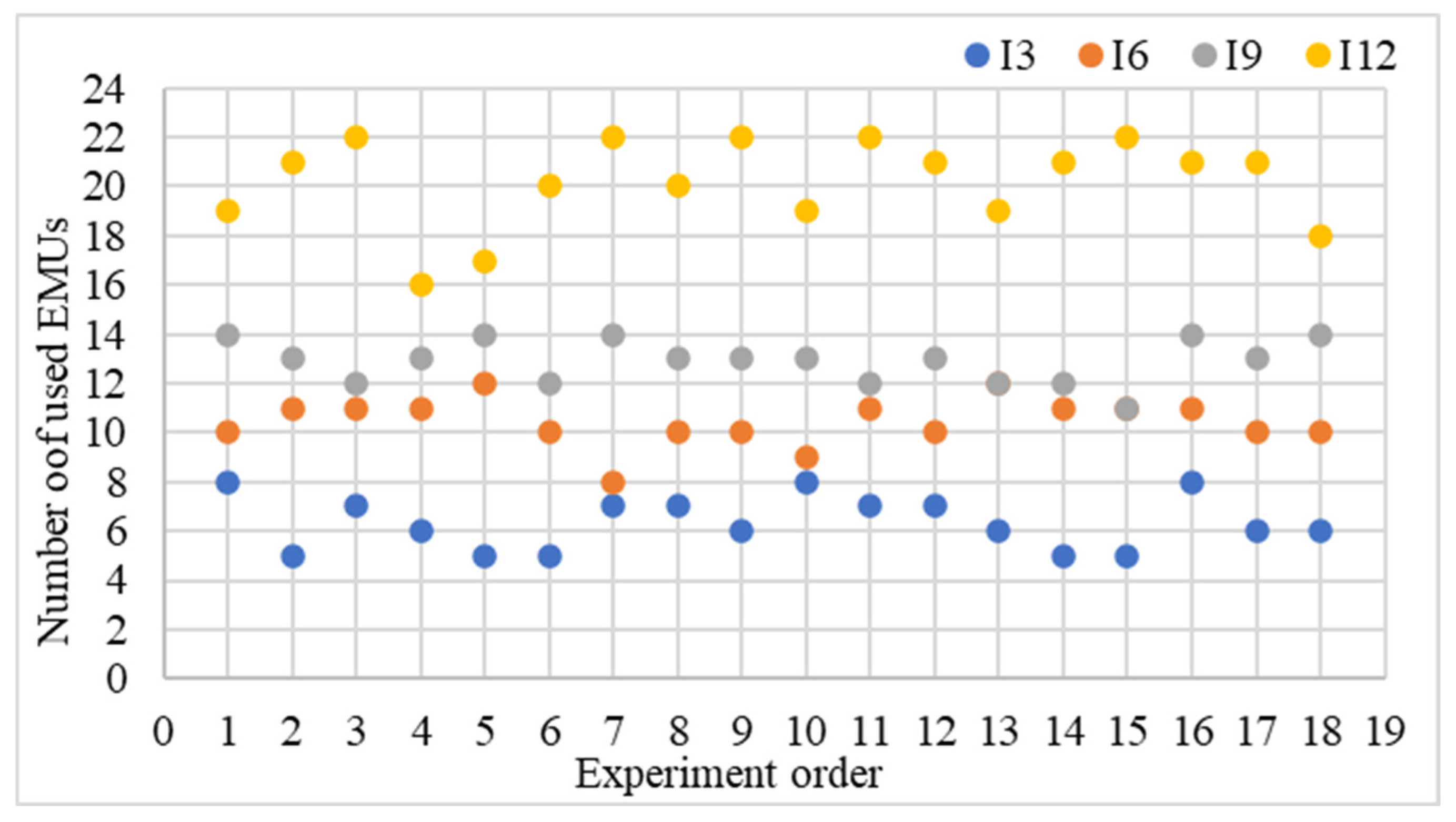
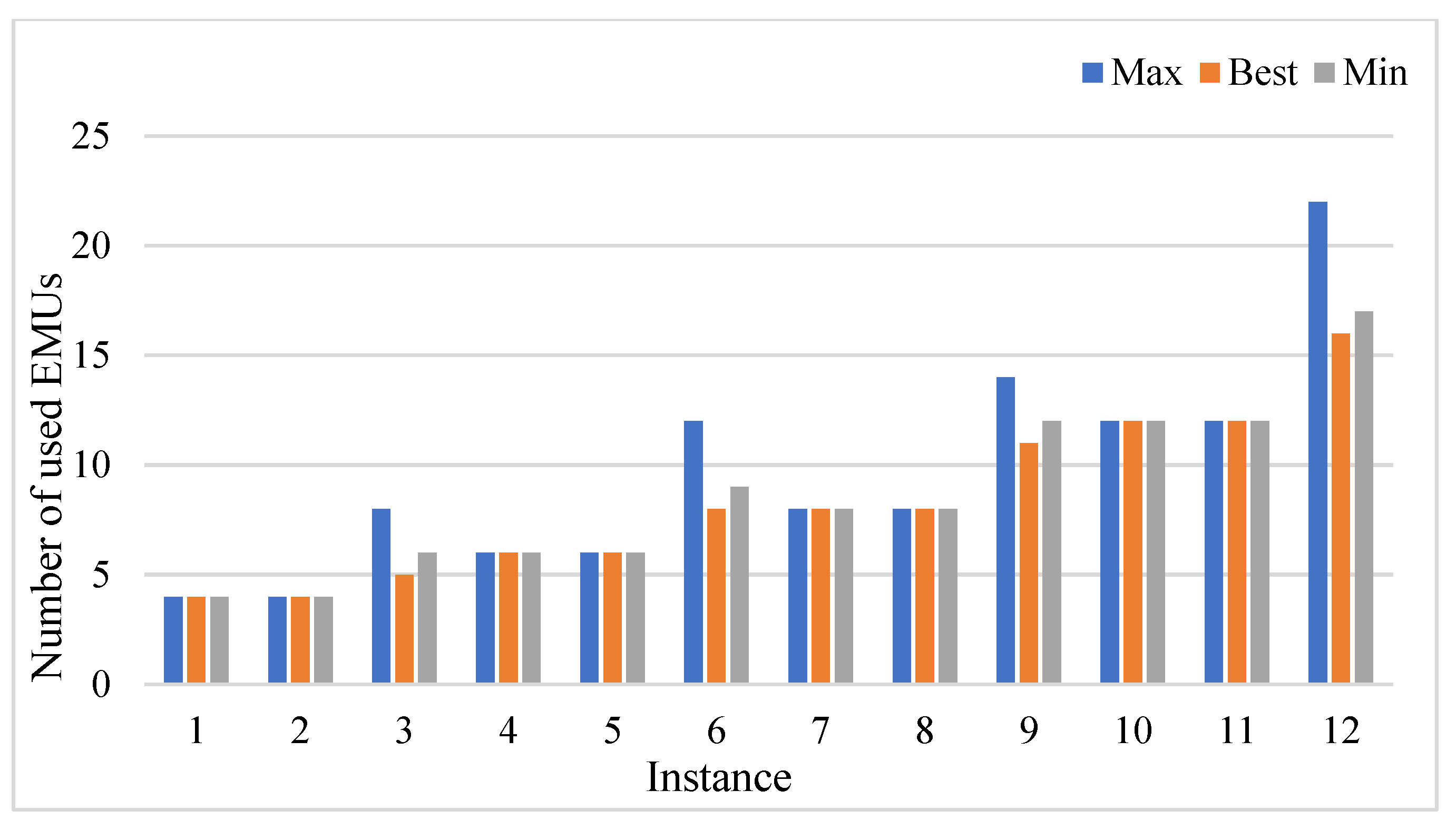
Figure 8 displays the variation in the number of denied passengers for Instances 7 to 12 across all parameter configurations. For instances 1 to 5, their objective values were identical across all runs. Figure 9 displays only the best value and the two values with the maximum and minimum difference from the best value. Instances 9 and 12 show relatively higher variations which may be attributed to the fact that the planning horizon for both instances is one week. The planning horizon for the other shown instances is either 1 or 2 days. The maximum observed percentage of denied passengers across all experiments was 0.69%, while the minimum was 0.20%. These results demonstrate that the proposed SA approach provides a reliable and effective solution to the RSRPP delivering high-quality results even for instances of significant scale and complexity. Here, $\alpha \in (0,1)$ is the cooling rate, $I_{max}$ is the maximum number of iterations, and T is the initial temperature.

6.3.2. Results When Minimizing Objective 2 (Number of Used EMUs)

As for Objective 2, which aims to minimize the number of used EMUs as formulated in Equation (2), the best results obtained for each of the 12 test instances across all SA parameter configurations are presented in

Table 9. Results for the best objective obtained for each of the 12 instances when minimizing objective 2.

Instance	Number of Used EMUs	Number of Denied Passengers	Percentage of Denied Passengers	Solution Time (s)	α	Imax	T
1	4	631	0.50	4	-	-	-
2	4	986	0.40	6	-	-	-
3	5	4852	0.58	27	0.99	10,000	2
4	6	1028	0.42	5	-	-	-
5	6	1828	0.38	9	-	-	-
6	8	27,087	1.61	2218	0.99	20,000	1
7	8	2414	0.99	5	-	-	-
8	8	4727	0.98	9	-	-	-
9	11	32,974	2.07	1046	0.95	10,000	4
10	12	4961	1.04	12	-	-	-
11	12	13,667	1.44	21	-	-	-
12	16	63,578	1.92	1903	0.99	10,000	1

. For each instance, the table reports the minimum number of EMUs used, the associated solution time, and the parameter configuration at which this result was achieved. More detailed results, including the number of denied passengers and the corresponding computation times for each of the 18 parameter configurations, are provided in Appendix A (

Table A3. Number of used EMUs when minimizing objective 2.

α	Imax	T	I1	I2	I3	I4	I5	I6	I7	I8	I9	I10	I11	I12
0.99	5000	1	4	4	8	6	6	10	8	8	14	12	12	19
		2	4	4	5	6	6	11	8	8	13	12	12	21
		4	4	4	7	6	6	11	8	8	12	12	12	22
	10,000	1	4	4	6	6	6	11	8	8	13	12	12	16
		2	4	4	5	6	6	12	8	8	14	12	12	17
		4	4	4	5	6	6	10	8	8	12	12	12	20
	20,000	1	4	4	7	6	6	8	8	8	14	12	12	22
		2	4	4	7	6	6	10	8	8	13	12	12	20
		4	4	4	6	6	6	10	8	8	13	12	12	22
0.95	5000	1	4	4	8	6	6	9	8	8	13	12	12	19
		2	4	4	7	6	6	11	8	8	12	12	12	22
		4	4	4	7	6	6	10	8	8	13	12	12	21
	10,000	1	4	4	6	6	6	12	8	8	12	12	12	19
		2	4	4	5	6	6	11	8	8	12	12	12	21
		4	4	4	5	6	6	11	8	8	11	12	12	22
	20,000	1	4	4	8	6	6	11	8	8	14	12	12	21
		2	4	4	6	6	6	10	8	8	13	12	12	21
		4	4	4	6	6	6	10	8	8	14	12	12	18
Mean			4	4	6	6	6	10	8	8	13	12	12	20
Standard deviation			0	0	1	0	0	1	0	0	1	0	0	2

and

Table A4. Solve time (s) when minimizing objective 2.

α	Imax	T	I1	I2	I3	I4	I5	I6	I7	I8	I9	I10	I11	I12
0.99	5000	1	4	6	394	5	9	538	6	9	511	12	21	1135
		2	4	6	14	5	9	549	6	9	583	12	21	950
		4	4	6	317	5	9	561	6	9	504	12	21	954
	10,000	1	7	12	868	10	18	1135	11	18	1022	25	42	1903
		2	7	11	27	10	17	1047	11	18	1020	24	42	1879
		4	7	12	702	10	17	1189	11	18	1133	24	42	1857
	20,000	1	14	23	1422	20	35	2218	23	35	2050	49	84	3895
		2	14	23	1187	20	35	2296	22	36	2089	49	84	3698
		4	15	23	1552	21	35	2145	22	35	2092	49	84	3704
0.95	5000	1	4	6	302	5	9	522	6	9	515	12	21	955
		2	4	6	337	5	9	619	5	9	688	12	21	927
		4	4	6	320	5	9	531	6	9	508	12	21	980
	10,000	1	7	12	616	10	18	1106	11	18	1038	25	42	1916
		2	7	12	28	10	17	1099	11	18	1052	25	42	1861
		4	7	12	27	10	18	1045	11	18	1046	24	42	1858
	20,000	1	15	23	1353	21	35	2325	22	35	2040	49	84	3714
		2	14	23	1249	20	35	2210	22	36	2050	49	84	3707
		4	15	23	1426	20	36	2210	22	36	2283	49	84	3780

, respectively).

The SA algorithm was able to solve all instances within a reasonable time frame, with solve times ranging from 4 s to 2218 s. For instances with a planning horizon of one or two days, parameter variation affected only the solve time, and the solution quality remained unchanged across all configurations. In these cases, the algorithm consistently identified the optimal number of EMUs, matching the results obtained by the MILP model. In contrast, for instances involving a full-week planning horizon, variations in parameter settings impacted not only the runtime but also the final objective value. This sensitivity to the search parameters reflects the increased complexity and size of the solution space in longer planning horizons. As the number of feasible sequences increases, the effectiveness of the cooling rate and iteration budget in exploring the solution space becomes more significant. Figure 10 illustrates the variation in the number of used EMUs across all 18 parameter configurations for selected instances. It highlights how parameter sensitivity increases with problem scale, particularly for Instance 12, which shows the widest range in EMU usage. Figure 11 complements this analysis by showing, for each instance, the best solution as well as the two configurations that yielded the most significant positive and negative deviations from that solution. The observed patterns confirm that for more complex instances, proper tuning of the SA parameters is critical to achieving effective fleet minimization without compromising service feasibility.

To determine the best value for each of the SA algorithm parameters when minimizing objective (1) (total ratio of denied passengers to passenger demand), the average percentage of denied passengers at each of the parameter combinations was calculated. The percentage of denied passengers at each of the 12 instances was obtained and then the average value for each of the 18 combinations was recorded in

Table 10. The average percentage of denied passengers and the average EMU usage percentage at each of the different SA parameter combinations.

Experiment Order	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
Average Percentage of denied passengers	0.47	0.52	0.44	0.44	0.46	0.47	0.35	0.39	0.46	0.47	0.50	0.46	0.46	0.41	0.40	0.36	0.37	0.40
Average EMU usage percentage	35.3	34.2	35.3	33.8	34.1	33.3	34.6	34.7	34.6	34.7	35.3	34.9	34.5	34.0	33.9	36.2	34.4	34.0

. As for objective (2) (number of used EMUs), to be able to compare different instances with different sizes, the EMU usage percentage for each instance was calculated for each of the 18 parameter combinations. The EMU usage percentage here is calculated from the ratio between the number of used EMUs and the total number of available EMUs. According to the minimum values for the average percentage of denied passengers and the average EMU usage percentage, the best parameter combination based on the available results was selected. Based on the results in Table 10, the recommendation for the best parameter combination of α, $I_{max}$, and T for objective (1) is 0.99, 20,000, and 0.2, while for objective (2) it is 0.99, 10,000, and 4.

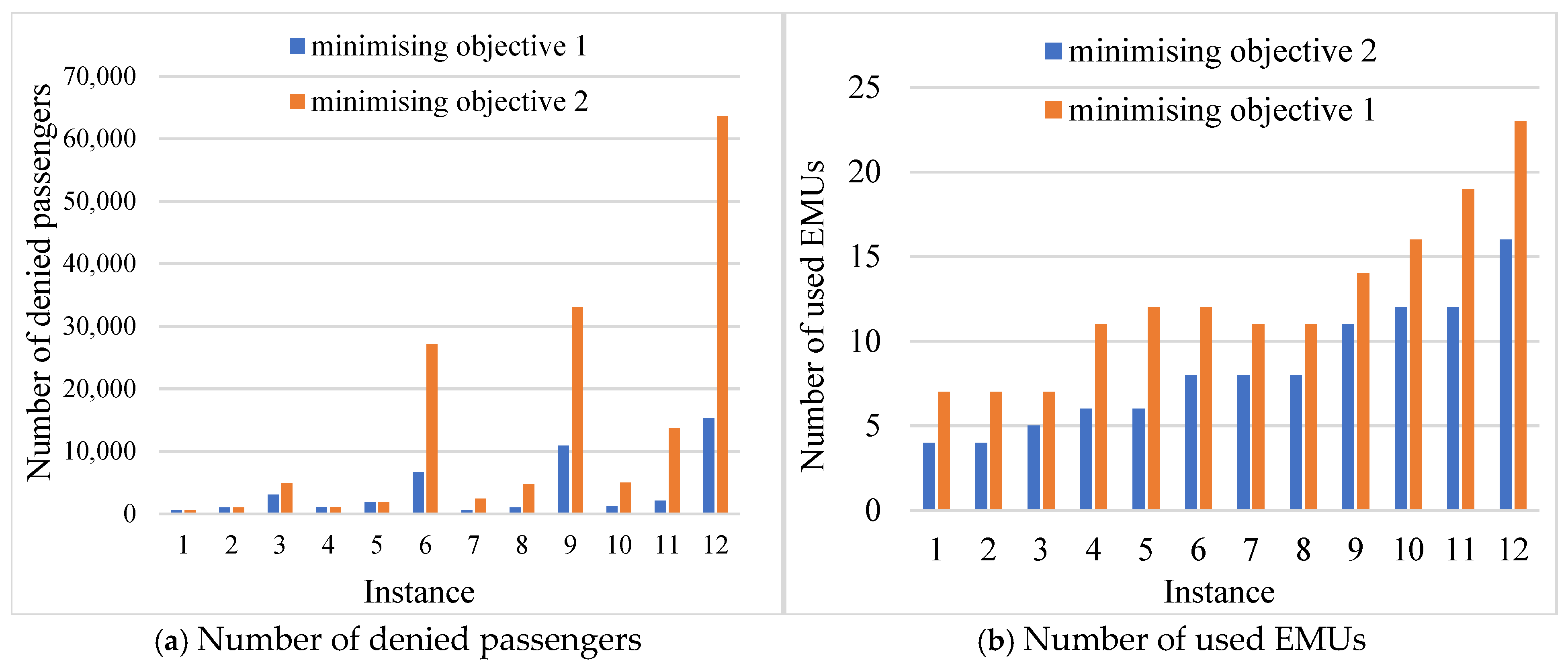
To highlight the trade-off between the two objectives adopted in this study, Figure 12 illustrates the values for the number of denied passengers and the number of used EMUs when the objective or fitness function is switched between minimizing denied passengers and minimizing the number of EMUs. The figure reveals that the solution outcomes differ substantially depending on the optimization goal. The variation in the number of used EMUs reached up to 100%, while the variation in the number of denied passengers peaked at 526%. These results underscore the inherent tension between operational efficiency and passenger service quality. When the objective is to reduce the number of EMUs, the algorithm sacrifices passenger satisfaction to a larger extent. Conversely, when minimizing denied passengers, additional rolling stock is deployed to meet the demand. It is also evident that for Instances 1, 2, 4, and 5, the number of denied passengers remained unchanged across both objectives. This consistency may be attributed to the relatively small size and lower complexity of these instances, which limits the solution space and the potential for trade-off-induced variability.

6.3.3. An Illustrative Case Study

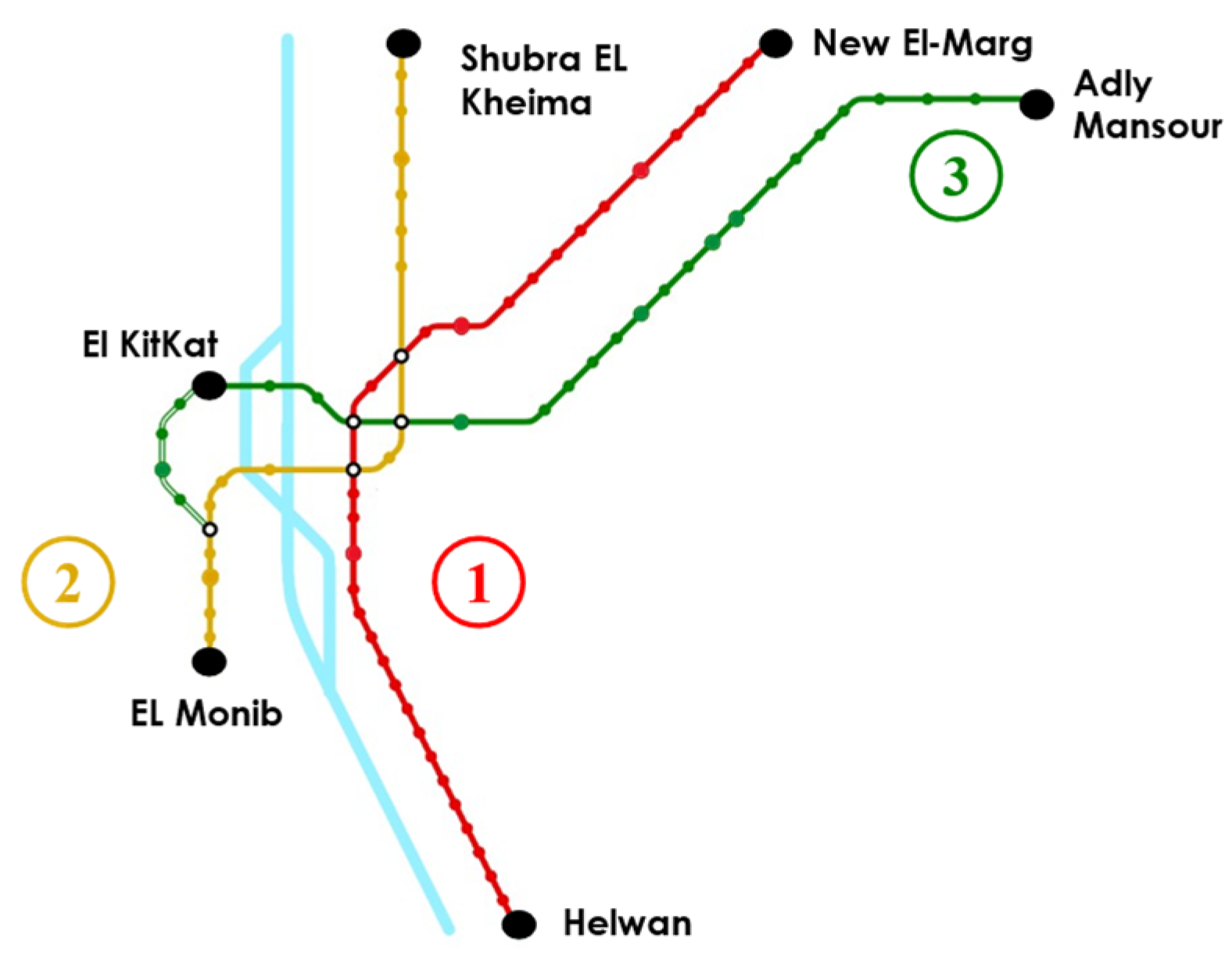
The Cairo Metro Network as shown in Figure 13 includes line 1 (red line) which consists of 35 stations and is about 44 km long. Line 2 (yellow line) covers a distance of about 21.6 km and has 20 stations. Finally, line 3 (green line), which is still being expanded has 18 operational stations spanning the length of 17.7 km.

The SA algorithm was used to solve the RSRP problem for a full week timetable for the Cairo Metro Network including all three lines.

Table 11. Case study input’s details.

Number of Lines	Number of Trips Per Hour	Planning Horizon (Days)	Number of Available EMUs	Total Passenger Demand
3	6	7	60	8,350,554

shows the details for the case study. The first daily trip starts at 5 am while the last trip starts before 12 am with trip scheduled every 10 min. This means that for each of the three lines, there are six trains leaving each hour. The total number of trips for the full week is about 4580 trips.

Table 12. Results for the case study when minimizing objective 1 and objective 2 separately.

	Number of Denied Passengers	Number of Used EMUs	Solve Time (s)	α	Imax	T
Minimizing objective 1	126,074	55	4930	0.99	20,000	0.2
Minimizing objective 2	145,469	51	5400	0.99	10,000	2

shows the values for the number of denied passengers, number of EMUs used, and solve time for the case study when minimizing objective 1 and objective 2. The values used for the SA parameters are also shown in the table. The SA algorithm was able to provide satisfactory solutions in both cases with a full week plan for the assignment, routing, and maintenance scheduling within a maximum of 5400 s. Considering the problem’s large size, Figure 14 shows solution representation only for the first ten trips in the trip sequence for EMUs 1 to 5 when optimizing objective 2.

6.4. Comparison Between MILP and SA Algorithm

The results obtained from the SA algorithm and the MILP model for the 12 test instances are summarized in

Table 13. Comparative analysis of MILP and SA solution approaches for the 12 instances: solution outputs and solution time.

Instance	Min O1						Min O2
	MILP			SA			MILP			SA
	Number of Denied Passengers	Gap %	Solution Time (s)	Number of Denied Passengers	Gap %	Solution Time (s)	Number of Used EMUs	Gap %	Solution Time (s)	Number of Used EMUs	Gap %	Solution Time (s)
1	631	0	13	631	0	8	4	0	9	4	0	4
2	986	0	538	986	0	13	4	0	62	4	0	6
3	4624	35	21,600	3046	0	86	5	0	1723	5	0	27
4	1028	0	3009	1028	0	14	6	0	57	6	0	5
5	1828	0	12,565	1828	0	25	6	0	727	6	0	9
6	---	---	21,600	6620		98	---	---	21,600	8		2218
7	511	0	478	511	0	27	8	0	75	8	0	5
8	---	---	2584	970		89	8	0	1034	8	0	9
9	---	---	21,600	14,220		523	---	---	21,600	11		1046
10	2644	63.7	9389	1158		64	12	0	727	12	0	12
11	---	---	21,600	2063		228	---	---	21,600	12		21
12	---	---	21,600	15,263		855	---	---	21,600	16		1903

. A comparison of the objective values and computation times clearly demonstrates the superior performance of the SA algorithm in solving the RSRPP with integrated deadhead routing and maintenance scheduling. The SA algorithm consistently achieved optimal solutions for all instances in which the MILP model also found the optimum. Furthermore, for instances where the MILP solution process was time-intensive or limited by solver capabilities, the SA algorithm was able to produce high-quality solutions within significantly reduced computational times. The difference in solution time was especially pronounced in larger instances, where the SA algorithm exhibited considerable efficiency gains. This computational advantage highlights the scalability and practical applicability of the proposed SA approach, particularly in real-world operational contexts where time constraints and solution feasibility are critical. The results confirm that while the MILP model provides theoretical guarantees of optimality, the SA algorithm offers a computationally tractable and effective alternative, especially for large-scale and time-sensitive urban rail scheduling problems.

A key factor contributing to the SA algorithm’s performance is the design of its neighborhood operators. The use of problem-specific operations—such as swap and reinsert—enables the algorithm to locally adjust trip sequences in a way that preserves feasibility with respect to mileage, maintenance, and timing constraints. These operators avoid the combinatorial explosion that exact solvers face when modeling large-scale instances with binary variables and multiple routing constraints. By operating on a list-based solution structure, the SA algorithm can rapidly explore feasible alternatives without re-solving the entire model. This targeted and adaptive search strategy gives SA a distinct advantage over MILP methods when solving large, complex, or tightly constrained rolling stock rotation problems.

6.5. Practical Implications for Urban Rail Operators

The findings of this study offer several practical insights for urban rail transit agencies and metro network operators:

• Optimized EMU Allocation: The proposed MILP and SA frameworks can help decision-makers efficiently assign rolling stock across multiple trips, ensuring full coverage of high-demand services while minimizing excess vehicle usage.
• Deadhead Reduction: By explicitly modeling and optimizing deadhead movements, operators can reduce non-revenue mileage, thereby lowering energy consumption and operational costs.
• Integrated Maintenance Scheduling: The integration of mileage-based maintenance into trip assignment enables more proactive planning of vehicle availability, reducing unscheduled downtime and extending asset life.
• Scalability for Planning Tools: The SA algorithm provides a scalable decision support tool that transportation authorities can use to generate robust rolling stock plans for large networks within an acceptable compute time.

These implications are especially relevant for dense urban systems, like the Cairo Metro, where rolling stock resources are constrained and service demand is constantly increasing. The modeling approach can be adapted for use in long-term investment planning, operational simulation, and disruption response strategies.

7. Conclusions

In this study, the complex challenges of urban rail transit operations have been explored, with a specific focus on the efficient management of rolling stock rotation, which includes deadhead routing and maintenance scheduling. A MILP model tailored for the Cairo Metro network was introduced. The model was first solved as a single objective model to minimize the number of denied passengers and the number of used EMUs separately. Computational experiments were conducted on multiple randomized instances derived from real-world data. The results demonstrated the MILP model’s capability in producing optimum solutions for instances with a shorter planning horizon. However, due to the computational complexity of the exact methods, especially for larger instances, a SA metaheuristic algorithm was proposed incorporating a structured solution representation and custom local search operators to ensure feasibility with respect to mileage and maintenance constraints.

The computational study confirmed the effectiveness of the SA algorithm in solving both single-objective formulations: minimizing denied passengers and minimizing the number of used EMUs. The SA algorithm obtained solutions for all 12 instances within a maximum of 2218 s. For larger instances and a full-week case study covering the entire Cairo Metro Network, the SA algorithm generated feasible, high-quality solutions in significantly less time than the MILP approach. Moreover, the results emphasized the inherent trade-off between passenger service levels and operational resource utilization.

The adopted approach successfully addressed the issues of incorporating maintenance scheduling into the RSRP problem for the URT, and the exploration of implementing SA as the solution approach. The limitation of this study includes the limited network size of two lines only, in addition to not considering the physical limitations of the stations’ capacity to accommodate multiple EMUs. Another limitation for the modeling approach is the assumption that the maintenance location is at the starting or ending station for the metro line, which is not necessarily the real case. However, this assumption has limited impact on the case study results. In the largest instance (7-day horizon), only one out of three maintenance locations was affected, and scheduled maintenance activities occurred infrequently in smaller instances. The additional deadhead distance due to this assumption was estimated to be less than 5% of the total deadhead mileage.

Future research directions include the exploration of advanced exact or hybrid solution methods, such as Benders Decomposition, Branch-and-Price, and Column Generation, to further improve scalability. Metaheuristics, like Adaptive Large Neighborhood Search (ALNS) or Genetic Algorithms, could also be adapted to enhance solution diversity and convergence. Moreover, incorporating additional operational constraints—such as maintenance depot capacity, crew availability, dynamic passenger demand patterns, rush-hour constraints, and time-dependent demand profiles—could lead to more realistic and implementable planning outcomes.

In addition, future studies may explore the integration of broader sustainability objectives, such as energy efficiency, carbon emission reduction, and passenger wellbeing, into the planning framework. Embedding such dimensions would allow the model to support both operational and environmental goals in line with modern urban transport policies.

Another promising direction is the differentiation of line-specific operational characteristics, including variations in maintenance costs, energy consumption, passenger density, and urban integration challenges across metro lines. Accounting for such heterogeneity would enhance the model’s adaptability to complex, real-world rail networks, like the Cairo Metro, and improve its usefulness for strategic infrastructure planning.