Abstract
Background: The rapid growth of international maritime trade has intensified operational challenges at marine terminals due to increased interaction between vessels, trucks, and trains. Key issues include berth congestion, inefficient truck arrivals, and underutilization of terminal resources. Ensuring coordinated planning among transport modes and fostering collaboration between stakeholders such as vessel operators, logistics providers, and terminal managers is critical to mitigating these inefficiencies. Methods: This study proposes a multi-agent, multi-objective coordination model that synchronizes vessel berth allocation with truck appointment scheduling. A solution method combining prioritized planning with a neighborhood search heuristic is introduced to explore Pareto-optimal trade-offs. The performance of this approach is benchmarked against well-established multi-objective evolutionary algorithms (MOEAs), including NSGA-II and SPEA2. Results: Numerical experiments demonstrate that the proposed method generates a greater number of Pareto-optimal solutions and achieves higher hypervolume indicators compared to MOEAs. These results show improved balance among objectives such as minimizing vessel waiting times, reducing truck congestion, and optimizing terminal resource usage. Conclusions: By integrating berth allocation and truck scheduling through a transparent, multi-agent approach, this work provides decision-makers with better tools to evaluate trade-offs in port terminal operations. The proposed strategy supports more efficient, fair, and informed coordination in complex multimodal environments.
1. Introduction
The unprecedented growth of international maritime trade over the last three decades has resulted in significantly increased cargo volumes, heavily affecting marine terminal operations globally. Ports face daily issues such as congestion, air pollution, and delays that hinder their effectiveness and competitiveness. During peak hours, irregular truck arrivals and equipment shortages on the landside as well as increased vessel traffic on the seaside exacerbate these problems and highlight operational inefficiencies. These problems can create a domino effect on other port activities, further reducing productivity [1].
Port operations inherently involve a multimodal aspect because they serve as critical hubs where different transportation modes, such as maritime, road, rail, converge to facilitate the movement of goods. Hence, the aforementioned issues can be addressed by enabling terminals’ transition towards an advanced multimodal transport system that leverages digital technologies and cooperation across stakeholders. Achieving coordination within multimodal systems requires streamlining administrative boundaries, fostering flexible and polycentric forms of management across modes, and increasing system resilience as emphasized by the Strategic Transport Research and Innovation Agenda [2]. Effective coordination is crucial because of the diverse and often conflicting goals of different stakeholders, varying private and public values, and differing preferences that must be harmonized to optimize the overall system performance.
Coordination among stakeholders in a multimodal marine terminal can be achieved across strategic, tactical, and operational levels. At the strategic level, stakeholders, including shipping lines, terminal operators, and logistics companies, can engage in collaborative planning to align long-term goals and investments. At the tactical level, coordination can be enhanced through data sharing among stakeholders and collaborative decision support systems that facilitate day-to-day operational decisions concerning interrelated activities, such as berth allocation, truck scheduling, and cargo processing. Tactical planning assumes some degree of information system integration and many ports already use systems such as Port Community Systems (PCSs). Operational coordination further involves real-time decisions and the interplay of various actors, including not only terminal operators and carriers but also port authorities, tug services, pilots, truck companies, and shippers.
This study focuses on the coordination of multimodal terminal operations at a tactical level, an area previously explored in works such as [3,4]. However, these studies often rely on a fixed set of rules and centralize decision-making around a single actor. This overlooks the inherently distributed nature of coordination in multimodal terminals, where numerous independent stakeholders operate with distinct objectives, constraints, and procedures. Additionally, terminal planning is typically multi-objective, further complicating coordination and raising critical questions about how to ensure fairness and transparency in decision-making processes, issues that remain insufficiently addressed in the literature [5]. These observations highlight a clear gap, namely the lack of distributed modeling approaches that reflect the autonomy of different actors while enabling fair, multi-objective coordination in port terminal operations.
To address this, the paper sets as its main objective developing a novel approach to model collaboration among terminal stakeholders in a distributed manner using a Multi-Agent System (MAS) framework. This approach aims to tackle the challenge of synchronizing vessel arrivals with truck scheduling in order to reduce delays and congestion in a coordinated manner. In addition, the study seeks to support fair and transparent multi-objective decision-making by applying Pareto optimality and to develop an effective solution method that combines prioritized planning with neighborhood search to enhance computational performance. This combination of distributed coordination, multi-objective fairness, and optimization represents a novel and comprehensive approach not yet explored in existing terminal operations literature.
The proposed system models stakeholder collaboration through an MAS approach, integrating data (e.g., arrival schedules) from actors (e.g., logistics companies) and modes (e.g., vessels, trucks) to facilitate distributed, multi-objective planning. Pareto optimal solutions are sought to promote fairness among actors, with the terminal acting as an external coordinator responsible for the orchestration of different agents. A novel algorithm is developed based on prioritized planning in combination with a neighborhood search heuristic algorithm to enhance solution quality. The algorithm’s performance is benchmarked against established multi-objective optimization algorithms, demonstrating its ability to produce more Pareto front contributions and increased hypervolume in a range of simulated terminal scenarios.
The rest of this paper is organized as follows. Section 2 provides an overview of the problem setting and modeling choices to be employed for this supply-chain-related problem. Section 3 and Section 4 provide a formal description of the model and the solution methodologies used to enhance the collaborative scheduling. Section 5 presents numerical results to assess the added value of the proposed approach for a case study relating to medium-sized terminals. Finally, Section 6 provides conclusions and future research avenues.
2. Problem Description and Modeling Approach
2.1. Problem Description
Scheduling operations for multimodal freight transport in a synchronized manner involves effectively addressing the needs and objectives of multiple stakeholders with contrasting agendas. In this study, the problem revolves around the interactions between three distinct actors forming a multimodal chain, in an environment similar to the one depicted in Figure 1.
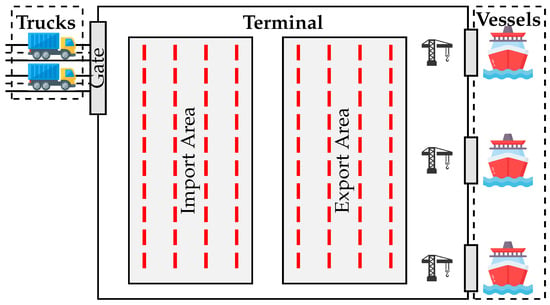
Figure 1.
Terminal layout for the examined supply chain.
The examined problem centers on synchronizing two interdependent processes: truck scheduling through an appointment system and berth allocation for inbound vessels. These processes share limited terminal resources and must be planned fairly and efficiently in a distributed environment where actors have conflicting objectives. Within this problem, the first actor is the vessels, which generate traffic from the seaside and expect quick access to a compatible berth and timely exit from the port to continue to subsequent destinations. The second actor is the logistics companies, which generate landside traffic by dispatching trucks to the terminal to pick up or deliver cargo associated with the incoming vessels. The decision making of logistics companies is centered around reducing their deviation cost from their desired processing time-period arising from potential delays in vessel arrivals and departures or truck congestion. Finally, the terminal is acting as an intermediate point in the multimodal chain, orchestrating the transition between different transportation modes and processing the demand. The terminal is also expected to ensure that certain service levels are maintained by tracking Key Performance Indicators (KPIs). Such KPIs include the maximum arrival rate of trucks per hour, cargo levels in the storage areas, as well as limits related to resources such as internal vehicles to perform drayage operations.
The system’s actors are interconnected since they share resources such as berths, cargo handling equipment, and arrival windows. The requirement to synchronize processes among several stakeholders, who can have competing goals and little knowledge of one another’s operations, further emphasizes the distributed aspect and need for distributed modeling methodology for this problem. Building on this, we further segment the problem setting it into two interrelated, distinct tasks: (1) truck scheduling at marine terminals, which is relevant for logistics companies; and (2) berth allocation for inbound vessels, which directly impacts the vessels. Given the terminal’s pivotal role as a coordinator, its own operations are affected by aspects of both tasks.
2.1.1. Truck Scheduling at Marine Terminals
Uncoordinated arrivals of trucks in marine terminals is a major problem caused by the unpredictability and rising volume of truck arrivals. A widely adopted solution to this problem in the literature is the implementation of a Truck Appointment System (TAS) [6]. Appointment systems are designed to reduce the impact of a concurrent influx of arrivals by limiting the number of trucks admitted during each time period. A time period is the temporal interval used to measure access rights in an appointment system (e.g., 1 h). TASs are often considered mandatory [7] for all trucks entering the port. This study also assumes a mandatory appointment system, where all logistics companies must request specific slots for their trucks. A slot grants a truck the right to access the terminal within a designated time period. The proposed system, however, does not operate on a simple First-Come, First-Serve (FCFS) basis. Decentralization has been proposed as a way to enable collaborative appointment scheduling between trucking companies and terminals [8]. Inspired by this concept, our work adopts a similar philosophy. In line with [9], the proposed system arbitrates between conflicting truck requests based on company preferences, with the overall objective of minimizing the maximum deviation cost from the original requests for all logistics companies. This objective introduces fairness in truck scheduling operations among different logistics companies. Fairness is introduced through an arbitration process that aims to reduce the incurred deviations per company.
Trucks are anticipated to enter the marine terminal to fulfill specific tasks. These tasks can be categorized into pickup tasks, involving the retrieval of cargo from the terminal, and delivery tasks, which entail transporting cargo to be exported through the terminal. The complexities of truck drayage within a marine terminal vary with the type of task [10]. In this study, all scheduled tasks are assumed to be related to a vessel’s arrival at the terminal. This operational framework aligns with the principles outlined in [11], wherein the concept of vessel-dependent time-windows is introduced. A Vessel-Dependent Time-Window (VDTW) is defined as a set of time periods during which specific trucks, based on their tasks, are granted terminal access. Separate time-windows are designated for pickups and deliveries: delivery jobs are expected to be scheduled near the vessel’s arrival, while pickup jobs occur after the vessel has unloaded its cargo. This study omits any interactions between trucks performing different jobs, similar to [12], with aspects such as minimizing empty runs [9,13] not being considered.
2.1.2. Berth Allocation for Inbound Vessels
The Berth Allocation Problem (BAP) is a well-established topic in operations research. It involves optimizing the assignment of berthing locations and time slots to arriving vessels at the quay, taking into account relevant constraints [14]. A crucial objective is often the minimization of vessel waiting and exit times through optimal berth assignments. Approaches to BAPs can be classified as proactive, reactive, or hybrid [15]. Our approach is classified as proactive, as it is fully embedded in the planning phase. For the purposes of this study, the vessel arrival schedule is assumed to be deterministic and fixed and is examined over a full week in a tactical planning context, following a similar setup to [16]. The occurrence of delays and any other disruptions is not studied. In contrast to previous studies on VDTWs [17], a bidirectional impact between VDTWs and berth planning is assumed, indicating mutual influence between the two. This suggests that immediate access to the terminal from the seaside is not guaranteed, as congestion may occur due to vessels occupying berths with active VDTWs, which can make mooring impossible during specific time periods and incur waiting times. Immediate access may also be hindered if it leads to high deviation costs for logistics companies. Berth size and vessel compatibility are also considered, implying that not all vessels can use all berths. Finally, vessel exit times depend on factors such as berth productivity, which is influenced by the number of quay cranes, available internal vehicles, and the drayage time costs within the terminal. To model the intricacies of cargo handling by the terminal and its effect on vessel departure, a macroscopic approach is used to determine productivity rates, as previously proposed by [18]. This approach computes the processing time for loading and unloading vessels based on terminal resources and cargo levels, while also measuring the conditions of import and export areas and the demand for internal vehicles. This study does not incorporate vessel-specific weights or priority levels to differentiate between vessel types such as motherships and feeders. Additionally, transshipment activities and multimodal transport connections, which can significantly influence vessel turnaround times, are not explicitly modeled. These simplifications were made to focus on the core coordination mechanisms under controlled assumptions. Extending the problem to account for vessel heterogeneity and broader port operations, however, does not contrast with the selected approach to model the problem.
2.2. Modeling Approach
To the best of the authors’ knowledge, the defined problem setting has not been previously studied. An important difference with existing literature is that vessels may be delayed to reduce truck congestion at the landside. Therefore, to select an appropriate solution methodology, inspiration was drawn from problems in the literature that share similar features. The MAS modeling paradigm is considered highly suitable for this problem because of the involvement of multiple autonomous yet interdependent stakeholders, each with distinct goals and incomplete information about others. Previous approaches to modeling container terminal operations using MAS are well-documented in the literature. For example, ref. [19] introduces a micro-level MAS framework for container terminals, while ref. [20] examines MAS-based coordination of barge and terminals to improve hinterland transport planning. Likewise, ref. [18] focuses on the coordination of internal trucks to manage cargo unloading operations. However, the previous models have a more limited scope, as agents only represent internal terminal functions without addressing stakeholder coordination and multimodal collaboration.
A closely related problem from MAS that inspires our modeling approach is the Multi-Agent Pickup and Delivery Problem (MAPD), which shares several design similarities. Multi-agent pickup and delivery is the problem of allocating tasks for agents and finding the shortest paths without collisions. Both involve multiple interrelated agents, each with its own objectives and limited knowledge of others’ plans, creating potential conflicts in decision-making. Additionally, both problems take into account dynamic scheduling and time constraints, which can disrupt planned operations. Finally, resource sharing and coordination are critical in both cases, as agents must efficiently allocate and manage shared resources to optimize overall system performance while balancing individual priorities. Solving MAPD problems often involves prioritization techniques and heuristics to enhance optimization. For instance, ref. [21] applies prioritized planning to develop efficient paths, combined with Large Neighborhood Search (LNS) for iterative solution improvement. Similarly, ref. [22] integrates task deadlines into a priority-based framework, using bounding and pruning techniques to maximize task assignments. Ref. [23] also leverages prioritization to ensure collision-free routes when assigning multiple goals to agents, striking a balance between managing conflicting objectives and task completion, with LNS aiding the search process. A key difference between the examined problem and MAPD problems is the less apparent presence of a unified optimization goal in the latter case. While MAPD studies typically involve independent agents working toward system-wide optimization, the examined problem lacks a clear, single optimization goal due to the varying, sometimes conflicting, objectives of different stakeholders. This complexity necessitates balancing these competing interests rather than pursuing a single objective, often addressed in the literature through multi-objective representations.
Multi-objective optimization is a common approach in scheduling operations with multiple, possibly conflicting goals, which is a key characteristic of the examined problem. Examples include job shop scheduling [24], timetabling [25], and machine scheduling [26]. In supply chain-related problems with multiple objectives, examples include truck scheduling in cross-docking centers, where the focus is on maximizing reliability against breakdowns while minimizing outbound truck tardiness [27], ship scheduling in congested marine terminals, balancing environmental, economic, and social objectives [28], and integrated terminal management, minimizing ship service times and yard crane operational costs [29]. The standard methodology for solving these problems are multi-objective evolutionary algorithms (MOEAs), like NSGA-II [30] and SPEA2 [31].
This paper introduces an approach inspired by both MOEAs and MAS to facilitate collaborative scheduling in multimodal terminal operations by utilizing distributed agents to enable multi-actor decision-making to tackle the issues outlined in Section 2.1. The use of priorities is also exploited to guide the optimization of the system based on KPIs. Each agent is guided by its own decision making model. Identification of conflicts and compromise solutions for the interacting agents is performed through terminal coordination and optimization with either existing MOEAs or a novel solution methodology inspired from prioritized search.
3. Model Formulation
The problem statement involves three distinct actor groups, each with specific requirements and objectives, which are modeled as decision-making agents within an MAS. The first group, consisting of vessels, is represented by the berth allocation agent, which seeks to minimize both waiting times and processing times for the vessels, by ensuring a berth allocation for timely mooring and cargo handling. The second group, comprising logistics companies, is represented by the truck arrival management agent, aiming to incur reduced deviation costs by aligning truck arrivals with their preferred time periods and optimizing pickup and delivery schedules. Lastly, we define the terminal processes agent that acts as an independent coordinating agent, responsible for overseeing the system processes and verifying the feasibility of all solutions by balancing the needs of the vessels and logistics companies, while maintaining smooth terminal operations. While the framework features a terminal coordinator, its function is not to dictate actions but to facilitate information exchange and conflict resolution between agents. The coordinator acts as a neutral intermediary, identifying conflicts over shared resources and enabling agents to adjust their plans in order to identify mutual beneficial solutions. This design ensures that the decentralized nature of the MAS is preserved, with coordination achieved through adaptation rather than central control.
The proposed approach assumes that agents collaborate by exchanging solutions, represented by their associated costs, in order to converge on a mutually acceptable outcome. While this assumption facilitates the exploration of coordinated decision-making, it may not fully reflect the current business priorities or operational constraints faced by terminal stakeholders. In particular, the model does not explicitly account for the asymmetry of power among actors, such as the disproportionate influence of shipping lines compared to smaller logistics providers or trucking companies. Although this imbalance is partially captured by the sequential structure of the multi-agent system, where vessels act first, the broader institutional and governance issues surrounding stakeholder inequality and trust remain beyond the scope of this study. Instead, the primary objective is to assess the viability and effects of different coordination and prioritization mechanisms in cargo handling. Demonstrating the value of such mechanisms is a necessary first step toward future work that may address practical barriers to collaboration, including data sharing, trust, and power imbalances.
The overall goal of the MAS is to determine Pareto optimal solutions by deploying search algorithms that take into account all requirements set by the involved agents. In Section 3.1, the berth allocation agent is described, followed by the truck arrival management agent in Section 3.2, and by the terminal processes agent in Section 3.3. Given the involved agents are interrelated, many parameters and variables are shared across them. For conciseness, these parameters and variables will be introduced only when they first appear in the tables within this section. In Figure 2, a schematic representation illustrates the interactions among variables, parameters and processes (to be introduced in the following sections) within the proposed MAS.
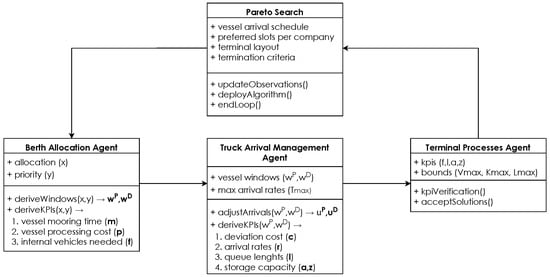
Figure 2.
Representation of agent interactions.
3.1. Berth Allocation Agent
The berth allocation agent is responsible for vessel-related operations. All sets, parameters and variables necessary to describe this agent are listed in Table 1. Allocation of berths to each vessel v is defined by variable , while priority of vessels per berth is an ordered set consisting of all vessel indices assigned to that berth, from higher to lower priority. A vessel v is granted access for mooring at time unit , and based on allocated berth , the processing time for loading/unloading operations can be defined. Within the interval , the berth is considered occupied, with representing the exit time of the vessel from the berth. The processing and mooring times for each vessel are measured in time-units (e.g., one minute) within the considered planning period.

Table 1.
Sets, parameters and variables used by the berth allocation agent.
With respect to the berth compatibility, each vessel v is characterized by a vessel length . Similarly, each berth b is assigned a maximum vessel length that it can service. Smaller vessels can use berths designed for larger vessels, but the reverse is not possible. Assignment of a larger vessel to an incompatible berth will result in an arbitrarily large processing time . Finally, the existence of priorities as established by asserts that no vessel with higher priority for the same berth should experience delays due to a vessel with lower priority. Let be the ordered list of vessels assigned to berth A, where . For each , the following condition must hold:
where denotes the mooring (start) time of vessel , and is its processing time. This essentially ensures that a vessel with higher priority will never be delayed by a lower-priority vessel, although a lower-priority vessel may still be served earlier if it does not interfere with the higher-priority vessel’s schedule (as shown on the right hand side of Condition (1)). The relationship between priority y and mooring time m is further explained with an example in Figure 3.
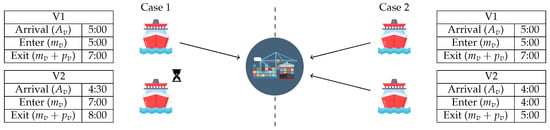
Figure 3.
Two cases of execution of vessel schedules approaching the same berth with V1 having priority over V2. V1 has a 2-hour processing time, while V2 has a 1-hour processing time. In Case 1, V2 arrives 30 min before V1 but must wait due to V1’s priority. In Case 2, V2 arrives an hour earlier and can be served by 5:00, when V1 arrives, despite the lower priority.
Processing time of cargo is the main determinant of the vessels’ exit time from the terminal. For this particular problem, a vessel is considered to carry only cargo in the form of Twenty-foot Equivalent Units (TEUs). Cargo is either designated for exports () and must be loaded onto vessel v, or it is designated for imports () and must be unloaded from vessel v. The amount of TEUs to be processed evidently affects the processing time but so does the productivity of the assigned berth, as each berth has a specific number of available quay cranes , and TEUs that can be processed per time-period based on mode and . When in single mode (), cranes will exclusively load or unload cargo with no overlap. When in double mode (), loading of containers can take place in parallel to unloading and vice-versa. Derivation of processing times for vessels follows a process similar to [18] as follows:
where is the amount of TEUs to be processed in single mode and the amount of cargo to be processed in double mode. Processed cargo in a specific mode is calculated in Equations (2) and (3), asserting that as many TEUs as possible will be processed in double mode and the rest in single mode. Then, the processing time is defined in Equation (4), contingent on the individual processing times per crane mode as defined in Equations (5) and (6).
Depending on whether a vessel has more TEUs to load than unload, double mode processing will occur before or prior to single mode. When there are more TEUs to be loaded to the vessel than unloaded, the vessel will first be processed in double mode. This ensures that unloading will finish before loading, leaving more time for the truck-pickup-related windows. Conversely, when there are more TEUs to be unloaded than loaded, the vessel will first be processed in single mode. This ensures loading does not start earlier than needed, thus allowing more time for deliveries to arrive later.
The processing mode also impacts the time-windows and for each vessel, which take values . A time-period i represents a set of time-units within the examined working week (e.g., all minutes in a single hour). The time-unit indicating the start of cargo loading is associated with the last possible time-period for delivery jobs, establishing the upper bound of . In contrast, the time-unit marking the completion of cargo unloading designates the first possible period of . Deliveries are assumed to occur at any time before the upper bound of , and pickups after the lower bound of , although they are generally expected to take place within 12 h of the respective bounds.
Overall, the decision-making agent responsible for berth allocation aims to minimize the waiting and processing times for all vessels. Its objective function (termed the vessel_process function), subject to the requirements outlined earlier, is defined as:
3.2. Truck Arrival Management Agent
The truck arrival management agent is responsible for operations related to logistics companies and trucks. All sets, parameters and variables necessary to describe this agent are listed in Table 2. Each truck that accesses the terminal is considered to be dependent on a vessel and owned by a Logistics Company . Additionally, each truck has a distinct job type as either a pickup or a delivery. A single truck is assumed to carry one TEU within the terminal and each truck has its own preferred arrival time-period . The sum of preferred arrival time-periods define as the number of trucks that company l prefers to send for delivery jobs related to vessel v during time-period i. Similarly, represents the preferred number of trucks for pickup jobs. The stated preferred arrival periods for trucks simulate the appointment process in the proposed model.

Table 2.
Sets, parameters and variables used by the truck arrival management agent.
Each company is assumed to be characterized by a deviation factor . This deviation factor represents how averse a company is to deviations from their preferred schedule. When the preferred arrival schedule is deemed infeasible, a cost is calculated as described in Equation (8).
where denotes the amount of trucks that need to be deviated at a specific time period for a logistics company and is the time-period difference between period i and the first feasible time period. The exponential factor is selected to discourage assignments that differ to a large extent from a truck’s preferred arrival period. A preferred arrival schedule may be deemed infeasible in two particular cases. The first cases relate to the timing of truck arrivals not aligning with the vessel’s arrival and handling processes. We denote this form of infeasibility as hard. In this case, the preferred arrival schedule can be accepted by the truck arrival management agent, given the berth allocation agent’s solution , if the following conditions hold:
Such infeasibility requires correction by incurring costs to logistics companies and rescheduling the trucks to the next feasible period. For instance, if trucks are planned for pickup in time-period 5 but the vessel moors in time-period 6 and finishes unloading by time-period 8, the trucks must be rescheduled to time-period 9, i.e., the earliest time-period when pickup can occur. Hard deviations are calculated using Algorithm 1.
The second case of schedule infeasibility concerns the maximum arrival quota per time-period (). In this scenario, deviations are required to reduce arrivals to , ensuring compliance with constraints set by the terminal processes agent. This type of infeasibility is classified as soft, as it does not imply an infeasible schedule but instead affects terminal productivity. To address soft deviations, Algorithm 2 is applied, as illustrated through a graphical example in Figure 4.
| Algorithm 1: hard() |
| 1 |
| 2 |
| 3 for do |
| 4 for do |
| 5 for do |
| 6 if then |
| 7 |
| 8 |
| 9 |
| 10 |
| 11 else if then |
| 12 |
| 13 |
| 14 |
| 15 |
| 16 for do |
| 17 |
| 18 return |
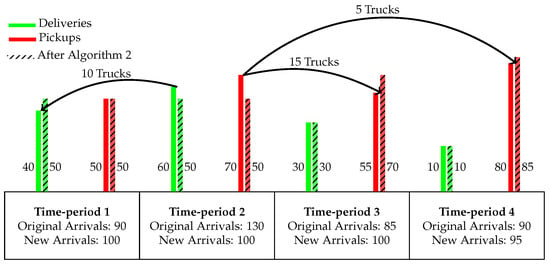
Figure 4.
Transformation of arrival rates after Algorithm 2.
The algorithm begins by identifying congested periods and sorting them from the most to the least congested. In Figure 4, we consider an example where the maximum arrival quota per time-period is set at 100 trucks and only one time-period needs correction. In this context, time-period 2 exceeds this limit by having 30 more truck arrivals than the set limit, indicating a soft violation. For each period i with a soft violation, if traffic is higher in the prior period over the subsequent , pickup jobs are selected for deviation to time-period , as slightly delaying a pickup is allowed by our strategy. If traffic is higher in the subsequent period over the prior , delivery jobs are selected for deviation to time-period , as slightly anticipating delivery jobs is allowed by our strategy as well. If adjacent periods have equal traffic, deviations alternate between pickups and deliveries. In the given example, time-period 3 initially has a lower arrival rate than time-period 1, prompting the rescheduling of five pickups from time-period 2 to time-period 3. After the initial five shifted trucks, the arrival rate of time-period 3 matches that of time-period 1, prompting the rescheduling to alternate between periods 1 and 3. As a result, 10 deliveries are shifted to time-period 1, and 10 more pickups are moved to time-period 3 leading to a total of 15 pickups delayed to time-period 3, bringing both periods to the quota. As indicated by Algorithm 2, if both neighboring periods reach , the adjustment window is extended by one additional period to time-periods and . In this example, the remaining five trucks needing rescheduling from time-period 2 are shifted to time-period 4, after extending the adjustment window by one additional period.
This process ensures that deliveries are never shifted to later periods, nor pickups to earlier ones, as such changes may cause hard violations. The algorithm thus maintains schedule feasibility while optimizing terminal productivity by managing soft deviations efficiently. Hard deviations are addressed first, followed by soft deviations. To reduce the arrival rates, the rule is used to minimize the maximum deviation cost per logistic company, including the deviation cost already incurred by hard deviations. Deviations are selected in a way that the company that incurred the least cumulative cost is selected for each truck deviation. The algorithm computing the soft deviation costs is provided in Algorithm 2.
Overall, the truck arrival management agent aims to minimize the amount of incurred deviation costs towards the logistics companies. Its objective function, subject to the requirements outlined by Algorithms 1 and 2 is defined as:
| Algorithm 2: soft() |
| 1 |
| 2 for do |
| 3 if then |
| 4 ; |
| 5 while do |
| 6 if then |
| 7 |
| 8 |
| 9 if then |
| 10 |
| 11 |
| 12 |
| 13 |
| 14 |
| 15 else |
| 16 |
| 17 |
| 18 if then |
| 19 |
| 20 |
| 21 |
| 22 |
| 23 |
| 24 |
| 25 |
| 26 return |
3.3. Terminal Processes Agent
The terminal processes agent is responsible for operations related to the terminal and overall coordination of the system. All parameters and variables associated with the terminal are listed in Table 3.

Table 3.
Parameters and variables used in the model used by the terminal processes agent.
The terminal’s decision-making is centered around managing requirements related to congestion, space, and available equipment. Four key metrics are considered: arrival rates, constrained by the maximum limit (addressed in the previous section); queue length at the gate, limited by ; cargo space in import and export areas, constrained by ; and internal vehicles used, limited by .
To model truck arrivals at the gate, a non-homogeneous Poisson distribution for the derived arrival rates r by the truck arrival management agent is used. Service times are treated as independent and identically distributed, consistent with the M/G/k queuing model, for k lanes as in existing literature [32,33]. To handle cases when arrival rates exceed service rates, the stationary backlog-carryover method is used [34,35], which allows queues to build up in overloaded periods, and waiting jobs can be transferred to a subsequent period. The queues effectively serve as constraints by determining the feasibility of a solution. If the queues become too long, the agent rejects the solution altogether. The derivation of equations to determine the queuing approximation for l can be found in Appendix A.
Cargo quantities in the yard are updated based on the actual pickup and delivery rates and , as provided by the truck arrival management agent, and are also contingent in the processing modes followed as explained in Section 3.1. For clarity of the formulations in Table 4, subsets relating to specific moments in the cargo handling process are formulated and measured in time periods. Essentially, the time-periods that a vessel will process cargo in, either in single or double mode, are isolated based on the mooring time and processing time derived by the berth-allocation agent. As previously discussed, based on whether there are more imports or exports, a different sequencing of cargo processing is performed. The total TEUs in import (z) and export areas (a) can then be computed based on Equations (11)–(18). For a specific vessel, cargo processing may begin after an associated time-period has started and conclude before a period ends. Equations (11)–(14) define the actual amount of cargo processed for each period within the subsets outlined in Table 4 based on the mooring and processing times of the vessel. Three cases are thus possible: cargo processing starting partway through an involved period, cargo processed throughout the entirety of a period, and cargo processing concluding before a period ends. The use of arrival rates in Equations (16) and (18) is appropriate for measuring TEUs, as it is assumed that each arriving truck carries a single TEU. Storage capacity at the import and export areas is considered finite for a maximum TEU.

Table 4.
Subsets used in the model, specific to the terminal.
Finally, a maximum number of internal vehicles is considered available. The amount of TEUs a vehicle can process within a single period is defined as for double mode, for single mode moves towards the import area and for the export area. Building on that, Equations (19)–(21) define the amount of vehicles needed per processing mode and vessel for the processing times of vessels as defined by the berth allocation agent. These equations establish the amount of vehicles needed to match the productivity of the used mode and cranes. Then, the total number of internal vehicles needed can be computed from Equation (22).
Overall, the terminal processes agent has no explicit optimization goal; thus, its decision-making is represented by a constraint satisfaction function termed , which checks whether variables that are directly related to r remain below upper bounds, returning False if any are violated.
4. Solution Methodology
Searching for Pareto optimal solutions that improve and satisfy the individual objectives of all agents depends on an efficient search algorithm as previously signaled in Figure 2. Due to the problem’s complexity, nonlinearity, and large solution space, metaheuristic methods are used. We consider multi-objective evolutionary optimization algorithms and a novel technique that combines prioritized planning with neighborhood search for developing the search algorithm. These methods balance conflicting objectives and refine solutions locally based on the requirements and functions defined in Section 3. Specifically, the vessel_process and incur_deviation must be minimized, while the terminal_constraints functions must be satisfied during the solution process.
4.1. Multi-Objective Evolutionary Algorithms
A common approach to solving multi-objective optimization problems involves population based algorithms that utilize evolutionary computation. Multi-Objective Evolutionary Algorithms (MOEAs) can efficiently generate a diverse set of trade-off solutions, focusing on convergence, diversity, and coverage of the examined solution space. These algorithms form the foundation of multi-objective optimization problems and have been extensively studied in the literature. To solve the problem presented in this study using MOEAs, the employed methodology, detailed in Figure 5, employs the following steps:

Figure 5.
Methodology employed for use of multi-objective evolutionary algorithms.
- Step 1: Initialize Problem Parameters— This includes determining the number of vessels, available berths, logistics companies involved, and specific requirements such as vessel-to-berth compatibility.
- Step 2: Generate Initial Set of Solutions—An initial set of solutions for berth allocation x and priority of vessels y per berth is generated and evaluated by assigning a simple FCFS priority based on the chronological arrival times of vessels, and then a random assignment of berths for each vessel, provided that the allocation is feasible with respect to vessel-to-berth compatibility. The generated x and y are defined as observations of the search algorithm.
- Step 3: Encoding of Observations—To facilitate the search process, observations of x and y must be encoded in a form that makes it easy to apply operators. To that end, we utilize real-encoding. For each vessel, a real number is generated randomly within the range from 0 to the total number of berths . The integer part of this number indicates the assigned berth for the vessel, while the fractional part represents the vessel’s priority among those allocated to the same berth. Vessels with the same integer part are sorted based on their fractional values to establish priority order. The chromosome structure is further illustrated in Figure 6.
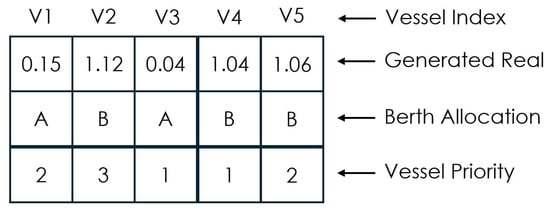 Figure 6. Encoded chromosome with reals.
Figure 6. Encoded chromosome with reals. - Step 4: Define evaluation method—The model defined in Section 3 must satisfy constraints during fitness evaluation. To handle constraint violations, hard constraints are transformed into soft constraints by adding high penalties to the objective value when violations occur. To compute the costs across agents, the vessel_process, incur_deviation and functions are deployed.
- Step 5: Select crossover and mutation operators—Generating diverse observations is crucial for the effectiveness of MOEAs as it helps explore a broader solution space and avoid premature convergence. To achieve this diversity, crossover and mutation operators are employed. For real-valued representations, a common crossover method is Simulated Binary Crossover (SBX). The SBX operator mimics the behavior of binary crossover for integers and is defined mathematically as follows:where . Variable is drawn from a beta distribution with an index of user-defined distribution to introduce variability in the crossover process. For mutation, polynomial mutation is commonly used. This method introduces small changes to individuals by altering their values with a polynomial distribution. The mutation operation is defined as:where is a polynomially distributed random variable and is a distribution index that controls the mutation magnitude:For all MOEAs these two operators were utilized with and for SBX and polynomial mutation, respectively.
- Step 6: Deploy Selected MOEAs—As previously established in Section 2.2, the common benchmark algorithms NSGA-II [30] and SPEA2 [31] are used.
4.2. Prioritized Search
MOEAs are relatively straightforward to implement and can effectively yield a satisfactory set of solutions for multi-objective optimization problems. However, achieving the set of all Pareto efficient solutions can be challenging due to the problem’s complexity and high dimensionality. A significant drawback is the excessive generation of redundant observations, as the operators used to create new solutions focus on diversity but lack a robust mechanism to incorporate local knowledge into the search process. For example, certain berths may be incompatible with specific vessels, yet the search algorithm evaluates these infeasible solutions, which, despite incurring minimal computational cost, detracts from overall optimization efficiency. To address these limitations, we propose a novel algorithm based on prioritized planning, which utilizes local knowledge to minimize redundancy and improve solution quality. The berth allocation variable x is assigned sequentially for each vessel according to y, leveraging priority trees, and outlined in Section 4.2.1. Subsequently, our approach employs a search algorithm, as described in Section 4.2.2, to determine the priority list y.
4.2.1. Priority Trees
In constructing a priority tree, we begin with a given priority list y and try to define the berth allocation . To define x, we assume that each vessel consistently selects a berth using a greedy approach, i.e., the one that minimizes any of the associated costs, always considering local conditions such as berth occupancy caused by other vessels. Each vessel is associated with a processing cost , and an incurred deviation cost for companies, , based on the selected berth. Given that the problem has two distinct objectives to minimize, different berth allocations may optimize different criteria. To address this, the algorithm may consider multiple berth allocations. When two different berths perform better for one objective but worse for the other, a branch occurs as no solution dominates the other.
In Figure 7, an example of the formation of priority trees is illustrated with three vessels and priorities V1 > V2 > V3. For vessel V1, berth B is selected since it is the greedy solution compared to the infeasible solution of berth A, which yields an infinite cost. For vessel V2, both berths yield minimum values for different costs, with berth A minimizing the total sum of and berth B minimizing the total sum of , resulting in new branches. For vessel , two branches and four allocations must be evaluated, and only greedy solutions must be kept. Allocation is disregarded because, for V3, allocation performs better in both objectives, thereby dominating solution . Allocations , , and are part of the final output of this process, but it is noted that allocation is dominated by allocation . This branch is dominated across all solutions, but not within solutions stemming from its root, and thus is discarded at a later stage, as indicated by Figure 7.
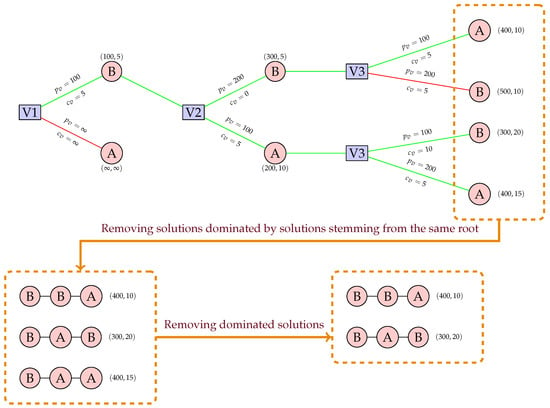
Figure 7.
Schematic representation of the branching process to create priorities.
We generally aim to retain non-dominated solutions originating from the same root, as they may lead to better final outcomes under the current priority constraints when examining vessels further down the priority list. However, this approach introduces significant redundancy, which can negatively affect performance as the number of vessels increases. To mitigate this, we apply a simple rule: we always keep at most the top k solutions. These are selected based on minimizing the sum of the two cost components. If, at any point, the number of branches from a root exceeds k, the least favorable solutions are discarded.
Algorithm 3 describes the process of creating priority-based trees, as visualized in Figure 7, for a given ordered priority y. We also introduce the concept of an archive , used to store indices of vessels where the greedy decision for berth allocation results in a branch, as shown in Figure 7. Information related to costs for the Berth Allocation Agent, Truck Arrival Management Agent, and occupancy constraints for the associated berths are stored in the ROOT dictionary (Algorithm 3, Line 2) and are updated for any given priority. Proceeding iteratively for every vessel , the processing time of each vessel and its impact on the vessel schedule is first computed (Algorithm 3, Line 12) using the vessel_process function. All possible berth allocations are evaluated iteratively, provided they are compatible with the vessel size (Algorithm 3, Line 11). Current best berth allocation for vessel processing and incurred deviation are stored in variables . Vessel processing costs are calculated for a single vessel, and conflicts with vessels of subsequent priorities are checked by updating the “curr” dictionary. Then, the hard deviation cost to the logistics companies caused by this vessel () and any effect to the current arrival rates applied to logistics companies is computed by Algorithm 1 (Algorithm 3, Line 13).
Based on the cumulative and , all potential branches relating to a greedy allocation are stored as previously explained (Algorithm 3, Line 14–22). When multiple branches are created, the vessel causing the split updates the archive () (Algorithm 3, Line 24). The archive is used to guide exploration of different priorities around this vessel later in the search process. Subsequently, occupancy constraints and current costs per agent are updated for all branches (Algorithm 3, Line 27–31). Finally, after processing all vessels, the derived branches are added to the found solutions after being updated to account for soft violations as per Algorithm 2 if they do not violate any terminal-related constraints (Algorithm 3, Line 32–37) such as maximum queue list and storage capacities.
| Algorithm 3: priority_tree(y,swap) |
| 1 sols, OPEN ← ∅, ∅ |
| 2 |
| 3 insert OPEN in ROOT |
| 4 for do |
| 5 children ← ∅ |
| 6 while OPEN do |
| 7 curr ← state from OPEN with index 0 |
| 8 remove OPEN from curr |
| 9 |
| 10 for do |
| 11 if then |
| 12 |
| 13 |
| 14 if and then |
| 15 |
| 16 |
| 17 else if then |
| 18 |
| 19 |
| 20 else if then |
| 21 |
| 22 |
| 23 if then |
| 24 update v in swap by 1 |
| 25 if then |
| 26 keep k trees with lowest total cost |
| 27 for do |
| 28 |
| 29 |
| 30 |
| 31 add child in children |
| 32 for child ∈ children do |
| 33 insert child in OPEN |
| 34 for child ∈ children do |
| 35 update child with soft(child) |
| 36 if then |
| 37 insert child in sols |
| 38 return sols, swap |
4.2.2. Search Algorithm
A search strategy is proposed that takes elements from neighborhood search to efficiently explore the solution space for different applied vessel priorities. Algorithm 4 is employed to search for non-dominated priorities by systematically refining the solution space through a combination of exploration and exploitation strategies. Below are the key steps of the search algorithm:
| Algorithm 4: priority_search(y,end,pb,pt) |
| 1 |
| 2 |
| 3 |
| 4 while True do |
| 5 sols, swap ← priority_tree(y, swap) |
| 6 non_dominated ← ∅ |
| 7 add sols in candidates |
| 8 |
| 9 for do |
| 10 |
| 11 for do |
| 12 if and is_dominated(i, j) then |
| 13 |
| 14 break |
| 15 if not dominated then |
| 16 add(i) in non_dominated |
| 17 |
| 18 for f do |
| 19 if ledger[BA][b] > f[] then |
| 20 |
| 21 if ledger[TAM][b] > f[] then |
| 22 |
| 23 Define |
| 24 if then |
| 25 select y from ledger[BA][sol] |
| 26 apply destroy operator on y |
| 27 yupdate y with a repair operator |
| 28 else if then |
| 29 select y from ledger[TAM][sol] |
| 30 apply destroy operator on y |
| 31 update y with a repair operator |
| 32 else |
| 33 select y from current front |
| 34 update y with a random operator |
| 35 if end then |
| 36 break |
| 37 return front |
- Initialization: The algorithm begins with an intuitively promising priority strategy. We utilize FCFS for the examined vessels and create the priority trees as previously explained in (Algorithm 3). Two termination criteria, collectively denoted as end, are considered:
- A pre-specified maximum number of iterations.
- Convergence to a certain Pareto front satisfying solution quality thresholds.
- Updating the Pareto Front: At each iteration, dominated solutions derived from the priority trees are discarded to create the current best Pareto front (Algorithm 4, Lines 6–17).
- Exploration and Exploitation: The algorithm uses exploration and exploitation to refine and diversify the solution space (Algorithm 4, Lines 18–34):
- Exploitation: A ledger maintains the best feasible priorities and allocations for each decision-making agent (Algorithm 4, Lines 18–22). To intensify the search near high-quality solutions, we apply a destroy-and-repair strategy: part of a solution is perturbed and then heuristically reconstructed (Algorithm 4, Lines 23–33). The process is applied to the current best solution of either the TAM or BA agent, chosen at random from the ledger. A destroy operator is followed by a repair operator, both selected randomly. The available operators are:Destroy operators apply targeted changes:
- −
- random_subsequence_removal: removes a contiguous block of n elements and then applies local reordering.
- −
- random_position_removal: removes k elements from random positions for broader variation.
Repair operators restore priority structure:- −
- random_reinsertion: reinserts removed elements at random positions to promote diversity.
- −
- greedy_reinsertion: reinserts each element in a weighted manner influenced by the archive.
- Exploration: To diversify the search space and avoid local optima, we apply a set of local operators that modify candidate solutions. One operator is selected at random in each iteration. The following operators are used:
- (a)
- insert—Inserts a random vessel into a different position in the sequence. To guide the exploration, we use the archive as a weight for vessel selection.
- (b)
- shuffle—Randomly shuffles a small segment of consecutive vessels.
- (c)
- reverse—Reverses the order of a selected segment in the sequence.
- (d)
- relocate—Moves a segment of vessels to a different position.
- (e)
- two_opt—Swaps two non-overlapping segments.
- Sampling Strategy: A specific sampling strategy is employed to balance exploration and exploitation throughout the iterations in our experiments:
- When exploiting, the decision to select a priority for a specific decision-making agent is made uniformly, with probabilities for berth allocation and truck arrival management set equally ().
- During the first 80% of iterations, the algorithm allocates 20% of iterations to exploitation and 80% to exploration ().
- For the final 20% of iterations, the balance shifts, with 80% of iterations focused on exploitation and 20% on exploration ().
Ultimately, the best observed Pareto front is returned as the output of Algorithm 4.
4.2.3. Scalability and Parallelization
The prioritized search algorithm, while reducing the solution space, can increase computational costs due to the need to form trees and perform computationally expensive operations, such as those in Algorithm 1, for each vessel individually. This computational cost grows with the number of vessels and berths, making single priority evaluations significantly more expensive. This issue is partially addressed by reducing the redundancy of examined branches (Algorithm 3, Lines 25–26), where only the top k priority vectors per branch are retained. In our experiments, we used to balance performance with computational efficiency. Scalability concerns related to increased vessel and berth numbers are further addressed through the evaluation in Section 5.2.
Another way to speed up computation, unlike MOEAs, which rely on iterative learning across generations, is through the parallelizable nature of Algorithm 4, which offers a practical advantage in large-scale problem settings. We propose a simple parallelization approach where multiple processes start from different priority strategies close to FCFS and independently follow the steps outlined in the previous section related to the search algorithm. This allows multiple processes to concurrently evaluate different priorities, significantly increasing the search capacity of the algorithm. However, without guidance some processes may get stuck in suboptimal solutions while others progress more effectively. To address this, we ensure that the best current observation from any individual process, with respect to a specific agent, is used to update the ledger (as defined in Algorithm 4) across all processes. The ledger helps guide processes stuck in poor regions of the solution space back toward the current optimum by recording and exploiting promising solutions. Since the ledger serves as the minimal form of communication across processes and can be updated asynchronously, the communication overhead remains negligible. The search process terminates once all processes complete their final iterations, ensuring that the prioritized search strategy maintains a comparable number of iterations across processes to MOEAs, even as the number of vessels or berths increases.
5. Case Study
5.1. Generation of Test Instances
The developed model and solution methodologies were tested for a medium-sized terminal in Norway over one week, with time-units measured in minutes and aggregated into hourly time-periods. A medium-sized terminal typically processes approximately 500,000 to 1,000,000 TEUs per year, which corresponds to around 10,000 to 20,000 TEUs per week [36]. The instances in this study are characterized by three distinct factors.
- The number of vessels approaching the terminal during the examined working period.
- The number of available berths for these ships.
- The level of incoming truck traffic to the terminal.
We report the values used for these three factors in all numerical experiments, together with other important parameters, in Table 5.

Table 5.
Summary of test data.
For the generated vessels, the expected arrival time is considered deterministic and known, while the length follows a uniform distribution within their respective vessel categories. The cargo amounts and are correlated with the size of the vessel. They are also proportional to incoming traffic obtained from loop detector data for heavy vehicles that were gathered in a road axis adjacent to the examined terminal. These were transformed to preferred pickup and delivery slots .
Truck traffic is distributed among 50 logistics companies, each with a deviation cost factor drawn from . Trucks are assigned randomly to vessels based with a constraint ensuring trucks are within 12 time-periods of the vessel’s arrival. The assignment to and depends on whether the sampled window is before or after the vessel’s arrival. Overall, traffic volumes varied from 3773 to 4449 trucks in low-traffic instances, 10,661 to 14,705 in medium traffic, and 17,275 to 21,748 in high-traffic scenarios.
Regarding the terminal geometry, the terminal features between two and four berths. With two berths, one is dedicated to vessels smaller than 100 m, while the other accommodates vessels of all sizes. When three or four berths are available, additional berths serve vessels up to 200 m in length. The berth for vessels under 100 m is equipped with a single quay crane, whereas the larger berths each have two or three quay cranes. Travel time from any berth to the import area is five minutes, while travel time from the berth to the export area is four minutes. The travel time between the import and export areas is set at one minute.
Regarding terminal productivity parameters, the crane throughput is set to 50 TEUs per period in double mode () and 31 TEUs per period in single mode (). Loading and unloading times for internal trucks are each set to one minute. Gate terminal productivity is 50 trucks per lane per period, with a total of two lanes available, both of which can be used for pickup and deliveries. Finally, regarding terminal operational parameters, the maximum truck arrival rate per period () is set to 125 trucks per lane. The maximum storage capacity in both the import and export areas () is 2000 TEUs. The maximum allowable queue length at any time () is 20 trucks, and the maximum number of internal trucks in use at any time () is 50.
5.2. Results and Discussion
The numerical campaign revolved around six core instances. Each instance is characterized by an identifier in the form , where represents the number of vessels approaching the terminal, represents the number of berths available, and represents the level of truck traffic. For example, instance 25-2-low represents an instance with 25 vessels, 2 berths, and low traffic. All numerical results were generated on an Intel Xeon Gold 6226R with 48 CPU cores and 192 GB of RAM. Both algorithms were implemented in Python, with the MOEAs employed using the existing pymoo package [37]. Each instance was executed for 5000 iterations, consisting of 25 generations with a population of 200 for the evolutionary algorithms, and 20 processes each with 250 iterations for the prioritized search. The parameters for exploration, crossover, and mutation for both algorithms have been previously described in Section 4. To assess the robustness of the algorithms against stochastic variations, each instance was solved five times for each algorithm, which was achieved by changing the random seed each time.
In Table 6, a comprehensive set of metrics evaluating the performance of each algorithm is presented. Specifically, the table includes Pareto front contributions (PF), hypervolumes (HVs), algorithm runtime in seconds, and iterations to the best Pareto front (ITB). The hypervolume measures the volume of the objective space that is dominated by the obtained set of non-dominated solutions and bounded by a predefined reference point. The reference point is selected just beyond the worst performance observed across all examined algorithms. Specifically, for each instance, it is defined by the maximum values of the Berth Allocation and Truck Arrival Management objectives observed in the proposed fronts across all solution methods. An algorithm with a larger hypervolume over the other indicates a better spread and convergence of the Pareto front approximation toward the true Pareto front.

Table 6.
Comparison of algorithms.
For these metrics, the average, minimum, and maximum values across the five runs are presented. The selection of five runs was made after confirming that the coefficient of variation related to hypervolumes had stabilized after five runs. It is important to note that the true Pareto front is unknown; therefore, the solutions are assessed based on the best results obtained across all solution algorithms. Finally, the combined performance of each algorithm, aggregated from all runs, is reported in the “Comb.” row for each instance.
The instances are further analyzed based on the traffic level used, beginning with the low-traffic scenarios. For these cases, the performance of the Prioritized Search algorithm was found to be comparable to, or better than that of NSGA-II and SPEA2. For the 20-2-low instance, NSGA-II showed slightly better consistency in identifying the best observed front, reflected in a higher average of Pareto front contributions. However, variability in both Pareto front contributions and hypervolumes remained marginal across all methods. In the 25-2-low instance, none of the algorithms identified the complete best observed Pareto front in a single run. Nonetheless, Prioritized Search achieved the highest number of Pareto front contributions across all runs. Interestingly, its average hypervolume performance was slightly lower than that of SPEA2 and NSGA-II. In the more complex 30-2-low instance, Prioritized Search further solidified its advantage. It consistently delivered more Pareto front contributions, higher hypervolumes, and faster convergence to the best observed front. While NSGA-II and SPEA2 each contributed only six solutions to the front, Prioritized Search contributed twelve, helping to uncover a front of 21 distinct solutions, underscoring the need for arbitration in such a multi-objective context. It is important to notice that the Prioritized Search algorithm exhibited a clear runtime advantage, being approximately 20-50% faster in runtime, and significantly better convergence to the best solution than the evolutionary algorithms. In Figure 8, the Pareto fronts identified by the solution algorithms and their overall convergence behavior are illustrated.
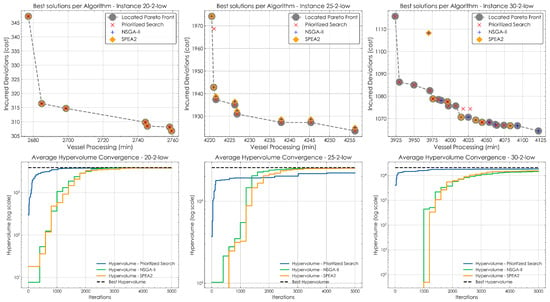
Figure 8.
Comparison of Pareto fronts and convergence across algorithms for instances of low traffic.
In the medium traffic instances 25-3, 30-3, and 35-3, the Prioritized Search algorithm consistently outperformed both NSGA-II and SPEA2 across all evaluated metrics. In the 25-3 instance, it was the only algorithm to contribute to the Pareto front, providing 16 non-dominated solutions and achieving the highest average hypervolume about 33% higher than the best-performing evolutionary algorithm. The 30-3 instance showed similar trends, with Prioritized Search contributing 10 solutions, compared to none by the evolutionary algorithms, and achieving an average hypervolume approximately 100% higher. In the 35-3 instance, Prioritized Search again dominated, contributing 17 solutions and reaching an average hypervolume that was over 50% higher than NSGA-II and SPEA2. Runtime analysis indicates that in the most complex case, Prioritized Search required about 10% more computation time on average, but reached its best solutions in 25% fewer iterations, suggesting better efficiency per iteration. In contrast, NSGA-II and SPEA2 not only failed to find high-quality trade-offs but also consumed comparable or greater computational resources. This inefficiency is compounded by their zero contributions to the combined Pareto fronts across all instances. Overall, it demonstrates clear advantages in convergence speed, solution quality, and computational efficiency in medium traffic scenarios, as illustrated in Figure 9.
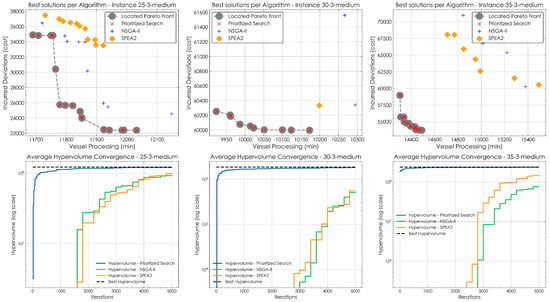
Figure 9.
Comparison of Pareto fronts and convergence across algorithms for instances of medium traffic.
In the high traffic instances 40-4, 45-4, and 50-4, Prioritized Search again showed a significant advantage over NSGA-II and SPEA2. In all three cases, the evolutionary algorithms failed to contribute any solutions to the combined Pareto fronts, while Prioritized Search contributed 43, 40, and 28 solutions, respectively. This dominance is again reflected in its consistently superior hypervolume values, indicating both better spread and convergence toward the optimal front. Although the complexity of the problem increased substantially, Prioritized Search remained effective, continuing to identify well-balanced solutions near the knee of the Pareto front. However, the increase in complexity came with a computational cost, as Prioritized Search exhibited longer runtimes than both NSGA-II and SPEA2 in all three high-traffic instances. These findings are visually summarized in Figure 10, which highlights the superior performance and robustness of Prioritized Search in demanding high-traffic scenarios.
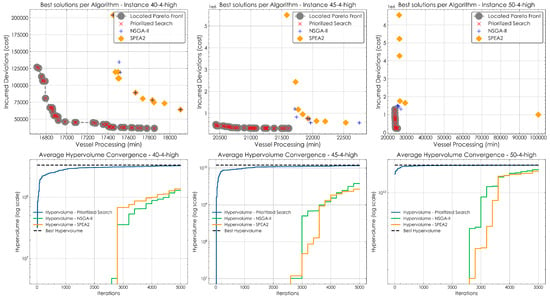
Figure 10.
Comparison of Pareto fronts and convergence across algorithms for instances of high traffic.
6. Conclusions
This paper introduces a novel approach to enhancing stakeholder coordination by synchronizing truck scheduling and berth allocation in a marine terminal. It presents an appointment system for trucks, building on the existing concept of vessel-dependent time-windows but allowing more flexibility for schedule deviations of vessels. A comprehensive model is proposed to facilitate terminal decision-making through orchestration of all interacting actor groups. Through effective terminal coordination, this model generates solutions that benefit all parties involved. Decision-making is achieved by distributed agents, focusing on representing the requirements imposed by different actors related to berth allocation, truck arrival processing and terminal operations. Additionally, the paper presents a new multi-agent, multi-objective solution methodology based on Prioritized Search for the proposed model, tested against common benchmark algorithms to validate its applicability and effectiveness.
The Prioritized Search method demonstrates increased performance by generating more Pareto front contributions and overall better convergence. Across all traffic scenarios, the Prioritized Search algorithm contributed a total of 180 Pareto-optimal solutions, compared to 21 by NSGA-II and 15 by SPEA2, highlighting a substantial advantage in solution discovery. Moreover, it consistently achieved higher hypervolume reaching up to 100% in medium traffic cases and maintained superior convergence efficiency, reaching the best solutions in 25–50% fewer iterations on average. The average runtime per iteration for medium-traffic instances was approximately 0.5 s for NSGA-II and SPEA2, and 0.3 s for the Prioritized Search. However, in higher-traffic instances, this increased to around 0.8 s for NSGA-II and SPEA2, and 2 s for the Prioritized Search. This indicates that while the Prioritized Search is more efficient in less congested scenarios, its runtime scales less favorably under heavier traffic conditions due to the increased complexity of coordinated decision-making. Nonetheless, even at half the number of iterations, the performance of the Prioritized Search in high-traffic instances remained superior, highlighting its effectiveness despite the increased computational cost. The solution algorithm is particularly effective at identifying solutions near the knee of the Pareto front across a range of traffic scenarios, consistently outperforming or matching NSGA-II and SPEA2. Although it incurs higher computational costs, especially in larger instances, this method delivers significantly superior solution quality due to its more focused and efficient exploration of the search space. Notably, it achieves these results while requiring fewer iterations on average, highlighting its ability to converge more quickly to high-quality trade-offs. In a more qualitative manner, the proposed approach highlights the potential of different prioritization techniques in vessel rotation and terminal cargo management through enhanced stakeholder collaboration and coordination.
Although the proposed coordination model yields promising results for medium-sized terminals, its applicability to larger ports merits further exploration. Power asymmetry warrants further investigation, as ports, particularly larger terminals, often have established relationships with specific stakeholders. These dynamics could be captured in the model through negotiation protocols or power-sensitive utility functions that reflect varying levels of influence. The model’s modular design facilitates such extensions. Validating the approach in a larger terminal would be a valuable direction for future research but may introduce challenges tied to a broader and more diverse stakeholder base, including data-sharing barriers and conflicting interests, issues more likely in the competitive environment of a major port. Real-world implementation should also address stakeholder reluctance toward oversight by clearly defining operational prerequisites and integration pathways for deploying the system within Port Community Systems. In terms of scalability, the computational cost of the Prioritized Search method, while capable of producing high-quality Pareto solutions, may limit its practicality in real-time or large-scale settings with constrained processing resources. Nevertheless, research avenues exist for improving the scalability of the approach. Another limitation of the current model is its reliance on deterministic vessel arrivals and fixed planning horizons. This reduces its responsiveness to real-world disruptions, such as delays or equipment failures. Furthermore, the model does not yet incorporate real-time data or reflect specific terminal technologies. For instance, in ports where Automated Guided Vehicles (AGVs) are deployed, the framework could be extended to represent AGV-based drayage operations.
Building on these limitations, possible extensions would focus on the further refining of the Prioritized Search algorithm. Enhancing the search strategy by incorporating more operators could potentially yield better outcomes through smarter exploration. Additionally, exploring alternative tree formation methods, such as depth-first search, might reduce computational costs associated with priority-based tree operations. An additional consideration would be to treat the terminal as an independent agent with its own objective value, taking into account other optimization criteria such as the minimization of empty runs. Applying this approach to a multi-terminal environment, where vessels and trucks may have to rotate between terminals could also introduce new complexities, enhancing our understanding of inter-terminal dynamics. Finally, the impact of dynamic scheduling, introduction of uncertainty in arrivals, and real-time data integration to enhance the adaptability of the proposed approach in disruptions could also be explored as well as the applicability to other domains, such as airport logistics or urban freight systems.
Author Contributions
Conceptualization, I.A.P., A.B. and A.S.; methodology, I.A.P., A.B. and A.S.; software, I.A.P.; validation, I.A.P., A.B. and A.S.; formal analysis, I.A.P., A.B. and A.S.; investigation, I.A.P., A.B. and A.S.; resources, A.B. and A.S.; data curation, I.A.P.; writing—original draft preparation, I.A.P.; writing—review and editing, I.A.P., A.B. and A.S.; visualization, I.A.P. and A.B.; supervision, A.B. and A.S.; project administration, A.S.; funding acquisition, A.B. and A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the European Union’s Horizon 2020 research and innovation program under the ORCHESTRA project, grant number 953618.
Data Availability Statement
The datasets utilized in this study are available upon request to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Stationary Backlog Carryover Queuing Approximation
For an expected arrival rate r:
where represents the expected trucks to be shifted to the next time-period based on the current arrival rate and service time of the gate and is the updated arrival rate. To compute the probability of traffic spilling over to the next-time-window, Erlang’s loss formula is applied. Parameter relates to Avg. gate service time.
To account for the modified arrival rate of trucks that are expected to be processed in a single time-period, the expected utilization rate of the gate is computed as follows:
For the computation of the expected queue length within each time window, the Cosmetatos approximation [38] is leveraged.
This approximation relies on the calculation of the waiting time for the queue (service times are exponentially distributed) and the expected waiting time for the queue (job service times are deterministic). Precise analytical derivations of queue performance metrics for these two queues are well-documented in [39].
queue
queue
References
- Akakura, Y. Analysis of offshore waiting at world container terminals and estimation of CO2 emissions from waiting ships. Asian Transp. Stud. 2023, 9, 100111. [Google Scholar] [CrossRef]
- European Commission. Strategic Transport Research and Innovation Agenda (STRIA)—Roadmap on Network and Traffic Management Systems; Technical report; European Commission Directorate-General for Research and Innovation: Brussels, Belgium, 2016.
- Zehendner, E.; Feillet, D. Benefits of a truck appointment system on the service quality of inland transport modes at a multimodal container terminal. Eur. J. Oper. Res. 2014, 235, 461–469. [Google Scholar] [CrossRef]
- Li, W.; Wu, Z.; Yang, P.; Cai, L. Collaborative Scheduling Optimization of Equipment in Multimodal Transport Harbor Considering Hybrid Operation Mode of “train-yard-vessel” and “train-vessel”. In Proceedings of the 2022 IEEE 18th International Conference on Automation Science and Engineering (CASE), Mexico City, Mexico, 20–24 August 2022; pp. 86–91. [Google Scholar] [CrossRef]
- Huynh, N.; Smith, D.; Harder, F. Truck Appointment Systems: Where We Are and Where to Go from Here. Transp. Res. Rec. 2016, 2548, 1–9. [Google Scholar] [CrossRef]
- Huynh, N.N.; Walton, C.M. Methodologies for Reducing Truck Turn Time at Marine Container Terminals; Technical report; University of Texas at Austin, Center for Transportation Research: Austin, TX, USA, 2005. [Google Scholar]
- Chen, X.; Zhou, X.; List, G.F. Using time-varying tolls to optimize truck arrivals at ports. Transp. Res. Part E Logist. Transp. Rev. 2011, 47, 965–982. [Google Scholar] [CrossRef]
- Phan, M.H.; Kim, K.H. Negotiating truck arrival times among trucking companies and a container terminal. Transp. Res. Part E Logist. Transp. Rev. 2015, 75, 132–144. [Google Scholar] [CrossRef]
- Parmaksizoglou, I.A.; Bombelli, A.; Sharpanskykh, A. A Novel Auction-Based Truck Appointment System for Marine Terminals. Logistics 2024, 8, 40. [Google Scholar] [CrossRef]
- Shiri, S.; Huynh, N. Optimization of drayage operations with time-window constraints. Int. J. Prod. Econ. 2016, 176, 7–20. [Google Scholar] [CrossRef]
- Chen, G.; Govindan, K.; Yang, Z. Managing truck arrivals with time windows to alleviate gate congestion at container terminals. Int. J. Prod. Econ. 2013, 141, 179–188. [Google Scholar] [CrossRef]
- Ma, M.; Fan, H.; Jiang, X.; Guo, Z. Truck Arrivals Scheduling with Vessel Dependent Time Windows to Reduce Carbon Emissions. Sustainability 2019, 11, 6410. [Google Scholar] [CrossRef]
- Schulte, F.; Lalla-Ruiz, E.; González-Ramírez, R.G.; Voß, S. Reducing port-related empty truck emissions: A mathematical approach for truck appointments with collaboration. Transp. Res. Part E Logist. Transp. Rev. 2017, 105, 195–212. [Google Scholar] [CrossRef]
- Bierwirth, C.; Meisel, F. A follow-up survey of berth allocation and quay crane scheduling problems in container terminals. Eur. J. Oper. Res. 2015, 244, 675–689. [Google Scholar] [CrossRef]
- Rodrigues, F.; Agra, A. Berth allocation and quay crane assignment/scheduling problem under uncertainty: A survey. Eur. J. Oper. Res. 2022, 303, 501–524. [Google Scholar] [CrossRef]
- Zhen, L. Tactical berth allocation under uncertainty. Eur. J. Oper. Res. 2015, 247, 928–944. [Google Scholar] [CrossRef]
- Ma, M.; Zhao, W.; Fan, H.; Gong, Y. Collaborative Optimization of Yard Crane Deployment and Inbound Truck Arrivals with Vessel-Dependent Time Windows. J. Mar. Sci. Eng. 2022, 10, 1650. [Google Scholar] [CrossRef]
- Yin, X.F.; Khoo, L.P.; Chen, C.H. A distributed agent system for port planning and scheduling. Adv. Eng. Inform. 2011, 25, 403–412. [Google Scholar] [CrossRef]
- Sun, Z.; Lee, L.H.; Chew, E.P.; Tan, K.C. MicroPort: A general simulation platform for seaport container terminals. Adv. Eng. Inform. 2012, 26, 80–89. [Google Scholar] [CrossRef]
- Feng, F.; Pang, Y.; Lodewijks, G. Integrate multi-agent planning in hinterland transport: Design, implementation and evaluation. Adv. Eng. Inform. 2015, 29, 1055–1071. [Google Scholar] [CrossRef]
- Chen, Z.; Alonso-Mora, J.; Bai, X.; Harabor, D.D.; Stuckey, P.J. Integrated Task Assignment and Path Planning for Capacitated Multi-Agent Pickup and Delivery. IEEE Robot. Autom. Lett. 2021, 6, 5816–5823. [Google Scholar] [CrossRef]
- Wu, X.; Liu, Y.; Tang, X.; Cai, W.; Bai, F.; Khonstantine, G.; Zhao, G. Multi-Agent Pickup and Delivery with Task Deadlines. In Proceedings of the IEEE/WIC/ACM International Conference on Web Intelligence and Intelligent Agent Technology, New York, NY, USA, 17–20 November 2022; WI-IAT ’21. pp. 360–367. [Google Scholar] [CrossRef]
- Xu, Q.; Li, J.; Koenig, S.; Ma, H. Multi-Goal Multi-Agent Pickup and Delivery. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; pp. 9964–9971. [Google Scholar] [CrossRef]
- Ahmadi, E.; Zandieh, M.; Farrokh, M.; Emami, S.M. A multi objective optimization approach for flexible job shop scheduling problem under random machine breakdown by evolutionary algorithms. Comput. Oper. Res. 2016, 73, 56–66. [Google Scholar] [CrossRef]
- Wu, Y.; Yang, H.; Tang, J.; Yu, Y. Multi-objective re-synchronizing of bus timetable: Model, complexity and solution. Transp. Res. Part C Emerg. Technol. 2016, 67, 149–168. [Google Scholar] [CrossRef]
- Bandyopadhyay, S.; Bhattacharya, R. Solving multi-objective parallel machine scheduling problem by a modified NSGA-II. Appl. Math. Model. 2013, 37, 6718–6729. [Google Scholar] [CrossRef]
- Amini, A.; Tavakkoli-Moghaddam, R. A bi-objective truck scheduling problem in a cross-docking center with probability of breakdown for trucks. Comput. Ind. Eng. 2016, 96, 180–191. [Google Scholar] [CrossRef]
- Wen, X.; Chen, Q.; Yin, Y.Q.; Lau, Y.y.; Dulebenets, M.A. Multi-Objective Optimization for Ship Scheduling with Port Congestion and Environmental Considerations. J. Mar. Sci. Eng. 2024, 12, 114. [Google Scholar] [CrossRef]
- Niu, B.; Liu, Q.; Wang, Z.; Tan, L.; Li, L. Multi-objective bacterial colony optimization algorithm for integrated container terminal scheduling problem. Nat. Comput. 2021, 20, 89–104. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the Strength Pareto Evolutionary Algorithm for Multiobjective Optimization. In Proceedings of the Evolutionary Methods for Design, Optimization and Control with Applications to Industrial Problems, Athens, Greece, 19–21 September 2001; Proceedings of the EUROGEN’2001. pp. 19–21. [Google Scholar]
- Minh, C.C.; Noi, N.V. Optimising truck arrival management and number of service gates at container terminals. Marit. Bus. Rev. 2023, 8, 18–31. [Google Scholar] [CrossRef]
- Minh, C.C.; Huynh, N. Planning-Level Tool for Assessing and Optimizing Gate Layout for Marine Container Terminals. Transp. Res. Rec. 2014, 2409, 31–39. [Google Scholar] [CrossRef]
- Stolletz, R. Analysis of passenger queues at airport terminals. Res. Transp. Bus. Manag. 2011, 1, 144–149. [Google Scholar] [CrossRef]
- Zhang, X.; Zeng, Q.; Chen, W. Optimization Model for Truck Appointment in Container Terminals. Procedia—Soc. Behav. Sci. 2013, 96, 1938–1947. [Google Scholar] [CrossRef]
- The World Bank. The Container Port Performance Index 2023: A Comparable Assessment of Performance Based on Vessel Time in Port; Technical report; The World Bank, Transport Global Practice: Washington, DC, USA, 2024. [Google Scholar]
- Blank, J.; Deb, K. Pymoo: Multi-Objective Optimization in Python. IEEE Access 2020, 8, 89497–89509. [Google Scholar] [CrossRef]
- Cosmetatos, G.P. Approximate Equilibrium Results for the Multi-Server Queue (GI/M/r). J. Oper. Res. Soc. 1974, 25, 625–634. [Google Scholar] [CrossRef]
- Bolch, G.; Greiner, S.; de Meer, H.; Trivedi, K.S. Queueing Networks and Markov Chains: Modeling and Performance Evaluation With Computer Science Applications; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).