Abstract
Background: Governments face critical decisions regarding road remediation projects, requiring careful economic evaluation, especially in countries like Slovakia where road infrastructure is crucial for attracting foreign investment. These decisions are complex, involving short-term and long-term costs and revenues, along with inherent uncertainty about future outcomes. Traditional economic assessments often fail to capture the full scope of these factors, potentially leading to suboptimal choices. Methods: This study proposes four probability-based models: the Short-term Model (SM), Long-term-Short-term Model (LSM), Social Long-term-Short-term Model (SLSM), and Long-term-Short-term Model with a Time Aspect (TLSM). These models incorporate probabilistic functions to calculate expected costs and profits, considering various factors such as reparation costs, financial compensations, social costs, and time-related costs, as well as long-term benefits like increased investment and lives saved. Results: The proposed models were partially validated through an ex post analysis of a past road remediation project on road 1/18 (E50) under the Strecno castle cliff in Slovakia. The analysis demonstrated the models’ utility for multi-criteria decision-making in transportation problems, highlighting their ability to capture the complex interplay of economic and societal factors. Conclusions: The models enable governments to maximize societal benefit while mitigating potential risks, contributing to a more sustainable and efficient transportation sector. Future research could focus on refining the models and adapting them to other sectors beyond transportation.
1. Introduction
Making economically sound decisions can lead to significant savings for governments, allowing them to allocate resources to other important sectors like healthcare or education. Decisions related to traffic problems are influenced by various financial and non-financial factors. It is essential to consider both short-term and long-term costs and benefits. Additionally, the economic assessment of traffic problems should include an evaluation of the costs incurred by companies due to implemented solutions.
This research addresses two key questions:
- What types of costs and revenues should governments consider to make economically efficient decisions in the short and long term for the benefit of the whole society?
- In the presence of uncertainty, how should governments evaluate road remediation projects to maximize benefits for society?
Since analyzing economic efficiency involves predicting future outcomes and therefore inherent uncertainty, our models utilize probabilistic functions and are based on quantifying uncertainty using the theory of expected returns and expected costs.
This paper presents four multi-aspect probability models designed to assess expected profits under uncertainty for multi-criteria evaluation in transportation:
- Short-term model (SM)
- Long-term-short-term model (LSM)
- Social long-term-short-term model (SLSM)
- Long-term-short-term model extended by a time aspect (TLSM)
Finally, we conduct a partial ex post validation of the proposed concepts and analyze a past road project to demonstrate their effectiveness. These models can be applied to various transport problems involving multiple companies and individuals.
Transportation projects often involve substantial infrastructure development and require significant financial investment. Therefore, making well-informed decisions is crucial in this domain. Economically sound decisions can result in considerable savings, which can then be allocated to other essential areas, such as healthcare or education. Economic decision-making relies on a thorough economic assessment of the problem, involving the quantification and subsequent comparison of costs and revenues. A comprehensive analysis that considers all aspects of the problem is essential for making informed decisions. In many countries, governments fail to consider all aspects of transportation problems, leading to a lack of systematic management in this area. This has been a significant issue in Slovakia, where transportation infrastructure is often seen as a critical factor for attracting foreign investment. The growth of vehicles on Slovak roads is alarming, with the number steadily increasing. In Figure 1, over 3.6 million vehicles were on Slovak roads in 2023, an 11.1% rise from 2019. Personal vehicles constituted 72.4% of all traffic. The trend of increasing vehicle numbers on Slovak roads is evident and clear.
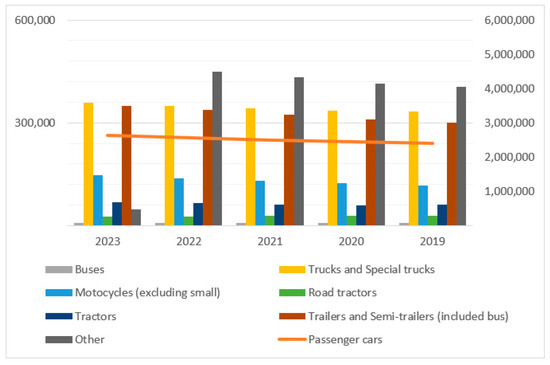
Figure 1.
Evolution of types of vehicle transport in Slovakia—2019–2023 [1].
In contrast, in Figure 2 there has been a continuous decline in the use of public transportation. The decrease from 2019 is −35.93%. The number of people using public transport decreased by 35.93% in the last five years to 173.276 million. Public transport decreased in all Slovak regions. There is a clear trend in Slovakia: less and less use of public transport. The transport where two or more people commute by the same transport means is decreasing very significantly. However, public transport saves costs for traveling, road infrastructure, and the environment. Instead, there is a large increase in personal transport, which burdens the Slovak road infrastructure significantly.
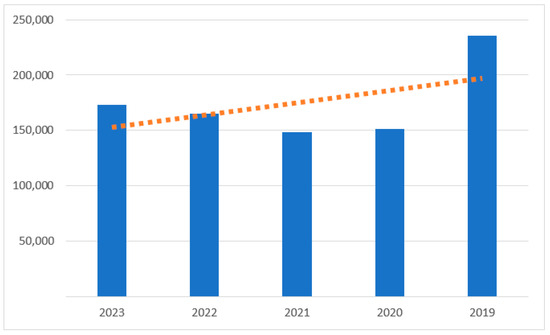
Figure 2.
Public transport in Slovakia—2019–2023 [2].
In addition to the rise in registered vehicles, the transportation of goods has also been increasing since 2020. In Slovakia, the transportation of goods has increased in most regions. It is therefore not surprising that the number of trucks on Slovak roads is also increasing. This trend negatively impacts the current state of transport infrastructure. Figure 3 illustrates the development of freight transport in Slovakia between 2019 and 2023, specifically the transport of goods on roads using trucks and special tracks.
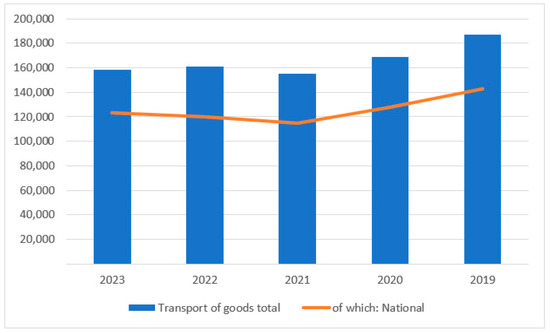
Figure 3.
Freight transportation of goods—2019–2023 [3].
As indicated in Figure 3, freight transportation has been decreasing since 2019, with an 18.23% decrease by 2023. However, based on the 4.16% increase observed in 2021, there is a strong estimate that freight transportation will continue to increase slowly. If the government does not address transportation more systematically, the situation may become unsustainable, leading to increased social costs and negative public sentiment.
The trends described above also affect road safety in Slovakia. In Slovakia, this trend is even more pronounced due to the lack of adequate and completed transport infrastructure, particularly motorways (see Figure 4).
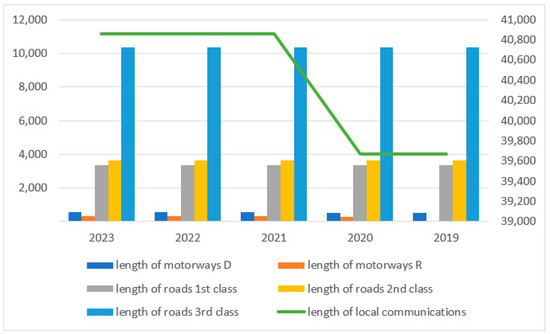
Figure 4.
Transport infrastructure in Slovakia—2019–2023 [4].
While there has been a decrease in road fatalities in Slovakia, the continuous growth in vehicle numbers poses a significant safety concern. Without a revised government strategy to improve the quality of Slovak roads, the number of fatalities and injuries may rise in the future as we see in Figure 5.
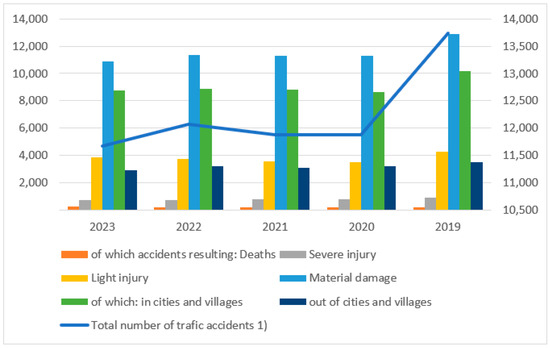
Figure 5.
Accidents on roads in Slovakia—2019–2023 [5].
The primary contribution of this paper is the proposal of economic models in the transportation field that account for uncertainty. We introduce several models: the short-term model (SM), the long-term-short-term model (LSM), the social LSM model (SLSM), and the LSM model with a time aspect (TLSM). These models can be used in the decision-making process for various transportation problems under conditions of uncertainty. Another contribution is the extension of these models by incorporating social and time aspects.
The motivation for this study comes from the critical need for governments to make economically sound decisions regarding road remediation projects. These projects often involve significant financial investments and have long-term consequences for society. However, traditional economic assessments often fail to capture the full complexity of these decisions, particularly the long-term impacts and inherent uncertainties. This can lead to suboptimal choices that do not maximize societal benefit. This study makes several key contributions to the field of transportation economics:
- Development of Comprehensive Models: We propose four probability-based models that provide a robust framework for evaluating road remediation projects under uncertainty. These models incorporate a wide range of costs and benefits, including short-term and long-term factors, social costs, and time-related costs.
- Integration of Uncertainty: The models explicitly address the issue of uncertainty by using probabilistic principles to express expected costs and profits. This allows decision-makers to better understand the potential risks and rewards associated with different project options.
- Partial ex post Validation: The concepts are partially validated through an ex post analysis of a past road project in Slovakia. This provides empirical evidence of the models’ utility for multi-criteria decision-making in transportation problems.
- Focus on Societal Benefit: The study emphasizes the importance of considering societal costs and benefits in addition to purely economic factors. This ensures that decisions are made in the best interests of the entire community.
In summary, this study provides a valuable tool for governments to make more informed and effective decisions regarding road remediation projects. By incorporating uncertainty, considering a wide range of costs and benefits, and focusing on societal welfare, the proposed models contribute to a more sustainable and efficient transportation sector.
2. Theoretical Research Implementation
This expanded literature review delves deeper into the complexities of economic modeling and evaluation in transportation, providing a comprehensive overview of recent research and highlighting key themes, methodologies, and future directions.
Accurate and comprehensive economic modeling is crucial for evaluating the viability and sustainability of transportation projects. Shi et al. investigated optimal concession contract design for Build-Operate-Transfer (BOT) road projects under asymmetric information, highlighting the importance of considering information asymmetry in project evaluation. Their research underscores the need for models that account for the different levels of information available to various stakeholders involved in transportation projects. Incorporating information asymmetry into economic models can lead to more realistic and robust evaluations, ultimately contributing to better decision-making. The studies deal with the capacity problem of roads. They investigate the impact of road construction on road traffic capacity. By analyzing traffic and road conditions and by putting forward specific measures, they propose a model which could improve the capacity of road traffic. With the accelerated process of urbanization, the construction of urban transportation infrastructure needs to be improved. This problem has been a focus of many studies all over the world. Scientists use different models and methodologies to suggest how the current state in the field of transport in specific regions of different countries could be improved [6,7,8,9,10].
Also, definitions of the optimal transport problem through Möbius transform were provided by Torra [11]. Optimizing routing decisions for a company’s fleet vehicles by addressing the Traveling Salesperson Problem (TSP) and Vehicle Routing Problem (VRP) also has the ultimate goal of reducing transportation costs according to Malhotra [12]. Xiang [13] proposes a fuzzy compromise method with an improved S-type membership function for multi-objective transportation decision-making, which evaluates both individual objectives and the overall objectiveness as a whole. The method transforms the multi-objective transportation linear programming model into a multi-objective transportation fuzzy compromise programming model and expresses its satisfaction by the global utility function.
Kozubek [14] conducted an ex post analysis of road investments, emphasizing the need to incorporate long-term perspectives and societal impacts in economic assessments. This study highlights the limitations of traditional cost–benefit analyses that often focus on short-term financial gains and overlook the broader societal implications of transportation projects. By incorporating long-term perspectives and societal impacts, economic models can provide a more holistic view of project viability, ensuring that decisions align with broader societal goals and contribute to sustainable development.
MCDA has emerged as a crucial tool for evaluating transportation projects, enabling the integration of multiple criteria and stakeholder preferences. Jasiuniene et al. applied MCDA to road network safety ranking, demonstrating its effectiveness in incorporating diverse factors such as accident rates, traffic volume, and road characteristics. Their study showcases the versatility of MCDA in handling complex decision-making processes with multiple, often conflicting objectives. By incorporating diverse criteria and stakeholder preferences, MCDA provides a more nuanced and comprehensive evaluation of transportation projects, facilitating informed decision-making that considers various perspectives and priorities [15,16].
Rudzianskaite-Kvaraciejiene et al. explored the use of MCDA for evaluating road investment project effectiveness, highlighting its ability to handle complex decision-making processes with multiple objectives. Their research emphasizes the importance of considering both quantitative and qualitative factors in transportation project evaluation, allowing for a more holistic assessment of project impacts. MCDA provides a structured framework for integrating these diverse factors, facilitating transparent and objective decision-making that balances various considerations and promotes sustainable transportation solutions [17,18,19].
Nowadays, road safety has become a major concern in most modern societies. One of the major problems in the transport area is how to systematically identify, assess, remove, and mitigate road risks in planning, designing, building, and using them. The determination of more dangerous road locations can be helpful in better scheduling road safety projects and in protecting people’s lives. Many propose a multivariate model for identifying and ranking dangerous accident locations according to their total expected cost to society using Bayesian estimation. Jamroz et al. present a system of tools for mitigating road risks and a concept of how these tools could be developed in Poland. They suggest methods for long-term forecasts of accidents and accident cost estimation as well as a set of rules for dangerous road risk classification. Koman et al. raise the electromobility element, which enters road infrastructure and influences life in cities [19,20,21,22].
Given the inherent uncertainties in transportation systems, researchers have explored methods to incorporate uncertainty and risk into economic models. Yuan et al. developed a risk assessment framework for electric power investment in Belt and Road Initiative nations, highlighting the importance of considering uncertainties related to policy, technology, and market conditions. Their study emphasizes the need for robust risk assessment frameworks that can capture the dynamic and unpredictable nature of transportation systems. By incorporating uncertainty and risk into economic models, decision-makers can better anticipate potential challenges and make more informed decisions that mitigate risks and enhance project resilience [20,23].
On the other hand, according to some researchers, today, in the era of technologies, cooperative systems applying infrastructure-to-vehicle (I2V) communication to intelligent transportation systems (ITS) are considered a key means to ensure safe and efficient driving in the increasingly overloaded infrastructure. In one study, the authors investigated driver behavior with cooperative systems based on infrastructure-to-vehicle communication. Based on the results of the COOPERS project, they found that I2V communication systems appear to influence driver behavior positively. Drivers remain calmer in stressful situations, and the direct influence on road safety can be observed in reduced driving speeds before dangerous situations occur. Thus, a positive indication for driver support during dangerous situations can be obtained. Their study underscores the importance of understanding the behavioral implications of new technologies, as these can significantly impact the effectiveness and adoption of transportation solutions. Incorporating behavioral considerations into economic models can lead to more accurate predictions and better inform the development and implementation of new technologies [24,25].
The second big problem is the financial aspect of transport infrastructure, both for building new infrastructure and for repairing current infrastructure. It is therefore no surprise that the focus is on the problem of selecting the most effective road investment projects, which is becoming more and more acute. Some papers deal with the problem of how to finance effective road projects, as road investments are often appraised from economic, social, and environmental viewpoints separately. One study, which is based on the principle of sustainable development, proposes a methodology for selecting the most effective road projects based on a combination of economic, social, and environmental aspects [14,17].
More often, such studies begin by examining the construction of active sports centers that are visited by large numbers of athletes and spectators. It is more than appropriate to have a suitable infrastructure to satisfy the transport needs of this segment. Valuing the current financial situation is important for the implementation of digital technologies in transport and human capital management in this area [26,27,28].
This review highlights the diverse range of research on economic modeling and evaluation in transportation. Future studies should focus on integrating these approaches to develop comprehensive frameworks that consider economic, social, environmental, and technological factors, enabling informed decision-making for sustainable transportation systems. This integration requires interdisciplinary collaboration and the development of innovative methodologies that can capture the complex interactions between various factors influencing transportation systems.
Furthermore, future research should prioritize the development of user-friendly decision support tools based on these comprehensive frameworks, making them accessible to decision-makers in government and industry. These tools can facilitate informed decision-making by providing clear and concise insights into the economic, social, and environmental implications of transportation projects, ultimately contributing to the development of sustainable and resilient transportation systems that serve the needs of present and future generations.
3. Materials and Methods
Evaluating the economic efficiency of road remediation projects requires a thorough approach that considers various factors and their potential impacts on society. To address this, this study proposes four distinct models, each capturing different aspects of the economic evaluation process. These models provide a framework for decision-making, enabling governments to assess the short-term and long-term costs and benefits of road remediation projects while also incorporating the inherent uncertainty associated with future outcomes.
The following sections detail each of the four models:
- 1. Short-term model (SM): This model focuses on the immediate costs and revenues of road remediation projects, providing a short-term perspective on economic efficiency.
- 2. Long-term-short-term model (LSM): Expanding on the SM model, the LSM model incorporates long-term considerations, allowing for a more comprehensive evaluation of costs and benefits over an extended period.
- 3. Extensions of LSM model: This section introduces two extensions of the LSM model, further refining the economic evaluation process.
- 3.1. Social extension: SLSM model: The SLSM model incorporates social costs into the analysis, providing a broader societal perspective on the impacts of road remediation projects.
- 3.2. Time extension: TLSM model: Recognizing the value of time, the TLSM model incorporates time-related costs and benefits into the evaluation, providing a more nuanced understanding of the economic efficiency of road remediation projects.
It is clear that a number of factors influence decision-making regarding traffic problems. Some of the mentioned factors can be directly expressed in financial form, but some factors are not explicitly defined in financial form. However, even these factors must be taken into account when making decisions in the transport area. Thus, the economic analysis should take into account all the factors that are connected with the mentioned problem, both financial and non-financial.
To properly evaluate the economic cost of a traffic problem, such as deciding on reconstruction, it is necessary to consider both long-term and short-term aspects (costs) and revenues. Long-term costs and revenues are not typically included in a standard economic assessment.
In the economic assessment of the transport problem, it is also necessary to address the costs that the implemented solution will impose on the citizens of the country.
Additionally, since the aforementioned analysis of economic efficiency concerns the future and is therefore associated with a certain degree of uncertainty, it is necessary to incorporate this degree of uncertainty into the economic analysis, which will serve to evaluate the economic efficiency of transport problems.
Based on the above, we decided to define the following research questions:
- RQ1: What types of costs and revenues should the government take into account to make an economically efficient decision in a short time period and in a long time period for the whole society?
- RQ2: Given uncertainty, how should the government evaluate a transport problem of road remediation to maximize the profit for society?
We use an economic approach to evaluate the decision-making process for road rehabilitation. Economic calculations exist as a generally acceptable means of indirect change. This procedure can be used to estimate the expected results of future actions or the results of past actions. Our suggested model uses two basic concepts:
- The cost–benefit analysis [29]—This concept of economic analysis can be applied in various areas when an economic actor decides between multiple options subject to uncertainty; the result is supposed to be economically optimal for the actor.
- Application of theory of expected profits adapted from [30]—Since it is not possible to explicitly determine some phenomena in the future, our model uses probabilistic form, and the expected mean value of the given variable is always taken into account.
The following Figure 6 presents our flowchart of our suggested models.
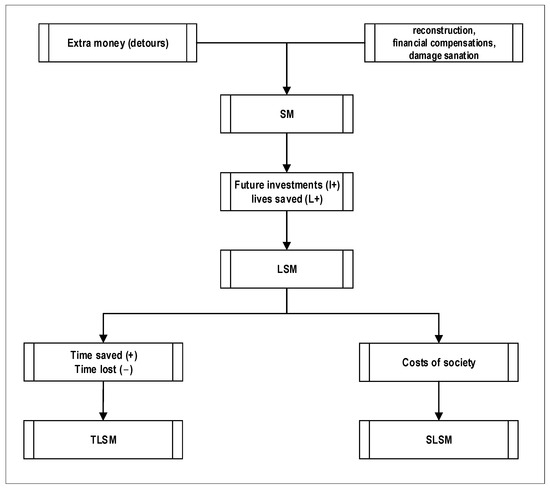
Figure 6.
Flowchart of our suggested models with their cost and revenue aspects.
The following Table 1 summarizes the different types of costs and benefits considered in the models.

Table 1.
Different types of costs and benefits considered in models.
3.1. Short-Term Model (SM)
Since the random variables that we will use in the model are not constant and exhibit a probability distribution, the basic principle of our decision criterion consists in choosing the variant that maximizes the expected short-term profit (SP),
where SP is a random variable which expresses the short-term profit, SR is a random variable which expresses short-term revenues, SC is a random variable which expresses short-term costs, and vi is the selected variant of solution selected from the set of all available variants V = {v1, v2, …, vk}, which are taken into consideration as possible solutions to the problem.
We define the benefit for government in the first sense of the word, as the government gains real benefits from vi realization, i.e., with additional money in the budget. We define expected short-term revenues as
where
- SR is a random variable which expresses the amount of extra euros that the government collects due to the increased amount of refueling caused by closures, detours, or restrictions. Moreover, SR is the sum of extra value-added tax and extra consumption tax collected by the government as a result of road closures and related detours.
- b is a value of the random variable SR.
- is the probability that the government will collect taxes in the amount of b EUR.
- is a probability density function of the random variable SR.
In the SM model, we define expected short-term costs as the sum of three types of costs: costs of remediation, financial compensation, and damage sanitation due to any accidents. Costs of remediation are the actual costs related to the remediation of the road. Of course, there is an option that the priority for remediation will be low, and that the road is remediated insufficiently or will not be remediated at all. In that case, the government must count on the option that there will be accidents related to the damage on the road, i.e., the government must count on the costs related to financial compensation as well as damage sanitation costs. The total expected costs of the SM model are defined as
where
- RC is a random variable which expresses direct costs of reconstruction (repair costs).
- FC is a random variable which expresses direct costs of financial compensation.
- DC is a random variable which expresses damage costs.
- r is a value of the random variable RC.
- c is a value of the random variable FC.
- d is a value of the random variable DC.
- is the probability that the remediation will cost r EUR.
- is the probability that the compensations will cost c EUR.
- is the probability that the damage sanitation will cost d EUR.
- are probability density functions of the random variable RC, FC, DC.
In the SM model, expected short-term profit is then defined as
where the notations are the same as defined earlier.
3.2. Long-Term-Short-Term Model (LSM)
In this section, we extend our basic SM model with a long-term component. The Long-term-short-term (LSM) model is based on two time aspects—short period and long period. In this case, total profits (TP) are expressed as the sum of expected total profit in the short term (also denoted as expected immediate profit) and expected profit in the long term (i.e., expected future profits, indirect profits), i.e.,
where TP is a random variable which expresses total profit, TR is a random variable which expresses total revenue, TC is a random variable which expresses total costs, is a random variable which expresses short term revenues, is a random variable which expresses long term revenues, is a random variable which expresses short term costs, are long term costs, and vi is the variant of solution selected from the set of all available variants V = {v1, v2, …, vk}, which are taken into consideration as possible solutions to the problem.
As stated earlier, we define the expected revenues in the short term as
where
- SR is a random variable which expresses the amount of extra euros that the government collects due to the increased amount of refueling caused by closures, detours, or restrictions. Moreover, SR is the sum of extra value-added tax and extra consumption tax collected by the government as a result of road closures and related detours.
- b is a value of the random variable SR.
- is the probability that the government will collect taxes in the amount of b EUR.
- is a probability density function of the random variable SR.
We define expected revenues in the long term as the sum of expected revenues from future investments and expected revenues from saved lives for the given variant vi, i.e.,
where
- I+ is a random variable which expresses an increase in investment in the region compared to the current situation as a result of the implementation of the given variant (in EUR).
- L+ is a random variable which expresses an increase in saved lives (number of people) compared to the current situation as a result of the implementation of the given variant.
- i is a value of the random variable I+.
- l is a value of the random variable L+.
- is the probability that the government will additionally receive an investment in the amount of i EUR in the future.
- is the probability that the government will save l people the future as a result of the implementation of variant vi.
- is a probability density function of the random variable I+.
- is a probability density function of the random variable L+.
- w is the average amount of taxes that one person pays to the government during their lifetime.
Obviously, the expected total profits (TP) will have to take into account the costs associated with them. We define expected total costs in the LSM model as the sum of three types of costs, and their expression is the same as in the STM model, i.e., as defined by Equations (4)–(7). Based on the above, the expected total profits in the long term are defined as follows:
Total (short-term + long-term) expected profits are defined as
where
- SR, I+, L+, RC, DC, FC are random variables.
- b, i, l, r, d, c are values of the random variables SR, I+, L+, RC, DC, FC which we defined above.
- is the probability that a random variable VAR = {SR, I+, L+, RC, DC, FC} is equal to the value of k = {r, c, d, f}.
- are probability density functions of the random variables SR, I+, L+, RC, DC, FC.
Based on notations from [31] the discrete version for total expected profits is defined as
where
- SR, I+, L+, RC, DC, FC are random variables.
- bj, ij, lj, rj, dj, cj are values of the random variables SR, I+, L+, RC, DC, FC.
- is the probability that a discrete random variable VAR = {SR, I+, L+, RC, DC, FC} is equal to the value of xj.
- are probability functions of the discrete random variables SR, I+, L+, RC, DC, FC.
3.3. Extensions of LSM Model
3.3.1. Social Extension: SLSM Model
In this section, the LSM model is extended by incorporating social costs. For comparing benefits and costs of the selected variant, one should consider the costs to society as well. We define these costs as extra costs of vi variant, which society (citizens/drivers) must pay due to increased consumption of fuels caused by restrictions and detours, i.e.,
where
- F is a random variable which expresses the amount of extra euros that the drivers have to pay for extra fuel due to the increased amount of refueling caused by closures, detours, or restrictions.
- f is a value of the random variable I+.
- is the probability that the drivers will pay f EUR because of purchases of extra fuel.
- is a probability density function of the random variable F.
The total expected costs after incorporating these losses can be expressed as
where
- RC, DC, FC, F are random variables.
- r, f, d, c are values of random variables RC, FC, DC, F which we defined above.
- fk are denoted as the probability density functions of these random variables, k = {r, c, d, f} and
- is the probability that a random variable VAR = {SR, I+, L+, RC, DC, FC} is equal to the value of k = {r, c, d, f}.
- are probability density functions of the random variables RC, FC, DC, F.
3.3.2. Time Extension: TLSM Model
As time is an important variable in the economy, we decided to incorporate the time aspect into our models. The idea is that if travelers save time, it can be spent on the production of additional goods and services, which can have a multiplier effect on the country’s economy. The extension by the time aspect can be incorporated into our models for two reasons. First, in the case of road closures, reconstruction, or detours, drivers/passengers will lose time. Secondly, thanks to the reconstruction or creation of a safer and faster road, drivers/passengers can save a significant amount of time. For this reason, we define TS as time saved, which will be defined as the amount of time that drivers/passengers gain per year thanks to the performed reconstruction, i.e.,
where
- TS is a random variable which expresses the amount of time that one driver/passenger saves thanks to realization of the selected variant vi.
- s is a value of the random variable TS.
- is the probability that a driver saves s amount of time.
- is a probability density function of the random variable TS.
We also define TL as a random variable that expresses the total time that one driver/passenger will lose in a year due to the closures or detours caused by the variant vi.
- z is a value of the random variable TL, which is defined as the amount of time that a driver loses due to the realization of the selected variant vi.
- TL is a random variable which expresses the amount of time that a driver loses due to the realization of the selected variant vi.
- z is a value of the random variable TL.
- is the probability that a driver loses z amount of time.
- is a probability density function of the random variable TL.
Based on the above, the expected Total Time Surplus (TTS) for the year of reconstruction (we assume in this case that the reconstruction will take a maximum of one year) can be defined as follows:
where
- TS, TL are random variables.
- s, z are values of random variables TS, TL which we defined above.
- is the probability that a random variable VAR = {TL, TS} is equal to the value of k = {s, z}.
- are probability density functions of the random variables TS, TL.
For subsequent years, if we assume that the reconstruction will take a maximum of one year, the total time surplus (TTS) can be defined as follows:
where
- TS is a random variable which expresses the amount of time that one driver/passenger saves thanks to realization of the selected variant vi.
- s is a value of the random variable TS.
- is the probability that a driver saves s amount of time.
- is a probability density function of the random variable TS.
It is obvious that in this case, it is necessary to define the number of people who will pass the given section during the year and also the number of years that will be taken into account in the case of calculating profits from the point of view of saving time. Last but not least, to quantify this model, it is necessary to define the average salary.
In the case of incorporating the time and costs for society, the expected total profit will include the following random variables:
The expected total profit TS-LSM model (i.e., after taking into account the aspects of time and society’s costs) can then be defined as
where
E[TP] = E[TR] − E[TC]
- SR, I+, L+, RC, FC, DC, F, TS, TL are random variables.
- r, f, d, c are values of random variables RC, FC, DC, F which we defined above.
- fk are denoted as the probability density functions of these random variables, k = {r, c, d, f}.
- is the probability that a random variable VAR = {SR, I+, L+, RC, FC, DC, F, TS, TL} is equal to the value of k = {b, i, l, r, c, d, f, s, z}.
- are probability density functions of the random variables SR, I+, L+, RC, FC, DC, F, TS, TL.
- n1 is a constant related to the sum of the number of drivers/passengers passing this route per given period, n2 is related to the number of drivers/passengers that have to use the detour caused the reconstruction in a given time period, and m is the average wage per hour.
Important note:
Resulting from theory of probability [31] it is important to note that in order for the above functions to be probability (density) functions of a random variable, the normalization condition must hold for all defined random variables mentioned above, i.e.,
Also, for all probability density functions of the random variables defined earlier the following conditions must be true [31]:
and must be defined for all values where x represents our defined random variables .
As for discrete versions of the random variables, in order for the above functions to be probability density functions of a random variable, the following normalization condition must hold for all defined random variables mentioned above
4. Results
In this section, the concepts of our models were applied to a selected problem in Slovak transport. Given that the solution was already implemented in our case, we verified the concepts of multi-criteria decision-making in transport proposed by us through partial ex post analysis.
We decided to apply and validate suggested principles to a transport problem in Slovakia, more specifically to one particular situation which took place in the past on the 1/18 road. Because of the growing economy in Slovakia, it is very likely that the volume of transport will rise in the coming years. It is therefore necessary to build new road infrastructure or at least extend and repair the existing infrastructure. However, the variety of country design is a big problem for the development of transport infrastructure in the whole country. Valleys of rivers varying with agricultural, forest, and mountain country pose challenges, regarding not only super elevations (climbing) but also geological variety of territories (possible soil slips, effect of weather, urbanization, forest logging, etc.).
One of the biggest transportation problems in Slovakia is the problem of route 1/18 (international route E50) underneath the cliff where the Strecno castle is located. It is the main road from the west of the county to the east. The situation underneath Strecno castle is a very serious problem in Slovakia due to several reasons. First, as we said before, there is a risk of rock falling on the road. However, as stated above, the problem of passage under the Strecno castle is not only about the danger of falling rocks and maintenance of the cliff. Secondly, due to lack of space, the road contains insufficient narrow lanes. The road does not meet the standards of a first-class road, it contains very narrow lanes, and it does not have emergency lanes and barriers. It is therefore no surprise that this also influences driving behavior. A review of the detailed Roadside Infrastructure for Safer European Roads accident database revealed that lateral positioning and speed of the vehicle were two of the primary factors leading to crashes. A study by van der Horst and de Ridder [31] found that roadside infrastructure influences driving behavior. Their driving simulator study investigated how roadside infrastructure affects drivers’ speed choices and lateral vehicle placement. Roadside features studied included trees, guardrails, barriers, panels, and emergency lanes. The study found that drivers tended to move laterally away from safety barriers upon approaching them and slightly slowed down. The type and size of a safety barrier appeared to be less important than its presence. Trees did not affect driver speed unless they were close (2 m) to the road edge on a rural road with an 80 km/h speed limit, and this effect faded quickly. There was no influence on speed if the trees were more than 4.5 m from the lane edge. The fact that trees along the road are not considered a hazard, and drivers do not adjust their behavior accordingly, makes them even more dangerous [32]. In addition, the road is consistently overloaded. According to the non-profit organization of the European Program for Routes Evaluations (EuroRAP), most Slovak roads, including this one, fall into the range with medium and high rate of risk (Europap). According to the newest report of the transport census from 2024, the number of vehicles passing the passage between Zilina and Martin was estimated to be 40,000 per day [32]. Finally, there is a problem with other natural aspects near this passage of route 1/18. As damages due to natural disasters and natural phenomena are well known to be dangerous for infrastructures, both during their construction and life-time, it is important to note these problems as well. Not only is the route surrounded by the high strong rock with Strecno castle from one side, but the river flows from the other side of the road. The biggest Slovak river, Vah, flows very close to this route. In case of increased volume of water in this river or in case of floods, there is a probability that this route will be flooded, and some part of the road will be affected by landslides (which is also likely to happen from the side of the castle cliff). Therefore, structures such as road-and-rail bridges crossing rivers affected by ice jamming and floods must be designed well; research on the region enables considering aspects for ensuring the security of construction. In the case of obstacles on the road, the driver’s behavior is affected. According to [31,33], roadside infrastructure and static objects near the road influence the driver. To sum up, this passage is cited as one of the most dangerous in the Slovak Republic.
Because this passage has many problems, the Country Office Zilina issues official information regarding crossing of this passage on the fly. It informs citizens about partial or total closures and how the transport is limited (e.g., lane narrowing, speed limits) as well as provides information about works on this passage (e.g., maintenance of Strecno rock). National print media often inform about current closures in this area, too. The number of cars, including those wandering around due to not having information about closures as well as not noticing road signs, is increasing. Except for the fact that this passage is the national road for citizens passing from the west of Slovakia to the east, it is also very heavily used by citizens of neighboring villages and cities. Often, media inform about problems with this passage, such as unsatisfactory transport situations and frequent accidents, including tragic accidents.
The biggest problem was the rock massif. The rock was moving, and there was a risk it could fall right on the road. In addition, drivers were endangered by falling small rocks from the castle cliff. Due to these reasons, it was necessary to deal with the unsatisfactory situation of this part of the road. Critical problems concerned the maintenance of this passage, e.g., readiness, overpassing routes, cleaning of castle cliff, and variable weather. Other sources of news and magazines stated these problems as well. Therefore, the Slovak Road Office IVSC Zilina had issued permission for partial closures of the passage in defined timed frames. In that time, cars were supposed to bypass this passage through the municipalities of Terchova and Zazriva; trucks had to bypass this passage through the city of Trencin. Obviously, these restrictions as well as total closures were problems not only for drivers but for the safety of citizens as well (police, health services, firefighting). In addition to that, these problems affected production plants and firms. The automobile plant KIA Motors therefore prepared for such a situation by securing material in advance. During closures, they only expected complications regarding employees. Resulting from all of this, the questions were as follows: How should the government solve the problem with the road under Strecno castle? The goal of government meetings was to address the remediation of the Strecno cliff, discuss remediation costs, and grant rights and responsibilities to the remediation investigator (i.e., Ministry of Internal Affairs of the Slovak Republic). The realized variant, approved by the government, meant the allocation of financial sources for remediation of the rock cliff of Strecno castle. Within this variant, the government selected the company which was to realize the selected variant of remediation.
In past years, the government approved the partial remediation of the cliff under the Strecno castle. This solution posed costs for securing the rock system as well as costs needed to secure the road below. By realizing this remediation process, the probability of accidents due to the rock system was lowered. We decided to analyze the realized solution according to criteria stated in the previous chapter. As we did not have enough data, we analyzed the situation according to the presented concept only partially.
During full closures, there were two official bypass routes: the shorter one crossed the village of Zazriva and was intended for personal vehicles. The bypass route across the city of Trencin was intended for trucks. Details about these bypass routes are listed in Table 2 and Figure 7.

Table 2.
Details of bypass routes for Strecno.
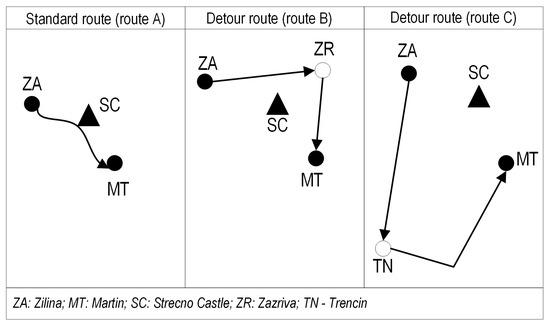
Figure 7.
The original route and bypass routes due to remediation on route 1/18.
The methodology for calculating costs to society (calculation of losses due to detours, which had to be made by personal vehicles as well as trucks) had several steps:
- First, we found out how many days the route under Strecno was closed.
- We then estimated the number of vehicles which had been diverted from the original route due to remediation—we found out how many days the route under Strecno was closed.
- We calculated the number of extra kilometers.
- Finally, the total extra fuel consumption in EUR was quantified as the sum of extra fuel consumption by personal vehicles, trucks, and motorcycles.
- According to results from every route, we estimated the extra costs to society (costs which drivers had to incur due to the closure of route 1/18).
An estimate of the decrease in the number of cars from the original route was made. We counted the number of days when the route was limited. In fact, there were two types of limitations on the route under Strecno Castle:
- 6.
- Partial restriction, two-way road in two choked lines (width of 3 m), the speed limit set to 30 km per hour.
- 7.
- Total closure, i.e., the transition through the passage was restricted and was guarded by police.
During the shutdown of the section, procedures related to the Strecno remediation had started, and the road had been either restricted partially or totally. According to the Ministry of Transport of the Slovak Republic, the following limitations were made: 47 days of total closure of the passage; from that:
- 8.
- 11 weekdays (from Monday to Friday) and 36 weekends
- 9.
- During weekends, the time of closure was set from Saturday 8 am until Sunday 4 pm.
- 10.
- During weekdays, it was a 24 h closure except for one day when the passage was closed only 3 h
- 11.
- In sum, the road was closed for 823 h.
The decrease in the number of vehicles on this route was calculated according to the number of hours when the road was closed. The approximate total decrease in the number of vehicles on this route was calculated as TOTAL= 823 h/24 h × 26,831 vehicles/day.
Based on the above information and on some approximate constants, we were able to partially quantify based on the presented approaches. The results are in Table 3.

Table 3.
Partial simplified quantification based on presented approaches.
5. Discussion
We presented the main results of our research. In this part, we summarize the basic concepts of our proposed models and summarize the answers to the research questions defined in the Introduction part.
RQ1: What types of costs and revenues should the government take into account to make an economically efficient decision in a short time period and in a long time period for the whole society? Types of costs: reparation costs, costs of financial compensation, damage costs, social costs, time costs. Types of revenues: extra revenues due to driver detours, extra investments, extra lives saved, extra time saved.
RQ2: Provided uncertainty, how should the government evaluate a transport problem of road remediation to maximize the profit for society? To assess the economic efficiency of traffic problems, we used the concept of the theory of expected profits. As it is not possible to explicitly determine some phenomena in the future, our models use probabilistic functions and are based on the quantification of uncertainty using the theory of expected returns and expected costs.
We proposed four models for assessing economic efficiency in transport:
The short-term model (SM) evaluates the economic efficiency of the transport proposal in the short term, taking into account reconstruction costs, financial compensation costs, and damage costs. As for revenues, it takes into account extra revenues from collected taxes, which were incurred by drivers due to the implementation of detours due to reconstruction.
- The long-term-short-term model (LSM) expands the concept of the SM model by taking into account long-term benefits, such as the increase in investment in the region and the increase in saved lives, compared to the current situation as a result of the implementation of the given variant.
- The social long-term-short-term model (SLSM) extends the LSM model by taking into account the costs to society (drivers) that arose due to increased fuel consumption caused by the implementation of detours.
- The long-term-short-term model with time aspect (TLSM) takes into account the time lost due to the implementation of the reconstruction and the further time gained thanks to the implementation of the given solution.
Limitations and Future Research
While this study offers a valuable framework for evaluating road remediation projects, it is essential to acknowledge its limitations. These limitations provide opportunities for future research to refine and expand upon the proposed models, enhancing their applicability and robustness. This section explores these limitations and outlines potential avenues for future research to address them.
Limitations of the Study:
- Data Availability: The study relies on estimations and average figures for certain parameters, such as the number of vehicles affected by road closures, which may not reflect the actual situation accurately. This reliance on estimations can affect the precision of the results and their ability to provide accurate implications in real-world scenarios.
- Regional Specificity: The models are validated using a specific road project in Slovakia, and their direct applicability to other regions with different geographical, economic, and social contexts may be limited. Factors such as terrain, traffic patterns, and economic activity can vary significantly between regions, potentially influencing the outcomes of road remediation projects.
- Project Scope: The study focuses primarily on road remediation projects, and the models may not be directly applicable to other types of transport projects, such as new road construction or public transportation initiatives. Each type of project has unique characteristics and considerations that may require adjustments to the models.
- Uncertainty Simplification: While the models incorporate uncertainty using probabilistic functions, they may not capture all types of uncertainty that can influence real-world outcomes. Factors such as political decisions, unforeseen events, or changes in economic conditions can introduce uncertainties that are not fully accounted for in the models.
- A limitation may also be the fact that, in practice, the probability density of a given random variable is unknown. This poses a problem in terms of solving the proposed models, since, in order to quantify individual variants, we need to have defined probability densities of individual random variables (e.g., the probability of collecting an additional amount of tax for all possible values of tax collection in EUR). One option to solve this is to approximately estimate these functions based on expert estimates in cooperation with experts. Another option is to use expert knowledge to create several possible scenarios of the development of the specified variant and calculate the expected values of random variables as discrete random variables, as stated in relation (18).
- Moreover, a model with a time aspect is also a limitation, since in this model, in order to be able to quantify it in monetary terms, it is necessary to know constants such as the number of people who will pass the given section during a period of time, the average wage, the reconstruction period, and also the number of years that we will take into account for calculating profits. In practice, this may be difficult to determine, and incorrect parameter settings may distort the results. This model may also be complicated by the fact that the number of people transported is not always equal to the number of cars, since there may be more than one person in a car or bus. This would also need to be considered in the time aspect model. In the case of drivers, the situation could be easier to estimate; however, it is the number of passengers which is more appropriate as the input number in the model.
- Other limitations also concern the validation of our concepts on the defined problem of road 1/18 in Slovakia. In this validation, we based our study on defined concepts rather than models in the true sense, since we did not have defined individual relevant probability (density) functions of random variables. However, since this was a validation of a solution that had already been implemented, we decided to partially investigate it using our concepts. However, during the validation itself, we did not have all the data available, and therefore, we did not include the variables I+ and L+ in the LSM model. Since this was only a partial road reconstruction, we assume that the I+ variable would not be significantly affected. However, in terms of lives saved, it is possible to assume that the reconstruction would have a certain impact on this variable, which was not quantified. Moreover, in the validation calculations, we used a large number of constants, some of which were only approximate and some that could be preliminary (e.g., the share of trucks, the average number of cars per day, the tax rate, or not taking into account the differences in the ratio of cars/trucks on weekdays and weekends). Setting the constants to other, more accurate values could also change the results compared to those we presented. However, rather than accurately quantifying the presented situation under Strecno Castle, we wanted to show the thought process of quantifying individual solutions to traffic problems. In the validation part, we also did not take into account unofficial detour routes, which could also change the results.
Key Points for Future Studies:
- Adaptation to Other Sectors: Future research could explore adapting the proposed models to other sectors beyond transportation, such as healthcare or environmental management, where economic evaluation under uncertainty is crucial.
- Integration of More Complex Uncertainty: Future studies could investigate incorporating more complex types of uncertainty into the models, such as using fuzzy logic or scenario planning to capture a wider range of potential outcomes.
- Refinement of Social Cost Estimation: Further research could refine the estimation of social costs by considering additional factors, such as environmental impacts or the distribution of costs and benefits across different population groups.
- In the future, it would be possible to focus on further expanding the models to include other aspects, or on thorough quantification of the model with a time aspect.
Development of Decision Support Tools: Future work could focus on developing user-friendly decision support tools based on the proposed models, making them more accessible to decision-makers in government and industry.
6. Conclusions
This paper contributes to the field of transportation economics by proposing four distinct models for evaluating road remediation projects: the Short-term Model (SM), Long-term-Short-term Model (LSM), Social Long-term-Short-term Model (SLSM), and Long-term-Short-term Model with a Time Aspect (TLSM). These models provide a framework for decision-making, enabling governments to assess the short-term and long-term costs and benefits of road remediation projects, while also incorporating the inherent uncertainty associated with future outcomes. These comparison is in Table 4.

Table 4.
The model comparison.
While the models offer a robust approach to evaluating road remediation projects, a more comprehensive explanation of their practical application and differentiation would enhance the manuscript’s clarity and impact. For instance, elaborating on specific scenarios or project types where each model would be most useful could guide decision-makers in selecting the most appropriate model for their needs.
Furthermore, incorporating more comprehensive case studies or real-world examples would demonstrate the practicality and versatility of the models across different geographic and economic contexts. This would not only showcase the models’ applicability but also provide valuable insights into their implementation and potential impact in diverse settings.
In conclusion, this paper provides a valuable contribution to the field of transportation economics by proposing four distinct models for evaluating road remediation projects. By further clarifying the models’ practical application and incorporating more comprehensive case studies, the manuscript can enhance its impact and provide decision-makers with a robust tool for evaluating road remediation projects in various contexts.
By incorporating uncertainty, considering a wide range of costs and benefits, and focusing on societal welfare, the proposed models can contribute to a more sustainable and efficient transportation sector.
Government actions influence citizens’ awareness of their country. Citizens need to know what is happening in the country and how problems that prevent them from meeting their needs are being solved. Transportation is one aspect of a functioning country and satisfied citizens. Good road infrastructure enables, among other things, fast mobility of people within the country. This increases work flexibility, which positively affects the country’s economy.
Slovakia faces several transportation challenges. The number of personal vehicles and trucks has been increasing rapidly, while road infrastructure has not kept pace, leading to congestion and safety concerns. This issue is particularly evident on road 1/11 (E50) under the Strecno castle cliff, considered one of the most dangerous passages in the country. The road is consistently overloaded, with narrow lanes, proximity to the Vah river, and the risk of rockfalls. The situation is exacerbated by its role as a major route for drivers traveling from western to eastern Slovakia.
The main contribution of this paper was the suggestion of four economic models to assess the economic efficiency. We suggested models with uncertainty which can be used for decision-making processes in transport problems with uncertainty. We built our models on expected costs which are related to the selected option of remediation.
We then applied our models to the remediation option chosen by the Slovak government. We found that this was a non-effective solution from the all-society point of view in the short term.
Today, every public institution, profit as well as non-profit organizations, groups, individuals, or the government, create social impact. According to Viturka [34], it is important to evaluate all realized actions, transport included, by a multiple-criteria function with incorporated social impacts of realized activities. We believe that our models enable even non-financial aspects to be considered in analyzing the economic efficiency of transport problems subject to uncertainty.
Author Contributions
Conceptualization, M.H., J.S. and J.D.; methodology, M.H., L.F. and J.D.; validation, M.H. and L.F.; formal analysis, M.H. and J.S.; investigation, M.H. and L.F.; resources, M.H.; data curation, M.H. and L.F.; writing—original draft, M.H., J.S. and L.F.; writing—review and editing, M.H. and L.F.; visualization, M.H.; supervision J.D.; project administration, L.F. and J.D.; funding acquisition, M.H. All authors participated in the research and shared joint responsibility for this work. All authors have read and agreed to the published version of the manuscript.
Funding
Funded by the EU NextGenerationEU through the Recovery and Resilience Plan for Slovakia under the project No. 09I05-03-V02-00011.
Data Availability Statement
The research data are stored in the internal storage facilities of the university in Žilina in the work files of employees.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Number of Motor Vehicles. Statistical Office of the SR, 2024. Available online: https://datacube.statistics.sk/?fbclid=IwAR0Iv3Bd7b9GNDil9CUVzA9rode6eVDhmKUj#!/view/sk/vbd_sk_win2/do3803rr/v_do3803rr_00_00_00_sk (accessed on 10 February 2025).
- Selected Road Public Transport Indicators. Statistical Office of the SR, 2024. Available online: https://datacube.statistics.sk/?fbclid=IwAR0Iv3Bd7b9GNDil9CUVzA9rode6eVDhmKUj#!/view/sk/vbd_sk_win2/do3801rr/v_do3801rr_00_00_00_sk (accessed on 10 February 2025).
- Road Transport–Expensive. Statistical Office of the SR, 2024. Available online: https://datacube.statistics.sk/?fbclid=IwAR0Iv3Bd7b9GNDil9CUVzA9rode6eVDhmpKUj#!/view/sk/VBD_SK_WIN/do1007rs/v_do1007rs_00_00_00_sk (accessed on 10 February 2025).
- Road Transport Infrastructure. Statistical Office of the SR, 2024. Available online: https://datacube.statistics.sk/?fbclid=IwAR0Iv3Bd7b9GNDil9CUVzA9rode6eVDhmKUj#!/view/sk/VBD_SK_WIN/do1012rs/v_do1012rs_00_00_00_sk (accessed on 10 February 2025).
- Road Transport Accidents. Statistical Office of the SR, 2024. Available online: http://datacube.statistics.sk/#!/view/sk/VBD_SK_WIN/do1012rs/v_do1012rs_00_00_00_sk (accessed on 10 February 2025).
- Shi, S.; Yin, Y.; Guo, X. Optimal choice of capacity, toll and government guarantee for build-operate-transfer roads under asymmetric cost information. Transp. Res. Part B-Methodol. 2016, 85, 56–69. [Google Scholar] [CrossRef]
- Anuar, W.K.; Lee, L.S.; Pickl, S. Benchmark dataset for multi depot vehicle routing problem with road capacity and damage road consideration for humanitarian operation in critical supply delivery. Data Brief 2022, 41, 107901. [Google Scholar] [CrossRef]
- Zakharov, A.V.; Zabalueva, T.R. Ensuring the integrity of the road network as the key to solving the problems of highway capacity in cities. Nexo Rev. Cient. 2021, 34, 103–111. [Google Scholar] [CrossRef]
- Stopka, O. Modelling Distribution Routes in City Logistics by Applying Operations Research Methods. PROMET-Traffic Transp. 2022, 34, 739–754. [Google Scholar] [CrossRef]
- Hussain, M.R.; Qayyum, M.; Hussain, M.E. Transportation Problem of LPP Involving Probability Density Function. Int. J. Recent Contrib. Eng. 2019, 7, 42–51. [Google Scholar] [CrossRef]
- Torra, V. The transport problem for non-additive measures. Eur. J. Oper. Res. 2023, 311, 679–689. [Google Scholar] [CrossRef]
- Malhotra, S.; Khandelwal, M. Solving XpressBees Logistics Problem by Using Exact and Heuristic Method. LOGI–Sci. J. Transp. Logist. 2022, 13, 37–48. [Google Scholar] [CrossRef]
- Xiang, Z.; Yang, J.; Naseem, M.H.; Xiang, Z. Solving the Multiobjective Transportation Decision-Making Problem Based on Improved S-Type Membership Function. J. Math. 2021, 2021, 4169352. [Google Scholar]
- Kozubek, P.R. An ex-post analysis of selected road investments in the Swietokrzyskie region in 2007–2016. Ekon. I Prawo-Econ. Law 2020, 19, 712–723. [Google Scholar] [CrossRef]
- Jasiuniene, V.; Ratkeviciute, K.; Peltola, H. Road Network Safety Ranking Using Accident Prediction Models. In Proceedings of the Vision Zero for Sustainable Road Safety in Baltic Sea Region, Vilnius, Lithuania, 5–6 December 2018; pp. 166–176. [Google Scholar]
- Baublys, A. Probability models for assessing transport terminal operation. Transport 2007, 22, 3–8. [Google Scholar] [CrossRef][Green Version]
- Rudzianskaite-Kvaraciejiene, R.; Apanaviciene, R.; Butauskas, A. Evaluation of Road Investment Project Effectiveness. Eng. Econ. 2010, 21, 368–376. [Google Scholar]
- Wang, Z.; Chen, L. Research on the Impact of Road Construction on Traffic Congestion. AEBMR-Adv. Econ. Bus. Manag. Res. 2016, 10, 209–212. [Google Scholar]
- AlHamad, S.; Almallah, M.; Naser, M.N.; Alhajyaseen, W.K.M.; de Roos, M.P. Examining the role of road safety audits worldwide: Exploring road safety expert’s opinions. Int. J. Inj. Control Saf. Promot. 2023, 30, 106–115. [Google Scholar] [CrossRef] [PubMed]
- Soeanu, A.; Debbabi, M.; Alhadidi, D.; Makkawi, M.; Allouche, M.; Bélanger, M.; Léchevin, N. Transportation risk analysis using probabilistic model checking. Expert Syst. Appl. 2015, 42, 4410–4421. [Google Scholar] [CrossRef]
- Jamroz, K.; Budzynski, M.; Kustra, W.; Michalski, L.; Gaca, S. Tools for road infrastructure safety management-Polish experiences. Transp. Res. Procedia 2014, 3, 730–739. [Google Scholar] [CrossRef]
- Koman, G.; Toman, D.; Jankal, R.; Krúpová, S. Public Transport Infrastructure with Electromobility Elements at the Smart City Level to Support Sustainability. Sustainability 2024, 16, 1091. [Google Scholar] [CrossRef]
- Yuan, J.H.; Zeng, Y.R.; Guo, X.X.; Ai, Y.; Xiong, M.P. Electric Power Investment Risk Assessment for Belt and Road Initiative Nations. Sustainability 2018, 10, 3119. [Google Scholar] [CrossRef]
- Bohm, M.; Fuchs, S.; Pfliegl, R.; Kolbl, R. Driver Behavior and User Acceptance of Cooperative Systems Based on Infrastructure-to-Vehicle Communication. Transp. Res. Rec. 2009, 2129, 136–144. [Google Scholar] [CrossRef]
- Kusnirova, D.; Durisova, M.; Bubeliny, O. Enhancing Stakeholder Value: Managerial Activities in the Value Creation Process for Suppliers and Buyer-Evidence from Slovak Enterprises. Adm. Sci. 2024, 14, 186. [Google Scholar] [CrossRef]
- Varmus, M.; Kubina, M.; Miciak, M.; Bosko, P.; Greguska, I. More Sustainable Sports Organizations’ Operation As A Result Of Fan Involvement Into The Processes Of Decision-Making And Community Building. Entrep. Sustain. Issues 2023, 11, 10. [Google Scholar] [CrossRef]
- Varmus, M.; Bosko, P.; Adámik, R.; Greguska, I. Sports Management in the Context of Sustainability. Entrep. Sustain. Issues 2024, 12, 240–252. [Google Scholar] [CrossRef] [PubMed]
- Štaffenová, N.; Kucharcíková, A. Digitalization in the Human Capital Management. Systems 2023, 11, 337. [Google Scholar] [CrossRef]
- Becker, G.S. Accounting for Tastes; Harvard University Press: Cambridge, MA, USA, 1996. [Google Scholar]
- Caplice, C. Single Period Inventory Model: Calculating Expected Profitability. CTL.SC1x-Supply Chain & Logistics Fundamentals. Available online: https://scx-static-assets.s3.amazonaws.com/SCx%20Key%20Concept%20Documents/MITx_MicroMasters_SCM_KeyConcepts.pdf (accessed on 15 February 2025).
- Van der Horst, R.; de Ridder, S. Influence of roadside infrastructure on driving behavior-Driving simulator study. Transp. Res. Rec. 2007, 2018, 36–44. [Google Scholar] [CrossRef]
- SSC. Slovak Road Administration: Work on the Rehabilitation of the Strečnian Rock Cliff Continues According to Plan, There Will Be Restrictions on Road I/18. 2024. Available online: https://www.ssc.sk/files/documents/tlacove_spravy/ts_1.8.2024_i18_strecno_kontrolny_den_obmedzenia.pdf (accessed on 15 February 2025).
- Dutta, B.; Vasudevan, V. An empirical study on the influence of on-road static obstacles on driver behaviour. Curr. Sci. 2021, 120, 699–706. [Google Scholar] [CrossRef]
- Viturka, M. Integrative model for evaluation of development potentials of regions and its application on an example of the Czech Republic. Econ. Manag. 2014, 17, 4–19. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).