Abstract
Background: The dynamic vehicle routing problem (DVRP) is a complex optimization problem that is crucial for applications such as last-mile delivery. Our goal is to develop an application that can make real-time decisions to maximize total performance while adapting to the dynamic nature of incoming orders. We formulate the DVRP as a vehicle routing problem where new customer requests arrive dynamically, requiring immediate acceptance or rejection decisions. Methods: This study leverages reinforcement learning (RL), a machine learning paradigm that operates via feedback-driven decisions, to tackle the DVRP. We present a detailed RL formulation and systematically investigate the impacts of various state-space components on algorithm performance. Our approach involves incrementally modifying the state space, including analyzing the impacts of individual components, applying data transformation methods, and incorporating derived features. Results: Our findings demonstrate that a carefully designed state space in the formulation of the DVRP significantly improves RL performance. Notably, incorporating derived features and selectively applying feature transformation enhanced the model’s decision-making capabilities. The combination of all enhancements led to a statistically significant improvement in the results compared with the basic state formulation. Conclusions: This research provides insights into RL modeling for DVRPs, highlighting the importance of state-space design. The proposed approach offers a flexible framework that is applicable to various variants of the DVRP, with potential for validation using real-world data.
1. Introduction
Last-mile delivery represents one of the most expensive and time-consuming operations in the entire supply chain [1]. This stage presents significant challenges due to real-life constraints, such as delivery windows, dynamic customer requests, limited driver capacity, and stochastic service and travel times.
To address these challenges and optimize last-mile delivery operations, many logistics companies have turned to tackling vehicle routing problems (VRPs), which involve determining the most efficient routes for a fleet of vehicles to visit a set of spatially distributed locations where customer requests are made. Traditional optimization methods for VRPs rely on deterministic data inputs, where all information is known beforehand [2]. However, in real-world operations, data inputs are often uncertain and subject to change, leading to the emergence of dynamic vehicle routing problems (DVRPs) [3,4,5].
The DVRP extends the VRP by considering the dynamic nature of real-world operations, where customer requests are uncertain and may occur during the day while drivers are on the road. This problem requires finding a solution that considers future stochastic developments and actions that must be taken in the presence of incomplete information. Despite its long history in operations research, the DVRP has gained attention in recent years due to innovative online services such as ride-sharing, ride-hailing, grocery delivery, emergency services, and waste collection [6,7,8,9,10,11].
An additional level of complexity in real-world problems is introduced by vehicle capacity and customer time preferences, leading to the problem known in optimization as the capacitated DVRP with time windows [12]. This problem introduces the constraint of limited vehicle capacity, which means that a vehicle can carry only a certain amount of goods. Time windows further complicate the problem by requiring deliveries to be made within specific time frames. These constraints are important in real-world scenarios, where logistics operations must comply with both physical vehicle limitations and customers’ expectations for timely deliveries. In the rest of this article, we will refer to the capacitated DVRP with time windows simply as the DVRP.
As the DVRP presents a challenging problem due to the complexity and high dynamics of the real-world environment, innovative solutions are needed to optimize last-mile delivery operations. One such solution is reinforcement learning (RL), a type of machine learning that enables an agent to learn an optimal policy by interacting with the environment and receiving feedback in the form of rewards [13]. In the context of the DVRP, RL can be used to train an agent to make decisions based on real-time feedback from the environment.
In this study, we explore the application of RL to solve the DVRP, where newly arrived orders must be immediately accepted or rejected. The problem is set in a dynamic environment, modeled as a geographical grid with distinct zones that generate customer orders at varying rates. Each order has specific characteristics, such as time windows and vehicle capacity constraints, and it must be fulfilled within a set period to avoid penalties. The delivery driver navigates this dynamic system, making decisions about the acceptance of arriving orders, when to restock at a central depot, and how to balance competing factors, such as travel distance, order fulfillment, and vehicle capacity. Our goal is to create an RL-based application that can make real-time decisions. We investigate the components in the state space that influence decision effectiveness and analyze how different factors impact the model’s performance. The main contributions of this study are the following: (1) a systematic comparison of different RL environments for solving DVRPs, including the modeling strategies; (2) the development of an RL model for the DVRP that is adaptable to various scenarios; (3) the proposal of key factors to consider when modeling DVRPs using RL.
The managerial implications of this study are particularly relevant in the context of increased digitization and data availability in logistics companies. As last-mile delivery problems become more complex, an RL-based approach to addressing the DVRP offers a promising direction for future logistics management [14,15]. Using historical data, companies can train decision-making models tailored to their specific operational environments, generating adaptive heuristic solutions optimized for company-specific patterns. Our comparative analysis of RL environments and the identification of influential factors can contribute to modeling strategies in addressing DVRP with RL. As the logistics industry continues to evolve, the integration of RL-based data-driven decision-making tools has the potential to improve operational efficiency and reduce complexity in last-mile delivery operations.
The remainder of this study is organized as follows: In Section 2, we review the relevant literature and provide a comparative analysis of existing approaches in the field. Section 3 shows a detailed description of the problem. In Section 4, we present the formal model formulation with details of the methodology. Section 5 introduces the details of the solution method used to address the problem. A computational study is presented in Section 6, where we first describe the experimental setup, followed by the various experiments with their results and analyses. Finally, conclusions and potential future work are discussed in Section 7.
2. Related Work
The rapid progress in computing hardware and the growth of available large-scale data in recent years have led academia and industry to shift their focus towards machine learning approaches to address complex combinatorial optimization problems [16]. When processing a large amount of historical data, the approximation strengths of deep neural networks (DNNs) and the decision-making abilities of RL can be used to tackle optimization problems. Such a combination has the potential to yield more generalizable solutions than those of traditional approaches. For example, several researchers have shown promising potential in addressing static VRPs with learning-based methods. Nazari et al. [17] solved a static version of the VRP using RL with a long short-term memory-based encoder. Kool et al. [18] developed an RL model based on attention layers to solve the static VRP. Delarue et al. [19] proposed focusing on solving individual problem instances rather than training a single model for multiple instances drawn from a similar distribution.
RL is a promising heuristic approach for tackling DVRPs due to the inherent structure of sequential decision-making problems, where a decision policy is required rather than a single solution vector. In theory, RL is well suited for DVRPs and dynamic optimization problems in general, as such problems can be modeled as Markov decision processes (MDPs), naturally capturing the evolution of stochastic and dynamic systems. Furthermore, integrating RL with DNN, which is known as deep reinforcement learning (DRL), has allowed complex large-scale decision problems to be addressed [20,21], allowing the offline training of complex decision policies that enable fast and efficient decision making in dynamic and uncertain environments.
The practical implementation of RL for DVRPs is challenging. State and action spaces can be complex and hard to formulate optimally, often requiring additional techniques, such as state aggregation or action factorization. Hildebrandt et al. [22] highlighted a significant issue with large action spaces in RL formulations, which has led to the categorization of approaches into two main types: assignment-based and routing-based problems [23]. Assignment-based problems do not require routing decisions and focus on research questions related to order acceptance and vehicle repositioning [24]. On the other hand, routing-based problems involve updating the route in the state and action spaces and have complex combinatorial action spaces that are challenging to construct or enumerate for a single state. Researchers have addressed this issue by suggesting that VRP solvers, rather than RL algorithms, are better equipped to search the action space [25]. To make action spaces less complex, action-space factorization can be performed, where RL is used to make assignment-based decisions, while routing decisions are handled by specialized VRP heuristics. This approach, as proposed by Chen et al. [26], allows for a more manageable RL formulation while still addressing the complexities of DVRPs.
In this study, we address the challenge of defining and formulating components of a state space for the DVRP. Given the complexities associated with routing-based problems in the DVRP, this study focuses on problem formulations that do not rely on the complete knowledge of the planned route. Specifically, we are interested in problems where decisions are related to the acceptance of orders and vehicle repositioning. By narrowing our scope to this class of problems, we hope to overcome some of the challenges that arise when dealing with complex and combinatorial action spaces that involve updating routes. By focusing on action spaces that do not involve complex routing decisions, we can leverage the strengths of RL algorithms to make effective decisions based on a simplified action space.
Our study is based on that of Balaji et al. [24], who proposed an approach to addressing a DVRP with acceptance decision making. Balaji et al. [24] incorporated a rich state representation and action space, which included acceptance decisions and repositioning actions. Specifically, their formulation introduced an action space that included the following options: (i) waiting for additional information, (ii) accepting a new order, (iii) moving one step closer to a previously accepted order, or (iv) moving one step closer to the depot. This approach allows for the formulation of an RL algorithm that can learn a policy for making an acceptance decision while simultaneously optimizing vehicle routing to maximize system performance. This formulation has the potential to address real-world DVRP scenarios, where acceptance decision making is critical for effective system performance in a dynamic complex environment.
Other researchers have explored another formulation to address the DVRP. The authors of [27,28,29] designed action spaces in which the focus is on moving to the customer without explicit acceptance or rejection decisions, with rewards based on travel distances rather than the value of the delivered orders. This approach draws on the static VRP environment [17,18]. To manage the complexities of the state space, Bono [27] proposed factorization of the state and encoding layers, while Pan et al. [28] suggested using distances to customers instead of customer locations in the state. These methodologies offer alternative ways to simplify the state space, potentially enhancing the applicability of RL in the DVRP.
Table 1 provides a comparison of various DRL environments for VRPs in the literature, highlighting the differences in vehicle types, VRP variants, state representations, action spaces, and reward structures in different studies.

Table 1.
Comparison of DRL environments for VRPs in the literature.
This demonstrates the diversity in problem formulations, from single- to multiple-vehicle scenarios and various VRP variants, including dynamic, capacitated, pickup and delivery, and time-windowed problems. The comparison reveals significant variations in state representations, ranging from basic customer information to complex planned route sets. The action spaces involve customer selection, order acceptance, and vehicle repositioning. The reward structures are primarily distance-based or value-based, reflecting different optimization goals.
Given the state of the current literature, several research gaps exist. Firstly, there is a lack of comparisons between different environments for solving DVRPs with RL. Instead, the literature tends to focus on highly problem-specific environments, making it difficult to compare the effectiveness of different models. Furthermore, the current state of research lacks an analysis of factors that impact the performance of RL-based approaches in DVRPs. The diversity of problem formulations in the literature makes it difficult to isolate and understand the impact of individual components in addressing VRPs with RL. To address these gaps, we aim to create an application for a DVRP with various constraints with simulation of a simplified real-life environment. The approach is motivated by the potential for RL solutions to be incorporated into real-life logistics solutions, as they can offer adaptability to dynamic conditions and continuous learning. As such, the primary objective of this study is to explore and combine the factors that impact the performance of the RL-based approach.
3. Problem Description
This study investigates a DVRP in which new orders arrive dynamically throughout the day. The problem is set in a geographical area represented by a grid map , which is divided into distinct zones that generate orders at varying rates. Each location in this grid is represented by a pair of integer coordinates that both fall within the range , and they define an individual cell within the grid. At each time step, multiple orders can emerge simultaneously, each with a fixed probability, and they are assigned to zones based on zone-specific probabilities. These orders carry rewards drawn from zone-specific truncated normal distributions with varying ranges, which are known at the time of appearing.
The central figure in this problem is the delivery driver, who must navigate this dynamic environment to maximize the total net reward over an episode, which represents a full delivery day. Each order must be delivered within a specified time window from its appearance and requires a fixed capacity from the driver. Failure to meet these time windows results in cost penalties. To fulfill these orders, the driver operates a vehicle with a limited capacity. This vehicle can return to a centrally located depot for restocking whenever necessary—whether it is empty and requires a full restock or is only partially loaded. This flexibility in restocking adds another layer of strategic decision making for the driver. The temporal aspect of the problem is defined by a predetermined total time for a full delivery day, which serves as the maximum time step. Throughout this period, the driver incurs a cost per time step and unit distance traveled, representing the monetary value of time and travel expenses.
In this environment, the driver makes a series of decisions. These include accepting or rejecting new orders as they appear, choosing which accepted customer to travel to next to satisfy specified time windows, managing the vehicle’s capacity efficiently, and strategically timing returns to the depot for restocking. Additionally, the driver can opt to wait strategically, doing nothing to potentially manage more profitable orders in the future. These decisions require balancing multiple factors: rewards of new orders, urgency of delivery time windows, vehicle capacity, travel costs, and benefits of strategic waiting. This ongoing decision-making process forms the core of the driver’s strategy to maximize rewards throughout the delivery day.
4. Model Formulation
The problem can be formulated as a Markov decision process (MDP), which is a widely used framework for modeling decision-making problems in a sequential and stochastic environment. In the context of the DVRP, the agent refers to the decision maker, specifically, to the vehicle driver responsible for accepting and routing orders. Consequently, throughout the text, the terms ’agent’ and ’driver’ are used interchangeably.
In the model, it is assumed that the agent can handle a maximum of N orders during any given time step, with each order being assigned one of three possible statuses: 0, 1, or 2. A status of 0 means that the order is currently inactive, having either been completed (delivered) or rejected. Upon arrival, each order is initially assigned a status of 1, signaling that it is available for acceptance. The agent is required to make an immediate decision whether to accept or reject this order. Once an order is accepted, its status transitions to 2, indicating that the order is in the delivery process. This structure enables the agent to disregard any orders that have already been delivered or rejected and to focus on the orders that are currently active and available to be processed. It also allows the agent to learn in a dynamic environment where the number of future orders is unknown and can vary over time. Figure 1 illustrates the overall methodology of the proposed DVRP model, showcasing the interactions among the agent, environment, and the decision-making process. This framework forms the basis for the detailed model components described below.
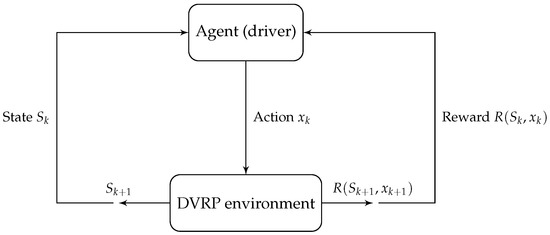
Figure 1.
RL framework for the DVRP.
Decision Point: A decision point k occurs when an agent must make a decision. The model involves two categories of decisions that the agent must make, which are acceptance and routing decisions. The model uses discrete time steps for routing decisions, indicated by , where T represents the total time for a full delivery day. The total number of decision points depends on the number of orders that arrived during T.
State: A state of the MDP consists of two parts: the pre-decision state and post-decision state . captures the necessary information required to make a decision and is represented as follows:
- The current time step: .
- The current location of the driver, , represented by the coordinates , where n represents the size of the grid that defines the geographical area.
- The locations of the orders are denoted as , represented by a set of tuples with the coordinates of each order’s location: , where for .
- The current status of each order: where for .
- The time elapsed since each order’s generation: where for .
- The rewards associated with each order: for .
- The available capacity of the driver to accommodate additional orders: .
Thus, the basic state is . The post-decision state represents the state of the environment after executing a decision at the decision point k. The components of the state are updated based on the specific decision made by the agent.
Action: At decision point k, the agent makes the decision in two categories: accepting or rejecting an order that has arrived and making the routing/repositioning decision. When an order appears with a status of 1, the agent must choose to accept or reject the order, after which the time step remains the same . Otherwise, the agent makes routing decisions with three options: staying stationary and waiting, moving a step closer to the depot, or moving a step closer to one of the accepted orders, resulting in a total of possible routing decision options.
Transition: The model involves two types of transitions, as illustrated in Figure 2:
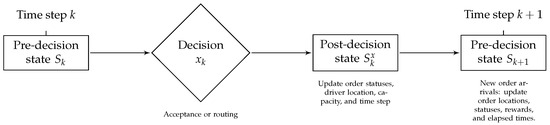
Figure 2.
Timeline of pre-decision and post-decision states.
1. Transition from pre-decision state to post-decision state : This transition represents the deterministic changes that occur immediately after the agent makes a decision at decision point k. The sequence of calculations depends on the type of decision.
- Acceptance decision point:
- -
- Order status: If the agent decides to accept an order that has arrived, its status changes from 1 (available) to 2 (in process). If the agent rejects the order, its status changes from 1 (available) to 0 (inactive).
- -
- Time step: The time step remains unchanged during the acceptance decision process, i.e., .
- Routing decision point:
- -
- Driver location: The driver’s location is updated based on the chosen routing action. The driver may move closer to the depot, move towards an accepted order, or stay stationary.
- -
- Order status: If the driver’s location matches the location of an accepted order (status 2), the order’s status is updated to 0 (completed).
- -
- Capacity update: If the driver’s location matches an accepted order and the order is completed, the driver’s available capacity is decreased by the amount that is required for the delivered order. If the driver has decided to go to the depot and arrives there, the driver’s available capacity is reset to the maximum capacity C. After a depot visit, the system continues to account for accepted orders as pending orders to deliver.
- -
- Time step: The time step increases by one unit to reflect the passage of time during the routing process, i.e., .
2. Transition from the post-decision state to the next pre-decision state : This transition represents the evolution of the environment and state variables from to , incorporating the effects of newly arrived orders and updating the state accordingly.
- Order arrival: At the transition from to , a new order may arrive probabilistically. The following updates are made:
- -
- Order locations: The location of a new order is added to .
- -
- Order statuses: New order is initially assigned a status of 1 (available) in .
- -
- Elapsed times: The elapsed time for a new order is initialized to 0.
- -
- Order rewards: The rewards associated with a new order are added to .
- Order updates:
- -
- Order processing status: The status and elapsed time of orders that are already in process are updated to reflect the time passage and any changes in the environment.
Reward function: The reward function depends on the decision made in state and is defined as , where
is a penalty for failing to deliver an accepted order within the specified timeframe, and represents the costs associated with time and travel.
5. Solution Method
In this study, we use the proximal policy optimization (PPO) algorithm due to its effective policy update mechanism based on the trust region policy optimization theorem [30], which ensures monotonic improvement of the policy. The algorithm alternates between sampling data through interaction with the environment and optimizing an objective function using a stochastic gradient ascent. PPO is a policy gradient method in RL, which means that it searches the space of policies instead of assigning values to state–action pairs.
PPO calculates two essential functions: the policy function, or ’actor’, which determines the agent’s action selection strategy based on observed states, and the value function, or ’critic’, which estimates the cumulative rewards associated with different states. The functions interact iteratively, where the value function guides the policy towards better actions, while the policy determines the agent’s behavior and influences the data used to estimate the value function.
The policy function represents the probability of taking action in state according to a policy . PPO optimizes this function using the following clipped surrogate objective:
where denotes the empirical mean over a finite batch of samples, approximating the expected value; is a function that restricts the value h to the range ; is the estimated advantage at the decision point k, representing how much better or worse an action is compared with the average action in a given state; and is a hyperparameter that limits the size of policy updates.
The value function estimates the expected cumulative reward from state . It is updated by minimizing the mean squared error:
where is the target value for state , which is calculated based on the observed rewards and estimated future values. This target helps the agent learn to accurately predict the long-term value of being in a particular state. represents the current estimate of the value function for state , parameterized by a policy , which corresponds to the weights of the function approximator. More details on the theoretical background of the algorithm can be found in [30].
To enhance decision making within this environment, we employ an action mask. The action mask comes into play by evaluating whether the agent has the necessary capacity to fulfill the orders. If the agent lacks sufficient capacity, it must return to the depot to restock. In this environment, the agent has a total of discrete actions to choose from. This includes two actions for the acceptance phase and actions available for the routing phase. When accepting an order, the agent receives a fraction of the order reward, with the remaining fraction being awarded upon successful delivery. This approach is designed to incentivize the agent to accept orders. The system encourages the agent to actively accept orders and strive to deliver them within the given time constraints. An episode refers to the entire sequence of decision points from the start to the end of a delivery day. It encompasses all of the acceptance and routing decisions made by the agent throughout the day.
Both the policy and value functions are parameterized using multilayer perceptron networks. These networks consist of two hidden layers, each with a dimension of 128 nodes. The input to the network is the current state of the environment, represented as a one-dimensional array. The length of the array is fixed, and it relies on the number of components and their transformations included in the state space. The output is a probability distribution over the set of all possible actions that the agent can take in the current step. To enhance the model performance, we normalize the state-space components and rewards to improve the model’s training efficacy by ensuring that all input features to the model have a similar scale.
6. Computational Study
This study is motivated by the need to develop an RL environment for the DVRP to identify the elements that impact system performance. The key aspect of interest is the state space, which serves as the foundation for the agent’s decision-making process and policy formation. With the state space, it is important to acknowledge the contributions of the action and reward spaces to the overall policy dynamics. However, these spaces are relatively limited in this DVRP formulation. The action space is constrained to choosing between acceptance and movement actions, while the reward space is defined by the objective function of the problem.
Through our investigation, we aim to identify patterns and relationships within the components of the state space. We experiment with various approaches, such as adding, removing, or modifying components to optimize the state space. By manipulating the components, we seek to gain valuable insights into how the problem policy can be improved. To accomplish our goal, we designed the following series of experiments.
- Exploring the basic state with different random seeds. The results of multiple runs with different random seeds are presented, and the best-performing run is selected for subsequent analyses.
- Impact of removing locations from the basic state: The effects of removing location information from the state space are discussed, and why this modification negatively affected the training process is analyzed.
- Incorporating a distance component into the basic state: The results obtained by including distance information for each location in the state space are investigated, and the impact on the model’s performance is discussed.
- The influence of one-hot encoding on model performance: How techniques involving data processing—specifically, one-hot encoding—can influence the performance of the model is demonstrated.
- Integrating derived features into the basic state: The outcomes of incorporating derived features, such as ratios for the order reward vs. time left for order delivery and the driver’s current load vs. the number of orders to deliver, into the state space are presented, and their effects on the model’s performance are analyzed.
- Combining state-space enhancements: The overall impact achieved by integrating multiple enhancements from previous subsections within the basic state is evaluated.
Table 2 provides an overview of the state-space components used in each experiment. It illustrates how we systematically modified the state space across our experiments, allowing us to isolate and analyze the impact of individual components on the model’s performance. Experiment 1 represented our basic state, from which experiments 2 through 6 were derived by modifying specific components. As shown, while some components remained constant across all experiments, others were selectively included or excluded to test their influence on the RL model’s effectiveness in solving the DVRP.

Table 2.
Overview of experiments and state-space components.
To evaluate the performance of the trained models, we conduct testing on a separate evaluation set consisting of 1000 scenarios. These scenarios are derived from the instance described in Section 6.1 and generated using a random seed distinct from the one used during the training phase.
6.1. Experimental Setup
We conducted experiments using an instance to evaluate the performance of our model. The geographical region was divided into four zones. The zones were defined based on the x-coordinate of each cell: the leftmost 30% of the grid belonged to zone 1, the next 30% belonged to zone 2, the following 20% belonged to zone 3, and the rightmost 20% belonged to zone 4. In the instance, there was a probability p that an order emerged at any given time step. In the case that an order emerged, it was assigned to zone z with probability . Orders in zone 1 had rewards in the range of , while orders in zones 2, 3, and 4 had rewards in the ranges , , and , respectively. Orders needed to be delivered within a -minute, requiring a capacity of q units. Failure to meet the time window incurred a cost penalty of f. The vehicle had a maximum capacity of C units, and the depot was located at the coordinates .
The instance parameters used in the experiments were as follows: , , , , , , , , , , , , , , , , , , , and . The hyperparameters of the solution method were , , , training batch = 128, learning rate = , and discount factor = 0.99.
The experiments were conducted on a MacBook Air equipped with an Apple M1 Chip that included an 8-Core CPU, 8-Core GPU, and a 16-core Neural Engine, running the macOS Big Sur operating system (version 11.2.3). We utilized Python 3.10.5 for coding, along with the Stable Baselines3 library [31] for implementing the PPO algorithm. We also leveraged parallelization to speed up the training process by using four threads, which led to a significant improvement (approximately 30%) in training speed. The model’s performance was evaluated using the total cumulative reward, which was calculated by summing the individual rewards (defined in Section 4) obtained at each decision point k over an episode.
6.2. Random Seed Analysis
First, we conducted six runs with different random seeds with the basic state described in the model formulation section. Figure 3 presents the training curves depicting the performance of each run over the training iterations. The x-axis represents the number of training iterations, while the y-axis shows the average cumulative rewards obtained. The graph illustrates a gradual increase in rewards during the training process, indicating that the model learned to optimize the DVRP solution. For readability, the graphs are clipped to skip the initial steps of training, as the rewards were low and would skew the y-axis scale.
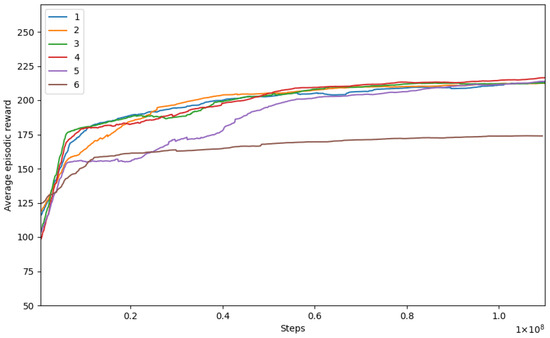
Figure 3.
Training curves for the basic state.
Table 3 provides insights into the performance metrics derived from the evaluation set. The “Reward” column displays the mean and standard deviation of cumulative rewards over scenarios, which represent the objective function outlined in the problem description. The “RS” column displays the random seeds employed in the basic state space.

Table 3.
Evaluation of different random seeds using the basic state.
Out of all of the runs, one specific run (number four, which is presented in bold in the table) with the highest performance was selected for further analysis. This run was chosen as a benchmark, as it set a higher standard compared with the other runs. It provided perspectives on how well the component analysis performed in relation to the other runs. A low training curve (referenced as run six) might indicate that the algorithm, under the influence of the currently selected random seed, has potentially converged to a suboptimal policy, possibly due to reaching a local optimum in the policy optimization landscape.
The curved run (number five) initially trailed behind the others, indicating a possibly less optimized pathway taken during the early stages of training. However, as the training progressed, this run exhibited a remarkable turnaround, eventually catching up with or even surpassing the performance of the other runs. This could be attributed to the algorithm eventually finding a more optimal policy through its exploration strategy.
6.3. The Impact of Location Removal
Next, we explored the impact of removing the location component of the orders, denoted as , from the state space. Our aim was to discern whether the location component influenced decisions or posed a challenge for the algorithm to learn meaningful insights. Figure 4 illustrates the training curves, comparing the run with the best performance of the basic state space (represented by the blue line) and the training curve where the location component was omitted (represented by the orange line). In the latter scenario, the rewards obtained during training consistently decreased. This finding suggests that the model faced challenges in learning without taking the location information into account. Table 4 provides an overview of the evaluation results when applying this policy to the evaluation set. The last column of the table represents the difference in the average reward mean compared with the benchmark run of the basic state (Section 6.2).
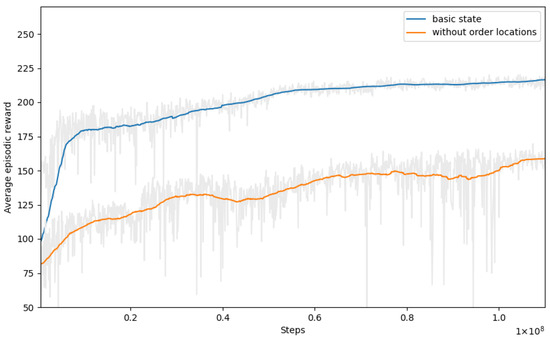
Figure 4.
Training curves with and without the location component.

Table 4.
Performance evaluation without the location component.
6.4. The Addition of the Distance Component
In this section, we added a component that stored the minimum distance from the driver’s position to each order location, measured in cells. These distances represented the minimum number of cell-to-cell movements required to reach the order locations from the driver’s current position. This addition was motivated by the insight that incorporating distance information can potentially help the model in making better decisions. By including the distance component in the state space, the model gained information about the spatial relationships between the driver and the orders.
Figure 5 displays the training graph for this extended state space. The graph illustrates that the model achieved higher rewards compared with those in the basic state space. This indicates that incorporating the distance component had a positive impact on the model’s performance, leading to better decision making. The same conclusion can be drawn from the results on the evaluation set presented in Table 5.
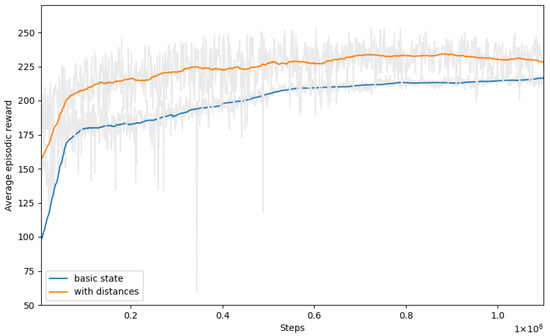
Figure 5.
Training curves with the distance component.

Table 5.
Performance evaluation with the distance component.
6.5. The Influence of One-Hot Encoding
In this section, we incorporated one-hot encoding into the state space as a component transformation technique. The first experiment aimed to encode order statuses by assigning a unique binary vector to each status category, enabling the model to differentiate between different statuses. In the second experiment, our focus shifted to applying encoding not only to the order statuses but also to the driver and order locations. For this experiment, we adopted a grid-based approach to represent the locations. Specifically, for both components, we created a grid where each cell was transformed into a binary value. A value of 0 indicated an empty cell, while a value of 1 represented the presence of the driver or order in that cell.
To provide a visual comparison of the training progress in both experiments, we plot the training curves in Figure 6. The training curve for the first experiment is represented by the orange color, and the second experiment is denoted by the green color; we also included the training curve of the run with the best performance from the basic state, visualized in blue color.
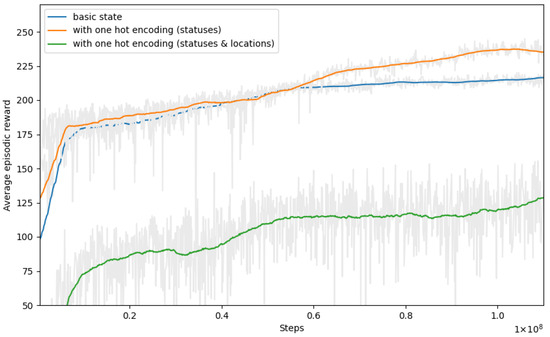
Figure 6.
Training curves for the encoding experiments.
The results presented in Table 6 indicate that the first experiment demonstrated improved performance, suggesting that selectively encoding individual components could improve learning. However, the second experiment showed lower performance compared with that of the basic state, which was likely due to the increased complexity of the state. The introduced encoding of multiple components may have made the state space too complex for effective learning. This suggests that encoding one component can improve learning without excessively complicating the state. In this scenario, the state space complexity remained manageable, leading to better performance.

Table 6.
Performance evaluation of the encoding experiments.
6.6. Ratio Integration
Next, we introduced two newly derived features to the state to potentially provide the agent with more valuable information for decision making. The first derived feature was the ratio of the rewards per order to the time left for order delivery. We included this feature instead of the rewards per order component . The second feature that we incorporated was the ratio of the driver’s remaining capacity to the total number of items in the queue for delivery. This feature gives the agent a sense of how much of the total outstanding demand it can fulfill with its remaining capacity. Similarly to the previous ratio, we integrated this value instead of the driver’s remaining capacity component . Figure 7 presents the training curves obtained by integrating these two derived features, while Table 7 displays the testing results on the evaluation set. The performance improvement compared with the benchmark of the basic state (blue line) was not significant for the first derived feature, but it revealed slightly higher results for the second derived feature.
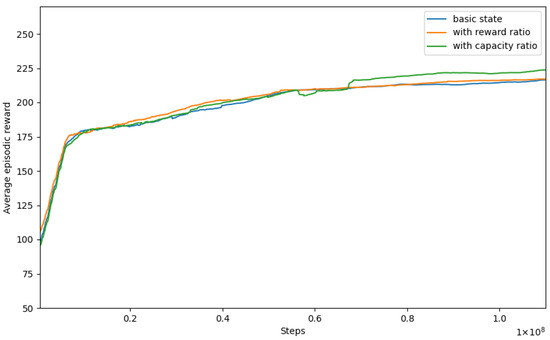
Figure 7.
Training curves with the derived ratios.

Table 7.
Performance evaluation with the derived ratios.
6.7. Combination of Enhancements
In the final phase of the experiment, we aimed to combine all of the enhancements discussed above into a single state space. This unified state space involved the basic state components from Section 6.2, such as vehicle location, the locations of the orders, the time elapsed since each order’s generation, and the current time step, as well as the newly introduced modifications, such as the one-hot encoding for order statuses (Section 6.5), distances from the current driver location to the orders (Section 6.4), the reward per order/time left ratio, and the driver capacity/total items in the queue ratio (Section 6.6). Figure 8 presents the training for different random seeds (the same as in Section 6.2) while integrating all enhancements from the previous subsections. Table 8 outlines the results on the evaluation set, where represents the difference in the average reward mean compared with the benchmark run of the basic state, and is the difference in the average reward mean compared with the appropriate random seed from Table 3, where each experiment outperformed the basic state.
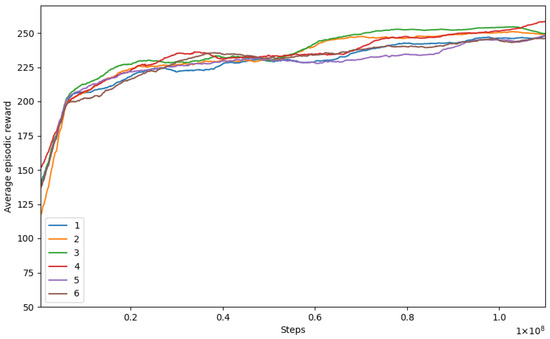
Figure 8.
Training curves with the combined state space.

Table 8.
Performance evaluation with the combined state space.
To compare the average reward means of the six runs, a paired-sample t-test was performed between the state space from Section 6.2 and the state space introduced in this section. This analysis was conducted on the same evaluation dataset of 1000 scenarios. The null hypothesis, which assumed no significant differences between the means, was rejected , indicating a statistically significant difference.
To provide a comprehensive overview of our experimental results, we compiled all outcomes from our experiments into a single table, which can be found in Appendix A. Table A1 presents a systematic comparison of the performance across all experimental configurations, including the variations in random seeds for the basic state and combined enhancements. This table offers a holistic view of how different modifications to the state space affected the model’s performance, allowing for easy comparison between different approaches.
7. Conclusions
In this research, we address a deep reinforcement learning model to tackle the dynamic vehicle routing problem with immediate acceptance or rejection of requests. Our approach offers a comprehensive Markov decision process formulation that integrates realistic variables, such as dynamic order arrivals, time windows, and capacity constraints, enhancing its relevance to practical scenarios. Through a computational study, we present a formulation for this complex dynamic problem and describe our solution method. The findings demonstrate that RL shows promise for tackling the DVRP in real-life settings, emphasizing the significance of careful and efficient modeling. The extensive analysis of various state-space configurations reveals that the selection and composition of components within the state space significantly impact the algorithm’s performance.
Our findings reveal several key insights. Conducting experiments with multiple random seeds allows for a comprehensive evaluation of the model. Additionally, even with a simple representation, certain components in the state space play a critical role and should be incorporated to address the problem effectively. Expanding the state space by incorporating relevant components, such as distance information in models with location components, can expedite learning for the RL agent. Furthermore, we explore derived features, such as ratios, and find that their impact on performance is relatively minimal in our experimentation. Careful consideration should be given to component transformation when designing the state space, such as by employing one-hot encoding. However, excessively expanding the state space can lead to reduced performance. Incorporating these key considerations into the modeling and design of RL algorithms for the problem at hand can yield valuable improvements in performance and contribute to more efficient routing solutions. The approach offers a flexible framework that can be applied to address a range of variations of the DVRP, extending its applicability beyond the specific problem studied in this research.
In future work, it is crucial to investigate the proposed findings using real-world settings and datasets, which would further validate the effectiveness of the approach and its potential in practical applications. Future research should also focus on scalability analysis, exploring how the model performs with larger problem instances, longer time horizons, and expanded geographic areas. The potential of transfer learning to quickly adapt the model to new environments or DVRP variations can be investigated, potentially allowing faster deployment in diverse scenarios. Furthermore, a key direction to explore is the development of hybrid approaches that combine RL with traditional optimization techniques or heuristics, particularly for the routing aspect of the problem. Although RL has shown promise in decision making for order acceptance and resource management, it can face challenges in optimizing complex routing decisions [22]. By integrating RL with specialized routing heuristics, one can potentially leverage the strengths of both methods, improving their overall performance and computational efficiency. These future directions aim to bridge the gap between theoretical RL models and practical DVRP applications, potentially leading to implementable solutions in the field of last-mile delivery.
Author Contributions
Conceptualization, A.K. and L.M.H.; methodology, A.K. and L.M.H.; software, A.K.; validation, A.K. and L.M.H.; formal analysis, A.K. and L.M.H.; investigation, A.K. and L.M.H.; resources, A.K. and L.M.H.; data curation, A.K. and L.M.H.; writing—original draft preparation, A.K.; writing—review and editing, L.M.H.; visualization, A.K. and L.M.H.; supervision, L.M.H.; project administration, A.K. and L.M.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author/s.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| VRP | Vehicle routing problem |
| DVRP | Dynamic vehicle routing problem |
| RL | Reinforcement learning |
| DNN | Deep neural network |
| DRL | Deep reinforcement learning |
| CVRP | Capacitated vehicle routing problem |
| MDP | Markov decision process |
| PPO | Proximal policy optimization |
Appendix A

Table A1.
Combined results of all experiments.
Table A1.
Combined results of all experiments.
| Experiment | Reward | ||
|---|---|---|---|
| 1.1. Basic state (RS 1) | 213.29 | 23.10 | −5.66 |
| 1.2. Basic state (RS 2) | 214.56 | 23.62 | −4.39 |
| 1.3. Basic state (RS 3) | 213.72 | 23.07 | −5.23 |
| 1.4. Basic state (RS 4) | 218.95 | 20.95 | 0 |
| 1.5. Basic state (RS 5) | 216.24 | 20.09 | −2.71 |
| 1.6. Basic state (RS 6) | 173.17 | 20.01 | −45.78 |
| 2. Removing locations | 166.06 | 26.14 | −52.89 |
| 3. Adding distances | 245.14 | 43.86 | 26.19 |
| 4.1. One-hot encoding (statuses) | 231.58 | 42.61 | 12.63 |
| 4.2. One-hot encoding (statuses and locations) | 126.13 | 47.36 | −92.82 |
| 5.1. Adding reward ratio | 219.32 | 22.21 | 0.37 |
| 5.2. Adding capacity ratio | 228.82 | 23.31 | 9.87 |
| 6.1. Combined state space (RS 1) | 258.24 | 36.99 | 39.29 |
| 6.2. Combined state space (RS 2) | 257.75 | 34.76 | 38.80 |
| 6.3. Combined state space (RS 3) | 252.61 | 38.11 | 33.66 |
| 6.4. Combined state space (RS 4) | 257.50 | 38.56 | 38.55 |
| 6.5. Combined state space (RS 5) | 245.82 | 45.86 | 26.87 |
| 6.6. Combined state space (RS 6) | 256.71 | 38.11 | 37.76 |
References
- Boysen, N.; Fedtke, S.; Schwerdfeger, S. Last-mile delivery concepts: A survey from an operational research perspective. OR Spectr. 2021, 43, 1–58. [Google Scholar] [CrossRef]
- Laporte, G. The vehicle routing problem: An overview of exact and approximate algorithms. Eur. J. Oper. Res. 1992, 59, 345–358. [Google Scholar] [CrossRef]
- Psaraftis, H.N. Dynamic vehicle routing problems. Veh. Routing Methods Stud. 1988, 16, 223–248. [Google Scholar]
- Pillac, V.; Gendreau, M.; Guéret, C.; Medaglia, A.L. A review of dynamic vehicle routing problems. Eur. J. Oper. Res. 2013, 225, 1–11. [Google Scholar] [CrossRef]
- Rios, B.H.O.; Xavier, E.C.; Miyazawa, F.K.; Amorim, P.; Curcio, E.; Santos, M.J. Recent dynamic vehicle routing problems: A survey. Comput. Ind. Eng. 2021, 160, 107604. [Google Scholar] [CrossRef]
- Zhang, J.; Woensel, T.V. Dynamic vehicle routing with random requests: A literature review. Int. J. Prod. Econ. 2023, 256, 108751. [Google Scholar] [CrossRef]
- Qin, Z.; Zhu, H.; Ye, J. Reinforcement learning for ridesharing: An extended survey. Transp. Res. Part Emerg. Technol. 2022, 144, 103852. [Google Scholar] [CrossRef]
- Zhan, X.; Szeto, W.; Chen, X.M. The dynamic ride-hailing sharing problem with multiple vehicle types and user classes. Transp. Res. Part Logist. Transp. Rev. 2022, 168, 102891. [Google Scholar] [CrossRef]
- Du, T.C.; Li, E.Y.; Chou, D. Dynamic vehicle routing for online B2C delivery. Omega 2005, 33, 33–45. [Google Scholar] [CrossRef]
- Créput, J.C.; Hajjam, A.; Koukam, A.; Kuhn, O. Dynamic vehicle routing problem for medical emergency management. In Self Organizing Maps-Applications and Novel Algorithm Design; Intechopen: London, UK, 2011; pp. 233–250. [Google Scholar]
- Sreelekshmi, V.; Nair, J.J. Dynamic vehicle routing for solid waste management. In Proceedings of the 2017 IEEE Region 10 Symposium (TENSYMP), Cochin, India, 14–16 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–5. [Google Scholar]
- Yang, Z.; van Osta, J.P.; van Veen, B.; van Krevelen, R.; van Klaveren, R.; Stam, A.; Kok, J.; Bäck, T.; Emmerich, M. Dynamic vehicle routing with time windows in theory and practice. Nat. Comput. 2017, 16, 119–134. [Google Scholar] [CrossRef]
- Kaelbling, L.P.; Littman, M.L.; Moore, A.W. Reinforcement learning: A survey. J. Artif. Intell. Res. 1996, 4, 237–285. [Google Scholar] [CrossRef]
- Yan, Y.; Chow, A.H.; Ho, C.P.; Kuo, Y.H.; Wu, Q.; Ying, C. Reinforcement learning for logistics and supply chain management: Methodologies, state of the art, and future opportunities. Transp. Res. Part Logist. Transp. Rev. 2022, 162, 102712. [Google Scholar] [CrossRef]
- Phiboonbanakit, T.; Horanont, T.; Huynh, V.N.; Supnithi, T. A Hybrid Reinforcement Learning-Based Model for the Vehicle Routing Problem in Transportation Logistics. IEEE Access 2021, 9, 163325–163347. [Google Scholar] [CrossRef]
- Bengio, Y.; Lodi, A.; Prouvost, A. Machine Learning for Combinatorial Optimization: A Methodological Tour d’Horizon. Eur. J. Oper. Res. 2020, 290, 405–421. [Google Scholar] [CrossRef]
- Nazari, M.; Oroojlooy, A.; Snyder, L.V.; Takác, M. Deep Reinforcement Learning for Solving the Vehicle Routing Problem. arXiv 2018, arXiv:1802.04240. [Google Scholar]
- Kool, W.; van Hoof, H.; Welling, M. Attention, Learn to Solve Routing Problems! In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018.
- Delarue, A.; Anderson, R.; Tjandraatmadja, C. Reinforcement Learning with Combinatorial Actions: An Application to Vehicle Routing. In Proceedings of the Advances in Neural Information Processing Systems, Virtual, 6–12 December 2020; Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M., Lin, H., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2020; Volume 33, pp. 609–620. [Google Scholar]
- Silver, D.; Huang, A.; Maddison, C.; Guez, A.; Sifre, L.; Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef]
- Berner, C.; Brockman, G.; Chan, B.; Cheung, V.; Debiak, P.; Dennison, C.; Farhi, D.; Fischer, Q.; Hashme, S.; Hesse, C.; et al. Dota 2 with Large Scale Deep Reinforcement Learning. arXiv 2019, arXiv:1912.06680. [Google Scholar]
- Hildebrandt, F.D.; Thomas, B.W.; Ulmer, M.W. Opportunities for reinforcement learning in stochastic dynamic vehicle routing. Comput. Oper. Res. 2022, 150, 106071. [Google Scholar] [CrossRef]
- Ulmer, M.W.; Goodson, J.C.; Mattfeld, D.C.; Thomas, B.W. On modeling stochastic dynamic vehicle routing problems. EURO J. Transp. Logist. 2020, 9, 100008. [Google Scholar] [CrossRef]
- Balaji, B.; Bell-Masterson, J.; Bilgin, E.; Damianou, A.; Garcia, P.M.; Jain, A.; Luo, R.; Maggiar, A.; Narayanaswamy, B.; Ye, C. ORL: Reinforcement Learning Benchmarks for Online Stochastic Optimization Problems. arXiv 2019, arXiv:1911.10641. [Google Scholar] [CrossRef]
- Joe, W.; Lau, H.C. Deep Reinforcement Learning Approach to Solve Dynamic Vehicle Routing Problem with Stochastic Customers. Proc. Int. Conf. Autom. Plan. Sched. 2020, 30, 394–402. [Google Scholar] [CrossRef]
- Chen, X.; Ulmer, M.W.; Thomas, B.W. Deep Q-learning for same-day delivery with vehicles and drones. Eur. J. Oper. Res. 2022, 298, 939–952. [Google Scholar] [CrossRef]
- Bono, G. Deep Multi-Agent Reinforcement Learning for Dynamic and Stochastic Vehicle Routing Problems. Ph.D. Thesis, Université de Lyon, Lyon, France, 2020. [Google Scholar]
- Pan, W.; Liu, S.Q.S. Deep reinforcement learning for the dynamic and uncertain vehicle routing problem. Appl. Intell. 2022, 53, 405–422. [Google Scholar] [CrossRef]
- Zhou, C.; Ma, J.; Douge, L.; Chew, E.P.; Lee, L.H. Reinforcement Learning-based approach for dynamic vehicle routing problem with stochastic demand. Comput. Ind. Eng. 2023, 182, 109443. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Raffin, A.; Hill, A.; Gleave, A.; Kanervisto, A.; Ernestus, M.; Dormann, N. Stable-Baselines3: Reliable Reinforcement Learning Implementations. J. Mach. Learn. Res. 2021, 22, 1–8. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).