Abstract
The ongoing issues in global supply chain disruptions have raised many concerns of port productivity, among which port congestion is a key issue. This article implements an integrated tactical–operational optimization framework which raises the capabilities of port information systems to deliver smarter decision-making processes in ports through a decision support system. To this end, we developed a library of multiple smart models for the optimization of port operations, independently engaged in parallel but mathematically coordinated to achieve autonomous real-time distributed optimization, using a novel event-driven structure to enable future implementations using digital twins. The framework was tested to benchmark different commercial solvers on several real instances for the port under study. The results show a strong improvement in port operational planning.
1. Introduction
Ports are critical nodes in international supply chains and play an essential role in the global economic and trade system, facilitating approximately 90% of world trade [1]. To achieve productivity and high service levels, ports must operate with maximum efficiency while facing numerous challenges. Recent global supply chain disruptions have heightened concerns about port productivity, with congestion being a significant issue [2]. This congestion exacerbates global supply chain stress, creating a ripple effect across many industries. Additionally, a faster-than-expected recovery in demand for goods has led to supply chain disruptions, such as container shortages and severe delays at some of the world’s busiest ports. To manage congestion, some ports have temporarily stopped accepting import/export orders [3] at times when the most sophisticated tools for operational efficiency reach their top performance. Shipping lines halted booking services to ports due to backlogs on the U.S. West Coast [4] and container availability imbalances from Asia [5,6].
Port congestion is a significant challenge faced by many ports worldwide and can arise from various factors. Common causes include overbooked terminal capacity, weather-related operational delays, strikes, the impact of war (whether real, cyber, or trade), vessel bunching, low productivity, insufficient yard space, port restrictions, location and access issues, and poor hinterland connections. These delays are prevalent in container terminals globally and are often attributed to the increase in both the number and size of container ships. However, the rise in container volumes also necessitates that container yards (CYs) clear the containers out of the port at the same or greater speed. Even before the COVID-19 pandemic, ports were struggling with congestion due to increasing global demand and a lack of digitalization in the maritime sector. Ports are under increasing pressure to better contribute to the economic, environment [7,8,9], and social [10] aspects of sustainability [11]. The grand challenge of effectively managing ports, while acquiring all of the angles for sustainable operations, requires the convergence of ideas and approaches from diverse disciplines. With the increasing introduction of digital and emerging technologies to ports [12], and more connectivity with stakeholders, managing operations at ports now benefits from faster flow of data between sensors, devices, equipment, and software applications to enable the smart infrastructure driving ports to becoming state-of-the-art facilities of the future. Digital technologies and increasing data exchange among all stakeholders yield higher gains in efficiency and predictability in ports.
The focus of our study is to implement tactical planning and scheduling models to optimize operations and commercial services for a container hub port. Our solution involves creating a framework that includes a set of optimization models aimed at (i) defining an operations timetable and (ii) allocating ships to docks and cranes to ships. This approach is designed to optimize the management of shipping services across the two terminals of the port.
With the primary goal of improving container port operational efficiency, we first examine the subproblems that arise in port planning. The most critical pain points to analyze for enhancing operational efficiency include the following:
- ▪
- The time that a vessel is at the berth needs to be minimized.
- ▪
- Land scarcity does not allow container terminals to meet the rapid growth of freight traffic.
- ▪
- The overall congestion increases operation variability and reduces throughput.
- ▪
- Operations on different subsystems need to be effectively coordinated.
- ▪
- The logistics of container terminals has reached a high degree of complexity.
The overall solution requires gathering and consolidating execution information from the different subsystems, leveraging optimization capabilities to tackle the complexity of the different interconnected subsystems and ultimately helping planners drive operational excellence and analyze terminal performances.
The motivation for this research article lies in addressing the pressing challenges facing global supply chains, particularly concerning port productivity and congestion. By developing an integrated tactical–operational optimization framework, we aim to enhance the capabilities of port information systems to facilitate smarter decision-making processes. This motivation stems from the recognition that traditional approaches to port operations planning may no longer suffice in addressing the complexities and uncertainties inherent in modern supply chain dynamics. The proposed framework leverages multiple smart models and a novel event-driven structure to achieve autonomous real-time distributed optimization, representing a significant advancement in port optimization methodologies. Through empirical testing and benchmarking on real instances, such as the Port of Cartagena in Colombia, the researchers demonstrate the potential for substantial improvements in port operational planning.
We identified the following gaps in the existing literature that need to be addressed for effective integrated port operation optimization:
- ▪
- Lack of Holistic Optimization Framework: The existing literature lacks comprehensive, enterprise-wide optimization frameworks that integrate all facets of port operations, from terminal management to hinterland logistics and supply chain integration.
- ▪
- Fragmented Optimization Efforts: Current research often focuses on individual components or subsystems within ports, resulting in fragmented optimization efforts that fail to consider the interconnectedness and interdependencies among various operational elements.
- ▪
- Insufficient Connectivity to Real-Time Data: There is a significant gap in achieving connectivity to live real-time data streams from diverse sources, such as IoT sensors, GPS tracking systems, and weather forecasts, which impedes the development of dynamic and adaptive optimization strategies.
- ▪
- Limited Dynamic and Adaptive Optimization: Many optimization models rely on static or historical data, which may not accurately reflect current operating conditions or account for unexpected disruptions. The lack of access to real-time data streams hinders the development of dynamic and adaptive optimization strategies.
- ▪
- Need for Advanced Data Analytics Techniques: There is a need for advanced data analytics techniques and machine learning algorithms to harness the vast amounts of real-time data generated within ports and their surrounding ecosystems, enabling smarter decision-making processes and more efficient operations.
These gaps highlight the need for a paradigm shift towards holistic, data-driven optimization frameworks that leverage real-time data and advanced analytics techniques to improve port operations and enhance decision-making processes. Addressing these gaps requires a paradigm shift towards holistic, enterprise-wide optimization frameworks that encompass all facets of port operations, from terminal management and berth scheduling to hinterland logistics and supply chain integration. Such frameworks should leverage advanced data analytics techniques and machine learning algorithms to harness the vast amounts of real-time data generated within ports and their surrounding ecosystems.
In what follows, Section 2 provides a comprehensive review of the extant literature, offering a broader look at existing studies and frameworks related to port optimization and operations planning. Building upon this foundation, Section 3 delineates the methods employed, focusing on the development of a robust modeling framework tailored to address the integrated event-driven tactical–operational port planning problem. Section 4 presents a detailed case study and corresponding results, supplemented by an economic analysis aimed at justifying the efficacy and practical applicability of the proposed framework within real-world port environments. Section 4 ends with managerial insights gleaned from this study’s findings, providing actionable recommendations for enhancing port operations and decision-making processes. Finally, Section 5 encapsulates the conclusions drawn from the research findings and outlines potential avenues for further studies, highlighting the ongoing pursuit of innovation and optimization in the realm of port management and logistics.
2. Literature Review
Port optimization has primarily been studied by addressing the various subproblems in port management separately. These subproblems include the well-studied berth scheduling and quay crane scheduling issues, yard optimization, port equipment scheduling, and energy efficiency objectives. However, few researchers have taken a comprehensive approach to port optimization that considers all of the challenges posed by port management.
2.1. Overview
Numerous survey articles on port operations exist in the current literature. Notable works focusing on yard management can be found in references [13,14,15,16,17]. Other authors focus on quayside operations, such as those outlined in [13,18,19]. Most of these surveys introduce the equipment used in container terminals and various optimization models, as seen in [20,21,22]. In [23], the authors examine port operations and decision support systems, emphasizing quay crane (QC) assignment and QC scheduling; yard operations including container stacking, yard vehicle dispatching, and yard crane (YC) scheduling; as well as integrated operations. Recent publications, such as [24,25], review new technologies and mathematical models for sea container terminals. In [26], the authors explore simulation modeling of port operations in container terminals. Additionally, a decision support system for integrated container handling operations is proposed in [27].
Moreover, as demonstrated in [12], the port industry has been advancing beyond scientific research, highlighting a pressing need to promote more rigorous and intelligent modeling structures to enhance port operational efficiency, productivity, and sustainability. Few authors have delved into the integration of environmental and social equity and inclusion constraints into port optimization systems, as evidenced by references [28,29]. In [30], the authors illustrate the advantages of digital transformation in maritime ports.
The efficiency of a port profoundly influences all those involved in its bustling trade activities [31]. Operational performance centers on productivity and encompasses physical quantities of items, levels of effort expended, the scale or scope of activities, and efficiency in resource transformation into products or services.
Port efficiency is interconnected with maritime, terminal, and hinterland operations, forming a continuum where inefficiencies in one dimension can affect the others. For example, issues in terminal operations can adversely impact maritime and hinterland operations, leading to delays. The efficiency of maritime access is a critical component of port performance, encompassing metrics such as the average anchorage time, which reflects the duration ships spend waiting for berthing slots. Lengthy wait times at anchorage may result from insufficient berthing slots capable of accommodating specific ship classes (e.g., draft and cargo type), as well as terminal productivity. Conversely, terminal operations serve as the primary performance indicator for assessing port efficiency.
Common metrics used to gauge terminal operations productivity comprise berth occupancy, cargo revenue per ton, capital equipment expenditure per ton of cargo, turnaround time, and the number of crew members employed to facilitate cargo operations.
2.2. The Port Continuum
In container terminal operations, several key processes are typically involved. However, the efficiency of transport operations beyond the terminal is often overlooked as a port indicator. This encompasses transportation and distribution activities serving the port’s clientele, primarily focusing on inland operations adjacent to the port area. In our previous research on hinterland efficiency [32], we demonstrated that inadequate transport infrastructure leads to longer travel times and increased costs, indirectly impacting the region’s productivity, as transportation costs directly affect sales prices. Consequently, this influences port choice for shipping lines [33], as decision making regarding port and path selection heavily relies on hinterland connection efficiency.
The capacity of the local road network in areas adjacent to the port is a crucial factor in hinterland operations. Additionally, in [34,35], we investigated the impact of freight brokering systems and transportation and logistics marketplaces on hinterland efficiency. These studies explored real-world implementations of an e-commerce platform that facilitates agile interaction, streamlining service and security negotiations. It offers geo-spatial sensory information to optimize driving efficiency, utilizing OBD-II technology to collect data on necessary conditions, along with a mobile platform for data input.
In the context of the remaining two segments of the port operational continuum, we will now position this study within the existing literature. Numerous authors have developed models and solutions for the berth allocation problem, as evidenced by references [36,37,38,39,40]. Integrated mathematical approaches addressing both berth allocation and quay crane scheduling can be found in [41,42,43]. Conversely, certain authors, such as those of [44,45,46], have proposed models addressing the integration of berth allocation and yard planning problems. Perhaps the most comprehensive modeling for port planning known to us is outlined in [47,48], where berth allocation, quay crane scheduling, and yard planning are integrated.
Regarding the maritime side of the continuum, the integrated modeling of vessel traffic and berth planning is presented in [49,50,51]. In a recent survey article [52], the authors noted that, to their knowledge, only one study has evaluated the performance of various mathematical formulations in an integrated manner. To our knowledge, our framework represents the most comprehensive port optimization framework presented to date, which is fully implemented using information systems.
From a different, but rather needed side, several authors have modeled integrated port and energy/environmental planning, for which [53,54,55,56,57] are very good sources. Last, an interesting framework for smart and sustainable port modeling is presented in [58]. Other studies exploring the concept of smart ports are [59,60,61]. Although not included in our current solution, our set of integrated modeling libraries allow for the introduction and embedding of environmental/energy considerations for port modeling. This will be part of a future work that will include the prediction of port emissions (not only the measurement of such) as a constraint in the optimization framework.
2.3. Digital Systems and Port Automation
More interestingly, none of today’s port operational problems could really be solved extensively and in real-time without the use of digital information systems. Information systems with built-in large-scale analytics and optimization engines are now capable of putting together tightly coupled tactical and operational optimization models. In this study, we address the problem of jointly solving integrated, interconnected tactical/operational planning models for a port with a focus on operational efficiency.
The introduction of intelligent devices able to share in real-time data has changed business models and the management of port decision support information systems. The reasons for this are mainly digitalization and automation, resulting in improved performances. These factors have changed the concept of logistics from physical to digital operations. The dematerialization of data has eliminated the expensive physical documents chain, while automation has increased levels of (cyber)security and efficiency. The major features of an evolved smart digital port are represented by (1) the combination of technology and widely adopted shared processes for collecting and distributing data and information to manage operations in (or out) or to (or from) a port, (2) the necessity of the processes to be shared by operators and the whole community of stakeholders, public or private, and (3) integration with the surrounding smart territory (city, region, or country) and with smart model transport infrastructures. The main benefits of smart port digitalization are clearly evidenced: a better transit response time of goods through ports, reduced costs to handle goods, a better response time of stakeholders to their customers, reduced usage of paper flow due to information being distributing electronically, improved track and trace efficiency, more efficiency, a shorter transit time, and higher integration with third parties (e.g., customs). In [1], we assessed how the application of digitalization could improve the response time for the case of multi-cargo port facilities. In a different study, the requirements and conditions to develop a customized IT system to improve operations for port terminal information systems were evidenced [2]. The results prove a strong need for decision-making tools, higher levels of interconnectivity with stakeholders, and governance structure. Currently, one of the most used platforms in ports are the so-called PCSs (Port Community Systems), defined as inter-organizational systems used for enabling commercial services and providing information exchange between a port to their customers and a variety of stakeholders, such as forwarders, carriers, and customs, among others [62,63]. One of the main concerns revealed by our previous research [12] is that industry is ahead of scientific research, meaning there is a gap between research and stakeholders. Research shows that scholars should move forward in developing pragmatic research and suggests future areas to consider for port information systems.
3. Materials and Methods: A Modeling Framework for the Integrated Event-Driven Tactical–Operational Port Planning Problem
Herein, we introduce a comprehensive mathematical modeling framework to address the integrated tactical and operational port planning problem, employing an innovative event-driven structure to seamlessly integrate the models into smart decision support information systems. Such an event-based modeling framework holds promise for providing a more accurate representation of the physical system’s behavior, thereby enhancing predictions and facilitating more effective decision making.
In contrast to conventional approaches, event-based modeling concentrates on the occurrence of discrete events rather than continuous variables. This approach offers greater flexibility and adaptability in modeling complex systems, particularly those exhibiting nonlinearity or discontinuous behavior. Moreover, event-based models can be updated in real-time, potentially allowing digital twins to respond promptly to changes in the physical system as they unfold.
We now explore the core methodology of this research, presenting a comprehensive framework crafted to tackle the intricate challenges inherent in contemporary port operations. Central to this section is the creation of a novel modeling approach specifically designed to incorporate tactical and operational considerations within a dynamic event-driven context. As ports navigate increasingly volatile and interconnected supply chain networks, the demand for agile decision-making processes capable of responding to real-time events becomes paramount. This section illustrates how the proposed modeling framework utilizes advanced optimization techniques coupled with an event-driven architecture to facilitate proactive planning and resource allocation, thereby enhancing the efficiency, resilience, and adaptability of port operations.
3.1. General Conceptualization
The system to be modeled comprises t port terminals and serves as a regional transshipment hub. This means that a unit arriving at one terminal may depart through another, necessitating intra-terminal movement and incurring operating costs. These terminals, located at different geographical points, facilitate joint operations.
Each terminal is equipped with m berthing lines or docks, distinguished by draft and structural capacity. These characteristics determine the types of ships that can be accommodated. Typically, these attributes vary within terminals, necessitating the segmentation of docks (s) where characteristics are homogeneous. Here, segment s refers to the relationship between docks.
Ships access the port via routes or itineraries provided by shipping companies, known as services (z). A service may be served by ships from various shipping lines but with similar operational characteristics. Within the model, these are identified as vessels (b). The reference ship is conceptualized as a fictitious vessel embodying the most adverse characteristics (e.g., the longest length, largest beam, highest tonnage, greatest height, fewest quay cranes, etc.) among all ships operating the service. Henceforth, the terms “reference ship” and “vessels” denote the reference ship or other vessels. Figure 1 shows the planning cycle for port operations.
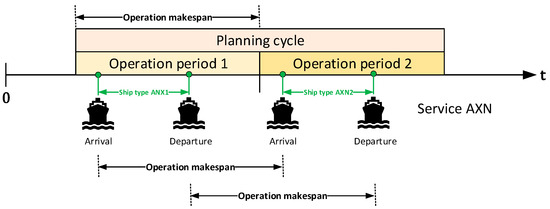
Figure 1.
Port operations planning cycle.
A recurring planning cycle serves as the foundation for decision making in operational and commercial tactical planning processes. This cycle consists of p operational periods during which service planning is conducted anew. Services may require ships to be served in all periods or only in select ones. In this instance, the planning cycle spans a fortnight (2 weeks), with each operational period lasting one week.
The mathematical model is constructed using a discrete event modeling structure, which employs the discrete event simulation paradigm in formulating optimization models. In this approach, events such as the arrival and departure of ships at the port are utilized. These two events capture the essential dynamics of the system that are necessary for decision making. Within the mathematical model, time is continuous, while space (represented by docks) is discrete and segmented.
We introduce an integrated tactical–operational planning framework designed to manage the diverse events encountered at a hub port. Initially, our focus is on addressing the midterm implications of assigning terminals to services for shipping lines. This involves a set of services with predefined itineraries and arrival patterns, each serviced by a fleet of vessels with specific characteristics. Additionally, there is a group of terminals equipped with docks and cranes of known specifications.
The objective is to allocate ships to docks at each terminal in order to minimize service waiting times throughout the year. While a service must be assigned to a specific terminal, the vessels of a service can be allocated to different docks within the same terminal. It is essential to determine both the maximum and average wait times per service, as well as to identify the time slots in the week with the most conflicts.
Subsequently, we proceed to address the berth and quay allocation problem, considering that services are already assigned to terminals with a specified number of movements per service per year. Additionally, we utilize a connectivity matrix between services, indicating the volume of containers exchanged between them.
The aim is to allocate services to terminals in a manner that minimizes inter-terminal transfers while ensuring that the average wait time remains within a predetermined percentage limit over the service duration, as set by the port. Agreements exist between shipping lines stipulating that a designated number of containers in transit are left at the port by one shipping line for subsequent pickup by another. Should container transfers between terminals occur, the associated costs are fully borne by the port. All models are closely interconnected and run (and learn) simultaneously. The interplay among these models is depicted in Figure 2.
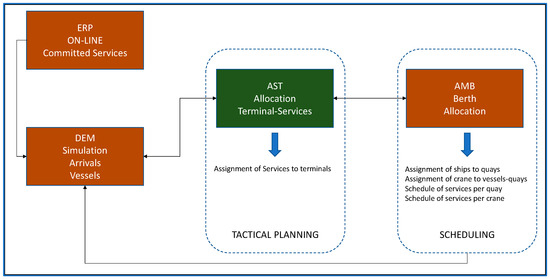
Figure 2.
The interconnectivity of the simulation and optimization models.
The information is first retrieved from the port’s enterprise resource planning (ERP) system and then fed into the different decision support models within the HAi Port Operations Information System [64].
The Allocation of Services and Terminals (AST) support model allocates terminals to all committed services of the shipping lines and generates a simulated allocation of potential occurrences for all terminals in the upcoming months. This model serves as a tactical planning tool and operates on a monthly basis, aligning with the forecasted service demand for the months ahead in the next semester or year. It is a continuous-time model that solves a mixed-integer programming problem.
At the berth level, the Allocation of Berths and Quay Cranes (ABQ) model operates an integrated berth allocation scheduling and quay crane assignment decision support framework; its primary aim is to assign vessels belonging to shipping services to specific docks within terminals and, subsequently, to allocate a set of cranes to service each vessel. This allocation is carefully managed while closely adhering to the operational constraints applicable to both vessels and each terminal, including its docks and cranes. A detailed hourly schedule of container transfers between terminals, factoring in the schedule for prior operations, is also meticulously formulated by employing a novel event-based model, as depicted in Figure 3; within this detailed schedule, each hour is meticulously mapped out with the assignment of vessels to docks, entailing the precise definition of the assigned dock, entry time, waiting period, operational duration, and exit time for each vessel.
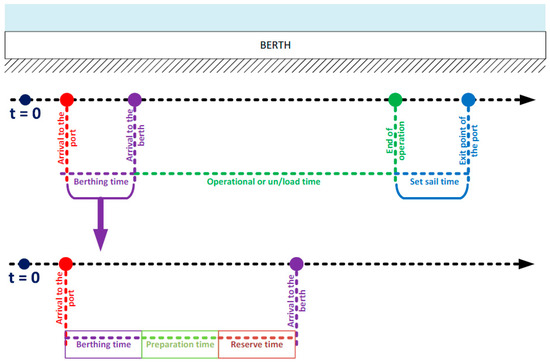
Figure 3.
Events that occur in a berth and quay allocation solution within the dwell time makespan.
A detailed schedule of container transfers between terminals, considering the schedule for prior operations, is also created. This model runs daily or every time an event occurs (which warrants the rescheduling of the ongoing schedule). It is based on continuous time modeling and solves a mixed-integer linear programming model. In what follows, we describe the mathematical groups and the solution methodology.
3.1.1. Mathematical Modeling Groups
In our modeling description, we opted to categorize the constraints (equations and inequalities) based on their functionality within the model. This approach not only organizes the constraints but also aids in explaining the implemented solution methodology later on. Table 1 shows the basic mathematical modeling main groups descriptions.

Table 1.
Model group descriptions.
3.1.2. Notation
In this section, we establish the notation employed in constructing the mathematical model. Initially, we define the indices utilized in the model, as presented in Table 2.

Table 2.
Definitions of indices.
We also define the sets. In the definition of sets, and to reduce their domain, the following notation is used: X and Y represent the sets of entities, x and y. The set represents the elements x that are related to the element y, that is, the ordered pairs (y,x). Table 3 defines all the sets used in the models.

Table 3.
Definitions of sets.
Table 4 describes the parameters for the various mathematical models presented in the next section.

Table 4.
Definitions of parameters.
We now formally describe the variables for the mathematical models (Table 5).

Table 5.
Definitions of variables.
The next section shows the mathematical formulation.
3.1.3. Mathematical Modeling
For the modeling description, we decided to group the constraints (equations and inequalities) according to their functionality within the model. In addition, they later facilitate the explanation of the implemented solution methodology.
Next, we present the different modeling groups that make up the planning/scheduling problem of the port operation analyzed in this research work.
Definitions of Times
This inequality guarantees that all events have a different time of occurrence (strictly increasing) in the timeline.
The time of entry of each ship can only be activated when it is assigned a docking segment.
The departure time of each ship can only be activated once and will be associated with the dock segment to which it was assigned.
The following expression coordinates the event line with the ship’s arrival at port events.
When the variable takes the value of 1, two inequalities are produced that are equivalent to an equality, making ; that is, the time of occurrence of the event e is equal to the time of entry of the ship to the port. This is represented by the following constraints:
The same idea is used to achieve the coordination between the timeline of events and the events cataloged as the departure of the ship from the port, generating the following equations:
The start time of each ship’s port operation must be greater than the earliest time that the ship can arrive at the port.
This restriction ensures that the completion time of the unloading/loading operation on each ship is greater than or equal to the completion time of the operation of each of the cranes that serve it.
Using the same concept used to coordinate the relationship between the variables , and , the coordination between the variables and is performed to determine the time a crane works on a ship.
When the variable takes the value of 1, the variable is equal to the difference in the instances of occurrence of the events and , which is represented by the following constraints:
Cranes can only operate on a ship if they have been assigned to service it.
Some ships have their own cranes that can be used in their service processes. The time of completion of the operation in these ships must be greater than or equal to the start time of the service operation plus the time of operation of their own cranes.
The following restriction is only activated when the ship b is unloaded/loaded with its own cranes without the intervention of the quay cranes.
The following equation ensures that the ships b of the “Container” service type that do not have their own cranes can use the maximum number of quay cranes allowed.
Equation (18) ensures that the departure time of the ship from the port must be equal to the time of completion of the operation plus the departure time.
For ships that transport vehicles, the difference between the time of departure and the start of the operation must be greater than the estimated unloading time.
The below equation calculates the deviation of the ship’s departure time in relation to the maximum departure date of the service window. The non-compliance fine is settled with respect to the ship’s expected date of departure .
This constraint, if necessary, allows the variable to take values other than zero, indicating that the ship b does not comply with the maximum departure date of its service window.
This constraint, when necessary, allows the variable to take values other than zero, indicating that the ship b leaves the port before the end of its attention window.
The following restriction allows, if necessary, a possible deviation of the departure time of each ship to be activated:
The below equation calculates the default time. It must be calculated in relation to the expected time of departure.
Equation (25) ensures that the average productivity of attention assigned to ship b is greater than or equal to the minimum productivity committed in the commercial negotiation.
Movements
Cargo movements, to and from, are only allowed when the ship b is being serviced during an event e in some segment of the dock m.
Equation (27) calculates the movements that are made on the ship type b between the events e and e + 1 as a function of the cranes that have been assigned to it.
The movements made must be equal to the expected movements. In the case of using the ship’s own cranes, it deactivates the movements that can be carried out by the dock cranes.
Resource Allocation
Each ship b entry must be allocated to a single event. This assignment considers the possible alternatives of the dock–dock segment–event combination.
The departure of each ship b must be assigned to a single event.
Each event e may or may not correspond to a change in the state of the system. In the case of a change in state, this must be the entry or exit of a ship.
Once a ship is assigned to a dock–dock segment for its attention (service), it must hold its position until it leaves the port.
The following equation allows the initial status of each ship to be included. All ships have not been assigned to any dock as the initial condition of the problem. At the operational level, it is one of the most important input parameters.
Each ship b must be assigned to a single dock segment between which it can dock.
Equation (35) ensures that only one ship b can be assigned to the berth segment s of a dock m during an event e.
If a ship is assigned to a dock segment, then only events related to this entity can be active.
Equation (37) guarantees that the crane c is assigned to one ship b at most in each of the events e that make up the timeline.
The variables can only be activated if the crane c attends the ship b in some event of the planning cycle.
During any event, the maximum number of cranes servicing the type b vessel may not exceed the maximum number of cranes allowed to service it in the port.
The sum of the lengths of the ships that are moored at a dock, at any time, cannot be greater than the operational length of the dock.
At any moment of the planning or operation horizon, ship–dock segment assignments that overlap or partially intersect, making the operation infeasible, should be avoided.
Planning Horizon
The length of the planning cycle is represented through the variable y and must be greater than or equal to each of the load and unload operation completion times.
The cranes cannot work more than the available time defined by the Resource Availability Factor (). This availability is restricted based on the planning horizon represented by the variable .
The operating time cannot be less than the expected departure time of the last ship to be served in the planning cycle.
Block–Yard Inventories
Service assignments to each terminal must be made by considering the maximum box handling capacity of each terminal. This parameter is determined by considering the historical efficiency of the cranes.
Equation (46) calculates the number of transfer units that are received at the terminal t for each type of service w.
Equation (47) calculates the number of units that have been received in the terminal t for the type of service w and that must be stored in the same terminal.
Equation (48) calculates the total number of units that have been received at the terminal t and that must be transported to another terminal to connect with the outgoing service.
Equation (49) calculates the expected flow of cargo to be handled at the terminal t for the type of service w.
Equation (50) calculates the expected flow of cargo to be handled at each terminal yard for each type of service.
Equation (51) establishes the maximum inventory peak that will be handled in any of the inventory cycles for each type of service.
The average inventory of the type of service w at the terminal t is proportional to the flow of units handled in the yard.
The variable determines the number of positions needed to handle the maximum projected inventory for the type of service w at the terminal t.
The storage area, for each type of service w, is a function of the number of storage positions required.
The area available in container yards can be used for vehicle handling. If the area has been designed for the storage of vehicles, it cannot be used for the storage of containers.
The sum of the areas used in each type of service w′ cannot be greater than the area available for the type of service w in the terminal t.
Service assignments to each terminal must be made considering the maximum box handling capacity of each terminal. This parameter is determined by considering the historical efficiency of the cranes.
This restriction is defined for several control instants (hours) to achieve adequate allocations to the operational capacity measured in movements.
Terminals and Services
Each service z must only be assigned to one terminal t within the port.
If a service z is assigned to be served at a terminal t, then ships b providing said service must be assigned to that same terminal.
This equation makes it possible to identify the pairs of services z that will be served at the same terminal t.
Together with the previous restriction, the following relationships are necessary to correctly identify when service z and service z‘ are served at the terminal t.
Coordination between Periods
This equation ensures that the segment–ship assignment (s ↔ b) is identical for ships belonging to the same service whose service window is carried out in different operating periods.
The difference in the entry instants of the ships that belong to the same service must be equal to the duration of a planning period (). The following restrictions relax the previous concept to facilitate the solution of the present problem:
Like the last two constraints, the following ones apply the same concept of relaxation in relation to the output instants:
Objective Function
The components of the objective function correspond to the cost of the transfers that must be made between terminals and the penalties incurred for non-compliance with the service window for each of the ships that must be served.
3.1.4. Solution Methodology
Ports operate in a highly dynamic environment where real-time decision making is critical. Our methodology is designed to provide solutions within a timeframe that is practical for real-time operations. This ensures that the port can respond swiftly to changing conditions and maintain operational efficiency.
The presented formulation encompasses two integrated optimization models. The first model is an assignment model, tasked with determining the services to be accommodated at each terminal, thereby assessing the cost associated with inter-terminal movements. The second model, a resource planning/scheduling model, focuses on determining the optimal utilization of docks and cranes to service each ship within its designated service window. This allocation model comprises various modeling blocks, including terminals and services and inventory in yards.
The resource scheduling model consists of blocks dedicated to resource allocation, time definition, coordination between periods, planning horizon, and movements. Solving this problem in its entirety presents a significant challenge for conventional commercial mathematical programming algorithms. Consequently, we propose an alternative methodology that facilitates a transition from an integrated scheme to a decoupled yet coordinated approach, as illustrated in Figure 4.
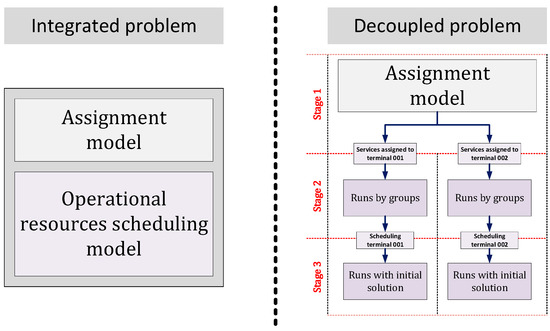
Figure 4.
Solution methodology.
The initial step in the solution methodology involves addressing the allocation stage. Given that the decisions regarding service assignments to terminals significantly influence the operational costs associated with any service scheme, resolving the assignment problem as a preliminary step is practical. This problem is efficiently solved within a short timeframe (less than 30 s), and the algorithms employed are capable of readily identifying the optimal solution in terms of quality.
Once the services allocated to each terminal are identified, we move on to their scheduling, marking Stage 2 of the process. To schedule these services, the methodology initially selects the first n ships based on their anticipated arrival dates at the port. Using this subset of services, it formulates a schedule aimed at minimizing the operational timeframe. Subsequently, it addresses the scheduling problem for the first 2n ships, adhering to their expected arrival dates while maintaining the previously obtained solution for the initial n ships. Figure 5, titled “Scheme of scheduling by groups”, illustrates the various instances of model execution.
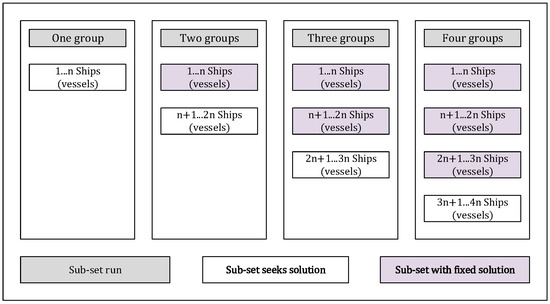
Figure 5.
Scheme of scheduling by groups.
In the column labeled “Two groups”, two distinct groups are highlighted. The first group encompasses the initial n ships, shaded in purple. This signifies that, in this instance, only this group, devoid of shading, will undergo scheduling as it already possesses a previous solution. Consequently, although the problem encompasses the first 2n ships, scheduling efforts are directed towards ships n + 1, …, 2n. Graphically illustrated in the column labeled “Four groups”, the problem is executed for a total of four groups, yet only the last n ships are actively programmed, given that the preceding three groups already have fixed solutions. Consequently, Stage 2 yields an initial feasible solution to the scheduling problem, paving the way for the proposed methodology to advance to Stage 3.
In Stage 3, the programming model is run for all the services that have been assigned to the terminal. The solution built in Stage 2 is provided as an initial solution to the programming problem of Stage 3.
In Stage 1, the mathematical model employed corresponds to the assignment model, aimed at minimizing the total cost associated with transfers between terminals. Transitioning to Stage 2, the scheduling model is utilized, with adjustments made by eliminating the equations pertaining to period coordination and the minimum boundary equation of the planning horizon within the respective block. This configuration constitutes the group scheduling model, focused on minimizing the scheduling horizon required for the ships (vessels) constituting the groups in each iteration.
In Stage 3, the programming model is applied without the equations concerning coordination between blocks of periods. Instead, a new set of restrictions is introduced to replace those relating to period coordination. Within this stage, the focus shifts towards minimizing penalties for non-compliance within the service window and for deviations in coordination between scheduling periods.
It is important to note that the model implemented at this stage differs from the one utilized to generate the initial solution due to two primary variances. Firstly, there are additional restrictions aimed at quantifying the deviation of service windows for services concluding the planning cycle. Secondly, the objective function differs. In Stage 2, the focus is on minimizing the planning horizon, whereas in Stage 3, the emphasis shifts to minimizing penalties associated with non-compliance within the service window alongside penalties for deviations from the service windows of services concluding the planning cycles.
The following equation measures the variance between the duration of the operational period and the disparity in the entry times of ships belonging to a service:
If the discrepancy between the entry times of ships within the service exceeds the duration of the operational cycle, then the variable assumes values greater than zero.
Similarly, if the variance between the entry times of ships within the service is less than the duration of the operational cycle, then the variable takes values greater than zero.
The model also guarantees that, at most, one of the deviation components between the difference in input instants and the operational cycle can be greater than zero.
The previous modeling method is also applied to the times of departure of ships from the port. The corresponding restrictions are presented below.
The objective function components of the integrated model comprise the transfer cost and the penalties incurred for non-compliance with service windows. In Stage 3, these two components remain, albeit with a distinction: the penalty cost stems from the deviations between the operational cycle duration and the disparity between the input and output instants, respectively.
The proposed solution methodology integrates two optimization models: an assignment model and a resource planning/scheduling model. The assignment model determines which services must be served at each terminal, optimizing the cost of moving between terminals. The resource planning/scheduling model determines how docks and cranes should be used to serve each of the ships within their service window.
The complexity of solving the integrated optimization problem in real-time port operations lies in the combinatorial nature of the problem and the multiple, often conflicting, objectives that need to be balanced. Traditional commercial mathematical programming algorithms struggle with such large-scale, complex problems due to their exponential growth in computational requirements as the problem size increases. Our methodology addresses this challenge by proposing a novel decoupling approach that retains coordination between the models while enabling efficient and scalable solutions.
Unlike traditional methods that attempt to solve the entire optimization problem in a single, monolithic process, our methodology decouples the problem into more manageable sub-problems. This decoupling is not a simple partitioning but a coordinated process that ensures the solutions of sub-problems are aligned and integrated. This approach leverages the strengths of decomposition techniques while maintaining the integrity of the overall optimization objective.
Our methodology employs a sequential refinement process, where the solution is progressively improved through multiple stages. Each stage builds on the results of the previous stage, allowing for iterative improvement and fine-tuning. This method ensures that initial solutions are quickly generated and then optimized further, balancing solution quality and computational efficiency. The introduction of a group scheduling mechanism is particularly innovative. By solving the scheduling problem for increasingly larger subsets of ships (e.g., first n, and then 2n, etc.) while fixing the solutions of previously solved groups, the methodology avoids the computational intractability of solving for all ships simultaneously. This staged approach enables the model to handle large-scale problems effectively and ensures that solutions are progressively refined.
The methodology employs different objective functions at different stages of the solution process. In Stage 2, the focus is on minimizing the planning horizon, which ensures efficient initial scheduling. In Stage 3, the focus shifts to minimizing penalties for service window non-compliance and deviations, reflecting the operational priorities of port management. This dynamic approach to objective functions allows for tailored optimization that meets specific operational goals at each stage.
The decoupled yet coordinated approach significantly reduces the computational burden compared to solving the integrated problem “as a whole”. By breaking down the problem and solving smaller, more manageable sub-problems, the methodology can scale to handle large ports with numerous terminals, ships, and resources without compromising on solution quality. The progressive refinement through stages ensures that the initial solutions are not only quickly obtained but also of high quality. The iterative process allows for continuous improvement, ensuring that the final solutions are near-optimal and practically viable. This is particularly important in complex port operations where minor improvements can lead to significant cost savings and efficiency gains.
The staged approach allows the methodology to be flexible and adaptable to different port settings and operational constraints. By adjusting the size of groups and the specific constraints in each stage, the methodology can be customized to fit the unique requirements of various ports, making it a versatile tool for a wide range of applications.
In summary, the proposed solution methodology offers a novel and justified approach to tackling the complex optimization problems faced in smart port operations. Its originality lies in the coordinated decoupling strategy, sequential refinement, group scheduling mechanism, and dynamic objective functions. The methodology is justified by its efficiency, scalability, improved solution quality, flexibility, and alignment with operational priorities, making it a robust framework for real-time tactical–operational optimization in port operations planning.
3.1.5. Integration with the Information System
To automatically run this mathematical framework as required, we embedded all of the mathematical models into a library of smart algorithms for the optimization of ports, independently engaged in parallel but mathematically coordinated to achieve Automated Real-Time Distributed Optimization (ARTDO) across the port system. We used the HAi optimization platform [64] to integrate the modeling framework as a set of massive distributed although interconnected parallel routines. The HAi optimization platform is the evolution of Optex, formerly a platform from DecisionWare Ltd.
We connected all of the data models and mathematical models with the port information system to automatically generate (and maintain) master tables for the terminals, dock segments, berths, vessels, quay cranes, port equipment, and support resources. Figure 6 shows a screenshot where each vessel is described on all its attributes (labels), such as boxes to hub, boxes to load, boxes to unload, length, with, draft, associated penalties/hr., number of movements (as per the BOL manifest), death weight (tonnage), etc.
Figure 6.
Screenshot image of HAi port optimization information system (labels in Spanish).
Due to the complexity of the real system, the DSS consists of multiple mathematical models which are integrated through the data stream, thereby generating the information required by the decision maker to address all hierarchic levels: strategy, tactic, operation, and real-time operations. The different models share information stored on a common database, including coherent and standardized information, to allow for data integration along with the decision-making chain in which some of the outputs of a model become the inputs of the models of subsequent stages, so this coordinated effort guarantees the “optimization” of the entire system. The latter is practically impossible to obtain with a single model.
From the base platform, we can generate mathematical modeling programs in high-level algebraic languages, like GAMS, GUROBI, IBM ILOG OPL, MOSEL, AIMMS, and AMPL. Our system is truly a generic meta-platform that works as an interface for multiple mathematical programming technologies.
The main large-scale concept used in our system is Real-Time Distributed Optimization (RT-DO); this is defined as the solution of a problem in which multiple agents work coordinately to permanently keep the system on the optimal path. The process begins with the load of the algebraic model by the modeler. This process attempts to fill the corresponding database to the MMIS and must follow the general guidelines described in subsequent steps. The process of defining the data model is generated simultaneously with the loading of mathematical models. The relations between the two models are strong, so the table structures are determined by the structure of the mathematical model, primarily by the relation between sets, parameters, variables, and constraints.
The information system generates a user interface without programming tasks. This involves organizing the shell windows in tables associated with a main table and the related secondary tables. This query is performed through the administrator who must build menus to provide access to end-users. Once the database is loaded into the MMIS, the next step is to interact with the main engine to begin the process of adjustment for the formulation of algebraic models. The analysis of the algebraic model involves interaction, coordinating two simultaneous activities: (a) reviewing the loaded algebraic formulation into the MMIS and (b) reviewing the results obtained with the models. This activity is carried out mainly with the RTF document generated by the system, where the user can see the exact formulation loaded into the MMIS and find errors in it and/or needs for adjustments due to imperfections in modeling.
Subsequently, the system is executed, and the results of the algebraic model are stored, a process carried out automatically by the system itself. After analyzing the progress and outcomes during the initial stages of implementation, adjustments to the MMIS and IDIS become necessary. This iterative process continues until the modeler deems that the implemented model yields accurate results and is prepared for delivery to the end-user. Ultimately, the end-user gains access to utilize the model, which is constructed based on the data stored in the IDIS and the results generated by the models.
4. Case Study and Computational Results
We implemented our methodology using datasets from the busiest container port in Colombia, South America, which currently holds the title of the most productive port in the Americas as of the 2023 ranking and ranks among the five most productive ports globally [65]. The objective of this mathematical optimization framework, coupled with interconnectivity, is to establish a planning scheme that accommodates all services within their designated service windows while minimizing associated operating costs. If one of the terminals had sufficient operating capacity, all services in that terminal and transfer costs would be zero.
Now, let us delve into our case study, focusing on the key components pertinent to the modeling framework. Firstly, we define a “service” as the numerous routes or itineraries offered by a shipping line company, which could be served by one or more vessels. Services serve as the foundations for tactical planning models. For each service, relevant data are required for constructing tactical planning models, including (1) the service name or label; (2) the type of planned arrival, categorized as regular or irregular (regular arrival services hold priority over irregular ones); (3) deviation; (4) the date of first arrival; (5) movements; and (6) the minimum required productivity. Figure 7 illustrates an example of a service line for ports in South America.
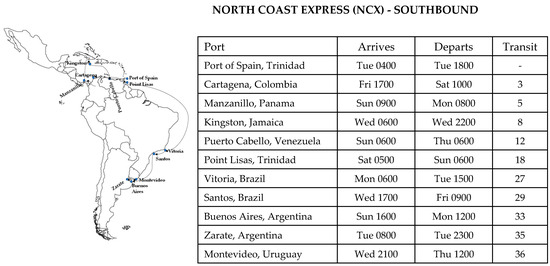
Figure 7.
An example of a shipping service with ports served.
We further provide additional details regarding the sample set of cranes intended for use in the case study. Figure 8 illustrates the crane characteristics, including the type, outreach, air draft, and productivity, along with the berths they are associated with.
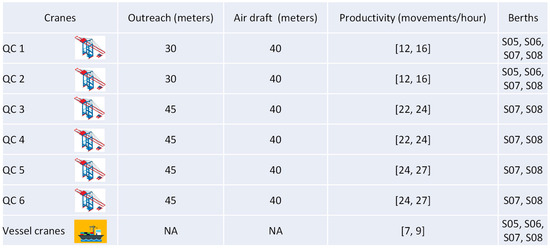
Figure 8.
Crane attributes.
An exemplary master table for services and vessels within the port information system can be observed in Table 2. Due to space constraints, the table was truncated for inclusion in this article. Readers can examine the service and its relationship with the vessel, along with the ETA and the anticipated number of crane movements for the operation. Table 6 shows an example for services and vessels in the system.

Table 6.
An excerpt of a master table for services and vessels.
Figure 9 below shows a sample container connectivity matrix of the port. This matrix shows the level of relationship between planned arrivals and departures.
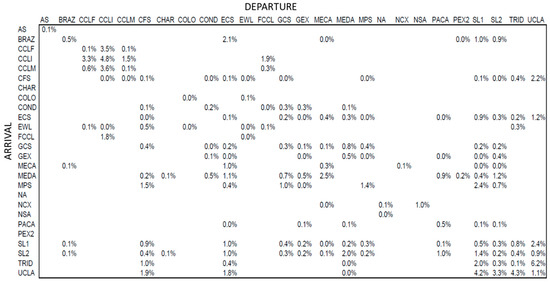
Figure 9.
Container connectivity matrix between terminals.
The connectivity matrix is the basis for the calculation of units transferred from service z to service z’. Whether both services are assigned to the same terminal is irrelevant. Subsequently, we ascertain the transshipment units that arrive at the port via terminal t and must stay there. Earlier, we established the total transshipment units received by each terminal and service type. Ultimately, we estimate the units that need to be transferred between terminals, determining the transportation cost between them. The yard’s capacity is modeled as follows: based on the estimated berth throughput and utilizing the transshipment rate, the yard throughput is calculated (refer to Table 7).

Table 7.
Yard storage requirements for container and vehicle.
Subsequently, considering the average stay time in yards, the planning cycle length, and the yard throughput, we can determine the average inventory level that must be managed in the yard for each service type. A safety or peak factor is applied to the average inventory level to safeguard port operations from potential variations. To facilitate container movements in the yard, certain stacking positions must remain unoccupied.
Next, it is crucial to apply a stacking factor to the average inventory. For containers, this factor typically hovers around 86%, while for vehicles, it is 100%. This calculation yields the number of inventory positions necessary for the port’s operations. By utilizing the storage density factor, we determine the required area for each type of service. Each terminal possesses a yard designed for either containers or vehicles depending on its initial purpose. A fundamental rule must be enforced: container yards can accommodate vehicles, but not vice versa.
Also, let us explain how the berths are modeled. Figure 10 shows a graphical description of what type of docking becomes a feasible assignment and which ones are not, detailing the relationship among berths, vessels, and quay (or vessel) cranes used. This representation allows us to have a better understanding of how the events will take place when implementing our solution methodology.
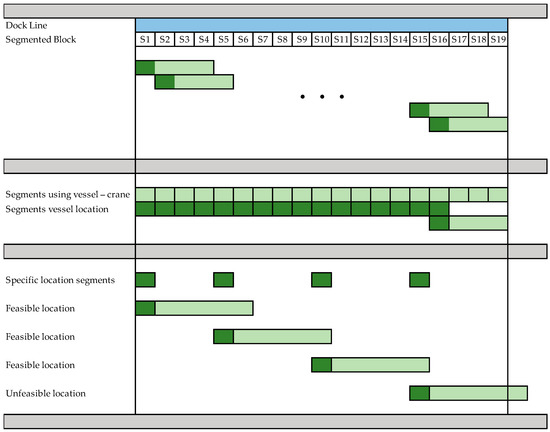
Figure 10.
How the berth is modeled.
Economic insights into the modeling framework: allocation vs. transfers and container moves
This sub-section presents an economic analysis of the solution used for our framework. The question that is addressed in this section is as follows: is the proposed solution approach appropriate? To answer this question, we should recall that the goal of this mathematical framework is to define a planning scheme that caters to all services within their service windows and whose associated operating cost is minimal. Additionally, we will use the allocation (assignment) model together with the reference database provided by the port.
The below table shows little differentiation in the costs per movement made by each one of the port cranes. This leads us to believe that, regardless of the segment, s, where the operation of unloading/loading is carried out, the operating cost will be almost the same. One might think that the cost of unloading/loading for a load level to be served is almost constant or has very little variation. This allows us to conclude that although these costs are important in the operation, they are not the most important factors when defining the optimal allocation of services to terminals. Table 8 shows the unitary costs per movement and each crane productivity.

Table 8.
Unit cost per movement and productivities of cranes.
If one of the terminals had ample operating capacity, then all services within that terminal and the associated transfer costs would be zero. However, due to the large number of elements in the connectivity matrix and the transshipment units, there will always be a rounding error. In the base scenario, this error amounts to USD 6806.50, which is equivalent to 100 average containers. We initially assign all services to one terminal (CTC) to estimate or gauge the impact of assigning a service to any terminal. The subsequent step involves relocating a service from the first terminal and assigning it to a second terminal (SPRC).
For example, when assigning the AS-N service to SPRC, there is a significant increase in transfer costs, totaling USD 65,062.50. This increase is primarily due to the transfers required from SPRC to CTC (447 containers), with 73 containers remaining at SPRC for transshipment to the same service. Furthermore, there are transfers of transshipments for the services initially assigned in CTC, which include AS-N as an output service.
Next, the AS-S service is relocated to SPRC, resulting in another sharp increase in transfer costs, reaching USD 119,515. The AZTE service, with 644 transfer containers, incurs transfer costs close to USD 196,993 when arbitrarily assigned to SPRC. This is because the model indicates that to minimize the cost of moving containers, it must rebalance service assignments to minimize the necessary transfers.
The service that has the largest number of transfer cases is UCLA-N-01, and to continue this exhibition, it will change the service terminal allocation. In the previous allocation case, the UCLA-N-01 service, which is currently attended in SPRC, will go to CTC.
This prompts the allocation model to propose a new service scheme, resulting in an associated transfer cost of USD 269,893, representing a 37.8% increase compared to the previous scenario. The services with the greatest cash flow determine the service allocation. Table 9 illustrates the area required for the weekly cycle based on the services in the base validation scenario.

Table 9.
Required area for weekly planning cycle.
Returning to the allocation model with the original data, the model defines the service scheme presented in the “Initial Allocation” table, with an associated transfer cost of USD 136,384.63.
From this solution, the service terminal is changed to the UCLA-N service while maintaining all other initial allocations. This generates a new transfer cost of USD 287,087.97. However, to avoid infeasibility, the capacity constraints (Equations (55)–(57)) must be relaxed.
Alternatively, if only the UCLA-N service is fixed while the original conditions are retained, and the model is allowed to propose a new scheme, the transfer cost is USD 247,779.
The new allocation can be observed in the table titled “allocation with UCLA-N in SPRC”. A comparison between this allocation and the initial allocation reveals a significant cost difference of nearly 81%, with six services changing their initial service terminals.
At this stage of the analysis, the second service in terms of flow volume, COVE, is allocated to SPRC by the model, while CTC becomes its service terminal. This change results in the model proposing a scheme with a transfer cost of USD 293,546. This alteration represents an increase of USD forty-six thousand, accounting for about 18.5% of the transfer cost of the immediately preceding case.
Subsequently, the UCLA-S service, like the UCLA-N and COVE services, is assigned to the SPRC terminal by the allocation model. If CTC is set as its terminal, the transfer cost rises to USD 328,681, indicating a 12% increase compared to the previous case.
The fourth flow generator is the MPS-W service, and it is allocated to the SPRC terminal according to the table labeled as “Initial allocation”. Table 10 shows the modifications to allocation of services.

Table 10.
Initial allocation (left); allocation with UCLA-N in SPRC (right).
In this new scenario, UCLA-S will be serviced by the terminal CTC. The model adjusts the allocation of services to achieve a transfer cost of USD 359,037, representing an increase of approximately USD 30,000. This solution will be locked in as the fixed solution.
The PEX3 service, as the fifth largest service flow generator, can only be served by the CTC terminal. Within the fixed solution, the JCS service is allocated to the CTC terminal. Retaining all other allocations from the fixed solution, this service undergoes a terminal switch. The new shipping cost amounts to USD 246,980, marking an increase of nearly USD 40,000 compared to the fixed solution. Table 11 outlines the marginal impact of altering the allocation of a service in the fixed solution.

Table 11.
The variations in the transshipment costs for the fixed solution.
So far, this discussion has empirically demonstrated the impact of poor allocation on operational costs. All services must be correctly assigned to the appropriate terminal; otherwise, we generate a negative impact on the port’s operational profit.
As evident from the previous paragraphs and in comparison, to the penalty costs, we can conclude that the most significant costs in the planning process are the transfer costs, which, at first glance, can be considerably higher than the penalty costs. Figure 11 compares the distribution of penalty costs among services with the behavior of the movements associated with the penalty costs that apply to each set of services.
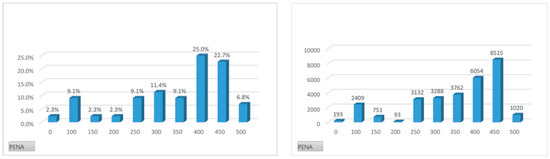
Figure 11.
Penalty cost distribution (left), penalty cost vs. moves (right).
The above graphs illustrate coherence in the provided information. It is noticeable that services with higher penalty costs must align with the group of services that generated the greater number of movements. It is worth emphasizing that the ultimate penalty cost will hinge on the delay of the reference vessel. However, generally, it will necessitate a considerable number of hours for it to be comparable to the marginal effect that allocating a service to a terminal has on the projected transfer cost.
4.1. Results, Benchmarks for Commercial Solvers, and Analysis
Table 12 below presents the computational results for a real-life case conducted on a customer. Only the solutions meeting the specific time threshold are displayed. The remaining results for other solvers are omitted from this table as they would not meet the customer’s expectations. These results serve to compare the performance of different solver engines in a real use case.

Table 12.
Benchmarks for different commercial solvers.
The gap (%) metric indicates how far the reported solution of each solver (Solvers 001, 002, and 004) is from the best bound for each subproblem. All three main solvers consistently meet the customer’s time threshold expectations. These results pertain to a specific time window and the conditions presented by the chosen port during that window, although the system operates daily.
Table 12 also reveals that Solver 001 consistently provides the best solution within the shortest computational time for two out of three main subproblems and closely approaches the solution for the third subproblem. This trend was observed in over 80% of the cases analyzed with real port data, although not consistently.
Given that all three solvers remained within the customer’s time constraints, we proceeded with a solution that selects the best outcome among the solutions provided by all three solvers.
4.2. Managerial Insights
In ref. [66], the authors emphasize that port container terminal operations are predominantly concerned with costs and profits from a managerial perspective. They suggest that developing a practical solution approach for real terminals requires cost analyses to be conducted and compared with the current situation. Consequently, studies focusing on cost and profit, which are often overlooked in integrated literature, should be undertaken.
To our knowledge, our study represents one of the most comprehensive analyses directed towards understanding port costs and profits. Not only do we offer a comprehensive framework alongside a smart information system that allows for framework enhancement as needed, but we also prioritize aligning with the understanding and preferences of port managers. Figure 12 shows one of the dashboards built for ease of understanding.
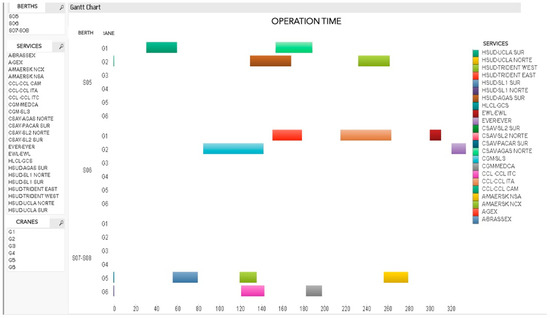
Figure 12.
Planning terminal–service allocations.
To facilitate readability for port managers, our information system incorporates a range of graphical displays. These displays cover various topics such as the schedule of services per berth/quay crane, detailing the arrival time, start time, completion time, and the services being attended.
The decision support information system employed by the port drives decisions across three primary areas: (1) planning terminal–service allocations, (2) planning events within the port, and (3) analyzing new commercial opportunities.
As discussed in [67] regarding port operations and management, the port industry, like others, is undergoing a digital transformation that affects existing business models and operational practices in various ways. This transformation within the port industry, facilitated by the adoption of various technological innovations, holds the potential to enhance profitability while addressing sustainability and operational efficiency at a systemic level. Leveraging available optimization technologies and information systems allows for the automation of decisions in an optimized manner.
This assertion is particularly relevant even in highly developed countries. For instance, numerous port improvement projects funded by the US DOT emphasize core topics such as port efficiency, sustainability, capacity, and resilience [68]. Carbon emissions should be considered in port operations [69]. It is our purpose to study this concept and embed it into our framework.
An information system designed to optimize port operations can offer valuable insights for port managers, aiding in improving efficiency, reducing costs, and enhancing customer satisfaction. Some key managerial insights that such a system can provide include real-time visibility of port operations, predictive analytics for resource planning, improved scheduling and synchronization, and performance monitoring and benchmarking. By facilitating informed decision making, resource optimization, and ongoing operational improvement, the system contributes to enhancing overall port operations.
5. Conclusions and Further Study
We approached the challenge of port optimization from a holistic perspective, considering the entire port continuum from sea-to-land interactions and extending to land-to-land (hinterland) operations. Our approach includes implementing a real-time distributed optimization mathematical framework within the HAi optimization platform.
Our solution methodology emphasizes a decoupled framework that allows us to deploy a comprehensive set of optimization libraries, enabling real-time distributed optimization mathematical models. This methodology significantly reduces the solution time for each run without sacrificing generality or solution quality. On the contrary, it enhances the autonomy and adaptability required for real-life implementations. By deploying multiple sub-models, our system can detect and manage changes, ensuring seamless interconnectivity between all distributed event-driven entities.
Furthermore, we developed a novel event-driven modeling structure to facilitate the interconnectivity of all sub-models within the framework and to fully integrate the modeling structures into the decision support information system.
Future work will focus on enhancing the capabilities of our mathematical modeling framework and its integration with information systems to encompass all aspects of the port continuum, including land-to-land operations. This integration will enable the optimization of events, such as gate appointments, truck traffic control, and integration with the yard management system.
We also hope to enhance our platform to incorporate emission inventories as constraints, initially based on desired levels and then predicted inventories. These inventories will account for emissions from vessels, port equipment, and trucks/vehicles interacting within the port. Additionally, we aim to integrate our solutions with any interconnected, real-time smart port framework to deliver optimized solutions that not only maximize operational productivity but also prioritize sustainability, considering the “people, planet, profit” approach.
AI-based solutions can play a crucial role in efficiently predicting critical factors, such as port emission inventories. By leveraging automated information from vessels, trucks, and port equipment, these solutions can plan the transition to a net-zero approach for port operations planning.
Author Contributions
Conceptualization, all authors; methodology, D.A. and J.V.-B.; software, D.A. and J.V.-B.; validation, C.D.P.-A. and J.V.-B.; formal analysis, D.A. and C.D.P.-A.; investigation, D.A. and J.V.-B.; resources, J.V.-B.; data curation, D.A.; writing—original draft preparation, D.A. and C.D.P.-A.; writing—review and editing, C.D.P.-A.; visualization, D.A. and J.V.-B.; supervision, C.D.P.-A. and J.V.-B.; project administration, J.V.-B.; funding acquisition, J.V.-B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Hypothalamus AI, Inc.
Data Availability Statement
Data are available upon request to the corresponding author. The authors require that people interested in the data sign an NDA.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gould, R. Shaping Shipping. International Organization for Standardization, 17 November 2020. Available online: https://www.iso.org/news/ref2588.html (accessed on 6 April 2023).
- Supply Chain Bottlenecks at U.S. Ports. Congressional Research Service. 10 November 2021. Available online: https://crsreports.congress.gov/product/pdf/IN/IN11800 (accessed on 16 January 2024).
- He, L. Shipping Delays Are back as China’s Lockdowns Ripple around the World. CNN Business, 6 May 2022. Available online: https://www.cnn.com/2022/05/06/business/china-lockdowns-global-port-chaos-supply-chains-intl-hnk/index.html (accessed on 21 February 2023).
- Capurro, M.E. Latin American Cargo Hits Snags Amid U.S. Port Backlog. Available online: https://www.bloomberg.com/news/newsletters/2021-05-03/supply-chains-latest-latin-american-cargo-hits-u-s-port-snarls (accessed on 21 February 2023).
- Carlos, J. Effects of Shipping Congestion on Latin America. Available online: https://www.tridge.com/stories/effects-of-shipping-congestion-on-latin-american (accessed on 21 February 2023).
- Fiber2Fashion News Desk. Congestion at China’s Yantian Port to have Ripple Effect Across World. Available online: https://www.fibre2fashion.com/news/textile-news/congestion-at-china-s-yantian-port-to-have-ripple-effect-across-world-274666-newsdetails.htm (accessed on 21 February 2023).
- Dinwoodie, J.; Tuck, S.; Knowles, H.; Benhin, J.; Sansom, M. Sustainable development of maritime operations in ports. Bus. Strat. Environ. 2012, 21, 111–126. [Google Scholar] [CrossRef]
- Wooldridge, C.F.; McMullen, C.; Howe, V. Environmental management of ports and harbours—Implementation of policy through scientific monitoring. Mar. Policy 1999, 23, 413–425. [Google Scholar] [CrossRef]
- Paternina-Arboleda, C.D.; Agudelo-Castañeda, D.; Voß, S.; Das, S. Towards Cleaner Ports: Predictive Modeling of Sulfur Dioxide Shipping Emissions in Maritime Facilities Using Machine Learning. Sustainability 2023, 15, 12171. [Google Scholar] [CrossRef]
- WCED. Our Common Future, 1st ed.; Oxford University Press: Oxford, UK, 1987. [Google Scholar]
- Lozano, R.; Fobbe, L.; Carpenter, A.; Sammalisto, K. Analysing sustainability changes in seaports: Experiences from the Gävle Port authority. Sustain. Dev. 2019, 27, 409–418. [Google Scholar] [CrossRef]
- Moros-Daza, A.; Amaya-Mier, R.; Paternina-Arboleda, C. Port Community Systems: A structured literature review. Transp. Res. Part A Policy Pr. 2020, 133, 27–46. [Google Scholar] [CrossRef]
- Carlo, H.J.; Vis, I.F.; Roodbergen, K.J. Storage yard operations in container terminals: Literature overview, trends, and research directions. Eur. J. Oper. Res. 2014, 235, 412–430. [Google Scholar] [CrossRef]
- Carlo, H.J.; Vis, I.F.; Roodbergen, K.J. Transport operations in container terminals: Literature overview, trends, research directions and classification scheme. Eur. J. Oper. Res. 2014, 236, 1–13. [Google Scholar] [CrossRef]
- Covic, F. A Literature Review on Container Handling in Yard Blocks. In Computational Logistics, Proceedings of the 9th International Conference, ICCL 2018, Vietri sul Mare, Italy, 1–3 October 2018; Cerulli, R., Raiconi, A., Voß, S., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2018; Volume 11184. [Google Scholar] [CrossRef]
- Lehnfeld, J.; Knust, S. Loading, unloading and premarshalling of stacks in storage areas: Survey and classification. Eur. J. Oper. Res. 2014, 239, 297–312. [Google Scholar] [CrossRef]
- Lu, Z.; Jiang, X.; Lee, L.H.; Chew, E.P. A Review on Yard Management in Container Terminals. Ind. Eng. Manag. Syst. 2013, 12, 289–304. [Google Scholar]
- Meisel, F.; Bierwirth, C. A unified approach for the evaluation of quay crane scheduling models and algorithms. Comput. Oper. Res. 2011, 38, 683–693. [Google Scholar] [CrossRef]
- Bierwirth, C.; Meisel, F. A follow-up survey of berth allocation and quay crane scheduling problems in container terminals. Eur. J. Oper. Res. 2015, 244, 675–689. [Google Scholar] [CrossRef]
- Stahlbock, R.; Voß, S. Operations research at container terminals: A literature update. OR Spectr. 2008, 30, 1–52. [Google Scholar] [CrossRef]
- Steenken, D.; Voß, S.; Stahlbock, R. Container terminal operation and operations research—A classification and literature review. OR Spectr. 2004, 26, 3–49. [Google Scholar] [CrossRef]
- Vis, I.F.A.; De Koster, R. Transshipment of containers at a container terminal: An overview. Eur. J. Oper. Res. 2003, 147, 1–16. [Google Scholar] [CrossRef]
- Murty, K.G.; Liu, J.; Wan, Y.-W.; Linn, R. A decision support system for operations in a container terminal. Decis. Support Syst. 2005, 39, 309–332. [Google Scholar] [CrossRef]
- Gharehgozli, A.; Roy, D.; de Koster, R. Sea container terminals: New technologies and OR models. Marit. Econ. Logist. 2016, 18, 103–140. [Google Scholar] [CrossRef]
- Kim, K.; Lee, H. Container Terminal Operation: Current Trends and Future Challenges. In Handbook of Ocean Container Transport Logistics; Lee, C.Y., Meng, Q., Eds.; International Series in Operations Research & Management Science; Springer: Cham, Switzerland, 2015; Volume 220. [Google Scholar] [CrossRef]
- Dragović, B.; Tzannatos, E.; Park, N.K. Simulation modelling in ports and container terminals: Literature overview and analysis by research field, application area and tool. Flex. Serv. Manuf. J. 2017, 29, 4–34. [Google Scholar] [CrossRef]
- Legato, P.; Mazza, R.M. A decision support system for integrated container handling in a transshipment hub. Decis. Support Syst. 2018, 108, 45–56. [Google Scholar] [CrossRef]
- Lozano, R. Envisioning sustainability three-dimensionally. J. Clean. Prod. 2008, 16, 1838–1846. [Google Scholar] [CrossRef]
- Sierra, L.A.; Yepes, V.; Pellicer, E. A review of multi-criteria assessment of the social sustainability of infrastructures. J. Clean. Prod. 2018, 187, 496–513. [Google Scholar] [CrossRef]
- Heilig, L.; Lalla-Ruiz, E.; Voß, S. Digital transformation in maritime ports: Analysis and a game-theoretic framework. NETNOMICS Econ. Res. Electron. Netw. 2017, 18, 227–254. [Google Scholar] [CrossRef]
- Notteboom, T.; Pallis, A.; Rodrigue, J.-P. Port Economics, Management and Policy; Routledge: New York, NY, USA, 2022. [Google Scholar] [CrossRef]
- Jubiz-Diaz, M.A.; Saltarin-Molino, M.A.; Arellana, J.; Paternina-Arboleda, C.D.; Yie-Pinedo, R. Effect of Infrastructure Investment and Freight Accessibility on Gross Domestic Product: A Data-Driven Geographical Approach. J. Adv. Transp. 2021, 2021, 5530114. [Google Scholar] [CrossRef]
- Gomez-Jacome, N.; Garcia-Llinas, G.; Paternina-Arboleda, C.D.; Jaller-Martelo, M. Caribbean Ports, Inland Logistics, and the Panama Canal Expansion: A Mode and Port Choice Analysis. In Computational Logistics, Proceedings of the 10th International Conference, ICCL 2019, Barranquilla, Colombia, 30 September–2 October 2019; Paternina-Arboleda, C., Voß, S., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2019; Volume 11756. [Google Scholar] [CrossRef]
- Moros-Daza, A.; Cassandro-De La Hoz, D.; Jaller-Martelo, M.; Paternina-Arboleda, C.D. Using Advanced Information Systems to Improve Freight Efficiency: Results from a Pilot Program in Colombia. In Computational Logistics, Proceedings of the 10th International Conference, ICCL 2019, Barranquilla, Colombia, 30 September–2 October 2019; Paternina-Arboleda, C., Voß, S., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2019; Volume 11756. [Google Scholar] [CrossRef]
- Bernal, W.N.; Jimenez-Barros, M.A.; Molinares, D.J.; Paternina-Arboleda, C.D. Developing Logistic Software Platforms: E-Market Place, a Case Study. In Computational Logistics, Proceedings of the 10th International Conference, ICCL 2019, Barranquilla, Colombia, 30 September–2 October 2019; Paternina-Arboleda, C., Voß, S., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2019; Volume 11756. [Google Scholar] [CrossRef]
- Rodrigues, F.; Agra, A. Berth allocation and quay crane assignment/scheduling problem under uncertainty: A survey. Eur. J. Oper. Res. 2022, 303, 501–524. [Google Scholar] [CrossRef]
- Monaco, M.F.; Sammarra, M. The Berth Allocation Problem: A Strong Formulation Solved by a Lagrangean Approach. Transp. Sci. 2007, 41, 265–280. [Google Scholar] [CrossRef]
- Nishi, T.; Okura, T.; Lalla-Ruiz, E.; Voß, S. A dynamic programming-based matheuristic for the dynamic berth allocation problem. Ann. Oper. Res. 2020, 286, 391–410. [Google Scholar] [CrossRef]
- Legato, P.; Mazza, R.M.; Gullì, D. Integrating tactical and operational berth allocation decisions via simulation–optimization. Comput. Ind. Eng. 2014, 78, 84–94. [Google Scholar] [CrossRef]
- Kramer, A.; Lalla-Ruiz, E.; Iori, M.; Voß, S. Novel formulations and modeling enhancements for the dynamic berth allocation problem. Eur. J. Oper. Res. 2019, 278, 170–185. [Google Scholar] [CrossRef]
- Meisel, F.; Bierwirth, C. A Framework for Integrated Berth Allocation and Crane Operations Planning in Seaport Container Terminals. Transp. Sci. 2013, 47, 131–147. [Google Scholar] [CrossRef]
- Kasm, O.A.; Diabat, A.; Cheng, T.C.E. The integrated berth allocation, quay crane assignment and scheduling problem: Mathematical formulations and a case study. Ann. Oper. Res. 2020, 291, 435–461. [Google Scholar] [CrossRef]
- Cheimanoff, N.; Fontane, F.; Kitri, M.N.; Tcherneva, N. Exact and heuristic methods for the berth allocation problem with multiple continuous quays in tidal bulk terminals. Expert Syst. Appl. 2022, 201, 117141. [Google Scholar] [CrossRef]
- Ma, H.L.; Chung, S.H.; Chan, H.K.; Cui, L. An integrated model for berth and yard planning in container terminals with multi-continuous berth layout. Ann. Oper. Res. 2019, 273, 409–431. [Google Scholar] [CrossRef]
- Zhen, L.; Chew, E.P.; Lee, L.H. An Integrated Model for Berth Template and Yard Template Planning in Transshipment Hubs. Transp. Sci. 2011, 45, 483–504. [Google Scholar] [CrossRef]
- Li, B.; Jiang, X.; Lei, J. Container Terminal Berth and Yard Collaborative Allocation for Import and Export Synchronous Operations by Computational Logistics. Discret. Dyn. Nat. Soc. 2022, 2022, 6008543. [Google Scholar] [CrossRef]
- Wang, K.; Zhen, L.; Wang, S. Gilbert Laporte. Column Generation for the Integrated Berth Allocation, Quay Crane Assignment, and Yard Assignment Problem. Transp. Sci. 2018, 52, 812–834. [Google Scholar] [CrossRef]
- Al-Hammadi, J.; Diabat, A. Anintegrated berth allocation and yard assignment problem for bulk ports: Formulation and case study. RAIRO—Oper. Res. 2017, 51, 267–284. [Google Scholar] [CrossRef]
- Jia, S.; Meng, Q.; Kuang, H. Equitable Vessel Traffic Scheduling in a Seaport. Transp. Sci. 2022, 56, 162–181. [Google Scholar] [CrossRef]
- Martin-Iradi, B.; Pacino, D.; Ropke, S. The Multi-Port Berth Allocation Problem with Speed Optimization: Exact Methods and a Cooperative Game Analysis. arXiv 2022. [Google Scholar] [CrossRef]
- Peng, W.; Bai, X.; Yang, D.; Yuen, K.F. A deep learning approach for port congestion estimation and prediction. Marit. Policy Manag. 2022, 50, 835–860. [Google Scholar] [CrossRef]
- Kizilay, D.; Eliiyi, D.T. A comprehensive review of quay crane scheduling, yard operations and integrations thereof in container terminals. Flex. Serv. Manuf. J. 2021, 33, 1–42. [Google Scholar] [CrossRef]
- Kizilay, D.; Eliiyi, D.T.; Van Hentenryck, P. Constraint and Mathematical Programming Models for Integrated Port Container Terminal Operations. In Integration of Constraint Programming, Artificial Intelligence, and Operations Research, Proceedings of the 15th International Conference, CPAIOR 2018, Delft, The Netherlands, 26–29 June 2018; van Hoeve, W.J., Ed.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2018; Volume 10848. [Google Scholar] [CrossRef]
- Mao, A.; Yu, T.; Ding, Z.; Fang, S.; Guo, J.; Sheng, Q. Optimal scheduling for seaport integrated energy system considering flexible berth allocation. Appl. Energy 2022, 308, 118386. [Google Scholar] [CrossRef]
- Wang, T.; Li, M.; Hu, H. Berth allocation and quay crane-yard truck assignment considering carbon emissions in port area. Int. J. Shipp. Transp. Logist. 2019, 11, 216–242. [Google Scholar] [CrossRef]
- Wang, T.; Wang, X.; Meng, Q. Joint berth allocation and quay crane assignment under different carbon taxation policies. Transp. Res. Part B Methodol. 2018, 117, 18–36. [Google Scholar] [CrossRef]
- Peng, Y.; Dong, M.; Li, X.; Liu, H.; Wang, W. Cooperative optimization of shore power allocation and berth allocation: A balance between cost and environmental benefit. J. Clean. Prod. 2021, 279, 123816. [Google Scholar] [CrossRef]
- Sankla, W.; Muangpan, T. Smart and sustainable port performance in Thailand: A conceptual model. J. Sustain. Dev. 2022, 15, 1–14. [Google Scholar] [CrossRef]
- Moros-Daza, A.; Solano, N.C.; Amaya, R.; Paternina, C. A multivariate analysis for the creation of Port Community System approaches. Transp. Res. Procedia 2018, 30, 127–136. [Google Scholar] [CrossRef]
- Heilig, L.; Voß, S. Port-Centric Information Management in Smart Ports: A framework and categorization. In Ports and Networks: Strategies, Operations and Perspectives; Geerlings, H., Kuipers, B., Zuidwijk, R., Eds.; Routledge: London, UK, 2017; p. 406. [Google Scholar] [CrossRef]
- Mi, W.; Liu, Y. Smart Ports, 1st ed.; Springer: Singapore, 2022. [Google Scholar] [CrossRef]
- International Port Community Systems Association (IPCSA). How to Develop a Port Community System, Tech. Rep., International Port Community Systems Association. 2015. Available online: https://ipcsa.international/wp-content/uploads/2020/07/ipcsa-guide-english-2015.pdf (accessed on 22 March 2024).
- Tsamboulas, D.; Ballis, A. Port community systems: Requirements, functionalities and implementation complications. In Proceedings of the 13th World Conference of Transport Research, Rio de Janeiro, Brazil, 15–18 July 2013; pp. 1–17. Available online: http://www.wctrs-society.com/wp-content/uploads/abstracts/rio/selected/2024.pdf (accessed on 26 March 2024).
- Velasquez-Bermudez, J.M.; Abril, D.; Paternina-Arboleda, C.D. Optimizing Port Operations to Cope with Shipping Congestion in South American Countries. OR/MS Today 2022, 49, 2. [Google Scholar]
- Humphreys, R.M.; Biju, N.O.; Tan, H.; Ashley, G.N.M.; Guillot, D.; Reja, B.; World bank Group Transport & S&P Global Market Intelligence. Transport Global Practice: The Container Port Performance Index 2021: A Comparable Assessment of Container Port Performance. Available online: https://thedocs.worldbank.org/en/doc/66e3aa5c3be4647addd01845ce353992-0190062022/original/Container-Port-Performance-Index-2021.pdf (accessed on 26 March 2023).
- Pallis, A.; Rodrigue, J.-P. Port Efficiency. In Port Economics, Management and Policy: A Comprehensive Analysis of the Port Industry; Routledge: New York, NY, USA, 2022; Available online: https://porteconomicsmanagement.org/pemp/contents/part6/port-efficiency/ (accessed on 26 September 2023).
- Chowdhury, M.M.; Alshareef, M.; Shaheen, M.M.; Majumdar, S. Smart Port Management Practices and Implementation: An Interpretive Structural Modelling Approach. Bangladesh Marit. J. 2022, 7, 249–262. [Google Scholar]
- Port Infrastructure Development Grants. U.S. Department of Transportation Maritime Administration. Available online: https://www.maritime.dot.gov/PIDPgrants (accessed on 17 July 2023).
- Eslamipoor, R. A Biobjective Model for Integrated Inventory and Transportation at Tactical and Operational Levels with Green Constraints. IEEE Trans. Eng. Manag. 2024, 71, 9764–9775. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).