Efficient Humanitarian Logistics: Multi-Commodity Location–Inventory Model Incorporating Demand Probability and Consumption Coefficients
Abstract
1. Introduction
2. Literature Review
3. Mathematical Modeling
3.1. Assumptions
- For two types of services, there are two sorts of commodities.
- Basic first aid is the first form of service, which requires the first type of product. Psychological medical aid is the second type of service, and it requires the second type of product.
- The nearest square or rectangular form is what we think of as products and available space.
- It is a straight line distance.
- The space allotted for each warehouse is considered, and it is assumed that 90% of the space is used for the ideal order quantity, which represents the level of service provided by each warehouse and distribution center, and 10% is set aside for managers and high-level decision makers’ precautionary storage.
- Products are not gender, age, or other features.
- The importance coefficients for the first and second products in each warehouse are and , respectively.
- Any product’s delivery time demand follows a normal distribution. In this statement, it is assumed that the delivery time is a normal distribution function with a mean of and a standard deviation of .
- Only one kind of service is provided by each J relief center.
- There is just one warehouse that covers each J relief center.
- For each of the products—one for the first kind of service and two for the second—presumably, the precautionary reserve might fall between the following ranges.
- There is no disease transmission between relief centers.
- The commodities are not substitutes and have independent demand, i.e.,
3.2. Defining the Notations
3.3. Development of Mathematical Model
- When the commodity type o is terminated: .
- When the commodity type two is terminated: .
- Both kinds of products have been finished. In such a situation, this state’s representation is equal to the total of the two states mentioned above.
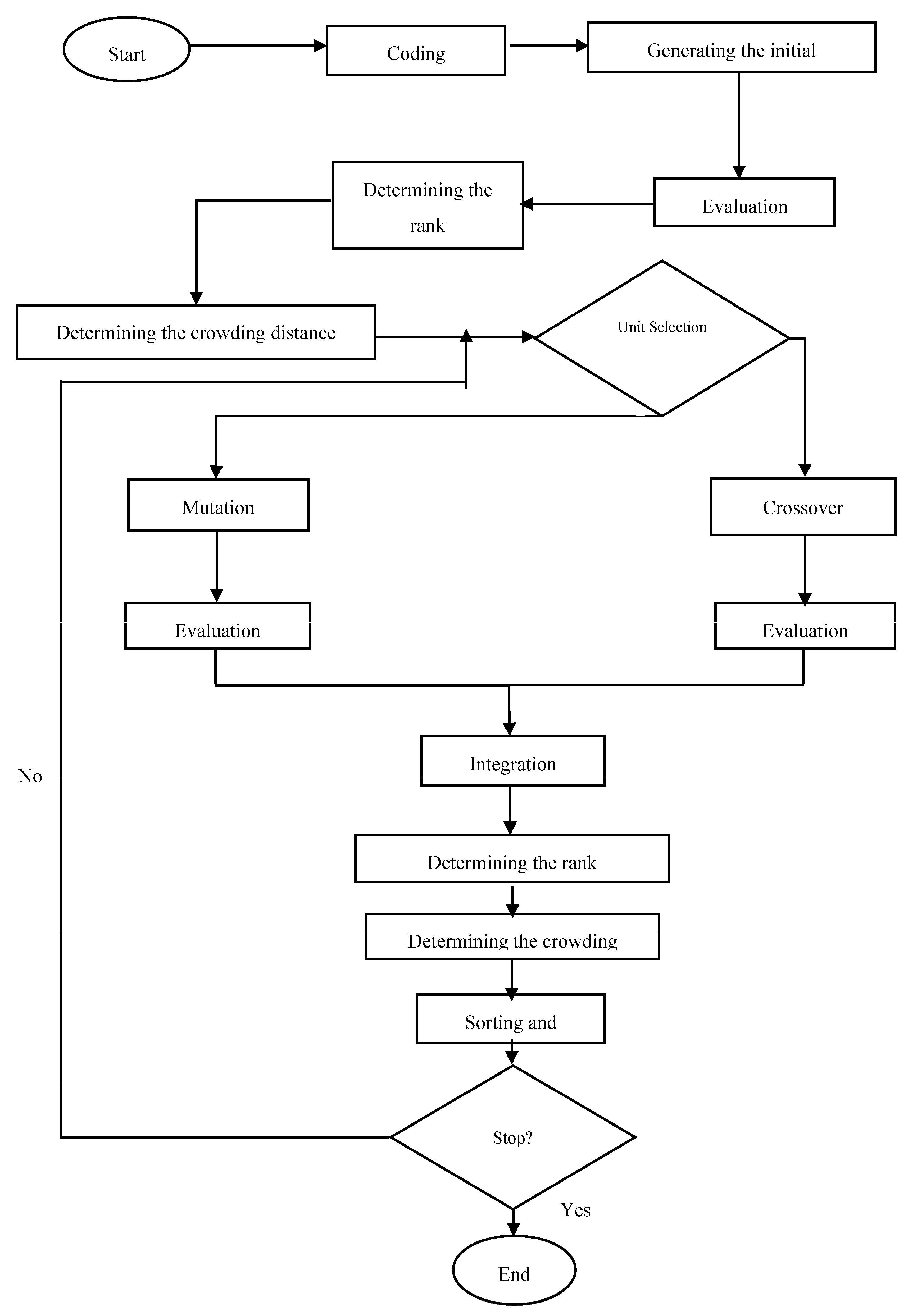
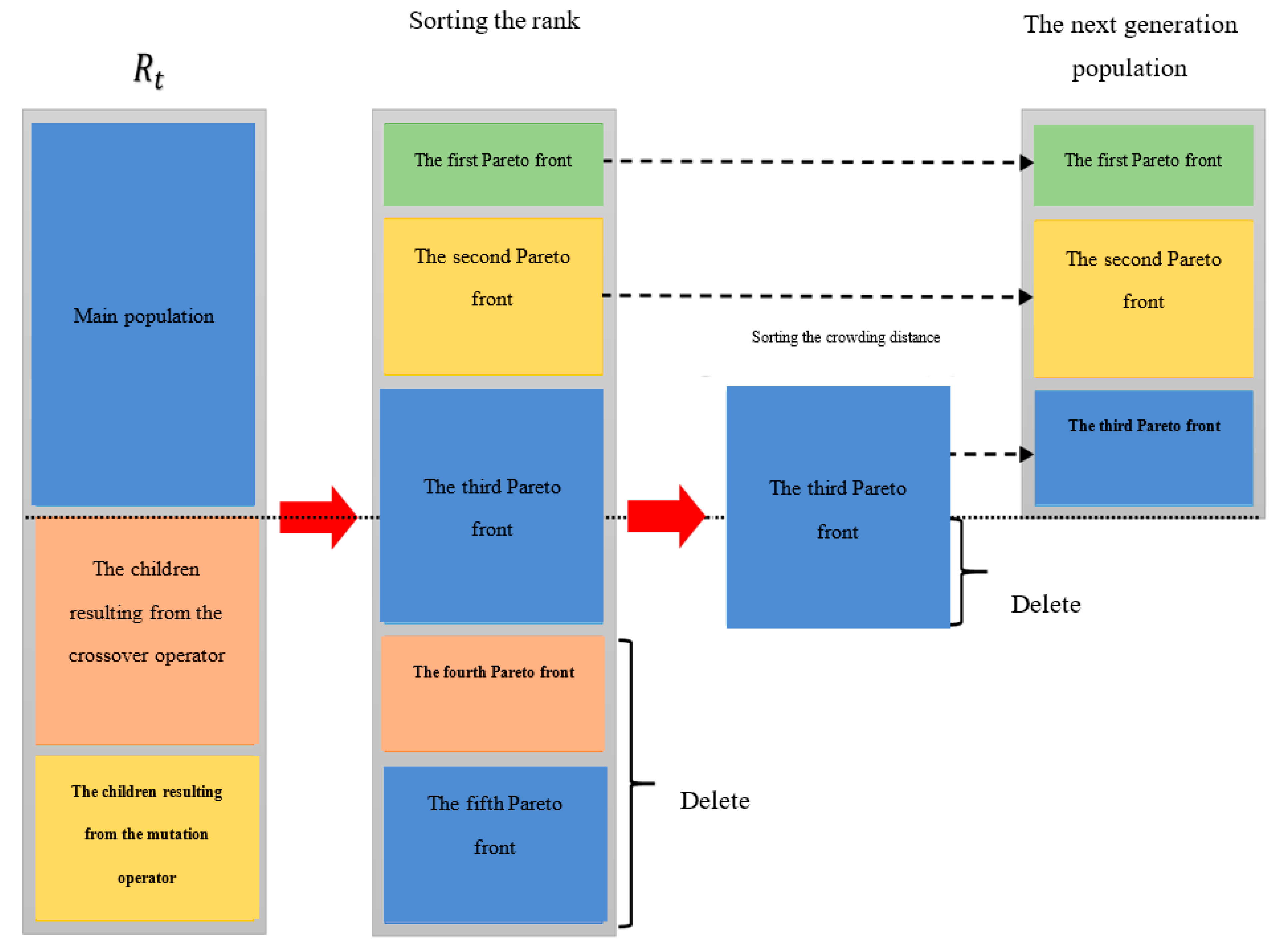
4. Solution Algorithm
- An answer that has more points than any other answer is unquestionably superior. Depending on how many superior answers there are, the answers are ranked and arranged.
- Competence (fitness) is assigned to the answers based on their rank and non-predominance of other answers.
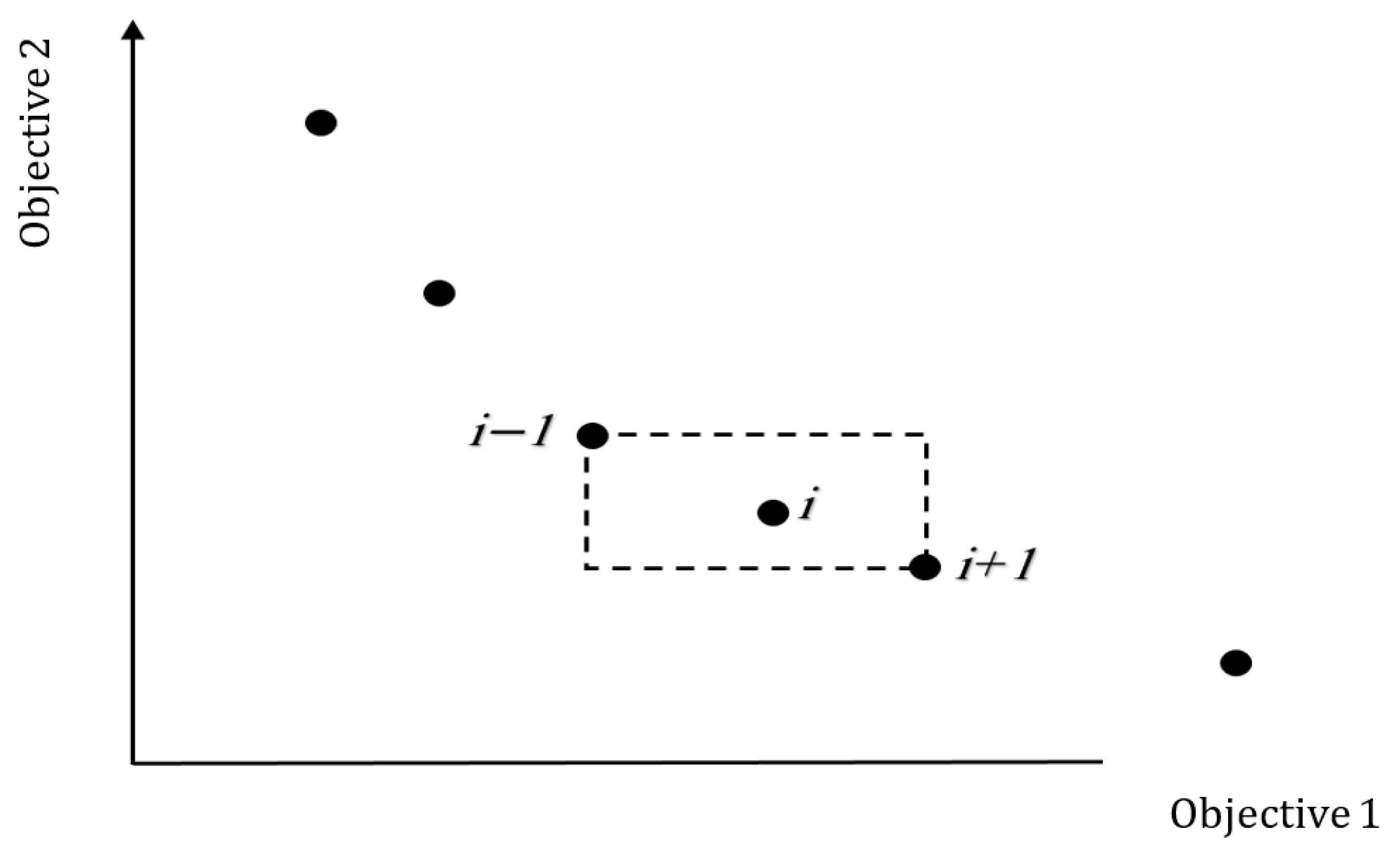
- To alter the answers’ dispersion positively and spread them equally over the search space, the crowding distance is utilized to choose amongst similar answers.
- Saving and preserving the non-dominant answers from the algorithm’s earlier phases (elitism).
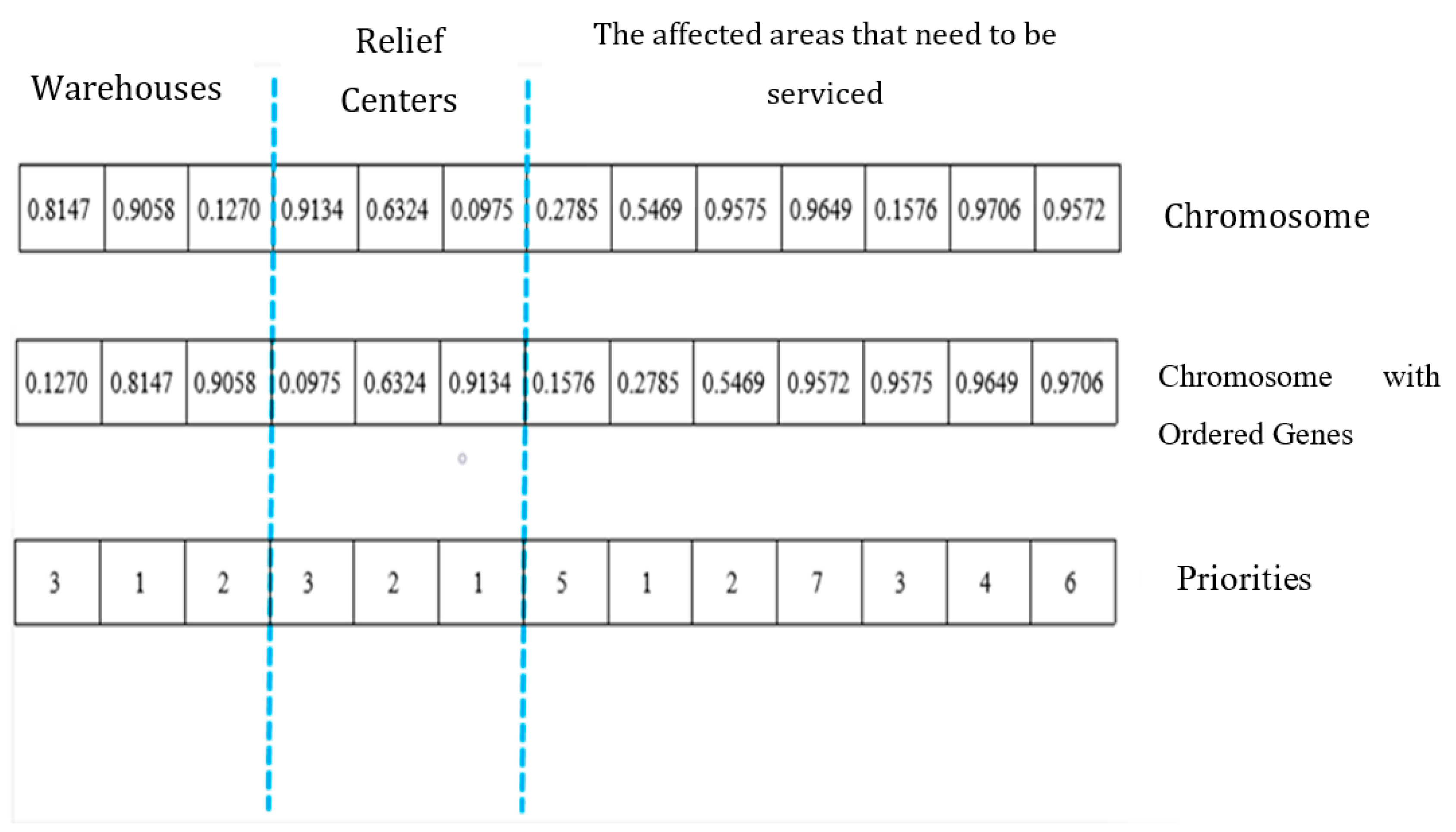
- Step 1. Coding
- Step 2. Establishing the initial population
- Step 3. Evaluation
- Step 4. Determining the rank
- Step 5. Determining the crowding distance
- Step 6. Parent selection
- Step 7. Crossover
- Step 8. Evaluation
- Step 9. Mutation
- Step 10. Evaluation
- Step 11. Integration
- Step 12. Determining the rank
- Step 13. Determining the crowding distance
- Step 14. Sorting and deletion
- Step 15. Analyzing the termination condition
5. Results and Model Solution
| Algorithm 1. The NSGA II algorithm pseudo code. |
| 1: Initial population: the number of population |
| 2: Generate random population S |
| 3: Evaluate object values |
| 4: Assign rank |
| 5: Generate children population for size S |
| 6: For i = 1: Max do |
| 7: For each parent and child do |
| 8: Assign rank |
| 9: Generate sets of non-dominated solutions |
| 10: Cross over and mutation |
| 11: Loop based on existing solution to next generation |
| 12: End For |
| 13: Select point on the lower front with high distance |
| 14: Generate next generation |
| 15: End For |
6. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kani, S. Demography of natural disaster (in Persian). Popul. Quraterly 2018, 26, 155–180. [Google Scholar]
- Townsend. Risk Insurance in village India. Econometria 1994, 62, 539–591. [Google Scholar] [CrossRef]
- Tomasini, R.; Van, W. Humanitarian Logistics; Palgrave Machillan: London, UK, 2009. [Google Scholar] [CrossRef]
- Van Wassenhove, L. Humanitarian aid logistics: Supply chain management in high gear. J. Oper. Res. Soc. 2006, 57, 475–489. [Google Scholar] [CrossRef]
- Thomas, A.K. Fro Logistics to supply chain Management: The path forward in the humanitarian Sector. Fritz Inst. 2005, 15, 1–15. [Google Scholar]
- CRED Crunch Newsletter. Disaster in Year Review 2020: Global Trends and Perspectives. Reliefweb. Available online: https://reliefweb.int/report/world/cred-crunch-newsletter-issue-no-62-may-2021-disaster-year-review-2020-global-trends-and (accessed on 14 May 2021).
- Cozzolino, A. Humanitarian Logistics Cross-sector Cooperation in Disaster Relief Management; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Jaher, M.; Jensen, L.-M.; Listou, T. Theory development in humanitarian logistics: A framework and three cases. Manag. Res. News 2009, 32, 1008–1023. [Google Scholar] [CrossRef]
- Pérez-Galarce, F.; Canales, L.J.; Vergara, C.; Candia-Véjar, A. An optimization model for the location of disaster refuges. Socio-Econ. Plan. Sci. 2017, 59, 56–66. [Google Scholar] [CrossRef]
- Melo, M.; Nickel, S.; Saldanha-da-Gama, F. Facility location and supply chain management—A review. Eur. J. Oper. Res. 2009, 196, 401–412. [Google Scholar] [CrossRef]
- Zandbiglari, K.; Ameri, F.; Javadi, M. Capability Language Processing (CLP): Classification and Ranking of Manufacturing Suppliers Based on Unstructured Capability Data. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Virtual, Online, 17–19 August 2021; American Society of Mechanical Engineers: New York, NY, USA, 2021; Volume 85376, p. V002T02A065. [Google Scholar]
- Tancrez, J.-S.; Lange, J.-C.; Semal, P. A location-inventory model for large three-level supply chains. Transp. Res. Part E Logist. Transp. Rev. 2012, 48, 485–502. [Google Scholar] [CrossRef]
- Diabat, A.; Richard, J.-P.P.; Codrington, C.W. A Lagrangian relaxation approach to simultaneous strategic and tactical planning in supply chain design. Ann. Oper. Res. 2011, 203, 55–80. [Google Scholar] [CrossRef]
- Diabat, A.; Dehghani, E.; Jabbarzadeh, A. Incorporating location and inventory decisions into a supply chain design problem with uncertain demands and lead times. J. Manuf. Syst. 2017, 43, 139–149. [Google Scholar] [CrossRef]
- Emami, A.; Hazrati, R.; Delshad, M.M.; Pouri, K.; Khasraghi, A.S.; Chobar, A.P. A novel mathematical model for emergency transfer point and facility location. J. Eng. Res. 2023, in press. [Google Scholar] [CrossRef]
- Kilic, F.; Kara, B.; Bozkaya, B. Locating temporary shelter areas after an earthquake: A case for Turkey. Eur. J. Oper. Res. 2015, 243, 323–332. [Google Scholar] [CrossRef]
- Espejo-Díaz, J.A.; Guerrero, W.J. A bi-objective model for the humanitarian aid distribution problem: Analyzing the trade-off between shortage and inventory at risk. In Proceedings of the Applied Computer Sciences in Engineering: 6th Workshop on Engineering Applications, WEA 2019, Santa Marta, Colombia, 16–18 October 2019; Proceedings 6. Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 752–763. [Google Scholar]
- Manopiniwes, W.; Irohara, T. Stochastic optimisation model for integrated decisions on relief supply chains: Preparedness for disaster response. Int. J. Prod. Res. 2017, 55, 979–996. [Google Scholar] [CrossRef]
- Ansari, M.; Borrero, J.S.; Lozano, L. Robust Minimum-Cost Flow Problems Under Multiple Ripple Effect Disruptions. INFORMS J. Comput. 2023, 35, 83–103. [Google Scholar] [CrossRef]
- Vahdani, B.; Soltani, M.; Yazdani, M.; Mousavi, S.M. A three level joint location-inventory problem with correlated demand, shortages and periodic review system: Robust meta-heuristics. Comput. Ind. Eng. 2017, 109, 113–129. [Google Scholar] [CrossRef]
- Demirbas, S.; Alp, E.M. Determination of equivalent warehouses in humanitarian logistics by reallocation of multiple item type inventories. Int. J. Disaster Risk Reduct. 2021, 66, 102603. [Google Scholar] [CrossRef]
- Yang, Y.; Yin, Y.; Wang, D.; Ignatius, J.; Cheng, T.; Dhamotharan, L. Distributionally robust multi-period loca-tion-allocation with multiple resources and capacity levels in humanitarian logistics. Eur. J. Oper. Res. 2023, 305, 1042–1062. [Google Scholar] [CrossRef]
- Liu, K.; Zhang, H.; Zhang, Z.-H. The efficiency, equity and effectiveness of location strategies in humanitarian logistics: A robust chance-constrained approach. Transp. Res. Part E Logist. Transp. Rev. 2021, 156, 102521. [Google Scholar] [CrossRef]
- Fuqua, D.; Hespeler, S. Commodity demand forecasting using modulated rank reduction for humanitarian logistics planning. Expert Syst. Appl. 2022, 206, 117753. [Google Scholar] [CrossRef]
- Stienen, V.; Wagenaar, J.; Hertog, D.D.; Fleuren, H. Optimal depot locations for humanitarian logistics service providers using robust optimization. Omega 2021, 104, 102494. [Google Scholar] [CrossRef]
- Chobar, A.P.; Adibi, M.A.; Kazemi, A. Multi-objective hub-spoke network design of perishable tourism products using combination machine learning and meta-heuristic algorithms. Environ. Dev. Sustain. 2022, 1–28. [Google Scholar] [CrossRef]
- Loree, N.; Aros-Vera, F. Points of distribution location and inventory management model for Post-Disaster Humanitarian Logistics. Transp. Res. Part E 2018, 116, 1–24. [Google Scholar] [CrossRef]
- Cotes, N.; Cantillo, V. Including deprivation costs in facility location models for humanitarian relief logistics. Socio-Econ. Plan. Sci. 2019, 65, 89–100. [Google Scholar] [CrossRef]
- Ghorbani, M.; Ramezanian, R. Integration of carrier selection and supplier selection problem in humanitarian logistics. Comput. Ind. Eng. 2020, 144, 106473. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Zarrinpoor, N. Designing an integrated humanitarian logistics network for the preparedness and response phases under uncertainty. Socio-Econ. Plan. Sci. 2023, 86, 101496. [Google Scholar] [CrossRef]
- Kawase, R.; Iryo, T. Optimal stochastic inventory-distribution strategy for damaged multi-echelon humanitarian logistics network. Eur. J. Oper. Res. 2023, 309, 616–633. [Google Scholar] [CrossRef]
- Roh, S.Y.; Seo, Y.J. The Pre-positioned Warehouse Location Selection for International Humanitarian Relief Logistics. Asian J. Shipp. Logist. 2018, 34, 297–307. [Google Scholar] [CrossRef]
- De, S.K. The goat search algorithms. Artif. Intell. Rev. 2023, 56, 8265–8301. [Google Scholar] [CrossRef]
- Boonmee, C.; Arimura, M.; Asada, M. Facility Location Optimization Model for Emergency Humanitarian Logistics. Int. J. Disaster Risk Reduct. 2017, 24, 485–498. [Google Scholar] [CrossRef]
- Yeh, C.T. An improved NSGA2 to solve a bi-objective optimization problem of multi-state electronic transaction network. Reliab. Eng. Syst. Saf. 2019, 191, 106578. [Google Scholar]
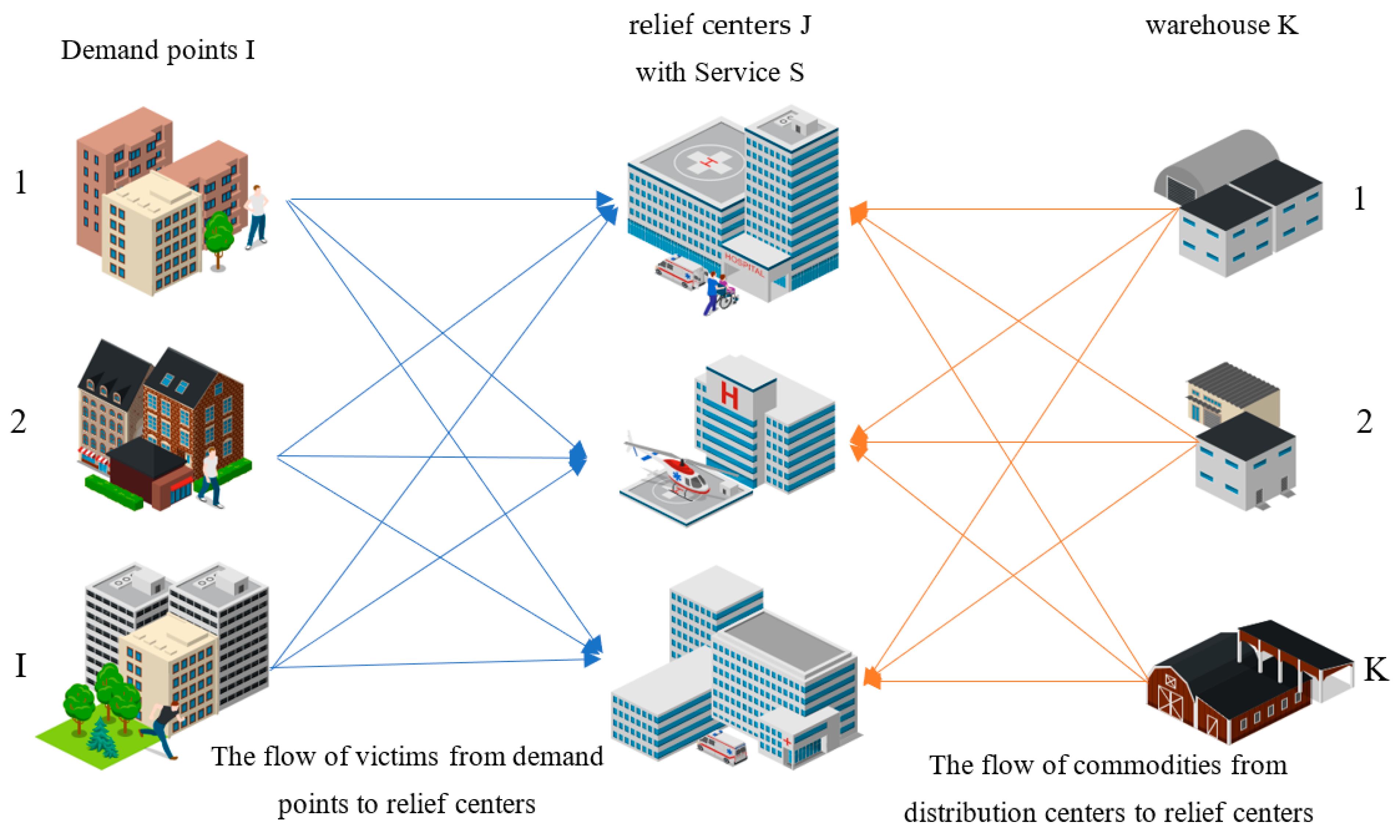
| Notation | Description |
|---|---|
| i | The set of demand points |
| The set of relief centers | |
| The set of warehouses | |
| The set of services | |
| The capacity of relief center j for services s | |
| The space occupied by each product unit for service s in warehouse k () | |
| 1 if the relief center is inside the warehouse’s service area; otherwise, 0. | |
| Number of injured people, demand point i, needing service s | |
| The fixed cost of establishing a relief jth center | |
| The fixed cost of establishing a kth warehouse | |
| The cost of delivering the injured person from the ith demand point to the jth relief center | |
| The cost of delivering service s-related commodities from warehouse k to jth relief center | |
| The demand from kth warehouse | |
| The demand in the time of product m delivery at kth warehouse | |
| The value of optimal order of product m in kth warehouse | |
| Available volume of kth warehouse () | |
| Maximum inventory (inventory level) of kth warehouse | |
| The maximum inventory (inventory level) of product m in kth warehouse | |
| Reorder point of kth warehouse | |
| Precautionary storage of kth warehouse | |
| Precautionary storage of the product m in kth warehouse | |
| Loss caused by a lack of products in kth warehouse | |
| The importance factor of service type one in kth warehouse | |
| The importance factor of service type two in kth warehouse | |
| The cost of lacking product one in the warehouse | |
| The cost of lacking product two in the warehouse | |
| Variable | Description |
| If the established warehouse k serves deployed relief center j, then the value is 1, otherwise, it is zero. | |
| 1 if service s is offered by the established relief center; otherwise, zero. | |
| 1 if warehouse k is established, otherwise zero. | |
| The number of people with the ith demand points in need of service s assigned to the established jth relief center. | |
| The number of people with ith demand points in need of service s assigned to the established jth relief center. |
| Number of Permutations (Ways to Reach the Answer) | Z2 | Z1 | Number of Services | Number of Warehouses | Number of Relief Centers | Number of Demand Points | # Sample Problem |
|---|---|---|---|---|---|---|---|
| 144 | 0.0008998 | 11,755 | 2 | 3 | 4 | 6 | 1 |
| 560 | 0.0121 | 16,983 | 2 | 4 | 7 | 10 | 2 |
| 1800 | 0.1045 | 22,036 | 2 | 6 | 10 | 15 | 3 |
| 6000 | 0.3026 | 38,654 | 2 | 10 | 15 | 20 | 4 |
| 11,050 | 0.499 | 42,741 | 2 | 13 | 17 | 25 | 5 |
| Changing Procedure of Z2 | Z2 | Changing Procedure of Z1 | Z1 | |
|---|---|---|---|---|
| Decreasing | 0.000401 | Increasing | 18,371 | −20% |
| Decreasing | 0.000621 | Increasing | 14,956 | −10% |
| Base | 0.0008998 | Base | 11,775 | 0% |
| Increasing | 0.001256 | Decreasing | 8523 | 10% |
| Increasing | 0.005482 | Decreasing | 4971 | 20% |
| Changing Procedure of Z2 | Z2 | Changing Procedure of Z1 | Z1 | |
|---|---|---|---|---|
| Decreasing | 0.000392 | Decreasing | 6672 | −20% |
| Decreasing | 0.000601 | Decreasing | 9563 | −10% |
| Base | 0.0008998 | Base | 11,775 | 0% |
| Increasing | 0.001658 | Increasing | 13,287 | 10% |
| Increasing | 0.010975 | Increasing | 15,986 | 20% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Delshad, M.M.; Chobar, A.P.; Ghasemi, P.; Jafari, D. Efficient Humanitarian Logistics: Multi-Commodity Location–Inventory Model Incorporating Demand Probability and Consumption Coefficients. Logistics 2024, 8, 9. https://doi.org/10.3390/logistics8010009
Delshad MM, Chobar AP, Ghasemi P, Jafari D. Efficient Humanitarian Logistics: Multi-Commodity Location–Inventory Model Incorporating Demand Probability and Consumption Coefficients. Logistics. 2024; 8(1):9. https://doi.org/10.3390/logistics8010009
Chicago/Turabian StyleDelshad, Majid Mehrabi, Adel Pourghader Chobar, Peiman Ghasemi, and Davoud Jafari. 2024. "Efficient Humanitarian Logistics: Multi-Commodity Location–Inventory Model Incorporating Demand Probability and Consumption Coefficients" Logistics 8, no. 1: 9. https://doi.org/10.3390/logistics8010009
APA StyleDelshad, M. M., Chobar, A. P., Ghasemi, P., & Jafari, D. (2024). Efficient Humanitarian Logistics: Multi-Commodity Location–Inventory Model Incorporating Demand Probability and Consumption Coefficients. Logistics, 8(1), 9. https://doi.org/10.3390/logistics8010009