The Existence and Uniqueness Conditions for Solving Neutrosophic Differential Equations and Its Consequence on Optimal Order Quantity Strategy

Abstract

Background: Neutrosophic logic explicitly quantifies indeterminacy while also maintaining the independence of truth, indeterminacy, and falsity membership functions. This characteristic assumes an imperative part in circumstances, where dealing with contradictory or insufficient data is a necessity. The exploration of differential equations within the context of uncertainty has emerged as an evolving area of research. Methods: the solvability conditions for the first-order linear neutrosophic differential equation are proposed in this study. This study also demonstrates both the existence and uniqueness of a solution to the neutrosophic differential equation, followed by a concise expression of the solution using generalized neutrosophic derivative. As an application of the first-order neutrosophic differential equation, we discussed an economic lot sizing model in a neutrosophic environment. Results: This study finds the conditions for the existing solution of a first-order neutrosophic differential equation. Through the numerical simulation, this study also finds that the neutrosophic differential equation approach is much better for handling uncertainty involved in inventory control problems. Conclusions: This article serves as an introductory exploration of differential equation principles and their application within a neutrosophic environment. This approach can be used in any operation research or decision-making scenarios to remove uncertainty and attain better outcomes.

1. Introduction

In the context of decision-making or computational procedures, almost all instances, such as measurement, observation, experimentation, quantification, and the analysis of data, inevitably involve a certain degree of uncertainty and ambiguity. It plays a pivotal role in drawing conclusions or making decisions when faced with dilemmas. In practice, it is impossible to eliminate uncertainty or imprecision from quantification and decision-making scenarios. Since the variables and parameters connected in the decision-making scenario are subject to uncertainty and unpredictability, dealing with these ambiguities or uncertainties requires a mathematical technique. In light of these challenges, Zadeh [1,2] introduced a groundbreaking concept known as “fuzzy set theory” to elucidate the presence of uncertainty in the literature of applied science, engineering, and management, which deals with the grade of membership of an element in a given set. Following this, several types of generalizations of fuzzy sets have been proposed by numerous researchers [3,4,5]. One of these generalizations is the neutrosophic set, which is presented by Smarandache [4,5]. The neutrosophic set theory offers a framework for modeling more intricate systems compared with fuzzy sets. In this framework, the membership value for falsity is not necessarily the complement of the membership value for truth. This theory introduces a level of indeterminacy besides the membership functions for truth and falsity and provides a more comprehensive framework to manage the inherent vagueness or uncertainty. As a result, neutrosophic set theory emerged as a new concept within the domain of fuzzy systems. Several researchers have worked on neutrosophic mathematics, such as neutrosophic topological space [6], neutrosophic calculus [7], neutrosophic vector spaces [8], and neutrosophic differential equations [9], etc. In this article, we establish a theorem that demonstrates both the existence and uniqueness of a solution to the neutrosophic differential equation ${\tilde{y}}^{\prime }\left(x\right)=f(x,y\left(x\right))$ with $y\left(x_0\right)=y_0$, where $f:I\times {\mathcal{N}}^n\to {\mathcal{N}}^n$ is levelwise continuous neutrosophic function and satisfies a generalized Lipschitz condition.

On the other hand, inventory control policy is a very important task related to operation research. The primary focus of this optimization problem is determining the optimal stock quantity to ensure maximum profits with a continuous unhindered supply chain operation. In this regard, Harris [10] first introduced a classical inventory model in 1913. However, the variables or parameters in a practical lot sizing model may not exist without uncertainty or vulnerability. Following the invention of the fuzzy set concept in 1965, Park [11] discussed an EOQ model using a fuzzy set theoretic approach to tackle the uncertainty involved in the system in 1987. After that, several studies [12,13,14,15,16,17,18,19] have investigated inventory control using this approach. As we have discussed in the above segment, a neutrosophic set is a more efficient approach than a fuzzy one to deal with uncertainty. Neutrosophic numbers are one of the extensions of fuzzy numbers. The determinacy on the membership of an element in each discourse provided by fuzzy number is generalized by the Intuitionistic fuzzy number, which includes a measure of indeterminacy as well. Neutrosophic numbers incorporate the notions of determinacy, hesitancy, and indeterminacy grade together, which makes itself the most generalized tool for carrying the sense of uncertainty in this direction. On the other hand, the fuzzy type 2 generalizes the membership function to be uncertain itself. The uncertainty regarding membership function may be suitable for risk analysis-based decision-making. The primary goal of the proposed order quantity model was to assume the dependence of the demand on several factors such as price, waiting time, stock, etc. The variability in the demand on the factors may stabilized by aggregating the notion of determinacy, hesitancy, and indeterminacy perceptions made by multiple decision makes. This is the reason to consider neutrosophic numbers in this regard. To the best of our knowledge, first, Mullai and Broumi [20] discussed an EOQ model in a neutrosophic environment. Very little work has been conducted on inventory control policy using the neutrosophic differential equation approach. In this study, we discussed an economic lot sizing model with price, stock level, and product warranty time-dependent demand in a neutrosophic uncertain environment and analyzed this using the neutrosophic differential equation approach.

After the introductory section, this article is structured as follows: Section 2 describes a literature survey on research related to the present study. Section 3 provides an overview of the important thoughts related to the theory of neutrosophic sets. Section 4 delves into the criteria for establishing the existence and uniqueness of solving the criteria of an NDE. Section 5 examines scenarios for the solution of a linear first-order NDE when dealing with various types of neutrosophic differentiability. Section 6 elaborates on an Economic Order Quantity (EOQ) model where the demand pattern is dependent on the selling price, warranty time, and stock level of items, employing the generalized neutrosophic differentiation method for neutrosophic-valued functions. Section 7 serves as the conclusion of this article.

2. Literature Review

The fundamental theory supporting this study is outlined thoroughly in two subsequent sections, namely neutrosophic calculus and the recent advancement of inventory modeling in a neutrosophic environment.

2.1. Neutrosophic Calculus and Differential Equation

Differential equations with imprecise parameters are generally used to address the inherent uncertainty or ambiguity in decision-making or computational procedures. The notion of fuzzy differential equations [21,22,23,24,25,26,27] was presented for this purpose, primarily considering the membership value. Subsequently, the intuitionistic fuzzy differential equation [28,29,30,31,32] was developed, incorporating both the concept of membership and non-membership value. Nevertheless, neither of these approaches accounted for the concept of indeterminacy. As a result, the neutrosophic differential equation (NDE) was conceived to model indeterminacy specifically. In this regard, Smarandache [33] defined the derivative of a neutrosophic-valued function. Son et al. [34] presented the notion of a “granular derivative” of a neutrosophic valued function, which is novel from a neutrosophic derivative. Sumathi and Priya [9] epitomized a first linear homogeneous order neutrosophic ordinary differential equation by taking the parameters as the triangular neutrosophic number and applying this concept to a bacteria culture model. After that, Sumathi and Sweety [35] discussed the solving approach of linear NDE of second order by taking the boundary conditions as trapezoidal neutrosophic numbers. Moi et al. [36] proposed the notion of a “generalized neutrosophic derivative” of a neutrosophic-valued function and discussed the solving approach of linear NDE. After that, Moi et al. [37] analyzed a neutrosophic boundary value problem using a different type of generalized neutrosophic derivative. The notion of neutrosophic Riemann integration is established by Biswas et al. [38]. Rahaman et al. [39] established the approach for solving linear and quadratic equations using Cauchy neutrosophic coefficients. Salama et al. [40] discussed an NDE by using a neutrosophic thick function. In this article, we have discussed the criteria for the existence and uniqueness of solving an initial value problem in a neutrosophic environment.

2.2. Inventory Model in Neutrosophic Environment

Three membership functions demonstrate how neutrosophic numbers handle uncertainties related to truth, indeterminacy, and falsity. Many researchers are currently applying the concept of neutrosophic logic to address uncertainty in inventory-related problems. For instance, Mondal et al. [41] introduced a lot-sizing model considering limited holding capacity through neutrosophic geometric programming. An inventory policy for seasonal goods with a logistic-growth demand function is discussed in a neutrosophic environment through neutrosophic norms by Mondal et al. [42]. Mullai and Surya [43] established a lot size model where a price discount policy is available considering demand rate, purchasing cost, and holding cost as a triangular neutrosophic number. They investigated how the application of neutrosophic set theory offers superior results in the lot sizing model compared with intuitionistic fuzzy or general fuzzy sets. Mullai and Surya [44] analyzed a neutrosophic inventory model with a full backlogging shortage using triangular neutrosophic numbers. De et al. [45] introduced a production inventory model assuming defective manufacturing by employing a combination of a game and a neutrosophic fuzzy method. Pal and Chakraborty [46] investigated an EPQ model for non-instantaneous degrading goods under shortages using a triangular neutrosophic number and found that this method gives better results than the crisp method. Garg et al. [47] presented a lot sizing strategy for container-taking triangular bipolar neutrosophic numbers. Rahaman et al. [48] discussed a lot size model with price and stock-dependent demand in the type-2 interval uncertain arena. Mohanta et al. [49] utilized neutrosophic logic in a scenario involving a perishable product-based lot size model considering a partial trade credit approach that varies over time. Recently, Bhavani and Mahapatra [50] introduced an inventory system with imperfect goods with generalized triangular neutrosophic numbers and solved it by using a meta-heuristic algorithm PSO.

Table 1. Comparison of this study with the previous article centered on the inventory model in an uncertain environment.

Author(s)	Year	Model Type	Demand Pattern Depends On	Nature of Impreciseness	Types of Imprecise Parameters	Solution Approach
Mondal et al. [41]	2018	EOQ	Constant	Neutrosophic	Neutrosophic set	Neutrosophic Geometric Programming
Mondal et al. [42]	2020	EOQ	Time-varying logistic growth	Neutrosophic	Generalized triangular neutrosophic number	Neutrosophic index value through weighted arithmetic mean approach
Mullai and Surya [44]	2020	EOQ	Constant	Neutrosophic	Triangular neutrosophic number	Neutrosophic index value through signed distance approach
De et al. [45]	2020	EPQ	Constant	Neutrosophic	Single-valued Neutrosophic Offset	Game and neutrosophic index value through sine-cut approach
Pal and Chakraborty [46]	2020	EOQ	Time	Neutrosophic	Triangular neutrosophic number	Neutrosophic index value through area removal approach
Bhavani and Mahapatra [50]	2022	EOQ	Price, quality, time	Neutrosophic	Generalized triangular neutrosophic	Meta-heuristic algorithm PSO
Momena et al. [19]	2023	EOQ	Price	Fuzzy	Triangular dense fuzzy set	Fuzzy differential equation approach
Rahaman et al. [48]	2023	EOQ	Price, stock	Type-2 interval uncertainty	Type-2 interval number	Type-2 interval differential equation approach
Mohanta et al. [49]	2023	EOQ	Price, advertisement frequency, downstream trade credit	Neutrosophic	Triangular neutrosophic number	Neutrosophic arithmetic operation approach
This article		EOQ	Price, product warranty time, stock	Neutrosophic	Triangular neutrosophic number	Neutrosophic differential equation approach

EOQ: Economic order quantity, EPQ: Economic production quantity.

describes contributions of the recently published literature in the mentioned direction

2.3. Research Gaps and Our Contribution

Based on the summary of the above discussion, we have identified specific research gaps that we aim to address in this article.

• It has come to our attention that the majority of studies [9,34,35,36,37,38,39,41,42,43,44,45,46,47,49,50] in neutrosophic set theory have focused on applying neutrosophic sets in various scientific disciplines. However, there has been minimal effort directed towards the comprehensive development of neutrosophic differential equations and their manifestation within the neutrosophic context. This creates a notable gap between the theory’s advancement and its practical implication.
• Only a limited number of articles [20,41,42,43,44,45,46,47,49,50] have studied tackling uncertainty in operations research issues using neutrosophic concepts. However, nearly all these investigations have employed data after de-neutrosophication, which led to an analysis rooted in crisp phenomena. To effectively deal with decision-making challenges in neutrosophic scenarios, it is advisable to approach the modeling and analysis using the framework of neutrosophic sets and calculus from start to finish.
• We noticed some studies [12,13,14,15,16,17,18,19] where the fuzzy differential equation approach is considered to describe lot-sizing models. However, almost no work has been conducted in inventory control theory using the neutrosophic differential equation approach. This gap motivates us to introduce the neutrosophic differential equation approach in an inventory control system.

To fill the gap in the existing literature, we included the following points in the current article.

• The manifestation of the solution strategy of a linear first-order neutrosophic differential equation has been discussed by taking two types of generalized neutrosophic derivatives of the neutrosophic valued function.
• Prior to the detailed manifestation of the neutrosophic differential equation under two types of generalized neutrosophic derivative, a theorem is established that demonstrates both the existence and uniqueness of the solution of the neutrosophic differential equation.
• A novel economic lot-sizing model with price, product warranty time, and stock-dependent demand is addressed using a neutrosophic differential equation approach by taking various parameters as single-valued triangular neutrosophic numbers.

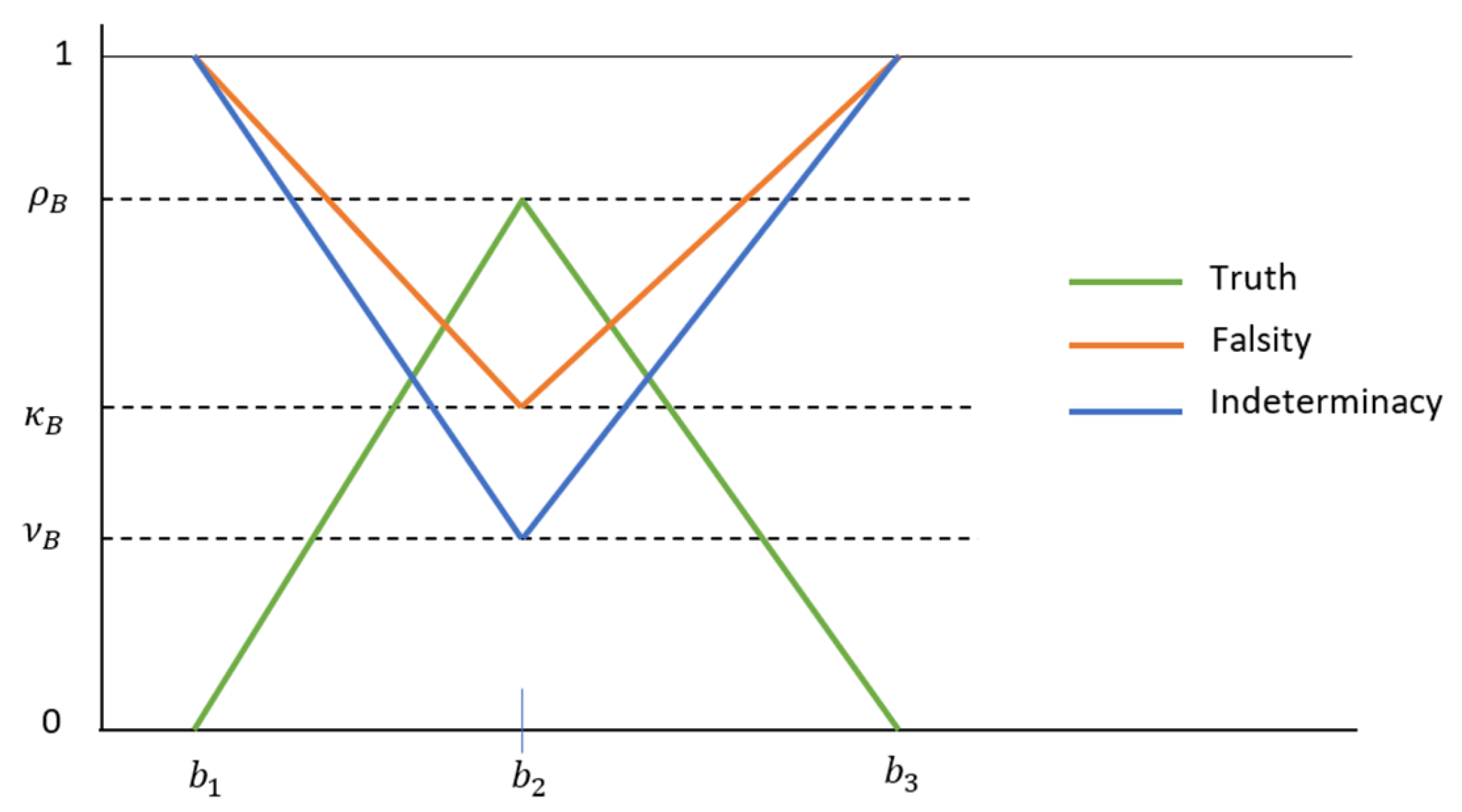
3. Preliminaries

Here, we provide some basic notions related to the theory of neutrosophic sets, neutrosophic number, and differentiability of a neutrosophic valued function.

Definition 1

([5]). Let $\mathit{X}$ be a space of points. Then, a neutrosophic set $\tilde{\mathit{B}}$ over $\mathit{X}$ is defined by a truth membership function ${\mathit{T}}_{\tilde{\mathit{B}}}\left(\mathit{\xi }\right)$, an indeterminacy function ${\mathit{I}}_{\tilde{\mathit{B}}}\left(\mathit{\xi }\right)$ and falsity membership function ${\mathit{F}}_{\tilde{\mathit{B}}}(\mathit{\xi })$ where ${\mathit{T}}_{\tilde{\mathit{B}}},{\mathit{I}}_{\tilde{\mathit{B}}},{\mathit{F}}_{\tilde{\mathit{B}}}:\mathit{X}\to ]{\mathbf{0}}^{\mathbf{-}},{\mathbf{1}}^{\mathbf{+}}[$ satisfying the relation ${\mathbf{0}}^{\mathbf{-}}\le {\mathit{T}}_{\tilde{\mathit{B}}}\left(\mathit{\xi }\right)+{\mathit{I}}_{\tilde{\mathit{B}}}\left(\mathit{\xi }\right)+{\mathit{F}}_{\tilde{\mathit{B}}}\left(\mathit{\xi }\right)\le {\mathbf{3}}^{\mathbf{+}}$.

Definition 2

([51]). Let $\mathit{X}$ be a space of points. Then, a single-valued neutrosophic set $\tilde{\mathit{B}}$ over $\mathit{X}$ is defined by $\tilde{\mathit{B}}=\left\{〈\mathit{\xi },\left({\mathit{T}}_{\tilde{\mathit{B}}}\left(\mathit{\xi }\right),{\mathit{I}}_{\tilde{\mathit{B}}}\left(\mathit{\xi }\right),{\mathit{F}}_{\tilde{\mathit{B}}}(\mathit{\xi })\right)〉:\mathit{\xi }\in \mathit{X}\right\}$ where ${\mathit{T}}_{\tilde{\mathit{B}}}\left(\mathit{\xi }\right)$, ${\mathit{I}}_{\tilde{\mathit{B}}}\left(\mathit{\xi }\right)$ and ${\mathit{F}}_{\tilde{\mathit{B}}}(\mathit{\xi })$ signifies the degree of membership, indeterminacy, and falsity of $\mathit{\xi }$ in $\mathit{X}$ with ${\mathit{T}}_{\tilde{\mathit{B}}},{\mathit{I}}_{\tilde{\mathit{B}}},{\mathit{F}}_{\tilde{\mathit{B}}}:\mathit{X}\to [\mathbf{0},\mathbf{1}]$ satisfying the relation $\mathbf{0}\le {\mathit{T}}_{\tilde{\mathit{B}}}\left(\mathit{\xi }\right)+{\mathit{I}}_{\tilde{\mathit{B}}}\left(\mathit{\xi }\right)+{\mathit{F}}_{\tilde{\mathit{B}}}\left(\mathit{\xi }\right)\le \mathbf{3}$.

Remark 1.

The neutrosophic set represents a broader concept compared with a fuzzy set. Implementing neutrosophic sets in practical applications might pose challenges. For real-world scenarios, it is more feasible to work with single-valued neutrosophic sets. Therefore, in the subsequent sections of this study, we will exclusively employ single-valued neutrosophic sets.

Definition 3

([52]). A single-valued triangular neutrosophic number ${\tilde{\mathit{B}}}_{\mathit{T}\mathit{N}}=〈\left({\mathit{b}}_{\mathbf{1}},{\mathit{b}}_{\mathbf{2}},{\mathit{b}}_{\mathbf{3}}\right);{\mathit{\rho }}_{\mathit{B}},{\mathit{\upsilon }}_{\mathit{B}},{\mathit{\kappa }}_{\mathit{B}}〉$ is a special type of neutrosophic set on $\mathbb{R}$ whose truth, indeterminacy, and falsity membership functions are represented graphically in Figure 1, which are defined as:

$${\mathit{T}}_{{\tilde{\mathit{B}}}_{\mathit{T}\mathit{N}}}\left(\mathit{\xi }\right)=\left\{\begin{array}{c}\left(\frac{\mathit{\xi }-{\mathit{b}}_{\mathbf{1}}}{{\mathit{b}}_{\mathbf{2}}-{\mathit{b}}_{\mathbf{1}}}\right){\mathit{\rho }}_{\mathit{B}}\hspace{1em}\hspace{0.17em}\mathit{w}\mathit{h}\mathit{e}\mathit{n} {\mathit{b}}_{\mathbf{1}}\le \mathit{\xi }\le {\mathit{b}}_{\mathbf{2}}\\ \hspace{1em} {\mathit{\rho }}_{\mathit{B}}\hspace{1em}\hspace{1em}\hspace{1em}\mathit{w}\mathit{h}\mathit{e}\mathit{n} \mathit{\xi }={\mathit{b}}_{\mathbf{2}}\hfill \\ \left(\frac{{\mathit{b}}_{\mathbf{3}}-\mathit{\xi }}{{\mathit{b}}_{\mathbf{3}}-{\mathit{b}}_{\mathbf{2}}}\right){\mathit{\rho }}_{\mathit{B}}\hspace{1em}\hspace{0.17em}\mathit{w}\mathit{h}\mathit{e}\mathit{n} {\mathit{b}}_{\mathbf{2}}\le \mathit{\xi }\le {\mathit{b}}_{\mathbf{3}}\\ \hspace{1em} \mathbf{0}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\mathit{o}\mathit{t}\mathit{h}\mathit{e}\mathit{r}\mathit{w}\mathit{i}\mathit{s}\mathit{e}\hfill \end{array}\right.$$

$$I_{{\tilde{B}}_{TN}}\left(\xi \right)=\left\{\begin{array}{c}\frac{b_2-\xi +{\upsilon }_B\left(\xi -b_1\right)}{b_2-b_1}\hspace{1em}when b_1\le \xi \le b_2\\ {\upsilon }_B\hspace{1em}\hspace{1em}\hspace{1em}when \xi =b_2\\ \frac{\xi -b_2+{\upsilon }_B\left(b_3-\xi \right)}{b_3-b_2}\hspace{1em}when b_2\le \xi \le b_3\\ \hspace{1em}\hspace{1em}1\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}otherwise\hfill \end{array}\right.$$

$$F_{{\tilde{B}}_{TN}}\left(\xi \right)=\left\{\begin{array}{c}\frac{b_2-\xi +{\kappa }_B\left(\xi -b_1\right)}{b_2-b_1}\hspace{1em}when b_1\le \xi \le b_2\\ {\upsilon }_B\hspace{1em}\hspace{1em}\hspace{1em}when \xi =b_2\\ \frac{\xi -b_2+{\kappa }_B\left(b_3-\xi \right)}{b_3-b_2}\hspace{1em}when b_2\le \xi \le b_3\\ \hspace{1em}\hspace{1em}1\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}otherwise\hfill \end{array}\right.$$

Figure 1. Graphical illustration of triangular neutrosophic number.

Figure 1. Graphical illustration of triangular neutrosophic number.

Definition 4

([53]). A triangular single-valued neutrosophic number of Type 1 is a special type of neutrosophic set on $\mathbb{R}$ is denoted as $\tilde{\mathit{B}}=\left({\mathit{m}}_{\mathbf{1}},{\mathit{m}}_{\mathbf{2},}{\mathit{m}}_{\mathbf{3}};{\mathit{l}}_{\mathbf{1}},{\mathit{l}}_{\mathbf{2}},{\mathit{l}}_{\mathbf{3}};{\mathit{k}}_{\mathbf{1}},{\mathit{k}}_{\mathbf{2}},{\mathit{k}}_{\mathbf{3}}\right)$ whose truth, indeterminacy, and falsity membership functions are represented graphically in Figure 2, which are defined as:

$$T_{\tilde{B}}\left(\xi \right)=\left\{\begin{array}{c}\frac{\xi -m_1}{m_2-m_1}\hspace{1em}when m_1\le \xi \le m_2\\ 1\hspace{1em}\hspace{1em}\hspace{1em}when \xi =m_2\\ \frac{m_3-\xi }{m_3-m_2}\hspace{1em}when m_2\le \xi \le m_3\\ \hspace{1em}0\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}otherwise\hfill \end{array}\right.$$

$$I_{\tilde{B}}\left(\xi \right)=\left\{\begin{array}{c}\frac{l_1-\xi }{l_2-l_1}\hspace{1em}when l_1\le \xi \le l_2\\ 0\hspace{1em}\hspace{1em}\hspace{1em}when \xi ={\xi }_2\\ \frac{\xi -l_2}{l_3-l_2}\hspace{1em}when l_2\le \xi \le l_3\\ 1\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}otherwise\hfill \end{array}\right.$$

$$F_{\tilde{B}}\left(\xi \right)=\left\{\begin{array}{c}\frac{k_1-\xi }{k_2-k_1}\hspace{1em}when k_1\le \xi \le k_2\\ 0\hspace{1em}\hspace{1em}\hspace{1em}when \xi =k_2\\ \frac{\xi -k_2}{k_3-k_2}\hspace{1em}when k_2\le \xi \le k_3\\ 1\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}otherwise\hfill \end{array}\right.$$

Figure 2. Graphical illustration of a triangular neutrosophic number of Type 1 with nine components.

Figure 2. Graphical illustration of a triangular neutrosophic number of Type 1 with nine components.

Definition 5

([52]). The $\left(\mathit{\zeta },\mathit{\eta },\mathit{\theta }\right)-$ representation of a neutrosophic set $\tilde{\mathit{B}}=\left\{〈\mathit{\xi },\left({\mathit{T}}_{\tilde{\mathit{B}}}\left(\mathit{\xi }\right),{\mathit{I}}_{\tilde{\mathit{B}}}\left(\mathit{\xi }\right),{\mathit{F}}_{\tilde{\mathit{B}}}(\mathit{\xi })\right)〉:\mathit{\xi }\in \mathit{X}\right\}$ over $\mathit{X}$ is written as ${\tilde{\mathit{B}}}_{\left(\mathit{\zeta },\mathit{\eta },\mathit{\theta }\right)}$ and is defined as ${\tilde{\mathit{B}}}_{\left(\mathit{\zeta },\mathit{\eta },\mathit{\theta }\right)}=\left\{〈\mathit{\xi },\left({\mathit{T}}_{\tilde{\mathit{B}}}\left(\mathit{\xi }\right),{\mathit{I}}_{\tilde{\mathit{B}}}\left(\mathit{\xi }\right),{\mathit{F}}_{\tilde{\mathit{B}}}(\mathit{\xi })\right)〉:\mathit{\xi }\in \mathit{X},{\mathit{T}}_{\tilde{\mathit{B}}}\left(\mathit{\xi }\right)\ge \mathit{\zeta },{\mathit{I}}_{\tilde{\mathit{B}}}\left(\mathit{\xi }\right)\le \mathit{\eta },{\mathit{F}}_{\tilde{\mathit{B}}}\left(\mathit{\xi }\right)\le \mathit{\theta }\right\}$, where $\mathit{\zeta },\mathit{\eta },\mathit{\theta }\in [\mathbf{0},\mathbf{1}]$.

Note 1.

The $\left(\mathit{\zeta },\mathit{\eta },\mathit{\theta }\right)-$representation of a Triangular Single Valued Neutrosophic number of Type 1 $\tilde{\mathit{L}}=\left({\mathit{m}}_{\mathbf{1}},{\mathit{m}}_{\mathbf{2},}{\mathit{m}}_{\mathbf{3}};{\mathit{l}}_{\mathbf{1}},{\mathit{l}}_{\mathbf{2}},{\mathit{l}}_{\mathbf{3}};{\mathit{k}}_{\mathbf{1}},{\mathit{k}}_{\mathbf{2}},{\mathit{k}}_{\mathbf{3}}\right)$ is commonly written as $〈\left[{\mathit{L}}_{\mathbf{1}}\left(\mathit{\zeta }\right),{\mathit{L}}_{\mathbf{2}}\left(\mathit{\zeta }\right)\right],\left[{\mathit{L}}_{\mathbf{1}}\left(\mathit{\eta }\right),{\mathit{L}}_{\mathbf{2}}\left(\mathit{\eta }\right)\right],[{\mathit{L}}_{\mathbf{1}}(\mathit{\theta }),{\mathit{L}}_{\mathbf{2}}(\mathit{\theta })]〉$ and is obtained as ${\mathit{L}}_{\mathbf{1}}(\mathit{\zeta })={\mathit{m}}_{\mathbf{1}}+\mathit{\zeta }\left({\mathit{m}}_{\mathbf{2}}-{\mathit{m}}_{\mathbf{1}}\right)$, ${\mathit{L}}_{\mathbf{2}}(\mathit{\zeta })={\mathit{m}}_{\mathbf{3}}-\mathit{\zeta }\left({\mathit{m}}_{\mathbf{3}}-{\mathit{m}}_{\mathbf{2}}\right)$, ${\mathit{L}}_{\mathbf{1}}(\mathit{\eta })={\mathit{l}}_{\mathbf{2}}-\mathit{\eta }\left({\mathit{l}}_{\mathbf{2}}-{\mathit{l}}_{\mathbf{1}}\right)$, ${\mathit{L}}_{\mathbf{2}}\left(\mathit{\eta }\right)={\mathit{l}}_{\mathbf{2}}+\mathit{\eta }\left({\mathit{l}}_{\mathbf{3}}-{\mathit{l}}_{\mathbf{2}}\right)$, ${\mathit{L}}_{\mathbf{1}}(\mathit{\theta })={\mathit{k}}_{\mathbf{2}}-\mathit{\theta }\left({\mathit{k}}_{\mathbf{2}}-{\mathit{k}}_{\mathbf{1}}\right)$ and ${\mathit{L}}_{\mathbf{2}}(\mathit{\theta })={\mathit{k}}_{\mathbf{2}}+\mathit{\theta }\left({\mathit{k}}_{\mathbf{3}}-{\mathit{k}}_{\mathbf{2}}\right)$.

Definition 6

([36]). Let $\tilde{\mathit{h}}:\mathit{I}\to \mathcal{N}$ be a neutrosophic-valued function defined on $\mathit{I}$ whose parametric representation is given as ${\left[\widetilde{\mathit{h}(\mathit{t})}\right]}_{\left(\mathit{\zeta },\mathit{\eta },\mathit{\theta }\right)}=〈\left[{\mathit{h}}_{\mathbf{1}}\left(\mathit{t};\mathit{\zeta }\right),{\mathit{h}}_{\mathbf{2}}\left(\mathit{t};\mathit{\zeta }\right)\right];\left[{\mathit{h}}_{\mathbf{1}}\left(\mathit{t};\mathit{\eta }\right),{\mathit{h}}_{\mathbf{2}}\left(\mathit{t};\mathit{\eta }\right)\right];[{\mathit{h}}_{\mathbf{1}}(\mathit{t};\mathit{\theta }),{\mathit{h}}_{\mathbf{2}}(\mathit{t};\mathit{\theta })]〉$ for all $\mathit{t}\in \mathit{I}$. Suppose ${\mathit{t}}_{\mathbf{0}}\in \mathit{I}$, then the generalized neutrosophic derivative of $\widetilde{\mathit{h}(\mathit{t})}$ at the point ${\mathit{t}}_{\mathbf{0}}\in \mathit{I}$ is defined as follows $\widetilde{{\mathit{h}}^{\prime }({\mathit{t}}_{\mathbf{0}})}=〈{\mathit{h}}_{\mathit{T}}^{\prime }\left({\mathit{t}}_{\mathbf{0}}\right),{\mathit{h}}_{\mathit{I}}^{\prime }\left({\mathit{t}}_{\mathbf{0}}\right),{\mathit{h}}_{\mathit{F}}^{\prime }\left({\mathit{t}}_{\mathbf{0}}\right)〉$ where ${\mathit{h}}_{\mathit{T}}^{\prime }\left({\mathit{t}}_{\mathbf{0}}\right)$, ${\mathit{h}}_{\mathit{I}}^{\prime }\left({\mathit{t}}_{\mathbf{0}}\right)$ and ${\mathit{h}}_{\mathit{F}}^{\prime }\left({\mathit{t}}_{\mathbf{0}}\right)$ are obtained as follows

 1.

$h_T^{\prime }\left(t_0\right)=\left[min\left\{h_1^{\prime }\left(t_0;\zeta \right),h_2^{\prime }\left(t_0;\zeta \right)\right\},max\left\{h_1^{\prime }\left(t_0;\zeta \right),h_2^{\prime }\left(t_0;\zeta \right)\right\}\right]$ if $h_1^{\prime }\left(t_0;\zeta \right)$ and $h_2^{\prime }\left(t_0;\zeta \right)$ exists.

 2.

$h_I^{\prime }\left(t_0\right)=\left[min\left\{h_1^{\prime }\left(t_0;\eta \right),h_2^{\prime }\left(t_0;\eta \right)\right\},max\left\{h_1^{\prime }\left(t_0;\eta \right),h_2^{\prime }\left(t_0;\eta \right)\right\}\right]$ if $h_1^{\prime }\left(t_0;\eta \right)$ and $h_2^{\prime }\left(t_0;\eta \right)$ exists.

 3.

$f_F^{\prime }\left(t_0\right)=\left[min\left\{h_1^{\prime }\left(t_0;\theta \right),h_2^{\prime }\left(t_0;\theta \right)\right\},max\left\{h_1^{\prime }\left(t_0;\theta \right),h_2^{\prime }\left(t_0;\theta \right)\right\}\right]$ if $h_1^{\prime }\left(t_0;\theta \right)$ and $h_2^{\prime }\left(t_0;\theta \right)$ exists.

$\widetilde{h^{\prime }(t)}$ is said to be neutrosophic differentiable of Type 1 at $t=t_0$, if

$${\left[\widetilde{h^{\prime }}\left(t_0\right)\right]}_{\left(\zeta ,\eta ,\theta \right)}=〈\left[h_1^{\prime }\left(t_0;\zeta \right),h_2^{\prime }\left(t_0;\zeta \right)\right]; \left[h_1^{\prime }\left(t_0;\eta \right),h_2^{\prime }\left(t_0;\eta \right)\right]; [h_1^{\prime }(t_0;\theta ),h_2^{\prime }(t_0;\theta )]〉$$

$\widetilde{h^{\prime }(t)}$ is said to be neutrosophic differentiable of Type 2 at $t=t_0$, if

$${\left[\widetilde{h^{\prime }}\left(t_0\right)\right]}_{\left(\zeta ,\eta ,\theta \right)}=〈\left[h_2^{\prime }\left(t_0;\zeta \right),h_1^{\prime }\left(t_0;\zeta \right)\right]; \left[h_2^{\prime }\left(t_0;\eta \right),h_1^{\prime }\left(t_0;\eta \right)\right]; [h_2^{\prime }(t_0;\theta ),h_1^{\prime }(t_0;\theta )]〉$$

4. Existence and Uniqueness Theorem for Solution to the First Order Linear Neutrosophic Differential Equations

Before going into the elaboration of the existence and uniqueness theorem for the solution to a first-order linear neutrosophic differential equation, we define some results that are relevant to this discussion.

Definition 7.

(Neutrosophic set on ${\mathbb{R}}^n$) Let $\mathcal{I}=[a,b]\subset \mathbb{R}$ be compact. The set of all neutrosophic numbers on ${\mathbb{R}}^n$ is denoted by ${\mathcal{N}}^n$ and is defined by

$$\begin{array}{c}{\mathcal{N}}^n=\{\langle \tilde{\xi };T\left(\tilde{\xi }\right),I\left(\tilde{\xi }\right),F\left(\tilde{\xi }\right)\rangle |T\left(\tilde{\xi }\right),I\left(\tilde{\xi }\right),F\left(\tilde{\xi }\right):\hspace{0.17em}{\mathbb{R}}^n\to \left[0,1\right],0\le T\left(\tilde{\xi }\right)+I\left(\tilde{\xi }\right)+F\left(\tilde{\xi }\right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\le 3 \forall \tilde{\xi }\in {\mathbb{R}}^n and satisfying 1-4\}\hfill \end{array}$$

 1.

$\tilde{L}=\langle \tilde{\xi };T\left(\tilde{\xi }\right),I\left(\tilde{\xi }\right),F\left(\tilde{\xi }\right)\rangle$ is normal, i.e., there exists an $\widetilde{{\xi }_0}\in {\mathbb{R}}^n$ such that $T\left(\widetilde{{\xi }_0}\right)=1$ and $I\left(\widetilde{{\xi }_0}\right)=F\left(\widetilde{{\xi }_0}\right)=0$.

 2.

The truth membership function $T(\tilde{\xi })$ is convex, i.e., $T\left(\mu \widetilde{{\xi }_1}+\left(1-\mu \right)\widetilde{{\xi }_2}\right)\ge min\left\{T\left(\widetilde{{\xi }_1}\right),T\left(\widetilde{{\xi }_2}\right)\right\}$, $\forall \widetilde{{\xi }_1}, \widetilde{{\xi }_2}\in {\mathbb{R}}^n$ and $0\le \mu \le 1$. The indeterminacy function $I\left(\tilde{\xi }\right)$ and the falsity membership function $F\left(\tilde{\xi }\right)$ is concave, i.e., $I\left(\mu \widetilde{{\xi }_1}+\left(1-\mu \right)\widetilde{{\xi }_2}\right)\ge max\left\{I\left(\widetilde{{\xi }_1}\right),I\left(\widetilde{{\xi }_2}\right)\right\}$, and $F\left(\mu \widetilde{{\xi }_1}+\left(1-\mu \right)\widetilde{{\xi }_2}\right)\ge max\hspace{0.17em}\left\{F\left(\widetilde{{\xi }_1}\right),\hspace{0.17em}F\left(\widetilde{{\xi }_2}\right)\right\}$ $\forall \widetilde{{\xi }_1},\widetilde{{\xi }_2}\in {\mathbb{R}}^n$ and $0\le \mu \le 1$.

 3.

$T\left(\tilde{\xi }\right)$ is upper semi-continuous and $I\left(\tilde{\xi }\right),\hspace{0.17em}F\left(\tilde{\xi }\right)$ is lower semi-continuous (Biswas et al. [38]).

 4.

Support of $\tilde{L}=\langle \tilde{\xi };T\left(\tilde{\xi }\right),I\left(\tilde{\xi }\right),F\left(\tilde{\xi }\right)\rangle$ is compact, i.e., $Supp\langle \tilde{L}\rangle =\left\{\tilde{\xi }\in \hspace{0.17em}{\mathbb{R}}^n:\hspace{0.17em}T\left(\tilde{\xi }\right)>0,I\left(\tilde{\xi }\right)<1,F\left(\tilde{\xi }\right)<1\right\}$ is compact.

Definition 8.

The $(\zeta ,\eta ,\theta )$-level set of a neutrosophic number $\tilde{L}=\langle \tilde{\xi };T\left(\tilde{\xi }\right),I\left(\tilde{\xi }\right),F\left(\tilde{\xi }\right)\rangle$ of ${\mathcal{N}}^n$ is defined as

$${\left[\tilde{L}\right]}_{\left(\zeta ,\eta ,\theta \right)}=\left\{\tilde{\xi }\in {\mathbb{R}}^n:T\left(\tilde{\xi }\right)\ge \zeta ,\hspace{0.17em}I\left(\tilde{\xi }\right)\le \eta ,F\left(\tilde{\xi }\right)\le \theta \right\}$$

If $g:{\mathbb{R}}^n\times {\mathbb{R}}^n\to {\mathbb{R}}^n$ is a function, then by extension principle, we can extend $g:{\mathcal{N}}^n\times {\mathcal{N}}^n\to {\mathcal{N}}^n$ for any $\tilde{L}=\langle \tilde{\xi };T_1\left(\tilde{\xi }\right),I_1\left(\tilde{\xi }\right),F_1\left(\tilde{\xi }\right)\rangle \in {\mathcal{N}}^n$ and $\tilde{M}=〈\tilde{\tau };T_2\left(\tilde{\tau }\right),I_2\left(\tilde{\tau }\right),F_2\left(\tilde{\tau }\right)〉\in {\mathcal{N}}^n$ by the equation

$$g\left(\tilde{L},\tilde{M}\right)\left(\tilde{\nu }\right)=\underset{\tilde{v}=g(\tilde{\xi },\tilde{\tau })}{sup}\langle \tilde{\nu };min\left\{T_1\left(\tilde{\xi }\right),T_2(\tilde{\tau })\right\},\hspace{0.17em}max\left\{I_1\left(\tilde{\xi }\right),I_2(\tilde{\tau })\right\},\hspace{0.17em}max\left\{F_1\left(\tilde{\xi }\right),F_2(\tilde{\tau })\right\}\rangle$$

Note 2.

It can be shown that

$${\left[g(\tilde{L},\tilde{M})\right]}_{(\zeta ,\eta ,\theta )}=g\left({\left[\tilde{L}\right]}_{(\zeta ,\eta ,\theta )},{\left[\tilde{M}\right]}_{(\zeta ,\eta ,\theta )}\right)$$

for all $\tilde{L},\tilde{M}\in {\mathcal{N}}^n$, $0\le \zeta ,\eta ,\theta \le 1$ and $g$ is continuous. Also, for any $\tilde{L},\tilde{M}\in {\mathcal{N}}^n$ and $\lambda \in R$ we can show that (see Biswas et al. [38])

$${\left[\tilde{L}+\tilde{M}\right]}_{(\zeta ,\eta ,\theta )}={\left[\tilde{L}\right]}_{(\zeta ,\eta ,\theta )}+{\left[\tilde{M}\right]}_{(\zeta ,\eta ,\theta )}$$

$${\left[\lambda \tilde{L}\right]}_{(\zeta ,\eta ,\theta )}=\lambda {\left[\tilde{L}\right]}_{(\zeta ,\eta ,\theta )}$$

where $0\le \zeta ,\eta ,\theta \le 1$.

Theorem 1.

For any $\tilde{L}=\langle \tilde{\xi };T\left(\tilde{\xi }\right),I\left(\tilde{\xi }\right),F\left(\tilde{\xi }\right)\rangle \in {\mathcal{N}}^n$ and ${\zeta }_i,{\eta }_i,{\theta }_i\in [0,1]$ $(i=1,2)$,

 1.

${\left[\tilde{L}\right]}_{({\zeta }_2,{\eta }_2,{\theta }_2)}\subseteq {\left[\tilde{L}\right]}_{({\zeta }_1,{\eta }_1,{\theta }_1)}$ where ${\zeta }_1<{\zeta }_2$, ${\eta }_1>{\eta }_2$, and ${\theta }_1>{\theta }_2$.

 2.

If $\left\{{\zeta }_n\right\}$ is a non-decreasing sequence converging to $\zeta$ and $\left\{{\eta }_n\right\}$ and $\left\{{\theta }_n\right\}$ are non-increasing sequences converging to $\eta$ and $\theta ,$ respectively, then

$$\bigcap _{n=1}^{\infty }{\left[\tilde{L}\right]}_{({\zeta }_n,{\eta }_n,{\theta }_n)}={\left[\tilde{L}\right]}_{(\zeta ,\eta ,\theta )}$$

Remark 2.

In this segment, we defined some results. In the next segment, we will define a metric on the set of all neutrosophic number ${\mathcal{N}}^n$. With the help of this metric, we will show the existence of the solution of a neutrosophic differential equation.

Definition 9.

Suppose two neutrosophic numbers $\tilde{L}$ $and$ $\tilde{M}$ of ${\mathcal{N}}^n$ are given in the parametric form representation by

$${\left[\tilde{L}\right]}_{\left(\zeta ,\eta ,\theta \right)}=〈\left[L_1\left(\zeta \right),L_2\left(\zeta \right)\right],[L_1(\eta ),L_2(\eta )],[L_1(\theta ),L_2(\theta )]〉$$

$${\left[\tilde{M}\right]}_{\left(\zeta ,\eta ,\theta \right)}=〈\left[M_1\left(\zeta \right),M_2\left(\zeta \right)\right],[M_1(\eta ),M_2(\eta )],[M_1(\theta ),M_2(\theta )]〉$$

where $\zeta ,\eta ,\theta \in \left[0,1\right]$. Then a metric $\Delta :{\mathcal{N}}^n\times {\mathcal{N}}^n\to R^{+}\cup \left\{0\right\}$ between $\tilde{L}$ $and$ $\tilde{M}$ is defined by the equation

$$\Delta \left(\tilde{L},\tilde{M}\right)=\underset{0\le \zeta ,\eta ,\theta \le 1}{sup}\mu \left({\left[\tilde{L}\right]}_{\left(\zeta ,\eta ,\theta \right)},{\left[\tilde{M}\right]}_{\left(\zeta ,\eta ,\theta \right)}\right)$$

$$=\underset{0\le \zeta ,\eta ,\theta \le 1}{sup}\left\{\mu \left(L\left(\zeta \right),M\left(\zeta \right)\right),\hspace{0.17em}\mu \left(L\left(\eta \right),M\left(\eta \right)\right),\hspace{0.17em}\mu \left(L\left(\theta \right),M\left(\theta \right)\right)\right\}$$

where $\mu \left(L\left(s\right),M\left(s\right)\right)$ is the Hausdorff metric defined by

$$\mu \left(L\left(s\right),M\left(s\right)\right)=\max \hspace{0.17em}\{‖L_1\left(s\right)-M_1\left(s\right)‖,‖L_2\left(s\right)-M_2\left(s\right)‖\}$$

for $s=\zeta ,\eta ,\theta$.

Note 3.

It can be shown that $\Delta$ is a metric in ${\mathcal{N}}^n$ and $\left({\mathcal{N}}^n,\Delta \right)$ is a complete metric space in ${\mathcal{N}}^n$.

Definition 10.

Suppose $\tilde{h}:\mathcal{T}\to {\mathcal{N}}^n$ is a neutrosophic valued function on $\mathcal{T}$ and the $\left(\zeta ,\eta ,\theta \right)$-level representation of $\widetilde{h(t)}$ is obtained as

$${\tilde{h}}_{\left(\zeta ,\eta ,\theta \right)}\left(t\right)={\left[\tilde{h}(t)\right]}_{\left(\zeta ,\eta ,\theta \right)}=〈\left[h_1\left(t;\zeta \right),h_2(t;\zeta )\right];\left[h_1\left(t;\eta \right),h_2(t;\eta )\right];\left[h_1\left(t;\theta \right),h_2(t;\theta )\right]〉$$

If the mapping ${\tilde{h}}_{\left(\zeta ,\eta ,\theta \right)}\left(t\right)$ is continuous at $t=t_0$ i.e., each $h_1\left(t;\zeta \right)$, $h_2(t;\zeta )$, $h_1\left(t;\eta \right)$, $h_2(t;\eta )$, $h_1\left(t;\theta \right)$ and $h_2(t;\theta )$ are continuous at $t=t_0$ concerning the metric $\Delta$ for all $\zeta ,\eta ,\theta \in [0,1]$ then $\widetilde{h(t)}$ is said to be levelwise continuous at $t_0\in \mathcal{T}$.

Definition 11.

A function $f:\mathcal{T}\times {\mathcal{N}}^n\to {\mathcal{N}}^n$ is defined to be levelwise continuous at some point $\left(t_0,{\tilde{x}}_0\right)\in \mathcal{T}\times {\mathcal{N}}^n$ if for any arbitrary $ϵ>0$ and fixed $\zeta ,\eta ,\theta \in [0, 1]$, there exists a $\delta \left(ϵ,\zeta ,\eta ,\theta \right)>0$ such that

$$\mu \left({\left[f\left(t,\tilde{x}\right)\right]}_{\left(\zeta ,\eta ,\theta \right)},{\left[f\left(t_0,{\tilde{x}}_0\right)\right]}_{\left(\zeta ,\eta ,\theta \right)}\right)<ϵ$$

whenever $\left|t-t_0\right|<\delta \left(ϵ,\zeta ,\eta ,\theta \right)$ and $\mu \left({\left[\tilde{x}\right]}_{\left(\zeta ,\eta ,\theta \right)},{\left[{\tilde{x}}_0\right]}_{\left(\zeta ,\eta ,\theta \right)}\right)<\delta \left(ϵ,\zeta ,\eta ,\theta \right)$ $\forall t\in \mathcal{T},\tilde{x}\in {\mathcal{N}}^n$.

Now, we will show the existence criteria for solving a linear first-order neutrosophic differential equation and its uniqueness. We take a neutrosophic differential equation.

$$\frac{d\widetilde{y(x)}}{dx}=f(x,\widetilde{y(x)}), \tilde{y}\left(x_0\right)=\widetilde{y_0}$$

(1)

where $\tilde{y}(x)$ is a neutrosophic-valued function of $x$ and $x\in \mathcal{I}=\left\{x:\left|x-x_0\right|\le \delta \le a\right\}$ is an independent variable, and $f:\mathcal{I}\times {\mathcal{N}}^n\to {\mathcal{N}}^n$ is also a neutrosophic-valued function.

Definition 12.

If the function $\tilde{y}:\mathcal{I}\to {\mathcal{N}}^n$ satisfies the integral equation

$$\tilde{y}\left(x\right)=y_0+{\int }_{x_0}^{x}f(z,y\left(z\right))dz$$

for all $x\in \mathcal{I}$ and $\widetilde{y(x)}$ is a levelwise continuous function on $\mathcal{I}$. Then $\widetilde{y(x)}$ is said to be a solution of the neutrosophic differential Equation (1).

Putting on the process of successive approximation, one can generate a sequence. $\left\{\widetilde{y_n(x)}\right\}$ such that

$$\widetilde{y_n(x)}=\widetilde{y_0}+{\int }_{x_0}^{x}f(z,\widetilde{y_{n-1}(z)})dz, n=1, 2, 3, \dots$$

(2)

where $\widetilde{y(x_0)}=\widetilde{y_0}$.

Theorem 2.

We define a closed ball $B(\widetilde{y_0},b)$ having a center at $\widetilde{y_0}\in {\mathcal{N}}^n$ and radius $b>0$ as

$$B\left(\widetilde{y_0},b\right)=\left\{\tilde{y}\in {\mathcal{N}}^n\hspace{0.17em}:\Delta \left(\tilde{y},\widetilde{y_0}\right)\le b\right\}$$

Consider the region as $\mathcal{R}=\mathcal{I}\times B\left(\widetilde{y_0},b\right)$. Suppose a function $f:\mathcal{R}\to {\mathcal{N}}^n$ which is levelwise continuous on $\mathcal{R}$ and

 1.

There exists a positive constant $k$ such that

$$\mu \left({\left[f\left(x,\tilde{y}\right)\right]}_{\left(\zeta ,\eta ,\theta \right)},{\left[f\left(x,\tilde{w}\right)\right]}_{\left(\zeta ,\eta ,\theta \right)}\right)\le k\mu \left({\left[\tilde{y}\right]}_{\left(\zeta ,\eta ,\theta \right)},{\left[\tilde{w}\right]}_{\left(\zeta ,\eta ,\theta \right)}\right)$$

for any two points $\left(x,\tilde{y}\right)$ and $\left(x,\tilde{w}\right)$ of $\mathcal{R}$ and for any $\zeta ,\eta ,\theta \hspace{0.17em}\in \left[0,1\right]$.

 2.

$∆\left(f\left(x,\tilde{y}\right),\tilde{0}\right)=\mathcal{K}$, $\tilde{0}\in {\mathcal{N}}^n$ for any $\left(x,\tilde{y}\right)\in \mathcal{R}$

Then the Equation (1) has a unique solution in $\left|x-x_0\right|\le \delta$, where $\delta =min\left\{a,\frac{b}{\mathcal{K}}\right\}$. Also, there exists a neutrosophic set-valued function $\tilde{y}:\mathcal{I}\to {\mathcal{N}}^n$ such that $\Delta \left({\tilde{y}}_n\left(x\right),y(x)\right)\to 0$ on $\left|x-x_0\right|\le \delta$ as $n\to \infty$.

Proof of Theorem 2.

By Equation (2), Equation (1) is equivalent to

$$\widetilde{y_1(x)}=\widetilde{y_0}+{\int }_{x_0}^{x}f(z,\widetilde{y_0(z)})dz$$

It is clear that $\widetilde{y_1}\left(x\right)$ is levelwise continuous on $\left|x-x_0\right|\le a$ and hence on $\left|x-x_0\right|\le \delta$. Also, for any $\zeta ,\eta ,\theta \hspace{0.17em}\in \left[0,1\right]$

$$\mu \left({\left[\widetilde{y_1}\right]}_{\left(\zeta ,\eta ,\theta \right)},{\left[\widetilde{y_0}\right]}_{\left(\zeta ,\eta ,\theta \right)}\right)=\mu \left({\left[\widetilde{y_0}+{\int }_{x_0}^{x}f\left(z,\widetilde{y_0(z)}\right)dz\right]}_{\left(\zeta ,\eta ,\theta \right)},{\left[\widetilde{y_0}\right]}_{\left(\zeta ,\eta ,\theta \right)}\right)$$

$$=\mu \left({\left[\widetilde{y_0}\right]}_{\left(\zeta ,\eta ,\theta \right)}+{\left[{\int }_{x_0}^{x}f\left(z,\widetilde{y_0(z)}\right)dz\right]}_{\left(\zeta ,\eta ,\theta \right)},{\left[\widetilde{y_0}\right]}_{\left(\zeta ,\eta ,\theta \right)}\right)$$

$$=\mu \left({\left[{\int }_{x_0}^{x}f\left(z,\widetilde{y_0(z)}\right)dz\right]}_{\left(\zeta ,\eta ,\theta \right)},\tilde{0}\right)$$

$$\le {\int }_{x_0}^x\mu \left({\left[f\left(z,\widetilde{y_0(z)}\right)\right]}_{\left(\zeta ,\eta ,\theta \right)},\tilde{0}\right)dz$$

If we take $\left|x-x_0\right|\le \delta$ then from the definition of $\Delta$, we can obtain

$$\Delta \left(\widetilde{y_1}\left(x\right),\widetilde{y_0}\right)\le \mathcal{K}\left|x-x_0\right|\le \mathcal{K}\delta =q$$

(3)

where $∆\left(f\left(x,\tilde{y}\right),\tilde{0}\right)=\mathcal{K}$. Hence $\left(x,\widetilde{y_1}\right)\in \mathcal{R}$. Next, we assume that ${\tilde{y}}_{n-1}\left(x\right)$ is levelwise continuous on $\left|x-x_0\right|\le \delta$ such that

$$\Delta \left(\widetilde{y_{n-1}}\left(x\right),\widetilde{y_0}\right)\le \mathcal{K}\left|x-x_0\right|\le \mathcal{K}\delta =q$$

and $\left(x,\widetilde{y_{n-1}}\right)\in \mathcal{R}$. From Definition 11, $\widetilde{y_n}\left(x\right)$ is levelwise continuous function on $\left|x-x_0\right|\le \delta$. Also, for any $\zeta ,\eta ,\theta \in \left[0,1\right]$

$$\mu \left({\left[\widetilde{y_n}\right]}_{\left(\zeta ,\eta ,\theta \right)},{\left[\widetilde{y_0}\right]}_{\left(\zeta ,\eta ,\theta \right)}\right)=\mu \left({\left[\widetilde{y_0}+{\int }_{x_0}^{x}f\left(z,\widetilde{y_{n-1}(z)}\right)dz\right]}_{\left(\zeta ,\eta ,\theta \right)},{\left[\widetilde{y_0}\right]}_{\left(\zeta ,\eta ,\theta \right)}\right)$$

$$=\mu \left({\left[\widetilde{y_0}\right]}_{\left(\zeta ,\eta ,\theta \right)}+{\left[{\int }_{x_0}^{x}f\left(z,\widetilde{y_{n-1}(z)}\right)dz\right]}_{\left(\zeta ,\eta ,\theta \right)},{\left[\widetilde{y_0}\right]}_{\left(\zeta ,\eta ,\theta \right)}\right)$$

$$=\mu \left({\left[{\int }_{x_0}^{x}f\left(z,\widetilde{y_{n-1}(z)}\right)dz\right]}_{\left(\zeta ,\eta ,\theta \right)},\tilde{0}\right)$$

$$\le {\int }_{x_0}^x\mu \left({\left[f\left(z,\widetilde{y_{n-1}(z)}\right)\right]}_{\left(\zeta ,\eta ,\theta \right)},\tilde{0}\right)dz$$

If we take $\left|x-x_0\right|\le \delta$ then from the definition of $\Delta$, we can obtain

$$\Delta \left(\widetilde{y_n(x)},\widetilde{y_0}\right)\le \mathcal{K}\left|x-x_0\right|\le \mathcal{K}\delta =q$$

for any $\left(x,\tilde{y}\right)\in \mathcal{R}$. Thus, $\left\{\widetilde{y_n(x)}\right\}$ is levelwise continuous function on $\left|x-x_0\right|\le \delta$ and $\left(x,\widetilde{y_n}\right)\in \mathcal{R}$ for all $n\in \mathbb{N}$ and $\left|x-x_0\right|\le \delta$. Again, for any $\zeta ,\eta ,\theta \hspace{0.17em}\in \left[0,1\right]$

$$\mu \left({\left[\widetilde{y_2(x)}\right]}_{\left(\zeta ,\eta ,\theta \right)},{\left[\widetilde{y_1(x)}\right]}_{\left(\zeta ,\eta ,\theta \right)}\right)$$

$$=\mu \left({\left[\widetilde{y_0}+{\int }_{x_0}^{x}f\left(z,\widetilde{y_1(z)}\right)dz\right]}_{\left(\zeta ,\eta ,\theta \right)},{\left[\widetilde{y_0}+{\int }_{x_0}^{x}f\left(z,\widetilde{y_0(z)}\right)dz\right]}_{\left(\zeta ,\eta ,\theta \right)}\right)$$

$$=\mu \left({\left[\widetilde{y_0}\right]}_{\left(\zeta ,\eta ,\theta \right)}+{\left[{\int }_{x_0}^{x}f\left(z,\widetilde{y_1(z)}\right)dz\right]}_{\left(\zeta ,\eta ,\theta \right)},{\left[\widetilde{y_0}\right]}_{\left(\zeta ,\eta ,\theta \right)}+{\left[{\int }_{x_0}^{x}f(z,\widetilde{y_0(z)})dz\right]}_{\left(\zeta ,\eta ,\theta \right)}\right)$$

$$=\mu \left({\left[{\int }_{x_0}^{x}f\left(z,\widetilde{y_1(z)}\right)dz\right]}_{\left(\zeta ,\eta ,\theta \right)},{\left[{\int }_{x_0}^{x}f\left(z,\widetilde{y_0(z)}\right)dz\right]}_{\left(\zeta ,\eta ,\theta \right)}\right)$$

$$\le {\int }_{x_0}^x\mu \left({\left[f\left(z,\widetilde{y_1(z)}\right)\right]}_{\left(\zeta ,\eta ,\theta \right)},{\left[f\left(z,\widetilde{y_0(z)}\right)\right]}_{\left(\zeta ,\eta ,\theta \right)}\right)dz$$

$$\le k{\int }_{x_0}^x\mu \left({\left[\widetilde{y_1\left(z\right)}\right]}_{\left(\zeta ,\eta ,\theta \right)},{\left[\widetilde{y_0\left(z\right)}\right]}_{\left(\zeta ,\eta ,\theta \right)}\right)dz$$

So,

$$\Delta \left(\widetilde{y_2}\left(x\right),\widetilde{y_1}(x)\right)\le {\int }_{x_0}^{x_1}k\Delta \left(\widetilde{y_1}\left(z\right),\widetilde{y_0}(z)\right)dz$$

(4)

By using Equation (3) in Equation (4) we attain,

$$\Delta \left(\widetilde{y_2}\left(x\right),\widetilde{y_1}(x)\right)\le \mathcal{K}k\frac{{\left|x-x_0\right|}^2}{2!}\le \mathcal{K}k\frac{{\delta }^2}{2!}$$

(5)

Next, we assume that

$$\Delta \left(\widetilde{y_n}\left(x\right),\widetilde{y_{n-1}}(x)\right)\le \mathcal{K}{k}^{n-1}\frac{{\left|x-x_0\right|}^n}{n!}\le \mathcal{K}{k}^{n-1}\frac{{\delta }^n}{n!}$$

(6)

Now, for any $\zeta ,\eta ,\theta \in \left[0,1\right]$,

$$\mu \left({\left[\widetilde{y_{n+1}}(x)\right]}_{\left(\zeta ,\eta ,\theta \right)},{\left[\widetilde{y_n(x)}\right]}_{\left(\zeta ,\eta ,\theta \right)}\right)$$

$$=\mu \left({\left[\widetilde{y_0}+{\int }_{x_0}^{x}f\left(z,\widetilde{y_n(z)}\right)dz\right]}_{\left(\zeta ,\eta ,\theta \right)},{\left[\widetilde{y_0}+{\int }_{x_0}^{x}f(z,\widetilde{y_{n-1}(z)})dz\right]}_{\left(\zeta ,\eta ,\theta \right)}\right)$$

$$=\mu \left({\left[\widetilde{y_0}\right]}_{\left(\zeta ,\eta ,\theta \right)}+{\left[{\int }_{x_0}^{x}f\left(z,\widetilde{y_n(z)}\right)dz\right]}_{\left(\zeta ,\eta ,\theta \right)},{\left[\widetilde{y_0}\right]}_{\left(\zeta ,\eta ,\theta \right)}+{\left[{\int }_{x_0}^{x}f(z,\widetilde{y_{n-1}(z)})dz\right]}_{\left(\zeta ,\eta ,\theta \right)}\right)$$

$$=\mu \left({\left[{\int }_{x_0}^{x}f\left(z,\widetilde{y_n(z)}\right)dz\right]}_{\left(\zeta ,\eta ,\theta \right)},{\left[{\int }_{x_0}^{x}f\left(z,\widetilde{y_{n-1}(z)}\right)dz\right]}_{\left(\zeta ,\eta ,\theta \right)}\right)$$

$$\le {\int }_{x_0}^x\mu \left({\left[f\left(z,\widetilde{y_n(z)}\right)\right]}_{\left(\zeta ,\eta ,\theta \right)},{\left[f\left(z,\widetilde{y_{n-1}(z)}\right)\right]}_{\left(\zeta ,\eta ,\theta \right)}\right)dz$$

$$\le k{\int }_{x_0}^x\mu \left({\left[\widetilde{y_n(z)}\right]}_{\left(\zeta ,\eta ,\theta \right)},{\left[\widetilde{y_{n-1}(z)}\right]}_{\left(\zeta ,\eta ,\theta \right)}\right)dz$$

So,

$$\Delta \left(\widetilde{y_{n+1}}\left(x\right),\widetilde{y_n}(x)\right)\le {\int }_{x_0}^{x}k\Delta \left(\widetilde{y_n}\left(z\right),\widetilde{y_{n-1}}(z)\right)dz$$

(7)

By using Equation (6) in the above equation, we attain,

$$\Delta \left(\widetilde{y_{n+1}}\left(x\right),\widetilde{y_n}(x)\right)\le \mathcal{K}{k}^n{\int }_{x_0}^x\frac{{\left|z-x_0\right|}^n}{n!}dz=\mathcal{K}{k}^n\frac{{\left|x-x_0\right|}^{n+1}}{\left(n+1\right)!}\le \mathcal{K}{k}^n\frac{{\delta }^{n+1}}{(n+1)!}$$

(8)

Thus,

$$\Delta \left(\widetilde{y_n}\left(x\right),\widetilde{y_{n-1}}(x)\right)\le \frac{\mathcal{K}}{k}\frac{{\left(k\delta \right)}^n}{n!}$$

(9)

for $n\in \mathbb{N}$ and $\left|x-x_0\right|\le \delta$. Since the series ${\sum }_{n=1}^{\infty }\frac{\mathcal{K}}{k}\frac{{\left(k\delta \right)}^n}{n!}$ is convergent, the series

$$\widetilde{y_0}\left(x\right)+\sum _{n=1}^{\infty }\left[\widetilde{y_n}\left(x\right)-\widetilde{y_{n-1}}\left(x\right)\right]$$

(10)

is convergent absolutely and uniformly in $\left|x-x_0\right|\le \delta$. Now,

$$\widetilde{y_n}\left(x\right)=\widetilde{y_0}\left(x\right)+\left[\widetilde{y_1}\left(x\right)-\widetilde{y_0}\left(x\right)\right]+\left[\widetilde{y_2}\left(x\right)-\widetilde{y_1}\left(x\right)\right]+\cdots +\left[\widetilde{y_n}\left(x\right)-\widetilde{y_{n-1}}\left(x\right)\right]$$

$$=\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l} \mathrm{s}\mathrm{u}\mathrm{m} \mathrm{o}\mathrm{f} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{s}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{e}\mathrm{s} (10)$$

and so, the sequence $\left\{\widetilde{y_n}\left(x\right)\right\}$ also converges uniformly in $\left|x-x_0\right|\le \delta$.

Since the series (10) has a general term $\widetilde{y_n}\left(x\right)-\widetilde{y_{n-1}}\left(x\right)$, from Equation (9) $\Delta \left(\widetilde{y_n}\left(x\right),\widetilde{y_{n-1}}(x)\right)\to 0$ uniformly on $\left|x-x_0\right|\le \delta$ as $n\to \infty$. So, $\exists$ a neutrosophic set-valued function $\tilde{y}:\mathcal{I}\to {\mathcal{N}}^n$ such that $\Delta \left(\widetilde{y_n}\left(x\right),\widetilde{y_{n-1}}(x)\right)\to 0$ uniformly on $\left|x-x_0\right|\le \delta$ as $n\to \infty$. Moreover, for any $\zeta ,\eta ,\theta \in \left[0,1\right]$,

$$\mu \left({\left[f(x,\widetilde{y_n}(x))\right]}_{\left(\zeta ,\eta ,\theta \right)},{\left[f(x,\tilde{y}(x))\right]}_{\left(\zeta ,\eta ,\theta \right)}\right)\le k\mu \left({\left[\widetilde{y_n}(x)\right]}_{\left(\zeta ,\eta ,\theta \right)},{\left[\tilde{y}(x)\right]}_{\left(\zeta ,\eta ,\theta \right)}\right)$$

(11)

From the definition of $\Delta$,

$$\Delta \left(f\left(x,\widetilde{y_n}\left(x\right)\right),f(x,\tilde{y}(x))\right)\le k\Delta \left(\widetilde{y_n}\left(x\right),\tilde{y}(x)\right)\to 0$$

(12)

uniformly on $\left|x-x_0\right|\le \delta$ as $n\to \infty$. Hence, from Theorem (2), we attain for $n\to \infty$

$$\widetilde{y(x)}=\widetilde{y_0}+{\int }_{x_0}^{x}f(z,\widetilde{y(z)})dz$$

(13)

This proves that $\widetilde{y(x)}$ is a solution of the neutrosophic differential Equation (1).

We now show that this solution is unique. If possible, let $\widetilde{y(x)}$ and $\widetilde{w(x)}$ be two solutions of (1) satisfying the initial conditions $\widetilde{y(x_0)}=\widetilde{y_0}$ and $\widetilde{w(x_0)}=\widetilde{y_0}$. Then, we have

$$\widetilde{y(x)}=\widetilde{y_0}+{\int }_{x_0}^{x}f(z,\widetilde{y(z)})dz$$

$$\widetilde{w(x)}=\widetilde{y_0}+{\int }_{x_0}^{x}f(z,\widetilde{w(z)})dz$$

For any $\zeta ,\eta ,\theta \in \left[0,1\right]$ and $n\in \mathbb{N}$,

$$\mu \left({\left[\widetilde{w(x)}\right]}_{\left(\zeta ,\eta ,\theta \right)},{\left[\widetilde{y_n}(x)\right]}_{\left(\zeta ,\eta ,\theta \right)}\right)$$

$$=\mu \left({\left[\widetilde{y_0}+{\int }_{x_0}^{x}f(z,\widetilde{w(z)})dz\right]}_{\left(\zeta ,\eta ,\theta \right)},{\left[\widetilde{y_0}+{\int }_{x_0}^{x}f(z,\widetilde{y_{n-1}}(z))dz\right]}_{\left(\zeta ,\eta ,\theta \right)}\right)$$

$$=\mu \left({\left[\widetilde{y_0}\right]}_{\left(\zeta ,\eta ,\theta \right)}+{\left[{\int }_{x_0}^{x}f\left(z,\widetilde{w(z)}\right)dz\right]}_{\left(\zeta ,\eta ,\theta \right)},{\left[\widetilde{y_0}\right]}_{\left(\zeta ,\eta ,\theta \right)}+{\left[{\int }_{x_0}^{x}f(z,\widetilde{y_{n-1}}(z))dz\right]}_{\left(\zeta ,\eta ,\theta \right)}\right)$$

$$=\mu \left({\left[{\int }_{x_0}^{x}f\left(z,\widetilde{w(z)}\right)dz\right]}_{\left(\zeta ,\eta ,\theta \right)},{\left[{\int }_{x_0}^{x}f\left(z,\widetilde{y_{n-1}}(z)\right)dz\right]}_{\left(\zeta ,\eta ,\theta \right)}\right)$$

$$\le {\int }_{x_0}^x\mu \left({\left[f\left(z,\widetilde{w(z)}\right)\right]}_{\left(\zeta ,\eta ,\theta \right)},{\left[f\left(z,\widetilde{y_{n-1}}(z)\right)\right]}_{\left(\zeta ,\eta ,\theta \right)}\right)dz$$

$$\le k{\int }_{x_0}^x\mu \left({\left[\widetilde{w(z)}\right]}_{\left(\zeta ,\eta ,\theta \right)},{\left[\widetilde{y_{n-1}}(z)\right]}_{\left(\zeta ,\eta ,\theta \right)}\right)dz$$

From the definition of $\Delta$, we attain,

$$\Delta \left(\widetilde{w(x)},\widetilde{y_n(x)}\right)\le {\int }_{x_0}^{x}k\Delta \left(\widetilde{w(z)},\widetilde{y_{n-1}(z)}\right)dz$$

(14)

For $n=1$,

$$\Delta \left(\widetilde{w(x)},\widetilde{y_1(x)}\right)\le {\int }_{x_0}^{x}k\Delta \left(\widetilde{w(z)},\widetilde{y_0(z)}\right)dz$$

(15)

On $\left|x-x_0\right|\le \delta$, $\Delta \left(\widetilde{w(z)},\widetilde{y_0}(z)\right)\le b$ and hence from (15), we attain,

$$\Delta \left(\widetilde{w(x)},\widetilde{y_1(x)}\right)\le bk\left|x-x_0\right|$$

(16)

Next, we assume on $\left|x-x_0\right|\le \delta$ that,

$$\Delta \left(\widetilde{w(x)},\widetilde{y_n(x)}\right)\le b{k}^n\frac{{\left|x-x_0\right|}^n}{n!}$$

(17)

Now,

$$\Delta \left(\widetilde{w(x)},\widetilde{y_{n+1}(x)}\right)\le {\int }_{x_0}^{x}k\Delta \left(\widetilde{w\left(z\right)},\widetilde{y_n(z)}\right)dz$$

(18)

Using the inequality (17) in (18), we attain

$$\Delta \left(\widetilde{w(x)},\widetilde{y_{n+1}(x)}\right)\le b{k}^{n+1}\frac{{\left|x-x_0\right|}^{n+1}}{(n+1)!}$$

(19)

Thus, by induction, we attain for any $n\in \mathbb{N}$

$$\Delta \left(\widetilde{w(x)},\widetilde{y_n(x)}\right)\le b{k}^n\frac{{\left|x-x_0\right|}^n}{n!}$$

(20)

on the interval $\left|x-x_0\right|\le \delta$. Since the series ${\sum }_{n=1}^{\mathrm{\infty }}{k}^n\frac{{\left|x-x_0\right|}^n}{n!}$ is convergent, we have $k^n\frac{{\left|x-x_0\right|}^n}{n!}\to 0$ as $n\to \mathrm{\infty }$. This implies that

$$\Delta \left(\widetilde{w(x)},\widetilde{y_n(x)}\right)=\Delta \left(\widetilde{y(x)},\widetilde{y_n(x)}\right)\to 0$$

on the interval $\left|x-x_0\right|\le \delta$ as $n\to \infty$. Thus, the uniqueness of the neutrosophic differential equation solution (1) has been proved. □

5. Manifestation of First-Order Linear Non-Homogeneous Neutrosophic Differential Equation in Different Cases

In this section, the solution strategy of the linear first-order non-homogeneous neutrosophic differential equation has been discussed, considering two types of generalized neutrosophic derivatives. A first-order linear non-homogeneous neutrosophic differential equation is taken in the form

$$\frac{d\tilde{y}(x)}{dx}=\tilde{A}\tilde{y}\left(x\right)+\tilde{B}$$

(21)

with the initial condition $\tilde{y}\left(0\right)=\tilde{\tau }$, where $\tilde{A}$, $\tilde{B}$ and $\tilde{\tau }$ are neutrosophic numbers. Suppose the parametric representation of $\tilde{A}$, $\tilde{B}$ and $\tilde{\tau }$ are given as

$${\tilde{A}}_{\left(\zeta ,\eta ,\theta \right)}=〈\left[A_1(\zeta ),A_2(\zeta )\right];\left[A_1(\eta ),A_2(\eta )\right];\left[A_1(\theta ),A_2(\theta )\right]〉$$

$${\tilde{B}}_{\left(\zeta ,\eta ,\theta \right)}=〈\left[B_1(\zeta ),B_2(\zeta )\right];\left[B_1(\eta ),B_2(\eta )\right];\left[B_1(\theta ),B_2(\theta )\right]〉$$

$${\tilde{\tau }}_{\left(\zeta ,\eta ,\theta \right)}=〈\left[{\tau }_1(\zeta ),{\tau }_2(\zeta )\right];\left[{\tau }_1(\eta ),{\tau }_2(\eta )\right];\left[{\tau }_1(\theta ),{\tau }_2(\theta )\right]〉$$

The existence of the solution is ensured by the preceding section. Based on the generalized neutrosophic differentiability of $\tilde{y}(x)$ of type 1 and type 2, two cases have been discussed.

5.1. When $\tilde{y}$ Is generalized Neutrosophic Differentiable of Type 1

The solution strategy of the Equation (21) is discussed through the $\left(\zeta ,\eta ,\theta \right)$-level representation. If we take the $\left(\zeta ,\eta ,\theta \right)$-cut of the neutrosophic differential Equation (21) and type 1 neutrosophic differentiability. Then, it gives the following components as

$$\frac{d{y}_1\left(x,\zeta \right)}{dx}=A_1\left(\zeta \right)y_1\left(x,\zeta \right)+B_1\left(\zeta \right)$$

(22)

$$\frac{d{y}_2\left(x,\zeta \right)}{dx}=A_2\left(\zeta \right)y_2\left(x,\zeta \right)+B_2\left(\zeta \right)$$

$$\frac{d{y}_1\left(x,\eta \right)}{dx}=A_1\left(\eta \right)y_1\left(x,\eta \right)+B_1(\eta )$$

$$\frac{d{y}_2\left(x,\eta \right)}{dx}=A_2\left(\eta \right)y_2\left(x,\eta \right)+B_2(\eta )$$

$$\frac{d{y}_1\left(x,\theta \right)}{dx}=A_1\left(\theta \right)y_1\left(x,\theta \right)+B_1(\theta )$$

$$\frac{d{y}_2\left(x,\theta \right)}{dx}=A_2\left(\theta \right)y_2\left(x,\theta \right)+B_2(\theta )$$

By solving the Equation (22), we obtain

$$y_1\left(x,,\zeta \right)e^{-A_1\left(\zeta \right)x}=-\frac{B_1\left(\zeta \right)}{A_1\left(\zeta \right)}{e}^{-A_1\left(\zeta \right)x}+c_1$$

Using the initial condition $y_1\left(0,\zeta \right)={\tau }_1(\zeta )$, we attain $c_1=\frac{B_1\left(\zeta \right)}{A_1\left(\zeta \right)}+{\tau }_1\left(\zeta \right)$. So, the solution is

$$y_1\left(x,\zeta \right)=\left(\frac{B_1\left(\zeta \right)}{A_1\left(\zeta \right)}+{\tau }_1\left(\zeta \right)\right)e^{A_1\left(\zeta \right)x}-\frac{B_1\left(\zeta \right)}{A_1\left(\zeta \right)}$$

Similarly, by solving the other equations, we obtain the solutions as

$$y_2\left(x,\zeta \right)=\left(\frac{B_2\left(\zeta \right)}{A_2\left(\zeta \right)}+{\tau }_2\left(\zeta \right)\right)e^{A_2\left(\zeta \right)x}-\frac{B_2\left(\zeta \right)}{A_2\left(\zeta \right)}$$

$$y_1\left(x,\eta \right)=\left(\frac{B_1\left(\eta \right)}{A_1\left(\eta \right)}+{\tau }_1\left(\eta \right)\right)e^{A_1\left(\eta \right)x}-\frac{B_1\left(\eta \right)}{A_1\left(\eta \right)}$$

$$y_2\left(x,\eta \right)=\left(\frac{B_2\left(\eta \right)}{A_2\left(\eta \right)}+{\tau }_2\left(\eta \right)\right)e^{A_2\left(\eta \right)x}-\frac{B_2\left(\eta \right)}{A_2\left(\eta \right)}$$

$$y_1\left(x,\theta \right)=\left(\frac{B_1\left(\theta \right)}{A_1\left(\theta \right)}+{\tau }_1\left(\theta \right)\right)e^{A_1\left(\theta \right)x}-\frac{B_1\left(\theta \right)}{A_1\left(\theta \right)}$$

$$y_2\left(x,\theta \right)=\left(\frac{B_2\left(\theta \right)}{A_2\left(\theta \right)}+{\tau }_2\left(\theta \right)\right)e^{A_2\left(\theta \right)x}-\frac{B_2\left(\theta \right)}{A_2\left(\theta \right)}$$

5.2. When $\tilde{\mathit{y}}$ Is Generalized Neutrosophic Differentiable of Type 2

If we take the $\left(\zeta ,\eta ,\theta \right)$-cut of the neutrosophic differential Equation (21) and type 2 neutrosophic differentiability. Then, it gives the following components as

$$\left\{\begin{array}{c}\frac{d{y}_2\left(x,\zeta \right)}{dx}=A_1\left(\zeta \right)y_1\left(x,\zeta \right)+B_1\left(\zeta \right)\\ \frac{d{y}_1\left(x,\zeta \right)}{dx}=A_2\left(\zeta \right)y_2\left(x,\zeta \right)+B_2\left(\zeta \right)\end{array}\right.$$

(23)

$$\left\{\begin{array}{c}\frac{d{y}_2\left(x,\eta \right)}{dx}=A_1\left(\eta \right)y_1\left(x,\eta \right)+B_1(\eta )\\ \frac{d{y}_1\left(x,\eta \right)}{dx}=A_2\left(\eta \right)y_2\left(x,\eta \right)+B_2(\eta )\end{array}\right.$$

(24)

$$\left\{\begin{array}{c}\frac{d{y}_2\left(x,\theta \right)}{dx}=A_1\left(\theta \right)y_1\left(x,\theta \right)+B_1(\theta )\\ \frac{d{y}_1\left(x,\theta \right)}{dx}=A_2\left(\theta \right)y_2\left(x,\theta \right)+B_2(\theta )\end{array}\right.$$

(25)

To solve the system (23) by Lagrange’s multiplier method, multiply the first equation by $\lambda$ and add with the second equation. By performing this, we attain

$$\frac{d}{dx}\left[y_1\left(x,\zeta \right)+\lambda y_2\left(x,\zeta \right)\right]=\lambda A_1\left(\zeta \right)\left\{y_1\left(x,\zeta \right)+\frac{A_2\left(\zeta \right)}{\lambda A_1\left(\zeta \right)}{y}_2\left(x,\zeta \right)+\frac{\lambda B_1\left(\zeta \right)+B_2\left(\zeta \right)}{\lambda A_1\left(\zeta \right)}\right\}$$

Choosing $\lambda$ such that $\lambda =\frac{A_2\left(\zeta \right)}{\lambda A_1\left(\zeta \right)}$. This gives two different values of $\lambda$ as $\sqrt{\frac{A_2\left(\zeta \right)}{A_1\left(\zeta \right)}}={\lambda }_1$, say and $-\sqrt{\frac{A_2\left(\zeta \right)}{A_1\left(\zeta \right)}}={\lambda }_2$, say. Then, the above equation becomes

$$\frac{dz(x)}{dx}=\lambda A_1\left(\zeta \right)z(x), \mathrm{where} z\left(x\right)=y_1\left(x,\zeta \right)+\lambda y_2\left(x,\zeta \right)+\frac{\lambda B_1\left(\zeta \right)+B_2\left(\zeta \right)}{\lambda A_1\left(\zeta \right)}$$

Then, $z\left(x\right)=k{e}^{\lambda A_1\left(\zeta \right)x}$

$$y_1\left(x,\zeta \right)+\lambda y_2\left(x,\zeta \right)+\frac{\lambda B_1\left(\zeta \right)+B_2\left(\zeta \right)}{\lambda A_1\left(\zeta \right)}=k{e}^{\lambda A_1\left(\zeta \right)x}$$

From the initial conditions $y_1\left(0,\zeta \right)={\tau }_1(\zeta )$ and $y_2\left(0,\zeta \right)={\tau }_2(\zeta )$, we attain

$$k={\tau }_1(\zeta )+\lambda {\tau }_2(\zeta )+\frac{\lambda B_1\left(\zeta \right)+B_2\left(\zeta \right)}{\lambda A_1\left(\zeta \right)}$$

Then, the solution is

$$y_1\left(x,\zeta \right)+\lambda y_2\left(x,\zeta \right)=\left({\tau }_1(\zeta )+\lambda {\tau }_2(\zeta )+\frac{\lambda B_1\left(\zeta \right)+B_2\left(\zeta \right)}{\lambda A_1\left(\zeta \right)}\right)e^{\lambda A_1\left(\zeta \right)x}-\frac{\lambda B_1\left(\zeta \right)+B_2\left(\zeta \right)}{\lambda A_1\left(\zeta \right)}$$

For two values of ${\lambda }_1$ and ${\lambda }_2$, we attain two simultaneous equations

$$y_1\left(x,\zeta \right)+{\lambda }_1{y}_2\left(x,\zeta \right)=k_1{e}^{{\lambda }_1{A}_1\left(\zeta \right)x}-l_1$$

(26)

$$y_1\left(x,\zeta \right)+{\lambda }_2{y}_2\left(x,\zeta \right)=k_2{e}^{{\lambda }_2{A}_1\left(\zeta \right)x}-l_2$$

(27)

where, $k_1={\tau }_1(\zeta )+{\lambda }_1{\tau }_2(\zeta )+\frac{{\lambda }_1{B}_1\left(\zeta \right)+B_2\left(\zeta \right)}{{\lambda }_1{A}_1\left(\zeta \right)}$, $l_1=\frac{{\lambda }_1{B}_1\left(\zeta \right)+B_2\left(\zeta \right)}{{\lambda }_1{A}_1\left(\zeta \right)}$, $k_2={\tau }_1(\zeta )+{\lambda }_2{\tau }_2(\zeta )+\frac{{\lambda }_2{B}_1\left(\zeta \right)+B_2\left(\zeta \right)}{{\lambda }_2{A}_1\left(\zeta \right)}$ and $l_2=\frac{{\lambda }_2{B}_1\left(\zeta \right)+B_2\left(\zeta \right)}{{\lambda }_2{A}_1\left(\zeta \right)}$. Solving the Equations (26) and (27) for $y_1\left(x,\zeta \right)$ and $y_2\left(x,\zeta \right)$, we attain

$$y_1\left(x,\zeta \right)=\frac{k_1{\lambda }_2{e}^{{\lambda }_1{A}_1\left(\zeta \right)x}-k_2{\lambda }_1{e}^{{\lambda }_2{A}_1\left(\zeta \right)x}}{{\lambda }_2-{\lambda }_1}+\frac{{\lambda }_1{l}_2-{\lambda }_2{l}_1}{{\lambda }_2-{\lambda }_1}$$

$$y_2\left(x,\zeta \right)=\frac{k_1{e}^{{\lambda }_1{A}_1\left(\zeta \right)x}-k_2{e}^{{\lambda }_2{A}_1\left(\zeta \right)x}}{{\lambda }_1-{\lambda }_2}+\frac{l_2-l_1}{{\lambda }_1-{\lambda }_2}$$

Similarly, by solving the systems (24) by Lagrange’s multiplier method, we attain

$$y_1\left(x,\eta \right)=\frac{k_3{\lambda }_4{e}^{{\lambda }_3{A}_1\left(\eta \right)x}-k_4{\lambda }_3{e}^{{\lambda }_4{A}_1\left(\eta \right)x}}{{\lambda }_4-{\lambda }_3}+\frac{{\lambda }_3{l}_4-{\lambda }_4{l}_3}{{\lambda }_4-{\lambda }_3}$$

$$y_2\left(x,\eta \right)=\frac{k_3{e}^{{\lambda }_3{A}_1\left(\eta \right)x}-k_4{e}^{{\lambda }_4{A}_3\left(\eta \right)x}}{{\lambda }_3-{\lambda }_4}+\frac{l_4-l_3}{{\lambda }_3-{\lambda }_4}$$

where, ${\lambda }_3=\sqrt{\frac{A_2\left(\eta \right)}{A_1\left(\eta \right)}}$, ${\lambda }_4=-\sqrt{\frac{A_2\left(\eta \right)}{A_1\left(\eta \right)}}$, $k_3={\tau }_1(\eta )+{\lambda }_3{\tau }_2(\eta )+\frac{{\lambda }_3{B}_1\left(\eta \right)+B_2\left(\eta \right)}{{\lambda }_3{A}_1\left(\eta \right)}$, $l_3=\frac{{\lambda }_3{B}_1\left(\eta \right)+B_2\left(\eta \right)}{{\lambda }_3{A}_1\left(\eta \right)}$, $k_4={\tau }_1(\eta )+{\lambda }_4{\tau }_2(\eta )+\frac{{\lambda }_4{B}_1\left(\eta \right)+B_2\left(\eta \right)}{{\lambda }_4{A}_1\left(\eta \right)}$ and $l_4=\frac{{\lambda }_4{B}_1\left(\eta \right)+B_2\left(\eta \right)}{{\lambda }_4{A}_1\left(\eta \right)}$. Similarly, by solving (25), we attain

$$y_1\left(x,\theta \right)=\frac{k_5{\lambda }_6{e}^{{\lambda }_5{A}_1\left(\theta \right)x}-k_6{\lambda }_5{e}^{{\lambda }_6{A}_1\left(\theta \right)x}}{{\lambda }_6-{\lambda }_5}+\frac{{\lambda }_5{l}_6-{\lambda }_6{l}_5}{{\lambda }_6-{\lambda }_5}$$

$$y_2\left(x,\theta \right)=\frac{k_5{e}^{{\lambda }_5{A}_1\left(\theta \right)x}-k_6{e}^{{\lambda }_6{A}_1\left(\theta \right)x}}{{\lambda }_5-{\lambda }_6}+\frac{l_6-l_5}{{\lambda }_5-{\lambda }_6}$$

where, ${\lambda }_5=\sqrt{\frac{A_2\left(\theta \right)}{A_1\left(\theta \right)}}$, say and ${\lambda }_4=-\sqrt{\frac{A_2\left(\theta \right)}{A_1\left(\theta \right)}}$, $k_5={\tau }_1(\theta )+{\lambda }_5{\tau }_2(\theta )+\frac{{\lambda }_5{B}_1\left(\theta \right)+B_2\left(\theta \right)}{{\lambda }_5{A}_1\left(\theta \right)}$, $l_3=\frac{{\lambda }_5{B}_1\left(\theta \right)+B_2\left(\theta \right)}{{\lambda }_5{A}_1\left(\theta \right)}$, $k_6={\tau }_1(\theta )+{\lambda }_6{\tau }_2(\theta )+\frac{{\lambda }_6{B}_1\left(\theta \right)+B_2\left(\theta \right)}{{\lambda }_6{A}_1\left(\theta \right)}$ and $l_6=\frac{{\lambda }_6{B}_1\left(\theta \right)+B_2\left(\theta \right)}{{\lambda }_6{A}_1\left(\theta \right)}$.

6. Inventory Control Problem as an Application

In this section, an economic order quantity (EOQ) model was taken using neutrosophic uncertainty to check the applicability of a first-order neutrosophic differential equation.

6.1. Notations

The following notations are taken to discuss the proposed model as an application of the neutrosophic initial value problem.

Table 2. Notations and their meanings in the article.

Notations	Descriptions
$a$	Constant part of market demand rate
$p$	Selling price per unit
$b$	Price sensitivity in demand rate
$t_w$	Warrantee time of items
$c$	Sensitivity of warrantee time in demand rate
$d$	Sensitivity of stock level in demand rate
$Q$	Initial stock level
$K$	Per cycle setup cost
$m$	Purchase cost per unit
$h_c$	Per unit holding cost
$I(t)$	Stock level at time $t$ (objective function)
$T$	Complete inventory cycle time (decision variable)

represents the meanings of the nations used in the article.

6.2. Hypothesis

• A hike in selling price can negatively impact the demand. The demand can be increased when the selling price is lowered. The demand can be proportional to the warranty time, as the demand can be boosted by enhancing the warranty period. In addition, the stocks in the showroom can induce additional demand. Thus, the demand is a linear function of warrantee time, price, and stock, i.e., $D(t)=a-bp+c{t}_w+dI(t)$, in which $a>0$ is the demand potential, $p>0$ is the selling price, $t_w>0$ is the warranty time, and $I(t)$ is the stock level at that moment.
• Lead time is zero.
• No shortage is allowed.
• Deterioration is not allowed.
• The lot size is finite, but the replenishment rate is infinite
• The time horizon is finite.

6.3. Formulation of the Model

Suppose $Q$ is the initial stock level of an EOQ model. The stock level experienced a continuous decrease throughout the entire time span due to customer demand. After this gradual decline, the inventory level reaches zero at the end of each lot cycle, i.e., at $t=T$. The following differential equation represents this model.

$$\frac{dI(t)}{dt}=-\left\{a-bp+c{t}_w+I(t)d\right\}$$

(28)

with $I\left(0\right)=Q$ and $I\left(T\right)=0$.

Solving (28) and using $I(T)=0$ we attain

$$I\left(t\right)=\frac{a-bp+c{t}_w}{d}\left\{e^{d\left(T-t\right)}-1\right\}$$

(29)

and using the condition $I\left(0\right)=Q$ we attain the initial stock level

$$Q=\frac{a-bp+c{t}_w}{d}\left\{e^{dT}-1\right\}$$

(30)

Holding cost (HC): The cumulative holding cost incurred overall retail activities within the period $[0,T]$ is calculated as follows:

$$HC=h_c{\int }_0^{T}I\left(t\right)dt=h_c{\int }_0^T\frac{a-bp+c{t}_w}{d}\left\{e^{d\left(T-t\right)}-1\right\}dt$$

$$=\frac{h_c(a-bp+c{t}_w)}{d^2}\left[e^{dT}-dT-1\right]$$

Purchase cost (PC): The overall expense associated with the purchasing of $Q$ items is determined by the following formula:

$$PC=mQ=\frac{m\left(a-bp+c{t}_w\right)}{d}\left\{e^{dT}-1\right\}$$

The cumulative cost is a summation of all potential costs. Consequently, the average total cost is acquired by dividing the cumulative cost by the cycle duration in the following manner.

$$G=\frac{K+HC+PC}{T}$$

So, the optimization problem is

$$\left\{\begin{array}{c}Min Z\\ Subject to (30)\\ 0\le t\le T\end{array}\right.$$

(31)

6.4. EOQ Model in Neutrosophic Environment

Let us assume that the crisp parameters $a$, $b$, $c,$ and $d$ are single-valued neutrosophic numbers. The neutrosophic numbers and the neutrosophic valued functions have their distinct arithmetic and calculus, respectively. The de-neutrosophication of the neutrosophic valued inputs and replacement of them in a crisp model is not a good idea in this regard. Because the model in the neutrosophic environment then becomes identical with the crisp representee except for little changes in the numerical values of the inputs. The utilization of neutrosophic calculus may be the best mathematical tool to describe the order quantity model in neutrosophic decision-making phenomena. Therefore, the model governed by the differential Equation (28) can be transformed into a neutrosophic uncertain environment, and this can be displayed through the neutrosophic differential equation as

$$\frac{d\widetilde{I\left(t\right)}}{dt}=-\left\{\tilde{a}-\tilde{b}p+\tilde{c}{t}_w+\tilde{d}\widetilde{I\left(t\right)}\right\}$$

(32)

with $\widetilde{I\left(0\right)}=\tilde{Q}$ and $\widetilde{I\left(T\right)}=0$.

6.4.1. When $\widetilde{\mathit{I}\left(\mathit{t}\right)}$ Is Type 1 Neutrosophic Differentiable (Case 1)

By taking $(\zeta ,\eta ,\theta )$-level of $\tilde{a}$, $\tilde{b}$, $\tilde{c}$, $\tilde{d}$ and applying the type 1 generalized neutrosophic differentiability of $\widetilde{I\left(t\right)}$, we attain the following components as a differential equation for $\widetilde{I\left(t\right)}$.

$$\frac{d{I}_1\left(t,\zeta \right)}{dt}=-a_2(\zeta )+b_1\left(\zeta \right)p-c_2\left(\zeta \right)t_w-d_2\left(\zeta \right)I_2\left(t,\zeta \right)$$

(33)

$$\frac{d{I}_2\left(t,\zeta \right)}{dt}=-a_1(\zeta )+b_2\left(\zeta \right)p-c_1\left(\zeta \right)t_w-d_1\left(\zeta \right)I_1\left(t,\zeta \right)$$

(34)

$$\frac{d{I}_1\left(t,\eta \right)}{dt}=-a_2(\eta )+b_1\left(\eta \right)p-c_2\left(\eta \right)t_w-d_2\left(\eta \right)I_2\left(t,\eta \right)$$

(35)

$$\frac{d{I}_2\left(t,\eta \right)}{dt}=-a_1(\eta )+b_2\left(\eta \right)p-c_1\left(\eta \right)t_w-d_1\left(\eta \right)I_1\left(t,\eta \right)$$

(36)

$$\frac{d{I}_1\left(t,\theta \right)}{dt}=-a_2(\theta )+b_1\left(\theta \right)p-c_2\left(\theta \right)t_w-d_2\left(\theta \right)I_2\left(t,\theta \right)$$

(37)

$$\frac{d{I}_2\left(t,\theta \right)}{dt}=-a_1(\theta )+b_2\left(\theta \right)p-c_1\left(\theta \right)t_w-d_1\left(\theta \right)I_1\left(t,\theta \right)$$

(38)

From Equations (33) and (34), we attain

$$\left\{\begin{array}{c}\frac{d{I}_1\left(t,\zeta \right)}{dt}=-d_2\left(\zeta \right)I_2\left(t,\zeta \right)-u_1\\ \frac{d{I}_2\left(t,\zeta \right)}{dt}=-d_1\left(\zeta \right)I_1\left(t,\zeta \right)-u_2\\ I_1\left(T,\zeta \right)=0=I_2\left(T,\zeta \right)\end{array}\right.$$

(39)

where $u_1=a_2(\zeta )-b_1\left(\zeta \right)p+c_2\left(\zeta \right)t_w$, $u_2=a_1(\zeta )-b_2\left(\zeta \right)p+c_1\left(\zeta \right)t_w$.

Now, we solve the system (39) by applying Lagrange’s multiplier method. Multiplying the second Equation of (39) by $\mu$ and adding with the first, we attain

$$\frac{d}{dt}\left[I_1\left(t,\zeta \right)+\mu I_2\left(t,\zeta \right)\right]=-\mu d_1\left(\zeta \right)I_1\left(t,\zeta \right)-d_2\left(\zeta \right)I_2\left(t,\zeta \right)-u_1-\mu u_2$$

$$\mathrm{i}.\mathrm{e}., \frac{d}{dt}\left[I_1\left(t,\zeta \right)+\mu I_2\left(t,\zeta \right)\right]=-\mu d_1\left(\zeta \right)\left\{I_1\left(t,\zeta \right)+\frac{d_2\left(\zeta \right)}{\mu d_1\left(\zeta \right)}{I}_2\left(t,\zeta \right)\right\}-\left(u_1+\mu u_2\right)$$

(40)

Choosing $\mu$ in a manner that $\frac{d_2\left(\zeta \right)}{\mu d_1\left(\zeta \right)}=\mu$, which gives two different values of $\mu$, say ${\mu }_1=+\sqrt{\frac{d_2\left(\zeta \right)}{d_1\left(\zeta \right)}}$ and ${\mu }_2=-\sqrt{\frac{d_2\left(\zeta \right)}{d_1\left(\zeta \right)}}=-{\mu }_1$ and the Equation (40) becomes

$$\frac{d}{dt}\left[I_1\left(t,\zeta \right)+\mu I_2\left(t,\zeta \right)\right]=-\mu d_1\left(\zeta \right)\left\{I_1\left(t,\zeta \right)+\mu I_2\left(t,\zeta \right)+\frac{\left(u_1+\mu u_2\right)}{\mu d_1\left(\zeta \right)}\right\}$$

$$\mathrm{Or}, \frac{du\left(t\right)}{dt}=-\mu d_1\left(\zeta \right)u\left(t\right), \mathrm{where} u\left(t\right)=I_1\left(t,\zeta \right)+\mu I_2\left(t,\zeta \right)+\frac{\left(u_1+\mu u_2\right)}{\mu d_1\left(\zeta \right)}$$

$$\mathrm{or}, u\left(t\right)=B{e}^{-\mu d_1\left(\zeta \right)t}$$

$$I_1\left(t,\zeta \right)+\mu I_2\left(t,\zeta \right)+\frac{\left(u_1+\mu u_2\right)}{\mu d_1\left(\zeta \right)}=B{e}^{-\mu d_1\left(\zeta \right)t}$$

This satisfies the initial conditions $I_1\left(T,\zeta \right)=0$ and $I_2\left(T,\zeta \right)=0$.

$$I_1\left(t,\zeta \right)+\mu I_2\left(t,\zeta \right)=\frac{\left(u_1+\mu u_2\right)}{\mu d_1\left(\zeta \right)}\left(e^{\mu d_1\left(\zeta \right)\left(T-t\right)}-1\right)$$

For two values ${\mu }_1$ and $-{\mu }_1$, we attain two simultaneous equations

$$I_1\left(t,\zeta \right)+{\mu }_1{I}_2\left(t,\zeta \right)=M_1\left(e^{{\mu }_1{d}_1\left(\zeta \right)\left(T-t\right)}-1\right)$$

(41)

$$I_1\left(t,\zeta \right)-{\mu }_1{I}_2\left(t,\zeta \right)=M_2\left(e^{-{\mu }_1{d}_1\left(\zeta \right)\left(T-t\right)}-1\right)$$

(42)

where $M_1=\frac{\left(u_1+{\mu }_1{u}_2\right)}{{\mu }_1{d}_1\left(\zeta \right)}$ and $M_2=-\frac{\left(u_1-{\mu }_1{u}_2\right)}{{\mu }_1{d}_1\left(\zeta \right)}$.

Solving the Equations (41) and (42) for $I_1\left(t,\zeta \right)$ and $I_2\left(t,\zeta \right)$ we attain,

$$I_1\left(t,\zeta \right)=\frac{M_1\left(e^{{\mu }_1{d}_1\left(\zeta \right)\left(T-t\right)}-1\right)+M_2\left(e^{-{\mu }_1{d}_1\left(\zeta \right)\left(T-t\right)}-1\right)}{2}$$

$$I_2\left(t,\zeta \right)=\frac{M_1\left(e^{{\mu }_1{d}_1\left(\zeta \right)\left(T-t\right)}-1\right)-M_2\left(e^{-{\mu }_1{d}_1\left(\zeta \right)\left(T-t\right)}-1\right)}{2{\mu }_1}$$

By using the initial condition $I_1\left(0,\zeta \right)=Q_1(\zeta )$ and $I_2\left(0,\zeta \right)=Q_2(\zeta )$ in the above equations, we obtained the lot size.

$$Q_1(\zeta )=\frac{M_1\left(e^{{\mu }_1{d}_1\left(\zeta \right)T}-1\right)+M_2\left(e^{-{\mu }_1{d}_1\left(\zeta \right)T}-1\right)}{2}$$

(43)

$$Q_2(\zeta )=\frac{M_1\left(e^{{\mu }_1{d}_1\left(\zeta \right)T}-1\right)-M_2\left(e^{-{\mu }_1{d}_1\left(\zeta \right)T}-1\right)}{2{\mu }_1}$$

(44)

Similarly, by solving systems (35) and (36) with the same approach, we attain

$$I_1\left(t,\eta \right)=\frac{M_3\left(e^{{\mu }_3{d}_1\left(\eta \right)\left(T-t\right)}-1\right)+M_4\left(e^{-{\mu }_3{d}_1\left(\eta \right)\left(T-t\right)}-1\right)}{2}$$

$$I_2\left(t,\eta \right)=\frac{M_3\left(e^{{\mu }_3{d}_1\left(\eta \right)\left(T-t\right)}-1\right)-M_4\left(e^{-{\mu }_3{d}_1\left(\eta \right)\left(T-t\right)}-1\right)}{2{\mu }_3}$$

where ${\mu }_3=\sqrt{\frac{d_2\left(\eta \right)}{d_1\left(\eta \right)}}$, $M_3=\frac{\left(u_3+{\mu }_3{u}_4\right)}{{\mu }_3{d}_1\left(\eta \right)}$, $M_4=-\frac{\left(u_3-{\mu }_3{u}_4\right)}{{\mu }_3{d}_1\left(\eta \right)}$, $u_3=a_2\left(\eta \right)-b_1\left(\eta \right)p+c_2\left(\eta \right)t_w$ and $u_4=a_1\left(\eta \right)-b_2\left(\eta \right)p+c_1\left(\eta \right)t_w$.

By using the initial condition $I_1\left(0,\eta \right)=Q_1(\eta )$ and $I_2\left(0,\eta \right)=Q_2(\eta )$ in the above equations, we obtained the lot size.

$$Q_1(\eta )=\frac{M_3\left(e^{{\mu }_3{d}_1\left(\eta \right)T}-1\right)+M_4\left(e^{-{\mu }_3{d}_1\left(\eta \right)T}-1\right)}{2}$$

(45)

$$Q_2(\eta )=\frac{M_3\left(e^{{\mu }_3{d}_1\left(\eta \right)T}-1\right)-M_4\left(e^{-{\mu }_3{d}_1\left(\eta \right)T}-1\right)}{2{\mu }_3}$$

(46)

Solutions of the system (37) and (38) are obtained as follows

$$I_1\left(t,\theta \right)=\frac{M_5\left(e^{{\mu }_5{d}_1\left(\theta \right)\left(T-t\right)}-1\right)+M_6\left(e^{-{\mu }_5{d}_1\left(\theta \right)\left(T-t\right)}-1\right)}{2}$$

$$I_2\left(t,\theta \right)=\frac{M_5\left(e^{{\mu }_5{d}_1\left(\theta \right)\left(T-t\right)}-1\right)-M_6\left(e^{-{\mu }_5{d}_1\left(\theta \right)\left(T-t\right)}-1\right)}{2{\mu }_5}$$

where ${\mu }_5=\sqrt{\frac{d_2\left(\theta \right)}{d_1\left(\theta \right)}}$, $M_5=\frac{\left(u_5+{\mu }_5{u}_6\right)}{{\mu }_5{d}_1\left(\theta \right)}$, $M_6=-\frac{\left(u_5-{\mu }_5{u}_6\right)}{{\mu }_5{d}_1\left(\theta \right)}$, $u_5=a_2\left(\theta \right)-b_1\left(\theta \right)p+c_2\left(\theta \right)t_w$ and $u_6=a_1\left(\theta \right)-b_2\left(\theta \right)p+c_1\left(\theta \right)t_w$.

By using the initial condition $I_1\left(0,\theta \right)=Q_1(\theta )$ and $I_2\left(0,\theta \right)=Q_2(\theta )$ in the above equations, we obtained the lot size.

$$Q_1(\theta )=\frac{M_5\left(e^{{\mu }_5{d}_1\left(\theta \right)T}-1\right)+M_6\left(e^{-{\mu }_5{d}_1\left(\theta \right)T}-1\right)}{2}$$

(47)

$$Q_2(\theta )=\frac{M_5\left(e^{{\mu }_5{d}_1\left(\theta \right)T}-1\right)-M_6\left(e^{-{\mu }_5{d}_1\left(\theta \right)T}-1\right)}{2{\mu }_5}$$

(48)

Here, several inventory-related costs are obtained.

Holding cost (HC): Inventory holding cost $\widetilde{\mathrm{H}\mathrm{C}}=〈\left[\mathrm{H}{\mathrm{C}}_1\left(\zeta \right),\mathrm{H}{\mathrm{C}}_2(\zeta )\right],\left[\mathrm{H}{\mathrm{C}}_1\left(\eta \right),\mathrm{H}{\mathrm{C}}_2(\eta )\right],\left[\mathrm{H}{\mathrm{C}}_1\left(\theta \right),\mathrm{H}{\mathrm{C}}_2(\theta )\right]〉$ of a cycle is given as

$$\mathrm{H}{\mathrm{C}}_1\left(\zeta \right)={\mathrm{h}}_{\mathrm{c}}{\int }_0^{\mathrm{T}}{\mathrm{I}}_1\left(\mathrm{t},\zeta \right)\mathrm{d}\mathrm{t}$$

$$\mathrm{H}{\mathrm{C}}_1\left(\zeta \right)=\frac{{\mathrm{h}}_{\mathrm{c}}}{2{\mu }_1{\mathrm{d}}_1(\zeta )}\left[{\mathrm{M}}_1\left({\mathrm{e}}^{{\mu }_1{\mathrm{d}}_1(\zeta )\mathrm{T}}-{\mu }_1{\mathrm{d}}_1\left(\zeta \right)\mathrm{T}-1\right)-{\mathrm{M}}_2\left({\mathrm{e}}^{-{\mu }_1{\mathrm{d}}_1(\zeta )\mathrm{T}}+{\mu }_1{\mathrm{d}}_1\left(\zeta \right)\mathrm{T}-1\right)\right]$$

$$\mathrm{H}{\mathrm{C}}_2\left(\zeta \right)={\mathrm{h}}_{\mathrm{c}}{\int }_0^{\mathrm{T}}{\mathrm{I}}_2\left(\mathrm{t},\zeta \right)\mathrm{d}\mathrm{t}$$

$$\mathrm{H}{\mathrm{C}}_2\left(\zeta \right)=\frac{{\mathrm{h}}_{\mathrm{c}}}{2{\mu }_1^2{\mathrm{d}}_1(\zeta )}\left[{\mathrm{M}}_1\left({\mathrm{e}}^{{\mu }_1{\mathrm{d}}_1(\zeta )\mathrm{T}}-{\mu }_1{\mathrm{d}}_1\left(\zeta \right)\mathrm{T}-1\right)+{\mathrm{M}}_2\left({\mathrm{e}}^{-{\mu }_1{\mathrm{d}}_1(\zeta )\mathrm{T}}+{\mu }_1{\mathrm{d}}_1\left(\zeta \right)\mathrm{T}-1\right)\right]$$

$$\mathrm{H}{\mathrm{C}}_1\left(\eta \right)={\mathrm{h}}_{\mathrm{c}}{\int }_0^{\mathrm{T}}{\mathrm{I}}_1\left(\mathrm{t},\eta \right)\mathrm{d}\mathrm{t}$$

$$\mathrm{H}{\mathrm{C}}_1\left(\eta \right)=\frac{{\mathrm{h}}_{\mathrm{c}}}{2{\mu }_3{\mathrm{d}}_1(\eta )}\left[{\mathrm{M}}_3\left({\mathrm{e}}^{{\mu }_3{\mathrm{d}}_1(\eta )\mathrm{T}}-{\mu }_3{\mathrm{d}}_1\left(\eta \right)\mathrm{T}-1\right)-{\mathrm{M}}_4\left({\mathrm{e}}^{-{\mu }_3{\mathrm{d}}_1(\eta )\mathrm{T}}+{\mu }_3{\mathrm{d}}_1\left(\eta \right)\mathrm{T}-1\right)\right]$$

$$\mathrm{H}{\mathrm{C}}_2\left(\eta \right)={\mathrm{h}}_{\mathrm{c}}{\int }_0^{\mathrm{T}}{\mathrm{I}}_2\left(\mathrm{t},\eta \right)\mathrm{d}\mathrm{t}$$

$$\mathrm{H}{\mathrm{C}}_2\left(\eta \right)=\frac{{\mathrm{h}}_{\mathrm{c}}}{2{\mu }_3^2{\mathrm{d}}_1(\eta )}\left[{\mathrm{M}}_3\left({\mathrm{e}}^{{\mu }_3{\mathrm{d}}_1(\eta )\mathrm{T}}-{\mu }_3{\mathrm{d}}_1\left(\eta \right)\mathrm{T}-1\right)+{\mathrm{M}}_4\left({\mathrm{e}}^{-{\mu }_3{\mathrm{d}}_1(\eta )\mathrm{T}}+{\mu }_3{\mathrm{d}}_1\left(\eta \right)\mathrm{T}-1\right)\right]$$

$$\mathrm{H}{\mathrm{C}}_1\left(\theta \right)={\mathrm{h}}_{\mathrm{c}}{\int }_0^{\mathrm{T}}{\mathrm{I}}_1\left(\mathrm{t},\theta \right)\mathrm{d}\mathrm{t}$$

$$\mathrm{H}{\mathrm{C}}_1\left(\theta \right)=\frac{{\mathrm{h}}_{\mathrm{c}}}{2{\mu }_5{\mathrm{d}}_1(\theta )}\left[{\mathrm{M}}_5\left({\mathrm{e}}^{{\mu }_5{\mathrm{d}}_1(\theta )\mathrm{T}}-{\mu }_5{\mathrm{d}}_1\left(\theta \right)\mathrm{T}-1\right)-{\mathrm{M}}_6\left({\mathrm{e}}^{-{\mu }_5{\mathrm{d}}_1(\theta )\mathrm{T}}+{\mu }_5{\mathrm{d}}_1\left(\theta \right)\mathrm{T}-1\right)\right]$$

$$\mathrm{H}{\mathrm{C}}_2\left(\theta \right)={\mathrm{h}}_{\mathrm{c}}{\int }_0^{\mathrm{T}}{\mathrm{I}}_2\left(\mathrm{t},\theta \right)\mathrm{d}\mathrm{t}$$

$$\mathrm{H}{\mathrm{C}}_2\left(\theta \right)=\frac{{\mathrm{h}}_{\mathrm{c}}}{2{\mu }_5^2{\mathrm{d}}_1(\theta )}\left[{\mathrm{M}}_5\left({\mathrm{e}}^{{\mu }_5{\mathrm{d}}_1(\theta )\mathrm{T}}-{\mu }_5{\mathrm{d}}_1\left(\theta \right)\mathrm{T}-1\right)+{\mathrm{M}}_6\left({\mathrm{e}}^{-{\mu }_5{\mathrm{d}}_1(\theta )\mathrm{T}}+{\mu }_5{\mathrm{d}}_1\left(\theta \right)\mathrm{T}-1\right)\right]$$

Purchasing cost (PC): the total purchasing cost $\widetilde{PC}=〈\left[P{C}_1\left(\zeta \right),P{C}_2(\zeta )\right],\left[P{C}_1\left(\eta \right),P{C}_2(\eta )\right],\left[P{C}_1\left(\theta \right),P{C}_2(\theta )\right]〉$ is given by $P{C}_1\left(\zeta \right)=m{Q}_1(\zeta )$, $P{C}_2\left(\zeta \right)=m{Q}_2(\zeta )$, $P{C}_1\left(\eta \right)=m{Q}_1(\eta )$, $P{C}_2\left(\eta \right)=m{Q}_2(\eta )$, $P{C}_1\left(\theta \right)=m{Q}_1(\theta )$ and $P{C}_2\left(\theta \right)=m{Q}_2(\theta )$.

Therefore, the total average cost of a complete inventory cycle can be obtained in the parametric form $\tilde{G}=〈\left[G_1\left(\zeta \right),G_2(\zeta )\right],\left[G_1\left(\eta \right),G_2(\eta )\right],\left[G_1\left(\theta \right),G_2(\theta )\right]〉$, where $G_1\left(\zeta \right)=\frac{K+H{C}_1\left(\zeta \right)+P{C}_1(\zeta )}{T}$, $G_2\left(\zeta \right)=\frac{K+H{C}_2\left(\zeta \right)+P{C}_2(\zeta )}{T}$, $G_1\left(\eta \right)=\frac{K+H{C}_1\left(\eta \right)+P{C}_1(\eta )}{T}$, $G_2\left(\eta \right)=\frac{K+H{C}_2\left(\eta \right)+P{C}_2(\eta )}{T}$, $G_1\left(\theta \right)=\frac{K+H{C}_1\left(\theta \right)+P{C}_1(\theta )}{T}$ and $G_2\left(\theta \right)=\frac{K+H{C}_2\left(\theta \right)+P{C}_2(\theta )}{T}$.

Therefore, mathematically, the optimization problem in the case of neutrosophic differentiability of Type 1 concerning the inventory model can be written in the form

$$\left\{\begin{array}{c}Min G_1\left(\zeta \right)\\ Min G_2\left(\zeta \right)\\ Min G_1\left(\eta \right)\\ Min G_2\left(\eta \right)\\ Min G_1\left(\theta \right)\\ Min G_2\left(\theta \right)\\ Subject to \left(43\right) to (48)\\ T>0 and 0\le \zeta ,\eta ,\theta \le 1\end{array}\right.$$

(49)

De-neutrosophication: Suppose, $G_{11}=\zeta G_1\left(\zeta \right)+\left(1-\zeta \right)G_2\left(\zeta \right)$, $G_{12}=\eta G_1\left(\eta \right)+\left(1-\eta \right)G_2\left(\eta \right)$ and $G_{13}=\theta G_1\left(\theta \right)+\left(1-\theta \right)G_2\left(\theta \right)$. In addition, let $Q_{11}=\zeta Q_1\left(\zeta \right)+\left(1-\zeta \right)Q_2(\zeta )$, $Q_{12}=\eta Q_1\left(\eta \right)+\left(1-\eta \right)Q_2(\eta )$ and $Q_{13}=\theta Q_1\left(\theta \right)+\left(1-\theta \right)Q_2(\theta )$. Then, the total average cost in de-neutrosophication form is $De\left(\tilde{G}\right)=\frac{G_{11}+G_{12}+G_{13}}{3}$ and optimal lot size in that form is $De\left(\tilde{Q}\right)=\frac{Q_{11}+Q_{12}+Q_{13}}{3}$. Therefore, the multi-objective optimization problem is transformed into a single-objective crisp problem as

$$\left\{\begin{array}{c}Min De\left(\tilde{G}\right)\\ subject to De\left(\tilde{Q}\right)\\ T>0 and 0\le \zeta ,\eta ,\theta \le 1\end{array}\right.$$

(50)

6.4.2. When $\widetilde{\mathit{I}\left(\mathit{t}\right)}$ Is Type 2 Neutrosophic Differentiable (Case 2)

In this case, the parametric representation of the differential Equation (32) is

$$\frac{d{I}_2\left(t,\zeta \right)}{dt}=-a_2(\zeta )+b_1\left(\zeta \right)p-c_2\left(\zeta \right)t_w-d_2\left(\zeta \right)I_2\left(t,\zeta \right)$$

(51)

$$\frac{d{I}_1\left(t,\zeta \right)}{dt}=-a_1(\zeta )+b_2\left(\zeta \right)p-c_1\left(\zeta \right)t_w-d_1\left(\zeta \right)I_1\left(t,\zeta \right)$$

(52)

$$\frac{d{I}_2\left(t,\eta \right)}{dt}=-a_2(\eta )+b_1\left(\eta \right)p-c_2\left(\eta \right)t_w-d_2\left(\eta \right)I_2\left(t,\eta \right)$$

$$\frac{d{I}_1\left(t,\eta \right)}{dt}=-a_1(\eta )+b_2\left(\eta \right)p-c_1\left(\eta \right)t_w-d_1\left(\eta \right)I_1\left(t,\eta \right)$$

$$\frac{d{I}_2\left(t,\theta \right)}{dt}=-a_2(\theta )+b_1\left(\theta \right)p-c_2\left(\theta \right)t_w-d_2\left(\theta \right)I_2\left(t,\theta \right)$$

$$\frac{d{I}_1\left(t,\theta \right)}{dt}=-a_1(\theta )+b_2\left(\theta \right)p-c_1\left(\theta \right)t_w-d_1\left(\theta \right)I_1\left(t,\theta \right)$$

From Equation (52), we attain

$$\frac{d{I}_1\left(t,\zeta \right)}{dt}+d_1\left(\zeta \right)I_1\left(t,\zeta \right)=-u_2$$

(53)

Solving the Equation (53) and using the condition $I_2\left(T,\zeta \right)=0$, we obtained

$$I_1\left(t,\zeta \right)=\frac{u_2}{d_1\left(\zeta \right)}\left(e^{d_1\left(\zeta \right)(T-t)}-1\right)$$

Similarly, by solving the other equations, we attain $I_2\left(t,\zeta \right)=\frac{u_1}{d_2\left(\zeta \right)}\left(e^{d_2\left(\zeta \right)(T-t)}-1\right)$, $I_1\left(t,\eta \right)=\frac{u_4}{d_1\left(\eta \right)}\left(e^{d_1\left(\eta \right)(T-t)}-1\right)$, $I_2\left(t,\eta \right)=\frac{u_3}{d_2\left(\eta \right)}\left(e^{d_2\left(\eta \right)(T-t)}-1\right)$, $I_1\left(t,\theta \right)=\frac{u_6}{d_1\left(\theta \right)}\left(e^{d_1\left(\theta \right)(T-t)}-1\right)$, $I_2\left(t,\theta \right)=\frac{u_5}{d_2\left(\theta \right)}\left(e^{d_2\left(\theta \right)(T-t)}-1\right)$.

Using the initial conditions, $I_1\left(0,\zeta \right)=Q_1(\zeta )$, $I_2\left(0,\zeta \right)=Q_2(\zeta )$, $I_1\left(0,\eta \right)=Q_1(\eta )$, $I_2\left(0,\eta \right)=Q_2(\eta )$, $I_1\left(0,\theta \right)=Q_1(\theta )$ and $I_2\left(0,\theta \right)=Q_2(\theta )$ we attain the lot size.

$$\left\{\begin{array}{c}{Q}_1(\zeta )=\frac{u_2}{d_1\left(\zeta \right)}\left(e^{d_1\left(\zeta \right)T}-1\right)\\ Q_2\left(\zeta \right)=\frac{u_1}{d_2\left(\zeta \right)}\left(e^{d_2\left(\zeta \right)T}-1\right)\\ Q_1(\eta )=\frac{u_4}{d_1\left(\eta \right)}\left(e^{d_1\left(\eta \right)T}-1\right)\\ Q_2(\eta )=\frac{u_3}{d_2\left(\eta \right)}\left(e^{d_2\left(\eta \right)T}-1\right)\\ Q_1(\theta )=\frac{u_6}{d_1\left(\theta \right)}\left(e^{d_1\left(\theta \right)T}-1\right)\\ Q_2(\theta )=\frac{u_5}{d_2\left(\theta \right)}\left(e^{d_2\left(\theta \right)T}-1\right)\end{array}\right.$$

(54)

By proceeding as case 1, we obtained the optimization problem in the case of type 2 neutrosophic differentiability (see Appendix A).

$$\left\{\begin{array}{c}Min De\left(\tilde{H}\right)\\ subject to De\left(\tilde{Q}\right)\\ T>0 and 0\le \zeta ,\eta ,\theta \le 1\end{array}\right.$$

(55)

6.5. Numerical Simulation and Graphical Representation

For numerical simulation of the crisp model, the following inputs are considered

$$K=50, a=150, b=0.25, p=10, c=0.4, t_w=1, d=0.15, h=0.75, m=6$$

The optimal solutions are obtained by using LINGO 20.0 software, which is given as $T=0.6205$, $Q=96.18,$ and $G=1046.10$.

Next, we consider the crisp parameters $a$, $b$, $c,$ and $d$ as triangular single-valued neutrosophic numbers of type 1 with nine components in the following way:

$$\tilde{a}=〈130,150,165;120,150,175;135,150,160〉$$

$$\tilde{b}=〈0.15,0.25,0.33;0.20,0.25,0.29;0.22,0.25,0.27〉$$

$$\tilde{c}=〈0.20,0.40,0.55;0.30,0.40,0.48;0.35,0.40,0.44〉$$

$$\tilde{d}=〈0.11,0.15,0.18;0.12,0.15,0.17;0.13,0.15,0.16〉$$

Then, the above inventory problem in crisp form is converted into a neutrosophic differential equation. The optimal results for two different cases are obtained according to the neutrosophic differentiability of type 1 and type 2.

Table 3. Optimal solutions for both the cases of neutrosophic differentiability.

Method	$\mathbf{Time} \mathbf{Cycle} (\mathit{T})$	$\mathbf{Lot} \mathbf{Size} (\mathit{Q})$	$\mathbf{Total} \mathbf{Average} \mathbf{Cost} (\mathit{G})$
Case 1 (type 1 generalised neutrosophic differentiability)	0.6638	87.90	902.22
Case 2 (type 2 generalised neutrosophic differentiability)	0.7426	90.40	831.12

displays the total average cost $(Z)$ along with the values of the decision variables, the total time cycle $(T),$ and lot size $(Q)$ for different cases. Figure 3 and Figure 4 compared the average cost and the cost functions among the crisp model, a neutrosophic model considering type 1 (case 1) and type 2 (case 2) generalized neutrosophic differentiability.

From Table 3, Figure 3 and Figure 4, it becomes evident that the objective of minimizing costs is better achieved when considering a neutrosophic environment and discussing them within a neutrosophic calculus framework. As a result, the suggested method for handling inventory dynamics is established based on numerical results. Among the two cases, case 2 appears to be more efficient in minimizing the average cost. Therefore, case 2 is best suited for achieving the most desirable scenario in terms of cost minimization, considering the feasible measurement of lot size and total inventory cycle.

6.6. Sensitivity Analysis and Managerial Implication

Case 2, which deals with the concept of type 2 neutrosophic differentiability in the context of a neutrosophic environment, unequivocally leads to the most favorable conclusion, as evident from the earlier discussion. We have conducted a sensitivity analysis to examine how precise variables affect the best possible outcome, including optimal quantities $(Q)$, ideal cycle durations $(T)$, and overall average costs $(G)$. During this analysis, we adjusted one parameter’s value within a range of −30% to +30% while keeping the other parameters constant at their initial values. The alterations in the optimal solution are presented in

Table 4. Changes of optimal results concerning the crisp cost parameters.

Crisp Parameter	Original Value	Change	$\mathbf{Time} \mathbf{Horizon} ({\mathit{T}}^{*})$	$\mathbf{Optimal} \mathbf{Lot} \mathbf{Size} ({\mathit{Q}}^{*})$	$\mathbf{Average} \mathbf{Cost} ({\mathit{G}}^{*})$
$K$	50	+30	0.843233	103.2786	850.0388
		+15	0.794674	97.0441	840.8811
		−15	0.686242	83.2528	820.6266
		−30	0.624332	75.4586	809.1819
$p$	10	+30	0.745265	90.0549	825.3756
		+15	0.743938	90.2281	828.2501
		−15	0.741306	90.5734	833.9975
		−30	0.740001	90.7456	836.8705
$t_w$	1	+30	0.742348	90.43412	831.6960
		+15	0.742483	90.4175	831.4100
		−15	0.742754	90.3843	830.8380
		−30	0.742890	90.3677	830.5520
$h$	0.75	+30	0.692913	84.0961	840.7866
		+15	0.716464	87.0787	836.0414
		−15	0.771897	94.13232	826.0144
		−30	0.804979	98.3642	820.6880
$m$	6	+30	0.694847	84.3407	1049.915
		+15	0.717530	87.2139	940.5986
		−15	0.770572	93.9632	721.4733
		−30	0.801985	97.9805	611.6251

and visualized in Figure 5.

We considered an EOQ model with selling price, stock, and warranty time in a neutrosophic environment. The mathematical analysis of the concerned model is performed in both cases of derivatives of the neutrosophic valued objective functions. Below is the list of the observed outcomes in a precise manner:

• The comparison among the optimal average cost in the mentioned cases exhibits that the best result can be obtained in the case of the type 2 differentiability of the neutrosophic valued function, while the worst among the three corresponds to the crisp result. The case regarding the type 1 differentiability of the neutrosophic valued function lies as an intermediate between these extreme cases.
• The ordering of the decision cycle span is the reverse of that of the average profit. That is the case corresponding to the type 1 differentiability of the neutrosophic valued function exhibits the largest span of the decision cycle, while the crisp case represents the smallest span of the decision cycle. Again, the case regarding the type 1 differentiability of the neutrosophic valued function lies as an intermediate between these extreme cases.
• The ordering pattern regarding the order size ($Q$) is not followed by either of the mentioned observations. Two cases of neutrosophic derivatives include the biggest and smallest order size.
• The rise of the setup cost $K$ results in a hike in average cost. The same pattern is revealed regarding the inventory maintenance cost $h$ per unit.
• A rise in the selling price ($p$) may lessen the demand. However, the same reduces the average cost in the proposed model.
• Increase in the warranty time ($t_w$) enhances the demand. However, the same increases the average cost as well.

Upon inspecting the tables and figures provided above, we have compiled the subsequent managerial implications:

• Price and stock influence demand and the cost reduction objective, which were discussed in many pieces of literature. The relational dependence of the market on the selling price is that a low selling price causes the demand to boost. On the other hand, the exhibition of stocks in showrooms also positively controls the market. In this study, we include the positive impact of warranty assurance on the demand pattern. The simultaneous influences of the mentioned issues on the average profit are detailed in this study. An optimal stock management strategy ensures that price enhancement may reduce the average cost of retail enterprises. On the contrary, the average cost increases as the span of warranty time offered by the retailer increases. These insights into the proposed model can be considered while implementing managerial policy.
• Furthermore, the decision-making process cannot be free from uncertainty in reality. So, crisp modeling cannot reflect the complexity involved in decision-making steps. It is better to describe the model as an acceptance-hesitance-rejection-based uncertain phenomenon, and neutrosophic theory corresponds to such uncertainty in mathematical notations. In this study, we view the proposed model in neutrosophic unsteady phenomena. Furthermore, the numerical result establishes that the decision-making under neutrosophic uncertainty not only reflects the decision phenomena more realistically but also provides better results to reduce the average cost for the retailer.

7. Conclusions

Neutrosophic set theory exhibits a more structured sense of uncertainty containing determinacy, hesitancy, and indeterminacy grading perceptions by decision influencers. Thus, the neutrosophic set theory may be applied to hypothesizing the demand pattern in a lot management retail scenario. In this regard, we noticed that few studies incorporated neotosophic theory in their study of inventory management. In those studies, the de-neotrosophication was conducted on the collected or assumed neutrosophic data, and then it was put in a traditional crisp model. The drawback of the existing approach is that it ignores the neutrosophic calculus for neutrosophic valued parameters and decision variables. In this study, we recommended the neutrosophic differential equation to marginalize the mentioned drawbacks while describing the economic order quantity model in the neutrosophic arena. Before going to the application of the neutrosophic differential equation for describing the inventory model, we established the existence and uniqueness criteria of the solution of the neutrosophic differential equation. Furthermore, we discussed an EOQ model with selling price, warranty time of the product, and stock level-dependent demand in a neutrosophic environment by taking various parameters as single-valued triangular neutrosophic numbers. This article serves as an introductory exploration of differential equation principles and their application within a neutrosophic environment. The suggested theory can be expanded in various directions, such as:

• The theory of neutrosophic differential calculus can emerge as a point for future research scope.
• This approach can be applied to address a differential equation of higher order. One can also investigate its utility in tackling both linear and nonlinear differential equations, as well as simultaneous differential equations.
• We have used the proposed theory to apply it to a simple EOQ model. We have kept our analysis brief because the primary focus was not on the inventory model. However, in the future, it can be extended by adding deterioration, time-dependent holding cost, partial backlogging shortage, all-unit quantity discount policy, and trade credit policy such as Momena et al. [54].
• One of the limitations of this study is that we discussed the proposed model by using hypothetical data. It will be a robust approach to formulating and optimizing models using real market data.