Locating Collection and Delivery Points Using the p-Median Location Problem
Abstract
1. Introduction
2. Background
2.1. E-Commerce and Home Delivery
2.2. Crowd Storage
2.3. Collection and Delivery Points and Their Positioning
2.4. Approaches to Solving the p-Median Location Problem
3. Methodology
- Number and spatial dispersion of households that can and want to play the role of CDPs (all or only some households in the service area have the conditions to be CDPs);
- Household storage capacity (unlimited or limited);
- Priority in decision making (more importance is given to operator or user preferences).
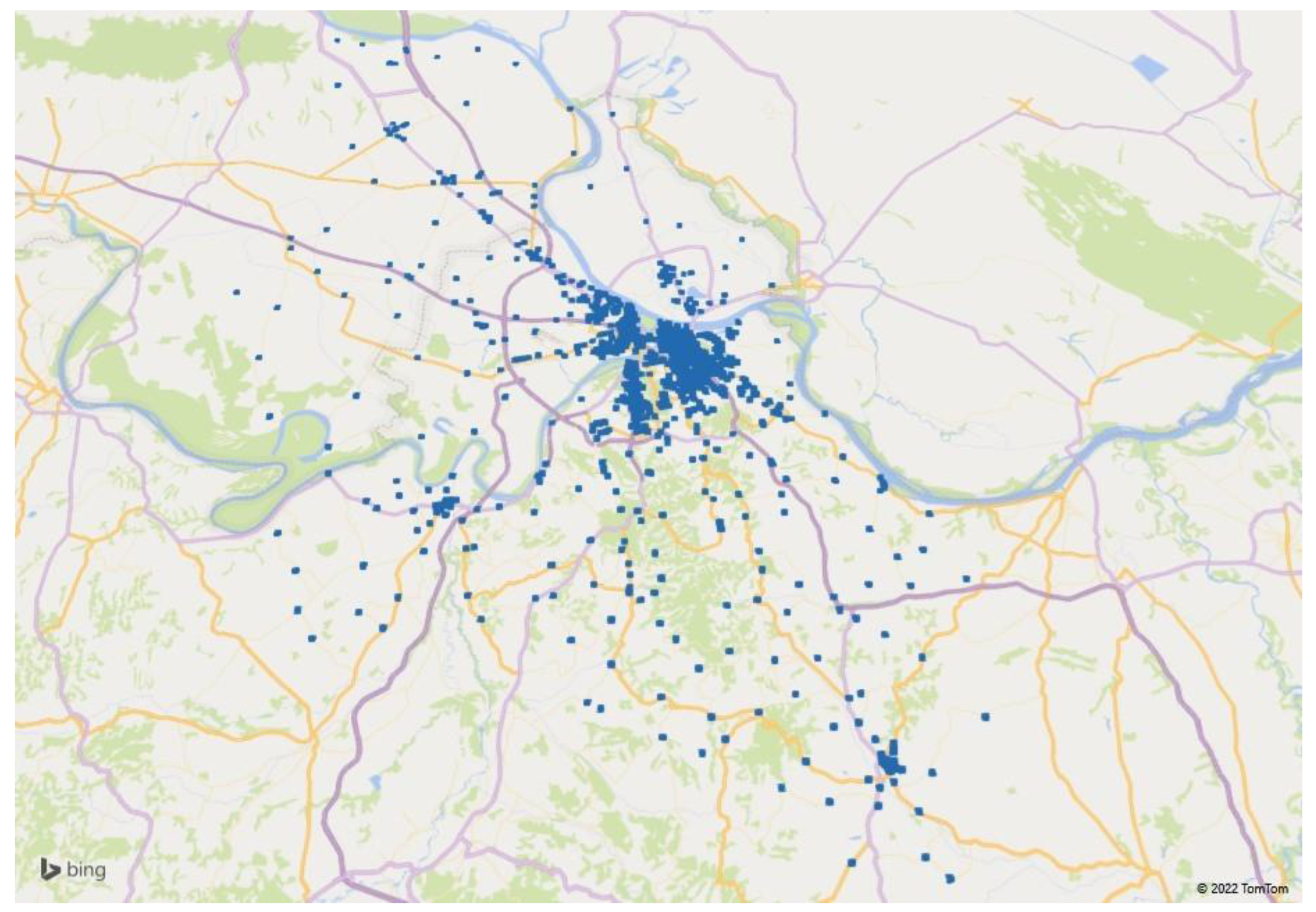
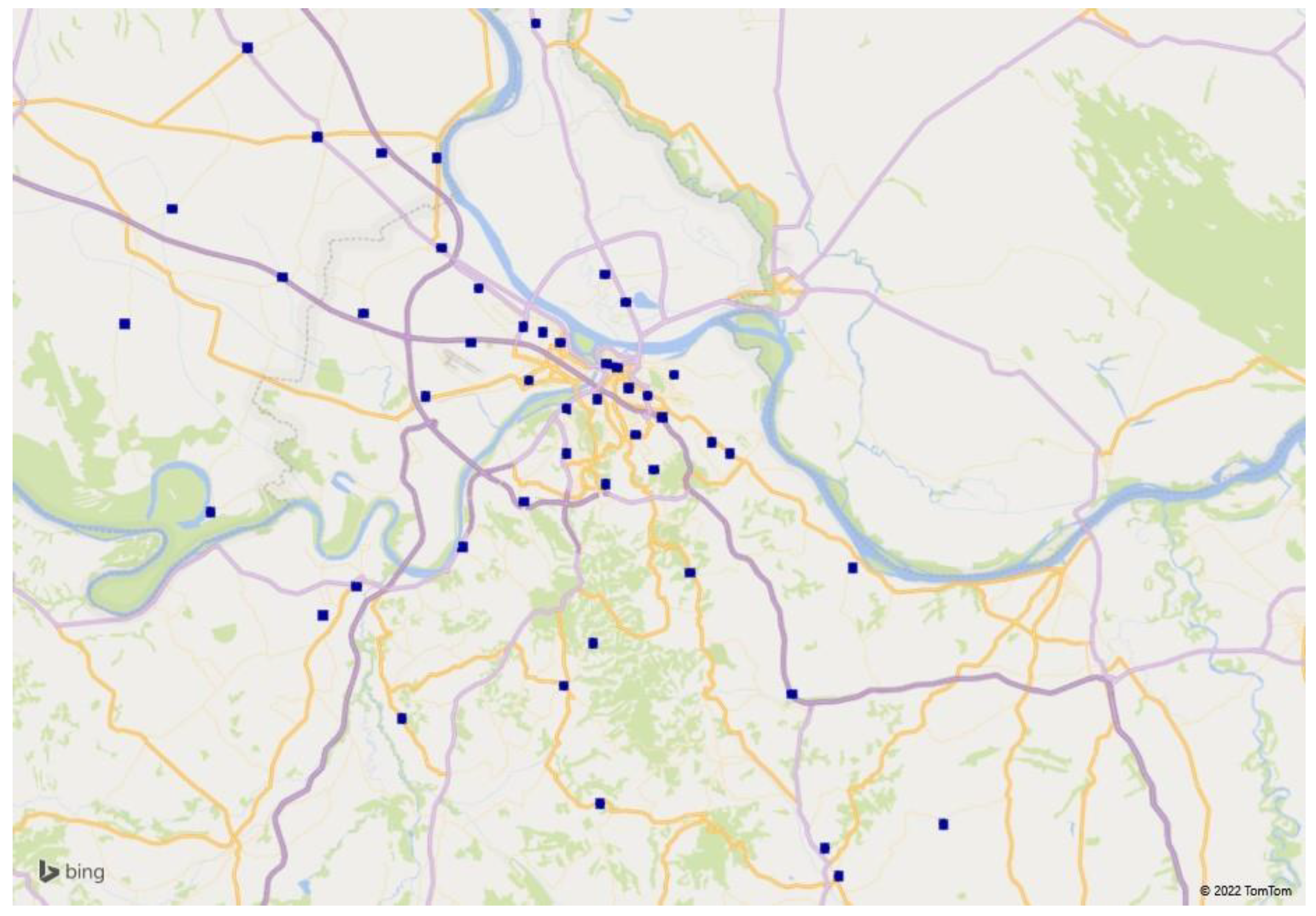
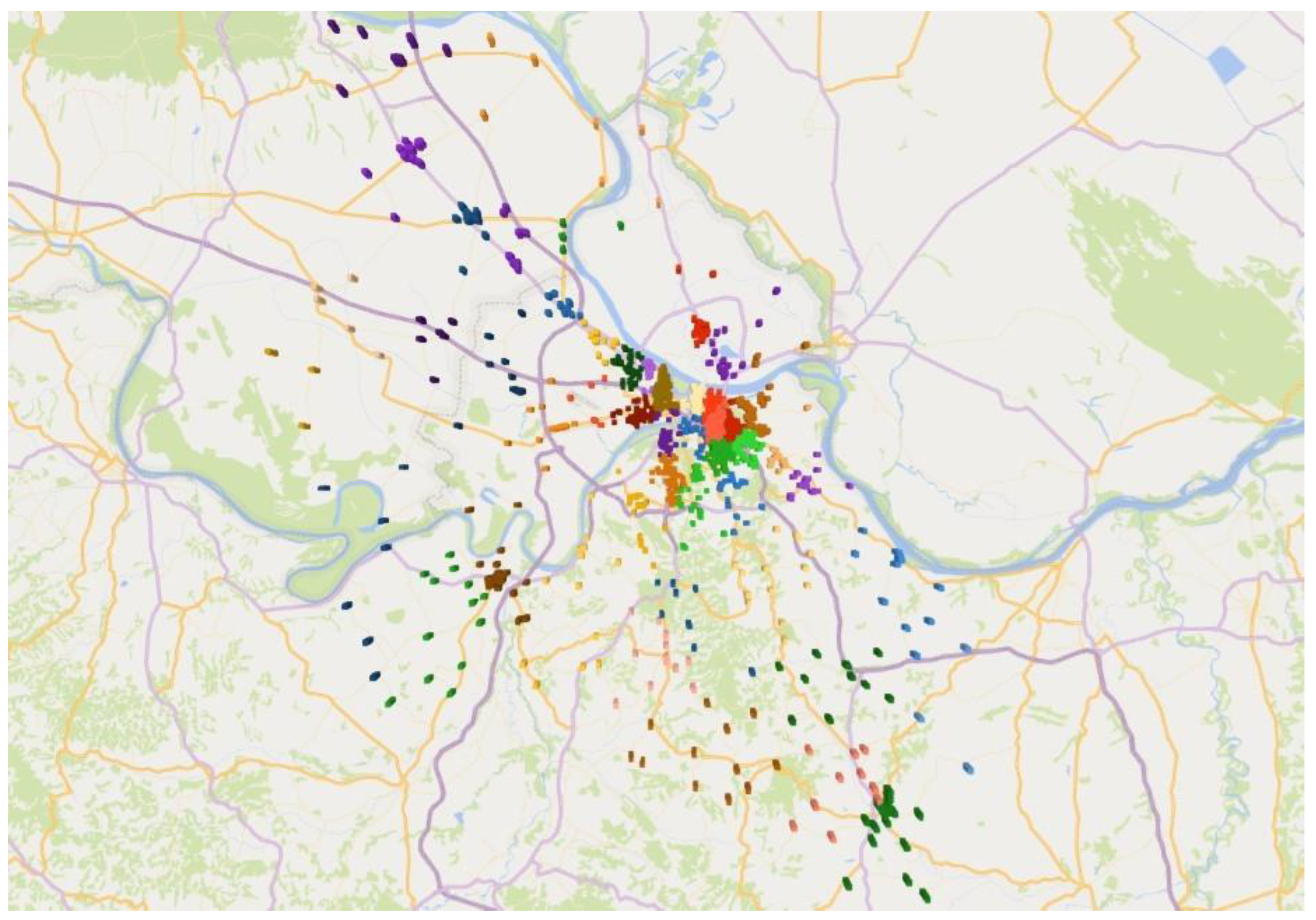
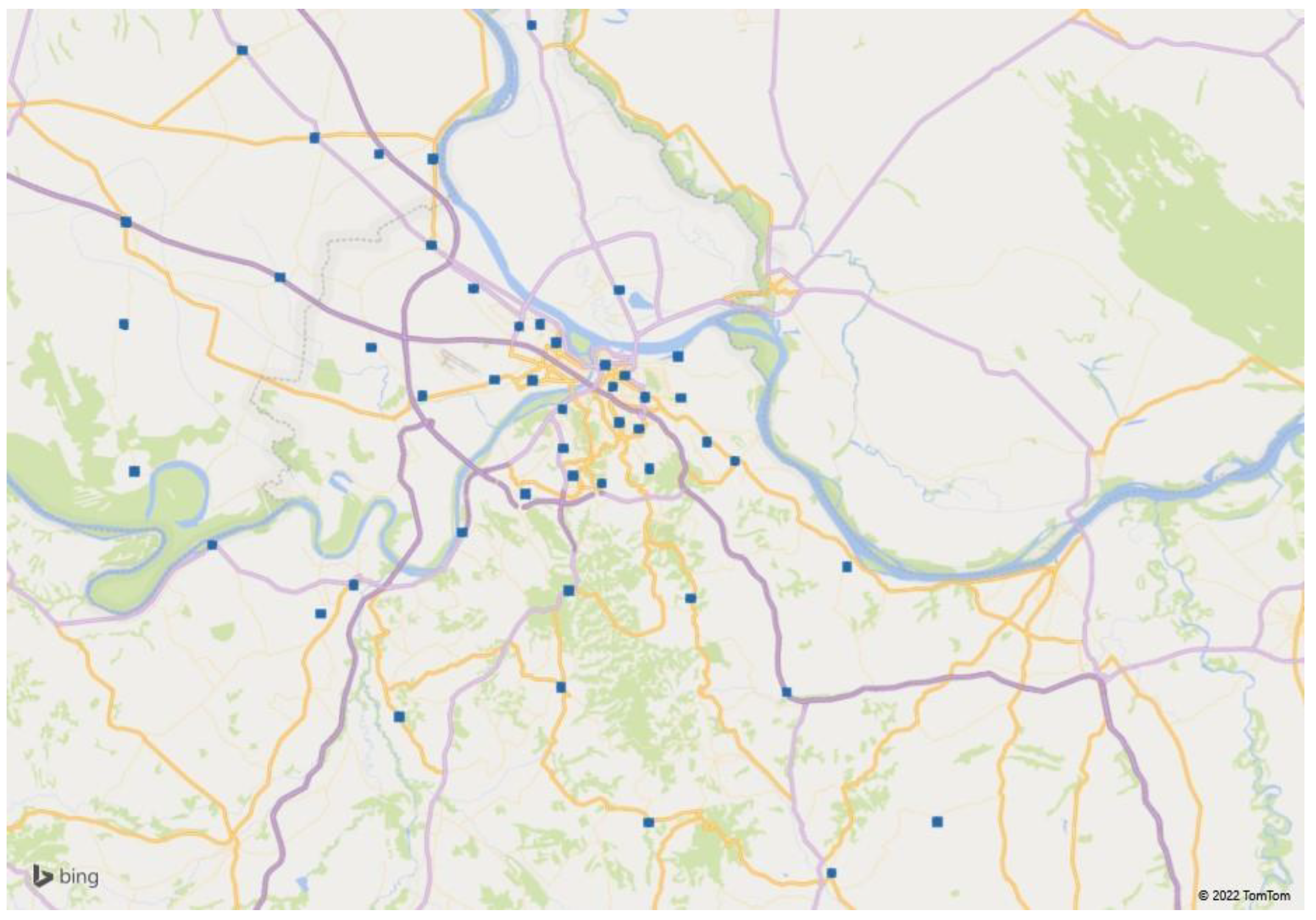
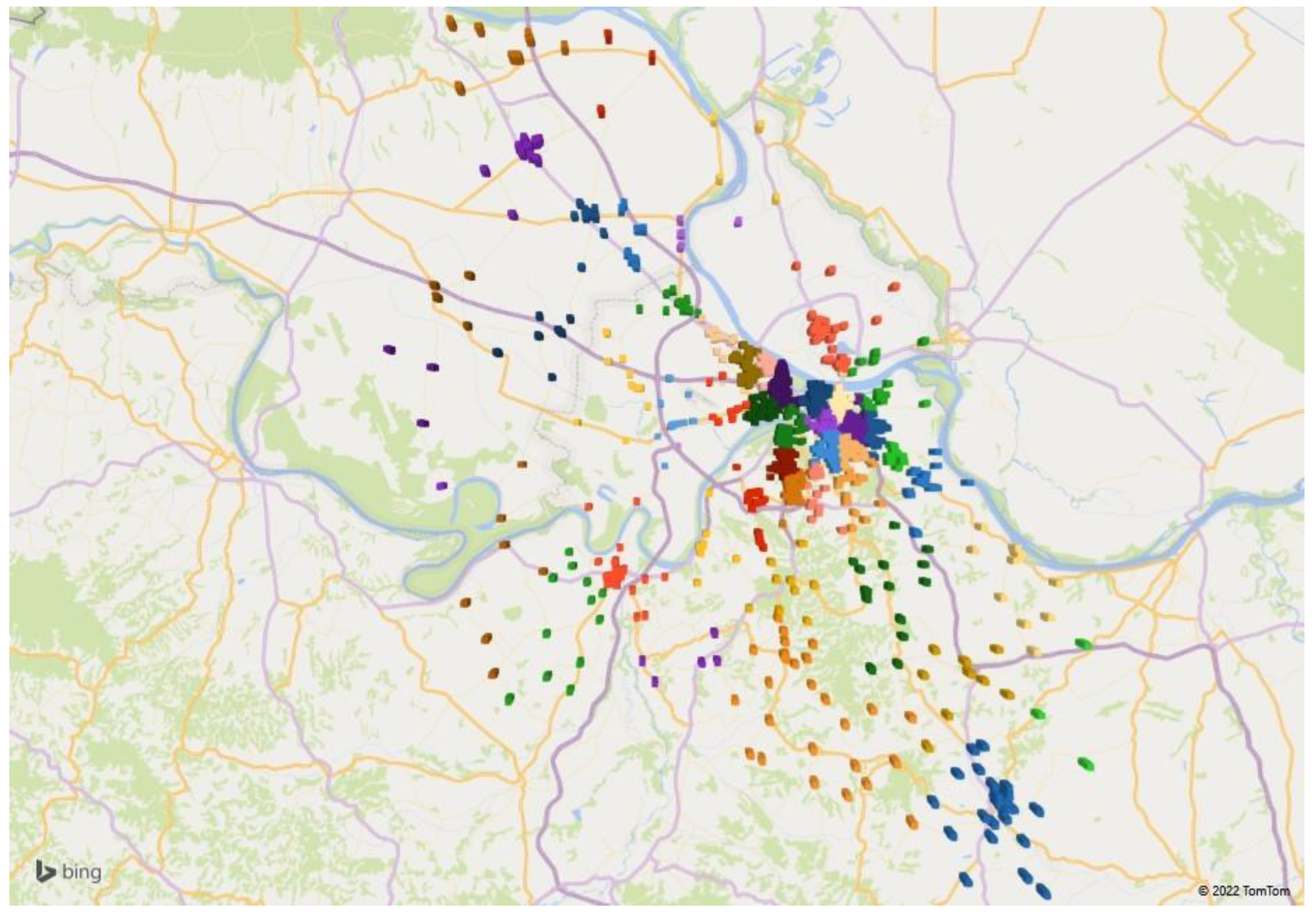
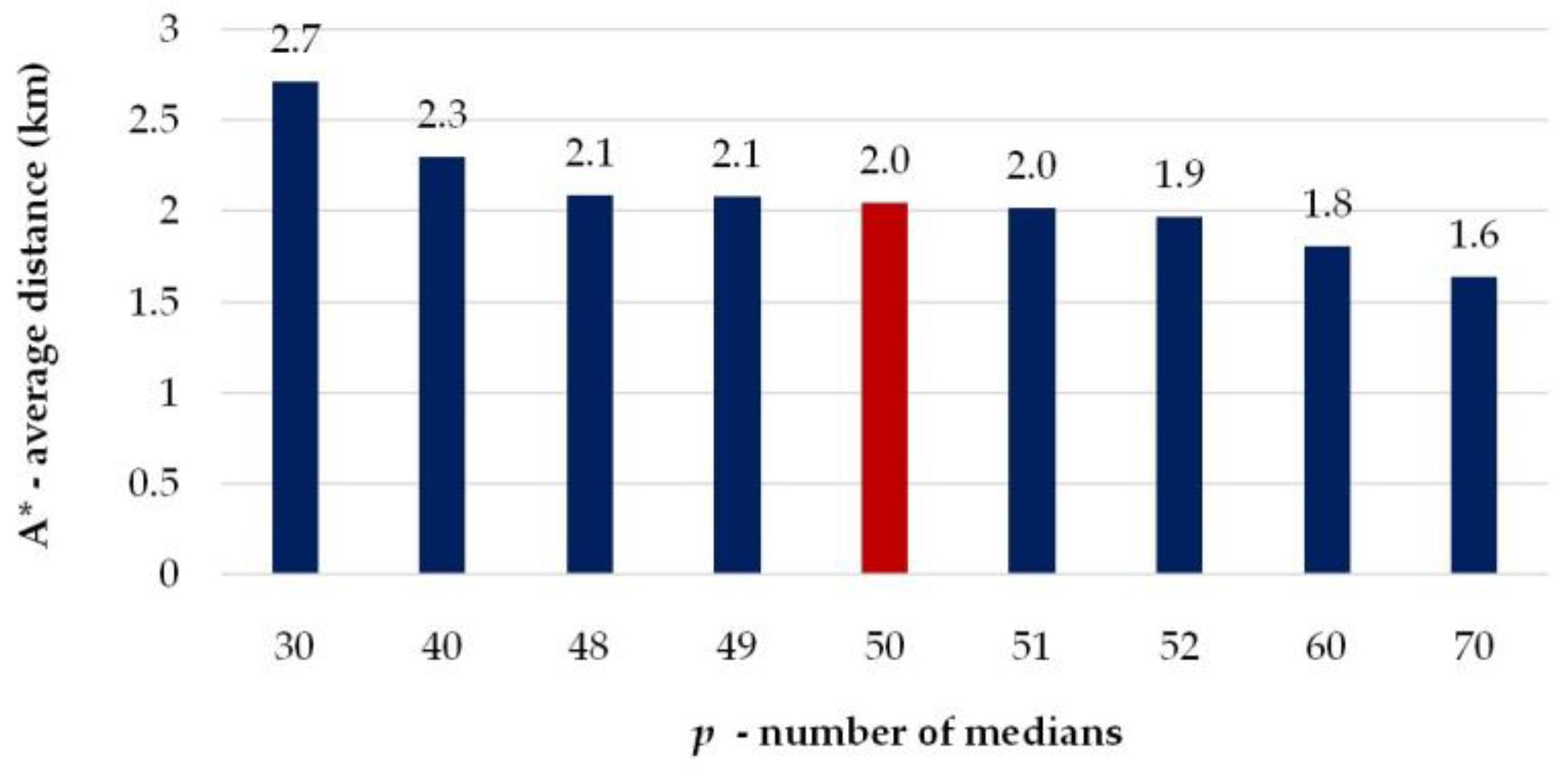
4. Locating CDPs in Users’ Households in the City of Belgrade
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tadić, S.; Veljović, M. Home delivery: A framework for structuring. Int. J. Traffic Transp. Eng. 2021, 11, 30–74. [Google Scholar]
- Chen, L.; Su, S. Optimization of the Trust Propagation on Supply Chain Network Based on Blockchain Plus. J. Intell. Manag. Decis. 2022, 1, 17–27. [Google Scholar] [CrossRef]
- Lin, K.Y.; Yao, Y. A Review of Digital Twin in Logistics: Applications and Future Works. J. Eng. Manag. Syst. Eng. 2022, 1, 32–42. [Google Scholar] [CrossRef]
- Hoffmann, T.; Prause, G. On the regulatory framework for last-mile delivery robots. Machines 2018, 6, 33. [Google Scholar] [CrossRef]
- Arishi, A.; Krishnan, K.; Arishi, M. Machine learning approach for truck-drones based last-mile delivery in the era of industry 4.0. Eng. Appl. Artif. Intell. 2022, 116, 105439. [Google Scholar] [CrossRef]
- Fazlollahtabar, H. Mathematical Modeling for Sustainability Evaluation in a Multi-Layer Supply Chain. J. Eng. Manag. Syst. Eng. 2022, 1, 2–14. [Google Scholar] [CrossRef]
- Alves, R.; Da Silva Lima, R.; Custódiode Sena, D.; Ferreira de Pinho, A.; Holguín-Veras, J. Agent-based simulation model for evaluating urban freight policy to e-commerce. Sustainability 2019, 11, 4020. [Google Scholar] [CrossRef]
- Tadić, S.; Krstić, M.; Veljović, M.; Zečević, S. Households in the function of collection and delivery points: Location decision problem. In Proceedings of the 5th Logistics International Conference, LOGIC2022, Belgrade, Serbia, 26–27 May 2022. [Google Scholar]
- Tadić, S.; Veljović, M.; Zečević, S. Crowd logistics: Household as a logistics service provider. Int. J. Traffic Transp. Eng. 2022, 12, 111–122. [Google Scholar]
- Morganti, E.; Seidel, S.; Blanquart, C.; Dablanc, L.; Lenz, B. The impact of e-commerce on final deliveries: Alternative parcel delivery services in France and Germany. Transp. Res. Procedia 2014, 4, 178–190. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, X.; Zhong, R.Y.; Huang, G.Q. E-commerce logistics in supply chain management: Practice perspective. Procedia Cirp 2016, 52, 179–185. [Google Scholar] [CrossRef]
- Żurek, J. E-commerce influence on changes in logistics processes. LogForum 2015, 11, 129–138. [Google Scholar] [CrossRef]
- Bask, A.; Lipponen, M.; Tinnilä, M. E-commerce logistics: A literature research review and topics for future research. Int. J. E-Serv. Mob. Appl. (IJESMA) 2012, 4, 1–22. [Google Scholar] [CrossRef]
- Alfonso, V.; Boar, C.; Frost, J.; Gambacorta, L.; Liu, J. E-commerce in the pandemic and beyond. BIS Bull. 2021, 36, 1–7. Available online: https://www.bis.org/publ/bisbull36.pdf (accessed on 1 February 2023).
- Bhatti, A.; Akram, H.; Basit, H.M.; Khan, A.U.; Raza, S.M.; Naqvi, M.B. E-commerce trends during COVID-19 Pandemic. Int. J. Future Gener. Commun. Netw. 2020, 13, 1449–1452. [Google Scholar]
- Unnikrishnan, A.; Figliozzi, M.A. A Study of the Impact of COVID-19 on Home Delivery Purchases and Expenditures. 2020. Available online: https://pdxscholar.library.pdx.edu/cgi/viewcontent.cgi?article=1576&context=cengin_fac (accessed on 1 February 2023).
- OBERLO. E-Commerce Share of Retail Sales (2021–2026). 2022. Available online: https://www.oberlo.com/statistics/ecommerce-share-of-retail-sales (accessed on 15 November 2022).
- Lee, H.L.; Whang, S. Winning the last mile of e-commerce. Sloan Manag. Rev. 2001, 42, 54–62. [Google Scholar]
- Bjerkan, K.Y.; Bjørgen, A.; Hjelkrem, O.A. E-commerce and prevalence of last mile practices. Transp. Res. Procedia 2020, 46, 293–300. [Google Scholar] [CrossRef]
- Viu-Roig, M.; Alvarez-Palau, E.J. The impact of E-Commerce-related last-mile logistics on cities: A systematic literature review. Sustainability 2020, 12, 6492. [Google Scholar] [CrossRef]
- Agatz, N.; Campbell, A.M.; Fleischmann, M.; Savels, M. Challenges and opportunities in attended home delivery. Veh. Routing Probl. Latest Adv. New Chall. 2008, 43, 379–396. [Google Scholar]
- Visser, J.; Nemoto, T.; Browne, M. Home Delivery and the Impacts on Urban Freight Transport: AReview. Procedia Soc. Behav. Sci. 2014, 125, 15–27. [Google Scholar] [CrossRef]
- Brown, J.R.; Guiffrida, A.L. Carbon emissions comparison of last mile delivery versus customer pickup. Int. J. Logist. Res. Appl. 2014, 17, 503–521. [Google Scholar] [CrossRef]
- Cheng, C.; Sakai, T.; Alho, A.; Cheah, L.; Ben-Akiva, M. Exploring the Relationship between Locational and Household Characteristics and E-Commerce Home Delivery Demand. Logistics 2021, 5, 29. [Google Scholar] [CrossRef]
- Kandula, S.; Krishnamoorthy, S.; Roy, D. A prescriptive analytics framework for efficient E-commerce order delivery. Decis. Support Syst. 2021, 147, 113584. [Google Scholar] [CrossRef]
- Jiang, Y.; Lai, P.; Chang, C.H.; Yuen, K.F.; Li, S.; Wang, X. Sustainable management for fresh food e-commerce logistics services. Sustainability 2021, 13, 3456. [Google Scholar] [CrossRef]
- Han, C.; Pervez, A.; Wu, J.; Shen, X.; Zhang, D. Home-delivery-oriented agri-food supply chain alliance: Framework, management strategies, and cooperation stability control. Sustainability 2020, 12, 6547. [Google Scholar] [CrossRef]
- Szmelter-Jarosz, A.; Rześny-Cieplińska, J. Priorities of urban transport system stakeholders according to crowd logistics solutions in city areas. A sustainability perspective. Sustainability 2019, 12, 317. [Google Scholar] [CrossRef]
- Mladenow, A.; Bauer, C.; Strauss, C. “Crowdlogistics”: The contribution of social crowds in logistics activities. Int. J. Web Inf. Syst. 2016, 12, 379–396. [Google Scholar] [CrossRef]
- Mehmann, J.; Frehe, V.; Teuteberg, F. Crowd logistics—A literature review and maturity model. In Innovations and Strategies for Logistics and Supply Chains: Technologies, Business Models and Risk Management, Proceedings of the Hamburg International Conference of Logistics (HICL), Hamburg, Germany, 24–25 September 2015; Epubli GmbH: Berlin, Germany, 2015; Volume 20, pp. 117–145. [Google Scholar]
- Arslan, A.M.; Agatz, N.; Kroon, L.; Zuidwijk, R. Crowd source ddelivery—A dynamic pickup and delivery problem with ad hoc drivers. Transp. Sci. 2019, 53, 222–235. [Google Scholar] [CrossRef]
- Tadić, S.; Veljović, M. Logistics flows of household. Tehnika 2020, 75, 225–237. [Google Scholar] [CrossRef]
- Rougès, J.F.; Montreuil, B. Crowd sourcing delivery: New interconnected business models to reinvent delivery. In Proceedings of the 1st International Physical Internet Conference, Québec City, QC, Canada, 28–30 May 2014. [Google Scholar]
- Alharbi, A.; Cantarelli, C.; Brint, A. Crowd Models for Last Mile Delivery in an Emerging Economy. Sustainability 2022, 14, 1401. [Google Scholar] [CrossRef]
- Tadić, S.; Veljović, M.; Krstić, M. Sustainability of the crowd logistics concept in urban and rural areas (In Serbian). In Proceedings of the Sixth Scientific and Professional Conference Politehnika 2021, Belgrade, Serbia, 10 December 2021. [Google Scholar]
- Seghezzi, A.; Mangiaracina, R.; Tumino, A.; Perego, A. ‘Ponyexpress’ crowdsourcing logistics for last-mile delivery in B2C e-commerce: An economic analysis. Int. J. Logist. Res. Appl. 2021, 24, 456–472. [Google Scholar] [CrossRef]
- Frehe, V.; Mehmann, J.; Teuteberg, F. Understanding and assessing crowd logistics business models—Using everyday people for last mile delivery. J. Bus. Ind. Mark. 2017, 32, 75–97. [Google Scholar] [CrossRef]
- Devari, A.; Nikolaev, A.G.; He, Q. Crowdsourcing the last mile delivery of online orders by exploiting the social networks of retail store customers. Transp. Res. Part E Logist. Transp. Rev. 2017, 105, 105–122. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, D.; Liu, Q.; Shen, F.; Lee, L.H. Towards enhancing the last-mile delivery: An effective crowd-tasking model with scalable solutions. Transp. Res. Part E Logist. Transp. Rev. 2016, 93, 279–293. [Google Scholar] [CrossRef]
- Carbone, V.; Roquet, A.; Roussat, C. The Rise of Crowd Logistics: A New Way to Co-Create Logistics Value. J. Bus. Logist. 2017, 38, 238–252. [Google Scholar] [CrossRef]
- Gould, J. Driven to Shop? Role of Transportation in Future Home Shopping. Transp. Res. Rec. J. Transp. Res. Board 1998, 1617, 149–156. [Google Scholar] [CrossRef]
- Van Duin, J.H.R.; DeGoffau, W.; Wiegmans, B.; Tavasszy, L.A.; Saes, M. Improving Home Delivery Efficiency by Using Principles of Address Intelligence for B2C Deliveries. Transp. Res. Procedia 2016, 12, 14–25. [Google Scholar] [CrossRef]
- Sampaio, A.; Savelsbergh, M.; Veelenturf, L.; Van Woensel, T. Crowd-based city logistics. In Sustainable Transportation and Smart Logistics: Decision-Making Models and Solutions; Faulin, J., Grasman, S., Juan, A., Hirsch, P., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 381–400. [Google Scholar]
- IMRG. Valuing Home Delivery Review; IMRG: London, UK, 2021. [Google Scholar]
- Yuen, K.F.; Wang, X.; Ng, L.T.W.; Wong, Y.D. An investigation of customers’ intention to use self-collection services for last-mile delivery. Transp. Policy 2018, 66, 1–8. [Google Scholar] [CrossRef]
- Piplani, R.; Saraswat, A. Robust optimisation approach to the design of service networks for reverse logistics. Int. J. Prod. Res. 2012, 50, 1424–1437. [Google Scholar] [CrossRef]
- McKinnon, A.C.; Tallam, D. Unattended delivery to the home: An assessment of the security implications. Int. J. Retail Distrib. Manag. 2003, 31, 30–41. [Google Scholar] [CrossRef]
- Kedia, A.; Kusumastuti, D.; Nicholson, A. Acceptability of collection and delivery points from consumers’ perspective: A qualitative case study of Christchurch city. Case Stud. Transp. Policy 2017, 5, 587–595. [Google Scholar] [CrossRef]
- Punakivi, M.; Yrjölä, H.; Holmström, J. Solving the last mile issue: Reception box or delivery box? Int. J. Phys. Distrib. Logist. Manag. 2001, 31, 427–439. [Google Scholar] [CrossRef]
- Che, Z.H.; Chiang, T.A.; Luo, Y.J. Multiobjective Optimization for Planning the Service Areas of Smart Parcel Locker Facilities in Logistics Last Mile Delivery. Mathematics 2022, 10, 422. [Google Scholar] [CrossRef]
- Lim, S.F.W.T.; Jin, X.; Srai, J.S. Consumer-driven e-commerce. Int. J. Phys. Distrib. Logist. Manag. 2018, 48, 308–332. [Google Scholar] [CrossRef]
- Weltevreden, J.W.J. B2C e-commerce logistics: The rise of collection-and-delivery points in The Netherlands. Int. J. Retail Distrib. Manag. 2008, 36, 638–660. [Google Scholar] [CrossRef]
- El-Araby, A.; Sabry, I.; El-Assal, A. A Comparative Study of Using MCDM Methods Integrated with Entropy Weight Method for Evaluating Facility Location Problem. Oper. Res. Eng. Sci. Theory Appl. 2022, 5, 121–138. [Google Scholar] [CrossRef]
- Maharjan, R. Modelling Establishment of Temporary Logistics Hub for Humanitarian Relief Operations. Ph.D. Dissertation, Tokyo Institute of Engineering, Tokyo, Japan, 2018. [Google Scholar]
- Iwan, S.; Kijewska, K.; Lemke, J. Analysis of parcel lockers’ efficiency as the last mile delivery solution—The results of the research in Poland. Transp. Res. Procedia 2016, 12, 644–655. [Google Scholar] [CrossRef]
- Lagorio, A.; Pinto, R. The parcel locker location issues: An overview of factors affecting their location. In Proceedings of the 8th International Conference on Information Systems, Logistics and Supply Chain: Interconnected Supply Chains in an Era of Innovation, ILS, Austin, TX, USA, 22–24 April 2020. [Google Scholar]
- Tong, D.; Ren, F.; Mack, J. Locating farmers’ markets with an incorporation of spatio-temporal variation. Socio-Econ. Plan. Sci. 2012, 46, 149–156. [Google Scholar] [CrossRef]
- Kedia, A.; Kusumastuti, D.; Nicholson, A. Locating collection and delivery points for goods’ last-mile travel: A case study in New Zealand. Transp. Res. Procedia 2020, 46, 85–92. [Google Scholar] [CrossRef]
- Wu, H.; Shao, D.; Ng, W.S. Locating self-collection points for last-mile logistics using public transport data. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Ho Chi Minh, Vietnam, 19–22 May 2015. [Google Scholar]
- Simoni, M.D.; Bujanovic, P.; Boyles, S.D.; Kutanoglu, E. Urban consolidation solutions for parcel delivery considering location, fleet and route choice. Case Stud. Transp. Policy 2018, 6, 112–124. [Google Scholar] [CrossRef]
- Deutsch, Y.; Golany, B. A parcel locker network as a solution to the logistics last mile problem. Int. J. Prod. Res. 2017, 56, 251–261. [Google Scholar] [CrossRef]
- Resende, M.G.; Werneck, R.F. A hybrid heuristic for the p-median problem. J. Heuristics 2004, 10, 59–88. [Google Scholar] [CrossRef]
- Brimberg, J.; Drezner, Z. A new heuristic for solving the p-median problem in the plane. Comput. Oper. Res. 2013, 40, 427–437. [Google Scholar] [CrossRef]
- Drezner, Z.; Brimberg, J.; Mladenović, N.; Salhi, S. New heuristic algorithms for solving the planar p-median problem. Comput. Oper. Res. 2015, 62, 296–304. [Google Scholar] [CrossRef]
- Gwalani, H.; Tiwari, C.; Mikler, A.R. Evaluation of heuristics for the p-median problem: Scale and spatial demand distribution. Comput. Environ. Urban Syst. 2021, 88, 101656. [Google Scholar] [CrossRef]
- Bozkaya, B.; Zhang, J.; Erkut, E. An efficient genetic algorithm for the p-median problem. In Facility Location: Applications and Theory; Springer: Manhattan, NY, USA, 2002; pp. 179–205. [Google Scholar]
- Alp, O.; Erkut, E.; Drezner, Z. An efficient genetic algorithm for the p-median problem. Ann. Oper. Res. 2003, 122, 21–42. [Google Scholar] [CrossRef]
- Correa, E.S.; Steiner, M.T.A.; Freitas, A.A.; Carnieri, C. A genetic algorithm for solving a capacitated p-median problem. Numer. Algorithms 2004, 35, 373–388. [Google Scholar] [CrossRef]
- Rolland, E.; Schilling, D.A.; Current, J.R. An efficient tabu search procedure for the p-median problem. Eur. J. Oper. Res. 1997, 96, 329–342. [Google Scholar] [CrossRef]
- França, P.M.; Sosa, N.M.; Pureza, V. An Adaptive Tabu Search Algorithm for the Capacitated p-Median Problem. Int. Trans. Oper. Res. 1999, 6, 665–678. [Google Scholar] [CrossRef]
- Kazakovtsev, L.A.; Orlov, V.; Stupina, A.A.; Kazakovtsev, V. Modied Genetic Algorithm with Greedy Heuristic for Continuous and Discrete p-Median Problems. Facta Universitatis. Ser. Math. Inform. 2015, 30, 89–106. [Google Scholar]
- Golden, B.L.; Skiscim, C.C. Using simulated annealing to solve routing and location problems. Nav. Res. Logist. Q. 1986, 33, 261–279. [Google Scholar]
- Osman, I.H.; Christofides, N. Capacitated clustering problems by hybrid simulated annealing and tabu search. Int. Trans. Oper. Res. 1994, 1, 317–336. [Google Scholar] [CrossRef]
- Cintrano, C.; Chicano, F.; Alba, E. Using metaheuristics for the location of bicycle stations. Expert Syst. Appl. 2020, 161, 113684. [Google Scholar] [CrossRef]
- Mu, W.; Tong, D. On solving large p-median problems. Environ. Plan. B Urban Anal. City Sci. 2020, 47, 981–996. [Google Scholar] [CrossRef]
- Vidović, M.; Zečević, S.; Kilibarda, M.; Vlajić, J.; Bjelić, N.; Tadić, S. The p-hub model with hub-catchment areas, existing hubs, and simulation: A case study of Serbian intermodal terminals. Netw. Spat. Econ. 2011, 11, 295–314. [Google Scholar] [CrossRef]
- Tang, C.; Tang, H.; Jia, A.; Yin, W. Application of P-median Method in the Location of Logistics Nodes. In IOP Conference Series: Earth and Environmental Science; IOPPublishing: Bristol, UK, 2020; Volume 526, p. 012196. [Google Scholar]
- Chen, D.; Xia, B.; Li, Z.; Huang, J. Application of P-median method in logistics node location. In IOP Conference Series: Earth and Environmental Science; IOPPublishing: Bristol, UK, 2020; Volume 526, p. 012175. [Google Scholar]
- İbrahim Miraç, E.; Eren, Ö. P-median and maximum coverage models for optimization of distribution plans: A case of United Nations Humanitarian response depots. In Smart and Sustainable Supply Chain and Logistics–Trends, Challenges, Methods and Best Practices; Golinska-Dawson, P., Tsai, K.M., Kosacka-Olejnik, M., Eds.; Springer Cham: New York, NY, USA, 2020; pp. 225–246. [Google Scholar]
- Hakimi, S.L. Optimum locations of switching centers and the absolute centers and medians of a graph. Oper. Res. 1964, 12, 450–459. [Google Scholar] [CrossRef]
- Mladenović, N.; Brimberg, J.; Hansen, P.; Moreno Pérez, J.A. The p-median problem: A survey of metaheuristic approaches. Eur. J. Oper. Res. 2007, 179, 927–939. [Google Scholar] [CrossRef]
- Teodorović, D. Transport Networks, 5th ed.; Faculty of Transport and Traffic Engineering, University of Belgrade: Belgrade, Serbia, 2016. (In Serbian) [Google Scholar]
- De Armas, J.; Juan, A.A.; Marquès, J.M.; Pedroso, J.P. Solving the deterministic and stochastic uncapacitated facility location problem: From a heuristic to a simheuristic. J. Oper. Res. Soc. 2017, 68, 1161–1176. [Google Scholar] [CrossRef]
- Jánošíková, L.; Herda, M.; Haviar, M. Hybrid genetic algorithms with selective crossover for the capacitated p-median problem. Cent. Eur. J. Oper. Res. 2017, 25, 651–664. [Google Scholar] [CrossRef]
- Bahalke, U.; Hamta, N.; Shojaeifard, A.R.; Alimoradi, M.; Rabiee, S. A New Heuristic Algorithm for Multi Vehicle Routing Problem with AND/OR-Type Precedence Constraints and Hard Time Windows. Oper. Res. Eng. Sci. Theory Appl. 2022, 5, 28–60. [Google Scholar] [CrossRef]
- Kuehn, A.A.; Hamburger, M.J. A heuristic program for locating warehouses. Manag. Sci. 1963, 9, 643–666. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt Jr, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Černý, V. Thermodynamical approach to the traveling salesman problem: An efficient simulation algorithm. J. Optim. Theory Appl. 1985, 45, 41–51. [Google Scholar] [CrossRef]
- Schneider, J.; Kirkpatrick, S. Stochastic Optimization; Springer Science & Business Media: Berlin, Germany, 2007. [Google Scholar]
- Filippone, M.; Masulli, F.; Rovetta, S. Simulated annealing for supervised gene selection. Soft Comput. 2011, 15, 1471–1482. [Google Scholar] [CrossRef]
- Hakimi, S.L. Optimum distribution of switching centers in a communication network and some related graph theoretic problems. Oper. Res. 1965, 13, 462–475. [Google Scholar] [CrossRef]
- Lučić, P. Assignment of Aircraft Crews to Work Tasks Using Metaheuristic Algorithms. Master’s Thesis, University of Belgrade, Belgrade, Serbia, 1996. (In Serbian). [Google Scholar]
- Rere, L.R.; Fanany, M.I.; Arymurthy, A.M. Simulated annealing algorithm for deep learning. Procedia Comput. Sci. 2015, 72, 137–144. [Google Scholar] [CrossRef]
- Iannaccone, G.; Marcucci, E.; Gatta, V. What Young E-Consumers Want? Forecasting Parcel Lockers Choice in Rome. Logistics 2021, 5, 57. [Google Scholar] [CrossRef]
- AGCOM. Allegato B AllaDelibera n. 629/20/CONS Documento per La ConsultazionePubblicaSulleMisure per Incentivare l’utilizzo Degli Armadietti Automatici per La Consegna e La Raccolta Dei Pacchi. 2020. Available online: https://www.agcom.it/documents/10179/20765769/Allegato+14-12-2020+1607956363583/ce1cce68-7327-46dc-a2b1-c5f620a96e5c?version=1.0 (accessed on 20 November 2022).


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tadić, S.; Krstić, M.; Stević, Ž.; Veljović, M. Locating Collection and Delivery Points Using the p-Median Location Problem. Logistics 2023, 7, 10. https://doi.org/10.3390/logistics7010010
Tadić S, Krstić M, Stević Ž, Veljović M. Locating Collection and Delivery Points Using the p-Median Location Problem. Logistics. 2023; 7(1):10. https://doi.org/10.3390/logistics7010010
Chicago/Turabian StyleTadić, Snežana, Mladen Krstić, Željko Stević, and Miloš Veljović. 2023. "Locating Collection and Delivery Points Using the p-Median Location Problem" Logistics 7, no. 1: 10. https://doi.org/10.3390/logistics7010010
APA StyleTadić, S., Krstić, M., Stević, Ž., & Veljović, M. (2023). Locating Collection and Delivery Points Using the p-Median Location Problem. Logistics, 7(1), 10. https://doi.org/10.3390/logistics7010010








