NARX Neural Network for Safe Human–Robot Collaboration Using Only Joint Position Sensor

Abstract

Background: Safety is the very necessary issue that must be considered during human-robot collaboration in the same workspace or area. Methods: In this manuscript, a nonlinear autoregressive model with an exog-enous inputs neural network (NARXNN) is developed for the detection of collisions between a manipulator and human. The design of the NARXNN depends on the dynamics of the manipulator’s joints and considers only the signals of the position sensors that are intrinsic to the manipulator’s joints. Therefore, this network could be applied and used with any conventional robot. The data used for training the designed NARXNN are generated by two experiments considering the sinusoidal joint motion of the manipulator. The first experiment is executed using a free-of-contact motion, whereas in the second experiment, random collisions by human hands are performed with the robot. The training process of the NARXNN is carried out using the Levenberg–Marquardt algorithm in MATLAB. The evaluation and the effectiveness (%) of the developed method are investigated taking into account different data and conditions from the used data for training. The experiments are executed using the KUKA LWR IV manipulator. Results: The results prove that the trained method is efficient in estimating the external joint torque and in correctly detecting the collisions. Conclusions: Eventually, a comparison is presented between the proposed NARXNN and the other NN architectures presented in our previous work.

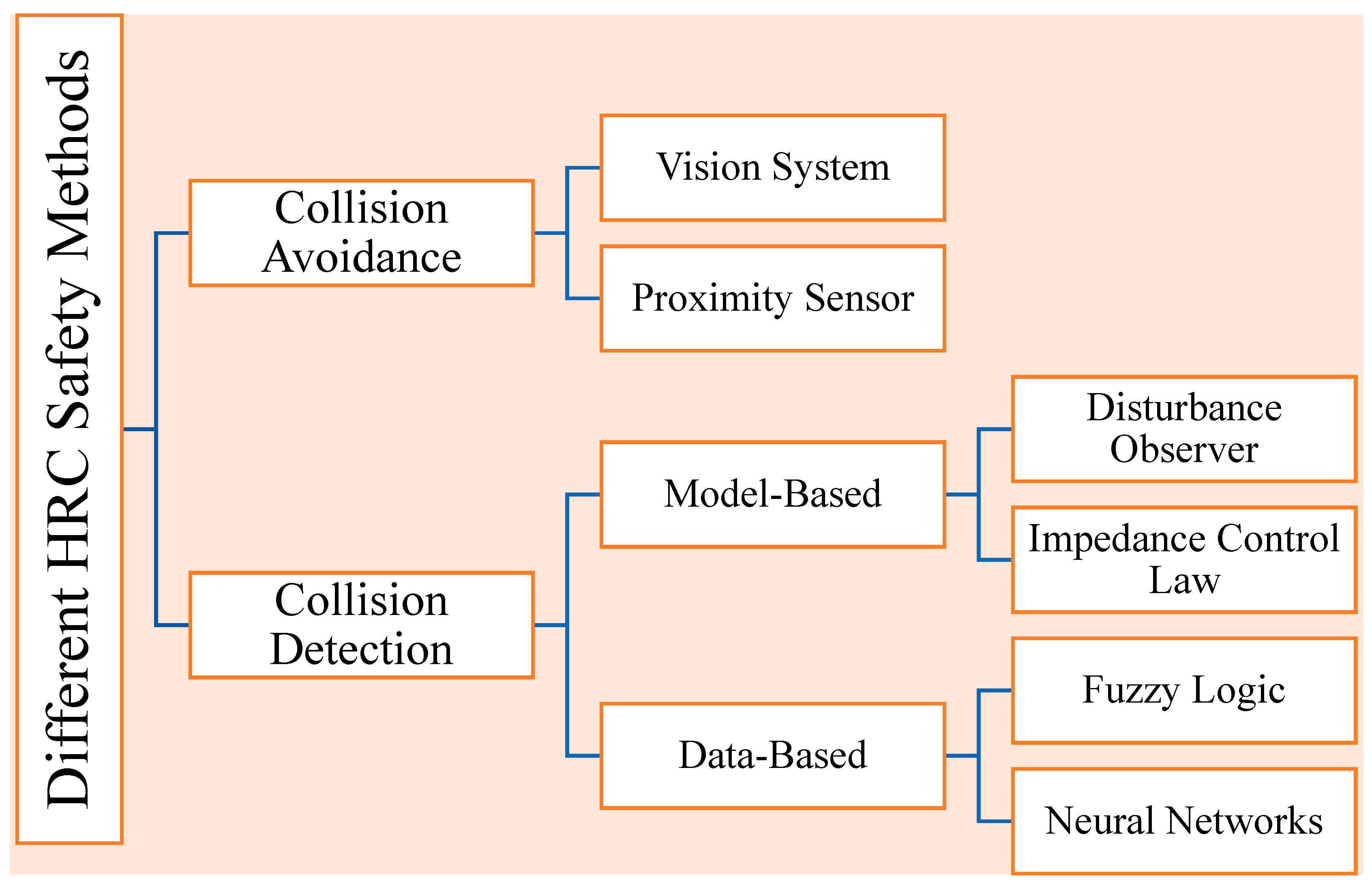
1. Introduction

During the collaboration between a human and manipulator, safety is the most relevant issue that needs to be considered in the procedural design. This is because when the human is close to the manipulator, injuries are expected to happen. Therefore, a safety system must exist for the robotic manipulator. The main challenge is to implement a cheap system, and at the same time, it should be easily adapted to the robot and have high effectiveness. Safety is also taken into accounts in the control system design of human–robot collaboration (HRC).

Researchers have put forth many efforts to develop a system for HRC safety, whether as a collision avoidance method or as a collision detection method. The classifications of these methods are presented in Figure 1.

Collision avoidance methods depend on the depth sensors and vision system, as presented in Refs. [1,2,3,4,5,6]. A proximity sensor-based approach was also proposed by Lam et al. in [7]. In this approach, five sensors of contactless and capacitive types and implemented antennas were used. These types of methods need modifications in the robot’s body, and the cost of the sensors is high.

Collision detection methods are classified into two types: model-based and data-based. Model-based methods depend mainly on the dynamic parameters of the robot’s model, whereas the data-based methods are based on data. The proposed approach in the current paper is a data-based method; therefore, most of our concentration focuses on these types of methods. Model-based methods are classified into two approaches: disturbance observer and impedance control law-based methods. In [8,9], the disturbance observer was presented. The approach depends on the signals of the torque sensors of the manipulator’s joints. Thus, this method could be applied and uses only collaborative robotic manipulators that contain joint torque sensors. Morinaga and Kosuge in [10] developed a collision-detection method depending on the impedance controller. Their approach used the torque signal (the error between the actual and the desired input torques of the robotic manipulator). The problems with the methods based on the robot’s model are that these methods are inaccurate and uncertain because there is uncertainty in the dynamic parameters determination [11,12,13,14]. Therefore, this negatively influences the effectiveness of the method to detect the collisions, and the fault alarms are increased [11]. In addition, the calculations of the inverse dynamics are very complex [15].

Data-based methods were considered for collision detection between a human and a manipulator. These methods depend on fuzzy logic and neural networks. In [16], Dimeas et al. used the fuzzy-logic-based method for collision detection. Their system was designed depending on the signals of both the joint position and the torque sensors. Their method was applied to a 2-DOF planar robot, and it was efficient in detecting the collisions. However, it can only be applied and used with the collaborative robots that contain a joint torque sensor. Furthermore, they used one fuzzy system for each joint, which means that they needed seven fuzzy systems if they applied their method to a 7-DOF robot. Therefore, this is very complex and needs more time and effort. In [14], S. Lu and his group used the NN-based approach for the detection of collisions. Their developed system was designed based on the history of the joint angles of the manipulator and the two external sensors (the base, and the wrist force/the torque sensors). Their method was investigated using 1-DOF and 2-DOF robotic manipulators. The effectiveness in the calculations of their method was presented by executing only one collision by the manipulator, but it was not investigated by using many random collisions. Kim et al., in [17], proposed a versatile modularized NN to detect collisions with a collaborative manipulator. The momentum observer torques were required for their method. In [18], four NN architectures were proposed: the auto regressive NN, the recurrent NN (RNN), the convolutional long short-term memory NN (CLSTMNN) and the mixed CLSTMNN. These architectures were designed based on position, velocity, and motor current.

In our previous work presented in [19,20,21,22,23,24], four NN architectures were designed and trained for the collision detection. These architectures were (1) multilayer feedforward NN having one hidden layer (MLFFNN-1), (2) multilayer feedforward NN having two hidden layers (MLFFNN-2), (3) the cascaded forward NN (CFNN), and (4) the recurrent NN (RNN). MLFFNN-1 was developed using both the position and torque sensors that are intrinsic to the manipulator’ joints. Thus, the application of this structure is only with the collaborative robotic manipulators that possess joint torque sensor. The experimental investigation of this structure was applied to the 1-DOF, 2-DOF planar, and 3-DOF robotic manipulators. The other three structures (MLFFNN-2, CFNN, and RNN) were developed using the position sensor only of the manipulator’s joint. Thus, the applications of these structures are with any conventional robot. MLFFNN-2 was investigated experimentally using 1-DOF and 2-DOF planar robotic manipulators, whereas CFNN and RNN were investigated experimentally using the 1-DOF manipulator. The effectiveness and the performance measure of these architecture were presented in different conditions and used different data from the training ones.

From this discussion, a data-based method is a desirable solution for the detection of robot collisions with humans. This type of method should avoid the explicit knowledge of the dynamic parameters of the robot model and the complex calculations of the inverse dynamics. Furthermore, it should be applied to any conventional robot, and its effectiveness (%) must be presented with the use of many different conditions and cases.

The work of the current paper is considered as an extension to our previous work presented in [19,20,21,22,23,24]. The main contribution and novelty of the current paper is discussed as follows. A NARXNN is developed to detect human–manipulator collisions. The NARXNN is designed depending only on the signals of the position sensors that are intrinsic to the manipulator’s joints. This qualifies the proposed method to be used with any conventional robot. The training of the designed NARXNN is executed using data with and without collisions and using Levenberg–Marquardt learning. The knowledge of the dynamic parameters of the robot model such as the inertia forces, the Coriolis and centrifugal forces, and the gravitational forces, is not needed in the proposed method, and these parameters are not available in most of the current robots. The test and the verification of the trained NARXNN are carried out using the same data that are used for the training. Furthermore, its effectiveness is investigated using different data and conditions from the training ones, considering many random collisions with the manipulator. The experiments are performed using KUKA LWR IV manipulator considering only one joint’s motion. However, the method can be applied with all joints of the robotic manipulator. The obtained results reveal that the trained NARXNN is an efficient method in estimating and detecting the collisions. A comparison is presented between the developed NARXNN and other previous NN architectures discussed in [19,20]. In addition, a comparison with other previously published methods is executed.

The rest of this manuscript is outlined as follows. Section 2 discusses the dynamics of the manipulator joints, why the NN is used, and the followed methodology/steps in the current work to detect the collision. Section 3 shows the design of the proposed NARXNN, and Section 4 illustrates the training and the testing of the designed NARXNN using the same data. Section 5 discusses the trained NARXNN’s evaluation considering many random collisions with the manipulator and using different data and conditions from the training ones. In Section 6, a comparison between the NARXNN and other NN architectures used for detecting the collisions is presented. Finally, Section 7 provides the main points that are discussed in this manuscript with some future work.

2. Dynamics of Manipulator Joints

The external torque of the manipulator’s joint ${\tau }_{ext}$ is determined from the dynamics equation of the manipulator as follows [25,26]:

$${\tau }_{ext}=M\left(\theta \right) \ddot{\theta }+C\left(\theta ,\dot{\theta }\right) \dot{\theta }+G\left(\theta \right)-\tau$$

(1)

The symbols used in this equation are defined in

Table 1. The meaning of the symbols used in the dynamic Equation (1).

Symbol	Meaning
$\theta \in {ℝ}^n$	A vector representing the positions of the manipulator joints
$\dot{\theta }\in {ℝ}^n$	A vector representing the velocities of the manipulator joints
$\ddot{\theta }\in {ℝ}^n$	A vector representing the accelerations of the manipulator joints
$M\left(\theta \right)\in {ℝ}^{n\times n }$	The inertia matrix of the manipulator
$C\left(\theta ,\dot{\theta }\right)\in {ℝ}^{n\times n }$	The Coriolis and centrifugal matrix of the manipulator
$G\left(\theta \right)\in {ℝ}^n$	The gravity vector of the manipulator
$\tau \in {ℝ}^n$	The actuator torque of the manipulator joints
$n$	The number of the links or the joints of the manipulator

.

As discussed in the introduction part, the parameters of this equation are not known in most of the current robots. This leads to difficulty in determining the external joint torque [15]. Furthermore, the techniques depending on the dynamic robot model are uncertain and inaccurate [11,12,13,14]. Therefore, this negatively influences the effectiveness for the detection of the collisions that occur between the human and manipulator.

According to this, a method depending on the NN’s structure is developed to save human–manipulator collaboration. The NN is efficient in approximating any function, whether linear or nonlinear [27,28,29]. In addition, it can be generalized under different conditions. The NN-based approach solves the inverse dynamics problems of the manipulator efficiently [30,31,32]. From the different NN architectures, NARXNN is proposed. NARXNN is the dynamic and recurrent NN, and it possesses the connections of feedback enclosing several network layers [33,34]. The structure of this NN is the nonlinear generalization of the well-known ARX models. This NN predicts the time series very well [35,36] and is widely used with the nonlinear dynamic systems [37,38].

In the current work, this NARXNN is trained using the Levenberg–Marquardt (LM) algorithm. The LM algorithm [39,40] is a second-order optimization method that has the advantage of fast convergence. In addition, it approximates the method of Newton. The LM algorithm can achieve a fast learning speed of the method of classical Newton and at the same time the convergence of the gradient descent [39,41]. Compared with other training algorithms, LM converges with less repetitions/iterations and in a shorter time. However, this algorithm needs larger data. For solving this issue, enough data are used in the current work.

The followed steps and methodology with the proposed NARXNN for the detection of the robot collisions with humans are presented in Figure 2. All these steps are discussed in detail in the next sections.

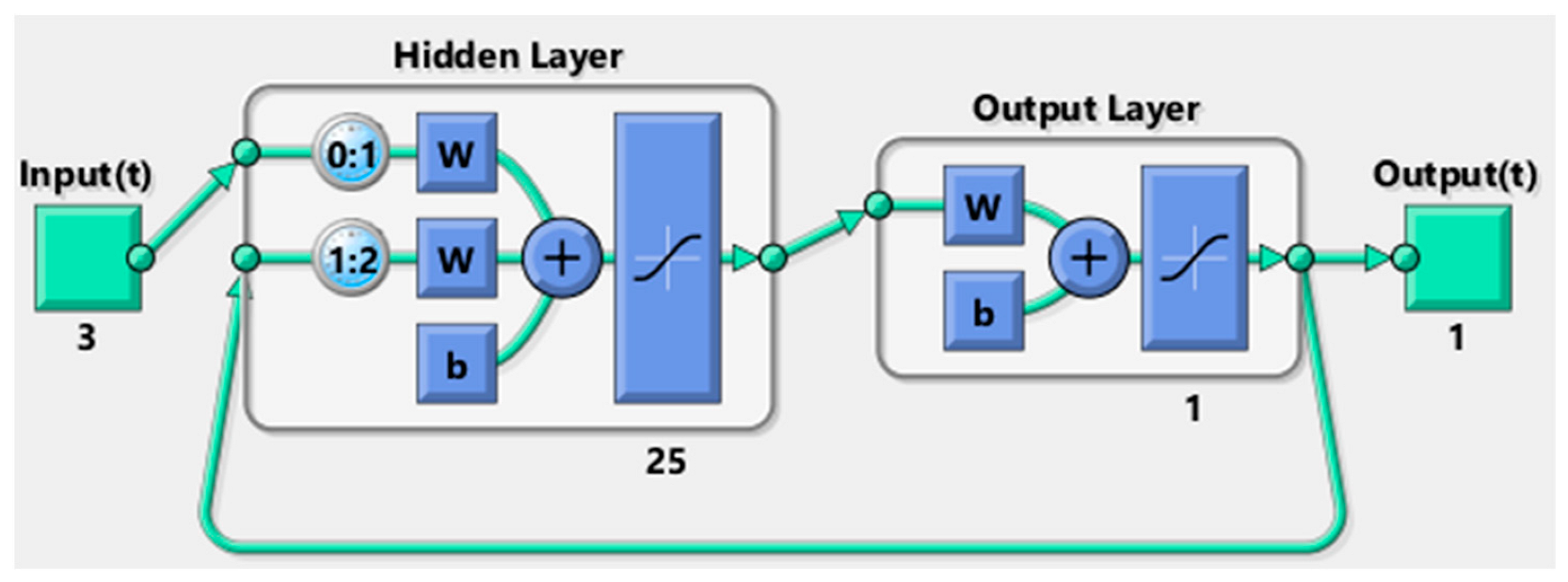
3. NARXNN Design

In this section, the design of the NARXNN for the detection of the robot collisions with humans is presented in detail.

The same sinusoidal motion presented in the previous work [19,20] is used here in the current work. This motion is executed using frequencies that are variable and are commanded to the E1′s joint of the KUKA LWR IV manipulator, as shown in Figure 3. Two experiments are considered. In the first experiment, the motion of the robot joint is free of contact, whereas in the second experiment, the human hand performs some random collisions with the robot during its motion.

The NARXNN is designed depending only on the positions’ sensors that are intrinsic to the manipulator’s joint. Therefore, the application and the use of this method are for any conventional robot. The main criteria to select the inputs of the NARXNN to achieve the high performance of the NN are (1) the smallest mean squared error (MSE), and therefore (2) the smallest training error. There are three inputs, and they are defined as follows:

(1)

The current position error of the joint $\tilde{\theta }\left(k\right)$, presenting the difference between the desired and the actual value of the joint’s position;

(2)

The previous position error of the joint $\tilde{\theta }\left(k-1\right)$;

(3)

The actual velocity of the joint ${\dot{\theta }}_{ac}\left(k\right)$.

The actual velocity of the joint is obtained from the KUKA robot controller (KRC). However, this velocity could be determined via the numerical differentiations of the joint’s position. The inputs for the case of a collision and for the in case of free-of-contact motion are shown in Figure 4.

In Figure 4, the red color curves represent the inputs in the case there is a collision, whereas the blue color curves represent the inputs in the case there is no collision. The spikes marked by the small blank circle represent the collisions. More details about these inputs are found in our previous work in Ref. [19].

The NARXNN architecture includes three types of layers as in the following order: the layer of input, the layer of hidden neurons that is nonlinear, where its activation function is the hyperbolic tangent (tanh), and the layer of output that is also nonlinear, where its activation function is the hyperbolic tangent (tanh). The output layer estimates the external joint torque ${\tau }_{ext}^{\prime }$. The input delay vector is $\left[0 1\right]$, and the output delay vector is $\left[1 2\right]$. This proposed architecture is presented in Figure 5. The equations representing the feedforward part of the NARXNN are given as follows.

The output of the hidden neuron $j$ that is in the hidden layer is given by

$$y_j={\phi }_j\left(h_j\right)={\phi }_j\left(\left({\displaystyle \sum }_{i=0}^3{w}_{ji}{x}_i\right)+(c_{j1}{\tau }_{ext}^{\prime }\left(k-1\right)\right)$$

(2)

where $x_i$ represents the inputs to the NN. $x_0=1$, $x_1=\tilde{\theta }\left(k\right)$, $x_2=\tilde{\theta }\left(k-1\right)$, and $x_3={\dot{\theta }}_{ac}\left(k\right)$. ${\tau }_{ext}^{\prime }\left(k-1\right)$ is the previous value of the estimated external joint of NARXNN. $w_{ji}$ is the weight between the input $i$ and the hidden neuron $j$, and $c_{j1}$ is the weight between the input ${\tau }_{ext}^{\prime }\left(k-1\right)$ and the hidden neuron $j$.

The activation function of the hidden layer is given by

$${\phi }_j\left(h_j\right)=\tanh \left(h_j\right)$$

(3)

The estimated external torque by the NARXNN, ${\tau }_{ext}^{\prime }$, is calculated by

$${\tau }_{ext}^{\prime }={\psi }_k\left(O\right)={\psi }_k\left({\displaystyle \sum }_{j=0}^n{b}_{1j}{y}_j\right)=\tanh \left({\displaystyle \sum }_{j=0}^n{b}_{1j}{y}_j\right)$$

(4)

where $b_{1j}$ is the weight between the hidden neuron $j$ and the estimated output of the NARXNN.

The external joint’s torque ${\tau }_{ext}$ is given/provided by KRC and is used only for training the designed NARXNN architecture. In any other type of robot where ${\tau }_{ext}$ is not given/existing, the external collision’s force can be measured by any type of external force sensor. The error of training $e\left(t\right)$ must be very small. This error is calculated from the following equation:

$$e\left(t\right)={\tau }_{ext}-{\tau }_{ext}^{\prime }$$

(5)

The training process of the designed NARXNN architecture is discussed in detail in the next section.

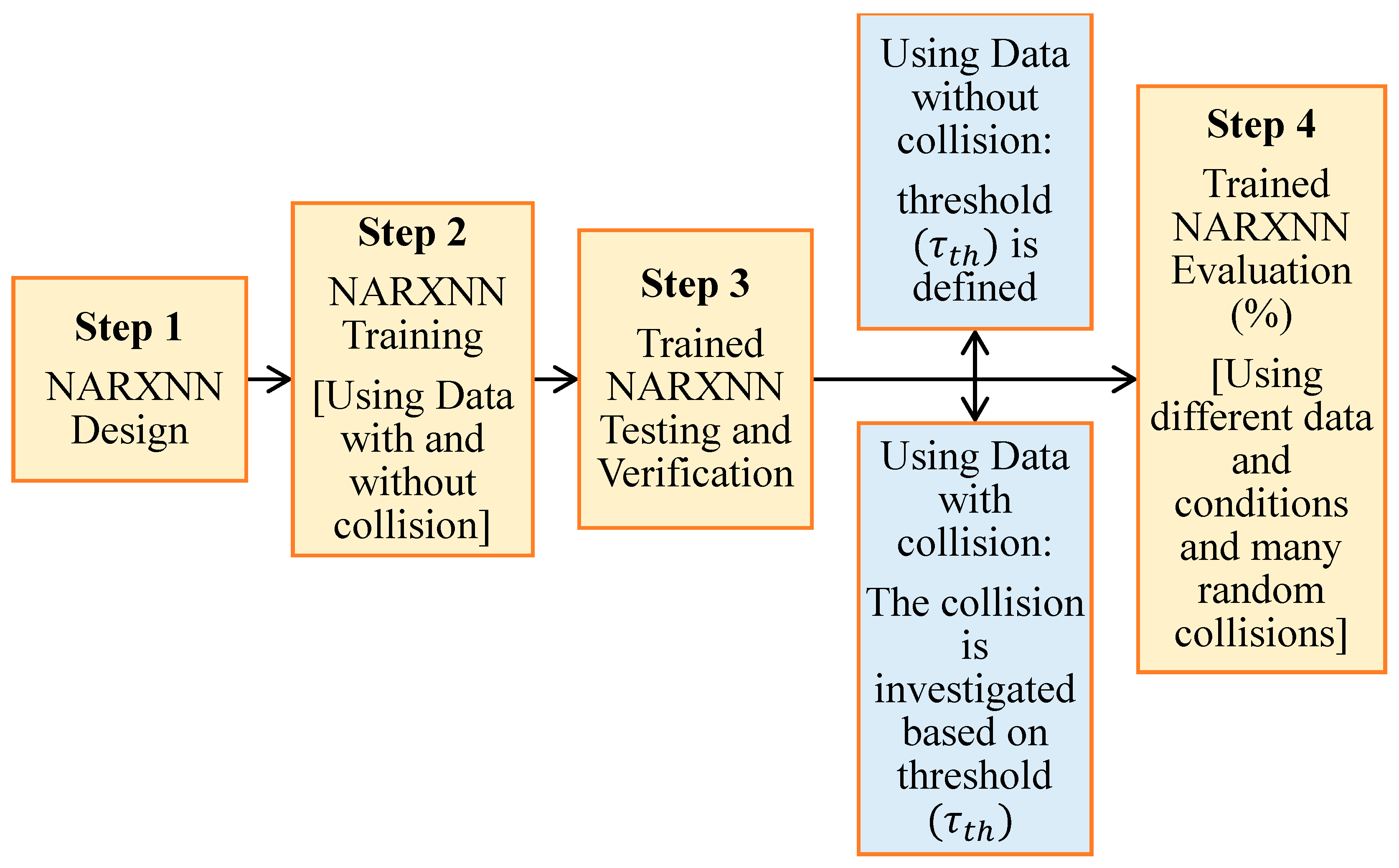
4. NARXNN Training Then Testing

In this section, the training process of the designed NARXNN is presented. In addition, the test of this trained NN structure is investigated. The following steps and methodology in these processes are summarized as follows:

(1)

Collect the data with and without collisions from the experiments with the KUKA LWR robot.

(2)

Initialize the parameters of the NARXNN and select the suitable number of hidden neurons.

(3)

Train the designed NARXNN, using the collected data with and without collisions.

(4)

After the training is completed, check the performance of the NARXNN by investigating the resulting MSE.

(5)

If the resulting MSE is a high value and is not satisfactory, go again to step 2.

(6)

If the resulting MSE is very small and close to zero (satisfactory), perform the following:

➢

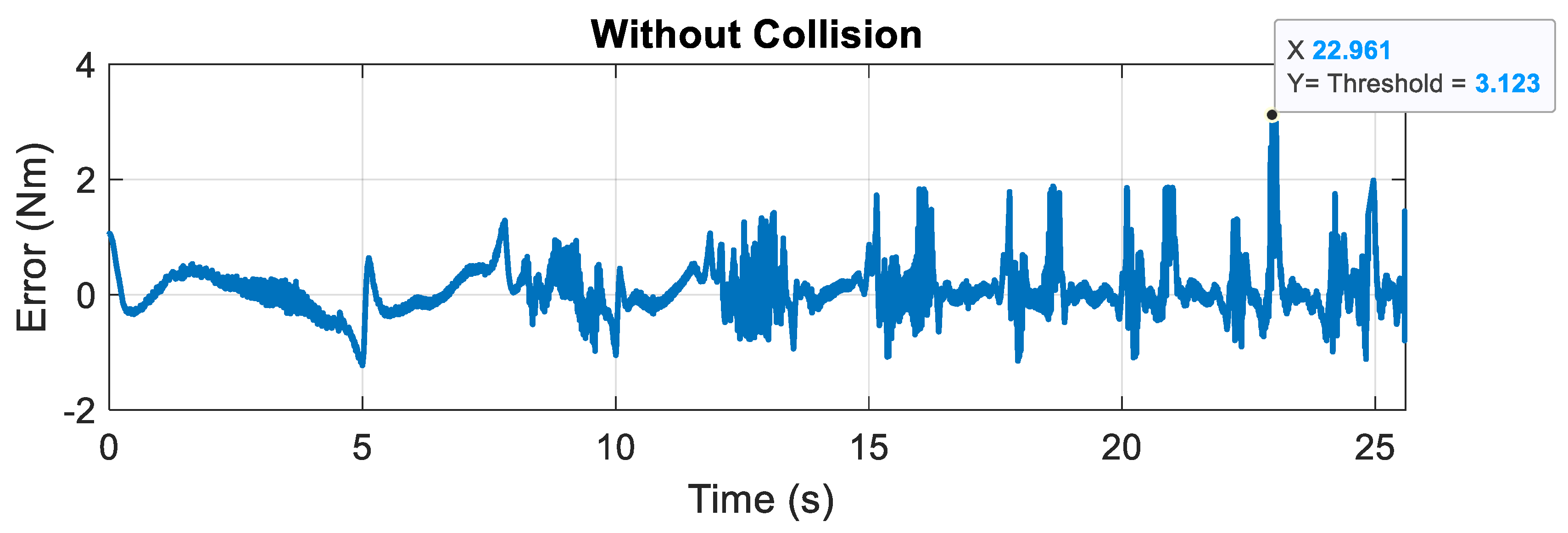
6.1 Test the trained NARXNN by using the data without collisions that is used for training and check the training/approximation error.

➢

6.2 If this training/approximation error is a low value and is satisfactory, calculate the collision threshold and then go to step 7.

➢

6.3 If this training/approximation error is a high value and is not satisfactory, go again to step 2.

(7)

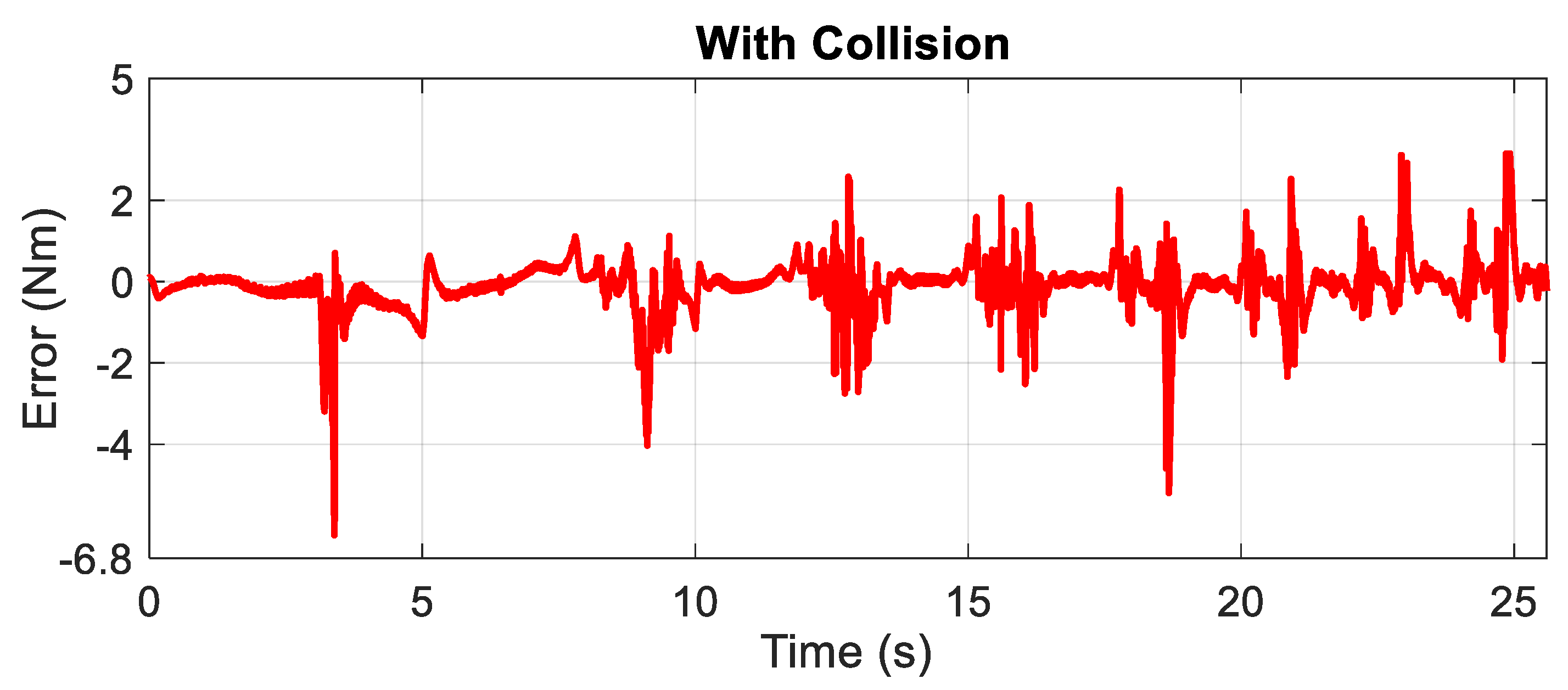
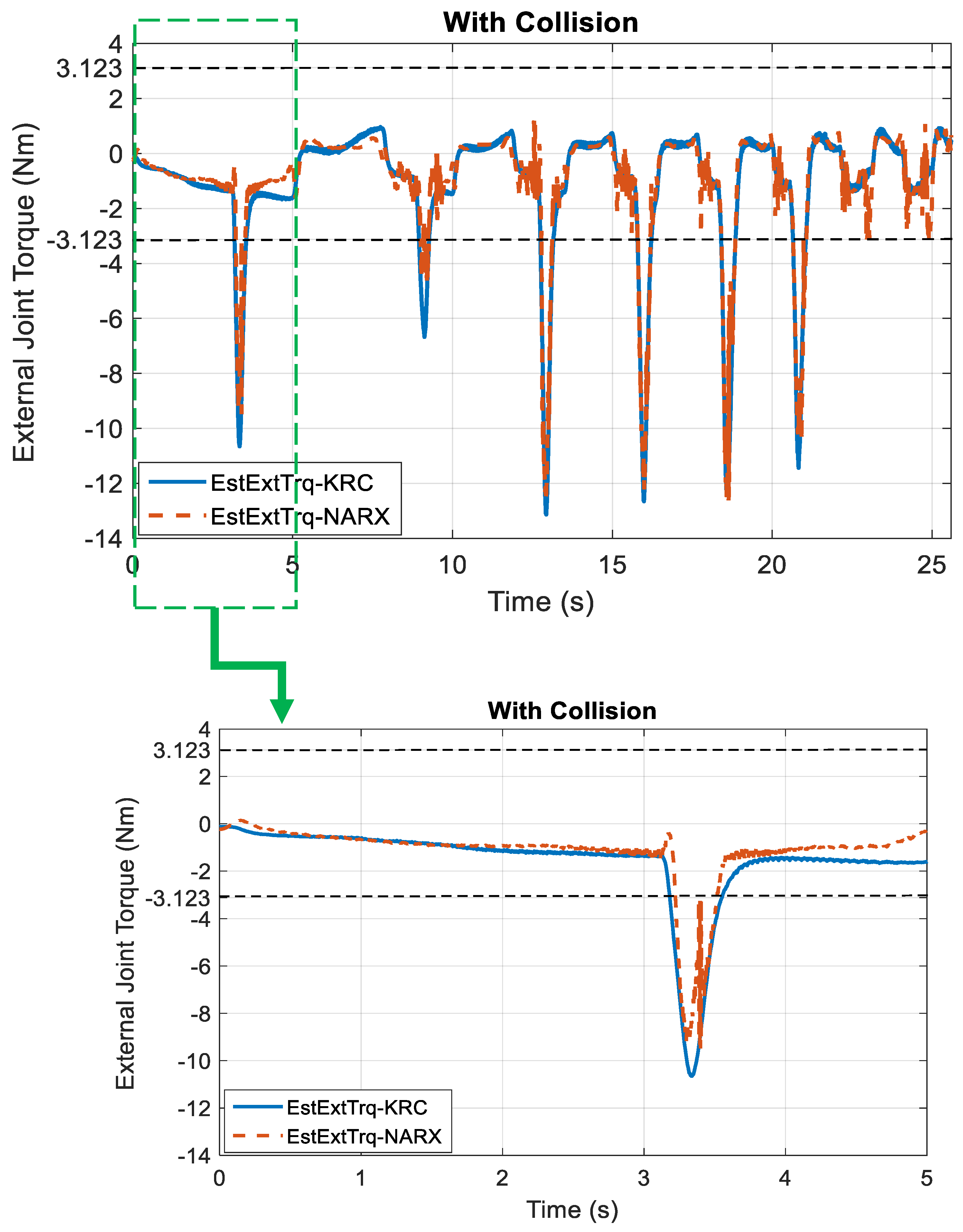
Test the trained NARXNN using the data with collision that is used for the training process and check the collisions using the determined collision threshold.

(8)

Check the effectiveness (%) of the trained NARXNN by performing many random different collisions with the robot based on the determined collision threshold.

All these steps are discussed and presented in detail in this section and the next sections.

The collected data from the executed experiments of the KUKA LWR manipulator in the first case where the motion has no collisions and in the second case where the collisions exist are used for training the designed NARXNN. The training occurs using the LM algorithm in MATLAB and using Intel(R) Core(TM) i5-8250U CPU @ 1.60 GHz processor. The number of pairs of input–output that are collected and used for the training process are 56358. These data are divided randomly into three parts: the first part comprising 80% is for training, the second part comprising 10% is used to make the validation, and the last part also comprising 10% is used to make the testing process. After investigating many different initializations of weights and many different numbers of the hidden neurons for finding the best parameters that achieve the high performance of the NARXNN, we obtained the following:

(1)

The hidden neuron number was 25.

(2)

The iteration/repetition number was 1000.

(3)

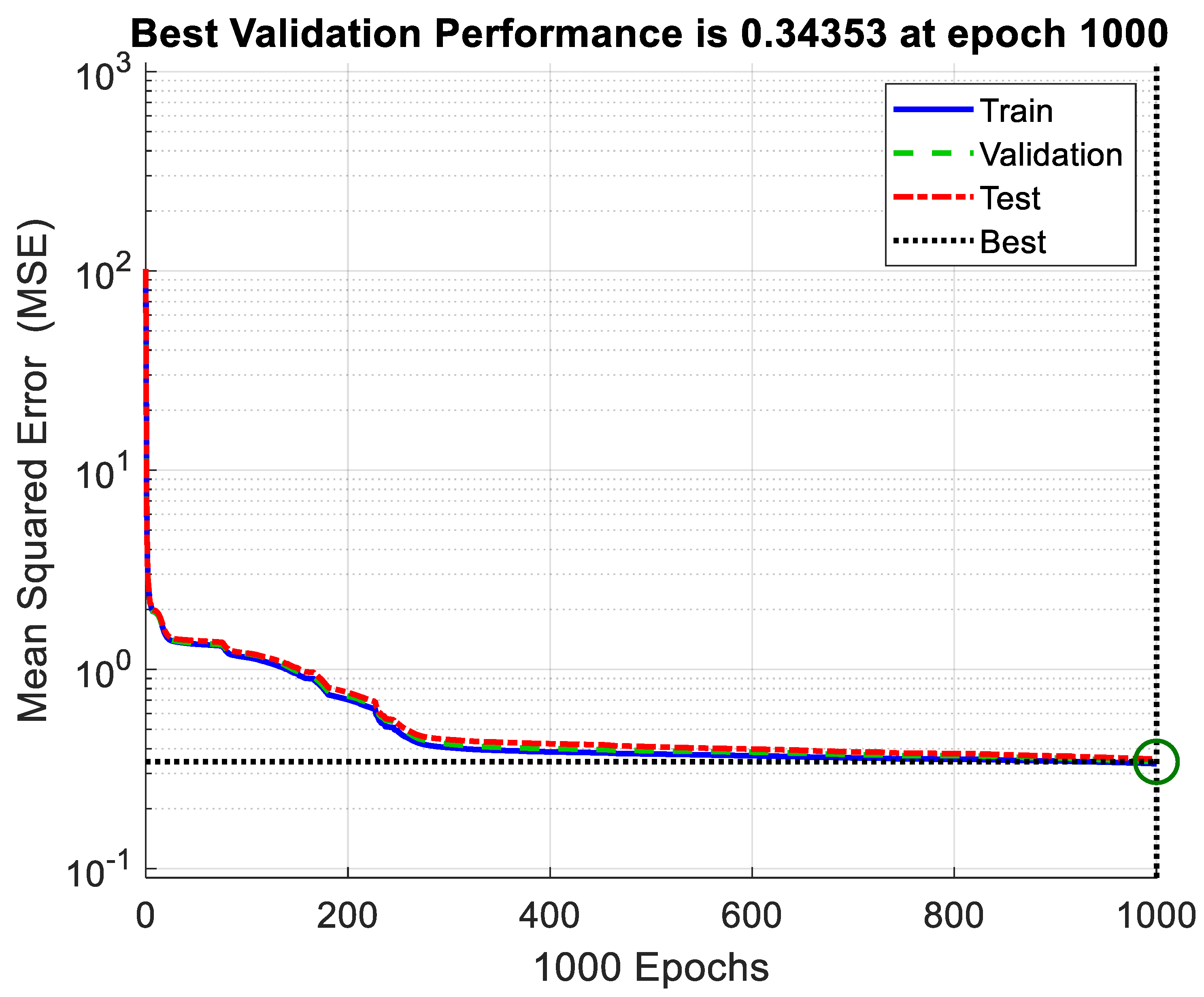
The lowest MSE was 0.34353. The equation used for calculating this MSE is given as follows:

$$\mathrm{MSE}={{\displaystyle \sum }}_{i=1}^n\frac{{\left({\tau }_{ext}\left(i\right)-{\tau }_{ext}^{\prime }\left(i\right)\right)}^2}{n}$$

(6)

(4)

The training time was 34 min and 28 s. This time had no importance because the important aim is to obtain a very well trained NARXNN that can detect and identify the robot’s collisions with humans efficiently. In addition, the training occurs offline.

The resulting MSE from the training process of the designed NARXNN is presented in Figure 6.

As shown in Figure 6, the resulting MSE is low and settles at the value of 0.34353. This proves that the designed NARXNN is trained well and is qualified for estimating the external joint’s torque.

After the process of training is finished in a complete way, this trained NARXNN is tested and verified using the same data that were used for the training. In the first step, using the data without collision, the approximating error that is the difference between the estimated external joint torque ${\tau }_{ext}^{\prime }$ and the provided one ${\tau }_{ext}$ is calculated and presented in Figure 7.

As shown in Figure 7, the approximating error in the case that there is no contact or collision is low. The average/mean of the absolute value of this error is $0.2759 \mathrm{Nm}$, and the standard deviation is $0.3342$. The collision threshold is represented as the maximum of the absolute value of this error, as defined in our previous work in [19,20,21,22,23,24]. Therefore, the collision threshold ${\tau }_{th}$ is equal to $3.123 \mathrm{Nm}$. The collision is detected once the external joint torque exceeds the collision threshold $\left(\left|{\tau }_{ext}^{\prime }\right|>{\tau }_{th}\right)$. The comparison between the defined collision’s threshold and ISO standards is presented as follows. In ISO/TS (15066) [42], the worst case for the reasons of safety is equal to $65 \mathrm{N}$, which represents the maximum value of the permissible force affecting the human face, creating pain or a minor injury, in the case of contact in a quasi-static condition. In the case of configurations of the KUKA LWR IV robotic manipulator, which represents the worst case for the human operator, the maximum external joint torque ${\tau }_{max}$ according to this force is equal to $30.42 \mathrm{Nm}$. By comparing the collision threshold by the maximum external torque ${\tau }_{max}$, the collision threshold is very low. This proves that the collaboration between the human and robot is in the region of safety, and the detection of the collision happens before causing pain or slight injurie. More discussions and illustrations about the collision threshold and how it is defined by other researchers are presented in our previous work [23,24,43].

In the second step, using the data with collision, the approximating error that is the difference between the estimated external joint’s torque ${\tau }_{ext}^{\prime }$ and the provided ${\tau }_{ext}$ is also calculated. This approximation error and the convergence between both torques are presented in Figure 8 and Figure 9.

As shown in Figure 8 and Figure 9, the approximation between the estimated external torque and the provided one, in the case of collisions, is good. This illustrates that the developed NARXNN is well trained. The average absolute value of this approximating error is $0.3965 \mathrm{Nm}$, and the corresponding standard deviation (std.) is $0.5839$. The approximation error in the case of collision is higher than the corresponding one in the case of no collision (Figure 7), which is logical. As shown in Figure 9, when a collision occurs, the estimated external joint torque exceeds the proposed threshold. This proves that the intended NARXNN is an efficient method for detecting the collision correctly.

The effectiveness (%) and the evaluation of the presented NARXNN using different data from the training data are presented in the next section.

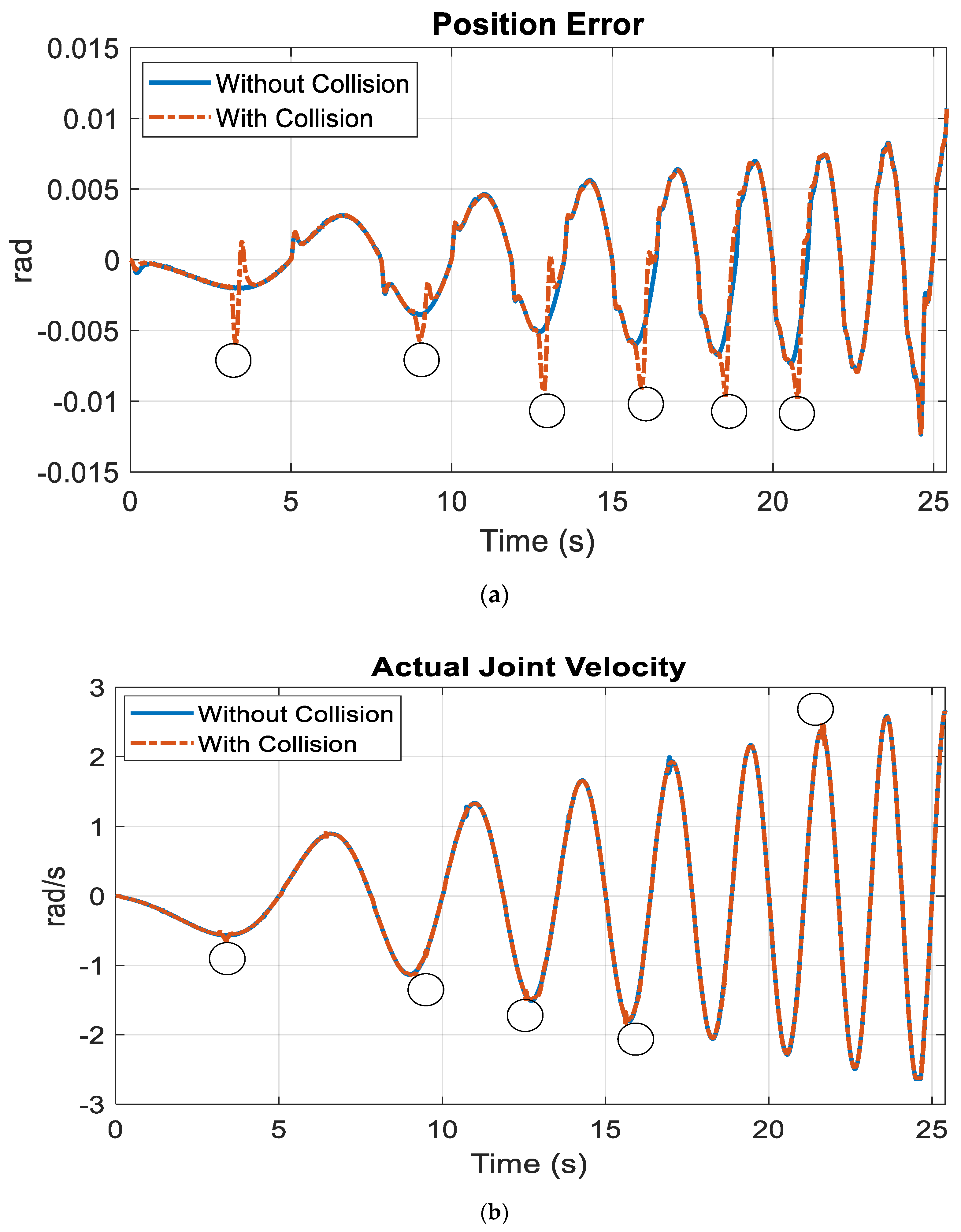
5. NARXNN Evaluation and Effectiveness

In this section, the effectiveness (%) of the NARXNN is investigated using different data from the training data. During the time of carrying out this study, the real robot did not exist to evaluate the NARXNN online (during the real-time work with the robot). Therefore, the NARXNN is evaluated and investigated offline by the same data presented in our previous papers [19,20]. These data are real and are obtained from the experimental work with the KUKA robot considering a sinusoidal motion with different velocities. During this motion, 25 random robot collisions were achieved with human hands at different directions and magnitudes. These achieved collisions are true negatives, TN. The evaluation of the NARXNN is illustrated in

Table 2. The effectiveness of the trained NARXNN considering the 25 executed random collisions.

The Trained NARXNN Effectiveness
The Parameter	The Number	The Percentage (%)
TN	25	100
TP	22	88
FN	3	12
FP	1	4
The overall effectiveness $\left(\frac{\mathrm{TP}-\mathrm{FP}}{\mathrm{TN}}\times 100\right)$	84%

considering the following parameters:

(1)

Correctly detected collisions are represented as true positives (TP).

(2)

Actual collisions not detected by the NARXNN are represented as false negatives (FN).

(3)

Alerts of collisions obtained by the trained NARXNN when no actual collision occurs are represented as false positives (FP).

From Table 2, the proposed trained NARXNN is an efficient method for the detection of the robot collision with the human. Its effectiveness is high (84%). Furthermore, the FP collision number is very low (4%), and this reveals that the NARXNN is robust. Its sensitivity to disturbances as well as unmodeled parameters is low.

The quantitative and qualitative comparison between the proposed trained NARXNN and the other previous NN architectures presented in our previous work [19,20] and other methods is discussed in the next section.

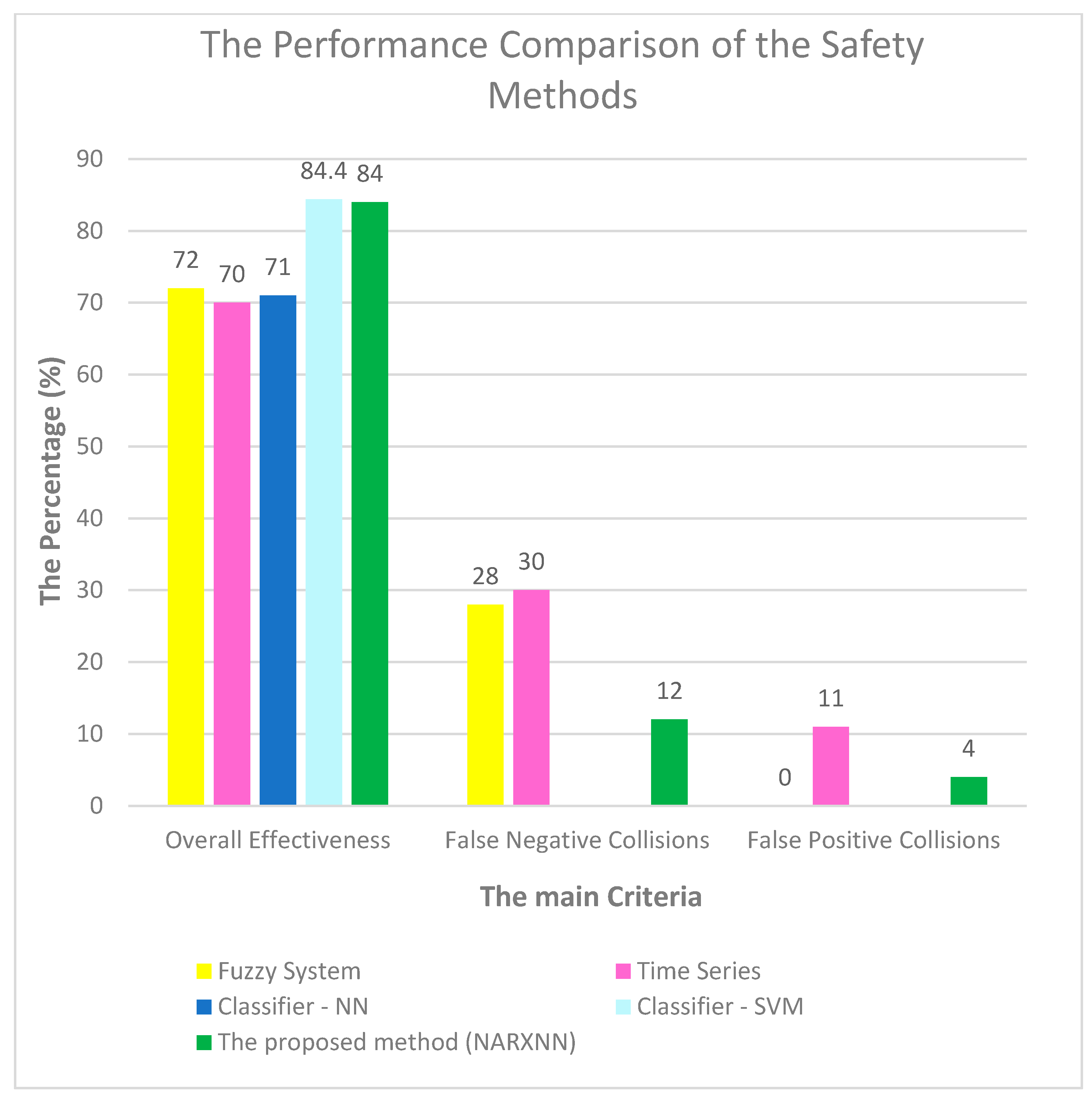
6. Quantitative and Qualitative Comparisons

In this section, a comparison between the proposed method and other previous published methods is presented.

Firstly, the comparison is presented between the proposed trained NARXNN and the previous NN architectures presented in our previous work [19,20]. These architectures are as follows:

▪

MLFFNN-1;

▪

MLFFNN-2;

▪

CFNN;

▪

RNN.

The comparison considers different parameters, as illustrated in

Table 3. The comparison between the developed NN structures (MLFFNN-1, MLFFNN-2, RNN, CFNN, NARXNN) for human–manipulator collision detection.

Parameter	NN’s Structure
	MLFFNN-1	MLFFNN-2	CFNN	RNN	NARXNN
Layers	3	4	3	3	3
Main Inputs	$\tilde{\theta }\left(k\right)$$, \tilde{\theta }\left(k-1\right)$$, {\dot{\theta }}_{ac}\left(k\right)$$, {\tau }_{msr}$	$\tilde{\theta }\left(k\right)$, $\tilde{\theta }\left(k-1\right)$, $\tilde{\theta }\left(k-2\right)$, ${\dot{\theta }}_{ac}\left(k\right)$, ${\dot{\theta }}_{ac}\left(k-1\right)$	$\tilde{\theta }\left(k\right)$$, \tilde{\theta }\left(k-1\right)$$, {\dot{\theta }}_{ac}\left(k\right)$,	$\tilde{\theta }\left(k\right)$$, \tilde{\theta }\left(k-1\right)$$, {\dot{\theta }}_{ac}\left(k\right)$,	$\tilde{\theta }\left(k\right)$$, \tilde{\theta }\left(k-1\right)$$, {\dot{\theta }}_{ac}\left(k\right)$,
Hidden neurons	90	35 in the first hidden layer, and 35 in the second hidden layer	35	20	25
Epochs/ Repetitions	932	1000	952	906	1000
Smallest MSE	0.040644	0.21682	0.392	0.43078	0.34353
Training time	29 min and 47 s	1 h, 53 min, and 18 s	4 min and 24 s	4 h, 41 min, and 53 s	34 min and 28 s
Average or mean of absolute of approximation error—case of free of contact motion	0.0955 Nm	0.2362 Nm	0.2992 Nm	0.3061 Nm	0.2759 Nm
Average or mean of absolute of approximation error—case of collision	0.1398 Nm	0.2779 Nm	0.4365 Nm	0.4456 Nm	0.3965 Nm
Collision threshold	1.6815 Nm	2.7423 Nm	3.4520 Nm	3.7500 Nm	3.123 Nm
FP collisions	8%	4%	0%	0%	4%
FN collisions	16%	16%	16%	20%	12%
Overall effectiveness	76%	80%	84%	80%	84%
Application	This structure is used in robots with torque sensors.	The structures are used with any conventional robot.

. $\tilde{\theta }\left(k\right)$ is the current error of position, $\tilde{\theta }\left(k-1\right)$ is the first previous error of position, $\tilde{\theta }\left(k-2\right)$ is the second previous error of position, ${\dot{\theta }}_{ac}\left(k\right)$ is the current actual velocity of joint, ${\dot{\theta }}_{ac}\left(k-1\right)$ is the previous actual velocity of the joint, and ${\tau }_{msr}$ is the measured joint torque.

From Table 3, the MSE, approximating the error mentioned in Section 4, and the collision threshold of the NARXNN structure are higher in comparison with the corresponding ones by MLFFNN-1 and MLFFNN-2 architectures. However, the effectiveness of the NARXNN for the detection of collisions is higher in comparison with other architectures. The NARXNN, MLFFNN-2, CFNN, and RNN structures are used with any conventional robot, whereas the MLFFNN-1 is used only with collaborative robotic manipulators, where the torque sensors exist, including the estimation of the torque signals of the joints.

Second, the effectiveness of the proposed method is compared with the corresponding one of other previously related approaches such as the fuzzy system [16], the time series-based approach [16], the classifier based on NN [44], the classifier based on support vector machine (SVM) [45], and Lu et al.’s approach based on NN [14]. This comparison includes the effectiveness of the method (%) in the collision detection and the number of FP and FN collisions and is presented in Figure 10. As shown in Figure 10, the proposed NARXNN and the classifier based on SVM have high effectiveness (%) compared with other methods. The problem with classifications is the neglect in the external force amplitude (collision). In addition, the classifier cannot be used as a practical system for this force estimation. The false positive collisions are very low with the proposed NARXXNN, and the fuzzy system compared with others. The effectiveness and the performance measure (%) of Lu et al.’s approach [14] were missing/not included.

7. Conclusions and Future Works

In this paper, a NARXNN was designed and trained to detect the collisions occurring between a human and the manipulator. For designing the proposed NARXNN, only the signals of the position sensors that are intrinsic to the manipulator’s joints were considered. This qualifies the NN structure to be used with any conventional robot or manipulator. The training of the NARXNN was executed using data generated from the experimental work with the KUKA LWR robotic manipulator considering two cases: the first case involved joint motion free of collision, and the second case was joint motion of random robot collisions with the human. The test and the verification of the NARXNN structure was investigated by the same training data. In addition, the effectiveness, and the evaluation (%) of the NARXNN were investigated by the use of different data and conditions from the training conditions. The results from this methodology prove that the approximation error between the estimated collision and the actual one is low. Furthermore, the trained NARXNN is efficient for estimating and detecting the collision with high percentage (84%). The number of FP collisions was very low (4%).

A comparison was presented between the current NARXNN and the previous NN architectures such as (1) MLFFNN-1, (2) MLFFNN-2, (3) CFNN, and (4) RNN. From this comparison, we concluded that the approximating error of NARXNN was higher compared with MLFNN-1 and MLFFNN-2. However, the effectiveness of the proposed NARXNN was higher. MLFFNN-2, CFNN, RNN, and NARXNN can be applied to any robot, whereas MLFFNN-1 can only be used with collaborative robotic manipulators where the signals of the joint torque sensors are available. The proposed NARXNN was compared with other previously published methods, and the comparison revealed that the proposed method has a high effectiveness (%) in detecting the collisions.

The results obtained in the current work motivate us to perform future work to further investigate the presented NN structures by executing many random collisions (e.g., two hundred collisions), and then, the trained NN effectiveness can be determined. In addition, new methods that depend on deep and machine learning can be investigated for human–manipulator collision detection.