Abstract
In the recent era, the rapidly increasing trend of e-commerce business creates opportunities for logistics service providers to grow globally. With this growth, the concern regarding the implementation of sustainability in logistic networks has received attention in recent years. Thus, in this work, we have focused on the vehicle routing problem (VRP) to deliver the products in a lesser time horizon with driver safety concern considerations in business (B2B) e-commerce platforms. We proposed a sustainable logistics network that captures the complexities of suppliers, retailers, and logistics service providers. A mixed-integer nonlinear programming (MINLP) approach is applied to formulate a model to minimize total time associated with order processing, handling, packaging, shipping, and vehicle maintenance. Branch-and-bound algorithms in the LINGO optimization tool and genetic algorithm (GA) are used to solve the formulated mathematical model. The computational experiments are performed in eight different case scenarios (small-sized problem to large-sized problem) to validate the model.
1. Introduction
There is an increasing trend of the e-commerce industry in recent years worldwide as more people are opting for online shopping. This is because of the range of products on the same platform, transparency of prices offered by sellers, convenience, discounts, and cashback offers provided by the e-commerce companies. Rising internet penetration into cities and rural areas of India further adds to the growth of e-commerce. Moreover, in the current scenario of COVID-19, to avoid personal contact, people have relied on online shopping, even for groceries and other basic household needs. Due to this, there is a significant growth of logistics companies, and the expected increment in it is expected to be USD 15.5 trillion within the forthcoming 10 years. Indian logistics companies’ raise is expected to be about 9–10 percent in a very short period [1].
The classic vehicle routing problem (VRP) puts attention on finding the shortest route that helps find the minimum time windows for the order delivery. Generally, the overall cost and time have a linear relation with the traveling distance [2]. The logistics service providers (LSPs) face new challenges like improving road safety concerns for drivers in driving time and road overcrowding. These challenges can be tackled by introducing some policies in favor of driver safety and road traffic. Policies may be responsible for tackling the difficulty level during efficient vehicle routes and enhancing the transport expenses regarding driver safety concerns [3]. Sustainability has become an essential factor for the financial performance as well as for implementation of a sustainable supply chain in practices in B2B e-commerce environment. Therefore, it is imperative to implement sustainability in practice by LSPs among the supply chain performers [4]. Moreover, there is a distinct silence in the sustainable B2B e-commerce logistics network design with drivers’ safety concerns when trying to achieve minimum order delivery time.
This research proposes a model for a sustainable logistics network for the VRP in B2B e-commerce. A mixed-integer nonlinear programming approach is used to formulate the mathematical model that captures the complexities of order processing, packaging, handling, and shipping times. It also considers the vehicle maintenance time due to accidents, damages, and other problems that arise when vehicles are driven at high speed.
The proposed MINLP model will enable us to minimize the total time window assigned for order delivery. The minimum traveling time is achieved by finding the optimized routes and increasing the vehicle’s speed under the limitation of the road traffic norms. In this study, we assumed that if vehicles are regularly moving at the speed of more than 70 km per hour then, additional time is required for vehicle maintenance. However, there is no maintenance time allowed for the vehicle having a speed below 70 km per hour. In this work, we attempt to minimize the time required for vehicle maintenance, which relates to the maintenance cost that comes under economic and social sustainability. There is a conflicting situation in between the minimum traveling time and the time required for vehicle maintenance. If we increase the speed of transport vehicles to achieve the minimum traveling time, then there is a more possibility of originating some damages and hazards during transportation. These damages are accountable for extra time as well as the cost required for their maintenance. In this study, the following research questions are guided:
- How to find the optimized delivery routes in a sustainable logistics network that help minimize the total delivery time horizon of an order in an e-commerce platform?
- How to mitigate the driver safety concern in the logistics system?
- How to minimize the order packaging and handling times to achieve the lesser delivery time horizon?
The rest of the paper is organized as follows: Section 2 provides the background of this research work. The problem description, along with mathematical formulation, is given in Section 3. The brief details of the considered solution methodologies used to solve the proposed model are provided in Section 4. A numerical example related to the first case scenario is given in Section 5. The computational experiments, results, and discussion, some managerial implications are demonstrated in Section 6. Finally, in Section 7, we have concluded the whole work and provided the limitation and future scope of this work.
2. Literature Review
H. K. Chen et al. [5] introduced the line haul-feeder VRP with virtual depots and time horizon. T. L. Chen et al. [6] have developed an MINLP comprehensive model to get the three decisions simultaneously; order batching, sequencing, and routing, within the least overall delay in the consumer orders delivery. A. Subramanyam et al. [7] aimed at a strategic decision-making problem with vehicle routing to allot the time horizons to consumers, which are affected by uncertainty in operations. D. Prajapati et al. [8] considered a VRP and focused on minimizing the transportation time with the time required for the maintenance of transport vehicles with economic sustainability. J.C. Molina et al. [9] focused on time windows in heterogeneous vehicle routing problems, which is a real extension of the standard VRP in that the routes to be designed with sharing of common resources. A. Muñoz-Villamizar et al. [10], studied a problem related to the e-commerce platform and measured the important disruption factors associated with last-mile delivery operations. The disruption causes delays, low service level, and high transportation costs during last-mile delivery transportation. Asefi et al. [11] investigate an integrated framework of the fleet size and mix vehicle routing problem for optimization of the cost-effective integrated solid waste management system. Y. Su et al. [12] developed an optimization strategy connected with an improved genetic algorithm to search valuable solutions for stakeholders’ preference more purposefully. Yousefi Nejad Attari et al. [13] addressed joint order batching measures of orders considering picker routing problems as a mixed-integer programming model by generating numerical experiments of small, medium, and large sizes. Gu Wenjuan et al. [14] addressed the commodity constrained split delivery vehicle routing problem in the scenarios in which customers need multiple commodities, which ascends when customers accept being delivered separately. Sabar, Nasser R. et al. [15] proposed an adaptive memetic approach that fits in new multi-parent crossover operators with multi-local search algorithms in an adaptive means. Araee Elham et al. [16] described a multi-objective model and stressed the progress of this mathematical structure in the area of optimal allocation of hazardous waste. Ancele, Yannis et al. [17] modeled and solved VRP with pickup and delivery with abundant attributes. The proposed model is then solved using a CPLEX optimization solver. Babaee Tirkolaee, Erfan et al. [18] addressed a new robust bi-objective multi-trip periodic capacitated arc routing problem with demand uncertainty to process the urban waste collection problem.
J. Lu et al. [19] studied a novel problem: time-dependent electric VRP that consists of routing electric vehicles in the fleet during serving the set of consumers and finding the speed of vehicles and departure time for each route. R.F. Fachini and V.A. Armentano [20] aimed to provide a service to the set of geographically dispersed consumers within their time windows through the capacitated and limited heterogeneous vehicles in a fleet. M. Keskin et al. [21] focused on electric VRP with time horizons and stochastic waiting time at the recharging stations, an advanced version of electric VRP with time horizons. Mostly, the vehicle routing approach neglects the necessity of refueling fleets [22].
P.N.K. Phuc and N.L.P. Thao [23] focused on explaining the VRP related to E-LSPs containing multiple pickup and delivery operations with heterogeneous fleets and time windows. They have used ant colony optimization (ACO) for the solution purpose of the proposed problem. D. Prajapati et al. [24] investigated an integrated sustainable vehicle routing, transportation, and supplier selection problem related to B2B e-commerce logistics. They have formulated an MINLP model to captures the complexities associated with the considered problem and solved it by using metaheuristics (i.e., the simulated annealing (SA) and invasive weed optimization (IWO)) and branch-and-bound algorithm in LINGO 18 software package. C.Y. Cheng et al. [25] proposed a hybrid particle swarm optimization (PSO) and ant colony optimization (ACO) algorithm for the solution of batch pickup and picker routing problems. A. Dwivedi et al. [26] proposed a sustainable agro-food grain supply chain network design and formulated an MINLP model to capture the realistic scenario. They have used genetic algorithm (GA), quantum-based GA, and LINGO optimization tool to select order set and vehicle allocation. Gutierrez Andres et al. [27] addressed a VRP with hard time windows attempted by a mixed stochastic program with recourse and chance constraints. Wu Weitiao et al. [28] presented a multi-period location-inventory-routing problem with time windows and fuel consumption and proposed a two-stage hybrid algorithm to solve this problem. The first stage was a customized genetic algorithm, and the second stage was a gradient descent algorithm. Tirkolaee, Erfan Babaee et al. [29] addressed an innovative model for the multi-trip green capacitated arc routing problem to minimize total cost. Due to NP-hardness, a hybrid genetic algorithm is developed and deployed. Babaee Tirkolaee, Erfan et al. [30] developed a hybrid augmented ant colony optimization algorithm based on an improved max–min ant system with a novel probability function and a simulated annealing algorithm to solve a chance-constrained programming model. Hamdia, Khader M. et al. [31] presented a procedure to optimize the architecture and the feature configurations of ML models with considerations of a supervised learning process. Goodarzian, Fariba et al. [32] proposed new heuristics to validate the model, two new meta-heuristic algorithms, which are an improved social engineering optimization (ISEO) and hybrid firefly and simulated annealing algorithm (HFFA-SA) have been established. Goodarzian, Fariba et al. [33] developed a new integrated production–transportation–ordering–inventory holding problem. The mathematical model developed is solved using two hybrid novel meta-heuristic algorithm (h1 and h2).
Based on the above literature, we have found that very few researchers have focused on minimizing the overall time required for delivery with the help of the best routes for order-vehicles assignment.
3. Problem Description
In this research work, we have considered a real-life B2B e-commerce logistics problem, which captures the sustainable VRP to minimize the total time horizon. This study focuses on developing a sustainable logistics network design related to the vehicle routing problem in the B2B e-commerce platform. The proposed network captures the complexities associated with the supplier, online retailers, and logistics service providers. The main aim is to minimize the delivery time horizon by finding the optimum vehicle routing and economical vehicle speed with sustainability and driver safety concerns. We have formulated an MINLP model to minimize the overall time required for the order’s delivery. This MINLP model consists of the time required for order processing, packaging, handling at supplier warehouse, traveling, and handling at retailer warehouse and time required for vehicle maintenance due to damage. For solution purposes, we have used two approaches as exact optimization approach, i.e., the branch-and-bound algorithm in LINGO 18 software package and metaheuristic approach, i.e., the genetic algorithm (GA) in MATLAB.
The graph G (Sk, Rl) is shown in Figure 1, where Sk is the set of supplier nodes, where k (k = 1, 2, …, K) is the indexing for suppliers, Rl is the set of retailer nodes, where l (l = 1, 2, …, L) is the indexing of retailers, and On is the set of orders placed by the retailers, where n (n = 1, 2, …, N) is the indexing of the orders. Availnk is the availability of orders at the supplier node, Demnl is the demand at retailer nodes, and xnkl is the binary decision variable, which helps in the selection of best possible routes with an availability constraint. Table 1 describes the terminologies (sets, parameters, decision variables) used in mathematical model.
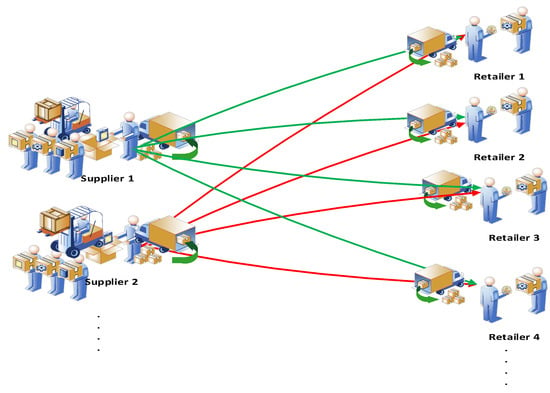
Figure 1.
A framework of B2B e-commerce logistics model.

Table 1.
Description of Terminology used in Mathematical Model.
OBObjective Function
Minimization {(order processing time) k + (order packaging time) k + (order handling time) k + (order traveling time) k → l + (vehicle maintenance time) k → l + (order processing time) l}
where,
Subjected to constraints
Equation (1) is the objective function, which computes the total time required for shipping of order batch from node k to node l. Equations (2)–(5) are used to compute the total order processing, packaging, handling at node k, and handling at node l, respectively. In contrast, Equations (6) and (7) are used to compute the total traveling and maintenance time, respectively. The constraints (8) ensure that the product’s availability at the supplier node should be greater than or is equal to the demanded quantity. Equation (9) restricted that the quantity moving from supplier point to destination point should be equal to the demanded quantity. Equation (10) was restricted to pick up order only once. Equation (11) decides the time required for maintenance. Equation (12) represents the binary decision variable for order pickup. Equation (13) shows the binary variable for the time required for the maintenance of vehicles.
4. Solution Methodology
The proposed work dealt with the order processing, packaging, handling and transportation times, and vehicle maintenance time required if vehicles are moving with more than 70 km per hour to achieve minimum transportation time. A mixed-integer nonlinear programming (MINLP) model is formulated, and the considered problem is broadly classified in VRP. Mostly, this type of problem is NP-hard in nature. IBM CPLEX [34,35], and LINGO optimization tool [26,36], were used to solve the vehicle routing problem, and the MINLP approach was used to formulate the mathematical model. The branch-and-bound algorithm in LINGO 18 software package and a meta-heuristic, i.e., genetic algorithm (GA), is used for the solution purpose of the proposed formulated model.
Genetic Algorithm
The genetic algorithm (GA) is developed in 1975 based on the evolutionary theory of survival of the fittest. The GA uses the natural biological system of reproduction and evolution. The basic GA has operators and operations such as selection, mutation, and crossovers. The GA was first used for the industry application in 1985 to design the optimized communication. Since then, the GA application has been widely used for constrained and unconstrained optimization problems.
Initially, chromosomes are created that are randomly generated solutions. The position in the chromosome is called a gene, and the value at each position is termed an allele. Then, these chromosomes are selected and added to the mating pool, which is termed selection. After that, crossover and mutation are applied to the parent chromosomes to generate new child chromosomes. The process of selection, crossover, and mutation is repeated until it meets the termination condition. The termination condition is said to be reached if the maximum number of generations are exhausted or the cost function values are stagnant.
Similarly, in the VRP problem, a chromosome is created, which is of a fixed size, and each element will store the set of design variables. The value of the design variable is based on the cost function. The cost function is the constraint under which we want to solve the problem. Then, through the selection process, the chromosomes are added to the mating pool, and operations like mutation and crossover are applied. The step-by-step procedure of GA is given in Figure 2.
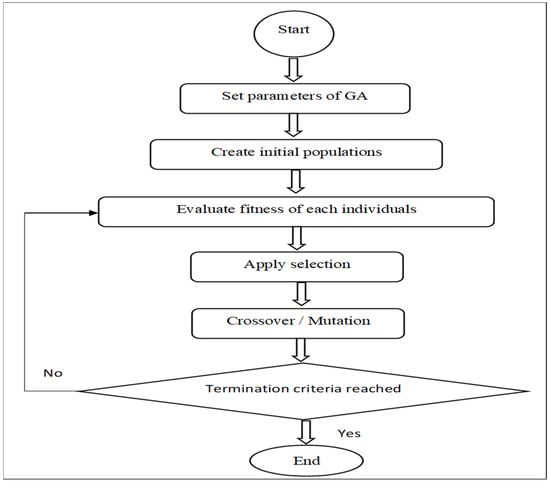
Figure 2.
Describes the flowchart of genetic algorithm.
5. Numerical Example
LINGO 18 and GA algorithm were used on a MATLAB 2014 (a) platform on a machine with the configuration—i5 processor (8.0 GHz), 64 bits, in Windows 10 platform—and determined the minimum total time horizons required for delivery of orders incurred in the B2B e-commerce logistics network.
5.1. Input Data for 1st Case Scenario
In this study, the proposed MINLP model is solved in eight different case scenarios, and the input data for the small-sized problem, i.e., the 1st case scenario, is given in Table 2, Table 3 and Table 4. There are two suppliers, three retailers, and three orders, and it is assumed that one order belongs to each retailer/demand point.

Table 2.
Total availability of products at the supplier points.

Table 3.
Demanded quantity of products from the retailer points.

Table 4.
Distance between the suppliers and retailers.
5.2. Output
In this case scenario, the total number of variables is 123, the total number of constraints is 19, and we found the total optimum time for the delivery of orders is 37.129 h within 0.30 s (computational time) from the exact optimization approach in LINGO 18 software package. However, the total optimum time for delivering orders is 42.019 h within 0.21 s (computational time) from GA, as presented in Table 4. The best possible routes for orders pickup and delivery are shown in Figure 3.
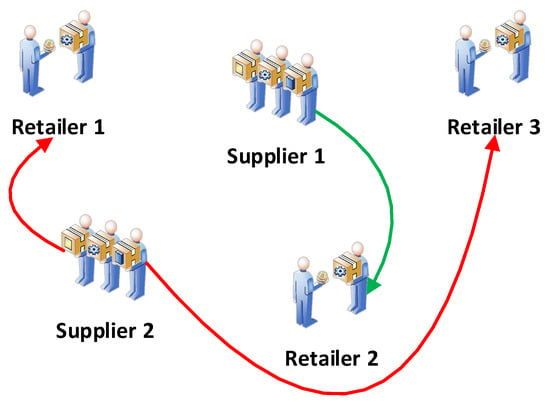
Figure 3.
Optimized vehicle route for order delivery.
6. Results and Discussion
6.1. Computational Experiments
We have performed the computational experiments in eight different case scenarios to validate the proposed model, as given in Table 5. In the last case scenario, i.e., the large-sized problem, there are 10 suppliers, 30 retailers, and 30 orders. The total number of variables and constraints are 20145 and 339, respectively. The total optimum time for delivering orders is 629.380 h with 149.34 s computational time, which are also given in Table 5.

Table 5.
Computational experiments of eight instances.
From Table 5, we can observe the conflicting situation in obtained values of the objective function and computational time for both approaches. In the small case scenario, there is a slight difference in computational time for both. However, in medium and large-size case scenarios, LINGO takes more time to get the feasible solution than GA, clearly portrayed in Figure 4 and numerically in Table 5. The values of the total time horizon (i.e., the objective function) have marginal differences while obtaining these from both approaches, i.e., branch-and-bound (B-and-B) and GA. However, the B-and-B algorithm performs better than the genetic algorithm, which is clearly presented in Figure 5 and numerically in Table 5. Figure 4 and Figure 5 are the comparative plots generated by using the first six instances. In these figures, series 2, i.e., the orange legend line, represents the data obtained from the branch-and-bound algorithm. In contrast, series 1, i.e., the blue legend line, represents GA’s data values. For the last two case scenarios, the results are achieved by GA only because the exact optimization approach in LINGO 18 software package takes large computation time.
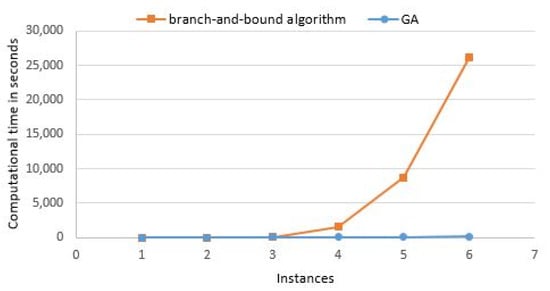
Figure 4.
Comparative plots in between computational time and number of instances.
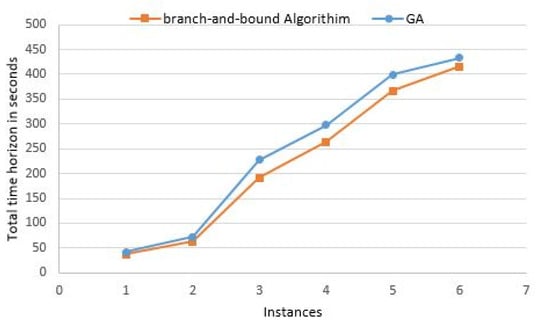
Figure 5.
Comparative plots in between total time horizon and number of instances.
6.2. Discussion
In today’s competitive situation, logistics has been positioned at the center of focus by company managers. In this regard, transportation is the most visible aspect of the supply chain that occupies a significant proportion of the logistics costs. As a result, companies try to create competitive merits by firming their transport section. The reduction of vehicle emissions is a key concern for many companies. They try to take approaches for decreasing their carbon footprint and therefore improving their green credentials. This research thus proposes a sustainable logistics network that captures the complexities associated with suppliers, retailers, and logistics service providers.
In this study, we considered a real-life B2B e-commerce logistics problem, which captures the sustainable VRP to minimize the total time horizon. The proposed network captures the complexities associated with the supplier, online retailers, and logistics service providers. The main aim is to minimize the delivery time horizon by finding the optimum vehicle routing and economical vehicle speed with sustainability and driver safety concerns. A mixed-integer nonlinear programming approach is applied to formulate a model to minimize total time associated with order processing, handling, packaging, shipping, and vehicle maintenance. The branch-and-bound algorithm in the LINGO optimization tool and genetic algorithm are used to solve the formulated mathematical model. The computational experiments are performed in 8 different case scenarios to validate the model. The branch-and-bound algorithm in LINGO 18 gave better results, but took more computational time than the genetic algorithm.
This research suggestively aids managers in selecting a solution that accounts for reducing total time horizons and considers driver safety concerns regarding the social-friendly aspects. Consequently, based on computational analyses presented in this work, we conclude that operational decisions can be significantly effective in reducing the total time horizon and improving the level of green ratio considering drivers’ safety concerns.
7. Conclusions
The rapid growth in the e-commerce market led to better and faster deliveries and a few challenges to overcome. Two of the major problems identified are sustainability concerns and safety factors. There is growing attention on sustainability in all sectors, and in e-commerce, it is even more. Thus, in this work, we have focused on the vehicle routing problem to deliver the products in a lesser time horizon with sustainability and driver safety considerations in the B2B e-commerce platform. In this study, we have developed a sustainable logistics network for B2B e-commerce. A mixed-integer nonlinear programming (MINLP) model is proposed to minimize the total time horizons, consisting of the order processing, packaging, handling, shipping times, and the time required for vehicle maintenance.
We have tested the proposed model in eight different case scenarios, which are demonstrated in the computational experiment. The optimized routes for orders pickup and delivery are found for all case scenarios, as shown in Figure 2 (first case scenario). The comparative results are provided in the computational experiments section. The obtained values of the objective function with the branch-and-bound algorithm in the LINGO 18 software package are slightly better than the genetic algorithm. However, the B-and-B algorithm takes more time to get feasible solutions than GA.
In this study, we have created a simulated data for making different case scenarios and to validate the proposed MINLP model. The limitation lies in the used data sets that allow only the theoretical overview of the findings. Accordingly, future researchers can shape the precise implications by testing the proposed sustainable logistics network related to the B2B e-commerce platform with research using real-life data sets. This study can be further extended by adding another objective function and bi-objective or multi-objective optimization that captures the overall cost associated with the logistics network in the B2B e-commerce platform.
Author Contributions
Conceptualization, S.P. and D.P.; methodology, D.P. and M.M.K.; software, D.P.; validation, S.P., D.P. and M.Z.; formal analysis and investigation, M.Z. and H.C.; writing—original draft preparation, D.P. and M.M.K.; writing—review and editing, S.P., M.Z.; supervision, S.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Simulated data-sets has been used.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Huang, Y.H.; Blazquez, C.A.; Huang, S.H.; Paredes-Belmar, G.; Latorre-Nuñez, G. Solving the Feeder Vehicle Routing Problem using ant colony optimization. Comput. Ind. Eng. 2019, 127, 520–535. [Google Scholar] [CrossRef]
- Li, J.; Wang, D.; Zhang, J. Heterogeneous fixed fleet vehicle routing problem based on fuel and carbon emissions. J. Clean. Prod. 2018, 201, 896–908. [Google Scholar] [CrossRef]
- Rincon-Garcia, N.; Waterson, B.; Cherrett, T.J.; Salazar-Arrieta, F. A metaheuristic for the time-dependent vehicle routing problem considering driving hours regulations—An application in city logistics. Transp. Res. Part A Policy Pract. 2020, 137, 429–446. [Google Scholar] [CrossRef] [Green Version]
- Ali, A.H.; Melkonyan, A.; Noche, B.; Gruchmann, T. Developing a Sustainable Logistics Service Quality Scale for Logistics Service Providers in Egypt. Logistics 2021, 5, 21. [Google Scholar] [CrossRef]
- Chen, H.K.; Chou, H.W.; Hsu, C.Y. The linehaul-feeder vehicle routing problem with virtual depots and time windows. Math. Probl. Eng. 2011, 2011, 759418. [Google Scholar] [CrossRef] [Green Version]
- Chen, T.L.; Cheng, C.Y.; Chen, Y.Y.; Chan, L.K. An efficient hybrid algorithm for integrated order batching, sequencing and routing problem. Int. J. Prod. Econ. 2015, 159, 158–167. [Google Scholar] [CrossRef]
- Subramanyam, A.; Wang, A.; Gounaris, C.E. A scenario decomposition algorithm for strategic time window assignment vehicle routing problems. Transp. Res. Part B Methodol. 2018, 117, 296–317. [Google Scholar] [CrossRef] [Green Version]
- Prajapati, D.; Zhou, F.; Cheikhrouhou, N.; Pratap, S. Minimizes the Time Window for Delivery of Orders in B2B E-commerce. In Proceedings of the 5th International Conference on Industrial Engineering (ICIE), Sochi, Russia, 18–19 November 2019; pp. 1–6. [Google Scholar]
- Molina, J.C.; Salmeron, J.L.; Eguia, I.; Racero, J. The heterogeneous vehicle routing problem with time windows and a limited number of resources. Eng. Appl. Artif. Intell. 2020, 94, 103745. [Google Scholar] [CrossRef]
- Muñoz-Villamizar, A.; Solano-Charris, E.L.; Reyes-Rubiano, L.; Faulin, J. Measuring Disruptions in Last-Mile Delivery Operations. Logistics 2021, 5, 17. [Google Scholar] [CrossRef]
- Asefi, H.; Shahparvari, S.; Chhetri, P.; Lim, S. Variable fleet size and mix VRP with fleet heterogeneity in Integrated Solid Waste Management. J. Clean. Prod. 2019, 230, 1376–1395. [Google Scholar] [CrossRef]
- Su, Y.; Jin, S.; Zhang, X.; Shen, W.; Eden, M.R.; Ren, J. Stakeholder-oriented multi-objective process optimization based on an improved genetic algorithm. Comput. Chem. Eng. 2020, 132, 106618. [Google Scholar] [CrossRef]
- Attari, M.Y.N.; Torkayesh, A.E.; Malmir, B.; Jami, E.N. Robust possibilistic programming for joint order batching and picker routing problem in warehouse management. Int. J. Prod. Res. 2021, 59, 4434–4452. [Google Scholar] [CrossRef]
- Gu, W.; Cattaruzza, D.; Ogier, M.; Semet, F. Adaptive large neighborhood search for the commodity constrained split delivery VRP. Comput. Oper. Res. 2019, 112, 104761. [Google Scholar] [CrossRef] [Green Version]
- Sabar, N.R.; Bhaskar, A.; Chung, E.; Turky, A.; Song, A. An Adaptive Memetic Approach for Heterogeneous Vehicle Routing Problems with two-dimensional loading constraints. Swarm Evol. Comput. 2020, 58, 100730. [Google Scholar] [CrossRef]
- Araee, E.; Manavizadeh, N.; Bosjin, S.A. Designing a multi-objective model for a hazardous waste routing problem considering flexibility of routes and social effects. J. Ind. Prod. Eng. 2020, 37, 33–45. [Google Scholar] [CrossRef]
- Ancele, Y.; Hà, M.H.; Lersteau, C.; Matellini, D.B.; Nguyen, T.T. Toward a more flexible VRP with pickup and delivery allowing consolidations. Transp. Res. Part C Emerg. Technol. 2021, 128, 103077. [Google Scholar] [CrossRef]
- Tirkolaee, E.B.; Goli, A.; Pahlevan, M.; Kordestanizadeh, R.M. A robust bi-objective multi-trip periodic capacitated arc routing problem for urban waste collection using a multi-objective invasive weed optimization. Waste Manag. Res. 2019, 37, 1089–1101. [Google Scholar] [CrossRef]
- Lu, J.; Chen, Y.; Hao, J.K.; He, R. The Time-dependent Electric Vehicle Routing Problem: Model and solution. Expert Syst. Appl. 2020, 161, 113593. [Google Scholar] [CrossRef]
- Fachini, R.F.; Armentano, V.A. Logic-based Benders decomposition for the heterogeneous fixed fleet vehicle routing problem with time windows. Comput. Ind. Eng. 2020, 148, 106641. [Google Scholar] [CrossRef]
- Keskin, M.; Çatay, B.; Laporte, G. A simulation-based heuristic for the electric vehicle routing problem with time windows and stochastic waiting times at recharging stations. Comput. Oper. Res. 2021, 125, 105060. [Google Scholar] [CrossRef]
- Neves-Moreira, F.; Amorim-Lopes, M.; Amorim, P. The multi-period vehicle routing problem with refueling decisions: Traveling further to decrease fuel cost? Transp. Res. Part E Logist. Transp. Rev. 2020, 133, 101817. [Google Scholar] [CrossRef]
- Nejad Attari, M.Y.; Torkayesh, A.E.; Jami, E.N. Ant Colony Optimization for Multiple Pickup and Multiple Delivery Vehicle Routing Problem with Time Window and Heterogeneous Fleets. Logistics 2021, 59, 28. [Google Scholar] [CrossRef]
- Prajapati, D.; Zhou, F.; Zhang, M.; Chelladurai, H.; Pratap, S. Sustainable logistics network design for multi-products delivery operations in B2B e-commerce platform. Sādhanā 2021, 46, 100. [Google Scholar] [CrossRef]
- Cheng, C.Y.; Chen, Y.Y.; Chen, T.L.; Yoo, J.J. Using a hybrid approach based on the particle swarm optimization and ant colony optimization to solve a joint order batching and picker routing problem. Int. J. Prod. Econ. 2015, 170, 805–814. [Google Scholar] [CrossRef]
- Dwivedi, A.; Jha, A.; Prajapati, D.; Sreenu, N.; Pratap, S. Meta-heuristic algorithms for solving the sustainable agro-food grain supply chain network design problem. Mod. Supply Chain Res. Appl. 2020. [Google Scholar] [CrossRef]
- Gutierrez, A.; Dieulle, L.; Labadie, N.; Velasco, N. A multi-population algorithm to solve the VRP with stochastic service and travel times. Comput. Ind. Eng. 2018, 125, 144–156. [Google Scholar] [CrossRef]
- Wu, W.; Zhou, W.; Lin, Y.; Xie, Y.; Jin, W. A hybrid metaheuristic algorithm for location inventory routing problem with time windows and fuel consumption. Expert Syst. Appl. 2021, 166, 114034. [Google Scholar] [CrossRef]
- Tirkolaee, E.B.; Hosseinabadi, A.A.R.; Soltani, M.; Sangaiah, A.K.; Wang, J. A Hybrid genetic algorithm for multi-trip green capacitated Arc routing problem in the scope of urban services. Sustainability 2018, 10, 1366. [Google Scholar] [CrossRef] [Green Version]
- Tirkolaee, E.B.; Mahdavi, I.; Esfahani, M.M.S.; Weber, G.W. A hybrid augmented ant colony optimization for the multi-trip capacitated arc routing problem under fuzzy demands for urban solid waste management. Waste Manag. Res. 2020, 38, 156–172. [Google Scholar] [CrossRef]
- Hamdia, K.M.; Zhuang, X.; Rabczuk, T. An efficient optimization approach for designing machine learning models based on genetic algorithm. Neural Comput. Appl. 2021, 33, 1923–1933. [Google Scholar] [CrossRef]
- Goodarzian, F.; Kumar, V.; Ghasemi, P. A set of efficient heuristics and meta-heuristics to solve a multi-objective pharmaceutical supply chain network. Comput. Ind. Eng. 2021, 158, 107389. [Google Scholar] [CrossRef]
- Goodarzian, F.; Kumar, V.; Abraham, A. Hybrid. Meta-Heuristic Algorithms for a Supply Chain Network Considering Different Carbon Emission Regulations Using Big Data Characteristics; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar] [CrossRef]
- Daultani, Y.; Cheikhrouhou, N.; Pratap, S.; Prajapati, D. Designing Forward and Reverse Supply Chain Network for Refurbished Products. In Proceedings of the 9th International Conference on Operations and Supply Chain Management, Ho Chi Minh City, Vietnam, 15–18 December 2019; pp. 1–7. [Google Scholar]
- Zhang, M.; Pratap, S.; Zhao, Z.; Prajapati, D.; Huang, G.Q. Forward and reverse logistics vehicle routing problems with time horizons in B2C e-commerce logistics. Int. J. Prod. Res. 2020, 1–20. [Google Scholar] [CrossRef]
- Prajapati, D.; Harish, A.R.; Daultani, Y.; Singh, H.; Pratap, S. A Clustering Based Routing Heuristic for Last-Mile Logistics in Fresh Food E-Commerce. Glob. Bus. Rev. 2020. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).