Figure 1.
A scene representing a worker’s reasoning to decide on search locations given temporal location information. (a)With just the current snapshot of the workspace, search for a workpiece defaults to chance for any worker. (b) Information on events leading up to the disappearance of workpiece 6, however, immediately introduces priority search locations of workpieces 12 and 14 based on simple reasoning of proximity. (c) The search strategy evolves along with the movement of workpieces as the initial suspected stack location, workpiece 12, is moved (d) This process can be chained with further changes in workpieces based on workers’ reasoning for the propagation of stacks.
Figure 1.
A scene representing a worker’s reasoning to decide on search locations given temporal location information. (a)With just the current snapshot of the workspace, search for a workpiece defaults to chance for any worker. (b) Information on events leading up to the disappearance of workpiece 6, however, immediately introduces priority search locations of workpieces 12 and 14 based on simple reasoning of proximity. (c) The search strategy evolves along with the movement of workpieces as the initial suspected stack location, workpiece 12, is moved (d) This process can be chained with further changes in workpieces based on workers’ reasoning for the propagation of stacks.
Figure 2.
Cameras attached to a worker’s gear to observe the immediate environment. (a) A worker’s helmet fitted with USB cameras to provide the field of view of the worker to our system. (b) Easy access to power switches, charging ports and an SD card slot allows for quick access and charging when the hardhat is not in use. (c) Internally, the hardhat houses the battery and Raspberry-Pi. This allows each mover to behave as an IoT device for information collection.
Figure 2.
Cameras attached to a worker’s gear to observe the immediate environment. (a) A worker’s helmet fitted with USB cameras to provide the field of view of the worker to our system. (b) Easy access to power switches, charging ports and an SD card slot allows for quick access and charging when the hardhat is not in use. (c) Internally, the hardhat houses the battery and Raspberry-Pi. This allows each mover to behave as an IoT device for information collection.
Figure 3.
Workpieces tagged with AR markers used for experiments at the shipyard. (a) Real-world workpieces within the shipyard viewed by a worker. (b) Test environment where the workpieces were moved by workers to evaluate our system under real-world mover behavior.
Figure 3.
Workpieces tagged with AR markers used for experiments at the shipyard. (a) Real-world workpieces within the shipyard viewed by a worker. (b) Test environment where the workpieces were moved by workers to evaluate our system under real-world mover behavior.
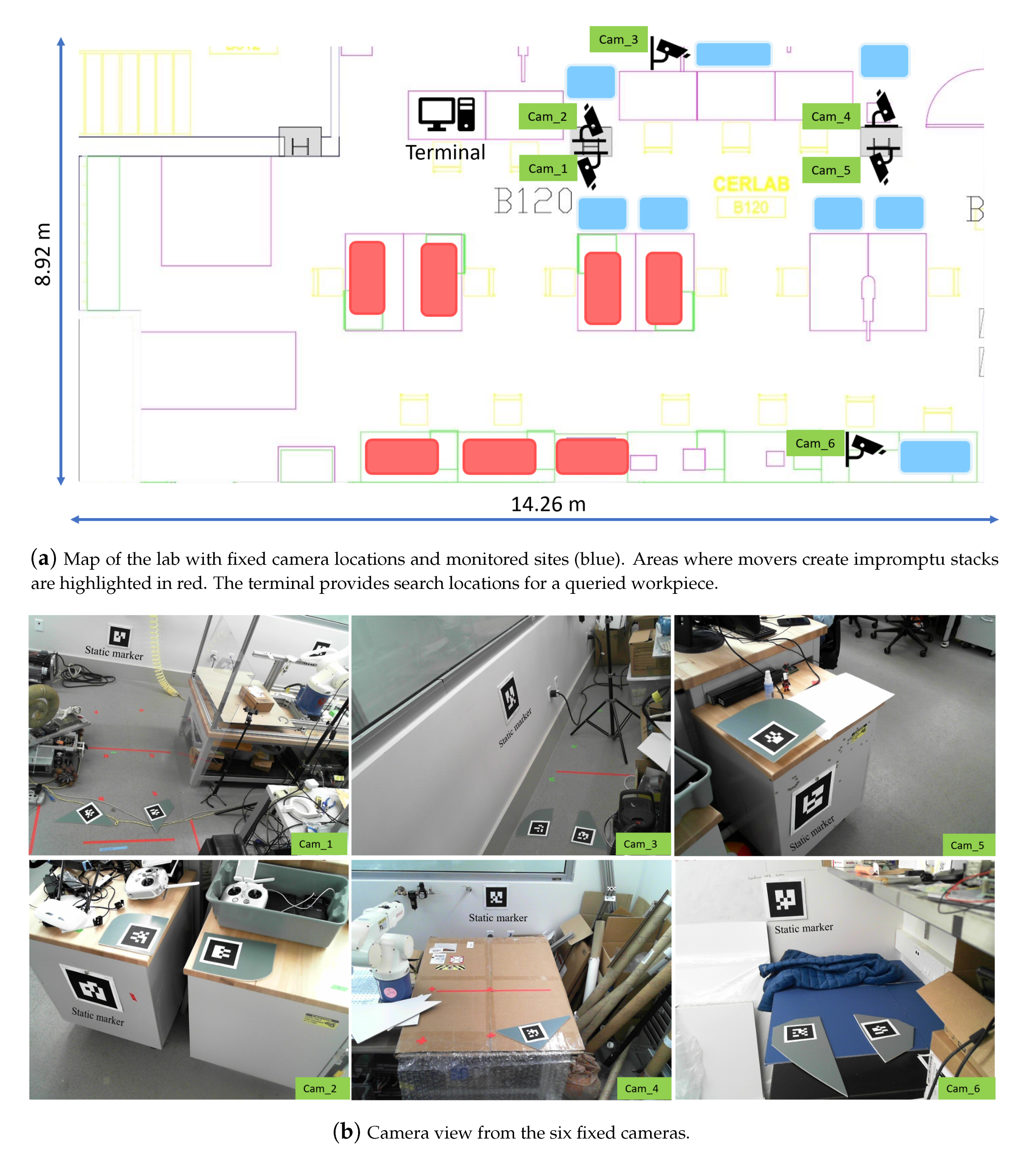
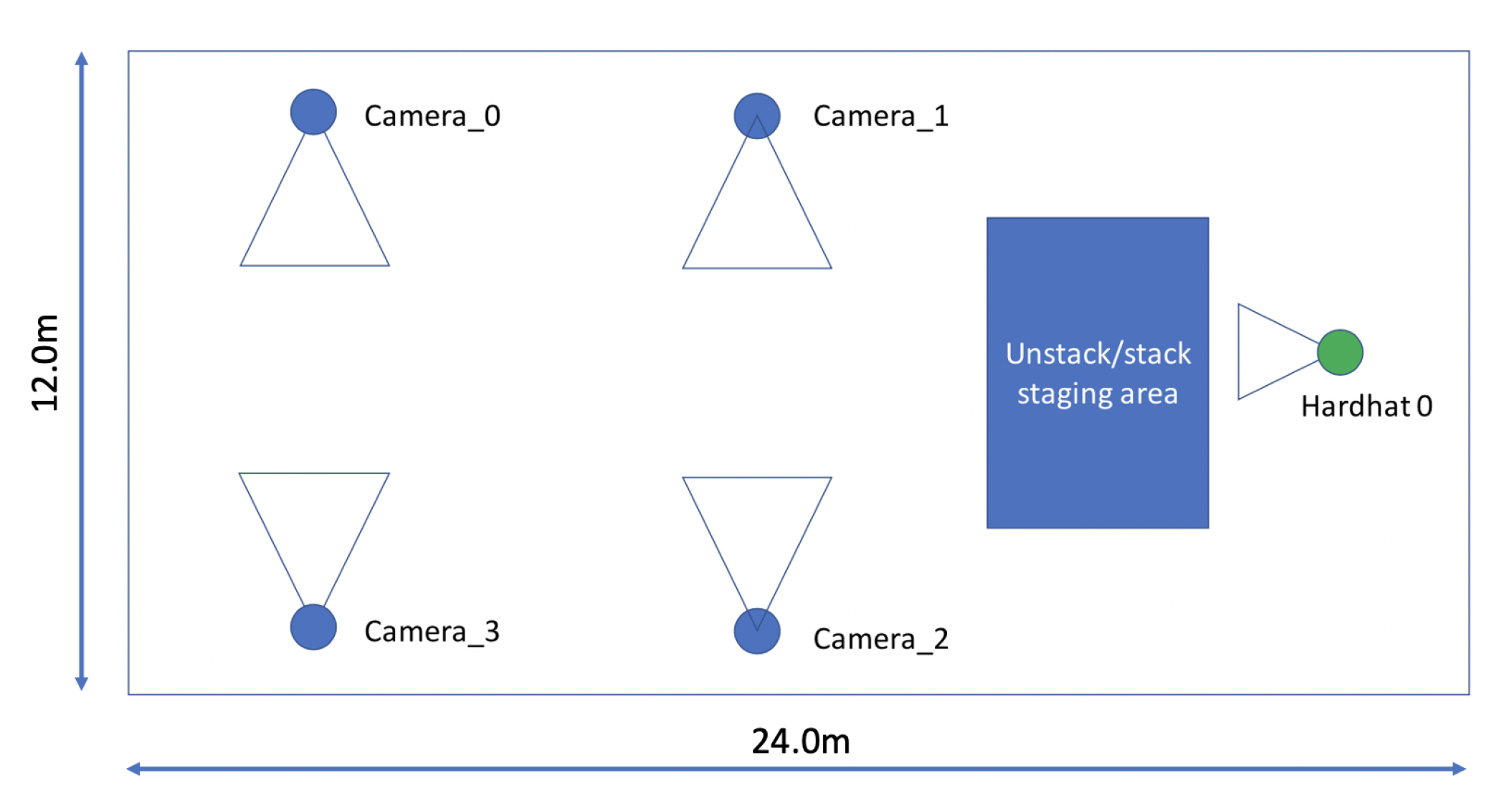
Figure 4.
Workspace scene setup in the lab. (a) Map of our lab with highlighted fixed camera and inventory storage locations. Areas being monitored by the fixed cameras are highlighted in blue whereas areas that are not constantly monitored but represent space where movers could make impromptu stacks are highlighted in red. (b) Images of storage locations containing workpieces (grey) and static markers (white) as viewed by the fixed cameras.
Figure 4.
Workspace scene setup in the lab. (a) Map of our lab with highlighted fixed camera and inventory storage locations. Areas being monitored by the fixed cameras are highlighted in blue whereas areas that are not constantly monitored but represent space where movers could make impromptu stacks are highlighted in red. (b) Images of storage locations containing workpieces (grey) and static markers (white) as viewed by the fixed cameras.
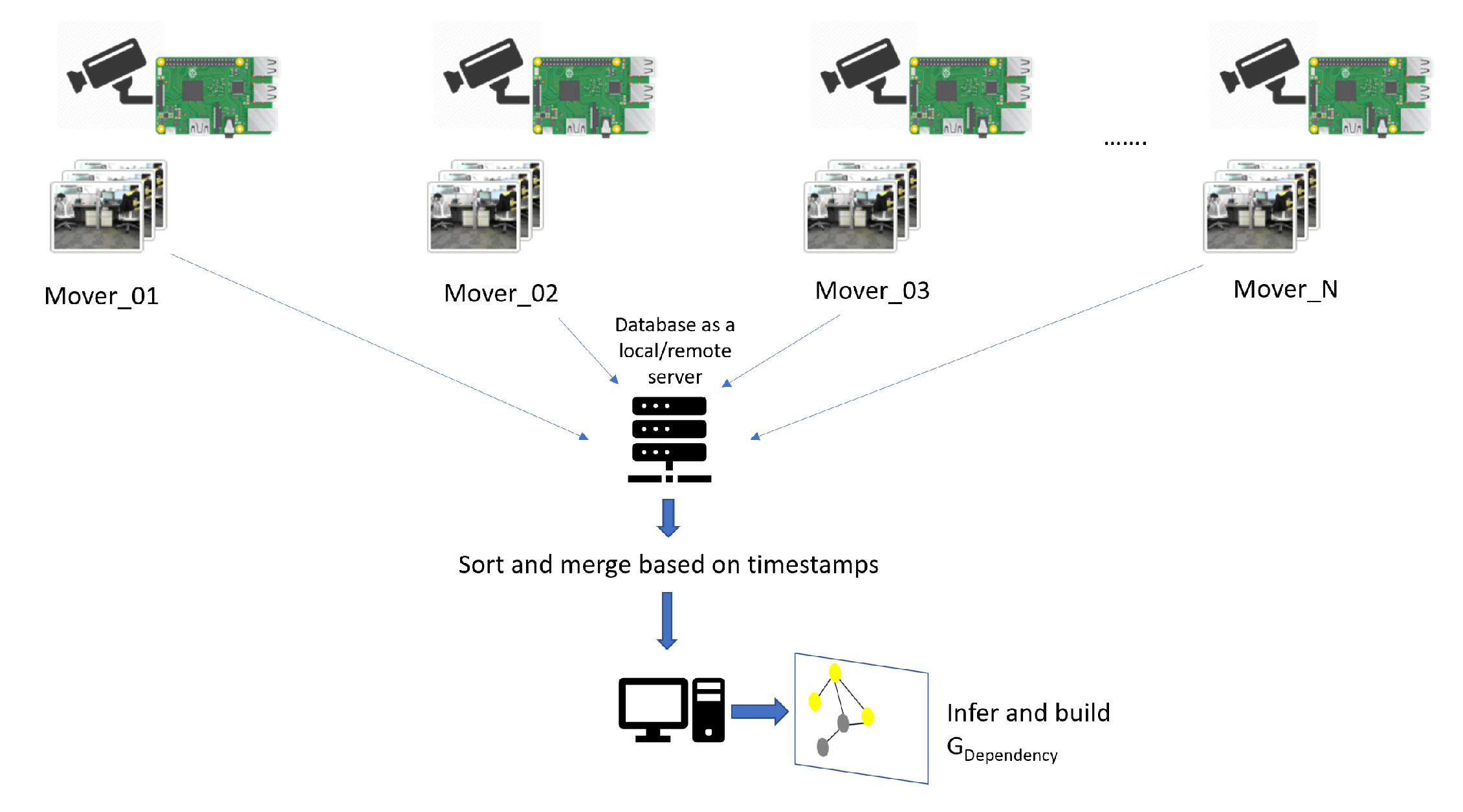
Figure 5.
Scalable IoT-type architecture for information collection. Each mover pushes their observed images onto a database when a connection is available. This architecture allows for images from observers across vast work areas to pool their data, allowing for workpieces to be tracked across the entire scope of the work site.
Figure 5.
Scalable IoT-type architecture for information collection. Each mover pushes their observed images onto a database when a connection is available. This architecture allows for images from observers across vast work areas to pool their data, allowing for workpieces to be tracked across the entire scope of the work site.
Figure 6.
Offline information collection setup when Wi-Fi is unavailable. For each mover wearing the hardhat as an IoT device, observations as images are transferred to the database immediately when the Wi-Fi signals are strong. However, when a mover is out of range or under poor Wi-Fi coverage, data are locally stored and pushed to the database when a connection can be established. This makes sure that all observations are available at the end of the day when all hardhats are within Wi-Fi range.
Figure 6.
Offline information collection setup when Wi-Fi is unavailable. For each mover wearing the hardhat as an IoT device, observations as images are transferred to the database immediately when the Wi-Fi signals are strong. However, when a mover is out of range or under poor Wi-Fi coverage, data are locally stored and pushed to the database when a connection can be established. This makes sure that all observations are available at the end of the day when all hardhats are within Wi-Fi range.
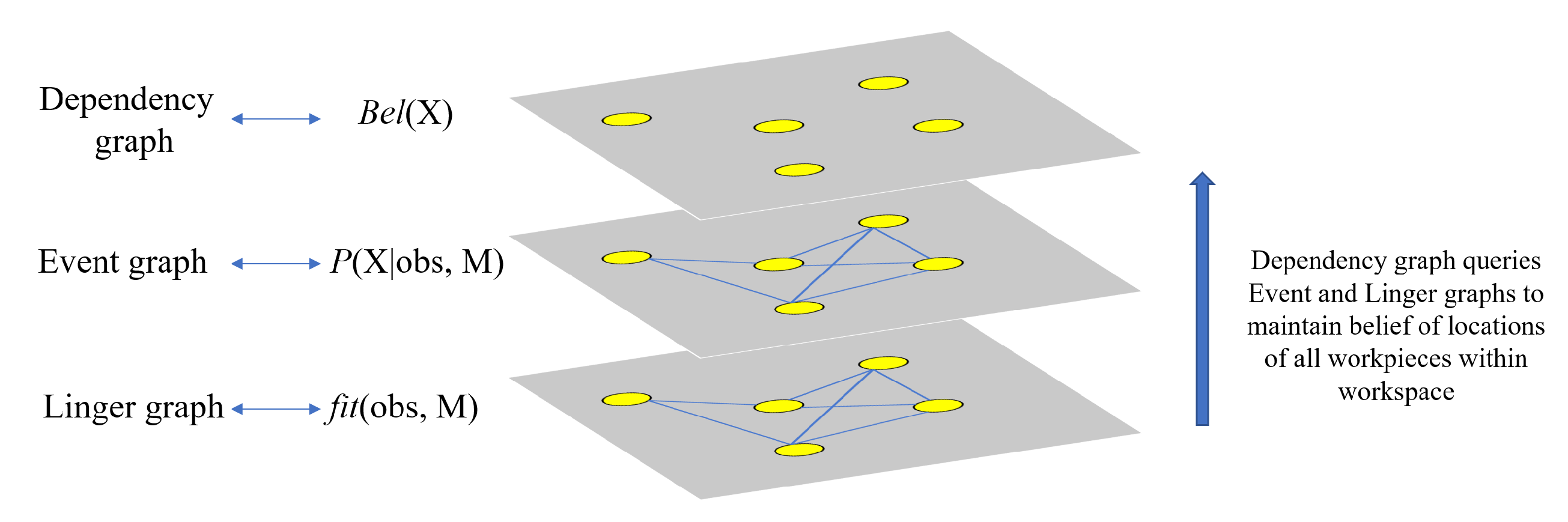
Figure 7.
Linger, event and dependency graphs to calculate stack fit, stack likelihood and overall belief of the positions of workpieces within a workspace, respectively. M represents the reasoning model based on human knowledge of the behavior of stacks and its propagation based on available detections of a workpiece.
Figure 7.
Linger, event and dependency graphs to calculate stack fit, stack likelihood and overall belief of the positions of workpieces within a workspace, respectively. M represents the reasoning model based on human knowledge of the behavior of stacks and its propagation based on available detections of a workpiece.
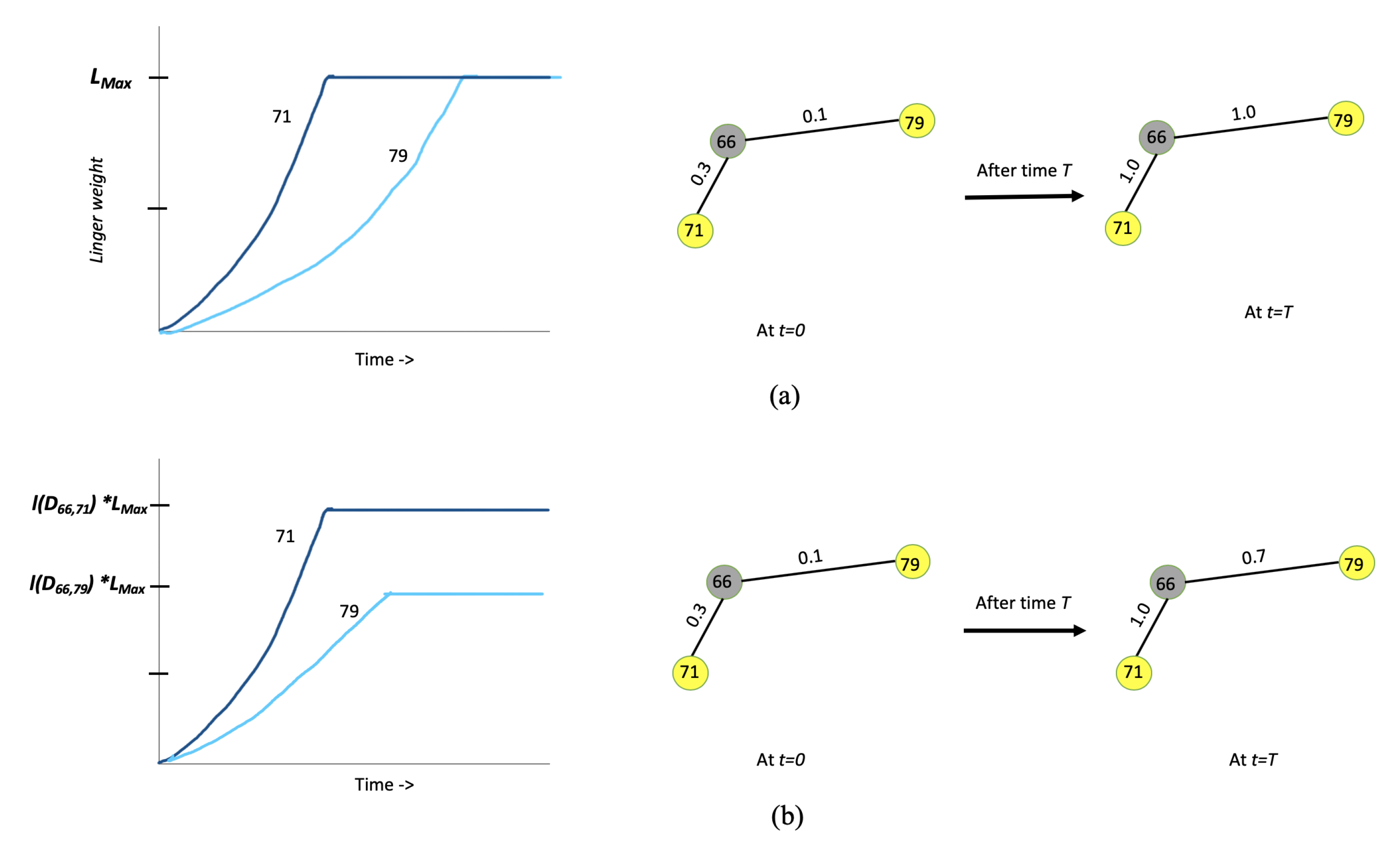
Figure 8.
Calculating pairwise fit for events between workpieces. (a) A representation of cases where linger weights are (top) increased when workpieces are within proximity and (bottom) when workpieces are out of proximity. (b) Examples of to increase and decrease weights based on proximity.
Figure 8.
Calculating pairwise fit for events between workpieces. (a) A representation of cases where linger weights are (top) increased when workpieces are within proximity and (bottom) when workpieces are out of proximity. (b) Examples of to increase and decrease weights based on proximity.
Figure 9.
Previous method (a) cannot differentiate workpieces within proximity after a certain period of time, making them all equally likely stack positions for a missing workpiece. Proposed approach (b) can differentiate most likely stack location even amongst workpieces within a neighborhood.
Figure 9.
Previous method (a) cannot differentiate workpieces within proximity after a certain period of time, making them all equally likely stack positions for a missing workpiece. Proposed approach (b) can differentiate most likely stack location even amongst workpieces within a neighborhood.
Figure 10.
When workpiece 1 becomes occluded near workpieces 2 and 3, stack order sets workpieces 2 and 3 as possible parent nodes for workpiece 1. This represents the case where workpiece 1 could be stacked under 2 or 3.
Figure 10.
When workpiece 1 becomes occluded near workpieces 2 and 3, stack order sets workpieces 2 and 3 as possible parent nodes for workpiece 1. This represents the case where workpiece 1 could be stacked under 2 or 3.
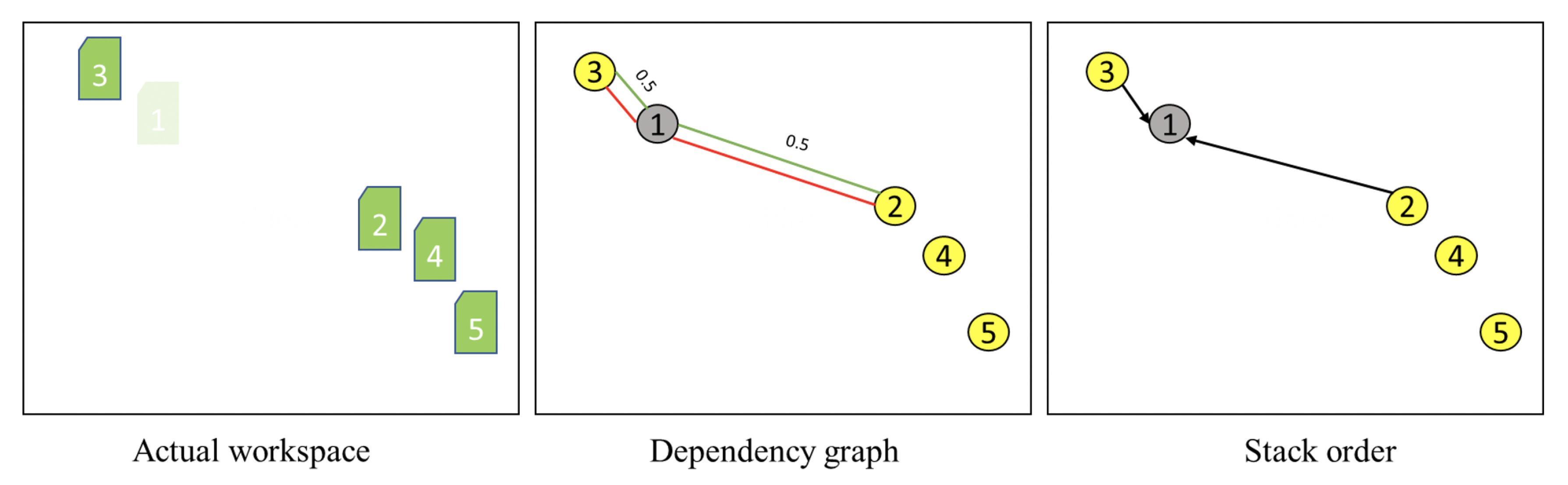
Figure 11.
The dependency graph state in our current approach and previous approach is exactly the same up to this scene.
Figure 11.
The dependency graph state in our current approach and previous approach is exactly the same up to this scene.
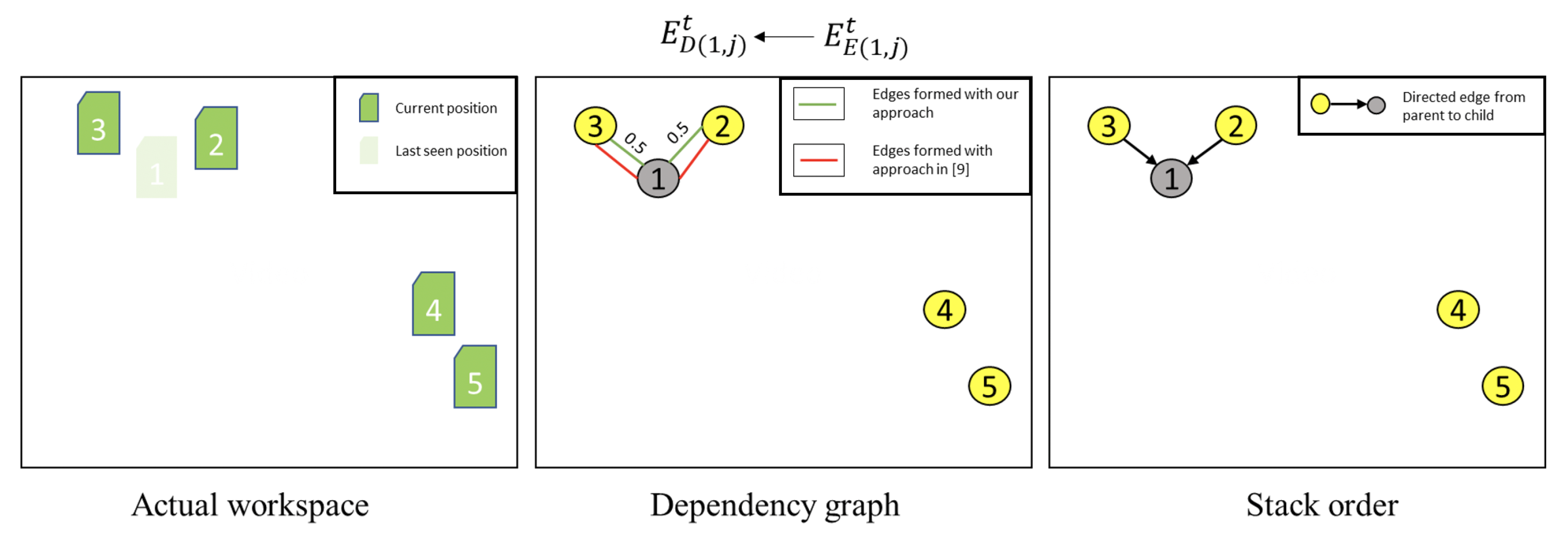
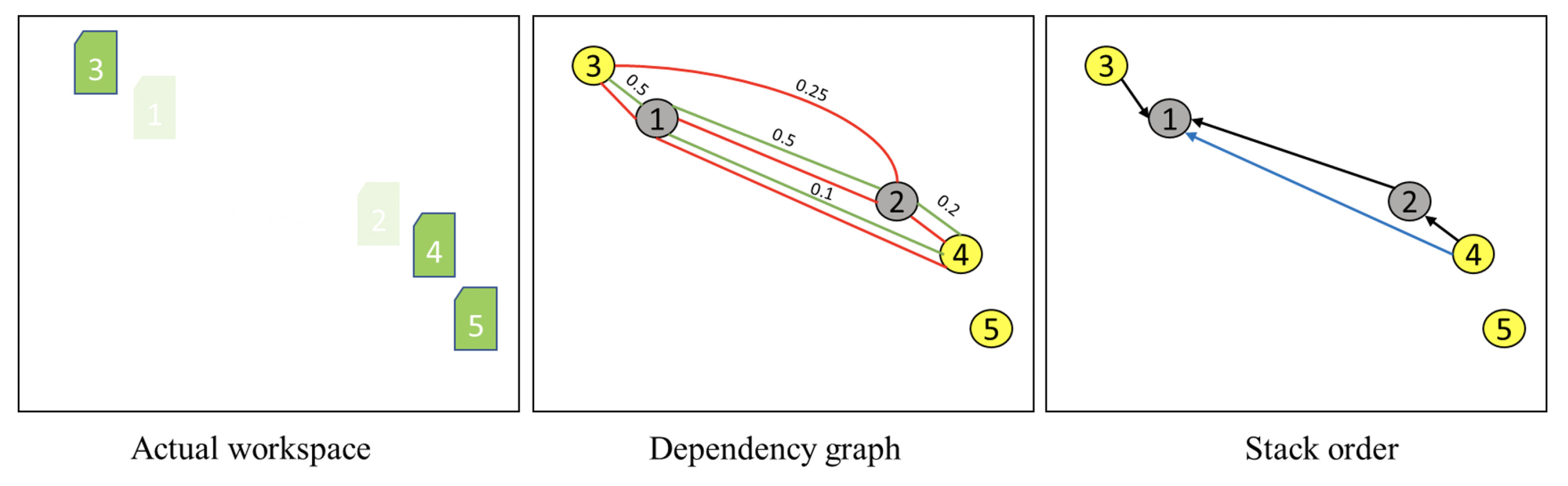
Figure 12.
Since the previous approach only used un-directed graphs and ignored stack order to build dependencies, an edge representing the possibility of workpiece 2 being stacked with 3 is spawned though it is an unnecessary search location. Using stack order, this can be avoided in our approach by limiting indirect edges to all ancestors and sibling nodes, as workpiece 3 is not an ancestor of 2. Since workpiece 4 is still an ancestor of 1, and since workpiece 1 could possibly be under 4, this indirect edge (blue) as a search location is still valid.
Figure 12.
Since the previous approach only used un-directed graphs and ignored stack order to build dependencies, an edge representing the possibility of workpiece 2 being stacked with 3 is spawned though it is an unnecessary search location. Using stack order, this can be avoided in our approach by limiting indirect edges to all ancestors and sibling nodes, as workpiece 3 is not an ancestor of 2. Since workpiece 4 is still an ancestor of 1, and since workpiece 1 could possibly be under 4, this indirect edge (blue) as a search location is still valid.
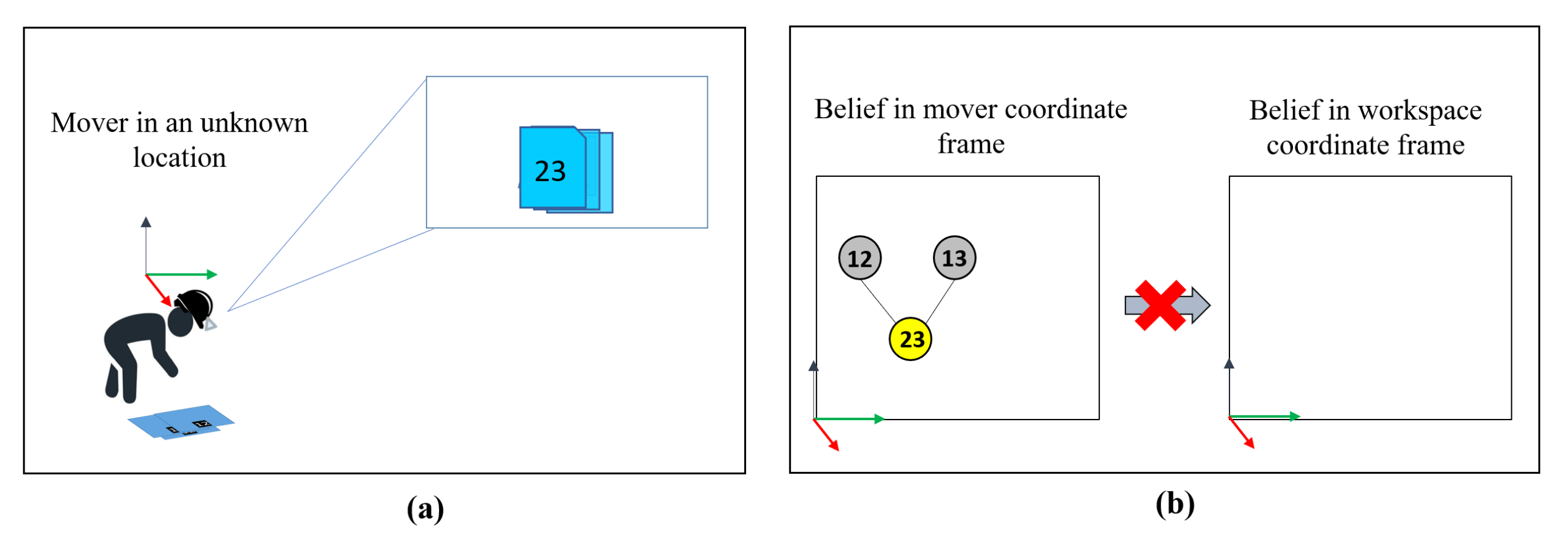
Figure 13.
Extracting critical information from local observations. (a) When a mover observes workpieces and stacks them while his/her position is unknown, dependencies between workpieces is locally extracted. (b) Since the positions of the worker and the workpieces are unknown, this information is not reflected in the dependency graph for the workspace.
Figure 13.
Extracting critical information from local observations. (a) When a mover observes workpieces and stacks them while his/her position is unknown, dependencies between workpieces is locally extracted. (b) Since the positions of the worker and the workpieces are unknown, this information is not reflected in the dependency graph for the workspace.
Figure 14.
Transferring locally observed stack information. When a mover observes the stacked workpieces when his/her own position with respect to the workspace is known, workpiece 23, the only visible member of the stack, is registered in the dependency graph. Additionally, since the earlier local dependency graph by the mover established that workpieces 12 and 13 were associated with 23, this information gets transferred to the workspace though they were never directly observed within the workspace.
Figure 14.
Transferring locally observed stack information. When a mover observes the stacked workpieces when his/her own position with respect to the workspace is known, workpiece 23, the only visible member of the stack, is registered in the dependency graph. Additionally, since the earlier local dependency graph by the mover established that workpieces 12 and 13 were associated with 23, this information gets transferred to the workspace though they were never directly observed within the workspace.
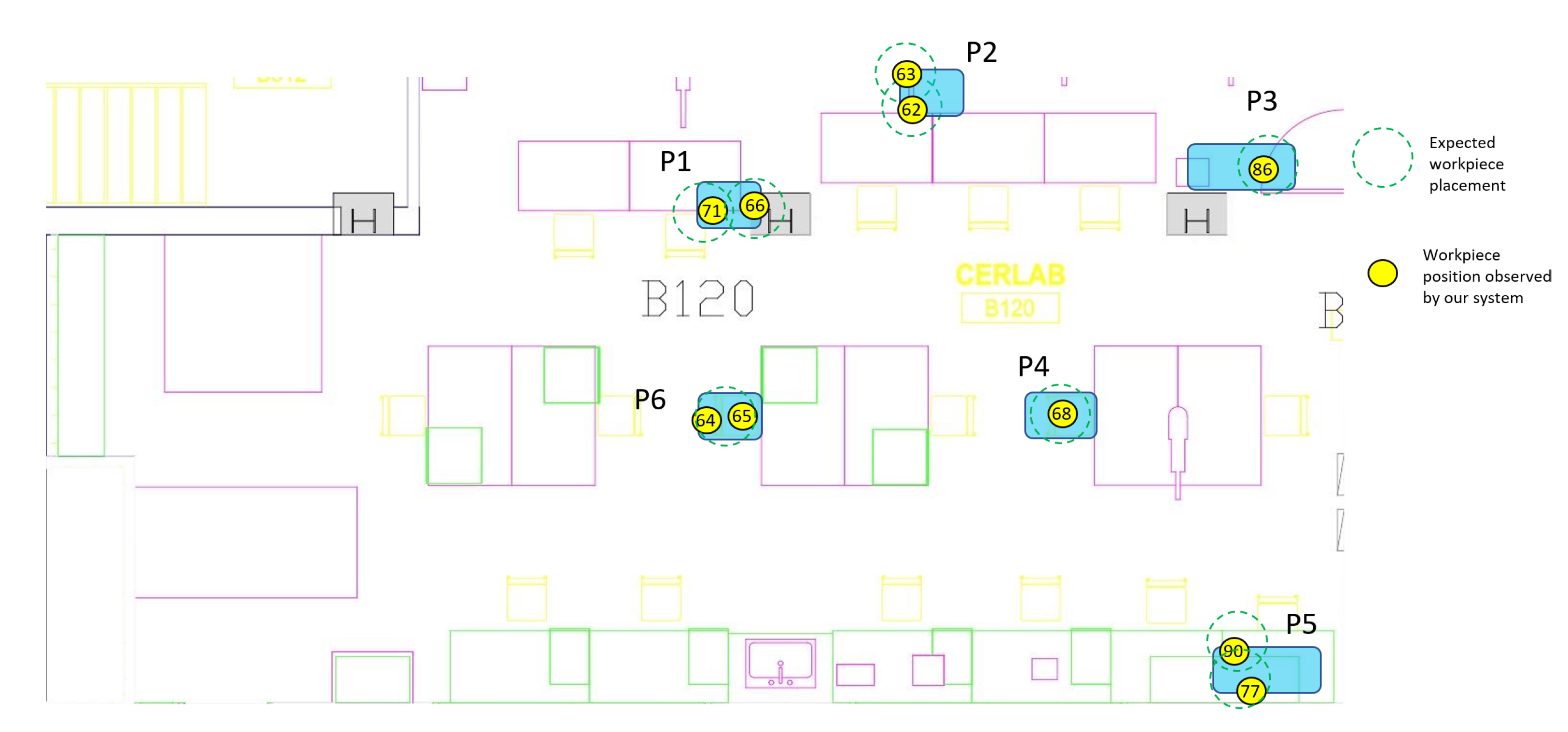
Figure 15.
Map of the workspace with observed workpieces after the first phase of the experiment. Expected (green) and observed (yellow) positions by our system plotted on a map. This information collection makes locations of workpieces available to the entire workforce and allows for fast pull times without need for manual logging.
Figure 15.
Map of the workspace with observed workpieces after the first phase of the experiment. Expected (green) and observed (yellow) positions by our system plotted on a map. This information collection makes locations of workpieces available to the entire workforce and allows for fast pull times without need for manual logging.
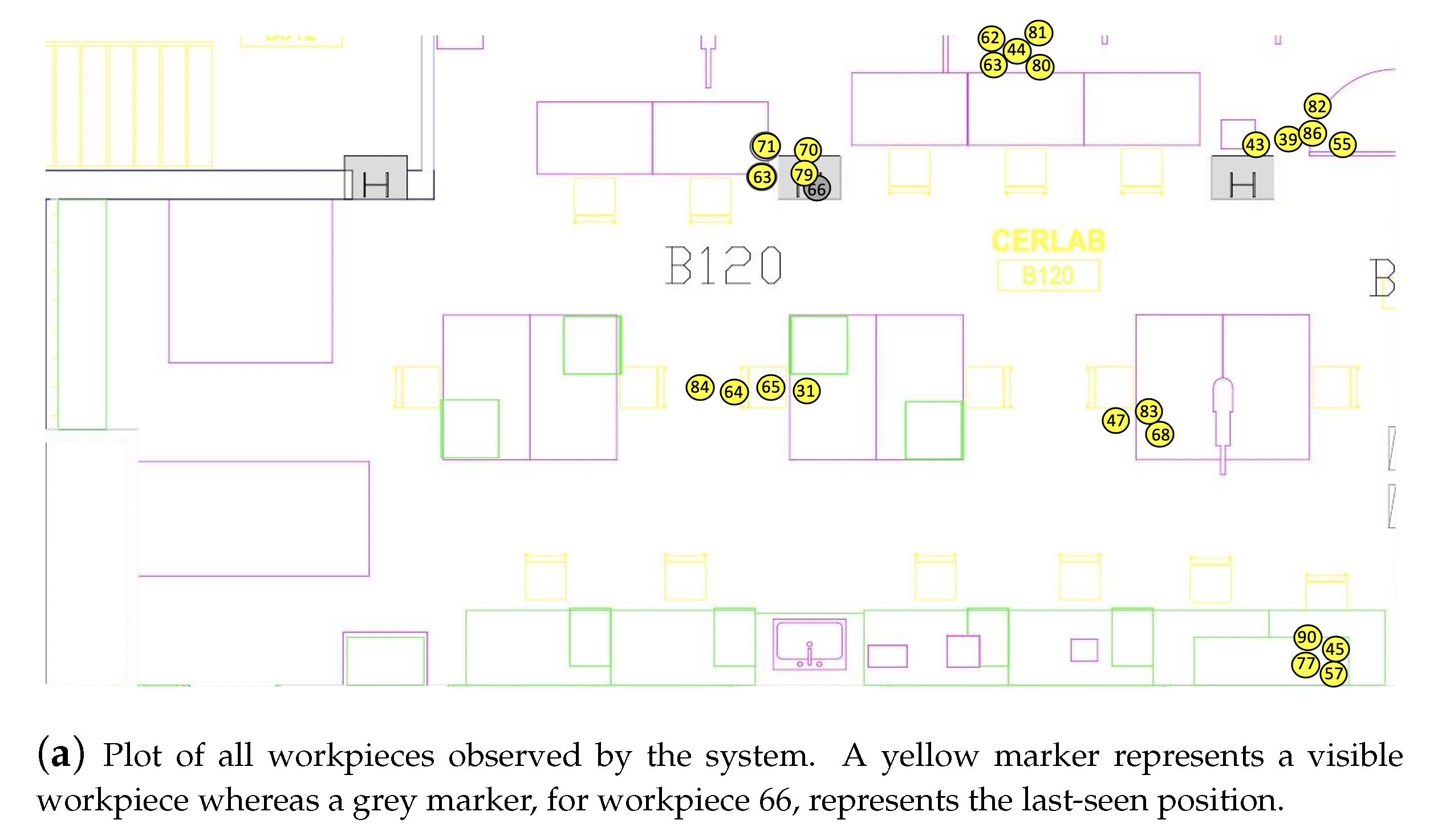
Figure 16.
Snapshot of the workspace and belief of our system after the second phase of the experiment. (a) Current location of all workpieces plotted by our system. Locations of recently observed workpieces (within a duration of 3.0 seconds) are highlighted in yellow, whereas workpieces that are deemed missing or occluded are highlighted in grey. (b) A query for the missing workpiece, workpiece 66, produces a plot of likely locations and their probabilities in finding workpiece 66 stacked under there. Workpiece 79 gets the highest confidence due to its proximity to 66, making it the first location to search.
Figure 16.
Snapshot of the workspace and belief of our system after the second phase of the experiment. (a) Current location of all workpieces plotted by our system. Locations of recently observed workpieces (within a duration of 3.0 seconds) are highlighted in yellow, whereas workpieces that are deemed missing or occluded are highlighted in grey. (b) A query for the missing workpiece, workpiece 66, produces a plot of likely locations and their probabilities in finding workpiece 66 stacked under there. Workpiece 79 gets the highest confidence due to its proximity to 66, making it the first location to search.
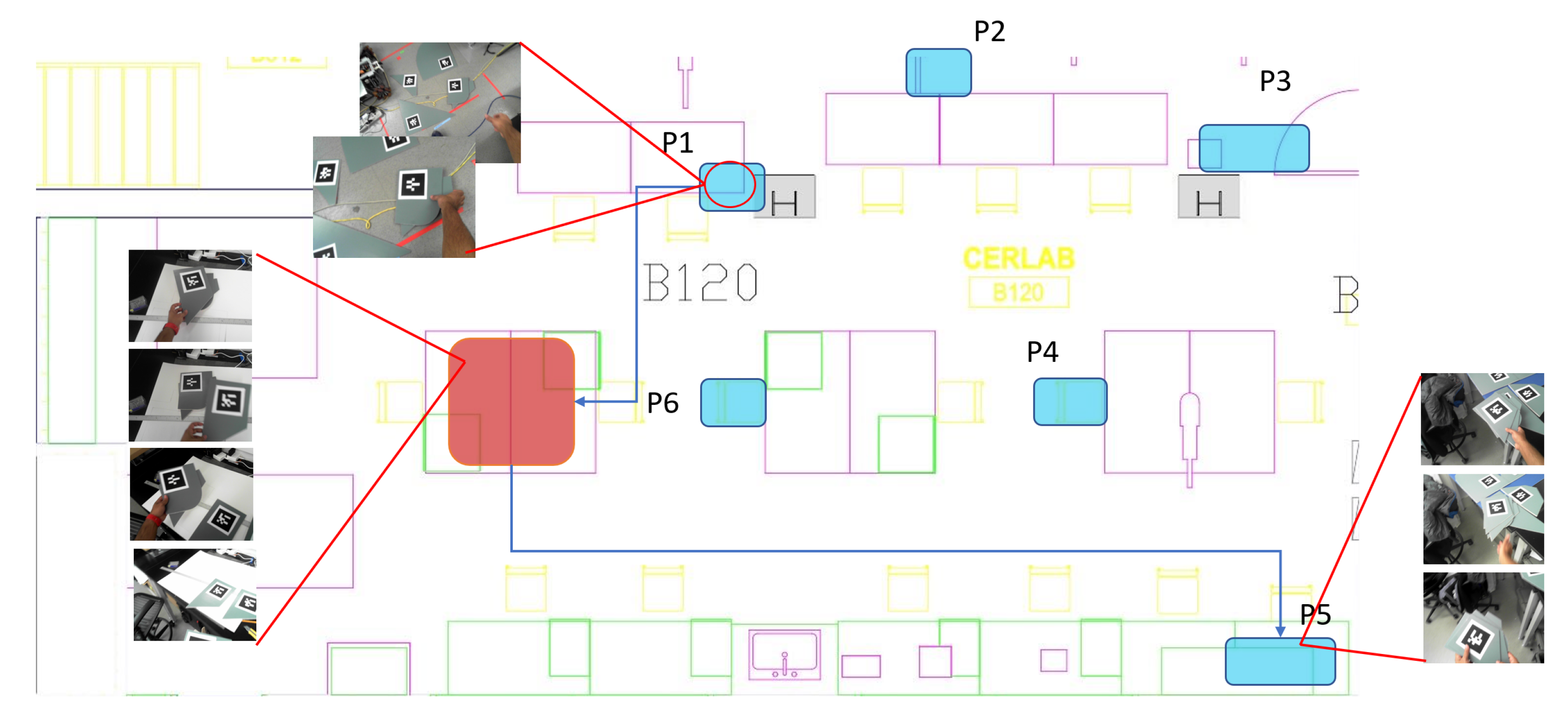
Figure 17.
Events, viewed by the hardhat camera of a mover, during the third and final phase of the experiment. The view at location P1 shows a mover picking up the stack with workpieces 79 and 66. The view at a random location (red) away from monitored areas shows the mover stacking workpieces 33 and 35 on the existing stack. The view at location P5 shows the mover placing the new stack with workpieces 66, 79, 33 and 35 on top of workpiece 77.
Figure 17.
Events, viewed by the hardhat camera of a mover, during the third and final phase of the experiment. The view at location P1 shows a mover picking up the stack with workpieces 79 and 66. The view at a random location (red) away from monitored areas shows the mover stacking workpieces 33 and 35 on the existing stack. The view at location P5 shows the mover placing the new stack with workpieces 66, 79, 33 and 35 on top of workpiece 77.
Figure 18.
Underlying graphs in our system calculating beliefs after displacement of workpiece 66 during the experiment. (a) A snapshot of the event weights and stack order of events that workpiece 66 could have encountered, as a directed graph, in the experiment run that displaced workpiece 66 to location P5. (b) The workpieces and their corresponding probability as search locations for the missing workpiece 66. Note that since workpiece 33’s location is unknown, it is not suggested as a search location. Additionally, workpieces 57, 45 and 90 are not considered, as there are no reasonable events connecting them to the directed graph either as an ancestor or a sibling.
Figure 18.
Underlying graphs in our system calculating beliefs after displacement of workpiece 66 during the experiment. (a) A snapshot of the event weights and stack order of events that workpiece 66 could have encountered, as a directed graph, in the experiment run that displaced workpiece 66 to location P5. (b) The workpieces and their corresponding probability as search locations for the missing workpiece 66. Note that since workpiece 33’s location is unknown, it is not suggested as a search location. Additionally, workpieces 57, 45 and 90 are not considered, as there are no reasonable events connecting them to the directed graph either as an ancestor or a sibling.
Figure 19.
Experimental setup and layout of testing space in the shipyard environment.
Figure 19.
Experimental setup and layout of testing space in the shipyard environment.
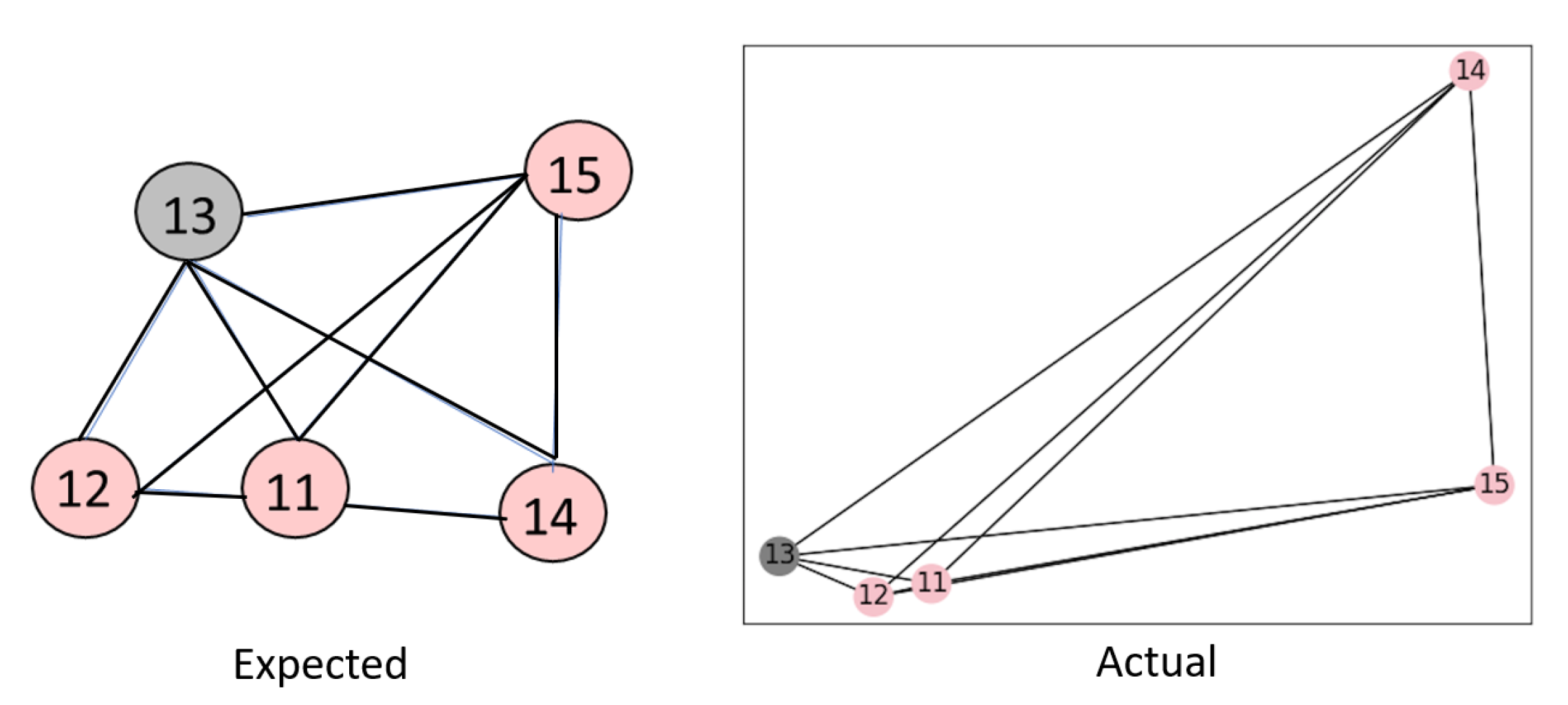
Figure 20.
Workpiece relations, as a graph, for the first experiment. The expected relation between workpieces from the scripted experiment (left) matches the relational graph published by our system (right).
Figure 20.
Workpiece relations, as a graph, for the first experiment. The expected relation between workpieces from the scripted experiment (left) matches the relational graph published by our system (right).
Figure 21.
Workpiece relations for the second experiment. Expected fully connected relation between workpieces (left) and the relational graph published by our system (right), which was able to infer the same relation.
Figure 21.
Workpiece relations for the second experiment. Expected fully connected relation between workpieces (left) and the relational graph published by our system (right), which was able to infer the same relation.
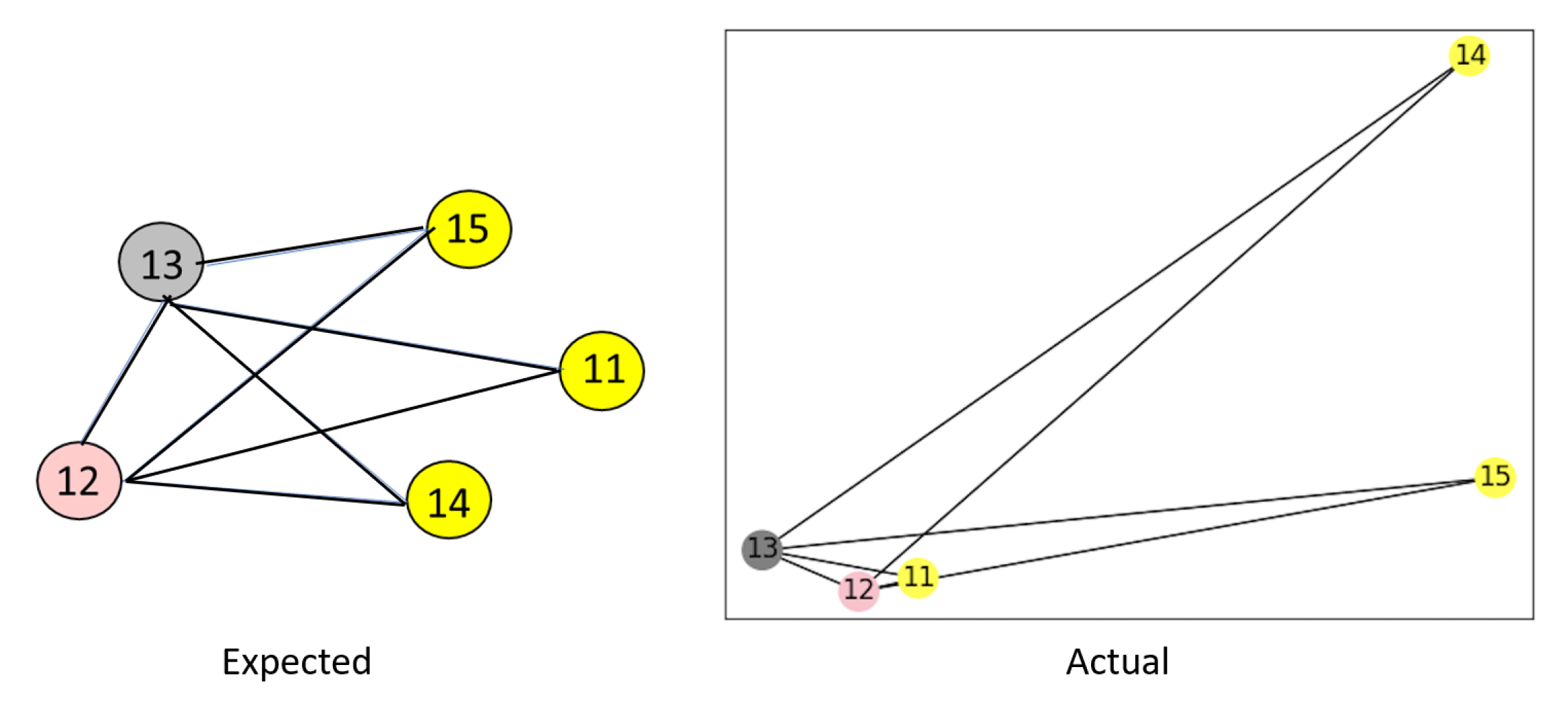
Figure 22.
Workpiece relation for the third stage of the experiment. Expected relation between workpieces after the stack was shuffled and split (left), which matches the output of our system (right).
Figure 22.
Workpiece relation for the third stage of the experiment. Expected relation between workpieces after the stack was shuffled and split (left), which matches the output of our system (right).
Table 1.
Cost of search in terms of number of workpieces to be visited and distance covered to find workpiece 66 displaced to various locations P1–P6. Least number of workpieces to be visited and the least distance covered during the search are highlighted in green.
Table 1.
Cost of search in terms of number of workpieces to be visited and distance covered to find workpiece 66 displaced to various locations P1–P6. Least number of workpieces to be visited and the least distance covered during the search are highlighted in green.
| Search Strategy | Status of Workpiece 66 | Average (P1–P6) |
|---|
| Metric | Visible | Stacked and Hidden out of View in Location |
|---|
| P1 | P2 | P3 | P4 | P5 | P6 |
|---|
| Last-seen location of workpiece 66 in known | Attempts | 1 | 1 | 7 | 12 | 16 | 19.5 | 23.5 | 13.2 |
| Distance | 0 m | 0 m | 2.5 m | 6.5 m | 10.5 m | 14.0 m | 20.0 m | 8.9 m |
| Previous method [15] | Attempts | 1 | 2.5 | 7 | 12 | 16 | 19.5 | 23.5 | 13.4 |
| Distance | 0 m | 0 m | 2.5 m | 6.5 m | 10.5 m | 14.0 m | 20.0 m | 8.9 m |
| Proposed approach | Attempts | 1 | 1 | 3 | 3 | 3 | 3 | 3 | 2.6 |
| Distance | 0 m | 0 m | 2.5 m | 5.0 m | 4.5 m | 6.6 m | 2.5 m | 3.5 m |
Table 2.
Totem pole and confidence of search locations for each experiment where workpiece 66 is moved to each of the six locations P1 to P6. The true location of workpiece 66 is highlighted in green. The locations are listed in the order of search locations along with their probability values as suggested by our system for each displacement.
Table 2.
Totem pole and confidence of search locations for each experiment where workpiece 66 is moved to each of the six locations P1 to P6. The true location of workpiece 66 is highlighted in green. The locations are listed in the order of search locations along with their probability values as suggested by our system for each displacement.
| Order of Search Locations for Workpiece 66 after Being Stacked and Displaced |
|---|
| P1 | P2 | P3 | P4 | P5 | P6 |
| Order | Prob. | Order | Prob. | Order | Prob. | Order | Prob. | Order | Prob. | Order | Prob. |
| 79 | 0.47 | 79 | 0.36 | 79 | 0.36 | 79 | 0.33 | 79 | 0.35 | 79 | 0.35 |
| 70 | 0.33 | 70 | 0.25 | 70 | 0.23 | 70 | 0.25 | 70 | 0.24 | 70 | 0.23 |
| 71 | 0.10 | 35 | 0.15 | 35 | 0.16 | 35 | 0.16 | 35 | 0.17 | 35 | 0.17 |
| 67 | 0.09 | 71 | 0.08 | 55 | 0.09 | 71 | 0.09 | 71 | 0.09 | 71 | 0.08 |
| | 62 | 0.07 | 71 | 0.08 | 47 | 0.08 | 77 | 0.09 | 65 | 0.08 |
| | 67 | 0.06 | 67 | 0.06 | 67 | 0.06 | 67 | 0.06 | 67 | 0.07 |