A Risk-Based Location-Allocation Approach for Weapon Logistics
Abstract
1. Introduction
2. Literature Review
2.1. Facility Location Problems
2.2. Overview of Military Optimization Problems
3. Mathematical Model
- N is the set of one or more candidate supply locations.
- M is the set of one or more demand points.
- P is the set of one or more product types.
- is the quantity of product type demanded by demand point .
- is the distance between candidate location and demand point .
- is the number of units of supplied by candidate location ; this variable is a decision variable in the model.
- is the number of units of that would have been supplied by candidate location if there was sufficient stock of product type ; this variable is also a decision variable in the model.
- is the available stock of product type ; that is, the number of units available for allocation to demand points.
- is the amount of stock available for supplying point ’s demand of product type .
- is equal to 1 if there is sufficient stock to supply the entire demand of product type ; and is equal to 0 if not.
- is the number of units of that could not be supplied because of insufficient stock.
- is the risk of allocating a unit of demand of demand point to candidate location . This parameter is used as a weight that increases the cost of risky locations. Thus, if one location is riskier than another location, the cost of allocation increases, and thus the location becomes less likely to be allocated any weapons.
- is the setup cost of allocating one unit of product type to candidate location .
- is the maximum quantity of units of product type allowed to be allocated to candidate location .Subject to the following:
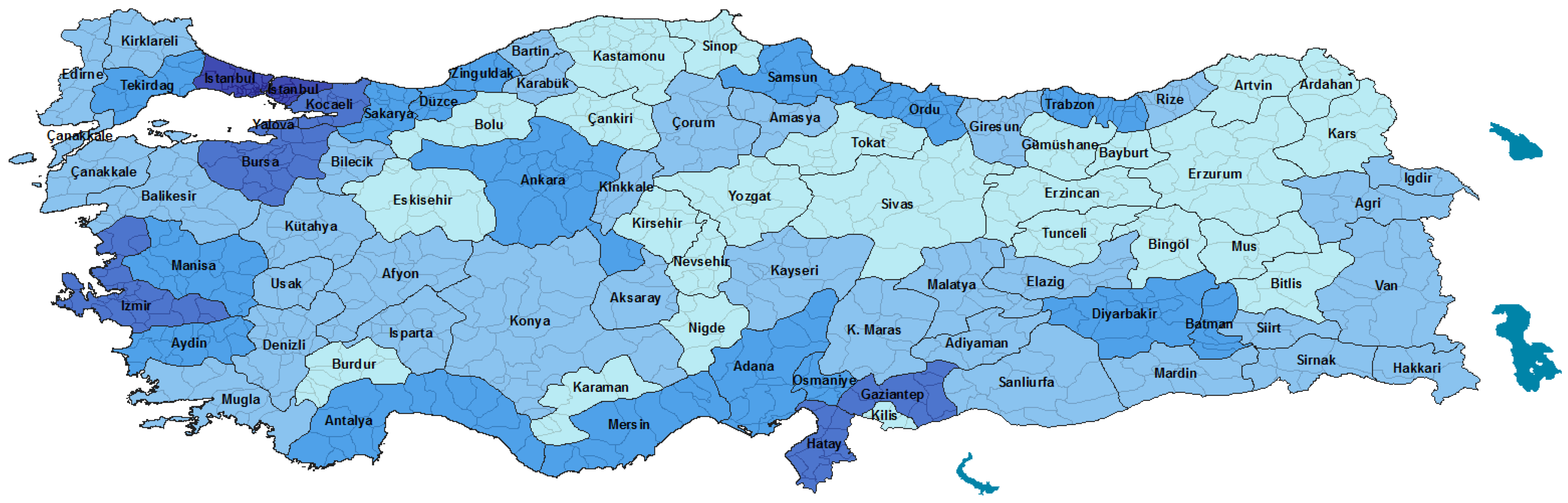
4. Case Study
4.1. Data Sources
4.2. Assumptions
4.2.1. Attack Scenarios
4.2.2. Nodes and Weapon Types
4.2.3. Supply
4.2.4. Demands
4.2.5. Risks
4.2.6. Setup Costs
4.2.7. Supply City Capacities
5. Solution Method
6. Results and Discussion
6.1. Solving Different Attack Scenarios
6.2. Limitations and Potential Improvements
6.3. Military Perspective Insights
7. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Weber, A. Theory of the Location of Industries; U.S. Department of Defense, Homeland Defense, Joint Publications 3-27: Washington, DC, USA, 2007.
- Kariv, O.; Hakimi, S.L. An algorithmic approach to network location problems. I: The p-centers. SIAM J. Appl. Math. 1979, 37, 513–538. [Google Scholar] [CrossRef]
- Kariv, O.; Hakimi, S.L. An algorithmic approach to network location problems. Ii: The p-medians. SIAM J. Appl. Math. 1979, 37, 539–560. [Google Scholar] [CrossRef]
- Melkote, S.; Daskin, M.S. Capacitated facility location/network design problems. Eur. J. Oper. Res. 2001, 129, 481–495. [Google Scholar] [CrossRef]
- Tran, T.H.; Scaparra, M.P.; O’Hanley, J.R. A hypergraph multi-exchange heuristic for the single-source capacitated facility location problem. Eur. J. Oper. Res. 2017, 263, 173–187. [Google Scholar] [CrossRef][Green Version]
- Revelle, C.S.; Eiselt, H.A.; Daskin, M.S. A bibliography for some fundamental problem categories in discrete location science. Eur. J. Oper. Res. 2008, 184, 817–848. [Google Scholar] [CrossRef]
- Sridharan, R. The capacitated plant location problem. Eur. J. Oper. Res. 1995, 2, 203–213. [Google Scholar] [CrossRef]
- Gendron, B.; Khuong, P.V.; Semet, F. Comparison of formulations for the two-level uncapacitated facility location problem with single assignment constraints. Comput. Oper. Res. 2017, 86, 86–93. [Google Scholar] [CrossRef][Green Version]
- Ravi, R.; Sinha, A. Multicommodity facility location. In Proceedings of the SODA ’04 Fifteenth Annual ACM-SIAM Symposium on Discrete Algorithms, New Orleans, LA, USA, 11–13 January 2004. [Google Scholar]
- Eiselt, H.A.; Sandblom, C.L. Decision Analysis, Location Models, and Scheduling Problems; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Schilling, D.A.; Jayaraman, V.; Barkhi, R. A review of covering problem in facility location. Locat. Sci. 1993, 1, 25–55. [Google Scholar]
- Toregas, C.; Swain, R.; ReVelle, C.; Bergman, L. The location of emergency service facilities. Oper. Res. 1971, 19, 1363–1373. [Google Scholar] [CrossRef]
- Beasley, J.E.; Chu, P.C. A genetic algorithm for the set covering problem. Eur. J. Oper. Res. 1996, 2, 392–404. [Google Scholar] [CrossRef]
- Eaton, D.J.; Daskin, M.S.; Simmons, D.; Bulloch, B.; Jansma, G. Determining emergency medical service vehicle deployment in austin, texas. Interfaces 1985, 1, 96–108. [Google Scholar] [CrossRef]
- Dyer, M.E.; Frieze, A.M. A simple heuristic for the p-centre problem. Oper. Res. Lett. 1985, 6, 285–288. [Google Scholar] [CrossRef]
- Davidović, T.; Ramljak, D.; Šelmić, M.; Teodorović, D. Bee colony optimization for the p-center problem. Comput. Oper. Res. 2011, 38, 1367–1376. [Google Scholar] [CrossRef]
- Irawan, C.A.; Salhi, S.; Drezner, Z. Hybrid meta-heuristics with VNS and exact methods: Application to large unconditional and conditional vertex p-centre problems. J. Heurist. 2016, 22, 507–537. [Google Scholar] [CrossRef]
- Callaghan, B.; Salhi, S.; Nagy, G. Speeding up the optimal method of drezner for the p-centre problem in the plane. Eur. J. Oper. Res. 2017, 257, 722–734. [Google Scholar] [CrossRef]
- Laporte, G.; Nickel, S.; da Gama, F.S. Location Science; Springer: Berlin, Germany, 2015. [Google Scholar]
- Goldman, A.J. Optimal center location in simple networks. Transp. Sci. 1971, 5, 212–221. [Google Scholar] [CrossRef]
- Ndiaye, F.; Ndiaye, B.M.; Ly, I. Application of the p-median problem in school allocation. Am. J. Oper. Res. 2012, 2, 253–259. [Google Scholar] [CrossRef]
- Dzator, M.; Dzator, J. An effective heuristic for the p-median problem with application to ambulance location. Opsearch 2013, 50, 60–74. [Google Scholar] [CrossRef]
- Cooper, L. Location-allocation problems. Oper. Res. 1963, 11, 331–343. [Google Scholar] [CrossRef]
- Aboolian, R.; Sun, Y.; Koehler, G.J. A location–allocation problem for a web services provider in a competitive market. Eur. J. Oper. Res. 2009, 194, 64–77. [Google Scholar] [CrossRef]
- Zhang, W.; Cao, K.; Liu, S.; Huang, B. A multi-objective optimization approach for health-care facility location-allocation problems in highly developed cities such as Hong Kong. Comput. Environ. Urban Syst. 2016, 59, 220–230. [Google Scholar] [CrossRef]
- Zarrinpoor, N.; Fallahnezhad, M.S.; Pishvaee, M. Design of a reliable hierarchical location-allocation model under disruptions for health service networks: A two-stage robust approach. Comput. Ind. Eng. 2017, 109, 130–150. [Google Scholar] [CrossRef]
- Jaiswal, N.K. Military Operations Research: Quantitative Decision Making; International Series in Operations Research & Management Science; Springer: Berlin, Germany, 1997. [Google Scholar]
- Ahuja, R.K.; Kumar, A.; Jha, K.C.; Orlin, J.B. Exact and heuristic algorithms for the weapon-target assignment problem. Oper. Res. 2007, 55, 1136–1146. [Google Scholar] [CrossRef]
- Leboucher, C.; Shin, H.S.; Le Ménec, S.; Tsourdos, A.; Kotenkoff, A.; Siarry, P.; Chelouah, R. Novel evolutionary game based multi-objective optimisation for dynamic weapon target assignment. IFAC Proc. Vol. 2014, 47, 3936–3941. [Google Scholar] [CrossRef]
- Kalyanam, K.; Rathinam, S.; Casbeer, D.; Pachter, M. Optimal threshold policy for sequential weapon target assignment. IFAC-PapersOnLine 2016, 49, 7–10. [Google Scholar] [CrossRef]
- Yan, Y.; Zha, Y.; Qin, L.; Xu, K. A research on weapon-target assignment based on combat capabilities. In Proceedings of the 2016 IEEE International Conference Mechatronics and Automation (ICMA), Harbin, China, 7–10 August 2016; pp. 2403–2407. [Google Scholar]
- Montoya, A.; Vélez–Gallego, M.C.; Villegas, J.G. Multi-product capacitated facility location problem with general production and building costs. NETNOMICS Econ. Res. Electron. Netw. 2016, 17, 47–70. [Google Scholar] [CrossRef]
- Interagency Working Group 5 For National Security Memorandum 84, The Warsaw Pact Threat to NATO, 1970. Available online: https://www.cia.gov/library/readingroom/docs/1970-05-01.pdf (accessed on 27 April 2018).
| Abbreviation | Weapon Type | |
|---|---|---|
| Category | Weapon | |
| AFV |  MBT | Main Battle Tanks |
 AIFV | Armored Infantry Fighting Vehicle | |
 APC | Armored Personnel Carrier | |
 ARV | Armored Recovery Vehicles | |
 RECCE | Reconnaissance | |
| AT |  MSL | Missiles |
 MSL SP | Self-propelled Missiles | |
 RCL | Recoilless Launchers | |
 GUNS | Guns | |
| ARTY |  SP | Self-Propelled Artillery |
 TOWED | Towed Artillery | |
 MOR | Mortars | |
 MRL | Multiple Rocket Launchers | |
| Weapon Type | Stock |
|---|---|
| Turkey: AFV: AIFV | 650 |
| Turkey: AFV: APC | 3643 |
| Turkey: AFV: ARV | 0 |
| Turkey: AT: GUNS | 0 |
| Turkey: AFV: MBT | 2504 |
| Turkey: ARTY: MOR | 5813 |
| Turkey: ARTY: MRL | 146 |
| Turkey: AT: MSL | 1363 |
| Turkey: AT: MSL SP | 365 |
| Turkey: AT: RCL | 3869 |
| Turkey: AFV: RECCE | 320 |
| Turkey: ARTY: SP | 1133 |
| Turkey: ARTY: TOWED | 760 |
| Turkey: Land Forces | 402,000 |
| AĞRI | ARDAHAN | ARTVİN | EDİRNE | GAZİANTEP | HAKKARİ | HATAY | IĞDIR | KARS | KİLİS | KIRKLARELİ | MARDİN | ŞANLIURFA | ŞIRNAK | VAN | TOTAL | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AIFV | 32 | 24 | 24 | 478 | 408 | 324 | 408 | 236 | 57 | 408 | 80 | 408 | 408 | 529 | 203 | 4027 |
| APC | 43 | 63 | 63 | 2614 | 250 | 868 | 250 | 257 | 106 | 250 | 64 | 250 | 250 | 905 | 214 | 6447 |
| ARV | 0 | 0 | 0 | 0 | 0 | 108 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 107 | 0 | 215 |
| GUNS | 0 | 15 | 15 | 63 | 0 | 0 | 0 | 0 | 20 | 0 | 63 | 0 | 0 | 0 | 0 | 176 |
| MBT | 36 | 41 | 41 | 1394 | 990 | 824 | 990 | 591 | 78 | 990 | 40 | 990 | 990 | 990 | 554 | 9539 |
| MOR | 4 | 21 | 21 | 2427 | 68 | 2141 | 68 | 1671 | 26 | 68 | 108 | 68 | 68 | 544 | 1666 | 8969 |
| MRL | 17 | 12 | 12 | 159 | 83 | 495 | 83 | 509 | 30 | 83 | 12 | 83 | 83 | 84 | 492 | 2237 |
| MSL | 0 | 10 | 0 | 0 | 730 | 0 | 365 | 0 | 0 | 365 | 0 | 365 | 365 | 365 | 0 | 2565 |
| MSL SP | 7 | 0 | 0 | 612 | 68 | 0 | 68 | 7 | 8 | 68 | 12 | 68 | 68 | 69 | 0 | 1055 |
| RCL | 0 | 0 | 0 | 4508 | 0 | 66 | 0 | 67 | 0 | 0 | 0 | 0 | 0 | 0 | 66 | 4707 |
| RECCE | 0 | 1 | 1 | 239 | 588 | 48 | 0 | 12 | 2 | 0 | 10 | 0 | 0 | 36 | 11 | 948 |
| SP | 12 | 22 | 22 | 611 | 83 | 121 | 83 | 110 | 36 | 83 | 24 | 83 | 83 | 108 | 97 | 1578 |
| TOWED | 44 | 23 | 23 | 565 | 338 | 706 | 338 | 720 | 67 | 338 | 12 | 338 | 338 | 369 | 676 | 4895 |
| Force | 13,950 | 5916 | 5916 | 101,650 | 36,666 | 143,666 | 36,666 | 130,616 | 19,867 | 36,666 | 8150 | 36,666 | 36,666 | 63,667 | 116,667 | 793,395 |
| Ankara | Bursa | Batman | |
|---|---|---|---|
| MBT | 658 | 366 | 88 |
| SP | 109 | 61 | 15 |
| TOWED | 338 | 188 | 45 |
| Problem Description and Solution Results | |
| Solution Time | ~14 min |
| # Decision Variables | 27,720 variables |
| # Bordering Cities | 15 |
| # Supply Cities | 66 |
| Total Cost | 755,210,884.00 |
| Solution Infrastructure | |
| Operating System | Windows 7 SP1 |
| RAM | 3 GB |
| CPU | Intel Core 2 Duo |
| Solver | CBC Solver |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Çetinkaya, C.; Haffar, S. A Risk-Based Location-Allocation Approach for Weapon Logistics. Logistics 2018, 2, 9. https://doi.org/10.3390/logistics2020009
Çetinkaya C, Haffar S. A Risk-Based Location-Allocation Approach for Weapon Logistics. Logistics. 2018; 2(2):9. https://doi.org/10.3390/logistics2020009
Chicago/Turabian StyleÇetinkaya, Cihan, and Samer Haffar. 2018. "A Risk-Based Location-Allocation Approach for Weapon Logistics" Logistics 2, no. 2: 9. https://doi.org/10.3390/logistics2020009
APA StyleÇetinkaya, C., & Haffar, S. (2018). A Risk-Based Location-Allocation Approach for Weapon Logistics. Logistics, 2(2), 9. https://doi.org/10.3390/logistics2020009




