A Food Transportation Framework for an Efficient and Worker-Friendly Fresh Food Physical Internet
Abstract
:1. Introduction
2. Overview of a Shared F Architecture
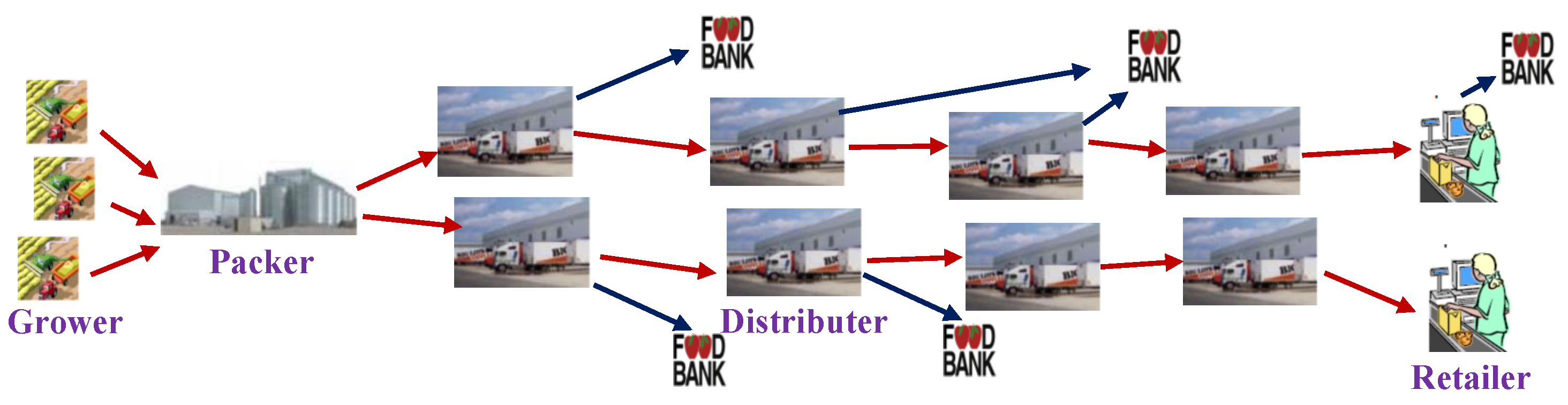
2.1. From Private Logistics to Shared Logistics
2.2. Modeling the Perishability Metric
3. Product Distribution and Truck Scheduling
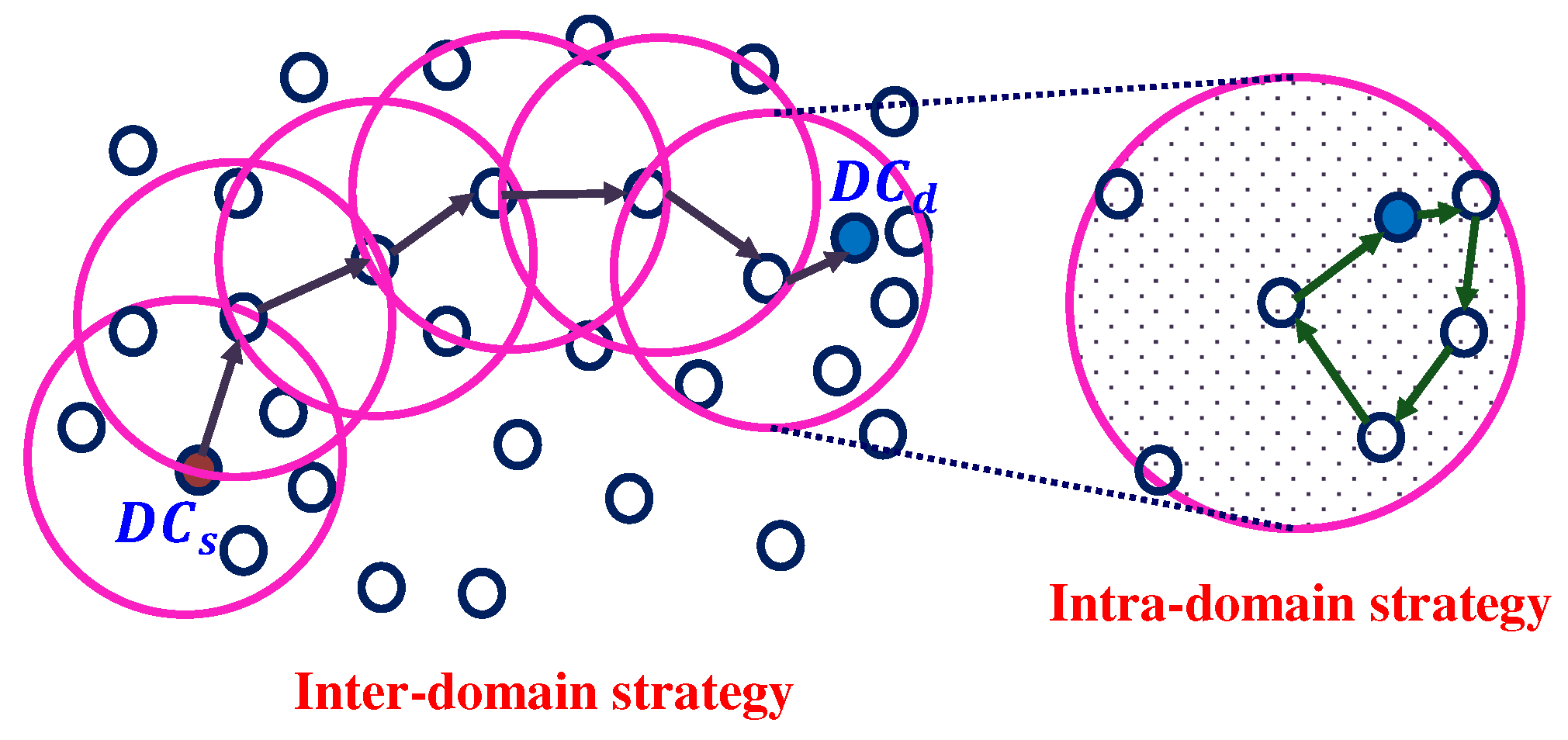
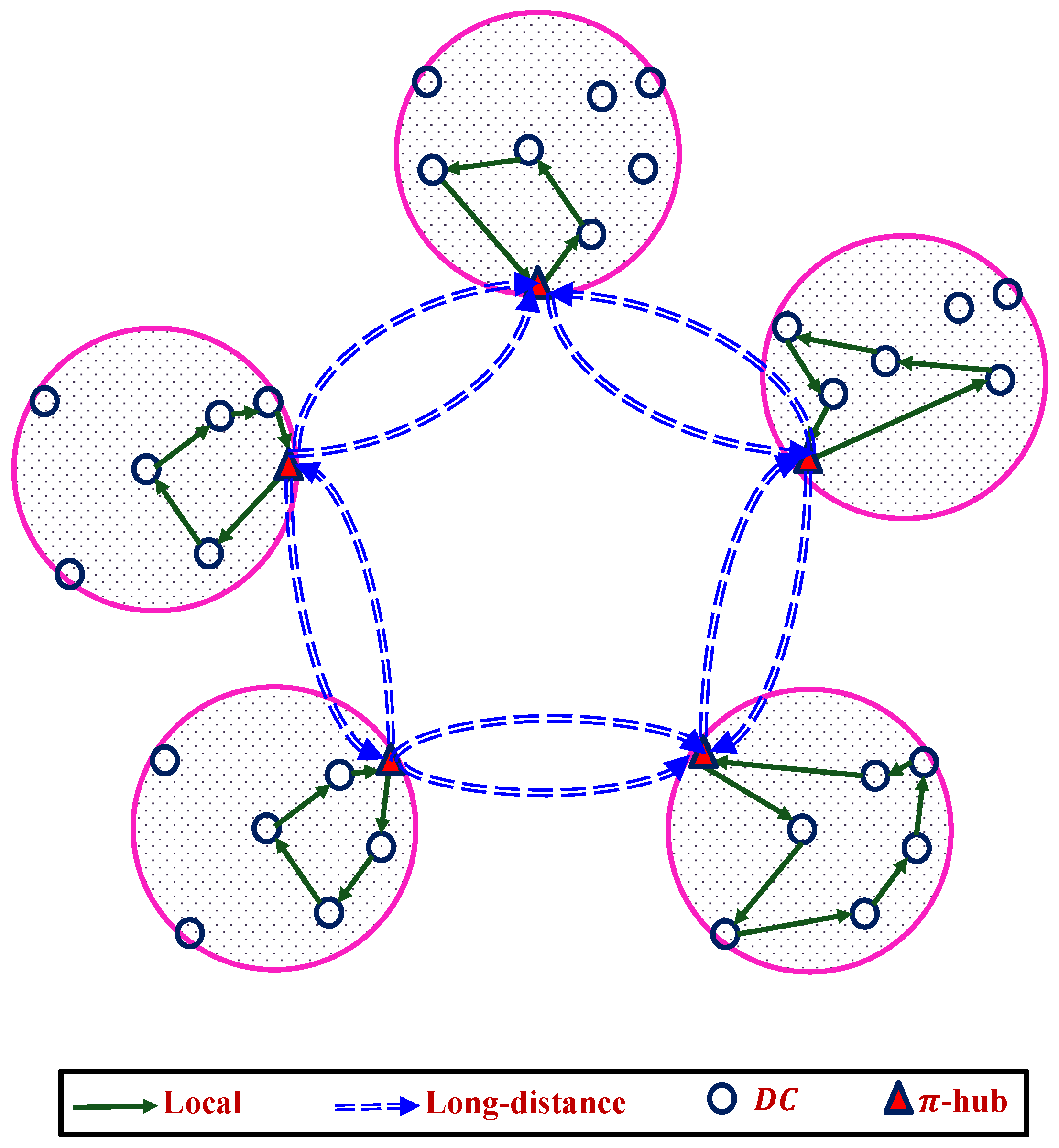
3.1. Inter-Domain Strategy
3.2. Intra-Domain Strategy
Problem Formulation of IntraDS
4. Performance Evaluation
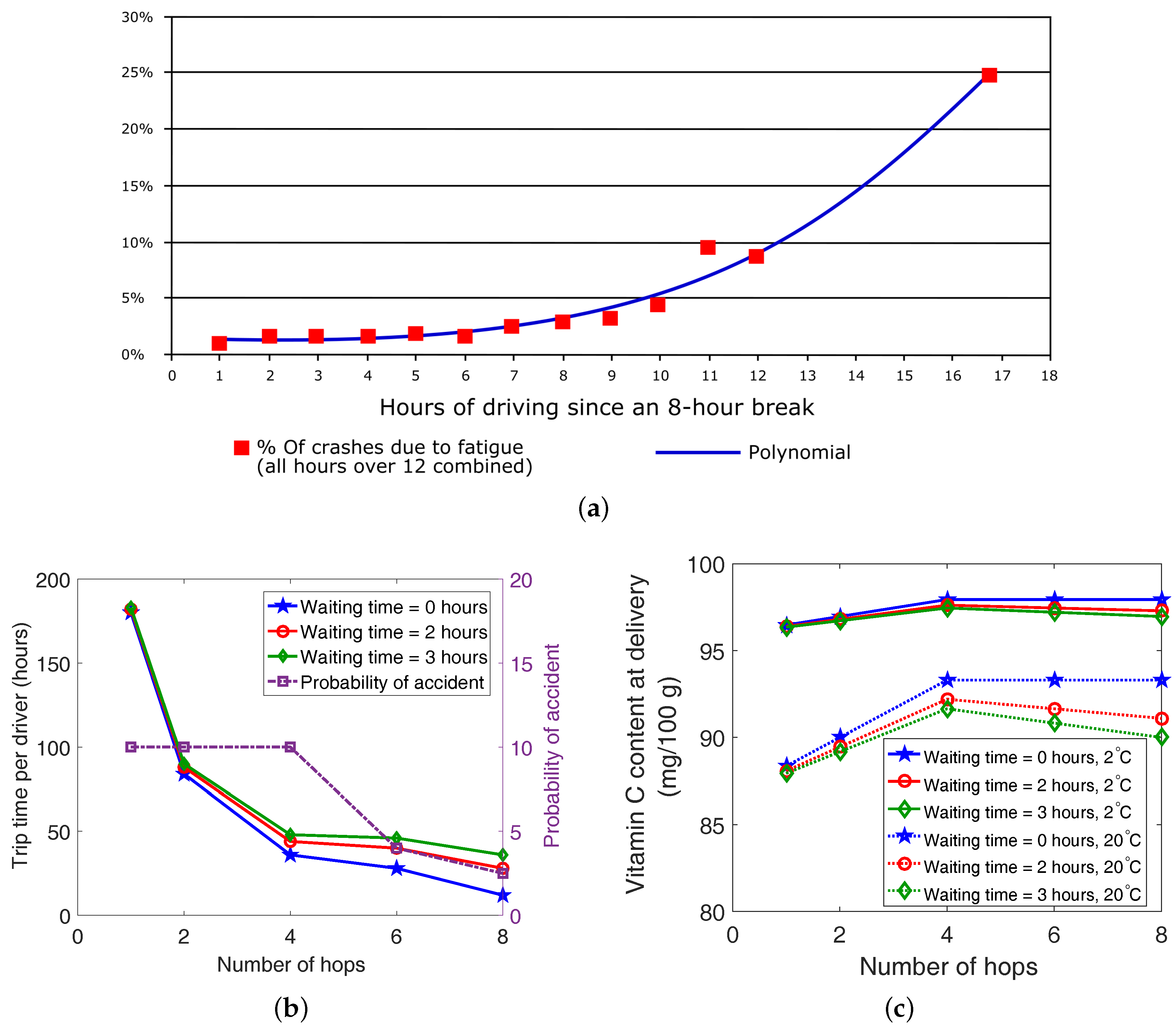
4.1. Performance of Inter-Domain Forwarding
4.2. Performance of Intra-Domain Forwarding
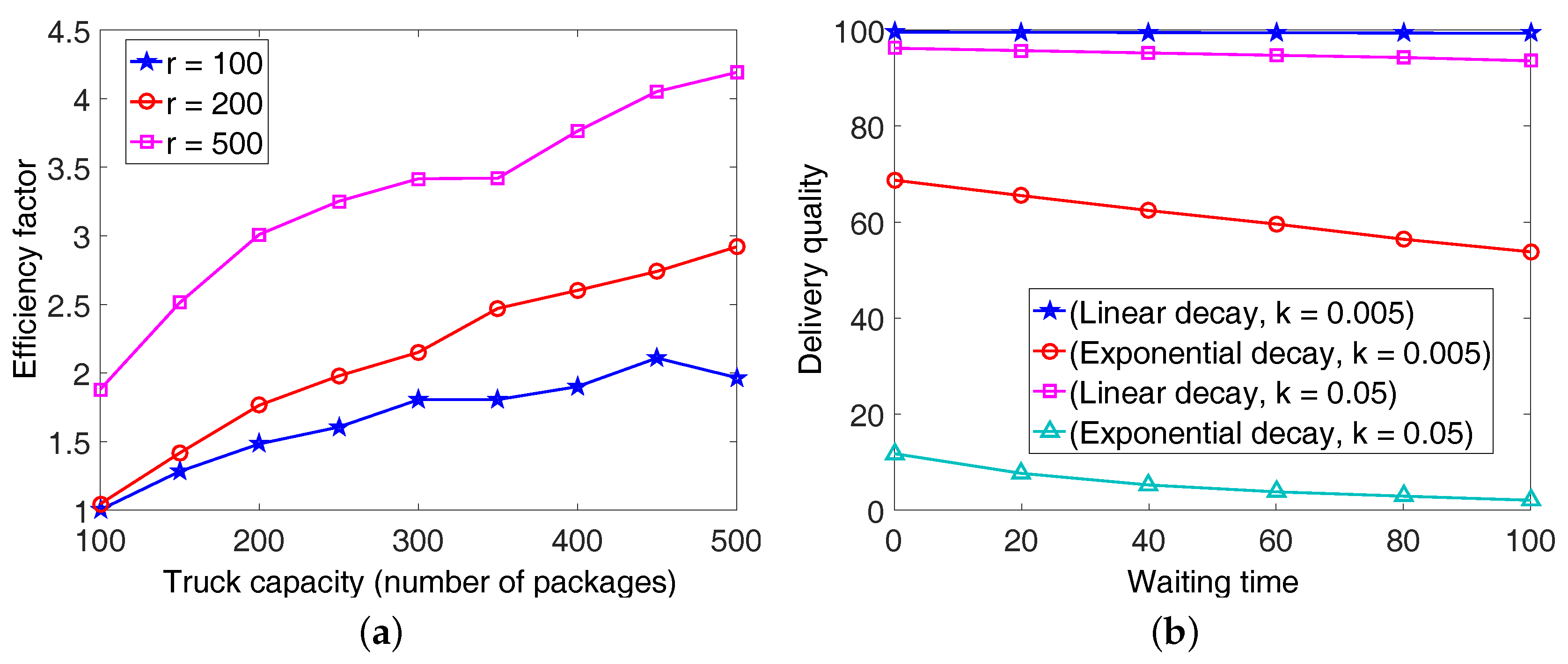
4.3. Performance Evaluation with a Larger Number of DCs
5. Related Works and Discussions
5.1. Related Works
5.2. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Montreuil, B. Towards a Physical Internet: Meeting the Global Logistics Sustainability Grand Challenge. Logist. Res. 2011, 3, 71–87. [Google Scholar] [CrossRef]
- Leuschner, R.; Carter, C.; Goldsby, T.; Rogers, Z. Third-Party Logistics: A Meta-Analytic Review and Investigation of its Impact on Performance. J. Supply Chain Manag. 2014, 50, 21–43. [Google Scholar] [CrossRef]
- GS1 Website. Available online: www.gs1.org/ (accessed on 1 December 2017).
- Montreuil, B.; University, L.; Meller, R.D. Towards a Physical Internet: The Impact on Logistics Facilities and Material Handling Systems Design and Innovation. In Proceedings of the International Material Handling Research Colloquium (IMHRC), Milwaukee, WI, USA, 21–24 June 2010. [Google Scholar]
- Sarraj, R.; Ballot, E.; Pan, S.; Montreuil, B. Analogies between Internet network and logistics service networks: Challenges involved in the interconnection. J. Intell. Manuf. 2014, 25, 1207–1219. [Google Scholar] [CrossRef]
- Pach, C.; Sallez, Y.; Berger, T.; Bonte, T.; Trentesaux, D.; Montreuil, B. Routing Management in Physical Internet Crossdocking Hubs: Study of Grouping Strategies for Truck Loading. In Proceedings of the IFIP International Conference on Advances in Production Management Systems (APMS), Ajaccio, France, 20–24 September 2014; pp. 483–490. [Google Scholar]
- Montreuil, B.; Meller, R.D.; Ballot, E. Physical Internet Foundations. In Service Orientation in Holonic and Multi Agent Manufacturing and Robotics; Springer: Berlin/Heidelberg, Germany, 2013; pp. 151–166. [Google Scholar]
- Ballot, E.; Gobet, O.; Montreuil, B. Physical Internet Enabled Open Hub Network Design for Distributed Networked Operations. In Service Orientation in Holonic and Multi-Agent Manufacturing Control; Springer: Berlin/Heidelberg, Germany, 2012; pp. 279–292. [Google Scholar]
- IPIC2016. Available online: http://www.pi.events/IPIC2016/ (accessed on 10 August 2016).
- Gunders, D. Wasted: How America Is Losing Up to 40 Percent of Its Food from Farm to Fork to Landfill. Natural Resources Defense Council (NRDC). Available online: https://www.nrdc.org/sites/default/files/wasted-food-IP.pdf (accessed on 1 December 2017).
- Pahl, J.; Voß, S. Integrating deterioration and lifetime constraints in production and supply chain planning: A survey. Eur. J. Oper. Res. 2014, 238, 654–674. [Google Scholar] [CrossRef]
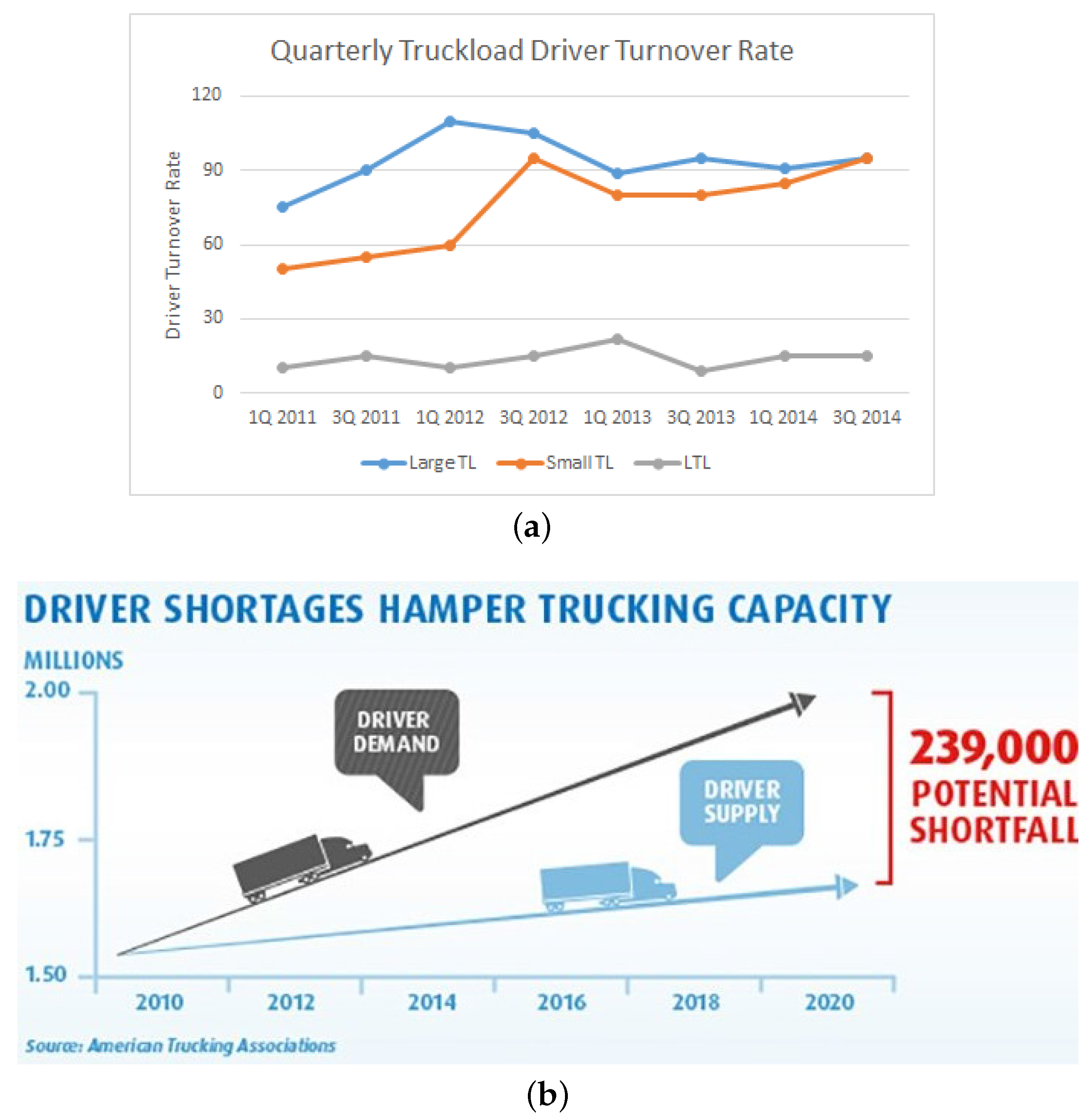
- Driver Shortage Report. Available online: https://www.linkedin.com/pulse/driver-shortage-better-pay-plan-dawn-strobel/ (accessed on 1 December 2017).
- Driver Turnover Report. Available online: http://www.conceptservicesltd.com/how-industry-leaders-are-combating-the-truck-driver-shortage/ (accessed on 1 December 2017).
- Laidler, K.J. The development of the Arrhenius equation. J. Chem. Educ. 1984, 61, 494–498. [Google Scholar] [CrossRef]
- Mazurek, A.; Pankiewicz, U. Changes of dehydroascorbic acid content in relation to total content of vitamin C in selected fruits and vegetables. Acta Sci. Pol. Hort. Cultus 2012, 11, 169–177. [Google Scholar]
- Kang, H.M.; Park, K.W.; Saltveit, M.E. Elevated growing temperatures during the day improve the postharvest chilling tolerance of greenhouse-grown cucumber (Cucumis sativus) fruit. Postharvest Biol. Technol. 2002, 24, 49–57. [Google Scholar] [CrossRef]
- Reddy, K.V. Effect of Method of Freezing, Processing and Packaging Variables on Microbiological and Other Quality Characteristics of Beef and Poultry; Retrospective Theses and Dissertations; Iowa State University Digital Repository: Ames, IA, USA, 1981; Available online: http://lib.dr.iastate.edu/rtd/6848/ (accessed on 2 January 2016).
- Quality Aspects Associated with Seafood. Available online: http://www.fao.org/docrep/003/T1768E/T1768E03.htm (accessed on 1 December 2017).
- Benjaafar, S.; Chen, X. On the Effectiveness of Emission Penalties in Decentralized Supply Chains. In Proceedings of the INFORMS Southeast Michigan Symposium, East Lansing, MI, USA, 3 October 2014. [Google Scholar]
- Applegate, D.L.; Bixby, R.E.; Chvatal, V.; Cook, W.J. The Traveling Salesman Problem: A Computational Study (Princeton Series in Applied Mathematics); Princeton University Press: Princeton, NJ, USA, 2007. [Google Scholar]
- Berbeglia, G.; Cordeau, J.F.; Laporte, G. Dynamic pickup and delivery problems. Eur. J. Oper. Res. 2010, 202, 8–15. [Google Scholar] [CrossRef]
- Ma, S.; Zheng, Y.; Wolfson, O. T-Share: A Large-Scale Dynamic Taxi Ridesharing Service. In Proceedings of the 2013 IEEE 29th International Conference on Data Engineering (ICDE), Brisbane, Australia, 8–12 April 2013; pp. 410–421. [Google Scholar]
- Hifi, M.; Kacem, I.; Nègre, S.; Wu, L. A Linear Programming Approach for the Three-Dimensional Bin-Packing Problem. Electron. Notes Discret. Math. 2010, 36, 993–1000. [Google Scholar] [CrossRef]
- Albrecht, J.A.; Schafer, H.W.; Zottola, E.A. Sulfhydryl and Ascorbic Acid Relationships in Selected Vegetables and Fruits. J. Food Sci. 1991, 56, 427–430. [Google Scholar] [CrossRef]
- Albrecht, J.A.; Schafer, H.W.; Zottola, E.A. Relationship of Total Sulfur to Initial and Retained Ascorbic Acid in Selected Cruciferous and Noncruciferous Vegetables. J. Food Sci. 1990, 55, 181–183. [Google Scholar] [CrossRef]
- Lee, S.K.; Kader, A.A. Preharvest and postharvest factors influencing vitamin C content of horticultural crops. Postharvest Biol. Technol. 2000, 20, 207–220. [Google Scholar] [CrossRef]
- FMCSA Report. Available online: https://www.fmcsa.dot.gov/regulations/hours-service/summary-hoursservice-regulations (accessed on 2 January 2016).
- FMCSA Report. Available online: https://www.fmcsa.dot.gov/rules-regulations/topics/hos/regulatoryimpact-analysis.htm (accessed on 2 January 2016).
- Fourer, R.; Gay, D.M.; Kernighan, B. Algorithms and Model Formulations in Mathematical Programming; Springer: New York, NY, USA, 1989; pp. 150–151. [Google Scholar]
- Pal, A.; Kant, K. SmartPorter: A Combined Perishable Food and People Transport Architecture in Smart Urban Areas. In Proceedings of the 2016 IEEE International Conference on Smart Computing (SMARTCOMP), St. Louis, MO, USA, 18–20 May 2016. [Google Scholar]
- Moler, C. Experiments with MATLAB. Available online: https://www.mathworks.com/moler/exm.html (accessed on 2 January 2016).
- Aiello, G.; Scalia, G.L.; Micale, R. Simulation analysis of cold chain performance based on time-temperature data. Prod. Plan. Control 2012, 23, 468–476. [Google Scholar] [CrossRef]
- Park, H.; Kim, Y.; Jung, S.; Kim, H.; Lee, S. Response of microbial time temperature indicator to quality indices of chicken breast meat during storage. Food Sci. Biotechnol. 2013, 22, 1145–1152. [Google Scholar] [CrossRef]
- Kim, Y.A.; Jung, S.W.; Park, H.R.; Chung, K.Y.; Lee, S.J. Application of a Prototype of Microbial Time Temperature Indicator (TTI) to the Prediction of Ground Beef Qualities during Storage. Korean J. Food Sci. Anim. Resour. 2012, 32, 448–457. [Google Scholar] [CrossRef]
- Bobelyn, E.; Hertog, M.L.; Nicolaï, B.M. Applicability of an enzymatic time temperature integrator as a quality indicator for mushrooms in the distribution chain. Postharvest Biol. Technol. 2006, 42, 104–114. [Google Scholar] [CrossRef]
- Ahumada, O.; Villalobos, J.R. Application of planning models in the agri-food supply chain: A review. Eur. J. Oper. Res. 2009, 196, 1–20. [Google Scholar] [CrossRef]
- Rantala, J. Optimizing the supply chain strategy of a multi-unit finish nursery. Silva Fenn. 2004, 38, 203–215. [Google Scholar] [CrossRef]
- Maia, L.O.A.; Lago, R.A.; Qassim, R.Y. Selection of postharvest technology routes by mixed-integer linear programming. Int. J. Prod. Econ. 1997, 49, 85–90. [Google Scholar] [CrossRef]
- Aramyan, L.; Ondersteijn, J.; Kooten, O.; Lansink, A.O. Performance Indicators in Agri-Food Production Chains; Springer: Dordrecht, Netherlands, 2006; Volume 15, pp. 47–64. [Google Scholar]
- Lin, Y.H.; Meller, R.D.; Ellis, K.P.; Thomas, L.M.; Lombardi, B.J. A decomposition-based approach for the selection of standardized modular containers. Int. J. Prod. Res. 2014, 52, 4660–4672. [Google Scholar] [CrossRef]
- Sallez, Y.; Montreuil, B.; Ballot, E. On the Activeness of Physical Internet Containers. In Service Orientation in Holonic and Multi-Agent Manufacturing; Springer: Berlin/Heidelberg, Germany, 2015; pp. 259–269. [Google Scholar]
- Pal, A.; Kant, K. Networking in the Real World: Unified Modeling of Information and Perishable Commodity Distribution Networks. In Proceedings of the IEEE International Physical Internet Conference (IPIC), Atlanta, GA, USA, 29 June–1 July 2016. [Google Scholar]
- Kant, K.; Pal, A. Internet of Perishable Logistics. IEEE Int. Comput. 2017, 21, 22–31. [Google Scholar] [CrossRef]
- Pal, A.; Kant, K. F2π: A Physical Internet Architecture for Fresh Food Distribution Networks. In Proceedings of the IEEE International Physical Internet Conference (IPIC), Atlanta, GA, USA, 29 June–1 July 2016. [Google Scholar]
- Matthews, K.R.; Sapers, G.M.; Gerba, C.P. The Produce Contamination Problem: Causes and Solutions; Academic Press: San Diego, CA, USA, 2014. [Google Scholar]
- GS1 Identification Keys. Available online: http://www.gs1.org/sites/default/files/docs/idkeys/GS1_ID_Keys_Reference_Card.pdf (accessed on 1 December 2017).
- Produce Traceability Initiative Best Practices for Repacking and Commingling. Available online: https://www.producetraceability.org/documents/Repacking_Best_Practice_Guide_v1_2_final_03232012.pdf (accessed on 1 December 2017).
- C2Sense. Available online: http://www.c2sense.com (accessed on 1 December 2017).
- FoodScan. Available online: http://www.israel21c.org/keeping-food-safe-from-farm-to-fork/ (accessed on 1 December 2017).
- Salmonella Sensing System: New Approach to Detecting Food Contamination Enables Real-Time Testing. Available online: http://phys.org/news/2013-10-salmonella-approach-food-contamination-enables.html (accessed on 18 March 2016).
- Pal, A.; Kant, K. Magnetic Induction Based Sensing and Localization for Fresh Food Logistics. In Proceedings of the 2017 IEEE 42nd Conference on Local Computer Networks (LCN), Singapore, 9–12 October 2017. [Google Scholar]
- Pal, A.; Kant, K. Sensing and Communications for Intelligent Fresh Food Distribution Logistics. submitted to ACM HotMobile. 2018. [Google Scholar]
- Hermann, M.; Pentek, T.; Otto, B. Design Principles for Industrie 4.0 Scenarios. In Proceedings of the 2016 49th Hawaii International Conference on System Sciences (HICSS), Koloa, HI, USA, 5–8 January 2016; pp. 3928–3937. [Google Scholar]
- Aurell, J.; Wadman, T. Vehicle Combinations Based on the Modular Concept. NVF-Reports. Available online: http://www.nvfnorden.org/lisalib/getfile.aspx?itemid=1589 (accessed on 2 December 2017).
- Meller, R. Functional Design of Physical Internet Facilities: A Road-based Transit Center; Faculté des Sciences de l’Administration, Université Laval: Quebec City, QC, USA, 2013. [Google Scholar]



| -Nodes | Operations |
|---|---|
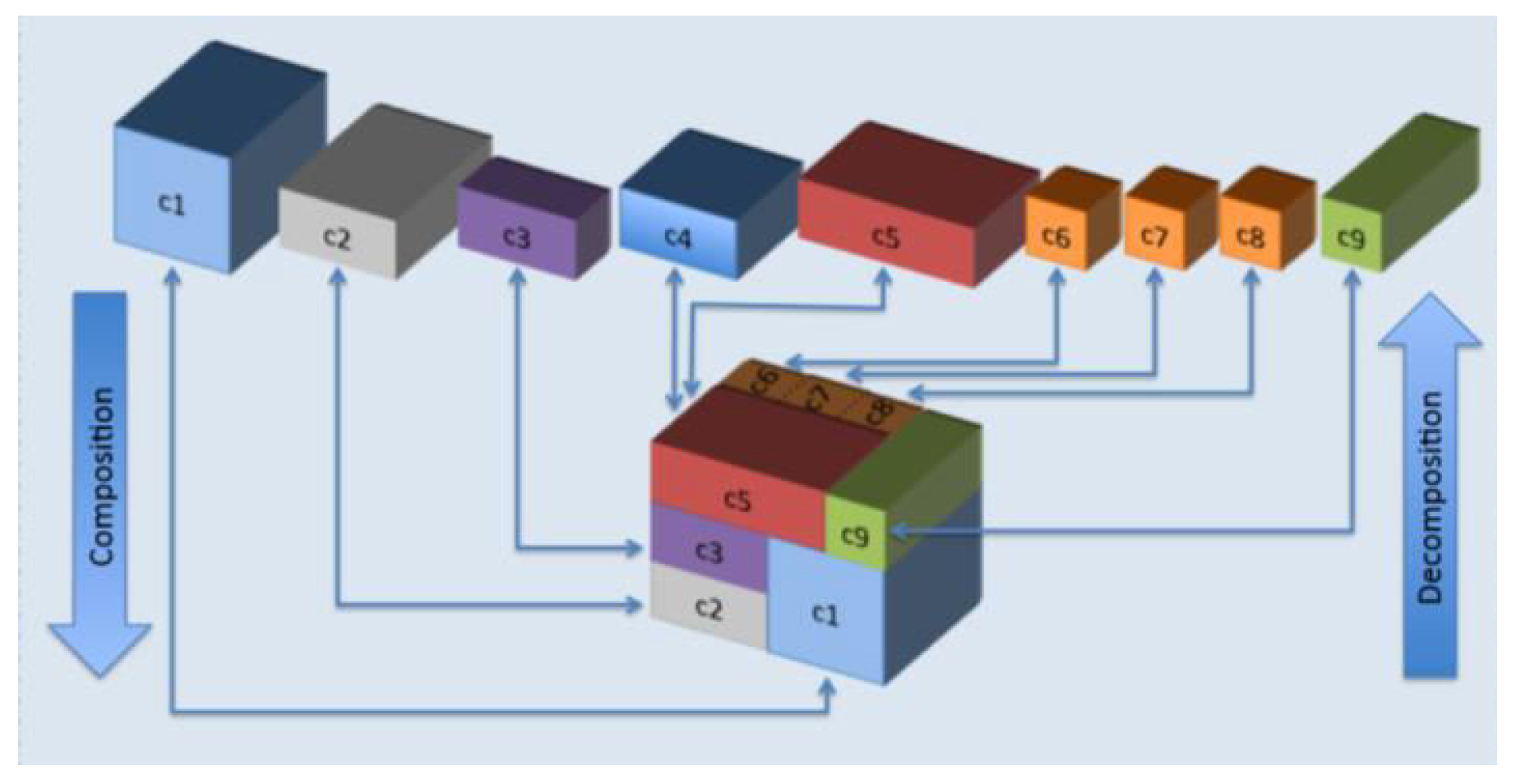
| -container | Containers that easily combine to create bigger and bigger containers so as to maximize space utilization and shipping efficiency, as shown in Figure 1 |
| -mover | Moves the -containers, such as -vehicles, -carriers, -conveyors, -handlers, etc. |
| -transit | Exchange points where the -containers are transferred from the inbound -vehicles to the outbound -vehicles |
| -switch | Unimodal transfer of -containers in between the -movers (like rail-rail or conveyor-conveyor -switches) |
| -bridge | One-to-one multi-modal transfer of -containers in between the -movers (like rail-road -bridge) |
| -hub | Multi-modal transfer of -containers from incoming -movers to outgoing -movers, i.e., it transfers the containers in between rail, road, water or air transportation |
| -sorter | Receive -containers from one or more entry points, sort and ship them to their specified exit points |
| -composer | Compose -containers for better space and shipping efficiency |
| -store | Store -containers |
| -gateway | Intersection points in between a private network and the physical Internet |
| Indices | ||
|---|---|---|
| i, j | ≜ | Index for distribution centers (1, …, ) that are within the coverage areas of the trucks |
| ℓ | ≜ | Index for transit-segments of the trucks (1, …, ) |
| t | ≜ | Index for types of products (1, …, ) |
| Transportation variables | ||
| ≜ | Number of type t loaded at for delivery at at the ℓ-th transit-segment | |
| ≜ | Number of type t unloaded at from at the ℓ-th transit-segment | |
| ≜ | Number of type t that are on the truck for delivery at from at the ℓ-th transit-segment | |
| ≜ | Truck load of type t at transit-segment ℓ | |
| ≜ | Delivery request from to of type t | |
| ≜ | Time of travel from to | |
| ≜ | Time when the truck delivers at in the ℓ-th transit-segment | |
| Decision Variables | ||
| ≜ | Whether or not the truck goes from to at the ℓ-th transit-segment | |
| A | B | C | D | E | |
|---|---|---|---|---|---|
| A | - | 2 | 3 | 3 | 3 |
| B | 2 | - | 2 | 3 | 3 |
| C | 3 | 2 | - | 1 | 1.5 |
| D | 3 | 3 | 1 | - | 1 |
| E | 3 | 3 | 1.5 | 1 | - |
| A | B | C | D | E | |
|---|---|---|---|---|---|
| A | - | X | X | X | X |
| B | - | - | X | - | - |
| C | X | - | - | - | X |
| D | X | - | - | - | X |
| E | X | - | X | X | - |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pal, A.; Kant, K. A Food Transportation Framework for an Efficient and Worker-Friendly Fresh Food Physical Internet. Logistics 2017, 1, 10. https://doi.org/10.3390/logistics1020010
Pal A, Kant K. A Food Transportation Framework for an Efficient and Worker-Friendly Fresh Food Physical Internet. Logistics. 2017; 1(2):10. https://doi.org/10.3390/logistics1020010
Chicago/Turabian StylePal, Amitangshu, and Krishna Kant. 2017. "A Food Transportation Framework for an Efficient and Worker-Friendly Fresh Food Physical Internet" Logistics 1, no. 2: 10. https://doi.org/10.3390/logistics1020010
APA StylePal, A., & Kant, K. (2017). A Food Transportation Framework for an Efficient and Worker-Friendly Fresh Food Physical Internet. Logistics, 1(2), 10. https://doi.org/10.3390/logistics1020010





