1. Introduction
The history of conventional economics and maritime economics as a branch of applied economics coincide in many facets of theoretical interpretations as well as practical uses. Therefore, it is not surprising to notice that many leading economists studied maritime related topics in their academic career. Paine [
1] in his seminal work,
Sea and Civilization, strikingly emphasizes that ‘
history is maritime history’. Every aspect of our modern maritime economics theory is basically born in the conventional economic theory and its incubation nests. Bulk shipping economics broadly leads maritime economics research, and it is a frontier, considering its history goes much before other segments of maritime economics such as liner shipping. The ruling school of maritime economics (the somewhat doctrine of maritime economics) is built by some fundamental hypotheses:
Freight rate is settled in an environment led by supply of bulk shipping services (usually attributed as fleet capacity) and demand for bulk shipping services (usually attributed as seaborne trade volume) (e.g. [
2]);
Supply of shipping services is very inelastic and rigid, while it is somewhat elastic in recession periods due to inactive fleet (e.g., laid-up tonnage) or slow steaming [
2,
3];
Shipping markets are efficient, at least in the long-run [
4,
5,
6];
Bulk shipping markets are perfectly competitive (for liner shipping markets, there are several scholars who indicate the weakness of market competition and existence of oligopoly e.g. [
7,
8];
Prices in the shipping business is mean-reverting (freight market memory) and stationary random walk series with no predictability (at least non-linear stationary [
9]);
Period freight rate is the expectation of future spot rate (i.e., term structure) ([
10,
11], among others).
In contrast to their central role, these hypotheses are sometimes accepted and rejected interchangeably in different periods of the literature, based on the period of time or the method used for testing procedures (classical versus time-varying, or linear versus non-linear approach) (e.g., Adland and Cullinane [
12] criticizes the traditional expectations theory assumed in previous studies and proposes an alternative approach).
Among these theoretical underpinnings of the maritime economics, the supply-demand framework plays a central role that is in close connection with other theories, and they are proof of each other at some point. Although the supply-demand framework is well-established in a theoretical basis (theoretical-laboratory economics), the measurement of real supply and demand is quite difficult in practice. Supply-demand framework is first developed by the so called fathers of economics in an era of physical discovery boom, and the theory is very much inspired from its mechanical perspective. The emergence of Austrian, behavioral, and institutional schools of economics broadly relies on the gap between the mechanical narrative of economics and the economic phenomenon in practice.
In maritime economics, measurement of supply and demand for shipping services is established over the ton–mile metric. Two dimensions of shipping services are thought to be essential: the volume of cargo being carried (ton), and the distance sailed (nautical mile) for the shipment. The product of these dimensions (ton–mile) is globally assumed as the scale of shipping services. In this paper, the ton–mile approach is revisited and critically reviewed with its historical backings and the basis on which the theory is built.
2. Supply and Demand for Shipping Services: Measurement Debate
Mainstream economics particularly emphasizes the supply-demand framework for the pricing of products and services. Pricing shipping services (i.e., freight rate formation) is thought to be a typical example of the supply-demand led Walrasian equilibrium mechanism, including some negligible external factors such as politics and social setting (in most studies, it is either ignored or assumed limited) [
2]. Based on this origin, supply-demand analysis is a key component in both academic and professional assessments of shipping markets. Before moving one step further, a comparative analysis of the shipping industry and other service industries would be timely and useful.
In the conventional service industry (e.g., restaurants, hotels), demand factors are usually measurable and present further assessments in addition to limited size of their markets. A restaurant in a city merely serves the society around the city, and short response time (customer visits, completion of service) makes it possible to count the number of customers and the volume of required services. A hotel located in a metropolitan area is designed for guests visiting that particular city in its relatively small boundaries. Numbers and requirements are readily available at any time. Most importantly, customers that are declined or not served in a timely manner (delayed) are known to key decision makers for designing and restructuring facilities and capacity. For example, a customer who waits in queue of a restaurant is explicitly known to managers. In modern restaurant chains, you may also find numerators that dynamically record requests and waiting times. Availability of both serviced and non-serviced customers is a great feature for future planning and pricing services. The capacity of restaurants can also be calculated roughly based on service time, number of seats, etc.
However, supply and demand are not measurable in various service industries, which produces a particular difficulty to economists. In Sasser [
13], the vulnerabilities of service industry analysis are discussed in four major dimensions:
- -
Services are direct; they cannot be inventoried.
- -
There is a high degree of producer-consumer interaction in the production of service.
- -
Services cannot be transported.
- -
Services’ output is intangible (subjective perception of service quality).
It is quite similar in the case of shipping service. Similar to hotels and restaurants, shipping service is a
Non-Storable and
Non-Transferable product. Shipping service capacity is available even when it is not employed. A critical question here is how to measure supply or demand for shipping services or rather shipping service itself. The “ton–mile” metric is used for measuring supply-demand for shipping services in the last century ([
2,
14], among others), and its origin actually goes back to railway transport.
2.1. The History of “Ton–Mile” and Its Rationale
In the modern economics of maritime transport, shipping service is assumed to be measured by the ton–mile metric. The definition of the ton–mile metric takes into account two major dimensions of shipping services: (1) size of cargo (ton) and (2) distance sailed (nautical mile). A century ago, shipping services were not specialized, and merchant ships were very similar to each other. Dry bulks were carried in bags, while wet bulks (e.g., vegetable oils) were carried in barrels. However, the modern form of the shipping industry is totally different than its ancestors. To understand the logic behind the ton–mile metric, a historical review would be timely and illuminating.
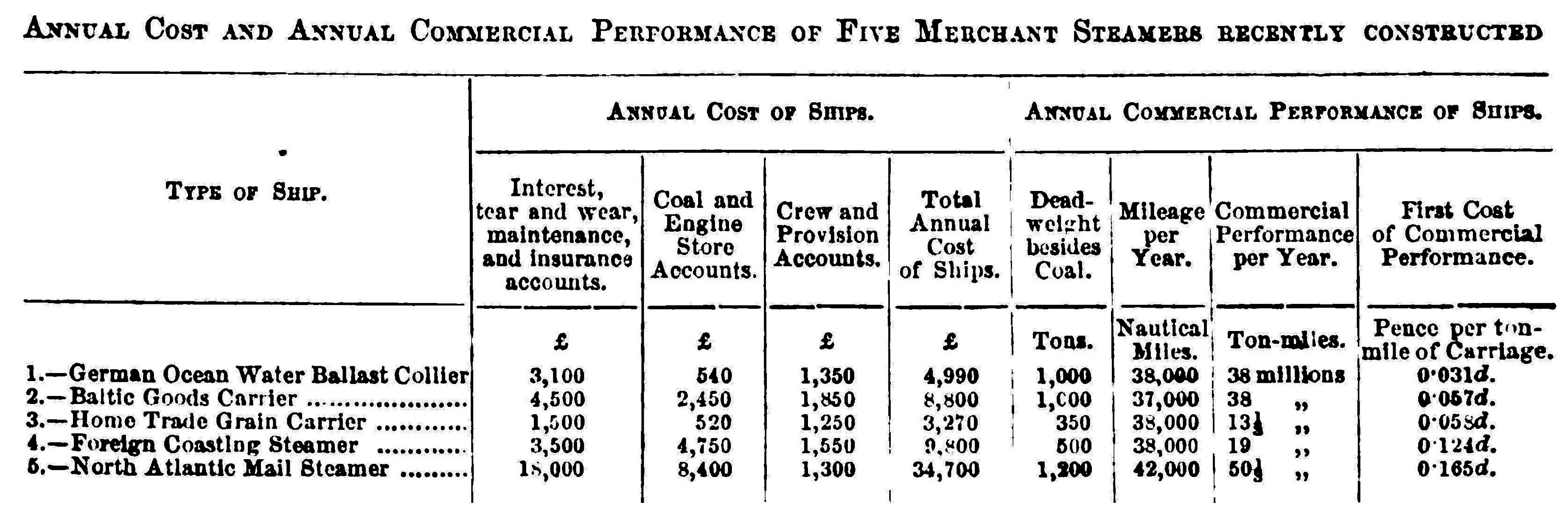
The term ‘ton–mile’ has been used for railway transport for the last couple of centuries. There are vast number of publications referring to ton–mile metrics when dealing with the production of railway transport services. However, its use for maritime transport goes back to 1871. To the best of our knowledge and extensive research, Walter Carl Bergius, a naval architect, first utilized the ton–mile metric for maritime transport in the Journal of the Society for Arts (Volume 19, p. 433) [
15]. He was the owner of Bergius and Co., Engineers and Naval Architects, Glasgow, and wrote an article titled, “On the commercial economy and performance of several types of merchant steamers on some of the principal lines of steam-ship traffic”. In his article, he explicitly indicated the railway transport analogy:
“The performance of the five ships is given in carriage units, called ‘ton–miles,’ computed in an analogous sense to ‘train-mile’ in railway terminology. A ton–mile is the performance accomplished in carrying one ton of deadweight for the distance of one nautical mile; therefore, if a ship carries 200 tons deadweight, besides her coal, upon load draught, and runs a distance of 35,000 nautical miles per annum, her total annual performance as a freight carrier is 35,000 × 200, equal to 7,000,000 ton–miles.”
Similar calculation for various carriers was presented (
Figure 1).
There are some publications that utilize and emphasize this approach in the last quarter of the 19th century. Thomas F. Woodlock wrote a book titled “
Ton–Mile Cost”, and discussed its methodology in railroad transport analysis ([
16], see
Figure 2). Although his book focuses on the railroad industry, its introduction generalizes the concept, and the author prefers ‘
transportation’ as title rather than a specific, ‘railroad transport’. Therefore, “Ton–Mile Cost” seems the first dedicated publication about measuring the transport service, and it is probably the only publication specifically written on the topic in history. The author has a very critical note just after the introduction of the concept in the first page of the first chapter:
“The passenger-mile is an abstraction, because it does not exist except as an arbitrary mental concept. The same is true of the ton–mile. Yet both are real and true measures of transportation, whereas neither of the component parts is alone a measure.”
The author clearly indicates that the ton–mile approach is just an abstraction, and it is absolutely not a complete measure of transport services. In addition to its limitation, the author mentions neither ‘demand’ nor ‘supply’ in the same context (these two terms are never used in the book). So, the author does not associate the ton–mile metrics with demand or supply.
In the 20th century, one of the pioneers of the econometrics and the theory of the maritime economics, Jan Tinbergen (First Nobel Laureate in Economics, 1969), utilized ton–mile metrics in his seminal work, “
Tonnage and Freight” [
14]. In contrast to previous uses of ton–mile metrics, Tinbergen associates it with the demand (i.e., demand index), while indicating the volume of tonnage and operating cost (i.e., coal price as marine bunker) as supply side indicators (‘supply picture’ in original text). After the book’s publication, seaborne trade volume (ton–miles) is frequently assumed to be a demand indicator in various publications of the field (e.g., [
3] p. 19). For example, Eriksen [
17] investigates demand for bulk shipping, and seaborne trade volume is again utilized as demand.
2.2. Challenges in the “Ton–Mile” Metric
In the theoretical economics, demand and supply are illustrated in identical units so as to analyze balance or imbalance of these two forces on prices (i.e., equilibrium). Seaborne trade volume, or in other words ton–mile (as the sum product) of ‘materialized’ (performed) shipments, is preferred as demand instead of supply. Stopford [
2] in his supply-demand framework justifies the approach and prefers ton–mile metrics for both supply and demand side ([
2]; p. 137). So, Stopford [
2] debiases the unit and balancing problem in the theoretical framework. The fundamental question is whether seaborne trade would be indicator for demand or supply of shipping services. It is clear that the size of a merchant shipping fleet describes the tonnage capacity for shipping; it is not the real size of shipping supply (dwt vs. ton–mile).
Tinbergen [
14] also indicates the accuracy problem behind the demand analysis. The neo-classical approach assumes unidirectional impact from demand to prices, and Tinbergen [
14] follows this principle while indicating that the contra-impact of price over the demand would be negligible or less than opposite. In other words, demand for shipping is fairly inelastic (demand driven market).
There are two problems behind the approach. First, seaborne trade (or ton–mile based on performed shipments) does not reflect shipments that are delayed or cancelled due to shortage of tonnage or unfeasible freight rates. There is no instrument to gauge its size and impact, and it is actually quite cyclical. When freight rates are calculated over a long-term average, shipowners usually fix their fleet easily, and their ships are very much productive. On the other hand, cargo owners may have difficulty in finding shipping space since the entire fleet is in a very productive and busy period. That will eventually cause problems such as rescheduling of shipments, delays, and parcel size changes (getting larger with higher freight rates). In the opposite period of the market, freight rates are lower than the long-term average, and the size of a fleet is typically in an oversupply cycle. In such circumstance, cargo owners will find tonnage easily, while shipowners will have difficulty employing their fleet. This eventually reduces productivity of the fleet (longer off-hire periods, slow steaming, lay-ups). In the first example, seaborne trade is a more reliable indicator for supply (full-capacity), while it is better indicator of demand in the second example. So, it is quite difficult to have a common interpretation of seaborne trade volume. In between different market periods, there will be various forms of demand-supply configurations that make it much more complicated. The productivity level of a shipping fleet changes through time, and it is very difficult to estimate its impact on seaborne trade volume statistics.
The second problem is that approach pretty much generalizes the demand for shipping, and it is implicitly assumed to be a static process. Even Tinbergen [
14] indicates various cargoes and tonnages around a century ago. Today, we know that there are several cargoes and corresponding parcel size configurations. In addition to that, parcel sizes are not static: they are dynamically settled in different climates of the global economy. For example, grain parcels may shift between Handymax (e.g., 45 k dwt) and Panamax (e.g., 70 k dwt) tonnages based on schedule and amount of trading activities. When demand for a given cargo increases, cargo owners may merge parcels into a single Panamax shipment rather than double Handymax shipments in a time lag. With growing global population and consumption, there is also a long-term rising trend in parcel sizes. Last but not least, there is cargo exchanges between general cargoes/bulk cargoes and container shipping, with increasing capacity of bulk cargo containers (particularly tank containers).
Back to its use in Bergius [
15], the ton–mile metric is explicitly a measure of transport, while attributing as a measure of demand or supply is always a biased approach considering the above mentioned features of the data. There is always a high positive correlation between dry bulk fleet capacity and dry bulk seaborne trade volume (e.g., over 0.85 for the last thirty years), and this causes multicollinearity problem in econometric models consisting of both demand and supply as independent variables. The measurement and analysis of shipping services have always been a great challenge regarding the collecting of relevant numbers, modelling in econometrical instruments, and interpreting the results. The predictability of the shipping markets is thought to be as low as the chances in flipping a coin.
3. The Adoption of Ton–Mile Metric in Maritime Economics Studies
Considering the maritime economics literature, the most cited scholarly publication that utilizes the ton–mile metric is written by Tinbergen [
14]. It is obvious that Tinbergen’s work has made a significant impact the field at its emergent stage. The persuasive power of Tinbergen is inevitable. He is known as one of fathers of modern econometrics and is also the first Nobel Laureate in Economics (originally
Bank of Sweden Prize in Economics). If we review the background of early developments in economics, it is not a secret that the age of Tinbergen arose from the transfer of ideas from developments in Physics. Beginning with the first quarter of the 1900s, the physical metaphor and the idea of explaining economic phenomenon with strict and abstract representations have grown dramatically [
18,
19]. A unique assumption of this approach is the measurability of economic actions. The econometric approach therefore requires the measurement of major components, including supply and demand. Therefore, the ton–mile metric is a solution to the measurement problem in the shipping services.
In subsequent years, the vast majority of the literature adopts the approach of Tinbergen, while a number of scholars prefer much more neutral position as in Metaxas [
20]. Metaxas ([
20], p. 274) states that, “
…the tramp freight market mechanism is not characterised by a stable equilibrium; demand is not always equal to the supply of tramp shipping tonnage at a price at which only normal profits are made.” He also underlines the lack of a real equilibrium in the market. Metaxas [
20] does not frame the shipping demand in the context of ton–mile measurement, but the weight of cargo (metric tons) transported by ships is investigated.
The Tinbergen doctrine of the ton–mile approach is reinforced by one of his colleagues and another Nobel Laureate, Tjalling C. Koopmans [
21], for tanker freight rates; Koopmans also clearly defined the ton–mile metric as measure of both shipping supply and demand.
In Charemza and Gronicki [
22], as well as in Beenstock and Vergottis ([
23], p. 17), the demand for dry cargo freight is represented by ton–mile measurement. Charemza and Gronicki [
22] utilize an indirect approach while still following the ton–mile approach. In the theoretical analysis of Tvedt ([
24], p. 343), the ton–mile metric plays an integral role as a demand indicator. Glen and Martin [
25] also assume the association between ton–mile metric and demand, instead of supply or both. Duru and Yoshida [
26] have developed the Beenstock-Vergottis model with life expectancy theory while implicitly assuming seaborne trade volume (again ton–mile) as the demand for shipping services.
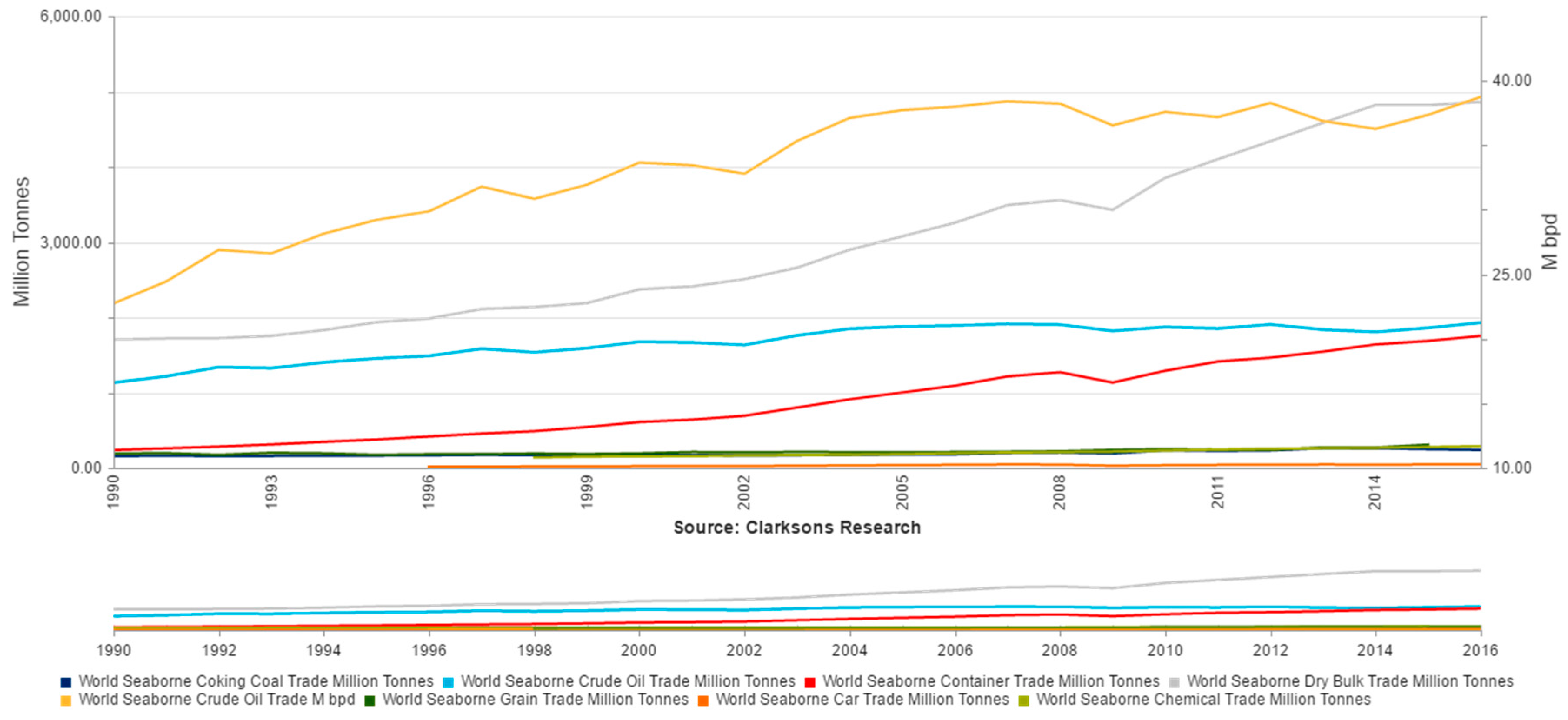
Considering the acceptance of the theory and uses of the ton–mile metric, it has become much more difficult to object to and revisit its weaknesses. The majority of past and ongoing research in maritime economics implicitly or explicitly assumes the ton–mile metric as an indicator of demand in various ship types (also TEU-mile in container shipping). On the other hand, the real explanatory power of seaborne trade is very low, since the seaborne trade volume for various cargoes has a steadily increasing trend without a significant decline, except in years with a market collapse (e.g., 2008) (
Figure 3).
It is common to find high level correlation between long-term datasets, since many of them are either positively or negatively trended. In a recent study, Munshi [
27] presented such spurious associations when proper data handling procedures are not followed.
There is also a critical reason behind the rationale of using the ton–mile metric. Econometric studies in maritime economics (also economics in general) are usually designed to observe relationships between variables (e.g., elasticities) in the historical data. The predictive power of those models is never tested and is presented in the current literature. The unique validation process for predictive power is the post-sample test of predictions generated by proposed models. The post-sample test of predictive properties of econometric models is ignored, and therefore the gap between statistical significance in past data and practical impact in real data always remained its undisclosed role in modelling shipping markets. The ton–mile metric (seaborne trade volume) is one example that suffers such inconsistencies.
4. Concluding Remarks
Taking into account the insufficiency of supply-demand measurement instruments, the use of the neo-classical framework has both theoretical and practical challenges. It is obviously not straightforward to employ seaborne trade as the volume of demand or supply, since it is technically not a complete representation of desired variable. Seaborne trade volume (ton–mile) may be a good predictor of demand at recession (oversupply, full utilization of shipments) or a good predictor of supply at upturn (undersupply, full utilization of fleet). In both case, various classifications of vessels and their cargo call into question the use of the ton–mile metric as a variable in conventional econometric analysis. Considering the changes in econometric models in every decade, the numbers that we utilize emphasize the potential of data omissions and/or the invalidity of an econometric approach.
Seaborne trade volume is still a good measure of the activity level in the industry without attributing either demand or supply. The extraction of the real volume of supply and demand from seaborne trade volume may be estimated through surveys and productivity indicators. Focus may be needed on the gap between numbers and ignored (uncounted) shipments, as well as on the average and highest productivity level of a shipping fleet. Some productivity indicators, such as lay-up tonnage and slow steaming estimations are presented in market reports, while converting this kind of data into real supply and demand figures is not well investigated or not presented as is (market predictions indirectly reflect such estimations).