AI Control for Pasteurized Soft-Boiled Eggs
Abstract
1. Introduction
1.1. AI Foods Processing
1.2. Pasteurized Soft-Boiled Eggs
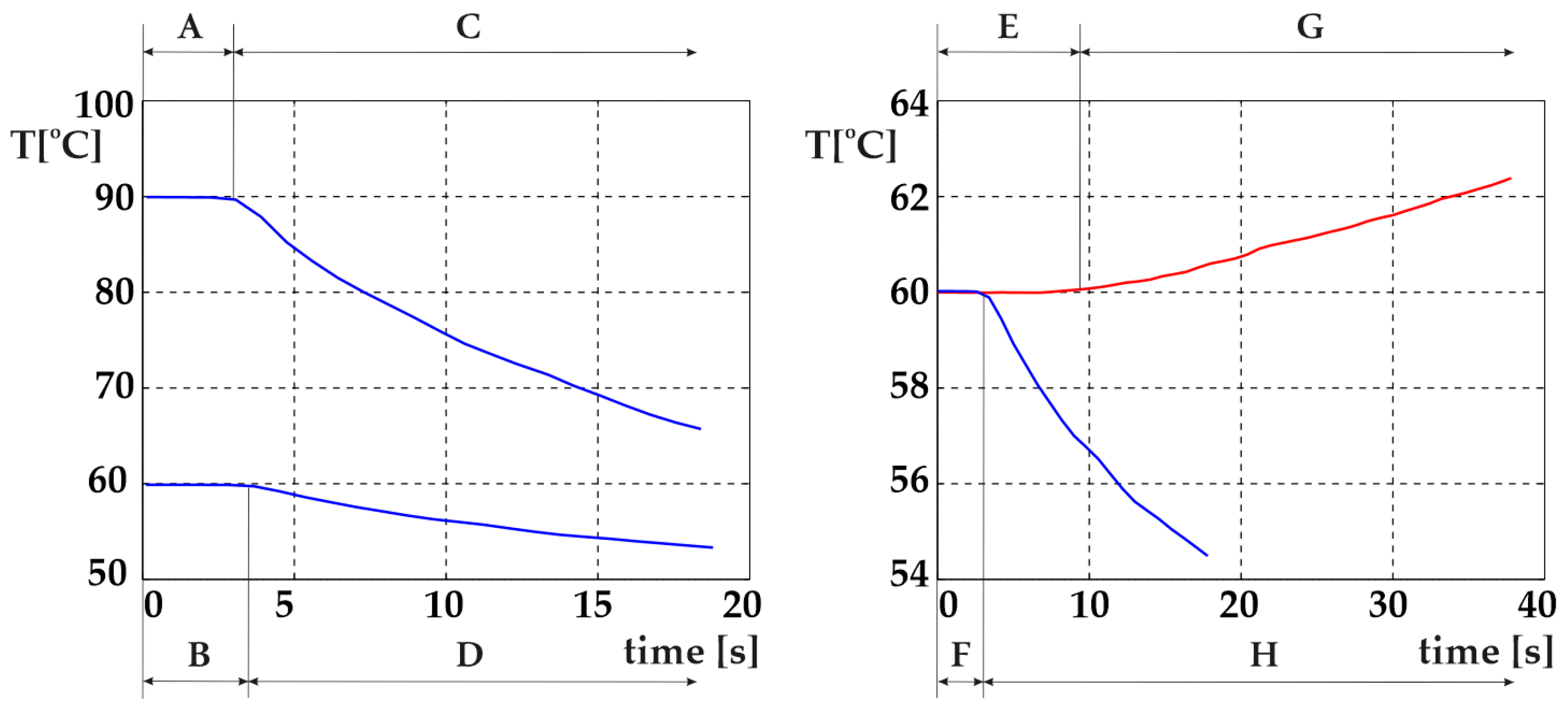
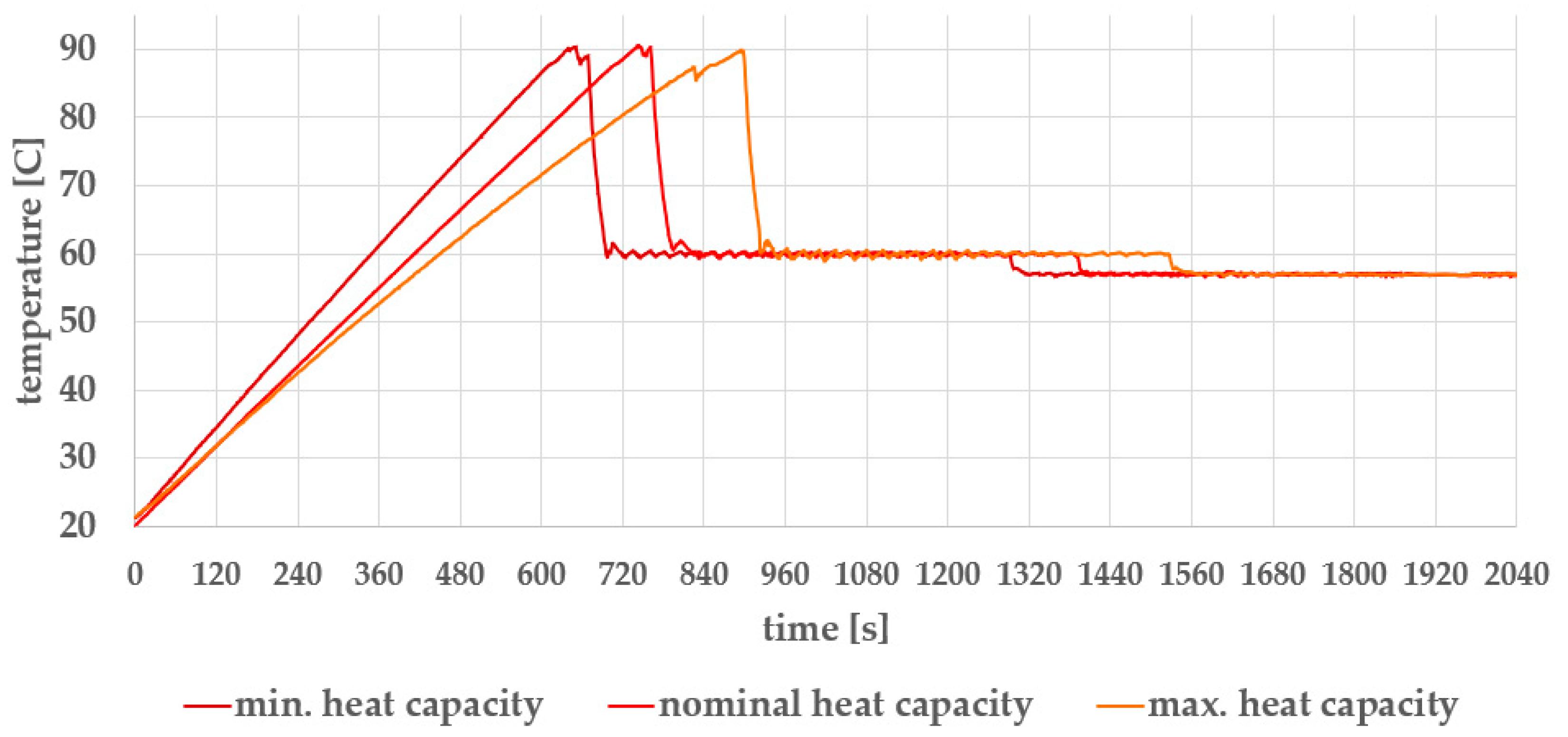
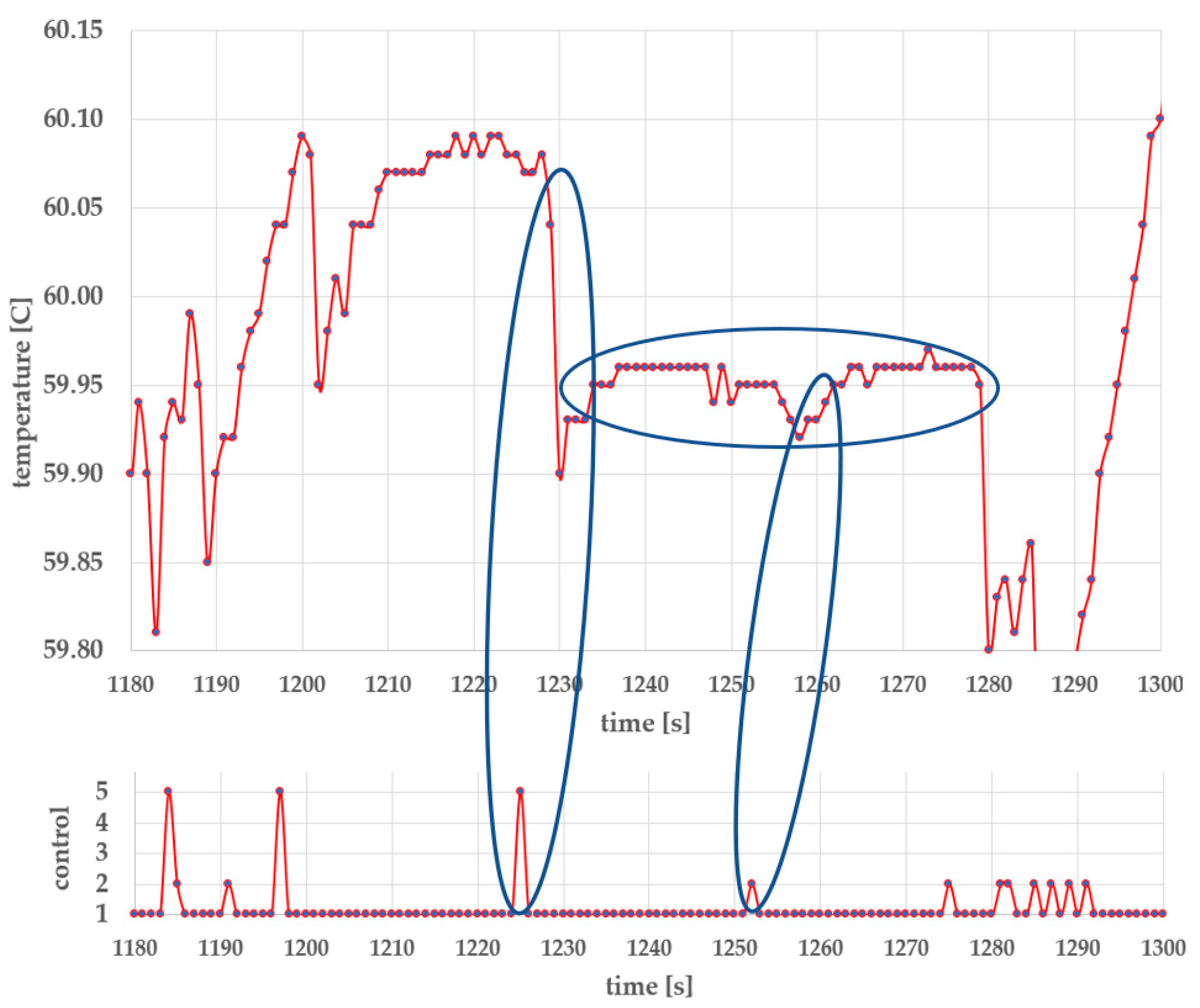
- Load sensitivity: The control algorithm performs well under full-load conditions (maximum number of eggs and water). However, when operating with partial loads—frequently required in practical use—the reduced heat capacity alters system dynamics, resulting in suboptimal control performance.
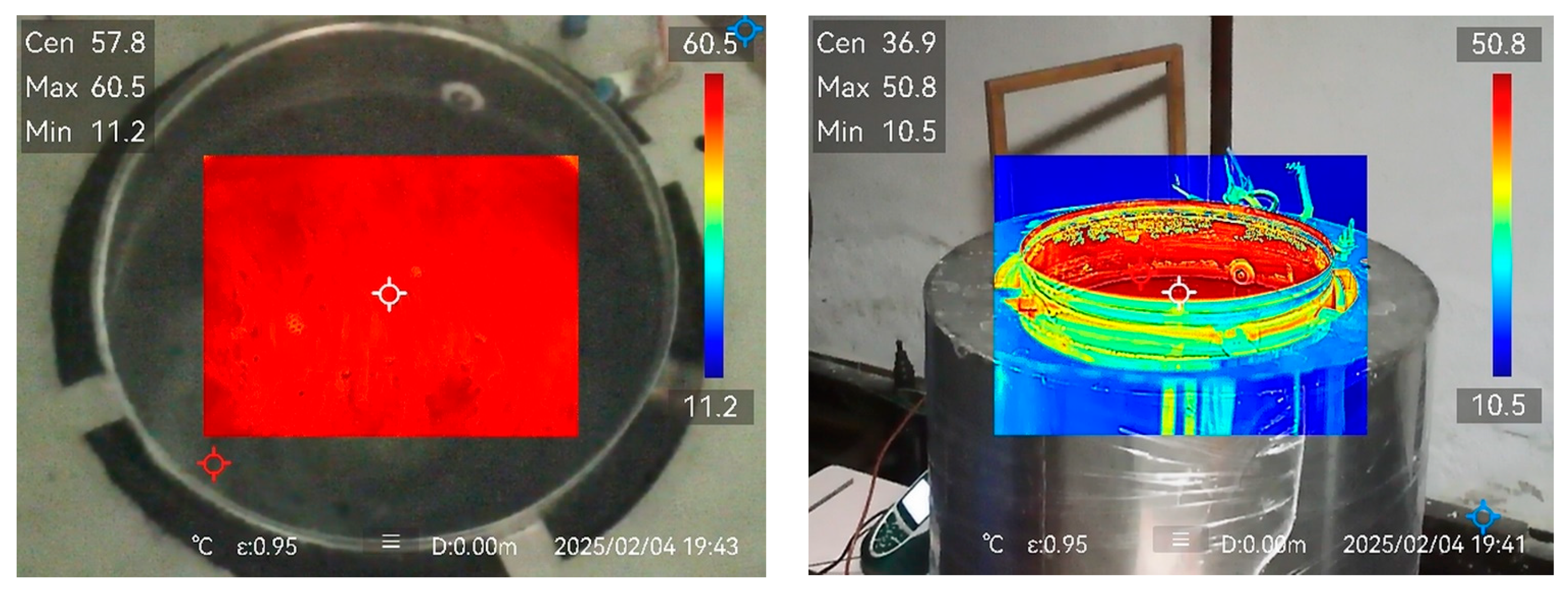
- Ambient temperature influence: Elevated room temperature, especially after prolonged operation (eggs can stay warm in the apparatus up to 6 h), contributes to firmer egg texture.
- Heater fouling: Limescale accumulation on the heater surface degrades heat transfer efficiency, thereby altering the thermal response of the system and impairing the accuracy of temperature control.
2. Reinforcement Learning Based Temperature Control
2.1. Etymology and Conceptual Origins of the Reinforcement Learning
2.2. RL Components
- The environment.
- The agent interacting with the environment.
- Observation—Before the agent takes an action, it observes the environment state, which serves as a part of information, based on which the agent decides which action to take.
- Action—An agent is interacting with the environment by taking actions based on its observations. Actions taken by the agent typically affect the state of the environment.
- Step—One step in the reinforcement system is defined as a cycle consisting of (a) the agent receiving observational information (and a reward, in the learning phase), (b) deciding which action to take, (c) taking the action, and (d) updating the environment state based on the agent’s action.
- Episode—One episode consists of multiple steps. For example, in a chess board game, one move on the chessboard is considered one step, and one game of chess is considered one episode.
- Reward—In the learning phase, i.e., the training phase, the agent is receiving rewards. These rewards serve as feedback for the agent, based on which the agent knows how well it is acting. The agent aims to collect as high a cumulative reward as possible throughout the steps of an episode. The agent learns to take actions that will lead to collecting the highest cumulative reward by the end of the episode.
- Policy—In the learning phase, the agent interacts with its environment with the goal of learning behavior policy that will earn him a high cumulative reward at the end of each episode. The agent is taking steps, one after another, episode after episode. The policy, which the agent is developing and refining throughout a sequence of episodes, defines a decision system. Based on current and previous observations, the decision system defines what action needs to be taken at each step: inputs are current and previous observations; output is the action to be taken. The decision system contains many learnable parameters, the values of which are defined during the learning phase.
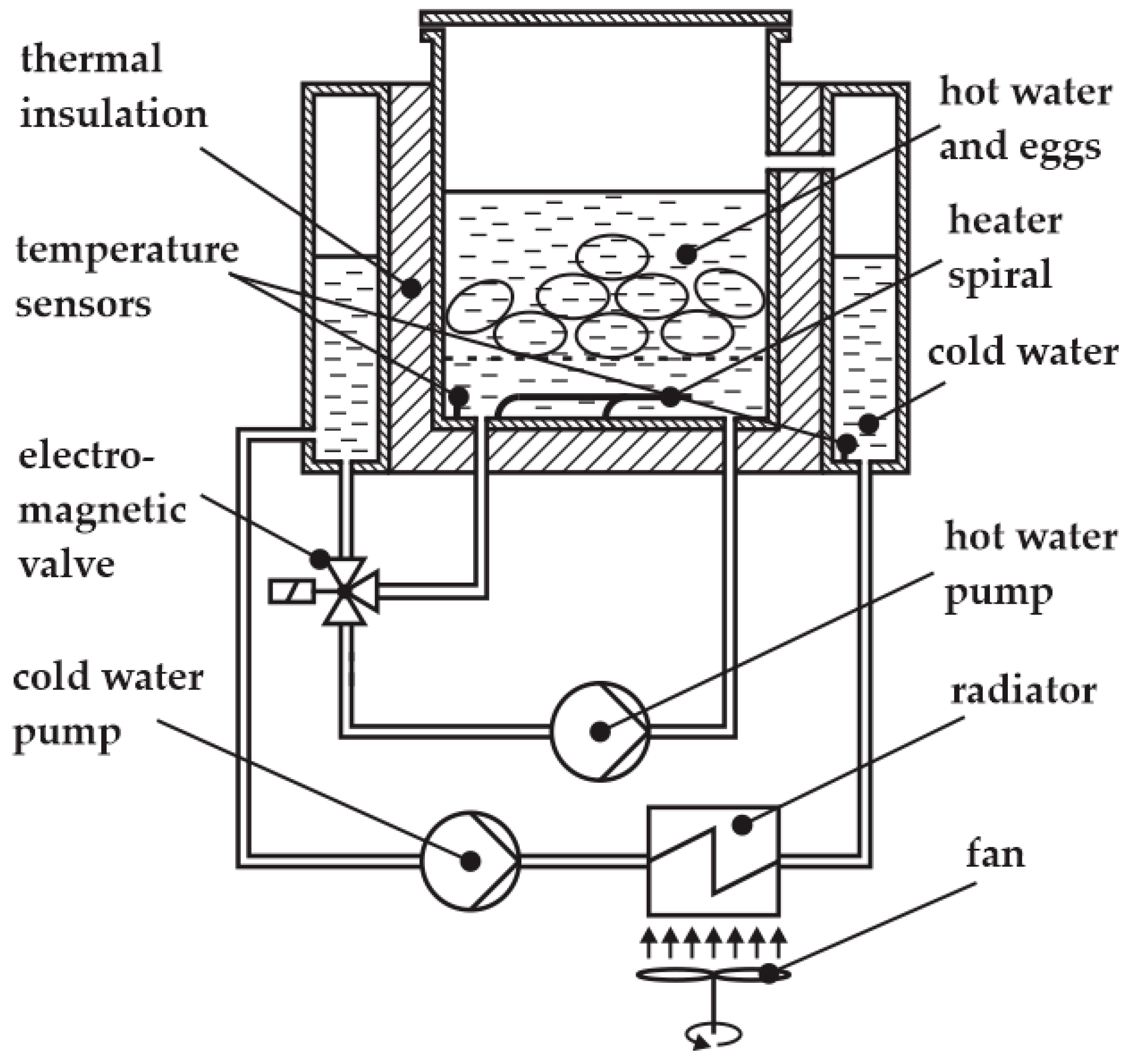
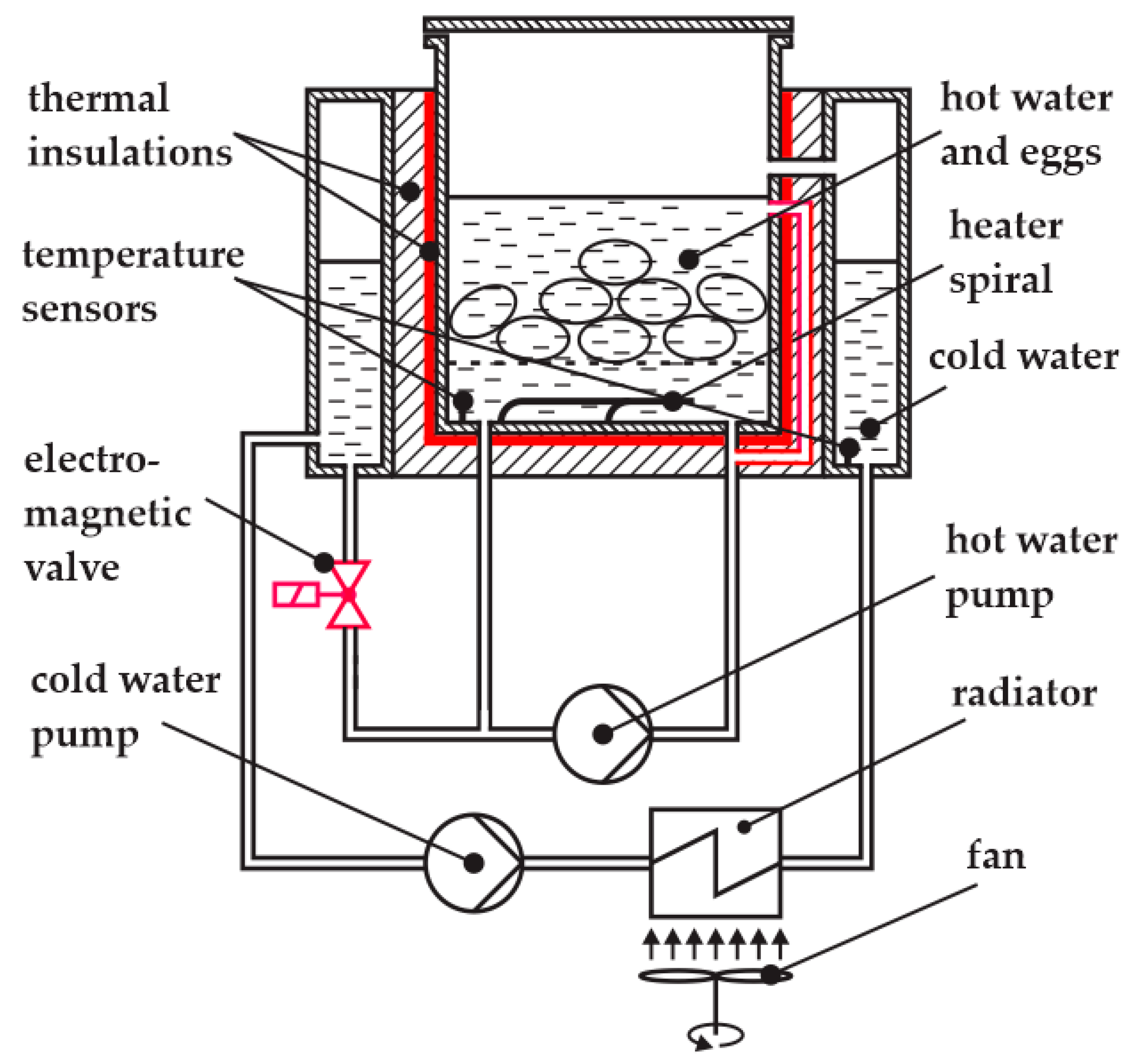
2.3. The Agent and the Egg Cooker
- Heater off, valve closed;
- Heater on, valve closed;
- Heater off, valve open;
- Heater on, valve open.
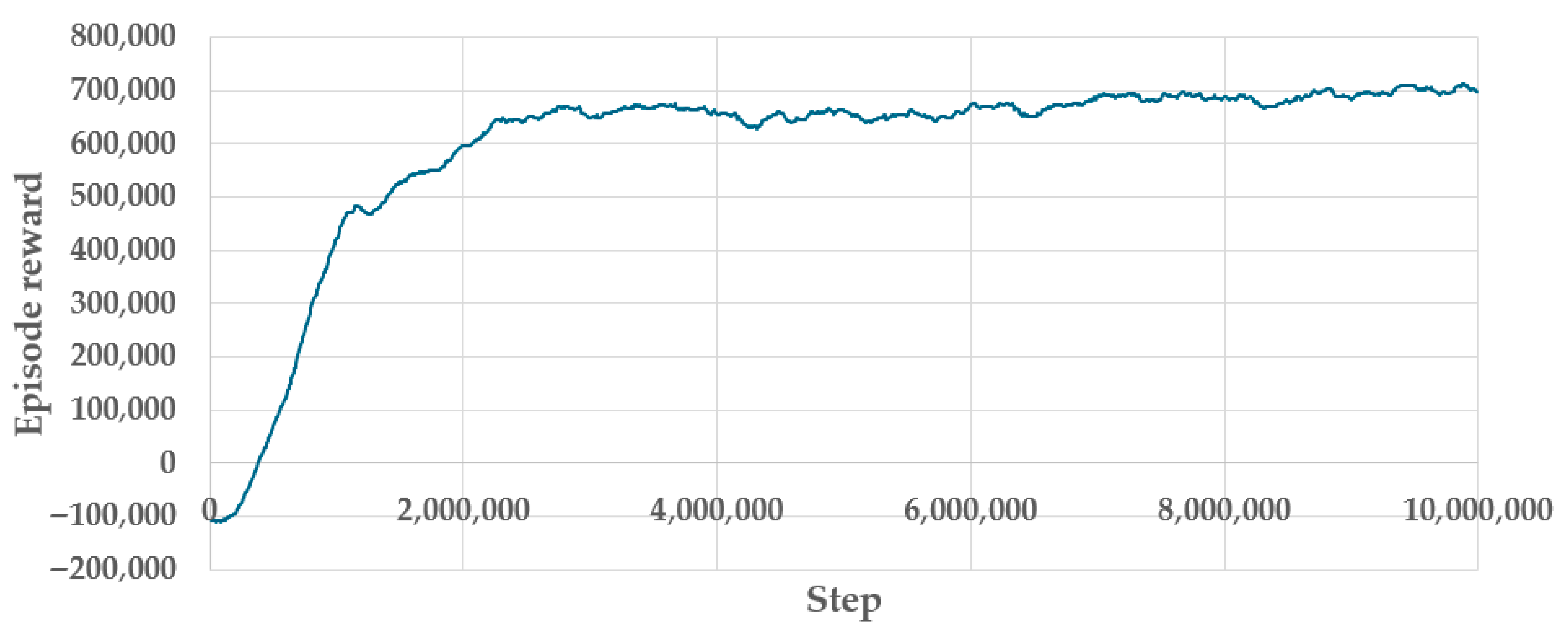
2.4. Learning in a Simulated Environment
- Initial temperature of the external (cold) water, with constant mass;
- Initial temperature of the device casing;
- Ambient temperature;
- Initial temperature of the eggs;
- Egg size;
- Egg age;
- Number of eggs;
- Mass of the heated water;
- Initial temperature of the heated water;
- Electrical supply voltage (), including variations from 230 V ± 15% (i.e., 195 V to 253 V, per EN 50,160 and IEC 61010-1 standards), and the voltage drop in a potential extension cord;
- Limescale deposits on the heating element.
2.5. Reinforcement Learning Algorithm Parameters and Workstation Configuration
2.6. The Apparatus Control
- Heater off, valve closed;
- Heater on, valve closed;
- Heater off, valve open;
- Heater on, valve open;
- Heater off, valve open to 20%.
2.7. The Apparatus Mechanical Improvements
- Water is now introduced into the vessel through a top-side inlet, while maintaining upward circulation from the bottom, in order to enhance overall water distribution.
- The three-way valve (Figure 2) was replaced with a simpler on/off valve (Figure 11), improving water circulation during the cooling phase. A secondary benefit is that the cooling power now exceeds the heating power to a lesser extent than in the original design, bringing the system closer to thermal symmetry.
- The thermal insulation of the inner vessel was improved. The new insulation is dual-layered. The inner insulation layer resists condensation, which can degrade conventional fibrous insulation materials. This protects the outer high-performance layer from moisture exposure and helps maintain long-term thermal performance. Assuming a thermal conductivity of approximately 0.020 W/m·K for aerogel and 0.08 W/m·K for silicone foam, the combined R-value of a 10 mm wall can reach approximately 0.625 (K·m2/W), significantly outperforming single-layer alternatives of the same thickness.
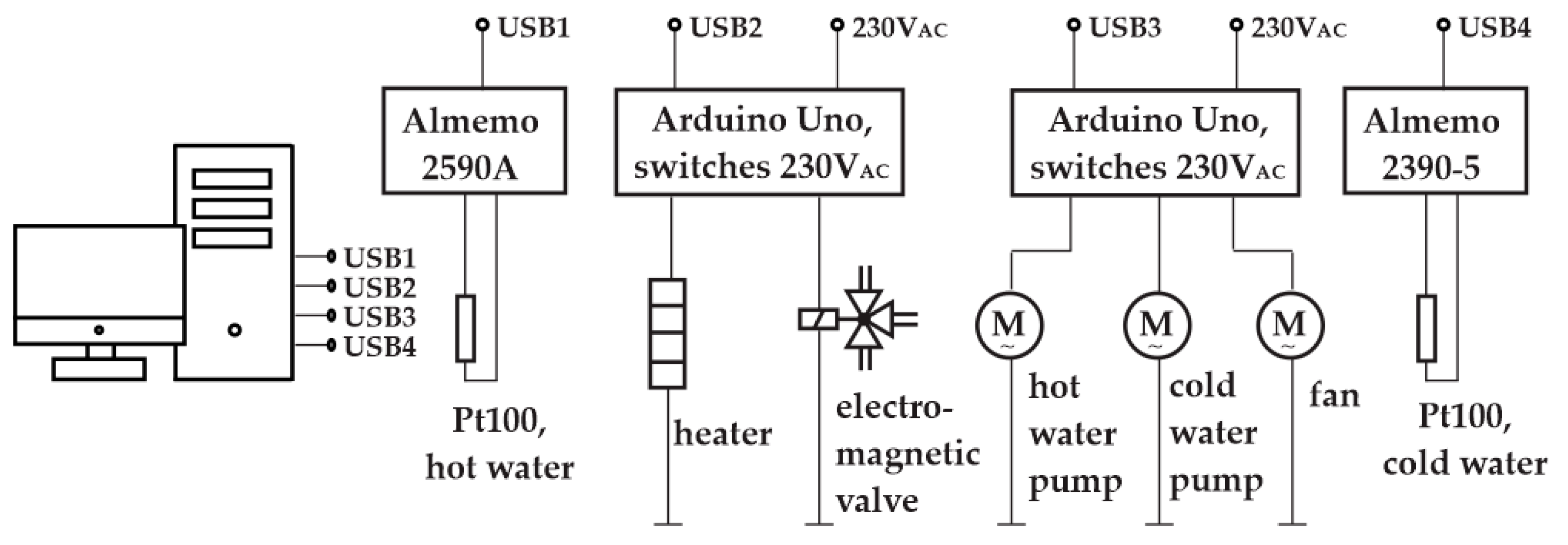
2.8. Methods for Porting the Algorithm to an Embedded System
2.8.1. Option A: Laboratory Python-Based DQN Control
2.8.2. Option B: Deployment via ONNX and NVIDIA Jetson
2.8.3. Option C: TensorFlow Lite (TFLite) Deployment
2.8.4. Option D: Apache TVM for Bare-Metal Deployment
2.8.5. Option E: Manual Optimization and Target-Specific Coding
3. Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CUDA | Compute unified device architecture |
| DQN | Deep Q-Network |
| HIL | Hardware-in-the-loop |
| MLP | Multilayer perceptron |
| ONNX | Open neural network exchange |
| ReLU | Rectified linear unit |
| RL | Reinforcement learning |
| TVM | Tensor virtual machine |
References
- Thingujam, B.; Jyoti, B.; Mansuri, S.M.; Srivastava, A.; Mohapatra, D.; Kalnar, Y.B.; Narsaiah, K.; Indore, N. Application of Artificial Intelligence in Food Processing: Current Status and Future Prospects. Food Eng. Rev. 2025, 17, 27–54. [Google Scholar] [CrossRef]
- Canatan, M.; Alkhulaifi, N.; Watson, N.; Boz, Z. Artificial Intelligence in Food Manufacturing: A Review of Current Work and Future Opportunities. Food Eng. Rev. 2025, 17, 189–219. [Google Scholar] [CrossRef]
- Wang, Q.; Yu, Q.; Fu, Y.; Zhou, L.; Fu, Y.; Huang, H. Application of Artificial Intelligence Techniques in Meat Processing: A Review. J. Food Process Eng. 2024, 47, e14297. [Google Scholar] [CrossRef]
- Yudhistira, I.; Wang, L.; Sadiq, M.B.; Fajarini, R.; Dissanayake, M.; Farid, M.M. Achieving Sustainability in Heat Drying Processing: Leveraging Artificial Intelligence. Compr. Rev. Food Sci. Food Saf. 2024, 23, 4621–4649. [Google Scholar] [CrossRef]
- Mandal, R. Applications of AI and ML in Food Process Engineering. In Microsoft Research Workshop on Food Security; Microsoft Research: Redmond, WA, USA, 2022; Available online: https://www.microsoft.com/en-us/research/wp-content/uploads/2022/11/Microsoft_Food-Security-Workshop_RMandal-presentation.pdf (accessed on 21 July 2025).
- Kovačević, S.; Banjac, M.K.; Kuzmanović, S.P. Artificial Intelligence and Experimental Design: The Flywheel of Innovating Food Processing Engineering. Processes 2025, 13, 846. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, M.; Mujumdar, A.S.; Li, C. AI-based processing of future prepared foods: Progress and prospects. Food Res. Int. 2025, 201, 115675. [Google Scholar] [CrossRef]
- Dhal, S.B.; Kar, D. Leveraging Artificial Intelligence and Advanced Food Processing Techniques for Enhanced Food Safety, Quality, and Security: A Comprehensive Review. Discov. Appl. Sci. 2025, 7, 75. [Google Scholar] [CrossRef]
- Song, X.; Zhang, X.; Dong, G.; Ding, H.; Cui, X.; Han, Y.; Huang, H.; Wang, L. AI in food industry automation: Applications and challenges. Front. Sustain. Food Syst. 2025, 9, 1575430. [Google Scholar] [CrossRef]
- Thapa, A.; Nishad, S.; Biswas, D.; Roy, s. A comprehensive review on artificial intelligence assisted technologies in food industry. Food Biosci. 2023, 56, 103231. [Google Scholar] [CrossRef]
- Suh, Y.K.; Park, J.; You, D. Review: AI for liquid–vapor phase-change heat transfer. arXiv 2023, arXiv:2309.01025. [Google Scholar]
- Kannapinn, M.; Pham, M.K.; Schäfer, M. Physics-based digital twins for autonomous thermal food processing: Efficient, non-intrusive reduced-order modeling. Innov. Food Sci. Emerg. Technol. 2022, 81, 103143. [Google Scholar] [CrossRef]
- Jiang, S.; Huang, Y.; Tang, X.; Wang, T.; Li, Q.; Wang, H.; Meng, X. Traditional cooking methods decreased the allergenicity of egg proteins. J. Food Sci. 2024, 89, 3847–3857. [Google Scholar] [CrossRef]
- Baker, R.C.; Hogarty, S.; Poon, W.; Vadehra, D.V. Survival of Salmonella typhimurium and Staphylococcus aureus in Eggs Cooked by Different Methods. Poult. Sci. 1983, 62, 1211–1216. [Google Scholar] [CrossRef] [PubMed]
- Mughini-Gras, L.; Enserink, R.; Friesema, I.; Heck, M.; Duynhoven, Y.; Pelt, W. Risk Factors for Human Salmonellosis Originating from pigs, cattle, broiler chickens and egg laying hens: A combined case-control and source attribution analysis. PLoS ONE 2013, 9, e87933. [Google Scholar] [CrossRef]
- Mihalache, O.A.; Monteiro, M.J.; Dumitrascu, L.; Neagu, C.; Ferreira, V.; Guimaraes, M.; Borda, D.; Teixeira, P.; Nicolau, A.I. Pasteurised eggs—A food safety solution against Salmonella backed by sensorial analysis of dishes traditionally containing raw or undercooked eggs. Int. J. Gastron. Food Sci. 2022, 28, 100547. [Google Scholar] [CrossRef]
- Shi, Y.; Chen, S.; Liu, Y.; Liu, J.; Xuan, L.; Li, G.; Li, J.; Zheng, J. Towards the perfect soft-boiled chicken eggs: Defining cooking conditions, quality criteria, and safety assessments. Poult. Sci. 2024, 103, 104332. [Google Scholar] [CrossRef]
- Abbasnehzad, B.; Hamdami, N.; Khodaei, D. Modeling of rheological characteristics of liquid egg white and yolk at different pasteurization temperatures. Food Meas. 2015, 9, 359–368. [Google Scholar] [CrossRef]
- Silva, F.; Gibbs, P. Thermal pasteurization requirements for the inactivation of Salmonella in foods. Food Res. Int. 2012, 45, 695–699. [Google Scholar] [CrossRef]
- Manas, P.; Pagan, R.; Alvarez, I.; Uson, S.C. Survival of Salmonella senftenberg 775W to current liquid whole egg pasteurization treatments. Food Microbiol. 2003, 20, 593–600. [Google Scholar] [CrossRef]
- Stadelman, W.J.; Singh, R.K.; Muriana, P.M.; Hou, H. Pasteurization of Eggs in the Shell. Poult. Sci. 1996, 75, 1122–1125. [Google Scholar] [CrossRef] [PubMed]
- Podržaj, P.; Jenko, M. A fuzzy logic-controlled thermal process for simultaneous pasteurization and cooking of soft-boiled eggs. Chemom. Intell. Lab. Syst. 2010, 102, 1–7. [Google Scholar] [CrossRef]
- Jenko, M. State-of-art precise control in foods processing: Pasteurization and lyophilization. Worldw. Megatrends Food Saf. Food Secur. 2024. [Google Scholar] [CrossRef]
- Koch, O. Method and Device for Preparing Chicken Eggs. U.S. Patent 6,162,478, 19 December 2000. [Google Scholar]
- Institute Fresenius. Mikrobiologische Uberprufung des Eierkochers “Golden Ei”, Auftrags Nr. 102/07465-00; Fresenius Institute: Berlin, Germany, 2002. [Google Scholar]
- Jenko, M.; Jeršek, B. Survival of Salmonella in soft-boiled eggs after thermal processing in the golden egg apparatus. In Food Processing, Innovation, Nutrition, Healthy Consumers: Book of Abstracts; 3rd Slovenian Congress on Food and Nutrition; Slovenian Nutrition Society: Ljubljana, Slovenia, 2007; ISBN 978-961-90571-2-4. [Google Scholar]
- Marsh, M.C.; Hossain, M.T.; Ewoldt, R.H. Egg yolk as a model for gelation: From rheometry to flow physics. Phys. Fluids 2025, 37, 4. [Google Scholar] [CrossRef]
- Laca, A.; Paredes, B.; Diaz, M. Possibilities of yolk rheological measurements to characterise egg origin and processing properties. Afinidad 2010, 67, 14–19. [Google Scholar]
- Chen, C.; An, J.; Wang, C.; Duan, X.; Lu, S.; Che, H.; Qi, M.; Yan, D. Deep reinforcement learning-based joint optimization control of indoor temperature and relative humidity in office buildings. Buildings 2023, 13, 438. [Google Scholar] [CrossRef]
- Thorndike, E.L. Animal Intelligence: An Experimental Study of the Associative Processes in Animals; American Psychological Association (APA): Washington, DC, USA, 1898; pp. 87–103. Available online: https://archive.org/details/animalintelligen00thoruoft/page/n1/mode/2up (accessed on 9 September 2025).
- Sutton, R.S. Learning to predict by the methods of temporal differences. Mach. Learn. 1988, 3, 9–44. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; MIT Press: Cambridge, MA, USA, 2018; pp. 13–22. ISBN 978-0-262-19398-6. [Google Scholar]
- Glassner, A. Deep Learning: From Basics to Practice; The Imaginary Institute: Milano, Italy, 2018; Volume 1, pp. 34–37. [Google Scholar]
- Glassner, A. Reinforcement learning. In Deep Learning: From Basics to Practice; The Imaginary Institute: Milano, Italy, 2018; Volume 2, pp. 1458–1557. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing atari with deep reinforcement learning. arXiv 2013, arXiv:1312.5602. [Google Scholar] [CrossRef]
- Raffin, A.; Hill, A.; Gleave, A.; Kanervisto, A.; Ernestus, M.; Dormann, N. Stable-Baselines3: Reliable reinforcement learning implementations. J. Mach. Learn. Res. 2021, 22, 1–8. Available online: https://dl.acm.org/doi/pdf/10.5555/3546258.3546526 (accessed on 9 September 2025).
- Acquarone, M.; Maino, C.; Misul, D.; Spessa, E.; Mastropietro, A.; Sorrentino, L.; Busto, E. Influence of reward function on the selection of reinforcement learning agents for hybrid electric vehicles real-time control. Energies 2023, 16, 2749. [Google Scholar] [CrossRef]
- Sedmak, I.; Može, M.; Kambič, G.; Golobič, I. Heat flux analysis and assessment of drying kinetics during lyophilization of fruits in a pilot-scale freeze dryer. Foods 2023, 12, 3399. [Google Scholar] [CrossRef]
- Bermudez, D.B.; Boyd, G.; Uknalis, J.; Niemira, B.A. Thermal resistance of avirulent salmonella enterica serovar typhimurium in albumen, yolk, and liquid whole egg. ACS Food Sci. Technol. 2024, 4, 2047–2057. [Google Scholar] [CrossRef]
- Jordan, J.S.; Gurtler, J.B.; Marks, H.M.; Jones, D.R.; Shaw, W.K. A mathematical model of inactivation kinetics for a four-strain composite of salmonella enteridis and oranienburg in commercial egg yolk. Food Microbiol. 2011, 28, 67–75. [Google Scholar] [CrossRef] [PubMed]
- Egg Answers. The Egg Safety Center of Commercial Egg Producers, by the FDA Egg Safety Rules and Regulatory Programs. Available online: https://eggsafety.org/faq/what-is-the-best-temperature-to-cook-an-egg/ (accessed on 14 July 2025).
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Sonoda, S.; Murata, N. Neural network with unbounded activation functions is universal approximator. Appl. Comput. Harmon. Anal. 2017, 43, 233–268. [Google Scholar] [CrossRef]
- Lorke, A.; Schneider, F.; Heck, J.; Nitter, P. Cybenko’s Theorem and the Capability of a Neural Network as Function Approximator. 2019. pp. 1–39. Available online: https://www.mathematik.uni-wuerzburg.de/fileadmin/10040900/2019/Seminar__Artificial_Neural_Network__24_9__.pdf (accessed on 14 July 2025).
- Egan, D.; Zhu, Q.; Prucka, R. A Review of reinforcement learning-based powertrain controllers: Effects of agent selection for mixed-continuity control and reward formulation. Energies 2023, 16, 3450. [Google Scholar] [CrossRef]
- Roth, A.M.; Liang, J.; Sriram, R.; Tabassi, E.; Manocha, D. MSVIPER: Improved policy distillation for reinforcement-learning-based robot navigation. arXiv 2022, arXiv:2209.09079. [Google Scholar]
- Liu, X.; Chen, W.; Tan, M. Fidelity-induced interpretable policy extraction for reinforcement learning. arXiv 2021, arXiv:2309.06097. [Google Scholar]





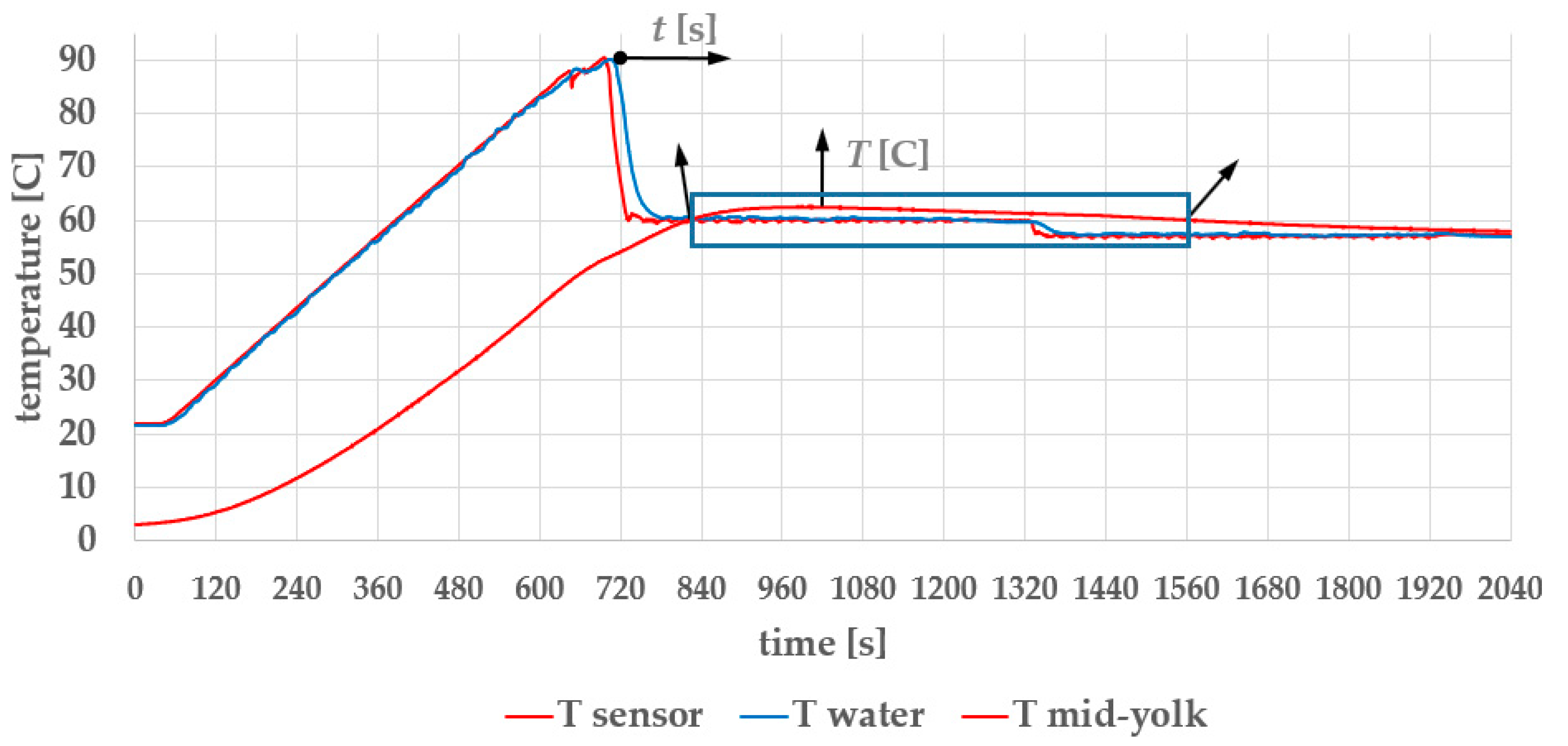
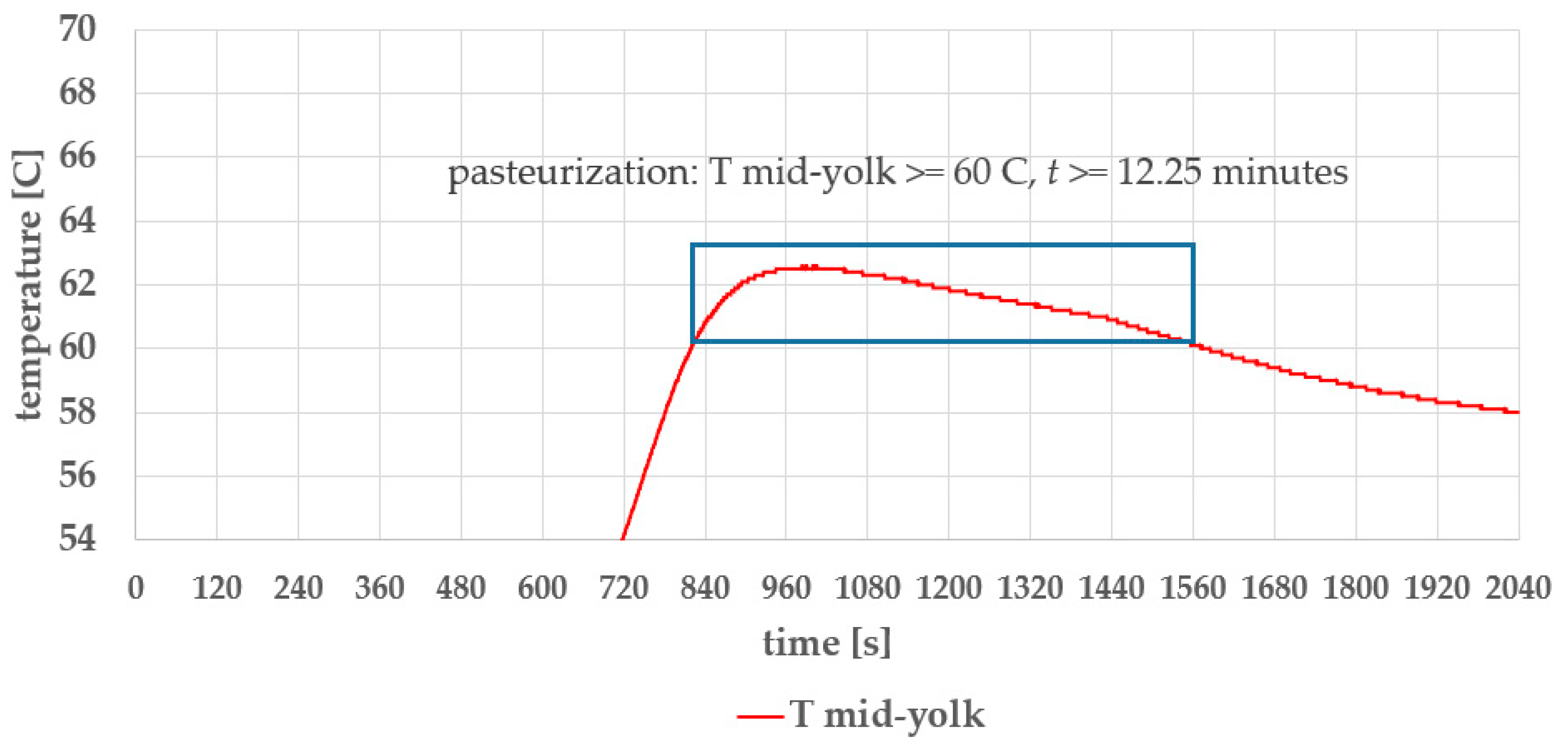
| Parameter | Min. Value | Nominal Value | Max. Value |
|---|---|---|---|
| [kg] | 5.00 | 7.50 | 12.00 |
| [W] | 2300 | 3600 | 4800 |
| [°C] | 10 | 20 | 35 |
| [kg/s] | 0.1 | 0.2 | 0.3 |
| [s] | 1 | 2.5 | 4 |
| [s] | 1 | 2 | 3 |
| 0.01 | 0.03 | 0.05 |
| Parameter | Value |
|---|---|
| Learning rate | 0.0001 |
| Buffer size | 1 million |
| Learning starts | 100 |
| Batch size | 32 |
| τ | 1.0 |
| γ | 0.99 |
| Train frequency | 4 |
| Gradient steps | 1 |
| Target update interval | 10,000 |
| Exploration fraction | 0.1 |
| Exploration initial ε | 1.0 |
| Exploration final ε | 0.05 |
| Maximum value for the gradient clipping | 10 |
| Controller | MSE [°C2] | Qualitative Outcome |
|---|---|---|
| RL (DQN agent) in simulation, NRUNs = 300 | 0.0271–0.0292 | Robust across scenarios, consistent cooking |
| RL (DQN agent) in target system | 0.0604–0.0620 | Verification: according to Section 2.8—Porting to an embedded system |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Podržaj, P.; Kozjek, D.; Škulj, G.; Požrl, T.; Jenko, M. AI Control for Pasteurized Soft-Boiled Eggs. Foods 2025, 14, 3171. https://doi.org/10.3390/foods14183171
Podržaj P, Kozjek D, Škulj G, Požrl T, Jenko M. AI Control for Pasteurized Soft-Boiled Eggs. Foods. 2025; 14(18):3171. https://doi.org/10.3390/foods14183171
Chicago/Turabian StylePodržaj, Primož, Dominik Kozjek, Gašper Škulj, Tomaž Požrl, and Marjan Jenko. 2025. "AI Control for Pasteurized Soft-Boiled Eggs" Foods 14, no. 18: 3171. https://doi.org/10.3390/foods14183171
APA StylePodržaj, P., Kozjek, D., Škulj, G., Požrl, T., & Jenko, M. (2025). AI Control for Pasteurized Soft-Boiled Eggs. Foods, 14(18), 3171. https://doi.org/10.3390/foods14183171








