Identifying the Producer and Grade of Matcha Tea through Three-Dimensional Fluorescence Spectroscopy Analysis and Distance Discrimination
Abstract
:1. Introduction
2. Materials and Methods
2.1. Matcha Tea Collection and Preparation
2.2. Methodologies
2.2.1. Three-Dimensional Fluorescence Spectroscopy
2.2.2. Dimensionality Reduction of Three-Dimensional Fluorescence Spectroscopy
- (1)
- Selection of the integral domains
- (2)
- Vectors of the integrated three-dimensional fluorescence spectroscopy
2.2.3. Discrimination Based on Different Distances
Different Distances
- (1)
- Mahalanobis distances
- (2)
- Three other distances
- ①
- Euclidean distances
- ②
- Manhattan distances
- ③
- Chebychev distances
- (3)
- Transformation of the distances
Discrimination
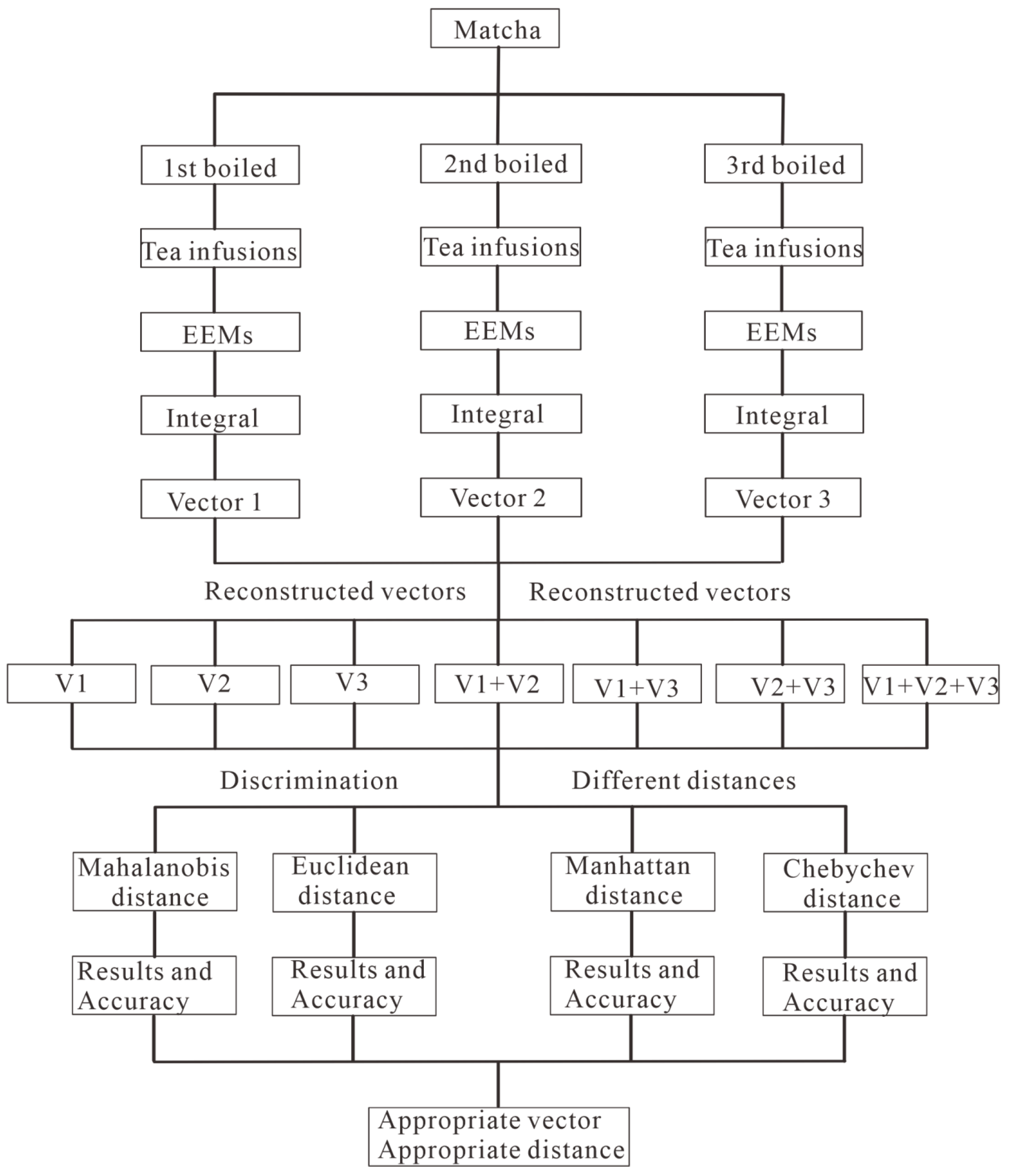
2.3. Construction of Technical System
2.3.1. Technical Route Diagram
- (1)
- Tea infusion extraction and three-dimensional fluorescence spectroscopy scanning. Matcha tea was extracted three times consecutively and the diluted tea infusion is scanned by three-dimensional fluorescence spectroscopy;
- (2)
- Reduce the dimension of EMMs by the integration. Then, the three-dimensional fluorescence spectroscopy of a tea fusion was integrated at three specific regions, and a tea fusion can provide seven reconstructed vectors based on the random combination of the three extractions;
- (3)
- Characteristic vectors training of the population. Following that, the trained characteristic vectors covering the three matchas and all of their grades were obtained by the average value of the training samples. In this study, 170 samples were used to test the discrimination. As for each one, the other 169 samples from the three manufacturers with 17 grades were trained;
- (4)
- Distance calculation and discrimination. After that, the four distances mentioned above were calculated between the vectors of the testing sample and the training population. The samples were discriminated by the minimum distance between them;
- (5)
- Accuracy evaluation and parameter optimization. The results calculated from different distances and vectors displayed a series of accuracies, from which the appropriate vector and distances were also identified.
2.3.2. Discriminative Patterns
2.4. The Accuracy Test
2.4.1. One-Step Pattern
2.4.2. Two-Step Pattern
3. Results and Discussions
3.1. Two-Step Discriminative Pattern
3.1.1. Identification of the Producing Area
- (1)
- Spatial distributions of tested samples in distance space
- (2)
- The accuracy of producer identification
3.1.2. Grade Discrimination
3.1.3. Accuracy of Discriminating Both Producing Area and Grade
3.2. One-Step Discriminative Pattern
4. Conclusions
- (1)
- The vector based on the integration of three-dimensional fluorescence spectroscopy of matcha tea infusion plays an important role in determining the accuracy of the discriminant. In total, the vectors calculated from the three-dimensional fluorescence spectroscopy of the first tea infusion exhibited an accuracy about 25–50% higher than the second and third tea infusion-based vectors. The vector based on more tea fusions had a higher accuracy;
- (2)
- The Mahalanobis distance had a higher accuracy that was up to 100% when the vector was appropriate, while the other three distances were about 60–90%. However, the Mahalanobis distance was challenged by the small number of training samples which is prone to lead to the matrix not being full in the calculation;
- (3)
- The two-step discriminative pattern, identifying the producer first and the grade second, showed a higher accuracy and a smaller uncertainty than the one-step discriminative pattern. This is because the correlations among samples from the same producer with different grades are not considered in the one-step discriminative pattern.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qin, O.Y.; Wang, L.; Park, B.; Kang, R.; Wang, Z.; Chen, Q.S.; Guo, Z.M. Assessment of matcha sensory quality using hyperspectral microscope imaging technology. LWT-Food Sci. Technol. 2020, 125, 109254. [Google Scholar]
- Qin, O.Y.; Yang, Y.C.; Park, B.; Kang, R.; Wu, J.Z.; Chen, Q.S.; Guo, Z.M.; Li, H.H. A novel hyperspectral microscope imaging technology for rapid evaluation of particle size distribution in matcha. J. Food Eng. 2020, 272, 109782. [Google Scholar]
- Qin, O.Y.; Wang, L.; Park, B.; Kang, R.; Chen, Q.S. Simultaneous Quantification of chemical constituents in matcha with visible-near infrared hyperspectral imaging technology. Food Chem. 2021, 350, 129141. [Google Scholar] [CrossRef]
- Kochman, J.; Jakubczyk, K.; Antoniewicz, J.; Mruk, H.; Janda, K. Health benefits and chemical composition of matcha green tea: A review. Molecules 2021, 26, 85. [Google Scholar] [CrossRef] [PubMed]
- Koláčková, T.; Kolofiková, K.; Sytařová, I.; Snopek, L.; Sumczynski, D.; Orsavová, J. Matcha tea: Analysis of nutritional composition, phenolics and antioxidant activity. Plant Foods Hum. Nutr. 2020, 75, 48–53. [Google Scholar] [CrossRef]
- Adnan, M.; Ahmad, A.; Ahmed, D.A.; Khalid, N.; Hayat, I.; Ahmed, I. Chemical composition and sensory evaluation of tea (Camellia sinensis) commercialized in Pakistan. Pak. J. Bot. 2013, 45, 901–907. [Google Scholar]
- Jakubczyk, K.; Kochman, J.; Kwiatkowska, A.; Kałduńska, J.; Dec, K.; Kawczuga, D.; Janda, K. Antioxidant properties and nutritional composition of matcha green tea. Foods 2020, 9, 483. [Google Scholar] [CrossRef]
- Ku, K.M.; Choi, J.N.; Kim, J.; Kim, J.K.; Yoo, L.G.; Lee, S.J.; Hong, Y.S.; Lee, C.H. Metabolomics analysis reveals the compositional differences of shade grown tea (Camellia sinensis L.). J. Agric. Food Chem. 2010, 58, 418–426. [Google Scholar] [CrossRef] [PubMed]
- Fujiki, H.; Sueoka, E.; Watanabe, T.; Suganuma, M. Synergistic enhancement of anticancer effects on numerous human cancer cell lines treated with the combination of EGCG, other green tea catechins, and anticancer compounds. J. Cancer Res. Clin. Oncol. 2015, 141, 1511–1522. [Google Scholar] [CrossRef]
- Zhang, L.; Ho, C.T.; Zhou, J.; Santos, J.S.; Armstrong, L.; Granato, D. Chemistry and biological activities of processed Camellia sinensis teas: A comprehensive review. Compr. Rev. Food Sci. Food Saf. 2019, 18, 1474–1495. [Google Scholar] [CrossRef]
- Ohishi, T.; Goto, S.; Monira, P.; Isemura, M.; Nakamura, Y. Anti-inflammatory action of green tea. Anti-Inflamm. Anti-Allergy Agents Med. Chem. 2016, 15, 74–90. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, J.; Lv, Y.; Jiang, Y.; Pan, J.; Zhu, Y.; Huang, M.; Zhang, S. Changes in intestinal microbiota of type 2 diabetes in mice in response to dietary supplementation with instant tea or matcha. Can. J. Diabetes 2020, 44, 44–52. [Google Scholar] [CrossRef]
- Guo, Z.M.; Barimah, A.O.; Yin, L.M.; Chen, Q.S.; Shi, J.Y.; El-Seedi, H.R.; Zou, X.B. Intelligent evaluation of taste constituents and polyphenols-to-amino acids ratio in matcha tea powder using near infrared spectroscopy. Food Chem. 2021, 353, 129372. [Google Scholar] [CrossRef]
- Bonuccelli, G.; Sotgia, F.; Lisanti, M.P. Matcha Green Tea (MGT) Inhibits the propagation of cancer stem cells (CSCs), by targeting mitochondrial metabolism, glycolysis and multiple cell signaling pathways. Aging 2018, 10, 1867–1883. [Google Scholar] [CrossRef]
- Kurauchi, Y.; Devkota, H.P.; Hori, K.; Nishihara, Y.; Hisatsune, A.; Seki, T.; Katsuki, H. Anxiolytic activities of matcha tea powder, extracts, and fractions in mice: Contribution of dopamine D1 receptor- and serotonin 5-HT1A receptor-mediated mechanisms. J. Funct. Foods 2019, 59, 301–308. [Google Scholar] [CrossRef]
- Chen, Q.S.; Zhang, D.L.; Pan, W.X.; Qin, O.Y.; Li, H.H.; Urmila, K.; Zhao, J.W. Recent developments of green analytical techniques in analysis of tea’s quality and nutrition. Trends Food Sci. Technol. 2015, 43, 63–82. [Google Scholar] [CrossRef]
- Yu, H.C.; Wang, J.; Xiao, H.; Liu, M. Quality grade identification of green tea using the eigenvalues of PCA based on the E-nose signals. Sens. Actuators B-Chem. 2009, 140, 378–382. [Google Scholar] [CrossRef]
- Palacios-Morillo, A.; Alcázar, A.; de Pablos, F.; Jurado, J.M. Differentiation of tea varieties using UV-Vis spectra and pattern recognition techniques. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2013, 103, 79–83. [Google Scholar] [CrossRef]
- Li, X.L.; He, Y. Discriminating varieties of tea plant based on Vis/NIR spectral characteristics and using artificial neural networks. Biosyst. Eng. 2011, 99, 313–321. [Google Scholar] [CrossRef]
- Firmani, P.; De Luca, S.; Buccit, R.; Marini, F.; Biancolillo, A. Near infrared (NIR) spectroscopy-based classification for the authentication of Darjeeling black tea. Food Control 2019, 100, 292–299. [Google Scholar] [CrossRef]
- Chen, Q.S.; Zhao, J.W.; Zhang, H.D.; Liu, M.H.; Fang, M. Qualitative identification of tea by near infrared spectroscopy based on soft independent modelling of class analogy pattern recognition. J. Near Infrared Spectrosc. 2005, 13, 327–332. [Google Scholar] [CrossRef]
- Chen, Q.S.; Zhao, J.W.; Liu, M.H.; Cai, J.R.; Liu, J.H. Determination of total polyphenols content in green tea using FT-NIR spectroscopy and different PLS algorithms. J. Pharm. Biomed. Anal. 2008, 46, 568–573. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.S.; Zhao, J.W.; Zhang, H.D.; Wang, X.Y. Feasibility study on qualitative and quantitative analysis in tea by near infrared spectroscopy with multivariate calibration. Anal. Chim. Acta X 2006, 572, 77–84. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.S.; Zhao, J.W.; Vittayapadung, S. Identification of the green tea grade level using electronic tongue and pattern recognition. Food Res. Int. 2008, 41, 500–504. [Google Scholar] [CrossRef]
- He, Y.; Li, X.L.; Deng, X.F. Discrimination of varieties of tea using near infrared spectroscopy by principal component analysis and BP model. J. Food Eng. 2007, 79, 1238–1242. [Google Scholar] [CrossRef]
- Liu, S.L.; Tsai, Y.S.; Ou, A.S.M. Classifying the variety, production area and season of Taiwan partially fermented tea by near infrared spectroscopy. J. Food Drug Anal. 2010, 18, 34–43. [Google Scholar] [CrossRef]
- Tan, S.M.; Luo, R.M.; Zhou, Y.P.; Xu, H.; Song, D.D.; Ze, T. Boosting partial least-squares discriminant analysis with application to near infrared spectroscopic tea variety discrimination. J. Chemom. 2012, 26, 34–39. [Google Scholar] [CrossRef]
- Li, X.L.; He, Y. Classification of tea grades by multi-spectral images and combined features. Trans. Chin. Soc. Agric. Mach. 2009, 40, 113–118, (Chines Journal with English Abstract). [Google Scholar]
- Wang, J.; Zeng, X.Y.; Du, S.P. Identification and grading of tea using computer vision. Appl. Eng. Agric. 2010, 26, 639–645. [Google Scholar]
- Jiang, F.; Qiao, X.; Zheng, H.; Yang, Q. Grade discrimination of machine-fried Longjing tea based on hyperspectral technology. Trans. Chin. Soc. Agric. Eng. 2011, 27, 343–348, (In Chinese Journal with English Abstract). [Google Scholar]
- Laddi, A.; Prakash, N.R.; Sharma, S.; Mondal, H.S.; Kumar, A.; Kapur, P. Significant physical attributes affecting quality of Indian black (CTC) tea. J. Food Eng. 2012, 113, 69–78. [Google Scholar] [CrossRef]
- Locquet, N.; Aït-Kaddour, A.; Cordella, C.B.Y. 3D fluorescence spectroscopy and its applications. Encycl. Anal. Chem. Appl. Theory Instrum. 2006, 1–39. [Google Scholar]
- Huo, D.Q.; Wu, Y.; Yang, M.; Fa, H.B.; Luo, X.G.; Hou, C.J. Discrimination of Chinese green tea according to varieties and grade levels using artificial nose and tongue based on colorimetric sensor arrays. Food Chem. 2014, 145, 639–645. [Google Scholar] [CrossRef] [PubMed]
- Hu, L.Q.; Yin, C.L. Development of a new three-dimensional fluorescence spectroscopy method coupling with multilinear pattern recognition to discriminate the variety and grade of green tea. Food Anal. Methods 2017, 10, 2281–2292. [Google Scholar] [CrossRef]
- Casale, M.; Pasquini, B.; Hooshyari, M.; Orlandini, S.; Mustorgi, E.; Malegori, C.; Turrini, F.; Ortiz, M.C.; Sarabia, L.A.; Furlanetto, S. Combining excitation-emission matrix fluorescence spectroscopy, parallel factor analysis, cyclodextrin-modified micellar electrokinetic chromatography and partial least squares class-modelling for green tea characterization. J. Pharm. Biomed. Anal. 2018, 159, 311–317. [Google Scholar] [CrossRef]
- Yu, X.L.; He, Y. Fast nondestructive identification of steamed green tea powder adulterations in matcha by visible spectroscopy combined with chemometrics. Spectrosc. Lett. 2018, 51, 112–117. [Google Scholar] [CrossRef]
- Wang, J.J.; Zareef, M.; He, P.; Sun, H.; Chen, Q.S.; Li, H.H.; Qin, O.Y.; Guo, Z.M.; Zhang, Z.Z.; Xu, D.L. Evaluation of matcha tea quality index using portable NIR spectroscopy coupled with chemometric algorithms. J. Sci. Food Agric. 2019, 99, 5019–5027. [Google Scholar] [CrossRef]
- Cimpoiu, C.; Cristea, V.M.; Hosu, A.; Sandru, M.; Seserman, L. Antioxidant activity prediction and classification of some teas using artificial neural networks. Food Chem. 2011, 127, 1323–1328. [Google Scholar] [CrossRef]
- Wu, J.Z.; Zareef, M.; Chen, Q.S.; Ouyang, Q. Application of visible-near infrared spectroscopy in tandem with multivariate analysis for the rapid evaluation of matcha physicochemical indicators. Food Chem. 2023, 421, 136185. [Google Scholar] [CrossRef]
- Ouyang, Q.; Liu, L.H.; Wang, L.; Zareef, M.; Wu, Z.; Li, H.Q.; Yin, J.; Chen, Q.S. Rapid determination of free amino acids and caffeine in matcha using near-infrared spectroscopy: A comparison of portable and benchtop systems. J. Food Compos. Anal. 2023, 115, 104868. [Google Scholar] [CrossRef]
- Fellman, J.B.; Hood, E.; Spencer, R.G.M. Fluorescence spectroscopy opens new windows into dissolved organic matter dynamics in freshwater ecosystems: A review. Limnol. Oceanogr. 2010, 55, 2452–2462. [Google Scholar] [CrossRef]
- Karoui, R.; Blecker, C. Fluorescence spectroscopy measurement for quality assessment of food systems-a review. Food Bioprocess Technol. 2011, 4, 364–386. [Google Scholar] [CrossRef]
- GB/T 34778-2017; Matcha. Standards Press of China: Beijing, China, 2017.
- Zhang, Q.Q.; Chen, J.X.; Wang, Q.; Wang, H.P. Study on physicochemical and sensory properties, polyphenolic composition and antioxidant capacity of matcha tea infusion. Food Mach. 2019, 35, 181–186, (In Chinese Journal with English Abstract). [Google Scholar]
- Liu, H.L.; Wu, X.J.; Tian, G.J. Three-dimensional fluorescence spectroscopy combined with parallel factor analysis as a complementary technique for green tea characterization. Chin. J. Lasers 2008, 35, 685–689, (In Chinese Journal with English Abstract). [Google Scholar]
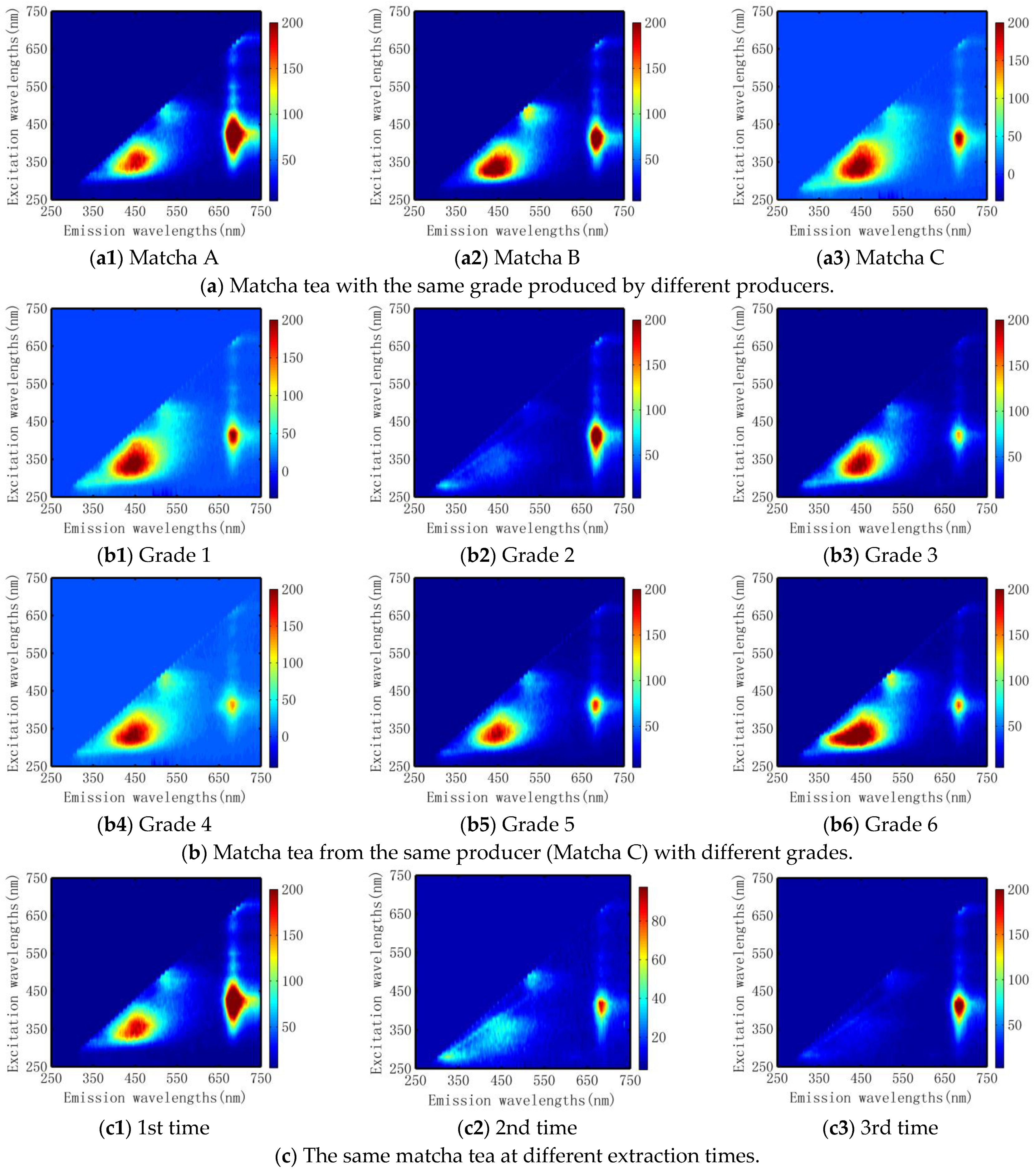


| Types | Place of Production | Year | Grade | Parallel Samples | Number of Samples | Times to Tea Infusion | Number of Tea Infusions |
|---|---|---|---|---|---|---|---|
| A | Guizhou | 2021 | 6 | 10 | 60 | 3 | 180 |
| B | Anhui | 2021 | 5 | 10 | 50 | 3 | 150 |
| C | Henan | 2021 | 6 | 10 | 60 | 3 | 180 |
| In total | - | - | 17 | - | 170 | - | 510 |
| Matcha | Distance | Tea Infusion | ||||||
|---|---|---|---|---|---|---|---|---|
| P1 | P2 | P3 | P1 + P2 | P1 + P3 | P2 + P3 | P1 + P2 + P3 | ||
| A | Euclidean | 90.00% | 85.00% | 83.33% | 95.00% | 95.00% | 83.33% | 98.33% |
| Manhattan/city block | 96.67% | 85.00% | 83.33% | 98.33% | 98.33% | 90.00% | 98.33% | |
| Chebychev | 86.67% | 85.00% | 78.33% | 88.33% | 93.33% | 78.33% | 93.33% | |
| Mahalanobis | 100.00% | 66.67% | 91.67% | 100.00% | 100.00% | 96.67% | 100.00% | |
| B | Euclidean | 86.00% | 74.00% | 58.00% | 90.00% | 84.00% | 74.00% | 86.00% |
| Manhattan/city block | 88.00% | 68.00% | 62.00% | 94.00% | 86.00% | 76.00% | 90.00% | |
| Chebychev | 76.00% | 74.00% | 60.00% | 78.00% | 76.00% | 70.00% | 78.00% | |
| Mahalanobis | 94.00% | 52.00% | 98.00% | 94.00% | 100.00% | 96.00% | 98.00% | |
| C | Euclidean | 91.67% | 66.67% | 66.67% | 76.67% | 80.00% | 66.67% | 71.67% |
| Manhattan/city block | 93.33% | 66.67% | 66.67% | 81.67% | 85.00% | 66.67% | 80.00% | |
| Chebychev | 85.00% | 65.00% | 66.67% | 70.00% | 81.67% | 66.67% | 70.00% | |
| Mahalanobis | 100.00% | 90.00% | 83.33% | 100.00% | 100.00% | 90.00% | 100.00% | |
| Mean | Euclidean | 89.41% | 75.29% | 70.00% | 87.06% | 86.47% | 74.71% | 85.29% |
| Manhattan/city block | 92.94% | 73.53% | 71.18% | 91.18% | 90.00% | 77.65% | 89.41% | |
| Chebychev | 82.94% | 74.71% | 68.82% | 78.82% | 84.12% | 71.76% | 80.59% | |
| Mahalanobis | 98.24% | 70.59% | 90.59% | 98.24% | 100.00% | 94.12% | 99.41% | |
| Matcha | Distance | Tea Infusion | ||||||
|---|---|---|---|---|---|---|---|---|
| P1 | P2 | P3 | P1 + P2 | P1 + P3 | P2 + P3 | P1 + P2 + P3 | ||
| A | Euclidean | 61.67% | 53.33% | 46.67% | 65.00% | 76.67% | 55.00% | 75.00% |
| Manhattan/city block | 63.33% | 58.33% | 48.33% | 66.67% | 76.67% | 60.00% | 81.67% | |
| Chebychev | 56.67% | 53.33% | 46.67% | 58.33% | 71.67% | 48.33% | 61.67% | |
| Mahalanobis | 96.67% | 76.67% | 80.00% | 100.00% | 100.00% | 90.00% | 100.00% | |
| B | Euclidean | 94.00% | 52.00% | 46.00% | 96.00% | 84.00% | 62.00% | 86.00% |
| Manhattan/city block | 92.00% | 46.00% | 52.00% | 92.00% | 82.00% | 62.00% | 78.00% | |
| Chebychev | 92.00% | 50.00% | 44.00% | 96.00% | 86.00% | 50.00% | 86.00% | |
| Mahalanobis | 100.00% | 88.00% | 70.00% | 100.00% | 100.00% | 100.00% | 100.00% | |
| C | Euclidean | 96.67% | 75.00% | 78.33% | 100.00% | 100.00% | 78.33% | 100.00% |
| Manhattan/city block | 98.33% | 80.00% | 78.33% | 100.00% | 98.33% | 76.67% | 100.00% | |
| Chebychev | 86.67% | 73.33% | 78.33% | 95.00% | 100.00% | 75.00% | 95.00% | |
| Mahalanobis | 96.67% | 91.67% | 86.67% | 100.00% | 100.00% | 100.00% | 100.00% | |
| Mean | Euclidean | 83.53% | 60.59% | 57.65% | 86.47% | 87.06% | 65.29% | 87.06% |
| Manhattan/city block | 84.12% | 62.35% | 60.00% | 85.88% | 85.88% | 66.47% | 87.06% | |
| Chebychev | 77.65% | 59.41% | 57.06% | 82.35% | 85.88% | 58.24% | 80.59% | |
| Mahalanobis | 97.65% | 85.29% | 79.41% | 100.00% | 100.00% | 96.47% | 100.00% | |
| Matcha | Distance | Tea Infusion | ||||||
|---|---|---|---|---|---|---|---|---|
| P1 | P2 | P3 | P1 + P2 | P1 + P3 | P2 + P3 | P1 + P2 + P3 | ||
| A | Euclidean | 55.50% | 45.33% | 38.89% | 61.75% | 72.84% | 45.83% | 73.75% |
| Manhattan/city block | 61.22% | 49.58% | 40.27% | 65.56% | 75.39% | 54.00% | 80.31% | |
| Chebychev | 49.12% | 45.33% | 36.56% | 51.52% | 66.89% | 37.86% | 57.56% | |
| Mahalanobis | 96.67% | 51.12% | 73.34% | 100.00% | 100.00% | 87.00% | 100.00% | |
| B | Euclidean | 80.84% | 38.48% | 26.68% | 86.40% | 70.56% | 45.88% | 73.96% |
| Manhattan/city block | 80.96% | 31.28% | 32.24% | 86.48% | 70.52% | 47.12% | 70.20% | |
| Chebychev | 69.92% | 37.00% | 26.40% | 74.88% | 65.36% | 35.00% | 67.08% | |
| Mahalanobis | 94.00% | 45.76% | 68.60% | 94.00% | 100.00% | 96.00% | 98.00% | |
| C | Euclidean | 88.62% | 50.00% | 52.22% | 76.67% | 80.00% | 52.22% | 71.67% |
| Manhattan/city block | 91.77% | 53.34% | 52.22% | 81.67% | 83.58% | 51.12% | 80.00% | |
| Chebychev | 73.67% | 47.66% | 52.22% | 66.50% | 81.67% | 50.00% | 66.50% | |
| Mahalanobis | 96.67% | 82.50% | 72.22% | 100.00% | 100.00% | 90.00% | 100.00% | |
| Mean | Euclidean | 74.68% | 45.62% | 40.36% | 75.28% | 75.28% | 48.78% | 74.25% |
| Manhattan/city block | 78.18% | 45.85% | 42.71% | 78.31% | 77.29% | 51.61% | 77.84% | |
| Chebychev | 64.40% | 44.39% | 39.27% | 64.91% | 72.24% | 41.79% | 64.95% | |
| Mahalanobis | 95.93% | 60.21% | 71.94% | 98.24% | 100.00% | 90.80% | 99.41% | |
| Matcha | Distance | Tea Infusion | ||||||
|---|---|---|---|---|---|---|---|---|
| P1 | P2 | P3 | P1 + P2 | P1 + P3 | P2 + P3 | P1 + P2 + P3 | ||
| A | Euclidean | 60.00% | 41.67% | 41.67% | 63.33% | 75.00% | 48.33% | 73.33% |
| Manhattan/city block | 60.00% | 48.33% | 43.33% | 65.00% | 75.00% | 58.33% | 78.33% | |
| Chebychev | 55.00% | 38.33% | 40.00% | 56.67% | 70.00% | 41.67% | 60.00% | |
| Mahalanobis | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | |
| B | Euclidean | 92.00% | 40.00% | 38.00% | 94.00% | 84.00% | 54.00% | 86.00% |
| Manhattan/city block | 92.00% | 34.00% | 46.00% | 90.00% | 82.00% | 56.00% | 76.00% | |
| Chebychev | 86.00% | 38.00% | 36.00% | 92.00% | 82.00% | 40.00% | 82.00% | |
| Mahalanobis | 20.00% | 20.00% | 20.00% | 20.00% | 20.00% | 20.00% | 20.00% | |
| C | Euclidean | 91.67% | 46.67% | 71.67% | 100.00% | 91.67% | 68.33% | 98.33% |
| Manhattan/city block | 95.00% | 53.33% | 75.00% | 96.67% | 91.67% | 73.33% | 98.33% | |
| Chebychev | 83.33% | 48.33% | 73.33% | 91.67% | 90.00% | 68.33% | 90.00% | |
| Mahalanobis | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | |
| Mean | Euclidean | 80.59% | 42.94% | 51.18% | 85.29% | 83.53% | 57.06% | 85.88% |
| Manhattan/city block | 81.76% | 45.88% | 55.29% | 83.53% | 82.94% | 62.94% | 84.71% | |
| Chebychev | 74.12% | 41.76% | 50.59% | 79.41% | 80.59% | 50.59% | 77.06% | |
| Mahalanobis | 5.88% | 5.88% | 5.88% | 5.88% | 5.88% | 5.88% | 5.88% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Zhou, X.; Lei, W. Identifying the Producer and Grade of Matcha Tea through Three-Dimensional Fluorescence Spectroscopy Analysis and Distance Discrimination. Foods 2023, 12, 3614. https://doi.org/10.3390/foods12193614
Xu Y, Zhou X, Lei W. Identifying the Producer and Grade of Matcha Tea through Three-Dimensional Fluorescence Spectroscopy Analysis and Distance Discrimination. Foods. 2023; 12(19):3614. https://doi.org/10.3390/foods12193614
Chicago/Turabian StyleXu, Yue, Xiangyang Zhou, and Wenjuan Lei. 2023. "Identifying the Producer and Grade of Matcha Tea through Three-Dimensional Fluorescence Spectroscopy Analysis and Distance Discrimination" Foods 12, no. 19: 3614. https://doi.org/10.3390/foods12193614
APA StyleXu, Y., Zhou, X., & Lei, W. (2023). Identifying the Producer and Grade of Matcha Tea through Three-Dimensional Fluorescence Spectroscopy Analysis and Distance Discrimination. Foods, 12(19), 3614. https://doi.org/10.3390/foods12193614






