Abstract
Rare-earth doped ceria materials are amongst the top choices for use in electrolytes and composite electrodes in intermediate temperature solid oxide fuel cells. Trivalent acceptor dopants such as gadolinium, which mediate the ionic conductivity in ceria by creating oxygen vacancies, have a tendency to segregate at grain boundaries and triple points. This leads to formation of ionically resistive blocking grain boundaries and necessitates high operating temperatures to overcome this barrier. In an effort to improve the grain boundary conductivity, we studied the effect of a modified sintering cycle, where 10 mol% gadolinia doped ceria was sintered under a reducing atmosphere and subsequently reoxidized. A detailed analysis of the complex impedance, conductivity, and activation energy values was performed. The analysis shows that for samples processed thus, the ionic conductivity improves when compared with conventionally processed samples sintered in air. Equivalent circuit fitting shows that this improvement in conductivity is mainly due to a drop in the grain boundary resistance. Based on comparison of activation energy values for the conventionally processed vs. reduced-reoxidized samples, this drop can be attributed to a diminished blocking effect of defect-associates at the grain boundaries.
1. Introduction
Rare-earth metal doped cerium oxide (CeO2) has received considerable attention in the past decades due to exciting possibilities for application as the electrolyte in intermediate temperature solid oxide fuel cells [1,2]. The primary reason for doped ceria being considered for such applications is its high oxygen ion conductivity and relative stability [3,4,5]. Doped ceria also affords enhanced surface kinetics for oxygen reduction reactions, and has been proposed for use as an electrolyte-cathode interlayer to improve operating temperatures for solid oxide fuel cells [6,7]. The ionic conductivity in CeO2 is mediated by the presence of oxygen vacancies obtained by doping with rare earth acceptor dopant oxides such as Gd2O3, Nd2O3, and Sm2O3, which have been found to be some of the best dopants for ceria. The vacancies are formed following Equation (1), where D is the dopant and is an oxygen vacancy. The vacancies allow for hopping of oxide ions under a concentration gradient, giving ionic conductivity.
It has been shown that the composition and microstructure of the ceramic material have a strong effect on its ionic conductivity [8,9,10,11,12,13,14]. For example, the resistance to ionic conduction is much higher for grain boundaries than for the grains or the bulk of the material [15,16,17]. The high resistance or the blocking nature of grain boundaries in the bulk has been ascribed to various causes like, amorphous phases, impurities, misorientation at the grain boundaries, and segregation of dopants and vacancies [15,18,19,20,21,22,23,24]. Due to their high energy, any point and extended defects present in the crystal structure of the grains, tend to accumulate at the grain boundaries during sintering. For cerium oxide-based materials, it is generally accepted that it is the high concentration of vacancies and dopants at grain boundaries which is chiefly responsible for the blocking nature of the grain boundaries [21,22,23,24,25,26]. For instance, atom probe tomography has shown that in Nd doped ceria, the Nd ions and oxygen vacancies segregate at the grain boundaries with the compositional difference extending up to 4–6 nm from the structural center of the boundaries [21]. Even for un-doped materials such as pure SrTiO3 and CeO2, it has been shown that grain boundaries are intrinsically non-stoichiometric, with a high concentration of vacancies at the boundaries, with the extent of accumulation changing with each type of grain boundary and tilt angle [22,23,24]. In general, it is understood that the high vacancy concentration causes the grain boundary core to have a net positive charge and in doped materials, acceptor dopants are hypothesized to segregate at the boundaries due to electrostatic attraction and to relieve elastic strain via structural relaxation [25,26].
One possible mechanism that has been proposed to explain the resistive effect of grain boundaries is the formation of defect-associates between the dopant ions and the vacancies at high dopant concentrations. The defect-associates or complexes effectively lock in the oxygen vacancies, reducing the ionic conductivity as dopant concentration increases [27]. This mechanism is also active in the grains at high dopant concentrations [18]. For grain boundaries in particular, the Mott-Schottky [28,29] model has been used and cited extensively to explain their blocking nature in both, doped and pure materials [12,15,30,31,32]. The Mott-Schottky model has a positively charged grain boundary core, with a high concentration of oxygen vacancies, which is compensated by oppositely charged defects, usually acceptor ions, and a depletion of oxygen vacancies in the adjacent region. The segregation of defects at grain boundaries, creates a space charge layer, forming a potential barrier for conduction at the interface [12,30]. It is important to note that although this model is widely accepted, it has not been proven experimentally with actual concentration data for different species at grain boundaries. In fact, none of the recent experimental data show the presence of a depletion zone at the grain boundaries [20,21,33]. Although it is not explicitly addressed or resolved in this work, it is essential to recognize this knowledge gap in the exact structure and nature of grain boundaries in doped ceramics.
In the case of rare-earth doped ceria, the key to attaining optimum ionic conductivity performance at intermediate temperature is to reduce the resistance of the grain boundaries. Various solutions have been proposed with varying degrees of success. The earliest and the simplest method was to modify the processing conditions in order to reduce the amount of grain boundaries [14,34]. For solid oxide fuel cells, the opposite strategy of increasing grain boundary density, albeit at the surface, has been shown to be beneficial, where the vacancies act as preferential sites for oxygen incorporation from air [35,36]. Techniques such as microwave sintering, spark plasma sintering, flash sintering, and pulsed laser deposition with thermal annealing have also achieved some success [18,37,38,39,40,41,42,43]. However, such “unconventional” sintering techniques usually require specialized equipment and are not easily amenable to bulk production.
All the above-mentioned approaches try to improve grain boundary ionic conductivity by taking advantage of the kinetics of dopant diffusion during the sintering process. For bulk materials however, another possible way of approaching the problem is by modifying the energetics of the system along with the kinetics. Esposito et al. [44] in their work on gadolinia doped ceria have shown that sintering in reducing atmospheres, reduces the Gd/Ce cation mismatch, mainly relating to the oxidation state and ion size, leading to a faster rate of mass diffusion. The grain growth and densification in conventional gadolinia doped ceria is otherwise inhibited due to a space charge effect and is explained by the solute drag model [45]. Esposito et al. [44] used this phenomenon to enable densification at lower sintering temperatures and also observed an increase in total conductivity and change in activation energy. They hint that this improvement is related to microstructural features and chemical heterogeneities at the grain boundaries, however no separation is made between the contributions of nature of grain boundaries versus that of microstructural effects like grain size and porosity [44]. The objective of this work was to separate the grain boundary effect from bulk effects in 10 mol% gadolinia doped ceria (10GDC) through analysis of complex impedance and conductivity data. In doing so, this paper provides insight into the relationship between defect-associates, higher grain boundary conductivity, and sintering in reducing atmospheres.
2. Results
To study the effect of sintering in a reducing atmosphere on the grain boundary and total ionic conductivity, disc shaped pellet samples of 10 mol% GDC were fabricated. The materials and processes used are detailed in the “Materials and Methods” section. The control samples were sintered at 1600 °C for 10 h in air with heating and cooling rates of 200 °C/h, conditions commonly used for sintering of doped ceria in bulk form [46,47,48,49]. For sintering under reduced atmosphere, the samples were sintered at 900 °C, 1000 °C, and 1100 °C, respectively for 20 h with a same cooling rate of 200 °C/h under an atmosphere of 4% H2-N2 mixture. Although multiple samples were manufactured, the 1100 °C samples were selected for comparison because they had a grain size closest to the conventionally sintered samples. This was assumed to facilitate the separation of the effect of grain size from segregation effects. The densities obtained for the samples thus prepared were in the range of 93–97% of the theoretical density measured as per ASTM (American Society of Testing and Materials) standard B962-15 [50]. Figure 1 shows the appearance of the two kinds of samples. Control samples had a cream color, whereas, the reduced samples showed shades of gray-black depending on the sintering conditions, as is commonly reported for non-stoichiometric ceria [51]. The reduced pellets after re-oxidation changed color again. Upon re-oxidation, the color of the samples became similar to that of the control samples. The two specific samples compared here had densities of 6.80 gm/cc for the conventionally sintered (94.33% of the theoretical 7.21 gm/cc) and 7.04 gm/cc (97.64% of the theoretical 7.21 gm/cc) for the reduced and reoxidized sample. The microstructures of the representative samples are shown in Figure 2. Similar to the observations by Esposito et al. [44] the reduced and reoxidized samples had sufficient mechanical integrity and did not seem affected by the multiple phase changes during processing.

Figure 1.
Appearance of 10GDC control pellet sintered at 1600 °C for 10 h (left), one sintered under 4% H2-N2 at 1100 °C for 20 h (center) and one following re-oxidation (right).

Figure 2.
Scanning electron micrographs showing the microstructures of the (a) 10GDC control pellet sintered at 1600 °C for 10 h and (b) sintered under 4% H2-N2 at 1100 °C for 20 h followed by re-oxidation. The black areas in the micrographs are porosity and thermally etched grain boundaries.
Impedance spectroscopy measurements were performed from 200 °C to 650 °C, as detailed in the “Materials and Methods” section, to study the effect of processing on ionic conductivity. Figure 3 shows a Nyquist plot obtained from impedance spectroscopy measurements at 300 °C for the two types of samples normalized for their dimensions. There was very little difference observed in the Nyquist plots for measurements performed during heating and cooling, indicating that there was no oxidation of the samples during the measurement. The plots for both the samples show three arcs, each from the impedance response of the grains, grain boundaries, and electrodes. Using equivalent circuit fitting, the resistive and capacitive nature, denoted by R and CPE (constant phase element) respectively, of each of the responses can be calculated [52,53]. The values thus obtained for Rg and Rgb, represent respectively the grain and grain boundary contribution to the resistance of the sample. The grain boundary resistance for the conventionally sintered sample is much higher than the grain boundary resistance for the sample sintered under reducing conditions, evidenced by the larger grain boundary arc for the former sample. After normalizing for sample dimensions, at 300 °C, the control sample had a grain boundary resistance of approximately 312 kΩ-cm, whereas the sample sintered under reducing conditions had a corresponding grain boundary resistance of approximately 40 kΩ-cm. As can be seen from the inset in Figure 3, the grain resistance also follows a similar trend, although the difference between the two samples is not as much as the difference for the grain boundary resistance. Both the grain and grain boundary resistance trends hold for the entire temperature range tested. Figure 4 shows the trends in grain boundary resistance to ionic conductivity for the sample sintered in a reducing atmosphere versus the control sample. While the estimation of grain boundary conductivity is difficult and often inaccurate due to errors in calculating the total grain boundary length and thickness in a sample, a comparison of resistances, normalized to sample dimensions, establishes the drop in the blocking behavior of grain boundaries.
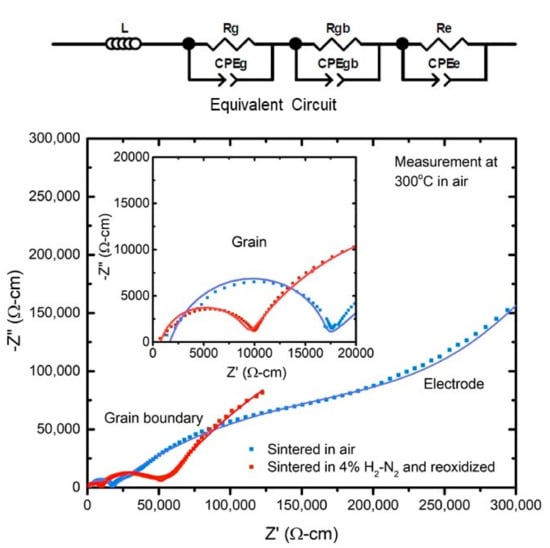
Figure 3.
Normalized Nyquist plot showing the comparison between the 10GDC control and H2 sintered samples measure at 300 °C in air, along with its equivalent circuit. The equivalent circuit is comprised of three pairs of parallel R-CPE elements in series with each other, R being the resistive component and CPE being a constant phase element representing the capacitive component. Here ‘g’ stands for grain, ‘gb’ stands for grain boundary, and ‘e’ stands for electrode and each R-CPE pair corresponds to each of the three arcs. There is an additional inductive element L for the measurement setup. The scatter plot is the measured data, and the line is the fit.
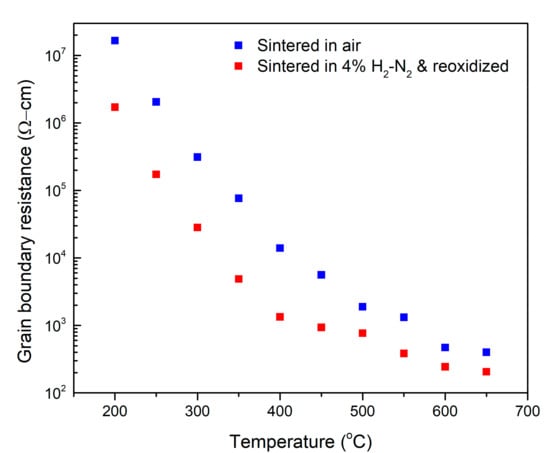
Figure 4.
A comparison of the grain boundary resistance with respect to temperature for the control sample and the reduced-reoxidized sample.
Since the proposed process utilizes a reducing atmosphere, the contribution of electronic conduction cannot be completely ruled out. However, any electronic contribution should be mostly through the grain boundaries parallel to the field, and this should lead to the appearance of a new resistance parallel to the original equivalent circuit. This however does not happen, and for both the conditions, the impedance data can be satisfactorily fit using the same equivalent circuit shown in Figure 3 with one inductor and three parallel R-CPE combinations in series with each other indicating that the samples have been oxidized to a large extent after re-oxidation. The same can be ascertained by the change of color from black/grey to cream color. Hence any electronic contribution to conductivity is expected to be minimal. For a more accurate conclusion, future work envisages transport number measurements to determine the electronic contribution to conductivity.
In contrast to grain boundary conductivity, the estimation of grain and total ionic conductivity for both the samples is fairly straightforward from the respective resistances and dimensions. The values of Rg obtained from equivalent circuit fitting of complex impedance data were used to calculate the grain ionic conductivity for the sample. The thickness of grain boundaries was neglected while calculating the grain ionic conductivity. The total ionic conductivity on the other hand was calculated from the sum of grain and grain boundary resistances, Rg + Rgb. Figure 5 shows an Arrhenius type plot of the grain and total conductivity for both groups of samples. The activation energy was calculated from the slope of the plot following Equation (2) where σ is the ionic conductivity, T is the temperature in Kelvin, σo is the pre-exponential factor, k is the Boltzmann constant and Ea is the activation energy.
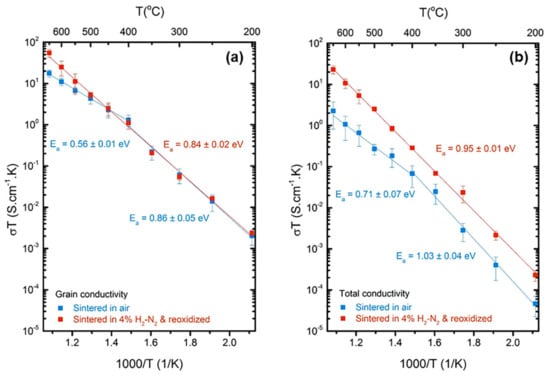
Figure 5.
Arrhenius type plot of (a) grain conductivity and (b) total conductivity with respect to temperature for the 10GDC control and 4% H2 balanced in N2 sintered-reoxidized samples.
There is not much difference between the grain conductivity for the two groups as expected for a small difference in the concentration of defects in the bulk of the material. However, there is a marked difference in the total conductivity of the two groups, with the reduced and reoxidized samples being more conductive by almost an order of magnitude. For example, at 350 °C, the total conductivity for the conventionally sintered sample is 3.95 × 10−5 S/cm, whereas that for the reducing atmosphere sintered sample is 1.09 × 10−4 S/cm with an increase of 6.99 × 10−5 S/cm or ~176%. On the other hand, the respective grain conductivities for conventionally and reducing atmosphere sintered samples are almost equal at 3.55 × 10−4 S/cm and 3.32 × 10−4 S/cm with a small decrease of 2.33 × 10−5 S/cm or ~6% which is within the error of the measurements. This difference becomes more prominent at higher temperatures, leading to almost an order of magnitude increase.
3. Discussion
The reason dopants segregate at the grain boundaries is to reduce the overall free energy of the system. The extent to which a dopant will form a uniform solid solution with ceria is dependent on several factors that to a first approximation are summarized in the Hume-Rothery rules [54]. The factors that affect the solid solution are, atomic or ionic size, electronegativity difference, similarity of crystal structure valency and the binding energy of defect clusters [54,55,56]. All other factors being similar, it is the crystal structure mismatch, cation mismatch, the defect charge difference between Gd+3 and Ce+4, and the tendency to form defect clusters that leads to the preferential segregation of Gd (or other similar dopants) at the grain boundaries. The 10 mol% gadolinia doped ceria (10GDC) is expected to have defect-associates in the grains along with higher order extended defect-associate structures at the grain boundaries. The hypothesis is that by sintering pressed gadolinia doped ceria (GDC) pellets in a reducing atmosphere of 4% H2-N2, the Ce+4 ions will get reduced to Ce+3. Various authors have shown this tendency for reduction of cerium oxide and studied the different phases formed under low pO2 atmospheres and different temperature conditions [55,56,57,58]. In essence, by reducing ceria, charged cation substitutional defects are not expected to form, but rather an effectively neutral substitutional defect is anticipated. Another possibility is that the dopant segregation is limited simply due to the low temperature afforded by high diffusion rates in a reducing atmosphere. In any case, all these factors combined are expected to lead to a more uniform microstructure without much dopant and vacancy segregation at the grain boundaries, thus improving both the grain boundary and total conductivity as seen in Figure 5.
It is important to note that the change in conductivity shown in Figure 5 can also be brought about by a difference in grain size. However, as can be seen from Figure 2, there is not much difference between the grain sizes of the two samples with their values being 2.64 ± 0.15 μm and 2.46 ± 0.36 μm, respectively for the conventionally processed and reduced and reoxidized samples. The grain size was measured using the intercept method as per ASTM standard E112-13 [59]. Similarly, given the density difference caused by different processing routes, it is important to quantify and correct for the effect of porosity on conductivity. As mentioned in the Results Section, the two specific samples discussed here have densities of 6.80 gm/cc and 7.04 gm/cc for the conventional, and the reduced and reoxidized samples respectively, with the latter being 3.4% higher. Based on the Maxwell correction for the effect of porosity on conductivity, as explained by McLachlan et al. [60], assuming discontinuous spherical pores, at 350 °C, a higher density of the reduced and reoxidized sample should result in a conductivity of 4.15 × 10−5 S/cm, an increase of 5.1%, which is much lower than the 176% jump observed. Porosity thus has a very small effect compared to the effect of processing in a reducing atmosphere. Having ruled out the effect of grain size and porosity, we can conclude that the large difference in total conductivity with almost no difference in grain conductivity indicates that most of the change in conductivity is due to the modification of the nature of the grain boundaries.
Both the grain and total ionic conductivity for the conventionally sintered samples show a change in slope, and subsequently activation energy, around 400 °C as can be seen in Figure 5. Similar behavior was reported by Esposito et al. [44] but only with respect to the total conductivity. A possible reason for such an activation energy change could be the presence of a larger number of defects associates which become free above a certain temperature. This behavior was first explained by Meyer and Neldel [61]. In this case, the temperature is around the same temperature where the Meyer-Neldel effect comes into play, the defect-associates break apart, and the activation energy required for conduction drops. This change in activation energy, represents an association enthalpy in addition to the migration enthalpy for the diffusion of vacancies. Based on values shown in Figure 5, both the grain and total conductivity for the air-sintered samples show about the same change in activation energy (~0.3 eV). This indicates that the blocking nature and defect structures at the grain boundaries remain unchanged through this transition, and only defect-associates in the grains dissociate. Interestingly, the 4% H2-N2 samples do not show this change in slope, indicating limited defect interaction to begin with in the grains. This limited defect interaction in the grains however does not have a big effect on the grain conductivity of the reduced-reoxidized samples with values being similar to those of air-sintered samples at low temperatures. As the temperature is increased, the difference between the grain and total conductivity for the reduced and reoxidized samples becomes smaller and smaller, as is expected due the grain boundaries becoming more and more conductive. This trend is however not as strong in the conventionally sintered samples due to more blocking grain boundaries. At higher temperatures, more and more charge carriers become free, which should eventually lead to the same conductivity for all samples. At this point, the total conductivity is expected to depend only on the dopant concentration, and even the defect structures at the grain boundaries are expected to dissociate.
4. Materials and Methods
A co-precipitation route was used for synthesizing phase pure 10 mol% doped gadolinia doped ceria powder where metal hydroxides are simultaneously precipitated from a solution containing precursor salts with an intimate mix of the metal species. The co-precipitation technique has been shown to produce phase pure powders with less siliceous impurities compared to the conventional powder processing route involving powder mixing and ball milling [18,62]. It also yields a smaller particle size which leads to better sintering kinetics [18,62]. Thus, high density pellets can be obtained using lower sintering temperatures and times [18,63]. Stoichiometric amounts of cerium nitrate (Ce(NO3)3·6H2O, 99.5%, Acros Organics, Fair Lawn, NJ, USA) and gadolinium nitrate hexahydrate (Gd(NO3)3·6H2O, 99.9%, Strem Chemicals, Newburyport, MA, USA) were mixed in de-ionized water forming an aqueous solution. Under magnetic stirring, an ammonium hydroxide solution (28–30 wt% NH3 solution in water Acros Organics, Fair Lawn, NJ, USA) was slowly added to this mixed solution till the pH was raised to 12. With the addition of ammonium hydroxide, a brownish precipitate separated out as shown in Equation (3). This precipitate was then washed with de-ionized water and dried in a drying oven at 120 °C for 12 h. The reaction is shown in Equation (4). Equations (5) and (6) show the conversion from Ce3+ to Ce4+ taking place in solution at a high pH and the corresponding reactions for Gd3+ and Ce3+ forming the respective hydroxide precipitates [47]. In case of low pH below 12, the complete conversion from Ce3+ to Ce4+ does not take place in the solution, but instead occurs during the drying and calcination steps in the presence of air.
The dried powder was ground using a mortar and pestle, then was calcined in air at 900 °C for 10 h. The calcination temperature and time used were previously optimized [18]. The calcined powder was ground again using a mortar pestle and checked for phase purity using X-ray diffraction. For pressing into pellets, the powder was sieved using a 212 µm sieve. It was uniaxially pressed into disc shaped pellets with 7 mm diameter under 150 MPa using a Carver Inc. (Wabash, IN, USA) 3912 uniaxial press. This was followed by cold isostatic pressing under 250 MPa using an MTI corporation CIP-50M isostatic press (MTI Corporation, Richmond, CA, USA). For isostatic pressing, the pellet was sealed in a common rubber balloon, which was then evacuated and tied up. The obtained green pellets were subsequently sintered at 1600 °C for 10 h in air with a heating and cooling rate of 200 °C/h in a CM Furnaces 1600 Series Rapid Temp Furnace (CM Furnaces, Inc., Bloomfield, NJ, USA) for the control samples. For reduced atmosphere sintering, the samples were sintered at 900 °C, 1000 °C, and 1100 °C, respectively for 20 h with the same cooling rate of 200 °C/h in a tube furnace (Barnstead Thermolyne 21100, Barnstead Thermolyne Corporation, Ramsey, MN, USA) under an atmosphere of 4% H2-N2 mixture (Airgas Inc., Radnor, PA, USA) with ~2 standard cubic feet per hour flow being maintained throughout. These temperatures were selected based on prior work by Esposito et al. [44]. The time of 20 h was selected by rough approximation as the concentration of hydrogen in the gas mixture was less than that used by Esposito et al. [44]. The reduced 10GDC samples thus obtained were subsequently reoxidized under an O2 (Airgas Inc., Radnor, PA, USA) atmosphere in the tube furnace at a much lower temperature of 900 °C for 24 h, with slow heating and cooling rates of about 50 °C/h. This condition was chosen to keep the temperature as low as possible, to avoid any other temperature effects on the sample.
For the microstructural analysis of bulk samples, the sintered ceramic samples were mechanically polished to a mirror finish using diamond lapping films down to 0.1 μm on an Allied Multiprep polisher (Allied High Tech Products, Inc., Rancho Dominguez, CA, USA). They were cleaned using sonication for 30 min. To make the grain boundaries visible, the control samples were thermally etched at 1400 °C for 1 h in air with rapid heating ramp rates of 600 °C/h. For the samples which were reduced and then reoxidized, where dopant segregation during thermal etching was a concern, they were etched using a 25 vol% HF solution in DI water with an exposure time of 4 min. The samples were then either observed directly under an optical microscope or coated with an approximately 10 nm thick layer of carbon for scanning electron microscopy (SEM).
For impedance spectroscopy and ionic conductivity measurements, the sample thickness of less than 1 mm ensured a relatively surface area vs. thickness, thus minimizing edge effects. The samples were polished using SiC polishing paper, cleaned using a sonicator and electroded with platinum paint (CL11-5349, Heraeus, Hanau, Germany). Each side was dried in a drying oven for 1 h at 120 °C, following which the samples were fired at 900 °C for 1 h. Platinum wires were attached onto the sample faces using silver paste for impedance measurements. The platinum wires were in turn tied to the gold wire electrodes, shielded with Pt coated alumina tubes, which were connected to the Solartron 1260 (Solartron Analytical, Farnborough, UK) using BNC connections. A Lindberg Blue M tube furnace (Lindberg/MPH, Riverside, MI, USA) was used to provide high temperatures. Complex impedance measurements were performed in 50 °C increments from 200 °C to 650 °C with an oscillating voltage of 500 mV in a frequency range from 0.1 Hz to 10 MHz under an air atmosphere. Nulling files for open and short circuit compensation were recorded for each data point before the actual sample measurement. Data was recorded using ZPlot® software (Scribner Associates Inc., Southern Pines, NC, USA). The complex impedance data so obtained was fitted using an equivalent circuit described in the Results Section and shown in Figure 3. These impedance measurements were performed during both heating and cooling to ensure there were no differences in the data pointing to a change in the condition of the samples after heating.
5. Conclusions
Using gadolinia doped ceria as an example, it was shown that by sintering under a reducing atmosphere and subsequently reoxidizing, the ionic conductivity can be drastically improved. The modified process also allows for sintering and densification at lower temperatures. In this particular example, an increase of one order of magnitude compared to a conventionally processed 10 mol% gadolinia doped ceria material was observed. At 350 °C, the total conductivity for the air-sintered sample was 3.95 × 10−5 S/cm, whereas that for the reduced-reoxidized sample was 1.09 × 10−4 S/cm. That is an increase of 6.99 × 10−5 S/cm or approximately 176%. Through a detailed analysis of the electrochemical impedance and conductivity data, it was established that this improvement in conductivity is mainly due to an improvement in the grain boundary conductivity of the material, and not a simple grain size or porosity effect. The decline in blocking effect of the grain boundaries can be attributed to less defect structures at the grain boundaries. However, higher resolution microscopic imaging and elemental analysis is required to further bolster this hypothesis. Although the improvement shown here is for gadolinia doped ceria, similar processing can be utilized for other oxide materials to reduce defect structures at grain boundaries and improve their electrical, optical, and mechanical properties.
Author Contributions
Conceptualization, S.S. and J.C.N.; methodology, J.C.N.; formal analysis, S.S.; experimental investigation, S.S., M.M. and J.H.K.; resources, J.C.N.; writing—original draft preparation, S.S.; writing—review and editing, S.S., M.M., J.H.K. and J.C.N.; supervision, J.C.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author, J.C.N., upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wachsman, E.D.; Lee, K.T. Lowering the temperature of solid oxide fuel cells. Science 2011, 334, 935–939. [Google Scholar] [CrossRef] [PubMed]
- Brett, D.J.; Atkinson, A.; Brandon, N.P.; Skinner, S.J. Intermediate temperature solid oxide fuel cells. Chem. Soc. Rev. 2008, 37, 1568–1578. [Google Scholar] [CrossRef] [PubMed]
- Inaba, H.; Tagawa, H. Ceria-based solid electrolytes. Solid State Ion. 1996, 83, 1–16. [Google Scholar] [CrossRef]
- Tuller, H.; Nowick, A. Doped ceria as a solid oxide electrolyte. J. Electrochem. Soc. 1975, 122, 255. [Google Scholar] [CrossRef]
- Eguchi, K.; Setoguchi, T.; Inoue, T.; Arai, H. Electrical properties of ceria-based oxides and their application to solid oxide fuel cells. Solid State Ion. 1992, 52, 165–172. [Google Scholar] [CrossRef]
- Bae, J.; Hong, S.; Koo, B.; An, J.; Prinz, F.B.; Kim, Y.-B. Influence of the grain size of samaria-doped ceria cathodic interlayer for enhanced surface oxygen kinetics of low-temperature solid oxide fuel cell. J. Eur. Ceram. Soc. 2014, 34, 3763–3768. [Google Scholar] [CrossRef]
- Bae, J.; Yang, H.; Son, J.; Koo, B.; Kim, Y.B. Enhanced Oxygen Reduction Reaction in Nanocrystalline Surface of Samaria-Doped Ceria via Randomly Distributed Dopants. J. Am. Ceram. Soc. 2016, 99, 4050–4056. [Google Scholar] [CrossRef]
- Omar, S.; Wachsman, E.D.; Nino, J.C. A co-doping approach towards enhanced ionic conductivity in fluorite-based electrolytes. Solid State Ion. 2006, 177, 3199–3203. [Google Scholar] [CrossRef]
- Xia, C.; Liu, M. Microstructures, conductivities, and electrochemical properties of Ce0. 9Gd0.1O2 and GDC–Ni anodes for low-temperature SOFCs. Solid State Ion. 2002, 152, 423–430. [Google Scholar] [CrossRef]
- Baure, G.; Zhou, H.; Chung, C.-C.; Buck, M.N.; Stozhkova, M.A.; Jones, J.L.; Nino, J.C. Comparison of the in-and across-plane ionic conductivity of highly oriented neodymium doped ceria thin films. Acta Mater. 2018, 147, 10–15. [Google Scholar] [CrossRef]
- Huang, H.; Gür, T.M.; Saito, Y.; Prinz, F. High ionic conductivity in ultrathin nanocrystalline gadolinia-doped ceria films. Appl. Phys. Lett. 2006, 89, 143107. [Google Scholar] [CrossRef]
- Avila-Paredes, H.J.; Choi, K.; Chen, C.-T.; Kim, S. Dopant-concentration dependence of grain-boundary conductivity in ceria: A space-charge analysis. J. Mater. Chem. 2009, 19, 4837–4842. [Google Scholar] [CrossRef]
- Tuller, H.L. Ionic conduction in nanocrystalline materials. Solid State Ion. 2000, 131, 143–157. [Google Scholar] [CrossRef] [Green Version]
- Christie, G.; Van Berkel, F. Microstructure—Ionic conductivity relationships in ceria-gadolinia electrolytes. Solid State Ion. 1996, 83, 17–27. [Google Scholar] [CrossRef]
- Guo, X.; Sigle, W.; Maier, J. Blocking grain boundaries in yttria-doped and undoped ceria ceramics of high purity. J. Am. Ceram. Soc. 2003, 86, 77–87. [Google Scholar] [CrossRef]
- Kim, S.K.; Khodorov, S.; Chen, C.-T.; Kim, S.; Lubomirsky, I. How to interpret current–voltage relationships of blocking grain boundaries in oxygen ionic conductors. Phys. Chem. Chem. Phys. 2013, 15, 8716–8721. [Google Scholar] [CrossRef] [PubMed]
- Gerhardt, R.; Nowick, A.S. Grain-boundary effect in ceria doped with trivalent cations: I, electrical measurements. J. Am. Ceram. Soc. 1986, 69, 641–646. [Google Scholar] [CrossRef]
- Omar, S. Enhanced Ionic Conductivity of Ceria-Based Compounds for the Electrolyte Application in SOFCs. Ph.D. Thesis, University of Florida, Gainesville, FL, USA, 2008. [Google Scholar]
- Gerhardt, R.; Nowick, A.; Mochel, M.; Dumler, I. Grain-boundary effect in ceria doped with trivalent cations: II, Microstructure and microanalysis. J. Am. Ceram. Soc. 1986, 69, 647–651. [Google Scholar] [CrossRef]
- Li, F.; Ohkubo, T.; Chen, Y.; Kodzuka, M.; Ye, F.; Ou, D.; Mori, T.; Hono, K. Laser-assisted three-dimensional atom probe analysis of dopant distribution in Gd-doped CeO2. Scr. Mater. 2010, 63, 332–335. [Google Scholar] [CrossRef]
- Diercks, D.R.; Tong, J.; Zhu, H.; Kee, R.; Baure, G.; Nino, J.C.; O’Hayre, R.; Gorman, B.P. Three-dimensional quantification of composition and electrostatic potential at individual grain boundaries in doped ceria. J. Mater. Chem. A 2016, 4, 5167–5175. [Google Scholar] [CrossRef]
- Kim, M.; Duscher, G.; Browning, N.D.; Sohlberg, K.; Pantelides, S.T.; Pennycook, S.J. Nonstoichiometry and the electrical activity of grain boundaries in SrTiO3. Phys. Rev. Lett. 2001, 86, 4056. [Google Scholar] [CrossRef] [Green Version]
- McGibbon, M.; Browning, N.; Chisholm, M.; McGibbon, A.; Pennycook, S.; Ravikumar, V.; Dravid, V. Direct determination of grain boundary atomic structure in SrTiO3. Science 1994, 266, 102–104. [Google Scholar] [CrossRef] [PubMed]
- Browning, N.; Buban, J.; Moltaji, H.; Pennycook, S.; Duscher, G.; Johnson, K.; Rodrigues, R.; Dravid, V.P. The influence of atomic structure on the formation of electrical barriers at grain boundaries in SrTiO3. Appl. Phys. Lett. 1999, 74, 2638–2640. [Google Scholar] [CrossRef]
- Guo, X.; Waser, R. Electrical properties of the grain boundaries of oxygen ion conductors: Acceptor-doped zirconia and ceria. Prog. Mater. Sci. 2006, 51, 151–210. [Google Scholar] [CrossRef]
- Fisher, C.A.; Matsubara, H. Molecular dynamics investigations of grain boundary phenomena in cubic zirconia. Comput. Mater. Sci. 1999, 14, 177–184. [Google Scholar] [CrossRef]
- Cantwell, P.R.; Tang, M.; Dillon, S.J.; Luo, J.; Rohrer, G.S.; Harmer, M.P. Grain boundary complexions. Acta Mater. 2014, 62, 1–48. [Google Scholar] [CrossRef]
- Schottky, W. Zur halbleitertheorie der sperrschicht-und spitzengleichrichter. Z. Phys. 1939, 113, 367–414. [Google Scholar] [CrossRef]
- Mott, N.F. The theory of crystal rectifiers. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1939, 171, 27–38. [Google Scholar]
- Guo, X.; Sigle, W.; Fleig, J.; Maier, J. Role of space charge in the grain boundary blocking effect in doped zirconia. Solid State Ion. 2002, 154, 555–561. [Google Scholar] [CrossRef]
- Guo, X.; Maier, J. Grain boundary blocking effect in zirconia: A Schottky barrier analysis. J. Electrochem. Soc. 2001, 148, E121. [Google Scholar] [CrossRef]
- Göbel, M.C.; Gregori, G.; Guo, X.; Maier, J. Boundary effects on the electrical conductivity of pure and doped cerium oxide thin films. Phys. Chem. Chem. Phys. 2010, 12, 14351–14361. [Google Scholar] [CrossRef]
- Frechero, M.A.; Rocci, M.; Sánchez-Santolino, G.; Kumar, A.; Salafranca, J.; Schmidt, R.; Díaz-Guillén, M.; Durá, O.; Rivera-Calzada, A.; Mishra, R. Paving the way to nanoionics: Atomic origin of barriers for ionic transport through interfaces. Sci. Rep. 2015, 5, 17229. [Google Scholar] [CrossRef] [Green Version]
- Durá, O.; De La Torre, M.L.; Vázquez, L.; Chaboy, J.; Boada, R.; Rivera-Calzada, A.; Santamaria, J.; Leon, C. Ionic conductivity of nanocrystalline yttria-stabilized zirconia: Grain boundary and size effects. Phys. Rev. B 2010, 81, 184301. [Google Scholar] [CrossRef] [Green Version]
- Lee, W.; Jung, H.J.; Lee, M.H.; Kim, Y.B.; Park, J.S.; Sinclair, R.; Prinz, F.B. Oxygen surface exchange at grain boundaries of oxide ion conductors. Adv. Funct. Mater. 2012, 22, 965–971. [Google Scholar] [CrossRef]
- Coppola, N.; Polverino, P.; Carapella, G.; Sacco, C.; Galdi, A.; Montinaro, D.; Maritato, L.; Pianese, C. Optimization of the electrical performances in Solid Oxide Fuel Cells with room temperature sputter deposited Gd0.1ce0.9o1.95 buffer layers by controlling their granularity via the in-air annealing step. Int. J. Hydrogen Energy 2020, 45, 12997–13008. [Google Scholar] [CrossRef]
- Ciacchi, F.; Nightingale, S.; Badwal, S. Microwave sintering of zirconia-yttria electrolytes and measurement of their ionic conductivity. Solid State Ion. 1996, 86, 1167–1172. [Google Scholar] [CrossRef]
- Mahboob, S.; Prasad, G.; Kumar, G. Impedance and ac conductivity studies on Ba (Nd0.2Ti0.6Nb0.2)O3 ceramic prepared through conventional and microwave sintering route. Bull. Mater. Sci. 2006, 29, 347–355. [Google Scholar] [CrossRef]
- Kabir, A.; Santucci, S.; Van Nong, N.; Varenik, M.; Lubomirsky, I.; Nigon, R.; Muralt, P.; Esposito, V. Effect of oxygen defects blocking barriers on gadolinium doped ceria (GDC) electro-chemo-mechanical properties. Acta Mater. 2019, 174, 53–60. [Google Scholar] [CrossRef]
- Cologna, M.; Rashkova, B.; Raj, R. Flash Sintering of Nanograin Zirconia in <5 s at 850 C. J. Am. Ceram. Soc. 2010, 93, 3556–3559. [Google Scholar] [CrossRef]
- Yu, M.; Grasso, S.; Mckinnon, R.; Saunders, T.; Reece, M.J. Review of flash sintering: Materials, mechanisms and modelling. Adv. Appl. Ceram. 2017, 116, 24–60. [Google Scholar] [CrossRef] [Green Version]
- An, J.; Bae, J.; Hong, S.; Koo, B.; Kim, Y.-B.; Gür, T.M.; Prinz, F.B. Grain boundary blocking of ionic conductivity in nanocrystalline yttria-doped ceria thin films. Scr. Mater. 2015, 104, 45–48. [Google Scholar] [CrossRef] [Green Version]
- Bae, J.; Lim, Y.; Park, J.-S.; Lee, D.; Hong, S.; An, J.; Kim, Y.-B. Thermally-induced dopant segregation effects on the space charge layer and ionic conductivity of nanocrystalline gadolinia-doped ceria. J. Electrochem. Soc. 2016, 163, F919. [Google Scholar] [CrossRef]
- Esposito, V.; He, Z.; Zhang, W.; Prasad, A.S.; Glasscock, J.A.; Chatzichristodoulou, C.; Ramousse, S.; Kaiser, A. Enhanced mass diffusion phenomena in highly defective doped ceria. Acta Mater. 2013, 61, 6290–6300. [Google Scholar] [CrossRef] [Green Version]
- Inaba, H.; Nakajima, T.; Tagawa, H. Sintering behaviors of ceria and gadolinia-doped ceria. Solid State Ion. 1998, 106, 263–268. [Google Scholar] [CrossRef]
- Zhang, T.; Ma, J.; Chan, S.; Kilner, J. Improvements in Sintering Behavior and Grain-Boundary Conductivity of Ceria-Based Electrolytes by a Small Addition of Fe2O3. J. Electrochem. Soc. 2004, 151, J84. [Google Scholar] [CrossRef]
- Higashi, K.; Sonoda, K.; Ono, H.; Sameshima, S.; Hirata, Y. Synthesis and sintering of rare-earth-doped ceria powder by the oxalate coprecipitation method. J. Mater. Res. 1999, 14, 957–967. [Google Scholar] [CrossRef]
- Sameshima, S.; Ono, H.; Higashi, K.; Sonoda, K.; Hirata, Y. Microstructure of rare-earth-doped ceria prepared by oxalate coprecipitation method. J. Ceram. Soc. Jpn. 2000, 108, 985–988. [Google Scholar] [CrossRef] [Green Version]
- Hong, S.J.; Virkar, A.V. Lattice parameters and densities of rare-earth oxide doped ceria electrolytes. J. Am. Ceram. Soc. 1995, 78, 433–439. [Google Scholar] [CrossRef]
- ASTM B962-15. Standard Test Methods for Density of Compacted or Sintered Powder Metallurgy (PM) Products Using Archimedes’ Principle; ASTM International: West Conshohocken, PA, USA, 2015. [Google Scholar]
- Basu, S.; Devi, P.S.; Maiti, H.S. Synthesis and properties of nanocrystalline ceria powders. J. Mater. Res. 2004, 19, 3162–3171. [Google Scholar] [CrossRef]
- Barsoukov, E.; Macdonald, J.R. Impedance Spectroscopy Theory, Experiment, and Applications, 2nd ed.; John Wiley &Sons, Inc.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Abram, E.; Sinclair, D.; West, A. A strategy for analysis and modelling of impedance spectroscopy data of electroceramics: Doped lanthanum gallate. J. Electroceram. 2003, 10, 165–177. [Google Scholar] [CrossRef]
- Hume-Rothery, W. Atomic Theory for Students of Metallurgy; The Institute of Metals: London, UK, 1952. [Google Scholar]
- Bevan, D. Ordered intermediate phases in the system CeO2 Ce2O3. J. Inorg. Nucl. Chem. 1955, 1, 49–59. [Google Scholar] [CrossRef]
- Bevan, D.; Kordis, J. Mixed oxides of the type MO2 (fluorite)—M2O3—I oxygen dissociation pressures and phase relationships in the system CeO2 Ce2O3 at high temperatures. J. Inorg. Nucl. Chem. 1964, 26, 1509–1523. [Google Scholar] [CrossRef]
- Hayles, J.; Bao, H. The reduction and oxidation of ceria: A natural abundance triple oxygen isotope perspective. Geochim. Cosmochim. Acta 2015, 159, 220–230. [Google Scholar] [CrossRef]
- Galusek, D.; Ghillányová, K. Ceramic oxides. In Ceramic Science and Technology; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2010; Volume 2, pp. 43–48. [Google Scholar]
- ASTM E112-13. Standard Test Methods for Determining Average Grain Size; ASTM International: West Conshohocken, PA, USA, 2003. [Google Scholar]
- McLachlan, D.; Hwang, J.-H.; Mason, T.O. Evaluating dielectric impedance spectra using effective media theories. J. Electroceram. 2000, 5, 37–51. [Google Scholar] [CrossRef]
- Starikov, E. ‘Meyer-Neldel Rule’: True history of its development and its intimate connection to classical thermodynamics. J. Appl. Solut. Chem. Model. 2014, 3, 15–31. [Google Scholar] [CrossRef]
- Segal, D. Chemical synthesis of ceramic materials. J. Mater. Chem. 1997, 7, 1297–1305. [Google Scholar] [CrossRef]
- Spiridigliozzi, L.; Dell’Agli, G.; Biesuz, M.; Sglavo, V.M.; Pansini, M. Effect of the Precipitating Agent on the Synthesis and Sintering Behavior of 20 mol% Sm-Doped Ceria. Adv. Mater. Sci. Eng. 2016, 2016, 6096123. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).