Prototype Material for New Strategy of Photon Energy Storage
Abstract
1. Introduction
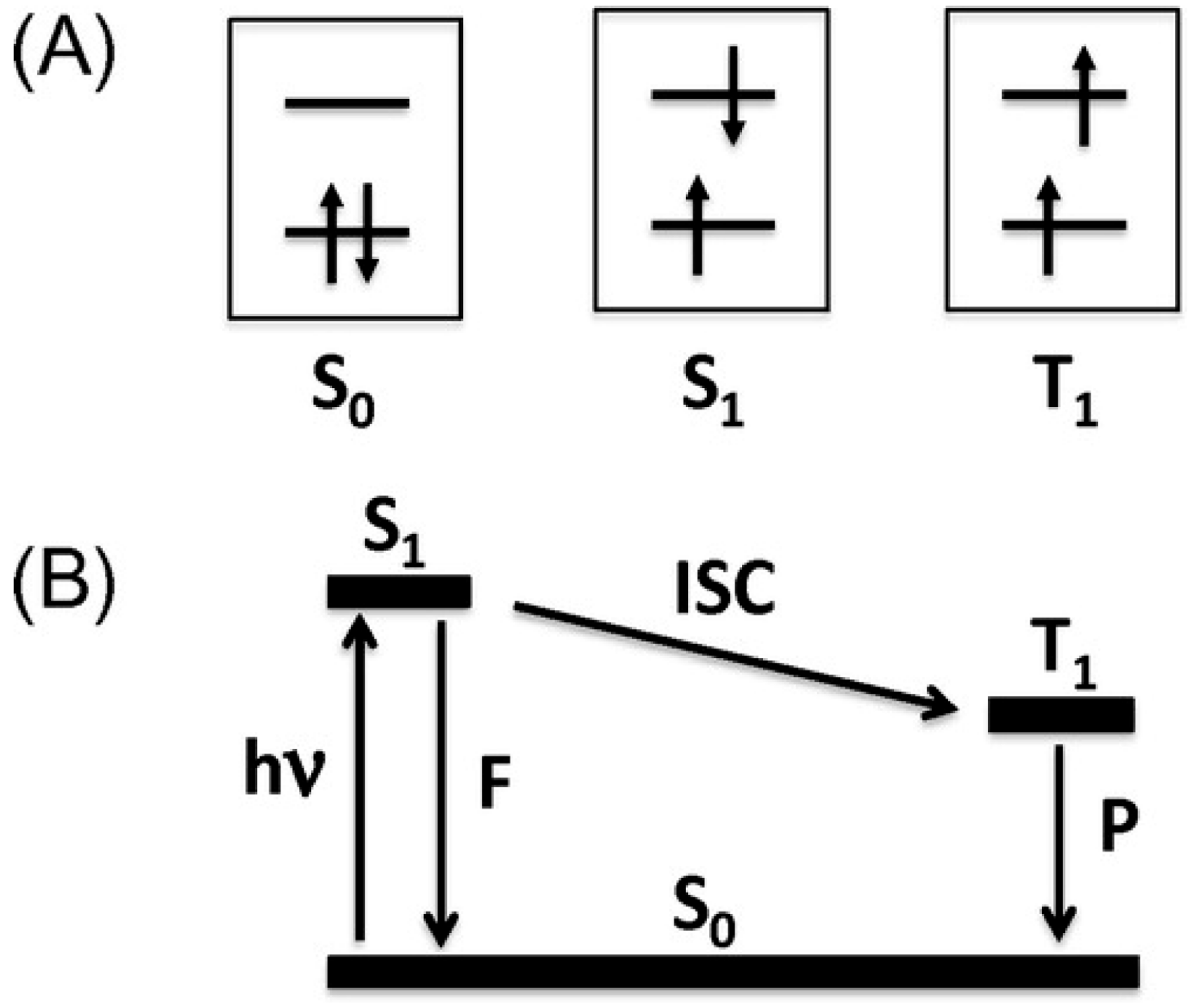
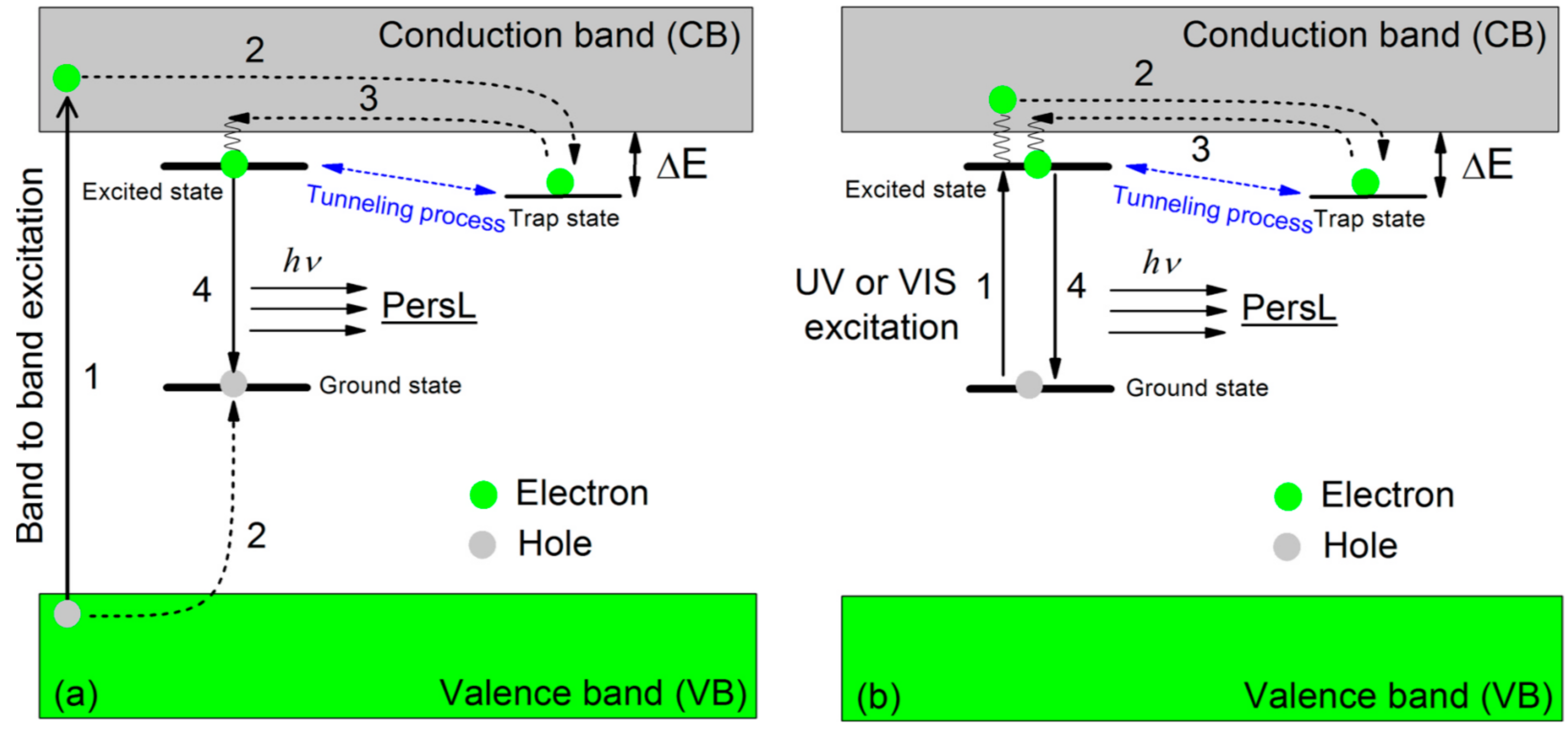
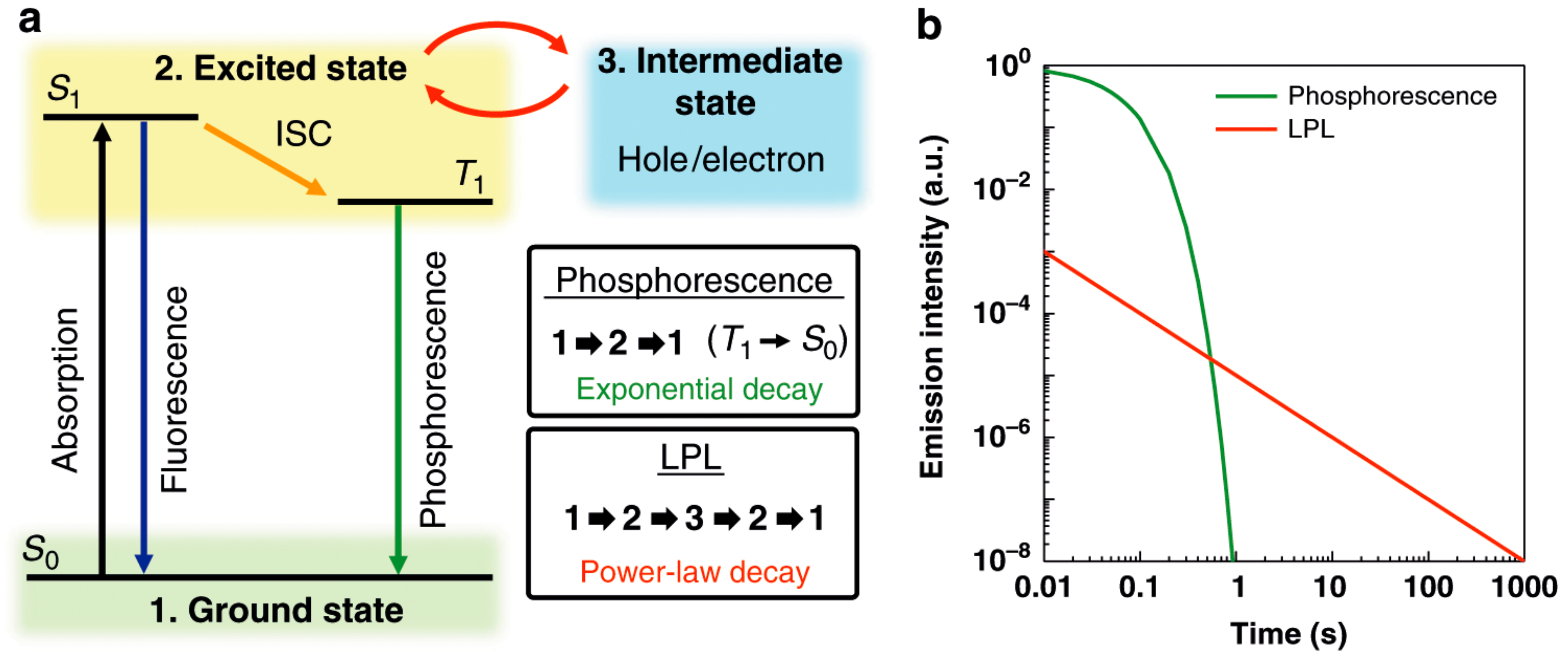
1.1. Photoluminescence and Related Phenomena
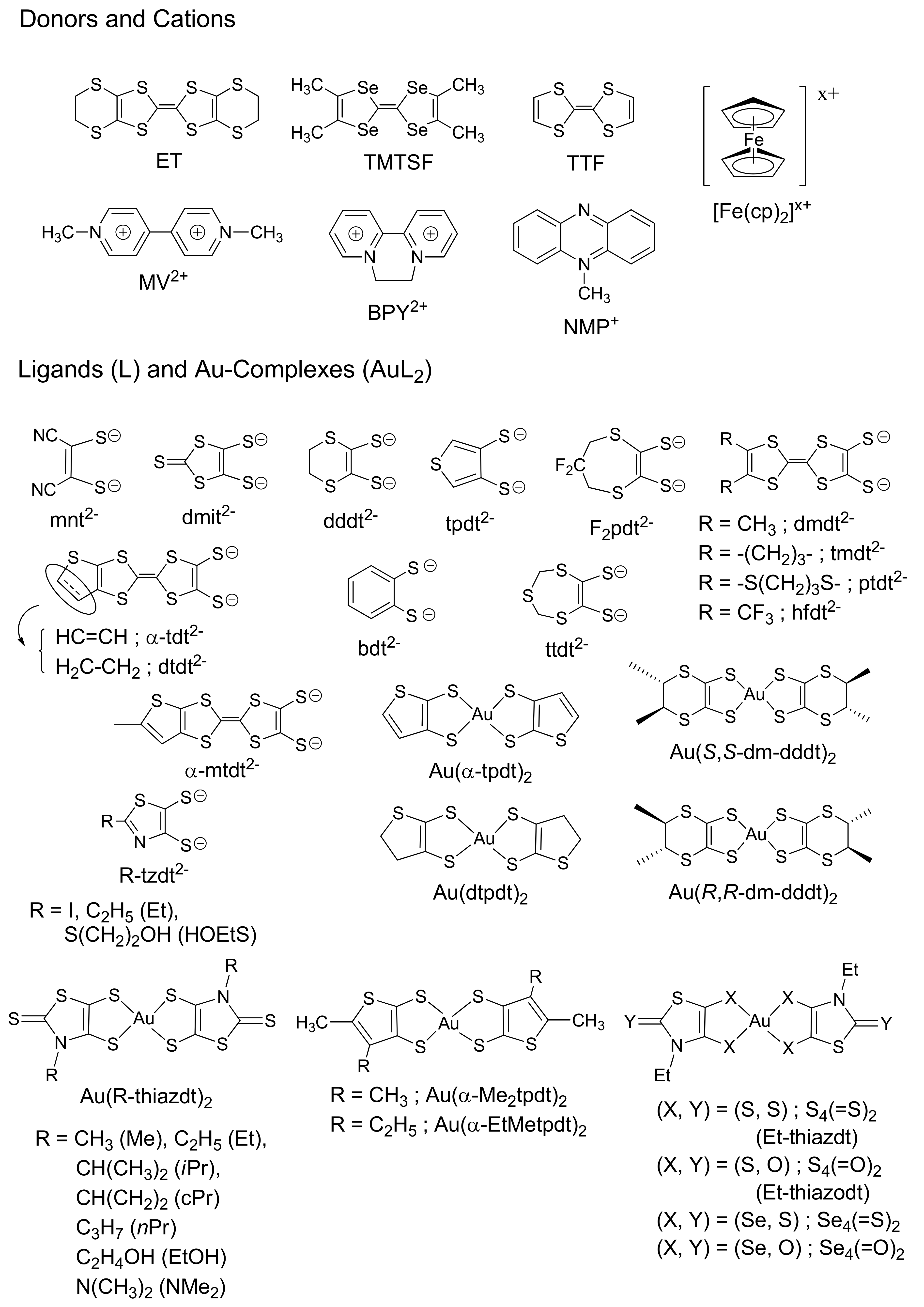
1.2. Au(III)-Dithiolene Complexes
2. Physical Properties of BPY[Au(dmit)2]2 (1): An Overview
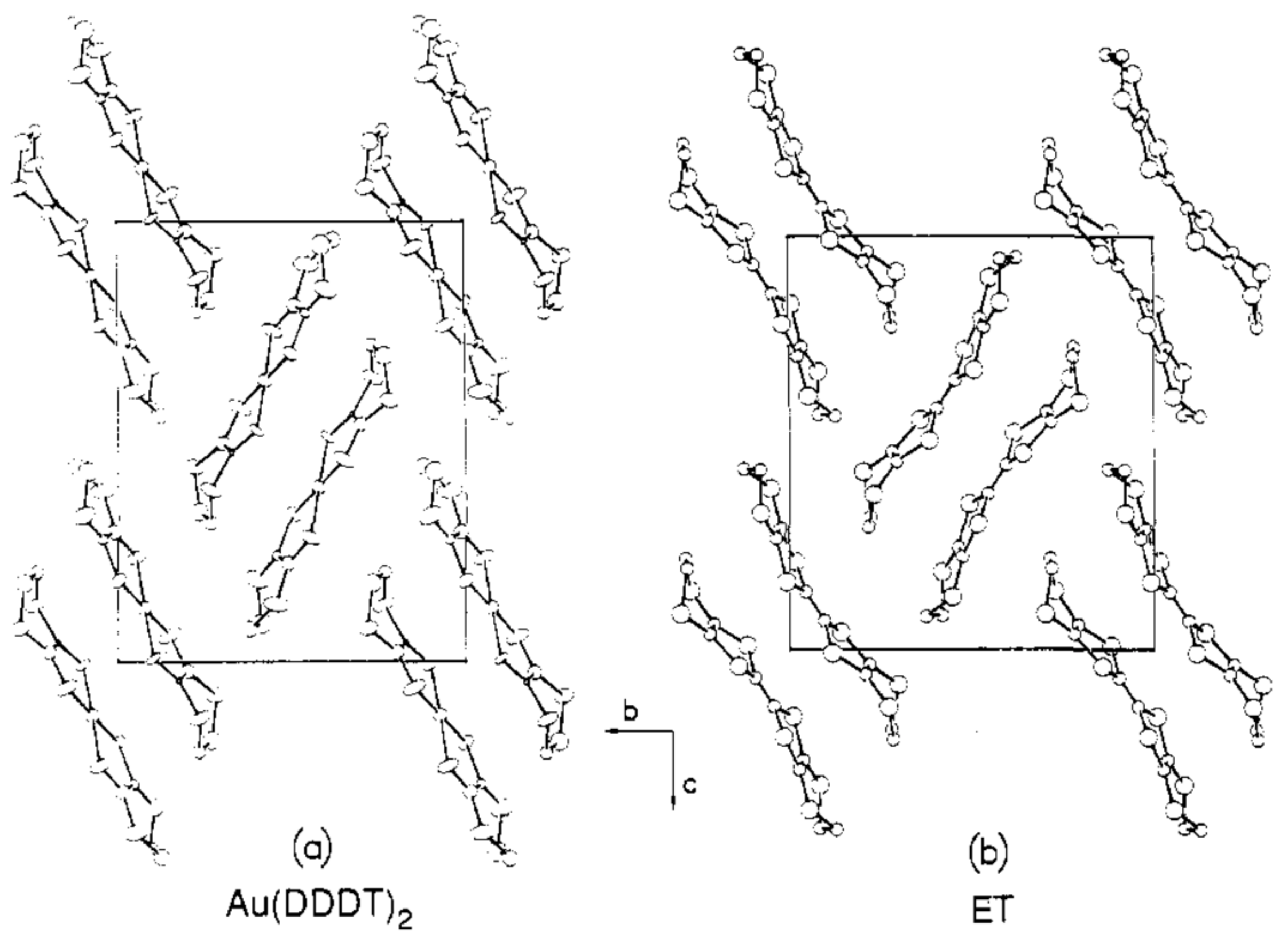
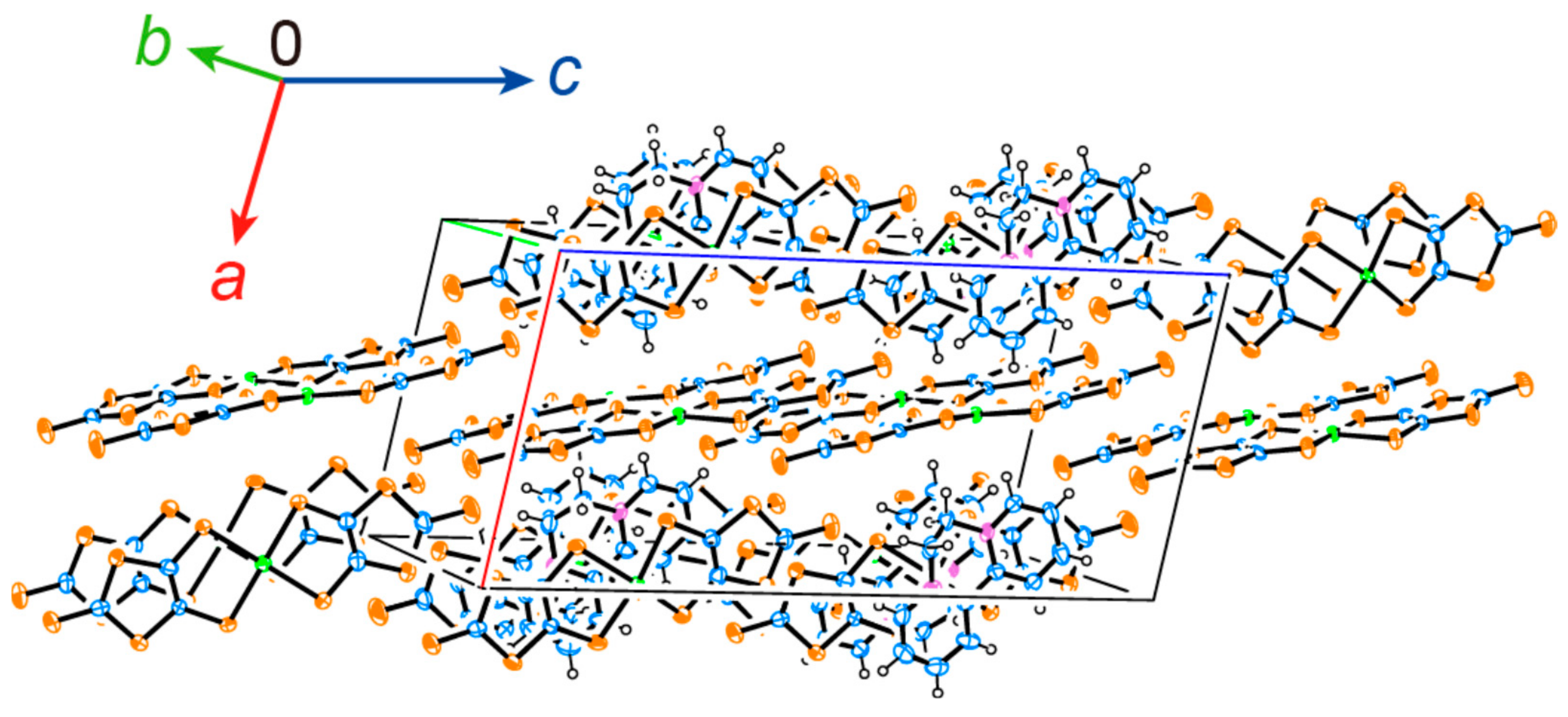
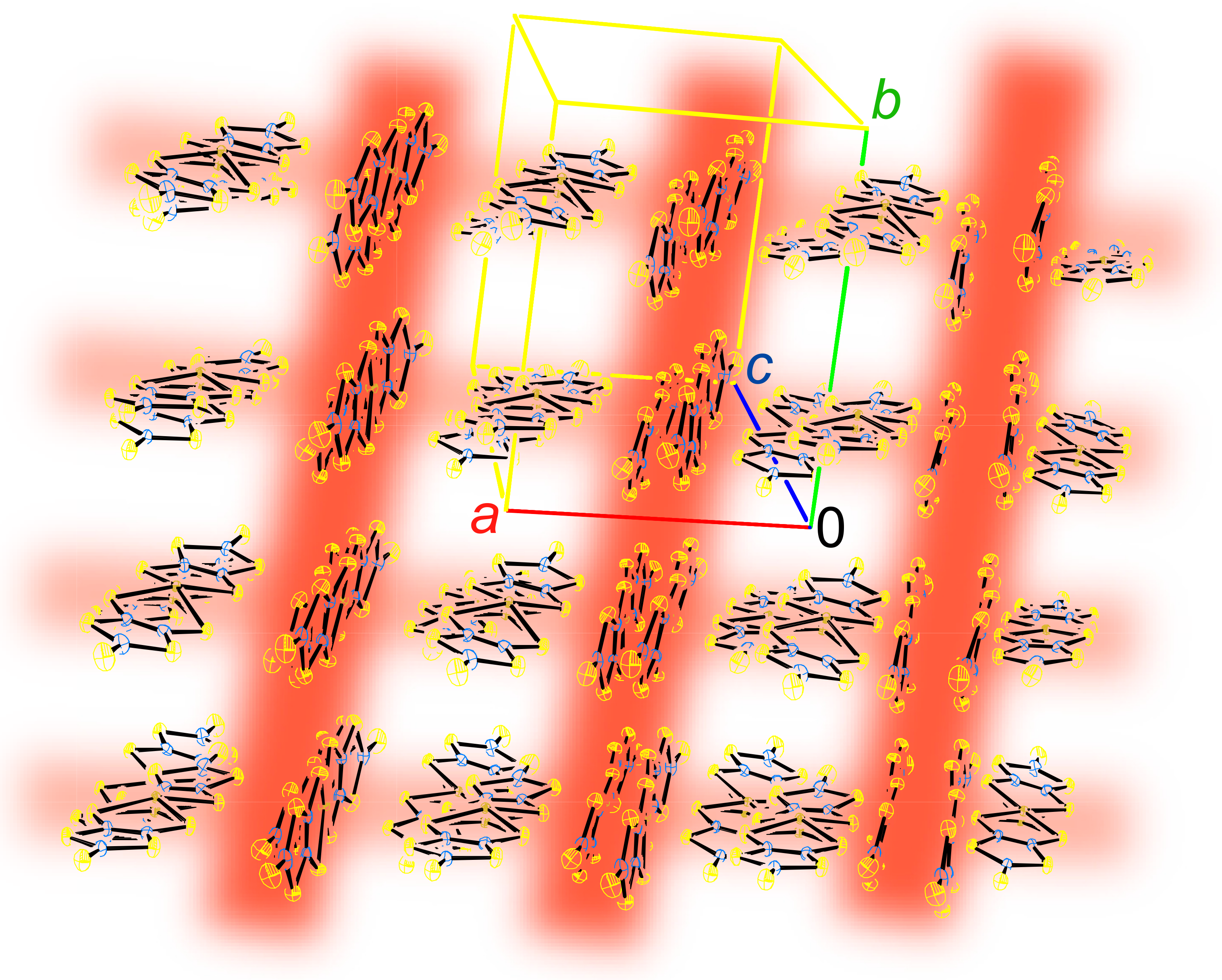
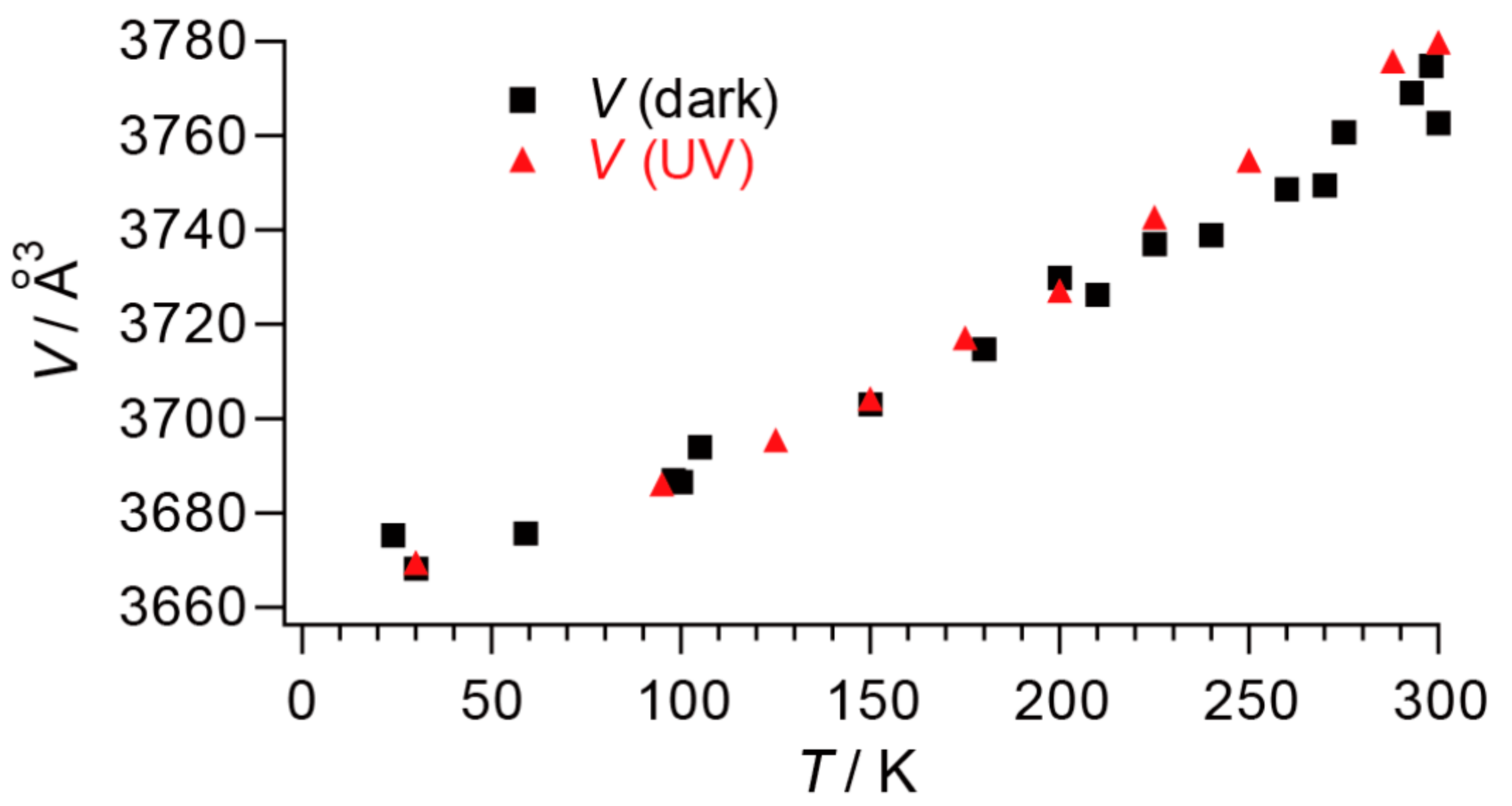
2.1. Crystal and Molecular Structure
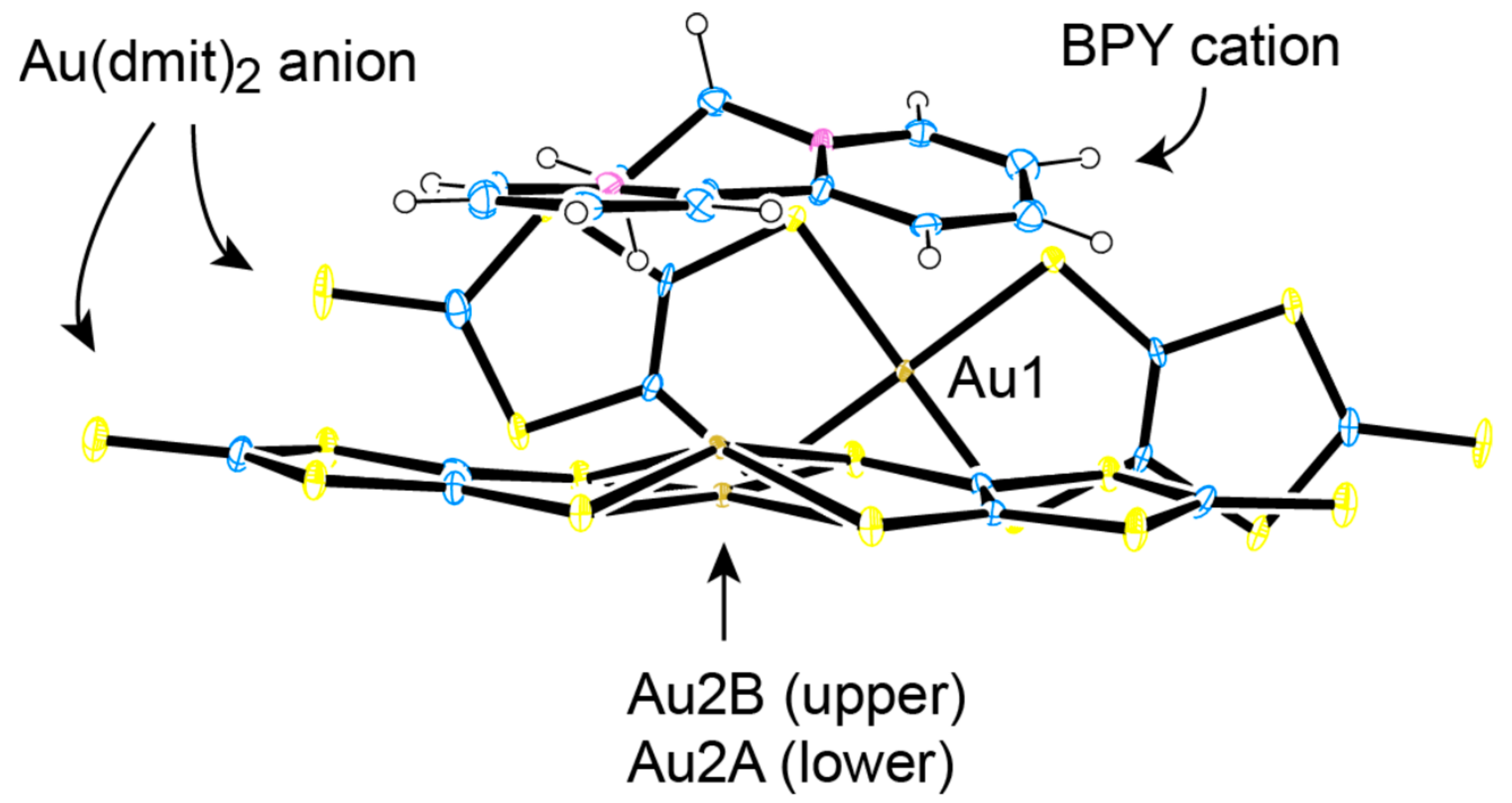
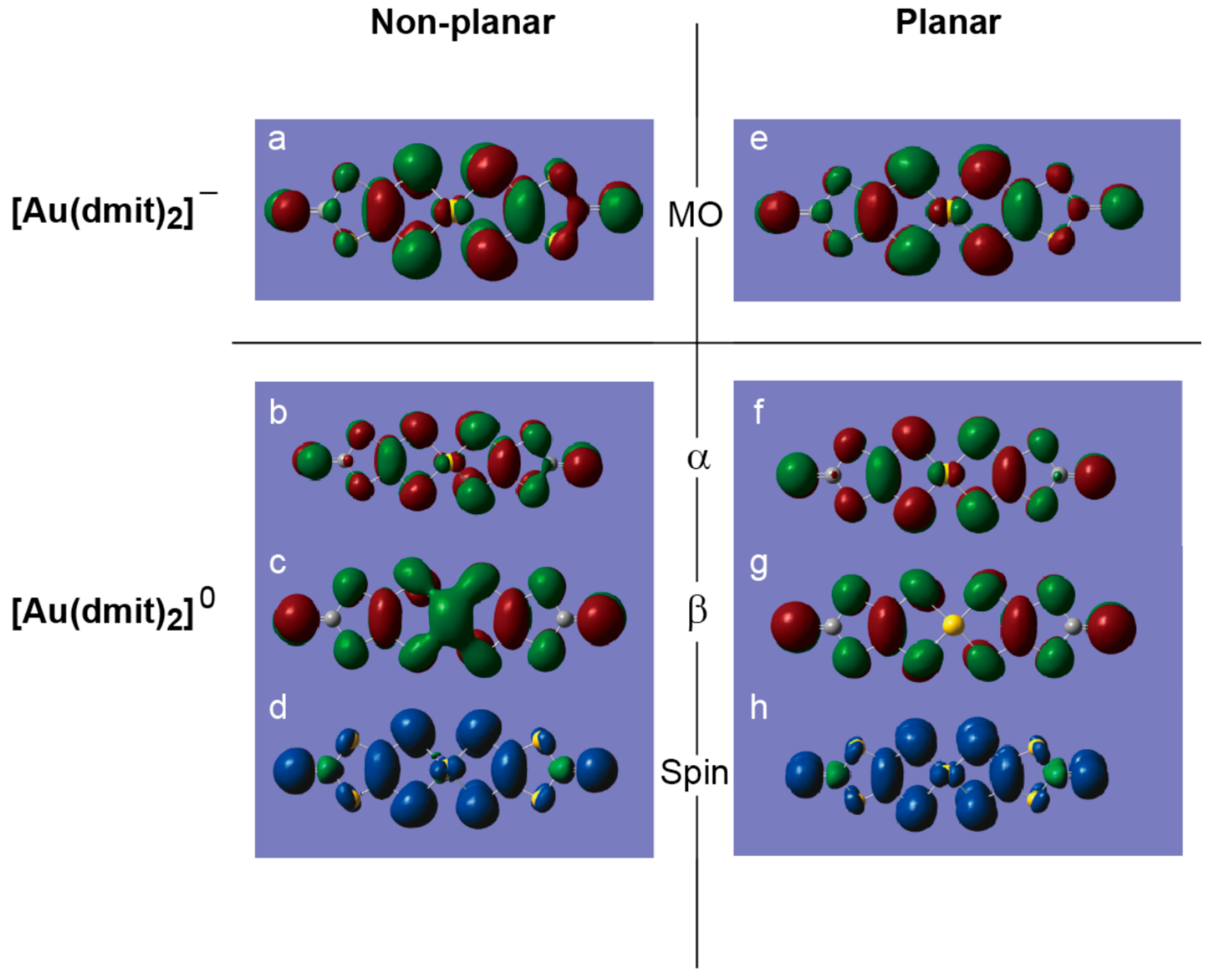
2.2. Charge, Spin, Coordination Geometry, and Cation-Anion Interaction
2.3. Phase Transition
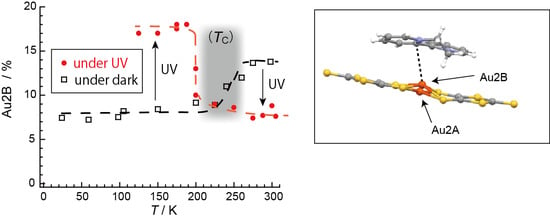
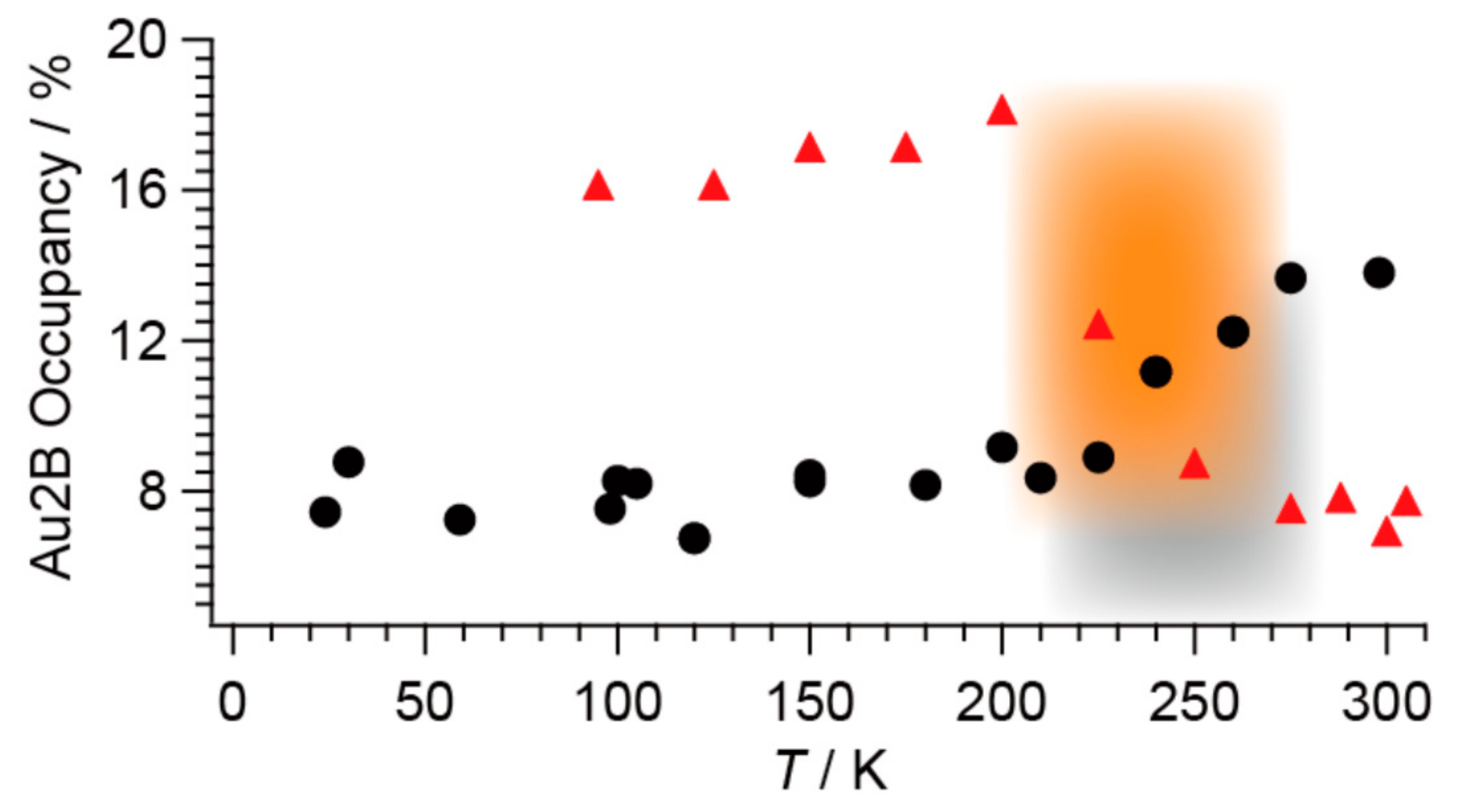
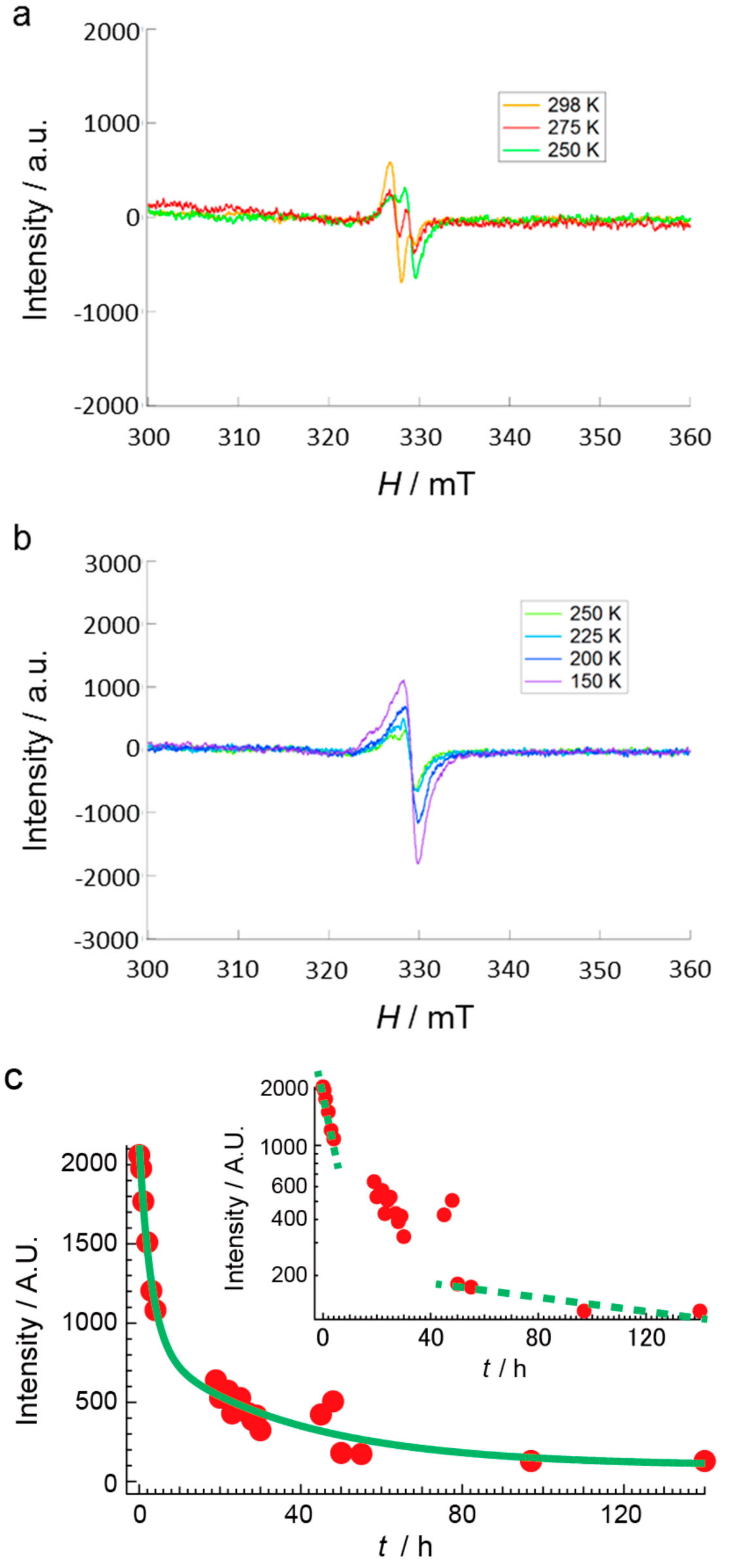
2.4. Unprecedentedly Long Relaxation Time of the UV-Excited State
3. Comparative Study on Related Materials
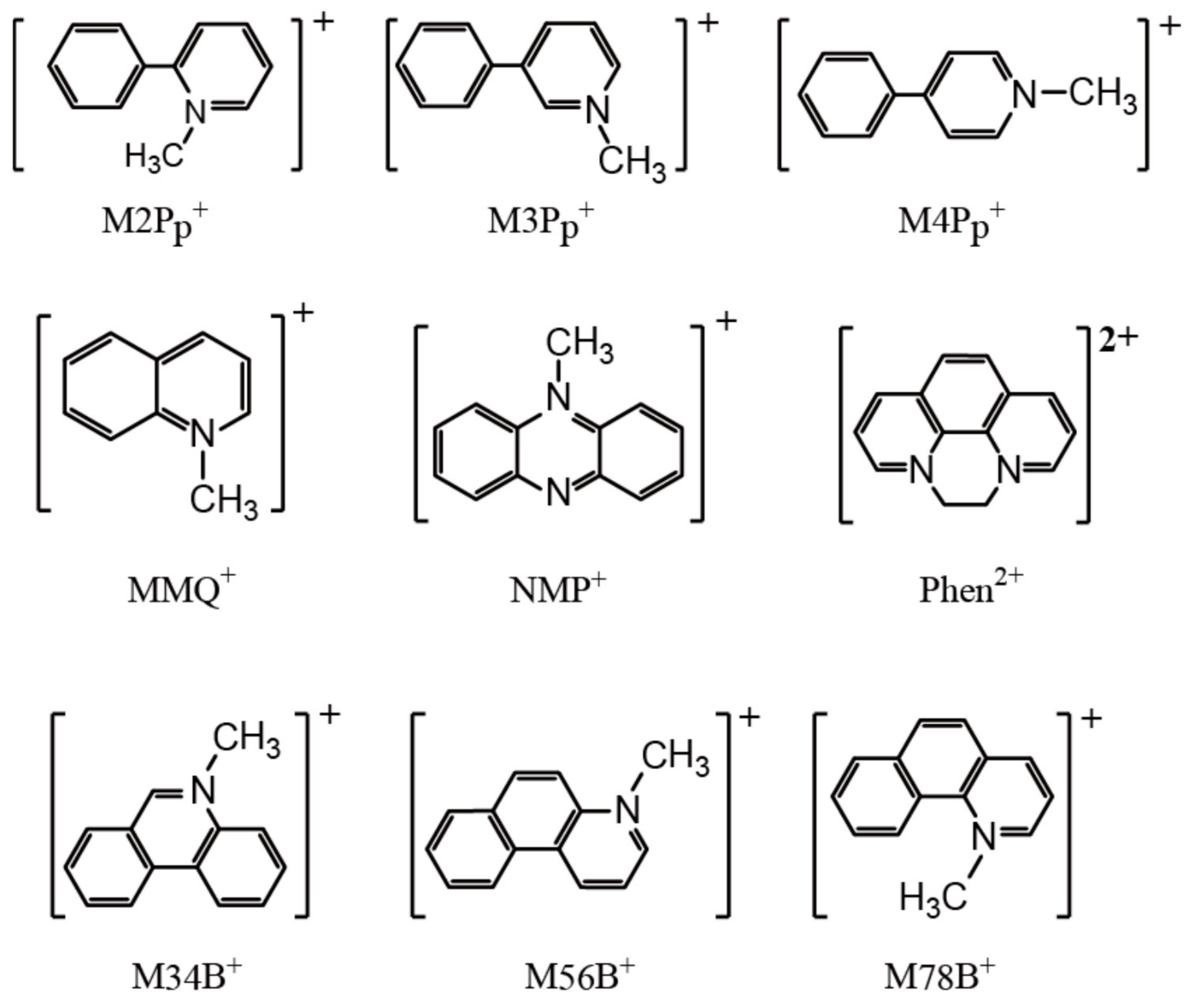
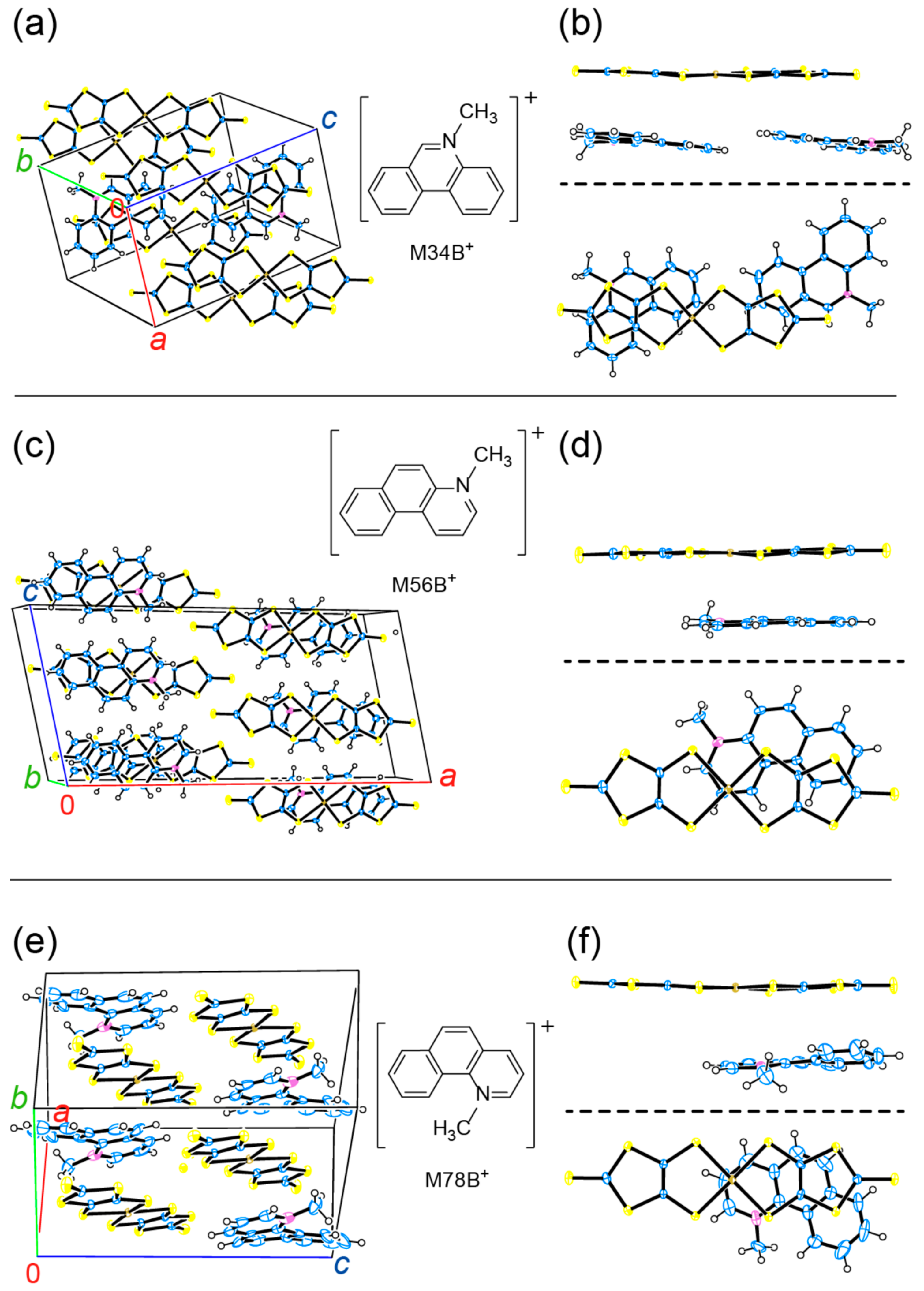
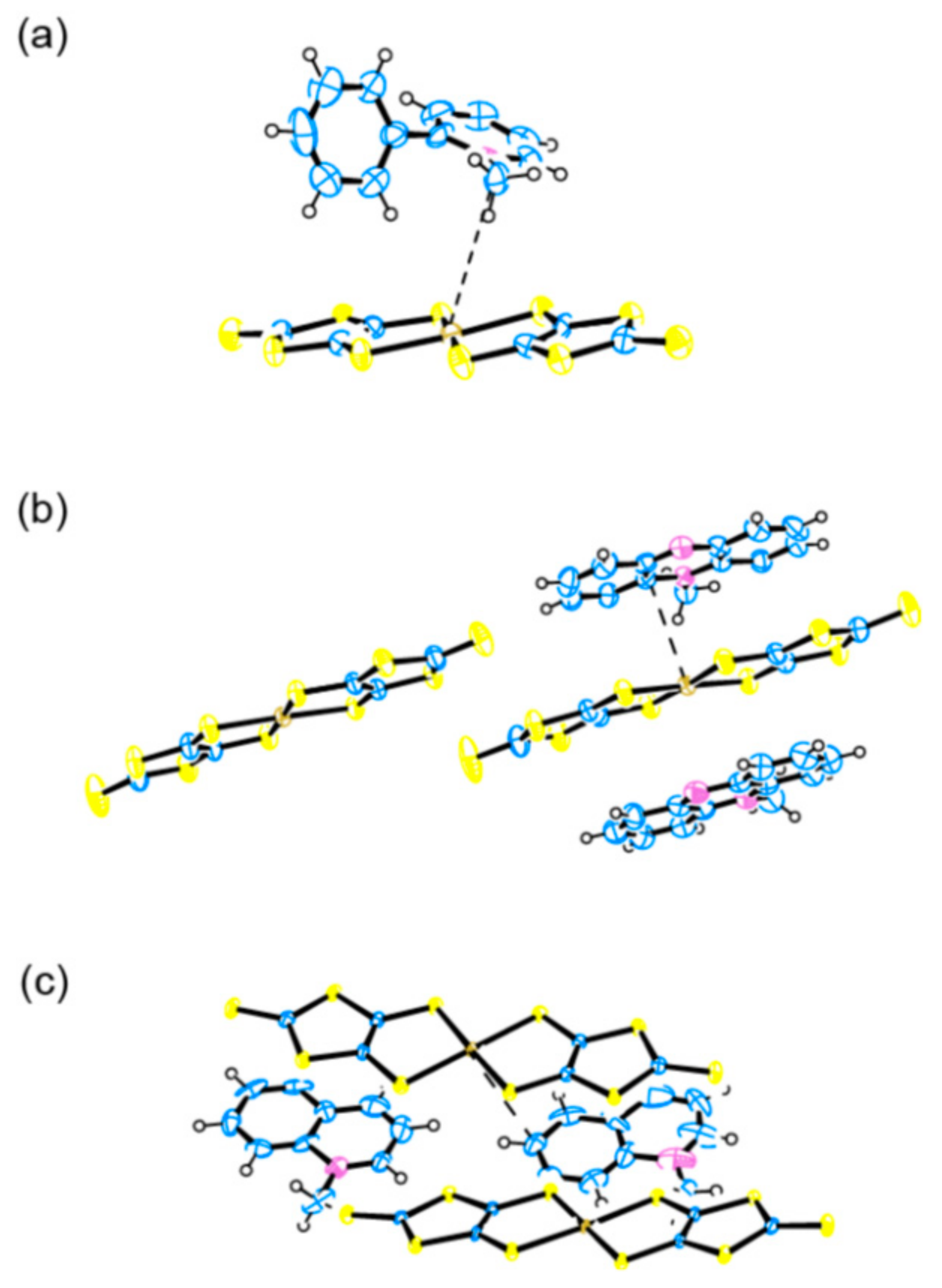
3.1. Selection of the Counter Cations
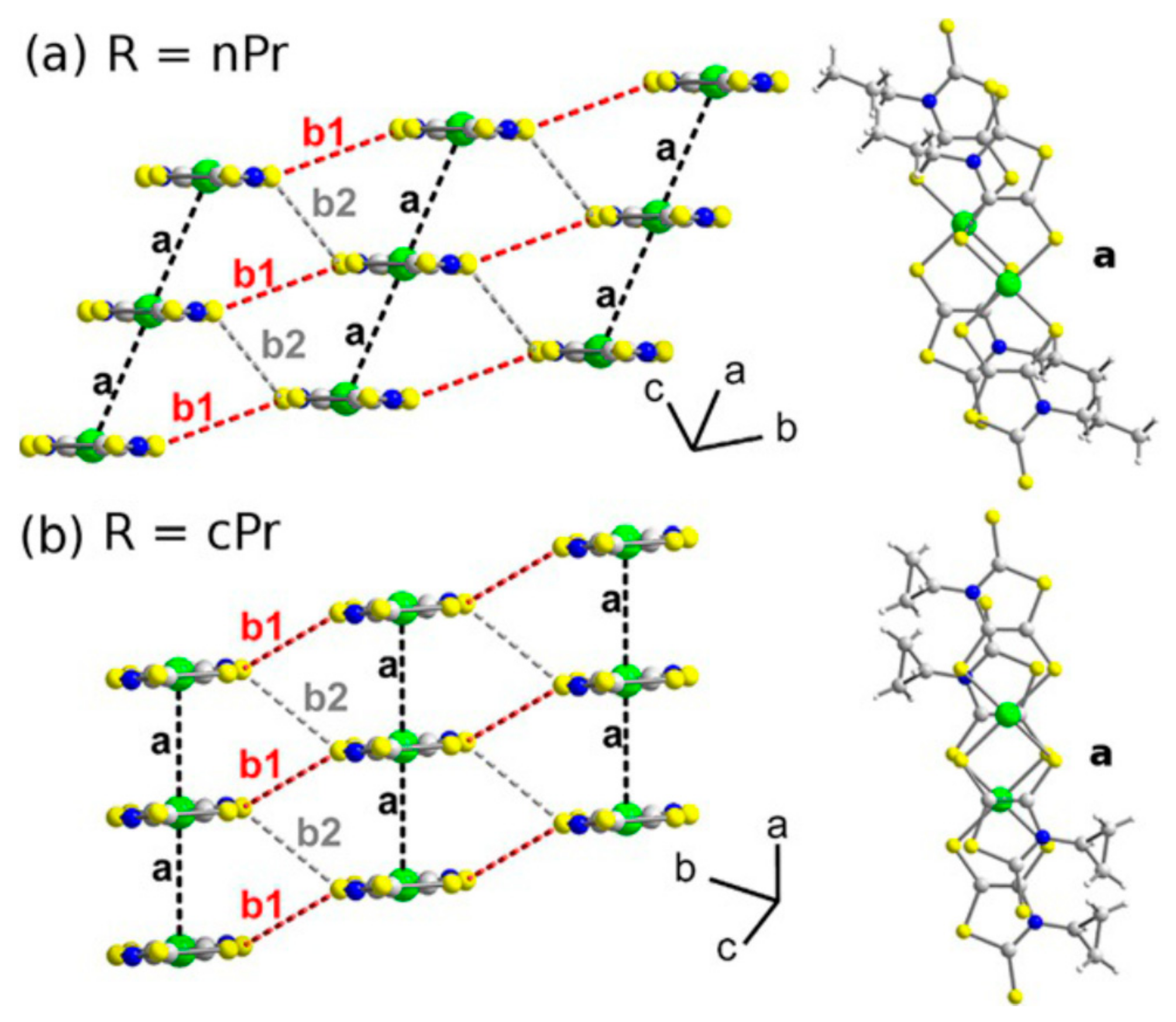
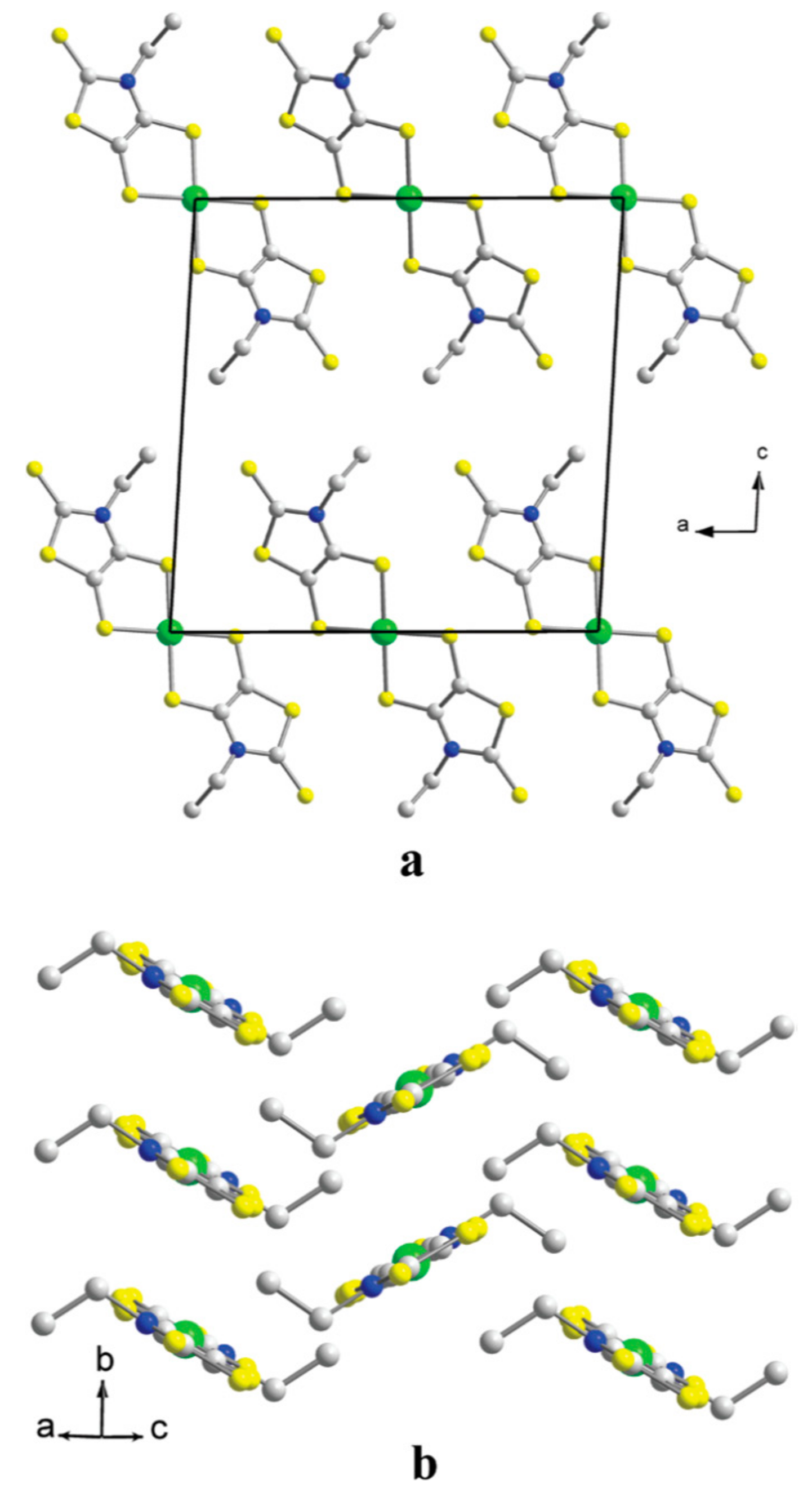
3.2. Comparison of the Resultant Salts
4. Future Prospects
Funding
Acknowledgments
Conflicts of Interest
References
- Kao, K.C. Dielectric Phenomena in Solids; Elsevier: San Diego, CA, USA, 2004; pp. 165–171. [Google Scholar]
- Naito, T. Development of Control Method of Conduction and Magnetism in Molecular Crystals. Bull. Chem. Soc. Jpn. 2017, 90, 89–136. [Google Scholar] [CrossRef]
- Naito, T. Optical Control of Electrical Properties in Molecular Crystals; States of Matter beyond Thermodynamic Restrictions. Chem. Lett. 2018, 47, 1441–1452. [Google Scholar] [CrossRef]
- Yuasa, H.; Kuno, S. Intersystem Crossing Mechanisms in the Room Temperature Phosphorescence of Crystalline Organic Compounds. Bull. Chem. Soc. Jpn. 2018, 91, 223–229. [Google Scholar] [CrossRef]
- Xu, J.; Tanabe, S. Persistent luminescence instead of phosphorescence: History, mechanism, and perspective. J. Lumin. 2019, 205, 581–620. [Google Scholar] [CrossRef]
- Matsuzawa, T.; Aoki, Y.; Takeuchi, N.; Murayama, Y. A new long phosphorescent phosphor with high brightness, SrAl2O4:Eu2+, Dy3+. J. Electrochem. Soc. 1996, 143, 2670–2673. [Google Scholar] [CrossRef]
- Jia, W.; Wang, Q.; Shi, H.; An, Z.; Huang, W. Manipulating the ultralong organic phosphorescence of small molecular crystals. Chem. Eur. J. 2020, 26, 4437–4448. [Google Scholar] [CrossRef]
- An, Z.; Zheng, C.; Tao, Y.; Chen, R.; Shi, H.; Chen, T.; Wang, Z.; Li, H.; Deng, R.; Liu, X.; et al. Stabilizing triplet excited states for ultralong organic phosphorescence. Nat. Mater. 2015, 14, 685–690. [Google Scholar] [CrossRef]
- Viana, B.; Sharma, S.K.; Gourier, D.; Maldiney, T.; Teston, E.; Scherman, D.; Richard, C. Long term in vivo imaging with Cr3+ doped spinel nanoparticles exhibiting persistent luminescence. J. Lumin. 2016, 170, 879–887. [Google Scholar] [CrossRef]
- Hu, L.; Wang, P.; Zhao, M.; Liu, L.; Zhou, L.; Li, B.; Albaqami, F.H.; El-Toni, A.M.; Li, X.; Xie, Y.; et al. Near-infrared rechargeable “optical battery” implant for irradiation-free photodynamic therapy. Biomaterials 2018, 163, 154–162. [Google Scholar] [CrossRef]
- Lin, Z.; Kabe, R.; Wang, K.; Adachi, C. Influence of energy gap between charge-transfer and locally excited states on organic long persistent luminescence. Nat. Commun. 2020, 11, 191. [Google Scholar] [CrossRef]
- Adachi, C. Third-generation organic electroluminescence materials. Jpn. J. Appl. Phys. 2014, 53, 060101. [Google Scholar] [CrossRef]
- Naito, T.; Watanabe, N.; Sakamoto, Y.; Miyaji, Y.; Shirahata, T.; Misaki, Y.; Kitou, S.; Sawa, H. A molecular crystal with an unprecedentedly long-lived photoexcited state. Dalton Trans. 2019, 48, 12858–12866. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Q.; Huang, C.; Li, F. Phosphorescent heavy-metal complexes for bioimaging. Chem. Soc. Rev. 2011, 40, 2508–2524. [Google Scholar] [CrossRef]
- Lima, J.C.; Rodríguez, L. Highlights on Gold TADF complexes. Inorganics 2019, 7, 124. [Google Scholar] [CrossRef]
- Sousa, S.A.; Leitão, J.H.; Silva, R.A.L.; Belo, D.; Santos, I.C.; Guerreiro, J.F.; Martins, M.; Fontinha, D.; Prûdencio, M.; Almeida, M.; et al. On the path to gold: Monoanionic Au bisdithiolate complexes with anitimicrobial and antitumor activities. J. Inorg. Biochem. 2020, 202, 110904. [Google Scholar] [CrossRef] [PubMed]
- Fontinha, D.; Sousa, S.; Morais, T.; Prudencio, M.; Leitao, J.H.; Le Gal, Y.; Lorcy, D.; Silva, R.A.L.; Velho, M.F.G.; Belo, D.; et al. Gold(III) bis(dithiolene) complexes: From molecular conductors to prospective anticancer, antimicrobial and antiplasmoidal agents. Metallomics 2020, 12, 974–987. [Google Scholar] [CrossRef]
- Pintus, A.; Aragoni, M.C.; Cinellu, M.C.; Maiore, L.; Isaia, F.; Lippolis, V.; Orru, G.; Tuveri, E.; Zucca, A.; Arca, M. [Au(pyb-H)(mnt)]: A novel gold(III) 1,2-dithiolene cyclometalated complex with antimicrobial activity (pyb-H = C-deprotonated 2-benzylpyridine; mnt = 1,2-dicyanoenthene-1,2-dithiolate). J. Inorg. Biochem. 2017, 170, 188–194. [Google Scholar] [CrossRef]
- Pop, F.; Avarvari, N. Chiral metal-dithiolene complexes. Coord. Chem. Rev. 2017, 346, 20–31. [Google Scholar] [CrossRef]
- Le Gal, Y.; Roisnel, T.; Auban-Senzier, P.; Bellec, N.; Íñiguez, J.; Canadell, E.; Lorcy, D. Stable Metallic State of a Neutral-Radical Single-Component Conductor at Ambient Pressure. J. Am. Chem. Soc. 2018, 140, 6998–7004. [Google Scholar] [CrossRef]
- Kato, R. Conducting metal dithiolene complexes: Structural and electronic properties. Chem. Rev. 2004, 104, 5319–5346. [Google Scholar] [CrossRef]
- Robertson, N.; Cronin, L. Metal bis-1,2-dithiolene complexes in conducting or magnetic crystalline assemblies. Coord. Chem. Rev. 2002, 227, 93–127. [Google Scholar] [CrossRef]
- Mercuri, M.L.; Deplano, P.; Pilia, L.; Serpe, A.; Artizzu, F. Interactions modes and physical properties in transition metal chalcogenolene-based molecular materials. Coord. Chem. Rev. 2010, 254, 1419–1433. [Google Scholar] [CrossRef]
- Garreau-de Bonneval, B.; Ching, K.I.M.-C.; Alary, F.; Bui, T.-T.; Valade, L. Neutral d8 metals bis-dithiolene complexes: Synthesis, electronic properties and applications. Coord. Chem. Rev. 2010, 254, 1457–1467. [Google Scholar] [CrossRef]
- Kobayashi, A.; Fujiwara, E.; Kobayashi, H. Single-Component Molecular Metals with Extended-TTF Dithiolate Ligands. Chem. Rev. 2004, 104, 5243–5264. [Google Scholar] [CrossRef] [PubMed]
- Davison, A.; Edelstein, N.; Holm, R.H.; Maki, A.H. The Preparation and Characterization of Four-Coordinate Complexes Related by Electron-Transfer Reactions. Inorg. Chem. 1963, 2, 1227–1232. [Google Scholar] [CrossRef]
- Bähr, G.; Schleitzer, H. Beiträge zur Chemie des Schwefelkohlenstoffs und Selenkohlenstoffs, II. Die Kondensierende Spontan-Entschwefelung von Salzen und Estern der Cyan-Dithioameisensäure. Freie Cyan-Dithioameisensäure. Chem. Ber. 1957, 90, 438–443. [Google Scholar] [CrossRef]
- Simmons, H.E.; Blomstrom, D.C.; Vest, R.D. Thiacyanocarbons. II. Chemistry of Disodium Dimercaptomaleonitrile. J. Am. Chem. Soc. 1962, 84, 4756–4771. [Google Scholar] [CrossRef]
- Gray, H.B.; Williams, R.; Bernal, I.; Billig, E. A Spin-Free Square Planar Cobaltous Complex. J. Am. Chem. Soc. 1962, 84, 3596–3597. [Google Scholar] [CrossRef]
- Steimecke, G.; Sieler, H.-J.; Kirmse, R.; Hoyer, E. 1,3-Dithiol-2-thion-4,5-dithiolat aus Schwefelkohlenstoff und Alkalimetall. Phosphorus Sulfur 1979, 7, 49–55. [Google Scholar] [CrossRef]
- Kirmse, R.; Stach, J.; Dietzsch, W.; Steimecke, G.; Hoyer, E. Single-Crystal EPR Studies on Nickel(III), Palladium(III), and Platinum(III) Dithiolene Chelates Containing the Ligands Isotrithionedithiolate, o-Xylenedithiolate, and Maleonitriledithiolate. Inorg. Chem. 1980, 19, 2679–2685. [Google Scholar] [CrossRef]
- Nakamura, T.; Tanaka, H.; Matsumoto, M.; Tachibana, H.; Manda, E.; Kawabata, Y. Conductive Langmuir-Blodgett films of transition metals with sulfur containing ligands. Synth. Met. 1988, 27, 601–608. [Google Scholar] [CrossRef]
- Nakamura, T.; Kojima, K.; Matsumoto, M.; Tachibana, H.; Tanaka, M.; Manda, E.; Kawabata, Y. Metallic Temperature Dependence in the Conductivity of Langmuir-Blodgett films of Tridecylmethylammonium-Au(dmit)2. Chem. Lett. 1989, 18, 367–368. [Google Scholar] [CrossRef]
- Matsubayashi, G.; Yokozawa, A. Spectroscopy and Electrical Conductivity of [Au(C3S5)2]n− and [Au(C3Se5)2]n− (n = 0–1) Complexes and X-ray Crystal Structure of [NBun4][Au(C3S5)2]. J. Chem. Soc. Dalton Trans. 1990, 1990, 3535–3539. [Google Scholar] [CrossRef]
- Hawkins, I.; Clark, R.A.; Wainwright, C.E.; Underhill, A.E. New Molecular Conductors Based on Metal Complex Anions. Mol. Cryst. Liq. Cryst. 1990, 181, 209–216. [Google Scholar] [CrossRef]
- Kotov, A.I.; Kushch, L.A.; Laukhina, E.E.; Khomenko, A.G.; Zvarykina, A.V.; Shibaeva, R.P.; Yagubskii, E.B.; Nagapetyan, S.S.; Struchkov, Y.T. Highly Conducting Complexes Based on Au(III)-Bis(1,3-dithio-2-thione-4,5-dithiolate). Synth. Met. 1991, 42, 2355–2358. [Google Scholar] [CrossRef]
- Wainwright, C.E.; Clark, R.A.; Underhill, A.E.; Marsden, I.R.; Allan, M.; Friend, R.H. Synthesis and Properties of New Molecular Metals Based on [Au(dmit)2] Anions. Synth. Met. 1991, 41–43, 2269–2274. [Google Scholar] [CrossRef]
- Shibaeva, R.P.; Rozenberg, L.P.; Kushch, L.A.; Kotov, A.I.; Khomenko, A.G.; Yagubskii, E.B.; Zavodnik, V.E. Synthesis, structure and conducting properties of Me4N[Au(dmit)2]2. Synth. Met. 1992, 46, 261–269. [Google Scholar] [CrossRef]
- Schiødt, N.C.; Bjørnholm, T.; Jacobsen, C.S.; Bechgaard, K. Magnetic and electrical properties of new aromatic 1,2-dithiolato-Au(III) and Au(IV) complexes. Synth. Met. 1993, 56, 2164–2168. [Google Scholar] [CrossRef]
- Belo, D.; Alves, H.; Lopes, E.B.; Duarte, M.T.; Gama, V.; Henriques, R.T.; Almeida, M.; Perez-Benitez, A.; Rovira, C.; Veciana, J. Gold Complexes with Dithiothiphene Ligands: A Metal Based on a Neutral Molecule. Chem. Eur. J. 2001, 7, 511–519. [Google Scholar] [CrossRef]
- Yagubskii, E.B.; Kotov, A.I.; Laukhina, E.E.; Ignatiev, A.A.; Buravov, L.I.; Khomenko, A.G.; Shklover, V.E.; Nagapetyan, S.S.; Struchkov, Y.T. New Class of Metal Bis-dithiolene Electroconducting Solids: Cation Complexes of Metals with dddt. Synth. Met. 1991, 42, 2515–2522. [Google Scholar] [CrossRef]
- Martin, L. Molecular conductors of BEDT-TTF with tris(oxalato) metallate anions. Coord. Chem. Rev. 2018, 376, 277–291. [Google Scholar] [CrossRef]
- Schultz, A.J.; Wang, H.H.; Soderholm, L.C.; Sifter, T.L.; Williams, J.M.; Bechgaard, K.; Whangbo, M.-H. Crystal Structures of [Au(DDDT)2]0 and [(n-Bu)4N][Ni(DDDT)2] and the Ligandlike Character of the Isoelectronic Radicals [Au(DDDT)2]0 and [Ni(DDDT)2]-. Inorg. Chem. 1987, 26, 3757–3761. [Google Scholar] [CrossRef]
- Branzea, D.G.; Pop, F.; Auban-Senzier, P.; Clérac, R.; Alemany, P.; Canadell, E.; Avarvari, N. Localization versus Delocalization in Chiral Single Component Conductors of Gold Bis(dithiolene) Complexes. J. Am. Chem. Soc. 2016, 138, 6838–6851. [Google Scholar] [CrossRef] [PubMed]
- Pennec, R.L.; Jeannin, O.; Auban-Senzier, P.; Fourmigué, M. Chiral, radical, gold bis(dithiolene) complexes. New J. Chem. 2016, 40, 7113–7120. [Google Scholar] [CrossRef]
- Kuppusamy, P.; Venkatalakshmi, N.; Manoharan, P.T. Crystal and molecular structure of N-methylphenazinium bis(maleonitriledithiolate)gold(III), [NMP+][Au(mnt)2]−. J. Cryst. Spectrosc. Res. 1985, 15, 629–641. [Google Scholar] [CrossRef]
- Wainwright, C.E.A.; Underhill, A.E. Molecular conductors based on the [Au(dmit)2] complex anion. Mol. Cryst. Liq. Cryst. 1993, 234, 193–198. [Google Scholar] [CrossRef]
- Geiser, U.; Schultz, A.J.; Wang, H.H.; Beno, M.A.; Williams, J.M. Structure of tetrathiafulvalenium bis(5,6-dihydro-1,4-dithiin-2,3-dithiolate)aurate(III), (TTF)[Au(DDDT)2]. Acta Crystallogr. Sect. C 1988, 44, 259–262. [Google Scholar] [CrossRef]
- Tenn, N.; Bellec, N.; Jeannin, O.; Piekara-Sady, L.; Auban-Senzier, P.; Iniguez, J.; Canadell, E.; Lorcy, D. A Single-Component Molecular Metal Based on a Thiazole Dithiolate Gold Complex. J. Am. Chem. Soc. 2009, 131, 16961–16967. [Google Scholar] [CrossRef]
- Filatre-Furcate, A.; Roisnel, T.; Fourmigué, M.; Jeannin, O.; Bellec, N.; Auban-Senzier, P.; Lorcy, D. Subtle Steric Differences Impact the Structural and Conducting Properties of Radical Gold Bis(dithiolene) Complexes. Chem. Eur. J. 2017, 23, 16004–16013. [Google Scholar] [CrossRef]
- Filatre-Furcate, A.; Bellec, N.; Jeannin, O.; Auban-Senzier, P.; Fourmigué, M.; Íñiguez, J.; Canadell, E.; Brière, B.; Lorcy, D. Single-Component Conductors: A Sturdy Electronic Structure Generated by Bulky Substituents. Inorg. Chem. 2016, 55, 6036–6046. [Google Scholar] [CrossRef]
- Le Gal, Y.; Roisnel, T.; Auban-Senzier, P.; Guizouarn, T.; Lorcy, D. Hydrogen-Bonding Interactions in a Single-Component Molecular Conductor: A Hydroxyethyl-Substituted Radical Gold Dithiolene. Inorg. Chem. 2014, 53, 8755–8761. [Google Scholar] [CrossRef] [PubMed]
- Hachem, H.; Jeannin, O.; Fourmigué, M.; Barrière, F.; Lorcy, D. Halogen bonded metal bis(dithiolene) 2D frameworks. CrystEngComm 2020, 22, 3579–3587. [Google Scholar] [CrossRef]
- Hachem, H.; Bellec, N.; Fourmigué, M.; Lorcy, D. Hydrogen bonding interactions in single component molecular conductors based on metal (Ni, Au) bis(dithiolene) complexes. Dalton Trans. 2020, 49, 6056–6064. [Google Scholar] [CrossRef] [PubMed]
- Higashino, T.; Jeannin, O.; Kawamoto, T.; Lorcy, D.; Mori, T.; Fourmigué, M. A Single-Component Conductor Based on a Radical Gold Dithiolene Complex with Alkyl-Substituted Thiophene-2,3-dithiolene Ligand. Inorg. Chem. 2015, 54, 9908–9913. [Google Scholar] [CrossRef]
- Rindorf, G.; Thorup, N.; Bjørnholm, T.; Bechgaard, K. Structure of bis(benzene-1,2-dithiolato)gold(IV). Acta Crystallogr. Sec. C 1990, 46, 1437–1439. [Google Scholar] [CrossRef]
- Yzambart, G.; Bellec, N.; Nasser, G.; Jeannin, O.; Roisnel, T.; Fourmigué, M.; Auban-Senzier, P.; Íñiguez, J.; Canadell, E.; Lorcy, D. Anisotropic Chemical Pressure Effects in Single-Component Molecular Metals Based on Radical Dithiolene and Diselenolene Gold Complexes. J. Am. Chem. Soc. 2012, 134, 17138–17148. [Google Scholar] [CrossRef]
- Dautel, O.J.; Fourmigué, M.; Canadell, E.; Auban-Senzier, P. Fluorine Segregation Controls the Solid-State Organization and Electronic Properties of Ni and Au Dithiolene Complexes: Stabilization of a Conducting Single-Component Gold Dithiolene Complex. Adv. Funct. Mater. 2002, 12, 693–698. [Google Scholar] [CrossRef]
- Silva, R.A.L.; Vieira, B.J.C.; Andrade, M.M.A.; Santos, I.C.; Rabaça, S.; Lopes, E.B.; Coutinho, J.T.; Pereira, L.C.J.; Almeida, M.; Belo, D. Gold and Nickel Extended Thiophenic-TTF bisdithiolene Complexes. Molecules 2018, 23, 424. [Google Scholar] [CrossRef]
- Takahashi, M.; Robertson, N.; Kobayashi, A.; Becker, H.; Friend, R.H.; Underhill, A.E. Synthesis, structure and properties of new dithiolene complexes containing a 1,3,5-trithiepin ring. J. Mater. Chem. 1998, 8, 319–324. [Google Scholar] [CrossRef]
- Sasa, M.; Fujiwara, E.; Kobayashi, A.; Ishibashi, S.; Terakura, K.; Okano, Y.; Fujiwara, H.; Kobayashi, H. Crystal structures and physical properties of single-component molecular conductors consisting of nickel and gold complexes with (trifluoromethyl)tetrathiafulvalenedithiolate ligands. J. Mater. Chem. 2005, 15, 155–163. [Google Scholar] [CrossRef]
- Kobayashi, A.; Zhou, B.; Kobayashi, H. Development of metallic crystals composed of single-component molecules. J. Mater. Chem. 2005, 15, 3449–3451. [Google Scholar] [CrossRef]
- Zhou, B.; Shimamura, M.; Fujiwara, E.; Kobayashi, A.; Higashi, T.; Nishibori, E.; Sakata, M.; Cui, H.B.; Takahashi, K.; Kobayashi, H. Magnetic Transitions of Single-Component Molecular Metal [Au(tmdt)2] and Its Alloy Systems. J. Am. Chem. Soc. 2006, 128, 3872–3873. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, W.; Fujiwara, E.; Kobayashi, A.; Fujishiro, Y.; Nishibori, E.; Takata, M.; Sakata, M.; Fujiwara, H.; Kobayashi, H. Highly Conducting Crystals Based on Single-Component Gold Complexes with Extended-TTF Dithiolate Ligands. J. Am. Chem. Soc. 2003, 125, 1486. [Google Scholar] [CrossRef] [PubMed]
- Zhou, B.; Yajima, H.; Idobata, Y.; Kobayashi, A.; Kobayashi, T.; Nishibori, E.; Sawa, H.; Kobayashi, H. Single-component Layered Molecular Conductor, [Au(ptdt)2]. Chem. Lett. 2012, 41, 154–156. [Google Scholar] [CrossRef]
- Filatre-Furcate, A.; Bellec, N.; Jeannin, O.; Auban-Senzier, P.; Fourmigué, M.; Vacher, A.; Lorcy, D. Radical or Not Radical: Compared Structures of Metal (M = Ni, Au) Bis-Dithiolene Complexes with a Thiazole Backbone. Inorg. Chem. 2014, 53, 8681–8690. [Google Scholar] [CrossRef]
- Mebrouk, K.; Kaddour, W.; Auban-Senzier, P.; Pasquier, C.; Jeannin, O.; Camerel, F.; Fourmigué, M. Molecular Alloys of Neutral Nickel/Gold Dithiolene Complexes in Single-Component Semiconductors. Inorg. Chem. 2015, 54, 7454–7460. [Google Scholar] [CrossRef]
- Schiødt, N.C.; Bjørnholm, T.; Bechgaard, K.; Neumeier, J.J.; Allgeier, C.; Jacobsen, C.S.; Thorup, N. Structural, electrical, magnetic, and optical properties of bis-benzene-1,2-dithiolate-Au(IV) crystals. Phys. Rev. B 1996, 53, 1773–1778. [Google Scholar] [CrossRef]
- Nunes, J.P.M.; Figueira, M.J.; Belo, D.; Santos, I.C.; Ribeiro, B.; Lopes, E.B.; Henriques, R.T.; Vidal-Gancedo, J.; Veciana, J.; Rovira, C.; et al. Transition metal bisdithiolene complexes based on extended ligands with fused terathiafulvalene and thiophene moieties: New single-component molecular metals. Chem Eur. J. 2007, 13, 9841–9849. [Google Scholar] [CrossRef]
- Kobayashi, H.; Kobayashi, A.; Sasaki, Y.; Saito, G.; Inokuchi, H. The Crystal and Molecular Structures of Bis(ethylenedithio)tetrathiafulvalene. Bull. Chem. Soc. Jpn. 1986, 59, 301–302. [Google Scholar] [CrossRef]
- Perochon, R.; Davidson, P.; Rouzière, S.; Camerel, F.; Piekara-Sady, L.; Guizouarn, T.; Fourmigué, M. Probing magnetic interactions in columnar phases of a paramagnetic gold dithiolene complex. J. Mater. Chem. 2011, 21, 1416–1422. [Google Scholar] [CrossRef]
- Cui, H.-B.; Kobayashi, H.; Ishibashi, S.; Sasa, M.; Iwase, F.; Kato, R.; Kobayashi, A. A Single-Component Molecular Superconductor. J. Am. Chem. Soc. 2014, 136, 7619–7622. [Google Scholar] [CrossRef] [PubMed]
- Alvarez, S.; Vicente, R.; Hoffmann, R. Dimerization and stacking in transition-metal bisdithiolenes and tetrathiolates. J. Am. Chem. Soc. 1985, 107, 6253–6277. [Google Scholar] [CrossRef]
- Espa, D.; Pilia, L.; Attar, S.; Serpe, A.; Deplano, P. Molecular engineering of heteroleptic metal-dithiolene complexes with optimized second-order NLO response. Inorg. Chim. Acta 2018, 470, 295–302. [Google Scholar] [CrossRef]
- Belo, D.; Almeida, M. Transition metal complexes based on thiophene-dithiolene ligands. Coord. Chem. Rev. 2010, 254, 1479–1492. [Google Scholar] [CrossRef]
- Valade, L.; Tanaka, H. Molecular Materials; Bruce, D.W., O’Hare, D., Walton, R.I., Eds.; John Wiley & Sons: Chichester, UK, 2010; Chapter 4; pp. 211–280. [Google Scholar] [CrossRef]
- Eid, S.; Fourmigué, M.; Roisnel, T.; Lorcy, D. Influence of the thiazole backbone on the structural, redox, and optical properties of dithiolene and diselenolene complexes. Inorg. Chem. 2007, 46, 10647–10654. [Google Scholar] [CrossRef]
- Buron-Le Cointe, M.; Collet, E.; Toudic, B.; Czarnecki, P.; Cailleau, H. Back to the structural and dynamical properties of neutral-ionic phase transitions. Crystals 2017, 7, 285. [Google Scholar] [CrossRef]
- Morimoto, T.; Miyamoto, T.; Okamoto, H. Ultrafast electron and molecular dynamics in photoinduced and electric-field-induced neutral-ionic transitions. Crystals 2017, 7, 132. [Google Scholar] [CrossRef]
- Horiuchi, S.; Kobayashi, K.; Kumai, R.; Ishibashi, S. Ionic versus electronic ferroelectricity in donor-acceptor molecular sequences. Chem. Lett. 2014, 43, 26–35. [Google Scholar] [CrossRef]
- Polman, A.; Kociak, M.; de Abajo, F.J.G. Electron-beam spectroscopy for nanophotonics. Nat. Mat. 2019, 18, 1158–1171. [Google Scholar] [CrossRef]
- Wang, L.; Allodi, M.A.; Engel, G.S. Quantum coherences reveal excited-state dynamics in biophysical systems. Nat. Rev. Chem. 2019, 3, 477–490. [Google Scholar] [CrossRef]
- Zhu, T.; Snaider, J.M.; Yuan, L.; Huang, L. Ultrafast dynamic microscopy of carrier and exciton transport. Ann. Rev. Phys. Chem. 2019, 70, 219–244. [Google Scholar] [CrossRef] [PubMed]
- Rossbach, J.; Schneider, J.R.; Wurth, W. 10 years of pioneering X-ray science at the free-electron laser FLASH at DESY. Phys. Rep. 2019, 808, 1–74. [Google Scholar] [CrossRef]
- Zhao, D.; Chia, E.E.M. Free carrier, exciton, and phonon dynamics in lead-halide perovskites studied with ultrafast terahertz spectroscopy. Adv. Opt. Mat. 2019, 1900783. [Google Scholar] [CrossRef]
- Xu, J.-Y.; Tong, X.; Yu, P.; Wenya, G.E.; McGrath, T.; Fong, M.J.; Wu, J.; Wang, Z.M. Ultrafast dynamics of charge transfer and photochemical reactions in solar energy conversion. Adv. Sci. 2018, 5, 1800221. [Google Scholar] [CrossRef]
- Chergui, M. Ultrafast photophysics and photochemistry of iron hexacyanides in solution: Infrared to X-ray spectroscopic studies. Coord. Chem. Rev. 2018, 372, 52–65. [Google Scholar] [CrossRef]
- Kobayashi, T. Development of ultrashort pulse lasers for ultrafast spectroscopy. Photonics 2018, 5, 19. [Google Scholar] [CrossRef]
- Fang, C.; Tang, L.; Oscar, B.G.; Chen, C. Capturing structural snapshots during photochemical reactions with ultrafast Raman spectroscopy: From materials transformation to biosensor responses. J. Phys. Chem. Lett. 2018, 9, 3253–3263. [Google Scholar] [CrossRef]
- Kraus, P.M.; Zürch, M.; Cushing, S.K.; Neumark, D.M.; Leone, S.R. Ultrafast X-ray spectroscopic revolution in chemical dynamics. Nat. Rev. Chem. 2018, 2, 82–94. [Google Scholar] [CrossRef]
- Kraus, P.M.; Wörner, H.J. Perspectives of attosecond spectroscopy for the understanding of fundamental electron correlations. Angew. Chem. Int. Ed. 2018, 57, 5228–5247. [Google Scholar] [CrossRef]
- Jiang, L.; Wang, A.-D.; Li, B.; Cui, T.-H.; Lu, Y.-F. Electrons dynamics control by shaping femtosecond laser pulses in micro/nanofabrication: Modeling, method, measurement and application. Light Sci. Appl. 2018, 7, 17134. [Google Scholar] [CrossRef]
- Oliver, T.A.A. Recent advances in multidimensional ultrafast spectroscopy. R. Soc. Open Sci. 2018, 5, 171425. [Google Scholar] [CrossRef] [PubMed]
- Young, L.; Ueda, K.; Gühr, M.; Bucksbaum, P.H.; Simon, M.; Mukamel, S.; Rohringer, N.; Prince, K.C.; Masciovecchio, C.; Meyer, M.; et al. Roadmap of ultrafast X-ray atomic and molecular physics. J. Phys. B At. Mol. Opt. Phys. 2018, 51, 032003. [Google Scholar] [CrossRef]
- Ichiryu, K.; Naito, T. Steady-state observation of interacting photochemical species in photoexcited solid states. Chem. Lett. 2020, 49, 1038–1042. [Google Scholar] [CrossRef]
- Guo, W.-X.; Wang, Y.-Y.; Hu, X.-L.; Yue, Q.; Gao, E.-Q. Homochiral helical coordination architectures built from biphenyl-based amino acid derivatives: Structural diversity tuned by varying conformation and configuration of N-donor ligands, sensing of acidic amino acids, and photoluminescence properties. Cryst. Growth Des. 2020, 20, 5072–5085. [Google Scholar] [CrossRef]
- Cho, Y.J.; Jeon, S.K.; Chin, B.D.; Yu, E.; Lee, J.Y. The Design of Dual Emitting Cores for Green Thermally Activated Delayed Fluorescent Materials. Angew. Chem. Int. Ed. 2015, 54, 5201–5204. [Google Scholar] [CrossRef]
- Hoffmann, S.T.; Schroegel, P.; Rothmann, M.; Albuquerque, R.; Strohriegl, P.; Koehler, A. Triplet excimer emission in a series of 4,4’-Bis(N-carbazolyl)-2,2’-biphenyl derivatives. J. Phys. Chem. B 2011, 115, 414–421. [Google Scholar] [CrossRef]



| L 2 | Formal Charge (n) | Counter Ion 3 | Stoichiometry (Cation: Anion) | Structural Feature 4 | Solid State Properties 5 | References |
|---|---|---|---|---|---|---|
| mnt | −1 | Et4N+ | 1:1 | - | Dia | [26] |
| mnt | −1 | NMP+ | 1:1 | Mixed stacking | - | [46] |
| dmit | −1 | nBu4N+ | 1:1 | Related to 1 | L 6 | [34] |
| dmit | −0.22 | nBu4N+ | 0.22:1 | - | Sem | [34] |
| dmit | - | TTF | 1:1 | - | Sem | [34] |
| dmit | - | Fe(cp)2 | 0.25:1 | - | Sem | [34] |
| dmit | - | TTF | 3:2 | - | Sem * | [35,47] |
| dmit | - | TMTSF | 3:2 | - | Sem * | [35,47] |
| dmit | - | ET | 1:1 | - | Sem * | [35,47] |
| dmit | −0.5 | Et4N+ | 1:2 (α) | - | Met | [36] |
| dmit | −0.5 | Et4N+ | 1:2 (β) | 2D | Sem | [36] |
| dmit | −0.5 | nBu4N+ | 1:2 (α) | - | H 6 | [36] |
| dmit | - | nBu4N+ | unknown (β) | - | Met | [36] |
| dmit | - | nBuEt3N+ | - | - | Met (~220 K) | [36] |
| dmit | - | nBu2Et2N+ | - | - | Met (~120 K) | [36] |
| dmit | - | nBu3EtN+ | - | - | Sem | [36] |
| dmit | −0.5 | Me4N+ | 1:2 | - | Sem | [36] |
| dmit | - | Me3S+ | unknown (α) | - | Sem | [36] |
| dmit | - | Me3S+ | unknown (β) | - | Met (~90 K) | [36] |
| dmit | - | Cat+ | - | - | Met (~100 K) | [36] |
| dmit | - | nBu3S+ | - | - | Met | [36] |
| dmit | −0.5 | Li+ | 1:2 | - | Met (~160 K) | [37] |
| dmit | −0.5 | Na+ | 1:2 | - | Met (~83 K) | [37] |
| dmit | −0.5 | K+ | 1:2 | - | Met (~60 K) | [37] |
| dmit | −0.5 | Me4N+ | 1:2 | Disordered anions | Sem | [38] |
| dddt | - | BF4− | - | - | H 6 | [41] |
| dddt | - | IBr2− | - | - | H 6 | [41] |
| dddt | - | SnCl6x− | - | - | Met (~150 K) | [41] |
| dddt | - | TTF | 1:1 | Disordered ethylene-group in anions | - | [48] |
| Me-thiazdt | −1 | Et4N+ | 1:1 | Disordered anions | - | [20] |
| Et-thiazdt 7 | −1 | Et4N+ | 1:1 | - | - | [49] |
| nPr-thiazdt | −1 | Ph4P+ | 1:1 | cis/trans8 | - | [50] |
| iPr-thiazdt | −1 | Ph4P+ | 1:1 | trans | - | [51] |
| cPr-thiazdt | −1 | Et4N+ | 1:1 | trans | - | [50] |
| EtOH-thiazdt | −1 | Et4N+ | 1:1 | cis/trans | - | [52] |
| NMe2-thiazdt | −1 | Ph4P+ | 1:1 | trans | - | [50] |
| I-tzdt | −1 | nBu4N+ | 1:1 | cis/trans9 | Dia | [53] |
| HOEtS-tzdt | −1 | Ph4P+ | 1:1 | trans | - | [54] |
| dm-dddt | −1 | nBu4N+ | 1:1 | Enantiopure separated anions | - | [44] |
| α-EtMetpdt | −1 | Ph4P+ | 1:1 | trans | - | [55] |
| α-Me2tpdt | −1 | Ph4P+ | 1:1 | Disordered anions 10 | - | [55] |
| bdt | −1 | nBu4N+ | 1:1 | - | - | [56] |
| S4(=O)2 11 | −1 | Ph4P+ | 1:1 | Separated anions | - | [57] |
| Se4(=S)2 | −1 | Et4N+ | 1:1 | Separated anions | - | [57] |
| Se4(=O)2 | −1 | Ph4P+ 12 | 1:1 | Separated anions | - | [57] |
| dtpdt | −1 | nBu4N+ | 1:1 | Zigzag chains | Dia | [40] |
| α-tpdt | −1 | nBu4N+ | 1:1 | - | Dia | [40] |
| tpdt | −1 | nBu4N+ | 1:1 | 2D | Dia | [40] |
| tpdt | ~−0.5 | nBu4N+ | ~1:2 | - | Curie | [40] |
| F2pdt | −1 | nBu4N+ | 1:1 | Separated anions | - | [58] |
| α-mtdt | −1 | nBu4N+ | 1:1 | cis-trans disorder | Dia | [59] |
| α-tbtdt | −2 | nBu4N+ | 2:1 | Dinuclear Au(I) | - | [59] |
| ttdt | −1 | nBu4N+ | 1:1 | - | - | [60] |
| ttdt | - | TTF | 1:1 | Separated dimers of cations and anions | - | [60] |
| L 1 | Structural Feature 2 | Conducting Properties 3 | Magnetic Properties 4 | References |
|---|---|---|---|---|
| dddt | Figure 5a | L | Dia | [43] |
| hfdt | Dimerized 2D | Sem | Almost Dia | [61] |
| tmdt | 3D | H * | AF (100–110 K) | [62,63,64] |
| dmdt | - | Met (~50 K) * | Pauli (~50 K) | [64] |
| ptdt | 2D | Met * | Pauli (~80 K) | [65] |
| Me-thiazdt | 3D | Met | Pauli | [20] |
| Et-thiazdt 5 | 2D | Sem | Pauli | [49,66] |
| nPr-thiazdt | trans, Uniform 1D | Sem | - | [50] |
| cPr-thiazdt | trans, Uniform 1D | Sem | - | [50] |
| iPr-thiazdt | Crisscross structure | Sem | Pauli | [51] |
| EtOH-thiazdt | 2D | Sem | CW | [52] |
| NMe2-thiazdt | trans, Crisscross structure | Sem | - | [50] |
| HOEtS-tzdt | Uniform 1D | Mott Ins | - | [54] |
| dm-dddt | Asymmetry in ligands | Sem | - | [44] |
| OC4 | Dimerized 1D | Sem | ST | [67] |
| α-EtMetpdt | Uniform 1D | Sem | - | [55] |
| α-Me2tpdt | - | Sem * | - | [55] |
| bdt | 1D with superstructure | Sem | Complicated behavior | [56,68] |
| S4(=O)2 6 | 1D | Sem | BF | [57] |
| Se4(=S)2 | Q2D | Sem | Pauli | [57] |
| Se4(=O)2 | Q2D | Sem | Pauli | [57] |
| F2pdt | Uniform 1D | Sem | BF | [58] |
| α-tpdt | - | Met (~15 K) * | Pauli | [40] |
| dtpdt | - | L * | Curie | [40] |
| α-tdt | - | Almost Met * | Large χ 7 | [59,69] |
| α-mtdt | - | Sem * | Pauli | [59] |
| dtdt | - | Almost Met * | Large χ 7 | [59,69] |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naito, T. Prototype Material for New Strategy of Photon Energy Storage. Inorganics 2020, 8, 53. https://doi.org/10.3390/inorganics8100053
Naito T. Prototype Material for New Strategy of Photon Energy Storage. Inorganics. 2020; 8(10):53. https://doi.org/10.3390/inorganics8100053
Chicago/Turabian StyleNaito, Toshio. 2020. "Prototype Material for New Strategy of Photon Energy Storage" Inorganics 8, no. 10: 53. https://doi.org/10.3390/inorganics8100053
APA StyleNaito, T. (2020). Prototype Material for New Strategy of Photon Energy Storage. Inorganics, 8(10), 53. https://doi.org/10.3390/inorganics8100053