Assessment of Double-Hybrid Density Functional Theory for Magnetic Exchange Coupling in Manganese Complexes
Abstract
1. Introduction
2. Test Set of Dinuclear Manganese Complexes
3. Selection of Functionals
4. Results and Discussion
4.1. Conventional Density Functionals
4.2. Double-Hybrid Density Functionals
4.3. Energetic Contributions to Exchange Coupling from Double-Hybrid Density Functionals
5. Computational Methods
6. Conclusions
Acknowledgments
Conflicts of Interest
References
- Mukhopadhyay, S.; Mandal, S.K.; Bhaduri, S.; Armstrong, W.H. Manganese Clusters with Relevance to Photosystem II. Chem. Rev. 2004, 104, 3981–4026. [Google Scholar] [CrossRef] [PubMed]
- Wu, A.J.; Penner-Hahn, J.E.; Pecoraro, V.L. Structural, Spectroscopic, and Reactivity Models for the Manganese Catalases. Chem. Rev. 2004, 104, 903–938. [Google Scholar] [CrossRef]
- Thompson, L.K.; Waldmann, O.; Xu, Z. Polynuclear Manganese Grids and Clusters—A Magnetic Perspective. Coord. Chem. Rev. 2005, 249, 2677–2690. [Google Scholar] [CrossRef]
- Gatteschi, D.; Sessoli, R.; Villain, J. Molecular Nanomagnets; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Boer, J.W.D.; Browne, W.R.; Feringa, B.L.; Hage, R. Carboxylate-Bridged Dinuclear Manganese Systems—From Catalases to Oxidation Catalysis. C. R. Chim. 2007, 10, 341–354. [Google Scholar] [CrossRef]
- Mullins, C.S.; Pecoraro, V.L. Reflections on Small Molecule Manganese Models that Seek to Mimic Photosynthetic Water Oxidation Chemistry. Coord. Chem. Rev. 2008, 252, 416–443. [Google Scholar] [CrossRef]
- Tsui, E.Y.; Kanady, J.S.; Agapie, T. Synthetic Cluster Models of Biological and Heterogeneous Manganese Catalysts for O2 Evolution. Inorg. Chem. 2013, 52, 13833–13848. [Google Scholar] [CrossRef] [PubMed]
- Hirahara, M.; Shoji, A.; Yagi, M. Artificial Manganese Center Models for Photosynthetic Oxygen Evolution in Photosystem II. Eur. J. Inorg. Chem. 2014, 2014, 595–606. [Google Scholar] [CrossRef]
- Yang, C.-I.; Zhang, Z.-Z.; Lin, S.-B. A Review of Manganese-Based Molecular Magnets and Supramolecular Architectures from Phenolic Oximes. Coord. Chem. Rev. 2015, 289–290, 289–314. [Google Scholar] [CrossRef]
- Young, K.J.; Brennan, B.J.; Tagore, R.; Brudvig, G.W. Photosynthetic Water Oxidation: Insights from Manganese Model Chemistry. Acc. Chem. Res. 2015, 48, 567–574. [Google Scholar] [CrossRef]
- Gerey, B.; Gouré, E.; Fortage, J.; Pécaut, J.; Collomb, M.-N. Manganese-calcium/strontium heterometallic compounds and their relevance for the oxygen-evolving center of photosystem II. Coord. Chem. Rev. 2016, 319, 1–24. [Google Scholar] [CrossRef]
- Krewald, V.; Pantazis, D.A. Understanding and tuning the properties of redox-accumulating manganese helicates. Dalton Trans. 2016, 45, 18900–18908. [Google Scholar] [CrossRef] [PubMed]
- Najafpour, M.M.; Renger, G.; Hołyńska, M.; Moghaddam, A.N.; Aro, E.-M.; Carpentier, R.; Nishihara, H.; Eaton-Rye, J.J.; Shen, J.-R.; Allakhverdiev, S.I. Manganese Compounds as Water-Oxidizing Catalysts: From the Natural Water-Oxidizing Complex to Nanosized Manganese Oxide Structures. Chem. Rev. 2016, 116, 2886–2936. [Google Scholar] [CrossRef]
- Paul, S.; Neese, F.; Pantazis, D.A. Structural models of the biological oxygen-evolving complex: Achievements, insights, and challenges for biomimicry. Green Chem. 2017, 19, 2309–2325. [Google Scholar] [CrossRef]
- De Graaf, C.; Broer, R. Magnetic Interactions in Molecules and Solids; Springer: Heidelberg, Germany, 2016; p. 246. [Google Scholar]
- Malrieu, J.P.; Caballol, R.; Calzado, C.J.; de Graaf, C.; Guihéry, N. Magnetic Interactions in Molecules and Highly Correlated Materials: Physical Content, Analytical Derivation, and Rigorous Extraction of Magnetic Hamiltonians. Chem. Rev. 2014, 114, 429–492. [Google Scholar] [CrossRef] [PubMed]
- Swart, M.; Costas, M. Spin States in Biochemistry and Inorganic Chemistry; John Wiley & Sons: Chichester, UK, 2016; p. 466. [Google Scholar]
- Krewald, V.; Pantazis, D.A. Applications of the Density Matrix Renormalization Group to Exchange-Coupled Transition Metal Systems. In Transition Metals in Coordination Environments: Computational Chemistry and Catalysis Viewpoints; Broclawik, E., Borowski, T., Radoń, M., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 91–120. [Google Scholar]
- Harris, T.V.; Kurashige, Y.; Yanai, T.; Morokuma, K. Ab initio Density Matrix Renormalization Group Study of Magnetic Coupling in Dinuclear Iron and Chromium Complexes. J. Chem. Phys. 2014, 140, 054303. [Google Scholar] [CrossRef] [PubMed]
- Roemelt, M.; Krewald, V.; Pantazis, D.A. Exchange Coupling Interactions from the Density Matrix Renormalization Group and N-Electron Valence Perturbation Theory: Application to a Biomimetic Mixed-Valence Manganese Complex. J. Chem. Theory Comput. 2018, 14, 166–179. [Google Scholar] [CrossRef] [PubMed]
- Kawakami, T.; Miyagawa, K.; Sharma, S.; Saito, T.; Shoji, M.; Yamada, S.; Yamanaka, S.; Okumura, M.; Nakajima, T.; Yamaguchi, K. UNO DMRG CAS CI Calculations of Binuclear Manganese Complex Mn(IV)2O2(NHCHCO2)4: Scope and Applicability of Heisenberg Model. J. Comput. Chem. 2018, 40, 333–341. [Google Scholar] [CrossRef] [PubMed]
- Roemelt, M.; Pantazis, D.A. Multireference Approaches to Spin-State Energetics of Transition Metal Complexes Utilizing the Density Matrix Renormalization Group. Adv. Theory Simul. 2019, 1800201. [Google Scholar] [CrossRef]
- Noodleman, L. Valence Bond Description of Anti-ferromagnetic Coupling in Transition-Metal Dimers. J. Chem. Phys. 1981, 74, 5737–5743. [Google Scholar] [CrossRef]
- Noodleman, L.; Davidson, E.R. Ligand Spin Polarization and Antiferromagnetic Coupling in Transition-Metal Dimers. Chem. Phys. 1986, 109, 131–143. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Takahara, Y.; Fueno, T. Ab-Initio Molecular Orbital Studies of Structure and Reactivity of Transition Metal-Oxo Compounds. In Applied Quantum Chemistry; Smith, V.H., Jr., Scheafer, H.F., III, Morokuma, K., Eds.; D. Reidel: Boston, MA, USA, 1986; pp. 155–184. [Google Scholar]
- Yamanaka, S.; Kawakami, T.; Nagao, H.; Yamaguchi, K. Effective Exchange Integrals for Open-Shell Species by Density Functional Methods. Chem. Phys. Lett. 1994, 231, 25–33. [Google Scholar] [CrossRef]
- Bencini, A.; Totti, F.; Daul, C.A.; Doclo, K.; Fantucci, P.; Barone, V. Density Functional Calculations of Magnetic Exchange Interactions in Polynuclear Transition Metal Complexes. Inorg. Chem. 1997, 36, 5022–5030. [Google Scholar] [CrossRef]
- Ruiz, E.; Rodriguez-Fortea, A.; Cano, J.; Alvarez, S.; Alemany, P. About the Calculation of Exchange Coupling Constants in Polynuclear Transition Metal Complexes. J. Comput. Chem. 2003, 24, 982–989. [Google Scholar] [CrossRef]
- Ciofini, I.; Daul, C.A. DFT Calculations of Molecular Magnetic Properties of Coordination Compounds. Coord. Chem. Rev. 2003, 238–239, 187–209. [Google Scholar] [CrossRef]
- Neese, F. Prediction of Molecular Properties and Molecular Spectroscopy with Density Functional Theory: From Fundamental Theory to Exchange-Coupling. Coord. Chem. Rev. 2009, 253, 526–563. [Google Scholar] [CrossRef]
- Bencini, A.; Totti, F. A Few Comments on the Application of Density Functional Theory to the Calculation of the Magnetic Structure of Oligo-Nuclear Transition Metal Clusters. J. Chem. Theory Comput. 2009, 5, 144–154. [Google Scholar] [CrossRef]
- Rudberg, E.; Sałek, P.; Rinkevicius, Z.; Ågren, H. Heisenberg Exchange in Dinuclear Manganese Complexes: A Density Functional Theory Study. J. Chem. Theory Comput. 2006, 2, 981–989. [Google Scholar] [CrossRef]
- Comba, P.; Hausberg, S.; Martin, B. Calculation of Exchange Coupling Constants of Transition Metal Complexes with DFT. J. Phys. Chem. A 2009, 113, 6751–6755. [Google Scholar] [CrossRef]
- Orio, M.; Pantazis, D.A.; Petrenko, T.; Neese, F. Magnetic and Spectroscopic Properties of Mixed Valence Manganese(III,IV) Dimers: A Systematic Study Using Broken Symmetry Density Functional Theory. Inorg. Chem. 2009, 48, 7251–7260. [Google Scholar] [CrossRef]
- Schinzel, S.; Kaupp, M. Validation of Broken-Symmetry Density Functional Methods for the Calculation of Electron Paramagnetic Resonance Parameters of Dinuclear Mixed-Valence MnIVMnIII Complexes. Can. J. Chem. 2009, 87, 1521–1539. [Google Scholar] [CrossRef]
- Pantazis, D.A.; Orio, M.; Petrenko, T.; Zein, S.; Bill, E.; Lubitz, W.; Messinger, J.; Neese, F. A New Quantum Chemical Approach to the Magnetic Properties of Oligonuclear Transition-Metal Complexes: Application to a Model for the Tetranuclear Manganese Cluster of Photosystem II. Chem. Eur. J. 2009, 15, 5108–5123. [Google Scholar] [CrossRef] [PubMed]
- Orio, M.; Pantazis, D.A.; Neese, F. Density Functional Theory. Photosynth. Res. 2009, 102, 443–453. [Google Scholar] [CrossRef] [PubMed]
- Baffert, C.; Orio, M.; Pantazis, D.A.; Duboc, C.; Blackman, A.G.; Blondin, G.; Neese, F.; Deronzier, A.; Collomb, M.-N. Trinuclear Terpyridine Frustrated Spin System with a MnIV3O4 Core: Synthesis, Physical Characterization, and Quantum Chemical Modeling of Its Magnetic Properties. Inorg. Chem. 2009, 48, 10281–10288. [Google Scholar] [CrossRef] [PubMed]
- Pantazis, D.A.; Krewald, V.; Orio, M.; Neese, F. Theoretical magnetochemistry of dinuclear manganese complexes: Broken symmetry density functional theory investigation on the influence of bridging motifs on structure and magnetism. Dalton Trans. 2010, 39, 4959–4967. [Google Scholar] [CrossRef] [PubMed]
- Schraut, J.; Arbuznikov, A.V.; Schinzel, S.; Kaupp, M. Computation of Hyperfine Tensors for Dinuclear MnIIIMnIV Complexes by Broken-Symmetry Approaches: Anisotropy Transfer Induced by Local Zero-Field Splitting. ChemPhysChem 2011, 12, 3170–3179. [Google Scholar] [CrossRef] [PubMed]
- Bovi, D.; Guidoni, L. Magnetic Coupling Constants and Vibrational Frequencies by Extended Broken Symmetry Approach with Hybrid Functionals. J. Chem. Phys. 2012, 137, 114107. [Google Scholar] [CrossRef]
- Krewald, V.; Neese, F.; Pantazis, D.A. On the Magnetic and Spectroscopic Properties of High-Valent Mn3CaO4 Cubanes as Structural Units of Natural and Artificial Water Oxidizing Catalysts. J. Am. Chem. Soc. 2013, 135, 5726–5739. [Google Scholar] [CrossRef]
- Krewald, V.; Retegan, M.; Cox, N.; Messinger, J.; Lubitz, W.; DeBeer, S.; Neese, F.; Pantazis, D.A. Metal Oxidation States in Biological Water Splitting. Chem. Sci. 2015, 6, 1676–1695. [Google Scholar] [CrossRef]
- Becke, A.D. Density-Functional Thermochemistry. III. The Role Of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula Into a Functional of the Electron-Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Staroverov, V.N.; Scuseria, G.E.; Tao, J.; Perdew, J.P. Comparative Assessment of a New Nonempirical Density Functional: Molecules and Hydrogen-Bonded Complexes. J. Chem. Phys. 2003, 119, 12129–12137. [Google Scholar] [CrossRef]
- Bühl, M.; Kabrede, H. Geometries of Transition-Metal Complexes from Density-Functional Theory. J. Chem. Theory Comput. 2006, 2, 1282–1290. [Google Scholar] [CrossRef] [PubMed]
- Kossmann, S.; Kirchner, B.; Neese, F. Performance of Modern Density Functional Theory for the Prediction of Hyperfine Structure: Meta-GGA and Double Hybrid Functionals. Mol. Phys. 2007, 105, 2049–2071. [Google Scholar] [CrossRef]
- Jensen, K.P. Bioinorganic Chemistry Modeled with the TPSSh Density Functional. Inorg. Chem. 2008, 47, 10357–10365. [Google Scholar] [CrossRef] [PubMed]
- Cirera, J.; Via-Nadal, M.; Ruiz, E. Benchmarking Density Functional Methods for Calculation of State Energies of First Row Spin-Crossover Molecules. Inorg. Chem. 2018, 57, 14097–14105. [Google Scholar] [CrossRef] [PubMed]
- Pantazis, D.A. Meeting the Challenge of Magnetic Coupling in a Triply-Bridged Chromium Dimer: Complementary Broken-Symmetry Density Functional Theory and Multireference Density Matrix Renormalization Group Perspectives. J. Chem. Theory Comput. 2019, 15, 938–948. [Google Scholar] [CrossRef] [PubMed]
- Goerigk, L.; Grimme, S. Double-Hybrid Density Functionals. Wires Comput. Mol. Sci. 2014, 4, 576–600. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical hybrid density functional with perturbative second-order correlation. J. Chem. Phys. 2006, 124, 034108. [Google Scholar] [CrossRef]
- Schwabe, T.; Grimme, S. Theoretical thermodynamics for large molecules: Walking the thin line between accuracy and computational cost. Acc. Chem. Res. 2008, 41, 569–579. [Google Scholar] [CrossRef]
- Goerigk, L.; Grimme, S. Efficient and Accurate Double-Hybrid-Meta-GGA Density Functionals—Evaluation with the Extended GMTKN30 Database for General Main Group Thermochemistry, Kinetics, and Noncovalent Interactions. J. Chem. Theory Comput. 2010, 7, 291–309. [Google Scholar] [CrossRef]
- Goerigk, L.; Grimme, S. A thorough benchmark of density functional methods for general main group thermochemistry, kinetics, and noncovalent interactions. Phys. Chem. Chem. Phys. 2011, 13, 6670–6688. [Google Scholar] [CrossRef]
- Goerigk, L.; Hansen, A.; Bauer, C.; Ehrlich, S.; Najibi, A.; Grimme, S. A Look at the Density Functional Theory Zoo with the Advanced GMTKN55 Database for General Main Group Thermochemistry, Kinetics and Noncovalent Interactions. Phys. Chem. Chem. Phys. 2017, 19, 32184–32215. [Google Scholar] [CrossRef]
- Mardirossian, N.; Head-Gordon, M. Thirty Years of Density Functional Theory in Computational Chemistry: An Overview and Extensive Assessment of 200 Density Functionals. Mol. Phys. 2017, 115, 2315–2372. [Google Scholar] [CrossRef]
- Schwabe, T.; Grimme, S. Calculation of Magnetic Couplings with Double-Hybrid Density Functionals. J. Phys. Chem. Lett. 2010, 1, 1201–1204. [Google Scholar] [CrossRef]
- Valero, R.; Costa, R.; de PR Moreira, I.; Truhlar, D.G.; Illas, F. Performance of the M06 family of exchange-correlation functionals for predicting magnetic coupling in organic and inorganic molecules. J. Chem. Phys. 2008, 128, 114103. [Google Scholar] [CrossRef]
- Gupta, T.; Rajeshkumar, T.; Rajaraman, G. Magnetic exchange in {GdIII–radical} complexes: Method assessment, mechanism of coupling and magneto-structural correlations. Phys. Chem. Chem. Phys. 2014, 16, 14568–14577. [Google Scholar] [CrossRef]
- Vogiatzis, K.D.; Klopper, W.; Mavrandonakis, A.; Fink, K. Magnetic properties of paddlewheels and trinuclear clusters with exposed metal sites. ChemPhysChem 2011, 12, 3307–3319. [Google Scholar] [CrossRef]
- Bossek, U.; Hummel, H.; Weyhermüller, T.; Wieghardt, K.; Russell, S.; van der Wolf, L.; Kolb, U. The [Mn2IV(μ-O)(μ-PhBO2)2]2+ Unit: A New Structural Model for Manganese-Containing Metalloproteins. Angew. Chem. Int. Ed. 1996, 35, 1552–1554. [Google Scholar] [CrossRef]
- Ménage, S.; Girerd, J.-J.; Gleizes, A. A [Mn2O(MeCO2)2(H2O)2(bipy)2]2+(bipy = 2,2′-bipyridine) Unit with Accessible Co-ordination Sites. Contribution to the Modelling of the Photosynthetic Oxygen Evolving Centre. J. Chem. Soc. Chem. Commun. 1988, 431–432. [Google Scholar] [CrossRef]
- Bossek, U.; Saher, M.; Weyhermuller, T.; Wieghardt, K. Asymmetric Mixed Valence Manganese Complexes Containing the [Mn(μ-O)2(μ-MeCo2)Mn]2+ Core and their Catalase Reactivity. J. Chem. Soc. Chem. Commun. 1992, 1780–1782. [Google Scholar] [CrossRef]
- Chan, G.K.-L.; Sharma, S. The Density Matrix Renormalization Group in Quantum Chemistry. Annu. Rev. Phys. Chem. 2011, 62, 465–481. [Google Scholar] [CrossRef]
- Pal, S.; Olmstead, M.M.; Armstrong, W.H. Syntheses, Structures, and Properties of [Mn2(μ-O)(2)(μ-O2CCH3)(fac-Bpea)2](ClΟ4)2 and Two Halide-Ligated Dioxo-Bridged Dimers Derived Therefrom—[Mn2(μ-O)2×2(mer-Bpea)2](ClO4)2 (X = F, Cl). Inorg. Chem. 1995, 34, 4708–4715. [Google Scholar] [CrossRef]
- Wieghardt, K.; Bossek, U.; Nuber, B.; Weiss, J.; Bonvoisin, J.; Corbella, M.; Vitols, S.E.; Girerd, J.J. Synthesis, Crystal Structures, Reactivity, and Magnetochemistry of a Series of Binuclear Complexes of Manganese(II), -(III), and -(IV) of Biological Relevance. The Crystal Structure of [L′MnIV(μ-O)3MnIVL′](PF6)2.H2O Containing an Unprecedented Short Mn···Mn distance of 2.296 Å. J. Am. Chem. Soc. 1988, 110, 7398–7411. [Google Scholar]
- Niemann, A.; Bossek, U.; Wieghardt, K.; Butzlaff, C.; Trautwein, A.X.; Nuber, B. A New Structure–Magnetism Relationship for Face-Sharing Transition-Metal Complexes with d3–d3 Electronic Configuration. Angew. Chem. Int. Ed. 1992, 31, 311–313. [Google Scholar] [CrossRef]
- Goerigk, L.; Mehta, N. A Trip to the Density Functional Theory Zoo: Warnings and Recommendations for the User. Aust. J. Chem. 2019. [Google Scholar] [CrossRef]
- Tao, J.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. Climbing the Density Functional Ladder: Nonempirical Meta-Generalized Gradient Approximation Designed for Molecules and Solids. Phys. Rev. Lett. 2003, 91, 146401. [Google Scholar] [CrossRef]
- Sun, J.; Ruzsinszky, A.; Perdew, J.P. Strongly Constrained and Appropriately Normed Semilocal Density Functional. Phys. Rev. Lett. 2015, 115, 036402. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward Reliable Density Functional Methods Without Adjustable Parameters: The PBE0 Model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Karton, A.; Tarnopolsky, A.; Lamère, J.-F.; Schatz, G.C.; Martin, J.M.L. Highly Accurate First-Principles Benchmark Data Sets for the Parametrization and Validation of Density Functional and Other Approximate Methods. Derivation of a Robust, Generally Applicable, Double-Hybrid Functional for Thermochemistry and Thermochemical Kinetics. J. Phys. Chem. A 2008, 112, 12868–12886. [Google Scholar]
- Grimme, S. Improved second-order Moller-Plesset perturbation theory by separate scaling of parallel- and antiparallel-spin pair correlation energies. J. Chem. Phys. 2003, 118, 9095–9102. [Google Scholar] [CrossRef]
- Kozuch, S.; Gruzman, D.; Martin, J.M.L. DSD-BLYP: A General Purpose Double Hybrid Density Functional Including Spin Component Scaling and Dispersion Correction. J. Phys. Chem. C 2010, 114, 20801–20808. [Google Scholar] [CrossRef]
- Kozuch, S.; Martin, J.M.L. DSD-PBEP86: In search of the best double-hybrid DFT with spin-component scaled MP2 and dispersion corrections. Phys. Chem. Chem. Phys. 2011, 13, 20104–20107. [Google Scholar] [CrossRef]
- Kozuch, S.; Martin, J.M.L. Spin-component-scaled double hybrids: An extensive search for the best fifth-rung functionals blending DFT and perturbation theory. J. Comput. Chem. 2013, 34, 2327–2344. [Google Scholar] [CrossRef]
- Jung, Y.; Lochan, R.C.; Dutoi, A.D.; Head-Gordon, M. Scaled opposite-spin second order Møller–Plesset correlation energy: An economical electronic structure method. J. Chem. Phys. 2004, 121, 9793–9802. [Google Scholar] [CrossRef]
- Paul, S.; Cox, N.; Pantazis, D.A. What Can We Learn from a Biomimetic Model of Nature’s Oxygen-Evolving Complex? Inorg. Chem. 2017, 56, 3875–3888. [Google Scholar] [CrossRef]
- Pantazis, D.A.; Ames, W.; Cox, N.; Lubitz, W.; Neese, F. Two Interconvertible Structures that Explain the Spectroscopic Properties of the Oxygen-Evolving Complex of Photosystem II in the S2 State. Angew. Chem. Int. Ed. 2012, 51, 9935–9940. [Google Scholar] [CrossRef]
- Beal, N.J.; Corry, T.A.; O’Malley, P.J. Comparison between Experimental and Broken Symmetry Density Functional Theory (BS-DFT) Calculated Electron Paramagnetic Resonance (EPR) Parameters of the S2 State of the Oxygen-Evolving Complex of Photosystem II in Its Native (Calcium) and Strontium-Substituted Form. J. Phys. Chem. B 2017, 121, 11273–11283. [Google Scholar]
- Amabilino, S.; Deeth, R.J. DFT Analysis of Spin Crossover in Mn(III) Complexes: Is a Two-Electron S = 2 to S = 0 Spin Transition Feasible? Inorg. Chem. 2017, 56, 2602–2613. [Google Scholar] [CrossRef]
- Cox, N.; Ames, W.; Epel, B.; Kulik, L.V.; Rapatskiy, L.; Neese, F.; Messinger, J.; Wieghardt, K.; Lubitz, W. Electronic Structure of a Weakly Antiferromagnetically Coupled MnIIMnIII Model Relevant to Manganese Proteins: A Combined EPR, 55Mn-ENDOR, and DFT Study. Inorg. Chem. 2011, 50, 8238–8251. [Google Scholar] [CrossRef]
- Ames, W.; Pantazis, D.A.; Krewald, V.; Cox, N.; Messinger, J.; Lubitz, W.; Neese, F. Theoretical evaluation of structural models of the S2 state in the oxygen evolving complex of photosystem II: Protonation states and magnetic interactions. J. Am. Chem. Soc. 2011, 133, 19743–19757. [Google Scholar] [CrossRef]
- Zheng, J.; Xu, X.; Truhlar, D.G. Minimally augmented Karlsruhe basis sets. Theor. Chem. Acc. 2011, 128, 295–305. [Google Scholar] [CrossRef]
- Cossi, M.; Rega, N.; Scalmani, G.; Barone, V. Energies, Structures, and Electronic Properties of Molecules in Solution with the C-PCM Solvation Model. J. Comput. Chem. 2003, 24, 669–681. [Google Scholar] [CrossRef]
- Peverati, R.; Head-Gordon, M. Orbital Optimized Double-Hybrid Density Functionals. J. Chem. Phys. 2013, 139, 024110. [Google Scholar] [CrossRef]
- Najibi, A.; Goerigk, L. A Comprehensive Assessment of the Effectiveness of Orbital Optimization in Double-Hybrid Density Functionals in the Treatment of Thermochemistry, Kinetics, and Noncovalent Interactions. J. Phys. Chem. A 2018, 122, 5610–5624. [Google Scholar] [CrossRef]
- Chan, B.; Goerigk, L.; Radom, L. On the Inclusion of Post-MP2 Contributions to Double-Hybrid Density Functionals. J. Comput. Chem. 2016, 37, 183–193. [Google Scholar] [CrossRef]
- Zhekova, H.R.; Seth, M.; Ziegler, T. Calculation of the exchange coupling constants of copper binuclear systems based on spin-flip constricted variational density functional theory. J. Chem. Phys. 2011, 135, 184105. [Google Scholar] [CrossRef]
- Groom, C.R.; Bruno, I.J.; Lightfoot, M.P.; Ward, S.C. The Cambridge Structural Database. Acta Cryst. 2016, B72, 171–179. [Google Scholar] [CrossRef]
- Neese, F. Software Update: The ORCA Program System, Version 4.0. Wires Comput. Mol. Sci. 2018, 8, e1327. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate ab initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H–Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Van Lenthe, E.; Baerends, E.J.; Snijders, J.G. Relativistic Regular Two-component Hamiltonians. J. Chem. Phys. 1993, 99, 4597–4610. [Google Scholar] [CrossRef]
- Van Lenthe, E.; Baerends, E.J.; Snijders, J.G. Relativistic Total-Energy Using Regular Approximations. J. Chem. Phys. 1994, 101, 9783–9792. [Google Scholar] [CrossRef]
- Pantazis, D.A.; Chen, X.Y.; Landis, C.R.; Neese, F. All-electron scalar relativistic basis sets for third-row transition metal atoms. J. Chem. Theory Comput. 2008, 4, 908–919. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F. Accurate Coulomb-Fitting Basis Sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef] [PubMed]
- Neese, F.; Wennmohs, F.; Hansen, A.; Becker, U. Efficient, Approximate and Parallel Hartree–Fock and Hybrid DFT Calculations. A ‘Chain-of-Spheres’ Algorithm for the Hartree–Fock Exchange. Chem. Phys. 2009, 356, 98–109. [Google Scholar] [CrossRef]
- Hellweg, A.; Hättig, C.; Höfener, S.; Klopper, W. Optimized accurate auxiliary basis sets for RI-MP2 and RI-CC2 calculations for the atoms Rb to Rn. Theor. Chem. Acc. 2007, 117, 587–597. [Google Scholar] [CrossRef]
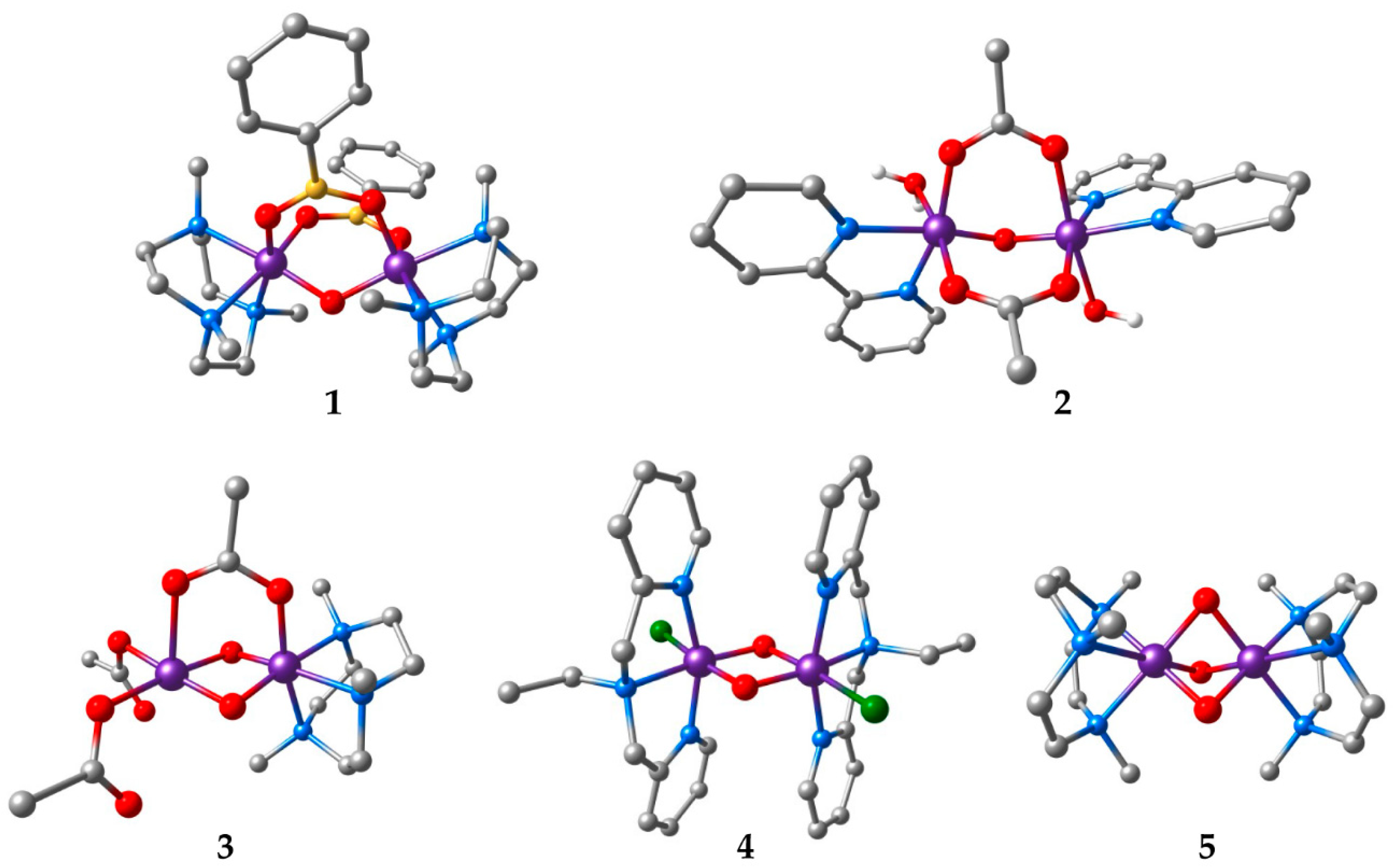
| Compound a | Refcode | Ox. States | R | J | Ref. | |
|---|---|---|---|---|---|---|
| 1 | [Mn2O(O2BPh)2(Me3tacn)2](PF6)2 | TIPFAZ | IV, IV | 3.185 | +10 | [63] |
| 2 | [Mn2O(OAc)2(H2O)2(bpy)2](PF6)2‚ 1.75H2O | GEFKAD | III, III | 3.131 | −3.4 | [64] |
| 3 | [Mn2O2(OAc)(Me3tacn)(OAc)2] | KUVPEW | III, IV | 2.665 | −90 | [65] |
| 4 | [Mn2O2Cl2(bpea)2](ClO4)2 | ZEQGOR | IV, IV | 2.756 | −147 | [67] |
| 5 | [Mn2O3(Me3tacn)2](PF6)2‚ H2O | VADDAF | IV, IV | 2.297 | −390 | [68] |
| Method | 1 | 2 | 3 | 4 | 5 | MAD |
|---|---|---|---|---|---|---|
| exp. | +10 | −3.4 | −90 | −147 | −390 | - |
| BLYP | −26.6 | −71.6 | −180.8 | −261.4 | −618.1 | −107.6 |
| TPSS | −13.4 | −48.7 | −147.7 | −216.7 | −549.7 | −71.2 |
| SCAN | −20.4 | −29.2 | −113.9 | −155.6 | −402.4 | −20.2 |
| TPSSh | +13.5 | −19.3 | −95.1 | −140.9 | −415.0 | −7.3 |
| B3LYP | +26.2 | −11.4 | −77.8 | −115.2 | −360.7 | +16.3 |
| PBE0 | +40.0 | +1.3 | −57.8 | −89.6 | −327.2 | +37.4 |
| Method | 1 | 2 | 3 | 4 | 5 | MAD |
|---|---|---|---|---|---|---|
| exp. | +10 | −3.4 | −90 | −147 | −390 | - |
| B2-PLYP | +13.1 | +4.6 | −83.8 | −109.9 | −326.8 | +23.5 |
| mPW2-PLYP | +19.6 | +6.0 | −72.5 | −101.8 | −317.7 | +30.8 |
| B2GP-PLYP | +13.3 | +11.7 | −79.8 | −135.1 | −332.6 | +19.6 |
| B2K-PLYP | +11.2 | +14.4 | −96.4 | −318.7 | −351.5 | −24.1 |
| B2T-PLYP | +15.6 | +9.2 | −73.6 | −114.6 | −323.2 | +26.8 |
| DSD-PBEP86 | −17.4 | +16.0 | −107.5 | −861.1 | −402.5 | −150.4 |
| DSD-PBEB95 | −15.5 | +11.2 | −97.6 | −230.6 | −394.1 | −21.2 |
| PWPB95 | +8.4 | −0.5 | −78.2 | −108.3 | −318.9 | +24.6 |
| JDFT | ΔJPT2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 | |
| B2-PLYP | +66.5 | +12.5 | −18.7 | −43.7 | −277.8 | −53.4 | −7.9 | −65.1 | −66.2 | −49.0 |
| mPW2-PLYP | +67.0 | +12.2 | −17.7 | −42.7 | −277.7 | −47.5 | −6.2 | −54.8 | −59.1 | −40.0 |
| B2GP-PLYP | +77.2 | +13.4 | −6.4 | −28.6 | −269.2 | −63.9 | −1.7 | −73.4 | −106.5 | −63.3 |
| B2K-PLYP | +83.2 | +13.2 | +3.3 | −13.1 | −261.1 | −71.9 | +1.2 | −99.7 | −305.6 | −90.4 |
| B2T-PLYP | +72.5 | +13.2 | −11.9 | −36.0 | −273.7 | −56.9 | −4.0 | −61.7 | −78.6 | −49.6 |
| DSD-PBEP86 | +94.0 | +16.1 | +12.7 | +9.9 | −244.8 | −111.4 | 0.0 | −120.2 | −871.1 | −157.7 |
| DSD-PBEB95 | +88.7 | +15.1 | +2.2 | −11.5 | −249.2 | −104.2 | −3.9 | −99.8 | −219.1 | −144.9 |
| PWPB95 | +67.1 | +12.9 | −22.8 | −50.3 | −278.4 | −58.7 | −13.3 | −55.4 | −58.0 | −40.4 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pantazis, D.A. Assessment of Double-Hybrid Density Functional Theory for Magnetic Exchange Coupling in Manganese Complexes. Inorganics 2019, 7, 57. https://doi.org/10.3390/inorganics7050057
Pantazis DA. Assessment of Double-Hybrid Density Functional Theory for Magnetic Exchange Coupling in Manganese Complexes. Inorganics. 2019; 7(5):57. https://doi.org/10.3390/inorganics7050057
Chicago/Turabian StylePantazis, Dimitrios A. 2019. "Assessment of Double-Hybrid Density Functional Theory for Magnetic Exchange Coupling in Manganese Complexes" Inorganics 7, no. 5: 57. https://doi.org/10.3390/inorganics7050057
APA StylePantazis, D. A. (2019). Assessment of Double-Hybrid Density Functional Theory for Magnetic Exchange Coupling in Manganese Complexes. Inorganics, 7(5), 57. https://doi.org/10.3390/inorganics7050057





