Abstract
Molecular systems containing magnetically interacting (exchange-coupled) manganese ions are important in catalysis, biomimetic chemistry, and molecular magnetism. The reliable prediction of exchange coupling constants with quantum chemical methods is key for tracing the relationships between structure and magnetic properties in these systems. Density functional theory (DFT) in the broken-symmetry approach has been employed extensively for this purpose and hybrid functionals with moderate levels of Hartree–Fock exchange admixture have often been shown to perform adequately. Double-hybrid density functionals that introduce a second-order perturbational contribution to the Kohn–Sham energy are generally regarded as a superior approach for most molecular properties, but their performance remains unexplored for exchange-coupled manganese systems. An assessment of various double-hybrid functionals for the prediction of exchange coupling constants is presented here using a set of experimentally characterized dinuclear manganese complexes that cover a wide range of exchange coupling situations. Double-hybrid functionals perform more uniformly compared to conventional DFT methods, but they fail to deliver improved accuracy or reliability in the prediction of exchange coupling constants. Reparametrized double-hybrid density functionals (DHDFs) perform no better, and most often worse, than the original B2-PLYP double-hybrid method. All DHDFs are surpassed by the hybrid-meta-generalized gradient approximation (GGA) TPSSh functional. Possible directions for future methodological developments are discussed.
1. Introduction
Oligonuclear complexes with magnetically interacting manganese ions have a long and rich history in chemistry, not only as synthetic analogues of essential biological clusters, such as the oxygen-evolving complex of photosystem II, but also in their own right, because of their magnetic, spectroscopic, and catalytic properties [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. From the perspective of quantum chemistry, a fundamental challenge in the description of the electronic structure of these systems is to model reliably the magnetic energy levels, that is, the energy levels associated with the magnetic “interaction” between the open-shell Mn ions [15]. This forms the basis for obtaining the full range of spin-dependent observables for a given system. By definition, this is a genuine multireference problem and in principle should be addressed with appropriate multireference quantum chemical methods [16,17,18,19,20,21,22]. However, the challenge of directly computing the full spectrum of energy states often can or has to be reduced for practical purposes to the more modest target of extracting pairwise exchange coupling constants that parameterize the magnetic energy levels in the framework of an effective spin Hamiltonian. This is often achieved at the level of Kohn–Sham density functional theory (DFT) using the broken-symmetry approach (BS-DFT) [23,24,25,26,27,28,29,30,31]. Various spectroscopic properties can be subsequently obtained using spin-projection techniques applied to single-determinant broken-symmetry solutions.
The BS-DFT approach has been used extensively in the study of exchange-coupled transition metal complexes, with documented achievements as well as failures. The chemical nature of a given system, the DFT functional, and the methodological details of the approach interact in physically non-transparent ways that lead to inconsistent and unpredictable behavior. This has so far precluded the establishment of a universally applicable BS-DFT approach, encouraging instead the empirical choice of an “optimal” functional for a specific type of chemical system. For manganese complexes a series of benchmark studies that compared generalized gradient approximation (GGA), meta-GGA, hybrid, and hybrid-meta-GGA functionals have suggested that hybrid functionals perform better than non-hybrid functionals for the prediction of exchange-coupling constants [32,33,34,35,36,37,38,39,40,41,42,43]. Pure GGA functionals tend to yield too large antiferromagnetic exchange couplings, a result attributed to excessive delocalization of spin density. Moderate admixture of Hartree–Fock (HF) exchange appears to provide an adequate counterbalance to this behavior for manganese systems, so that the calculated exchange coupling constants agree better with experiment when the BS-DFT results are used with spin projection. Still, there is no magic number for the exact exchange admixture and the best compromise for a given type of system depends on other features of the functional. Although the popular B3LYP hybrid functional (20% HF exchange) [44,45] has been used with reasonably good results, the hybrid-meta-GGA TPSSh functional (10% HF exchange) [46] is a better and more widely validated choice, not only for exchange coupling constants but for a range of molecular properties [34,47,48,49,50]. This choice of functional is not necessarily transferable, as demonstrated for example by the fact that TPSSh is no longer at the methodological sweet spot for the calculation of exchange coupling constants even for complexes of metal ions isoelectronic with manganese [51]. The adequate performance of a given functional for a restricted chemical space and the emergence of inconsistent behavior or large deviations outside this restricted space are typical of standard BS-DFT approaches.
Double-hybrid density functionals (DHDFs) [52] are regarded as “higher-rung” DFT methods compared to hybrid and meta-GGA functionals. They mix standard DFT exchange () and correlation () with HF exchange () and an additional second-order perturbation theory contribution ():
The contribution is obtained through a Møller–Plesset perturbational term (MP2) based on Kohn–Sham orbitals that are self-consistently optimized with respect to the first three terms:
The archetypal example is the B2-PLYP functional [53] that uses the B88 and LYP functionals for exchange and correlation, mixing HF exchange () and perturbational correction (). The percentage of HF exchange in DHDFs is usually considerably higher than that in most standard hybrid functionals. DHDFs have been shown to perform robustly and with generally superior results compared to other DFT methods in numerous benchmarks involving various types of energetics [52,54,55,56,57,58].
Studies involving exchange-coupled systems are comparatively scarce. Schwabe and Grimme [59] evaluated double-hybrid DFT on a set of organic compounds and a few simple copper complexes [60], supporting the good performance of the method. Rajaraman and coworkers [61] reported that the double-hybrid B2-PLYP functional performed better than hybrid functionals such as B3LYP, PBE0, or TPSSh for the description of magnetic coupling in Gd(III)–radical complexes. Vogiatzis et al. [62] also reported that B2-PLYP performs well within the BS-DFT approach for dinuclear paddlewheel complexes, however they also noted that it is inferior to B3LYP in the case of a trichromium system [62]. It is, therefore, not a given that the use of a double-hybrid functional automatically can ensure better results for exchange coupling problems across transition metal chemistry. The increase in the number of DHDFs over recent years further complicates the choice of method because new functionals are typically not tested for transition metal complexes with magnetically coupled ions. Double-hybrid DFT has similarly not been evaluated so far for manganese systems of relevance to biomimetic chemistry and molecular magnetism. The oxidation states Mn(III) and Mn(IV) are most relevant in this area, that is why previous assessments of theoretical methods for magnetic and spectroscopic properties of manganese complexes have made extensive use of oligonuclear complexes with Mn ions in these oxidation states [32,33,34,35,36,37,38,39,40,41,42,43]. In the present study a set of dinuclear Mn complexes are used to evaluate the performance of double-hybrid DFT for the prediction of exchange coupling constants. The manganese complexes comprising the database are crystallographically characterized compounds with experimentally determined exchange coupling constants that span the range from moderate ferromagnetic to strong antiferromagnetic coupling. A series of traditional as well as more modern DHDF formulations are included in the evaluation. The results are compared with those obtained by standard GGA, meta-GGA, hybrid-GGA and hybrid-meta-GGA functionals.
2. Test Set of Dinuclear Manganese Complexes
Five dinuclear complexes were selected for the present study as representative of various exchange coupling situations in manganese containing systems (see Table 1 and Figure 1). It is noted that the exchange coupling constants J in the present study adhere to the following form of the Heisenberg–Dirac–van Vleck Hamiltonian for the isotropic bilinear coupling of two spins S1 and S2:

Table 1.
Dinuclear manganese complexes considered in this study, with their crystallographic identifiers, Mn oxidation states, Mn···Mn distance R (in Å), and exchange coupling constant J (in cm−1).
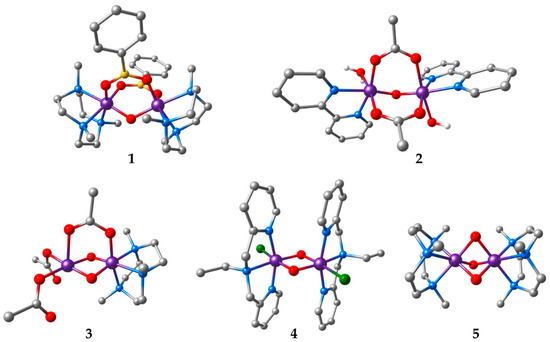
Figure 1.
Structures of the manganese complexes included in this study. Hydrogen atoms bound to carbons are omitted for clarity (Mn: purple; C: grey; N: blue; O: red; B: yellow; Cl: green).
Antiferromagnetic coupling is the most common situation in complexes comprising Mn(III) and Mn(IV) ions, so only one of the systems (complex 1) represents a case of ferromagnetic coupling, with a ground state spin of S = 3 [63]. The other complexes have low-spin ground states. Complex 2 is a weakly antiferromagnetically coupled Mn(III,III) dimer (S = 0) [64]. Complex 3 is a mixed-valence system with asymmetric ligation [65] that facilitates spin localization. This complex has a moderate antiferromagnetic coupling resulting in a spin doublet (S = 1/2) ground state and has been the subject of a recent study [20] that evaluated the use of the density matrix renormalization group [66] in the multireference treatment of exchange coupling [18,22]. Complex 4 is a classic example of a strongly coupled bis-μ-oxo Mn(IV,IV) system [67]. Finally, complex 5 reaches the far limit of strong antiferromagnetic coupling [68]. The tris-μ-oxo ligation in complex 5 brings the manganese ions in such close proximity that, in addition to ligand-mediated superexchange, direct metal–metal interaction contributes significantly in stabilizing the low-spin state [39]. This situation is common in face-sharing d3–d3 systems [51,69].
3. Selection of Functionals
Recent years have seen a surge in interest in DHDFs and, as a result, a rapid increase in the number of variants and modified forms [52,58,70]. In the present study we aim at a modest selection of functionals that is nevertheless representative of all widely available types of double-hybrid methods. A few non-double-hybrid methods were included to facilitate comparisons with the DHDFs. These are the GGA functional BLYP, the meta-GGA functionals TPSS [71] and SCAN [72], the hybrid functionals B3LYP (20% HF exchange) [44,45] and PBE0 (25% HF exchange) [73], and the hybrid-meta-GGA functional TPSSh (10% HF exchange) [46]. The selected double-hybrid functionals include B2-PLYP [53], which is the first modern functional where a PT2 contribution replaces part of the DFT correlation; it combines B88 for DFT exchange with LYP for DFT correlation, with a HF exchange coefficient and a PT2 coefficient . mPW2-PLYP is similar but uses mPW exchange with and . A series of reparametrized versions of the B2-PLYP functional are B2GP-PLYP ( and ), B2K-PLYP ( and ), and B2T-PLYP ( and ), which were respectively suggested as more suitable for general-purpose calculations, kinetics, and thermochemistry [74].
In the spin-component-scaled MP2 approach (SCS-MP2) [75] a separate scaling factor is used for the correlation energy contribution of opposite-spin () and same-spin () electron pairs. This is usually an improvement over MP2 because it can take account of the fact that same-spin correlation is already present at the HF level. SCS-MP2 was also used in the context of double-hybrid density functional theory. Here we test functionals from the dispersion-corrected spin-component-scaled double-hybrid family (DSD) [76,77,78], which follow the formula:
DSD-PBEP86 employs PBE exchange and P86 correlation with , , , and , while DSD-PBEB95 combines PBE exchange with B95 correlation and has coefficients , , , and . It is noted that the scaling factors for the SCS-MP2 part were reparametrized and do not follow the original SCS-MP2 definition [75]. Finally, the PWPB95 functional [55] uses reparametrized PW91 exchange and B95 correlation, but instead of SCS-MP2 it employs the scaled-opposite-spin approach (SOS-MP2) [79] that considers exclusively the correlation contribution of opposite-spin electron pairs. The factor in PWPB95 is fixed at 0.50 and the correlation terms are related as , with and .
4. Results and Discussion
4.1. Conventional Density Functionals
It is instructive to examine first the performance of conventional DFT methods, where the term encompasses GGA, meta-GGA, and hybrid-(meta)-GGA functionals. Table 2 lists exchange coupling constants computed with six representative functionals from these families. The trends are largely anticipated from past studies: functionals that do not incorporate any exact exchange strongly favor the broken-symmetry over the high-spin state, yielding exchange coupling constants that are too negative compared to experiment. In contrast, hybrid functionals stabilize the high-spin states to an extent that depends principally on the admixture of HF exchange.

Table 2.
Exchange coupling constants J (in cm−1) computed with selected conventional density functionals for the five manganese complexes studied in this work, compared with experimentally fitted values. Mean absolute deviations (MAD) in cm−1.
The BLYP functional performs very poorly, leading to unrealistically strong antiferromagnetic coupling constants for all complexes. The meta-GGA functional TPSS moves to the right direction, albeit without being able to sufficiently correct the GGA bias. The recently proposed SCAN functional is the best performing non-hybrid approach. It still fails to predict ferromagnetic coupling for complex 1, but improves over TPSS for all other complexes. The SCAN results suggest possible non-linearity because the results are rather poor in the weak coupling cases but improve significantly toward the strong exchange-coupling regime (complexes 4 and 5).
TPSSh and B3LYP predict correctly the sign of the exchange coupling constants for all complexes. TPSSh, with 10% HF exchange, shows the best overall performance among all methods: it achieves deviations from experiment of merely 3–6 cm−1 for complexes 1, 3, and 4, with the largest deviation being 25 cm−1 for the strongest antiferromagnetic coupling in the test set (complex 5). The good performance of TPSSh documented here is in agreement with previous studies on synthetic manganese complexes and bioinorganic model systems [34,35,36,38,40,41,42,43,80,81,82,83,84,85]. The increase in the percentage of HF exchange to 20% in the B3LYP functional leads to a slight overestimation of the stability of high-spin states and larger deviations from experiment. Only complex 2 appears to be better described by B3LYP compared with TPSSh. Further increase of HF exchange to 25% in PBE0 results in exaggerated ferromagnetic coupling for complex 1, too small antiferromagnetic coupling for 3–5, and qualitatively incorrect reversal of the ground spin state for 2 from low to high spin. The effect of additional diffuse functions [86] in the basis set was tested and found to be negligible (variation of less than 0.2 cm−1 in the computed exchange coupling constants) because they do not have a differential effect on the energies of the high-spin and broken-symmetry solutions. The conductor-like polarizable continuum model (CPCM) [87] was additionally tested with an infinite dielectric in order to investigate possible effects on the computed exchange coupling constants. Compared to the gas-phase results, the CPCM calculations show variations in the J values of less than 2 cm−1 for the antiferromagnetically coupled dimers and up to 9 cm−1 for complex 1. Given that these values were obtained under the extreme assumption of a perfect conductor, it is concluded that the continuum model has only a limited effect on the computed values as it does not strongly favor any particular solution. In conclusion, the various technical aspects of the calculations appear to be converged. In terms of the performance of individual functionals, even though exceptions exist at the quantitative level for specific complexes, TPSSh offers the most balanced performance.
4.2. Double-Hybrid Density Functionals
The exchange coupling constants obtained with double-hybrid functionals are listed in Table 3. Compared to the divergent behavior of the functionals discussed above, the variation among double-hybrids appears remarkably small, with the exception of a few erratic results that are discussed below. With the marginal exception of PWPB95, all DHDFs fail to predict antiferromagnetic coupling for complex 2, and all DHDFs overestimate the stability of the high-spin state.

Table 3.
Exchange coupling constants J (in cm−1) computed with selected double-hybrid density functionals for the five manganese complexes studied in this work, compared with experimentally fitted values. Mean absolute deviations (MAD) in cm−1.
A comparison between Table 2 and Table 3 shows that the DHDFs do not replicate the behavior of any conventional functional. For example, B2-PLYP produces the same exchange coupling constant as TPSSh for complex 1, but a qualitatively different result for complex 2, a similar error albeit with opposite sign than TPSSh for complex 3, and significantly greater errors than TPSSh for the more strongly coupled complexes 4 and 5. mPW2-PLYP tracks closely the B2-PLYP results, but with uniformly increased errors for all complexes. The reparametrized versions of B2-PLYP, i.e., the general-purpose B2GP-PLYP and the other two functionals (B2K-PLYP and B2T-PLYP) that were optimized for specific applications similarly show no improvement. Complex 4 yields an outlier for B2K-PLYP, which overestimates the strength of the antiferromagnetic coupling.
The two DSD functionals that make use of spin-component-scaled MP2 have similar problems with complex 4, yielding unrealistically large antiferromagnetic exchange coupling constants, particularly in the case of DSD-PBEP86. This is presumably related to the coefficients employed for the SCS-MP2 correction, to the overall MP2 contribution, or both. Moreover, both DSD functionals fail to predict the absolute and relative sign of the coupling for complexes 1 and 2.
PWPB95, which employs only an opposite-spin MP2 component, behaves much more reasonably. It is the only double-hybrid functional that might be considered an improvement over B2-PLYP. This is less in the sense of overall superior numerical agreement with experiment, and more because it is the only double-hybrid functional that marginally predicts weak antiferromagnetic coupling for complex 2.
An important conclusion from the above results is that there are only three well-behaved functionals among the selection used here: B2-PLYP, mPW2-PLYP, and PWPB95. Although the present test set is too small to support entirely general conclusions, the present results suggest that the B2x-PLYP and DSD functionals are likely inappropriate for the problem of exchange coupling. Presumably the parametrization of these functionals for specific uses or with training sets that target narrowly defined properties reduces their generality, resulting in erratic behavior and rendering them unsuitable for exchange-coupled systems. But an equally important conclusion is that despite the fact that the three well-behaved DHDFs do not display the wild fluctuations and inconsistencies observed with conventional functionals (as suggested by their MAD values in Table 3), there is no advantage in choosing any of them over TPSSh for the study of exchange coupling in manganese complexes.
4.3. Energetic Contributions to Exchange Coupling from Double-Hybrid Density Functionals
To gain insight into the behavior of the double-hybrid density functionals it is illuminating to decompose the final exchange coupling constant into the energy contribution from the Kohn–Sham orbitals and the perturbational theory component. This is presented in Table 4.

Table 4.
Density functional theory (DFT)-only exchange coupling constants JDFT (in cm−1) obtained from the Kohn–Sham orbitals of the double hybrid functionals by excluding the perturbational energy component, and the corresponding perturbational contribution (ΔJPT2) that leads to the final results of Table 3.
In general, energies based on the Kohn–Sham orbitals without the perturbational contribution are strongly in favor of the high-spin state (JDFT in Table 4). This is due to the high HF admixture in all DHDFs. Looking at these results alone, the usual and expected correlation between the percentage of HF exchange and the stabilization of the high-spin state that was discussed for the conventional hybrid functionals (Table 2) becomes immediately apparent. B2-PLYP, mPW2-PLYP, and PWPB95 appear practically identical here because the results are primarily defined by the fact that all three functionals have almost the same factor (0.50–0.55). Reparametrized functionals with higher factors yield even greater stabilization of the high-spin state. In terms of the methodological utility of these DHDFs in the prediction of exchange coupling constants, the question is, to what extent can the perturbational contribution correct the flawed JDFT picture.
The ΔJPT2 values in Table 4 are illuminating in this respect. Almost without exception the perturbational component correctly stabilizes the low-spin state, thereby enhancing antiferromagnetic coupling. For the functionals that were termed “well-behaved” above, the perturbational corrections are all very similar. What can be concluded on the basis of these results is that the perturbational correction for these functionals is well-controlled but never sufficient to fully recover the experimentally determined strength of antiferromagnetic coupling. Interestingly, the SOS-MP2 used in PWPB95 gives practically the same corrections as the MP2 component of B2-PLYP and mPW2-PLYP.
The B2x-PLYP functionals are less consistent in the magnitude of the MP2 corrections as a result of their higher and variable factors. Thus, in the case of B2K-PLYP () the perturbational corrections are more pronounced and it is precisely the MP2 component that causes the problem of a too negative exchange coupling constant for complex 4. The decomposition of the energetic contributions in Table 4 reveals clearly the origin of the weakness of the DSD functionals for the present application. Their weakness stems in large part from the SCS-MP2 approach used in these functionals, or more precisely from the associated , , and parameters that lead to very large and hence unreliable perturbational terms. These two families of DHDFs vividly demonstrate the pitfalls of pursuing property-specific functional parametrizations.
It is beyond the scope of this contribution to devise an improved double-hybrid functional for the present systems. Besides, the test set of complexes used here is too small and chemically restricted to form a meaningful basis for methodological developments of general utility. Nevertheless, the results presented above provide useful insights in this direction. It is suggested that the PWPB95 functional can be a starting point for future refinements: the rather moderate 50% HF exchange and the SOS-MP2 approach with high percentage of DFT correlation () appear to provide a reasonable balance between the different energetic components. In the context of BS-DFT applications, the implication is that it could be perfectly sufficient for the perturbational term to correct any deficiencies of the density functional contribution only for opposite-spin correlation.
The high admixture of HF exchange in some of the DHDFs tested here is known to be beneficial for specific applications, for example in predicting reaction barriers. However, it is detrimental for the present problem of exchange coupling, presumably because it places unrealistic demands on the perturbational contribution by creating poor Kohn–Sham orbitals. Several methodological developments not represented by the functionals tested in the present work are currently being pursued in the field of double-hybrid density functionals [52]. These include, for example, investigations into the effect of orbital optimization [88,89] and of post-MP2 contributions [90].
Regardless of where such theoretical advances will lead, an important point that needs to be stressed is that the commonly used training or reference data sets, with their focus on thermochemistry and kinetics, are not necessarily testing for the ability of functionals to handle aspects of the electronic structure that relate to spin-state energetics and exchange coupling. To facilitate progress in this area, appropriate benchmark sets must be developed to explicitly target challenging situations characteristic of open-shell transition metal chemistry. Small sets of copper dimers that are sometimes used in the literature [59,60,91] are insufficient for the purpose of evaluating general-purpose functionals for exchange coupling interactions. Such sets should encompass spin-state energetics of mononuclear transition metal complexes, spin-crossover systems, and diverse cases of magnetic exchange interactions. The present collection of complexes can be part of a large, unbiased, and inclusive future test set that should contain examples spanning many different transition metal ions with different unpaired electron counts. Ideally, of course, a “next generation” of DHDFs would rely less on reference-set parametrization and more on physically motivated improvements that would address fundamental challenges such as that of strong correlation in polynuclear exchange-coupled systems.
5. Computational Methods
The crystallographic coordinates were taken from the Cambridge Structural Database [92] (see Table 1 for Refcodes of the compounds). Counterions and solvent molecules were removed, hydrogens were added where necessary and their positions were optimized with ORCA [93] using the TPSS functional [71] and the D3 dispersion corrections proposed by Grimme [94]. The high-spin state was assumed for these optimizations. Following past practice, the crystallographic positions of heavy atoms were maintained in order to avoid introducing additional errors or bias in our comparison of methods. The zeroth-order regular approximation (ZORA) [95,96] was employed for treating scalar relativistic effects, in combination with ZORA-recontracted versions [97] of the def2-TZVP basis sets [98]. Fully decontracted def/J basis sets [99] were used for fitting the Coulomb integrals in the resolution of the identity (RI) approximation. Tight energy convergence criteria, enhanced integration grids (Grid6) and increased radial integration accuracy (IntAcc 6) were used throughout.
The calculation of exchange-coupling constants followed the standard broken-symmetry DFT procedure that utilizes the energy of the high-spin (ferromagnetic) solution and the energy of the broken-symmetry Kohn–Sham determinant that results from “flipping” the spin of the electrons at the metal site with the lowest local spin population in the high-spin solution. All broken-symmetry solutions were verified for correctness by examining the manganese spin populations to confirm the presence of the expected number of unpaired electrons on each metal site (all Mn ions in all complexes have a local high-spin configuration). Explicit inspection is crucial because the assigned spin multiplicity does not necessarily constrain the total number of unpaired electrons in a broken-symmetry calculation. In some cases, the orbital optimization procedure may converge to solutions where the electrons are locally spin-coupled at a metal ion, even though the correct broken-symmetry solution with local high-spin configurations is lower in energy. Such electron-coupled configuration represents an excited state that is not relevant for the exchange-coupling problem. In these cases, it is necessary to restart from the orbitals of the initial high-spin solution and to carefully monitor the self-consistent field procedure in the broken-symmetry calculation, adjusting appropriately the convergence algorithms to avoid changes in orbital occupations and accumulation of numerical errors. Exchange coupling constants were computed with the Yamaguchi formula [25] that smoothly covers weak to strong exchange coupling by scaling the energy difference between the high-spin and broken-symmetry solutions according to their spin expectation values:
Methodological details in terms of scalar relativity and all-electron basis sets were the same as discussed above. For hybrid functionals the chain-of-spheres approximation to exact exchange (COSX) [100] was employed with increased grid settings (GridX6 in ORCA convention) to speed up the calculation of exchange integrals without loss of accuracy. The resolution of the identity approach was used in the MP2 (or SCS-MP2) part of the calculation for all double-hybrid functionals, in combination with appropriate correlation fitting def2/C basis sets [101].
6. Conclusions
A set of dinuclear manganese complexes with various metal oxidation states and a broad range of exchange coupling constants was used to test the performance of representative conventional and double-hybrid density functionals. Among standard approaches, TPSSh was confirmed to be the best choice in line with past studies. Among the double-hybrid functionals, there appears to be little reason to prefer any of the more recent variants over the original B2PLYP. This sobering observation leads to an important conclusion concerning the development of new double-hybrid functionals: the minor or major adjustments and developments reported since 2006 offer no advantage for the problem of exchange coupling. Several double-hybrid density functionals, particularly some that incorporate high admixture of Hartree–Fock exchange or use the spin-component-scaled MP2 approach perform so poorly, that their use is discouraged. Analysis of the different energetic contributions suggests that erratic behavior by double-hybrid functionals is typically associated with large perturbational contributions. The results are not promising for applications to systems of higher nuclearity, where any weaknesses are expected to become even more pronounced. In terms of overall performance, no double-hybrid functional can compete with TPSSh, which remains the method of choice for exchange-coupled manganese systems. In addition to methodological advances that will address physical deficiencies of present density functionals, it is necessary to develop varied reference sets of exchange-coupled transition metal complexes, representative of electronically, chemically, and magnetically diverse systems, on which to assess any new methods.
Acknowledgments
The author is grateful for the support of the Max Planck Society.
Conflicts of Interest
The author declares no conflict of interest.
References
- Mukhopadhyay, S.; Mandal, S.K.; Bhaduri, S.; Armstrong, W.H. Manganese Clusters with Relevance to Photosystem II. Chem. Rev. 2004, 104, 3981–4026. [Google Scholar] [CrossRef] [PubMed]
- Wu, A.J.; Penner-Hahn, J.E.; Pecoraro, V.L. Structural, Spectroscopic, and Reactivity Models for the Manganese Catalases. Chem. Rev. 2004, 104, 903–938. [Google Scholar] [CrossRef]
- Thompson, L.K.; Waldmann, O.; Xu, Z. Polynuclear Manganese Grids and Clusters—A Magnetic Perspective. Coord. Chem. Rev. 2005, 249, 2677–2690. [Google Scholar] [CrossRef]
- Gatteschi, D.; Sessoli, R.; Villain, J. Molecular Nanomagnets; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Boer, J.W.D.; Browne, W.R.; Feringa, B.L.; Hage, R. Carboxylate-Bridged Dinuclear Manganese Systems—From Catalases to Oxidation Catalysis. C. R. Chim. 2007, 10, 341–354. [Google Scholar] [CrossRef]
- Mullins, C.S.; Pecoraro, V.L. Reflections on Small Molecule Manganese Models that Seek to Mimic Photosynthetic Water Oxidation Chemistry. Coord. Chem. Rev. 2008, 252, 416–443. [Google Scholar] [CrossRef]
- Tsui, E.Y.; Kanady, J.S.; Agapie, T. Synthetic Cluster Models of Biological and Heterogeneous Manganese Catalysts for O2 Evolution. Inorg. Chem. 2013, 52, 13833–13848. [Google Scholar] [CrossRef] [PubMed]
- Hirahara, M.; Shoji, A.; Yagi, M. Artificial Manganese Center Models for Photosynthetic Oxygen Evolution in Photosystem II. Eur. J. Inorg. Chem. 2014, 2014, 595–606. [Google Scholar] [CrossRef]
- Yang, C.-I.; Zhang, Z.-Z.; Lin, S.-B. A Review of Manganese-Based Molecular Magnets and Supramolecular Architectures from Phenolic Oximes. Coord. Chem. Rev. 2015, 289–290, 289–314. [Google Scholar] [CrossRef]
- Young, K.J.; Brennan, B.J.; Tagore, R.; Brudvig, G.W. Photosynthetic Water Oxidation: Insights from Manganese Model Chemistry. Acc. Chem. Res. 2015, 48, 567–574. [Google Scholar] [CrossRef]
- Gerey, B.; Gouré, E.; Fortage, J.; Pécaut, J.; Collomb, M.-N. Manganese-calcium/strontium heterometallic compounds and their relevance for the oxygen-evolving center of photosystem II. Coord. Chem. Rev. 2016, 319, 1–24. [Google Scholar] [CrossRef]
- Krewald, V.; Pantazis, D.A. Understanding and tuning the properties of redox-accumulating manganese helicates. Dalton Trans. 2016, 45, 18900–18908. [Google Scholar] [CrossRef] [PubMed]
- Najafpour, M.M.; Renger, G.; Hołyńska, M.; Moghaddam, A.N.; Aro, E.-M.; Carpentier, R.; Nishihara, H.; Eaton-Rye, J.J.; Shen, J.-R.; Allakhverdiev, S.I. Manganese Compounds as Water-Oxidizing Catalysts: From the Natural Water-Oxidizing Complex to Nanosized Manganese Oxide Structures. Chem. Rev. 2016, 116, 2886–2936. [Google Scholar] [CrossRef]
- Paul, S.; Neese, F.; Pantazis, D.A. Structural models of the biological oxygen-evolving complex: Achievements, insights, and challenges for biomimicry. Green Chem. 2017, 19, 2309–2325. [Google Scholar] [CrossRef]
- De Graaf, C.; Broer, R. Magnetic Interactions in Molecules and Solids; Springer: Heidelberg, Germany, 2016; p. 246. [Google Scholar]
- Malrieu, J.P.; Caballol, R.; Calzado, C.J.; de Graaf, C.; Guihéry, N. Magnetic Interactions in Molecules and Highly Correlated Materials: Physical Content, Analytical Derivation, and Rigorous Extraction of Magnetic Hamiltonians. Chem. Rev. 2014, 114, 429–492. [Google Scholar] [CrossRef] [PubMed]
- Swart, M.; Costas, M. Spin States in Biochemistry and Inorganic Chemistry; John Wiley & Sons: Chichester, UK, 2016; p. 466. [Google Scholar]
- Krewald, V.; Pantazis, D.A. Applications of the Density Matrix Renormalization Group to Exchange-Coupled Transition Metal Systems. In Transition Metals in Coordination Environments: Computational Chemistry and Catalysis Viewpoints; Broclawik, E., Borowski, T., Radoń, M., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 91–120. [Google Scholar]
- Harris, T.V.; Kurashige, Y.; Yanai, T.; Morokuma, K. Ab initio Density Matrix Renormalization Group Study of Magnetic Coupling in Dinuclear Iron and Chromium Complexes. J. Chem. Phys. 2014, 140, 054303. [Google Scholar] [CrossRef] [PubMed]
- Roemelt, M.; Krewald, V.; Pantazis, D.A. Exchange Coupling Interactions from the Density Matrix Renormalization Group and N-Electron Valence Perturbation Theory: Application to a Biomimetic Mixed-Valence Manganese Complex. J. Chem. Theory Comput. 2018, 14, 166–179. [Google Scholar] [CrossRef] [PubMed]
- Kawakami, T.; Miyagawa, K.; Sharma, S.; Saito, T.; Shoji, M.; Yamada, S.; Yamanaka, S.; Okumura, M.; Nakajima, T.; Yamaguchi, K. UNO DMRG CAS CI Calculations of Binuclear Manganese Complex Mn(IV)2O2(NHCHCO2)4: Scope and Applicability of Heisenberg Model. J. Comput. Chem. 2018, 40, 333–341. [Google Scholar] [CrossRef] [PubMed]
- Roemelt, M.; Pantazis, D.A. Multireference Approaches to Spin-State Energetics of Transition Metal Complexes Utilizing the Density Matrix Renormalization Group. Adv. Theory Simul. 2019, 1800201. [Google Scholar] [CrossRef]
- Noodleman, L. Valence Bond Description of Anti-ferromagnetic Coupling in Transition-Metal Dimers. J. Chem. Phys. 1981, 74, 5737–5743. [Google Scholar] [CrossRef]
- Noodleman, L.; Davidson, E.R. Ligand Spin Polarization and Antiferromagnetic Coupling in Transition-Metal Dimers. Chem. Phys. 1986, 109, 131–143. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Takahara, Y.; Fueno, T. Ab-Initio Molecular Orbital Studies of Structure and Reactivity of Transition Metal-Oxo Compounds. In Applied Quantum Chemistry; Smith, V.H., Jr., Scheafer, H.F., III, Morokuma, K., Eds.; D. Reidel: Boston, MA, USA, 1986; pp. 155–184. [Google Scholar]
- Yamanaka, S.; Kawakami, T.; Nagao, H.; Yamaguchi, K. Effective Exchange Integrals for Open-Shell Species by Density Functional Methods. Chem. Phys. Lett. 1994, 231, 25–33. [Google Scholar] [CrossRef]
- Bencini, A.; Totti, F.; Daul, C.A.; Doclo, K.; Fantucci, P.; Barone, V. Density Functional Calculations of Magnetic Exchange Interactions in Polynuclear Transition Metal Complexes. Inorg. Chem. 1997, 36, 5022–5030. [Google Scholar] [CrossRef]
- Ruiz, E.; Rodriguez-Fortea, A.; Cano, J.; Alvarez, S.; Alemany, P. About the Calculation of Exchange Coupling Constants in Polynuclear Transition Metal Complexes. J. Comput. Chem. 2003, 24, 982–989. [Google Scholar] [CrossRef]
- Ciofini, I.; Daul, C.A. DFT Calculations of Molecular Magnetic Properties of Coordination Compounds. Coord. Chem. Rev. 2003, 238–239, 187–209. [Google Scholar] [CrossRef]
- Neese, F. Prediction of Molecular Properties and Molecular Spectroscopy with Density Functional Theory: From Fundamental Theory to Exchange-Coupling. Coord. Chem. Rev. 2009, 253, 526–563. [Google Scholar] [CrossRef]
- Bencini, A.; Totti, F. A Few Comments on the Application of Density Functional Theory to the Calculation of the Magnetic Structure of Oligo-Nuclear Transition Metal Clusters. J. Chem. Theory Comput. 2009, 5, 144–154. [Google Scholar] [CrossRef]
- Rudberg, E.; Sałek, P.; Rinkevicius, Z.; Ågren, H. Heisenberg Exchange in Dinuclear Manganese Complexes: A Density Functional Theory Study. J. Chem. Theory Comput. 2006, 2, 981–989. [Google Scholar] [CrossRef]
- Comba, P.; Hausberg, S.; Martin, B. Calculation of Exchange Coupling Constants of Transition Metal Complexes with DFT. J. Phys. Chem. A 2009, 113, 6751–6755. [Google Scholar] [CrossRef]
- Orio, M.; Pantazis, D.A.; Petrenko, T.; Neese, F. Magnetic and Spectroscopic Properties of Mixed Valence Manganese(III,IV) Dimers: A Systematic Study Using Broken Symmetry Density Functional Theory. Inorg. Chem. 2009, 48, 7251–7260. [Google Scholar] [CrossRef]
- Schinzel, S.; Kaupp, M. Validation of Broken-Symmetry Density Functional Methods for the Calculation of Electron Paramagnetic Resonance Parameters of Dinuclear Mixed-Valence MnIVMnIII Complexes. Can. J. Chem. 2009, 87, 1521–1539. [Google Scholar] [CrossRef]
- Pantazis, D.A.; Orio, M.; Petrenko, T.; Zein, S.; Bill, E.; Lubitz, W.; Messinger, J.; Neese, F. A New Quantum Chemical Approach to the Magnetic Properties of Oligonuclear Transition-Metal Complexes: Application to a Model for the Tetranuclear Manganese Cluster of Photosystem II. Chem. Eur. J. 2009, 15, 5108–5123. [Google Scholar] [CrossRef] [PubMed]
- Orio, M.; Pantazis, D.A.; Neese, F. Density Functional Theory. Photosynth. Res. 2009, 102, 443–453. [Google Scholar] [CrossRef] [PubMed]
- Baffert, C.; Orio, M.; Pantazis, D.A.; Duboc, C.; Blackman, A.G.; Blondin, G.; Neese, F.; Deronzier, A.; Collomb, M.-N. Trinuclear Terpyridine Frustrated Spin System with a MnIV3O4 Core: Synthesis, Physical Characterization, and Quantum Chemical Modeling of Its Magnetic Properties. Inorg. Chem. 2009, 48, 10281–10288. [Google Scholar] [CrossRef] [PubMed]
- Pantazis, D.A.; Krewald, V.; Orio, M.; Neese, F. Theoretical magnetochemistry of dinuclear manganese complexes: Broken symmetry density functional theory investigation on the influence of bridging motifs on structure and magnetism. Dalton Trans. 2010, 39, 4959–4967. [Google Scholar] [CrossRef] [PubMed]
- Schraut, J.; Arbuznikov, A.V.; Schinzel, S.; Kaupp, M. Computation of Hyperfine Tensors for Dinuclear MnIIIMnIV Complexes by Broken-Symmetry Approaches: Anisotropy Transfer Induced by Local Zero-Field Splitting. ChemPhysChem 2011, 12, 3170–3179. [Google Scholar] [CrossRef] [PubMed]
- Bovi, D.; Guidoni, L. Magnetic Coupling Constants and Vibrational Frequencies by Extended Broken Symmetry Approach with Hybrid Functionals. J. Chem. Phys. 2012, 137, 114107. [Google Scholar] [CrossRef]
- Krewald, V.; Neese, F.; Pantazis, D.A. On the Magnetic and Spectroscopic Properties of High-Valent Mn3CaO4 Cubanes as Structural Units of Natural and Artificial Water Oxidizing Catalysts. J. Am. Chem. Soc. 2013, 135, 5726–5739. [Google Scholar] [CrossRef]
- Krewald, V.; Retegan, M.; Cox, N.; Messinger, J.; Lubitz, W.; DeBeer, S.; Neese, F.; Pantazis, D.A. Metal Oxidation States in Biological Water Splitting. Chem. Sci. 2015, 6, 1676–1695. [Google Scholar] [CrossRef]
- Becke, A.D. Density-Functional Thermochemistry. III. The Role Of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula Into a Functional of the Electron-Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Staroverov, V.N.; Scuseria, G.E.; Tao, J.; Perdew, J.P. Comparative Assessment of a New Nonempirical Density Functional: Molecules and Hydrogen-Bonded Complexes. J. Chem. Phys. 2003, 119, 12129–12137. [Google Scholar] [CrossRef]
- Bühl, M.; Kabrede, H. Geometries of Transition-Metal Complexes from Density-Functional Theory. J. Chem. Theory Comput. 2006, 2, 1282–1290. [Google Scholar] [CrossRef] [PubMed]
- Kossmann, S.; Kirchner, B.; Neese, F. Performance of Modern Density Functional Theory for the Prediction of Hyperfine Structure: Meta-GGA and Double Hybrid Functionals. Mol. Phys. 2007, 105, 2049–2071. [Google Scholar] [CrossRef]
- Jensen, K.P. Bioinorganic Chemistry Modeled with the TPSSh Density Functional. Inorg. Chem. 2008, 47, 10357–10365. [Google Scholar] [CrossRef] [PubMed]
- Cirera, J.; Via-Nadal, M.; Ruiz, E. Benchmarking Density Functional Methods for Calculation of State Energies of First Row Spin-Crossover Molecules. Inorg. Chem. 2018, 57, 14097–14105. [Google Scholar] [CrossRef] [PubMed]
- Pantazis, D.A. Meeting the Challenge of Magnetic Coupling in a Triply-Bridged Chromium Dimer: Complementary Broken-Symmetry Density Functional Theory and Multireference Density Matrix Renormalization Group Perspectives. J. Chem. Theory Comput. 2019, 15, 938–948. [Google Scholar] [CrossRef] [PubMed]
- Goerigk, L.; Grimme, S. Double-Hybrid Density Functionals. Wires Comput. Mol. Sci. 2014, 4, 576–600. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical hybrid density functional with perturbative second-order correlation. J. Chem. Phys. 2006, 124, 034108. [Google Scholar] [CrossRef]
- Schwabe, T.; Grimme, S. Theoretical thermodynamics for large molecules: Walking the thin line between accuracy and computational cost. Acc. Chem. Res. 2008, 41, 569–579. [Google Scholar] [CrossRef]
- Goerigk, L.; Grimme, S. Efficient and Accurate Double-Hybrid-Meta-GGA Density Functionals—Evaluation with the Extended GMTKN30 Database for General Main Group Thermochemistry, Kinetics, and Noncovalent Interactions. J. Chem. Theory Comput. 2010, 7, 291–309. [Google Scholar] [CrossRef]
- Goerigk, L.; Grimme, S. A thorough benchmark of density functional methods for general main group thermochemistry, kinetics, and noncovalent interactions. Phys. Chem. Chem. Phys. 2011, 13, 6670–6688. [Google Scholar] [CrossRef]
- Goerigk, L.; Hansen, A.; Bauer, C.; Ehrlich, S.; Najibi, A.; Grimme, S. A Look at the Density Functional Theory Zoo with the Advanced GMTKN55 Database for General Main Group Thermochemistry, Kinetics and Noncovalent Interactions. Phys. Chem. Chem. Phys. 2017, 19, 32184–32215. [Google Scholar] [CrossRef]
- Mardirossian, N.; Head-Gordon, M. Thirty Years of Density Functional Theory in Computational Chemistry: An Overview and Extensive Assessment of 200 Density Functionals. Mol. Phys. 2017, 115, 2315–2372. [Google Scholar] [CrossRef]
- Schwabe, T.; Grimme, S. Calculation of Magnetic Couplings with Double-Hybrid Density Functionals. J. Phys. Chem. Lett. 2010, 1, 1201–1204. [Google Scholar] [CrossRef]
- Valero, R.; Costa, R.; de PR Moreira, I.; Truhlar, D.G.; Illas, F. Performance of the M06 family of exchange-correlation functionals for predicting magnetic coupling in organic and inorganic molecules. J. Chem. Phys. 2008, 128, 114103. [Google Scholar] [CrossRef]
- Gupta, T.; Rajeshkumar, T.; Rajaraman, G. Magnetic exchange in {GdIII–radical} complexes: Method assessment, mechanism of coupling and magneto-structural correlations. Phys. Chem. Chem. Phys. 2014, 16, 14568–14577. [Google Scholar] [CrossRef]
- Vogiatzis, K.D.; Klopper, W.; Mavrandonakis, A.; Fink, K. Magnetic properties of paddlewheels and trinuclear clusters with exposed metal sites. ChemPhysChem 2011, 12, 3307–3319. [Google Scholar] [CrossRef]
- Bossek, U.; Hummel, H.; Weyhermüller, T.; Wieghardt, K.; Russell, S.; van der Wolf, L.; Kolb, U. The [Mn2IV(μ-O)(μ-PhBO2)2]2+ Unit: A New Structural Model for Manganese-Containing Metalloproteins. Angew. Chem. Int. Ed. 1996, 35, 1552–1554. [Google Scholar] [CrossRef]
- Ménage, S.; Girerd, J.-J.; Gleizes, A. A [Mn2O(MeCO2)2(H2O)2(bipy)2]2+(bipy = 2,2′-bipyridine) Unit with Accessible Co-ordination Sites. Contribution to the Modelling of the Photosynthetic Oxygen Evolving Centre. J. Chem. Soc. Chem. Commun. 1988, 431–432. [Google Scholar] [CrossRef]
- Bossek, U.; Saher, M.; Weyhermuller, T.; Wieghardt, K. Asymmetric Mixed Valence Manganese Complexes Containing the [Mn(μ-O)2(μ-MeCo2)Mn]2+ Core and their Catalase Reactivity. J. Chem. Soc. Chem. Commun. 1992, 1780–1782. [Google Scholar] [CrossRef]
- Chan, G.K.-L.; Sharma, S. The Density Matrix Renormalization Group in Quantum Chemistry. Annu. Rev. Phys. Chem. 2011, 62, 465–481. [Google Scholar] [CrossRef]
- Pal, S.; Olmstead, M.M.; Armstrong, W.H. Syntheses, Structures, and Properties of [Mn2(μ-O)(2)(μ-O2CCH3)(fac-Bpea)2](ClΟ4)2 and Two Halide-Ligated Dioxo-Bridged Dimers Derived Therefrom—[Mn2(μ-O)2×2(mer-Bpea)2](ClO4)2 (X = F, Cl). Inorg. Chem. 1995, 34, 4708–4715. [Google Scholar] [CrossRef]
- Wieghardt, K.; Bossek, U.; Nuber, B.; Weiss, J.; Bonvoisin, J.; Corbella, M.; Vitols, S.E.; Girerd, J.J. Synthesis, Crystal Structures, Reactivity, and Magnetochemistry of a Series of Binuclear Complexes of Manganese(II), -(III), and -(IV) of Biological Relevance. The Crystal Structure of [L′MnIV(μ-O)3MnIVL′](PF6)2.H2O Containing an Unprecedented Short Mn···Mn distance of 2.296 Å. J. Am. Chem. Soc. 1988, 110, 7398–7411. [Google Scholar]
- Niemann, A.; Bossek, U.; Wieghardt, K.; Butzlaff, C.; Trautwein, A.X.; Nuber, B. A New Structure–Magnetism Relationship for Face-Sharing Transition-Metal Complexes with d3–d3 Electronic Configuration. Angew. Chem. Int. Ed. 1992, 31, 311–313. [Google Scholar] [CrossRef]
- Goerigk, L.; Mehta, N. A Trip to the Density Functional Theory Zoo: Warnings and Recommendations for the User. Aust. J. Chem. 2019. [Google Scholar] [CrossRef]
- Tao, J.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. Climbing the Density Functional Ladder: Nonempirical Meta-Generalized Gradient Approximation Designed for Molecules and Solids. Phys. Rev. Lett. 2003, 91, 146401. [Google Scholar] [CrossRef]
- Sun, J.; Ruzsinszky, A.; Perdew, J.P. Strongly Constrained and Appropriately Normed Semilocal Density Functional. Phys. Rev. Lett. 2015, 115, 036402. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward Reliable Density Functional Methods Without Adjustable Parameters: The PBE0 Model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Karton, A.; Tarnopolsky, A.; Lamère, J.-F.; Schatz, G.C.; Martin, J.M.L. Highly Accurate First-Principles Benchmark Data Sets for the Parametrization and Validation of Density Functional and Other Approximate Methods. Derivation of a Robust, Generally Applicable, Double-Hybrid Functional for Thermochemistry and Thermochemical Kinetics. J. Phys. Chem. A 2008, 112, 12868–12886. [Google Scholar]
- Grimme, S. Improved second-order Moller-Plesset perturbation theory by separate scaling of parallel- and antiparallel-spin pair correlation energies. J. Chem. Phys. 2003, 118, 9095–9102. [Google Scholar] [CrossRef]
- Kozuch, S.; Gruzman, D.; Martin, J.M.L. DSD-BLYP: A General Purpose Double Hybrid Density Functional Including Spin Component Scaling and Dispersion Correction. J. Phys. Chem. C 2010, 114, 20801–20808. [Google Scholar] [CrossRef]
- Kozuch, S.; Martin, J.M.L. DSD-PBEP86: In search of the best double-hybrid DFT with spin-component scaled MP2 and dispersion corrections. Phys. Chem. Chem. Phys. 2011, 13, 20104–20107. [Google Scholar] [CrossRef]
- Kozuch, S.; Martin, J.M.L. Spin-component-scaled double hybrids: An extensive search for the best fifth-rung functionals blending DFT and perturbation theory. J. Comput. Chem. 2013, 34, 2327–2344. [Google Scholar] [CrossRef]
- Jung, Y.; Lochan, R.C.; Dutoi, A.D.; Head-Gordon, M. Scaled opposite-spin second order Møller–Plesset correlation energy: An economical electronic structure method. J. Chem. Phys. 2004, 121, 9793–9802. [Google Scholar] [CrossRef]
- Paul, S.; Cox, N.; Pantazis, D.A. What Can We Learn from a Biomimetic Model of Nature’s Oxygen-Evolving Complex? Inorg. Chem. 2017, 56, 3875–3888. [Google Scholar] [CrossRef]
- Pantazis, D.A.; Ames, W.; Cox, N.; Lubitz, W.; Neese, F. Two Interconvertible Structures that Explain the Spectroscopic Properties of the Oxygen-Evolving Complex of Photosystem II in the S2 State. Angew. Chem. Int. Ed. 2012, 51, 9935–9940. [Google Scholar] [CrossRef]
- Beal, N.J.; Corry, T.A.; O’Malley, P.J. Comparison between Experimental and Broken Symmetry Density Functional Theory (BS-DFT) Calculated Electron Paramagnetic Resonance (EPR) Parameters of the S2 State of the Oxygen-Evolving Complex of Photosystem II in Its Native (Calcium) and Strontium-Substituted Form. J. Phys. Chem. B 2017, 121, 11273–11283. [Google Scholar]
- Amabilino, S.; Deeth, R.J. DFT Analysis of Spin Crossover in Mn(III) Complexes: Is a Two-Electron S = 2 to S = 0 Spin Transition Feasible? Inorg. Chem. 2017, 56, 2602–2613. [Google Scholar] [CrossRef]
- Cox, N.; Ames, W.; Epel, B.; Kulik, L.V.; Rapatskiy, L.; Neese, F.; Messinger, J.; Wieghardt, K.; Lubitz, W. Electronic Structure of a Weakly Antiferromagnetically Coupled MnIIMnIII Model Relevant to Manganese Proteins: A Combined EPR, 55Mn-ENDOR, and DFT Study. Inorg. Chem. 2011, 50, 8238–8251. [Google Scholar] [CrossRef]
- Ames, W.; Pantazis, D.A.; Krewald, V.; Cox, N.; Messinger, J.; Lubitz, W.; Neese, F. Theoretical evaluation of structural models of the S2 state in the oxygen evolving complex of photosystem II: Protonation states and magnetic interactions. J. Am. Chem. Soc. 2011, 133, 19743–19757. [Google Scholar] [CrossRef]
- Zheng, J.; Xu, X.; Truhlar, D.G. Minimally augmented Karlsruhe basis sets. Theor. Chem. Acc. 2011, 128, 295–305. [Google Scholar] [CrossRef]
- Cossi, M.; Rega, N.; Scalmani, G.; Barone, V. Energies, Structures, and Electronic Properties of Molecules in Solution with the C-PCM Solvation Model. J. Comput. Chem. 2003, 24, 669–681. [Google Scholar] [CrossRef]
- Peverati, R.; Head-Gordon, M. Orbital Optimized Double-Hybrid Density Functionals. J. Chem. Phys. 2013, 139, 024110. [Google Scholar] [CrossRef]
- Najibi, A.; Goerigk, L. A Comprehensive Assessment of the Effectiveness of Orbital Optimization in Double-Hybrid Density Functionals in the Treatment of Thermochemistry, Kinetics, and Noncovalent Interactions. J. Phys. Chem. A 2018, 122, 5610–5624. [Google Scholar] [CrossRef]
- Chan, B.; Goerigk, L.; Radom, L. On the Inclusion of Post-MP2 Contributions to Double-Hybrid Density Functionals. J. Comput. Chem. 2016, 37, 183–193. [Google Scholar] [CrossRef]
- Zhekova, H.R.; Seth, M.; Ziegler, T. Calculation of the exchange coupling constants of copper binuclear systems based on spin-flip constricted variational density functional theory. J. Chem. Phys. 2011, 135, 184105. [Google Scholar] [CrossRef]
- Groom, C.R.; Bruno, I.J.; Lightfoot, M.P.; Ward, S.C. The Cambridge Structural Database. Acta Cryst. 2016, B72, 171–179. [Google Scholar] [CrossRef]
- Neese, F. Software Update: The ORCA Program System, Version 4.0. Wires Comput. Mol. Sci. 2018, 8, e1327. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate ab initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H–Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Van Lenthe, E.; Baerends, E.J.; Snijders, J.G. Relativistic Regular Two-component Hamiltonians. J. Chem. Phys. 1993, 99, 4597–4610. [Google Scholar] [CrossRef]
- Van Lenthe, E.; Baerends, E.J.; Snijders, J.G. Relativistic Total-Energy Using Regular Approximations. J. Chem. Phys. 1994, 101, 9783–9792. [Google Scholar] [CrossRef]
- Pantazis, D.A.; Chen, X.Y.; Landis, C.R.; Neese, F. All-electron scalar relativistic basis sets for third-row transition metal atoms. J. Chem. Theory Comput. 2008, 4, 908–919. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F. Accurate Coulomb-Fitting Basis Sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef] [PubMed]
- Neese, F.; Wennmohs, F.; Hansen, A.; Becker, U. Efficient, Approximate and Parallel Hartree–Fock and Hybrid DFT Calculations. A ‘Chain-of-Spheres’ Algorithm for the Hartree–Fock Exchange. Chem. Phys. 2009, 356, 98–109. [Google Scholar] [CrossRef]
- Hellweg, A.; Hättig, C.; Höfener, S.; Klopper, W. Optimized accurate auxiliary basis sets for RI-MP2 and RI-CC2 calculations for the atoms Rb to Rn. Theor. Chem. Acc. 2007, 117, 587–597. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).