Electronic Structure of Cubane-Like Vanadium–Nitrogen Cationic Clusters [V4N4]+ and [V6N6]+
Abstract
:1. Introduction
2. Results
2.1. Electronic Structure of [V4N4]+
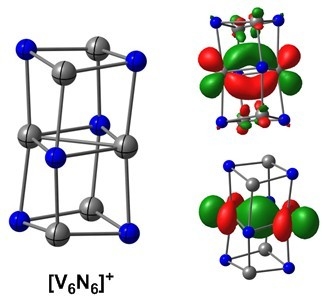
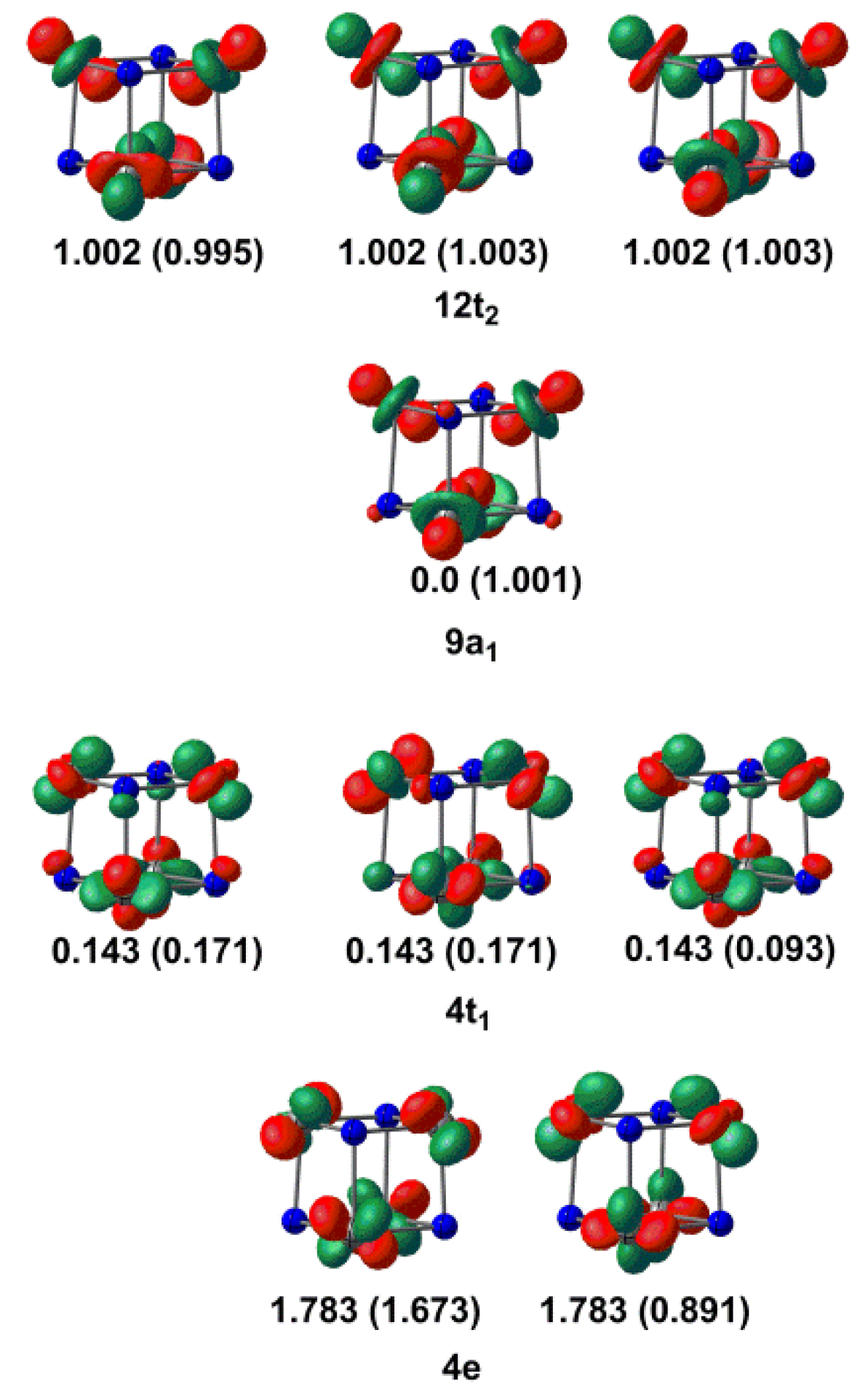
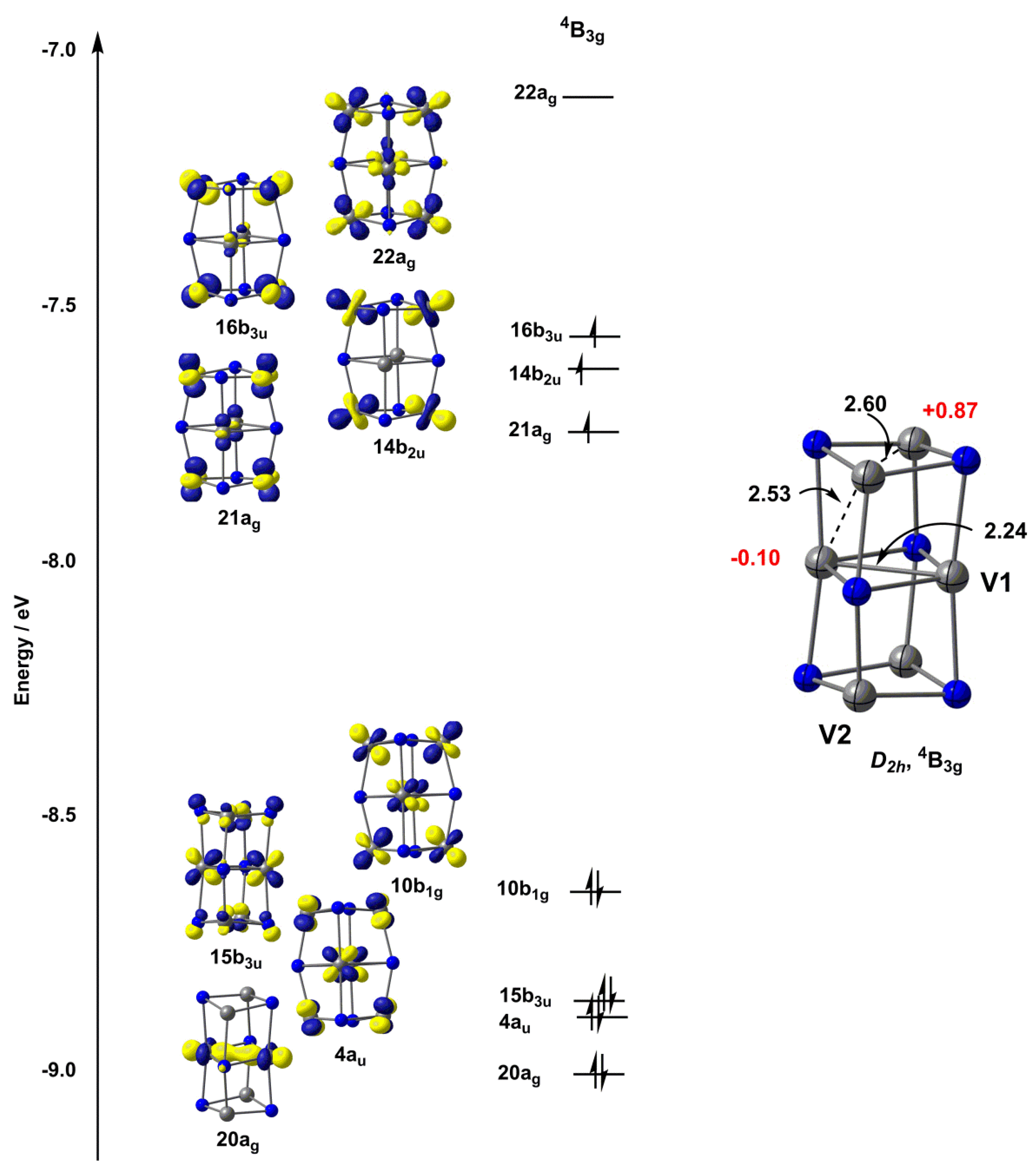
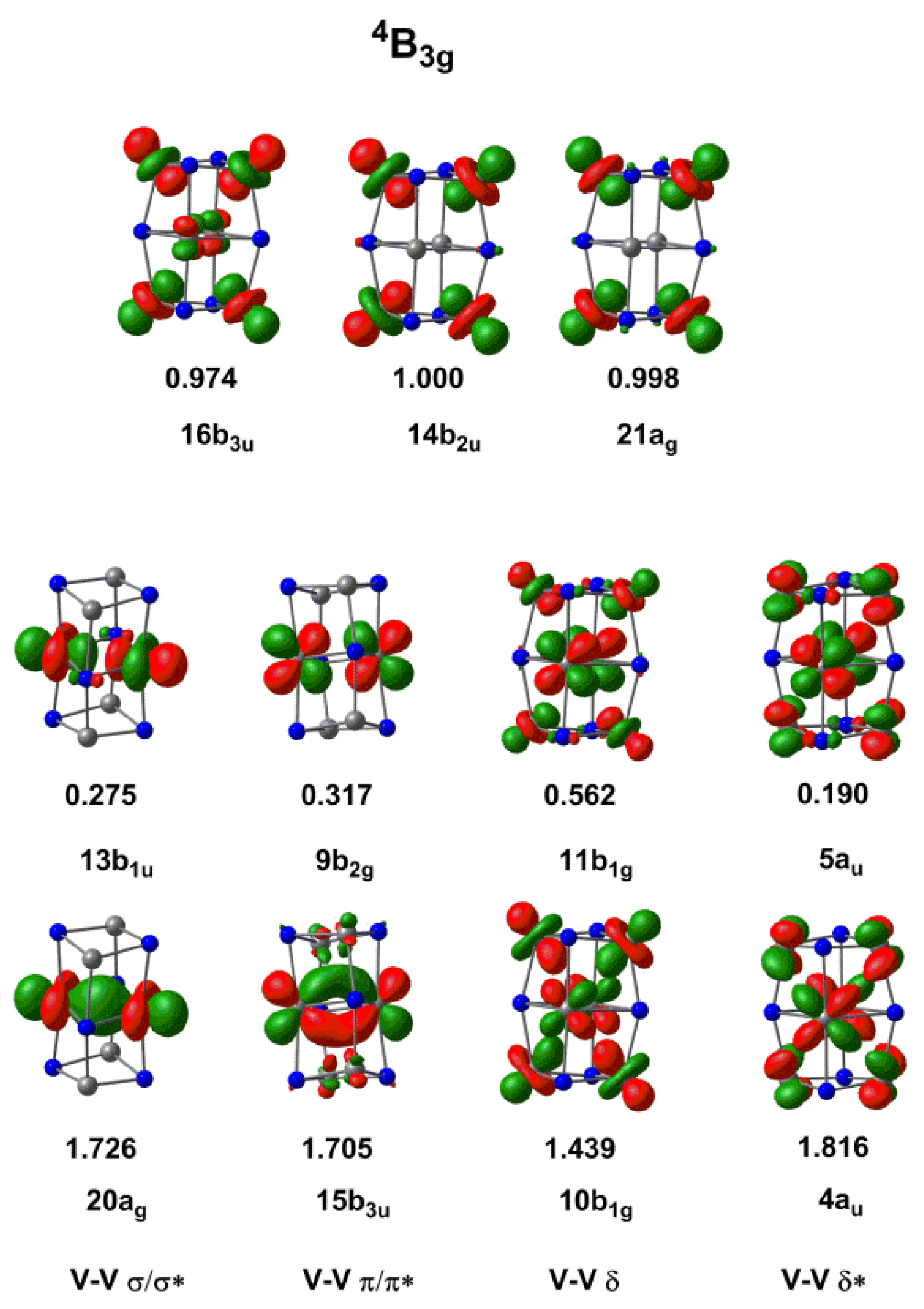
2.2. Electronic Structure of [V6N6]+
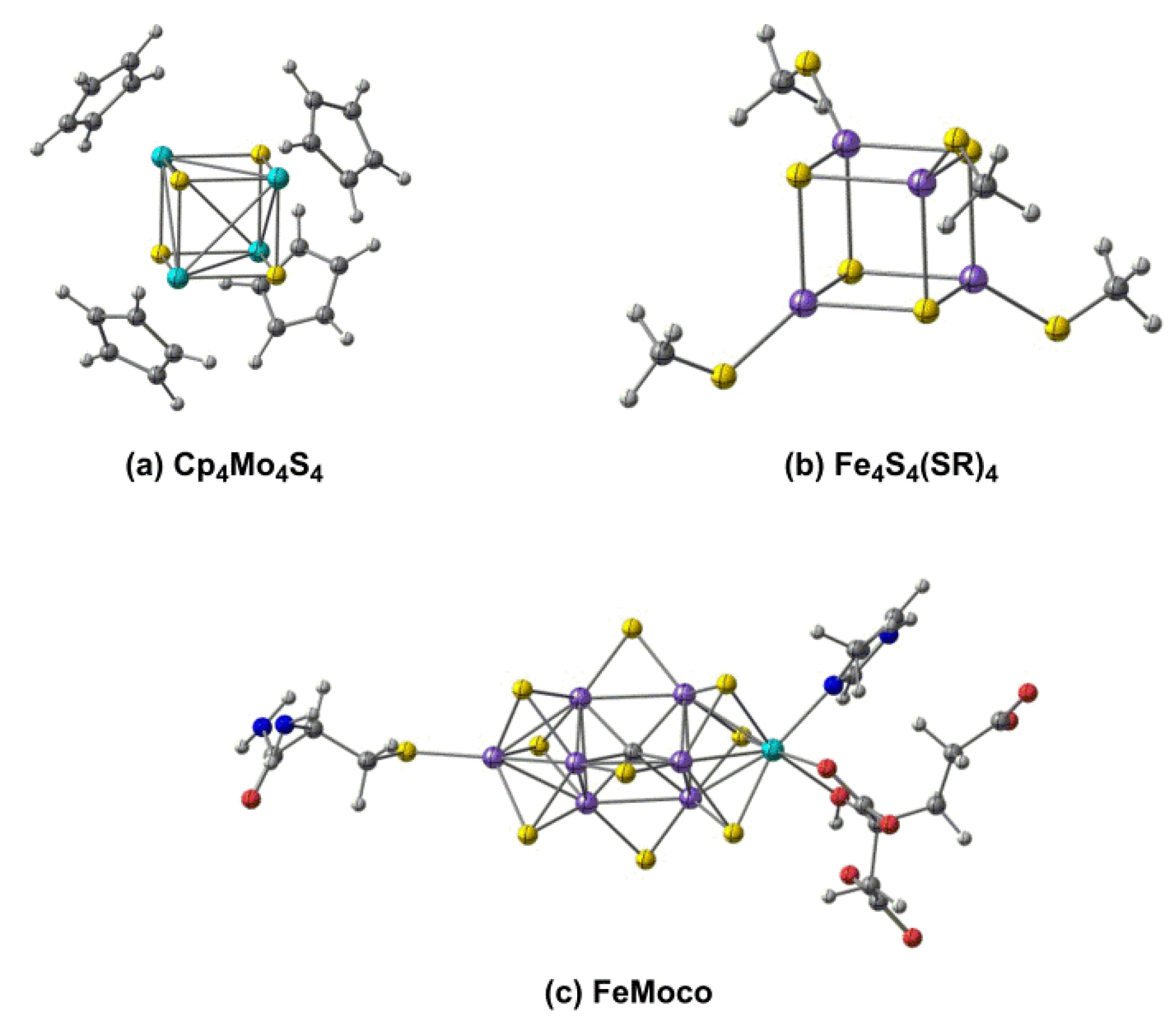
3. Discussion
4. Computational Methods
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Hargreaves, J.S.J. Heterogeneous catalysis with metal nitrides. Coord. Chem. Rev. 2013, 257, 2015–2031. [Google Scholar] [CrossRef]
- Guo, J.; Wang, P.; Wu, G.; Wu, A.; Hu, D.; Xiong, Z.; Wang, J.; Yu, P.; Chang, F.; Chen, Z.; et al. Lithium imide synergy with 3d transition-metal nitrides leading to unprecedented catalytic activities for ammonia decomposition. Angew. Chem. Int. Ed. 2015, 54, 2950–2954. [Google Scholar] [CrossRef]
- Lotz, C.R.; Sebba, F. Energies of activation for decomposition of ammonia catalysed by the nitrides of the 4th series transition elements. Trans. Faraday Soc. 1957, 53, 1246–1252. [Google Scholar] [CrossRef]
- Liao, M.Y.; Gotoh, Y.; Tsuji, H.; Ishikawa, J. Crystallographic structure and composition of vanadium nitride films deposited by direct sputtering of a compound target. J. Vac. Sci. Technol. A 2004, 22, 146–150. [Google Scholar] [CrossRef]
- Abghoui, Y.; Garden, A.L.; Howalt, J.G.; Vegge, T.; Skúlason, E. Electroreduction of N2 to ammonia at ambient conditions on mononitrides of Zr, Nb, Cr, and V: A DFT guide for experiments. ACS Catal. 2016, 6, 635–646. [Google Scholar] [CrossRef]
- Choi, D.; Blomgren, G.E.; Kumta, P.N. Fast and reversible surface redox reaction in nanocrystalline vanadium vitride supercapacitors. Adv. Mater. 2006, 18, 1178–1182. [Google Scholar] [CrossRef]
- McGill, W.J.; Sebba, F. The kinetics of ammonia decomposition over vanadium nitride. J. Catal. 1963, 2, 104–108. [Google Scholar] [CrossRef]
- Zhou, X.; Shang, C.; Gu, L.; Dong, S.; Chen, X.; Han, P.; Li, L.; Yao, J.; Liu, Z.; Xu, H.; et al. Mesoporous coaxial titanium nitride–vanadium nitride fibers of core–shell structures for high-performance supercapacitors. ACS Appl. Mater. Interfaces 2011, 3, 3058–3063. [Google Scholar] [CrossRef] [PubMed]
- Indlekofer, G.; Mariot, J.M.; Lengauer, W.; Beauprez, E.; Oelhafen, P.; Hague, C.F. Electronic structure of stoichiometric and substoichiometric vanadium nitrade from photoelectron spectroscopy. Solid State Commun. 1989, 72, 419–423. [Google Scholar] [CrossRef]
- Wu, G.; Yang, M.; Guo, X.; Wang, J. Comparative DFT study of N2 and NO adsorption on vanadium clusters Vn (n = 2–13). J. Comput. Chem. 2012, 33, 1854–1861. [Google Scholar] [CrossRef] [PubMed]
- Reddy, B.V.; Khanna, S.N. Structure and stability of TinNm clusters. Phys. Rev. B 1996, 54, 2240–2243. [Google Scholar] [CrossRef]
- Jakubikova, E.; Rappé, A.K.; Bernstein, E.R. Density functional theory study of small vanadium oxide clusters. J. Phys. Chem. A 2007, 111, 12938–12943. [Google Scholar] [CrossRef]
- Aetukuri, N.B.; Gray, A.X.; Drouard, M.; Cossale, M.; Gao, L.; Reid, A.H.; Kukreja, R.; Ohldag, H.; Jenkins, C.A.; Arenholz, E.; et al. Control of the metal–insulator transition in vanadium dioxide by modifying orbital occupancy. Nat. Phys. 2013, 9, 661–666. [Google Scholar] [CrossRef]
- Hirabayashi, S.; Ichihashi, M. Adsorption and dehydrogenation of ammonia on vanadium and niobium nitride cluster cations. Int. J. Mass Spectrom. 2016, 407, 86–91. [Google Scholar] [CrossRef]
- Pralong, V. Lithium intercalation into transition metal oxides: A route to generate new ordered rock salt type structure. Prog. Solid State Chem. 2009, 37, 262–277. [Google Scholar] [CrossRef]
- Burdett, J.K.; Mitchell, J.F. Nonstoichiometry in early transition metal compounds with the rock salt structure. Prog. Solid State Chem. 1995, 23, 131–170. [Google Scholar] [CrossRef]
- Liu, Q.Q.; Pan, H.L.; Tao, W.H.; Wu, H.T. New rock salt structure dielectric material Li2Ni3TiO6 at microwave frequency. J. Mater. Sci: Mater. Electron. 2017, 28, 9893–9899. [Google Scholar] [CrossRef]
- Nakamura, A.; Ukita, M.; Shimoda, N.; Furushima, Y.; Toyoura, K.; Matsunaga, K. First-principles calculations on slip system activation in the rock salt structure: Electronic origin of ductility in silver chloride. Philos. Mag. 2017, 97, 1281–1310. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Castleman, A.W., Jr. Growth of titanium nitride: From clusters to microcrystals. J. Chem. Phys. 1993, 98, 231–235. [Google Scholar] [CrossRef]
- Marksteiner, P.; Weinberger, P.; Neckel, A.; Zeller, R.; Dederichs, P.H. Electronic structure of substoichiometric carbides and nitrides of titanium and vanadium. Phys. Rev. B 1986, 33, 812–822. [Google Scholar] [CrossRef]
- Beinert, H.; Holm, R.H.; Münck, E. Iron–sulfur clusters: Nature’s modular, multipurpose structures. Science 1997, 277, 653–659. [Google Scholar] [CrossRef] [PubMed]
- Noodleman, L. A model for the spin states of high-potential iron–sulfur [Fe4S4]3+ proteins. Inorg. Chem. 1988, 27, 3677–3679. [Google Scholar] [CrossRef]
- Lancaster, K.M.; Roemelt, M.; Ettenhuber, P.; Hu, Y.; Ribbe, M.W.; Neese, F.; Bergmann, U.; DeBeer, S. X-ray emission spectroscopy evidences a central carbon in the nitrogenase iron-molybdenum cofactor. Science 2011, 334, 974–977. [Google Scholar] [CrossRef] [PubMed]
- Bjornsson, R.; Neese, F.; DeBeer, S. Revisiting the Mössbauer isomer shifts of the FeMoco cluster of nitrogenase and the cofactor charge. Inorg. Chem. 2017, 56, 1470–1477. [Google Scholar] [CrossRef]
- Krewald, V.; Neese, F.; Pantazis, D.A. On the magnetic and spectroscopic properties of high-valent Mn3CaO4 cubanes as structural units of natural and artificial water-oxidizing catalysts. J. Am. Chem. Soc. 2013, 135, 5726–5739. [Google Scholar] [CrossRef] [PubMed]
- McGrady, J.E. Periodic trends in metal–metal bonding in cubane clusters, (C5H5)4M4E4 [M = Cr, Mo, E = O, S]. J. Chem. Soc. Dalton Trans. 1999, 1393–1400. [Google Scholar] [CrossRef]
- Gorelsky, S.I. Complexes with a single metal–metal bond as a sensitive probe of quality of exchange-correlation functionals. J. Chem. Theor. Comput. 2012, 8, 908–914. [Google Scholar] [CrossRef]
- Spivak, M.; Arcisauskaite, V.; López, X.; McGrady, J.E.; de Graaf, C. A multiconfigurational approach to the electronic structure of trichromium extended metal atom chains. Dalton Trans. 2017, 46, 6202–6211. [Google Scholar] [CrossRef] [PubMed]
- Tao, J.M.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. Climbing the density functional ladder: Nonempirical meta-generalized gradient approximation designed for molecules and solids. Phys. Rev. Lett. 2003, 91, 146401:1–146401:4. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Truhlar, D.G. A new local density functional for main-group thermochemistry, transition metal bonding, thermochemical kinetics, and noncovalent interactions. J. Chem. Phys. 2006, 125, 194101:1–194101:18. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Perdew, J.P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B 1986, 33, 8822–8824. [Google Scholar] [CrossRef]
- Stefan, G.; Stephan, E.; Lars, G. Effect of the damping function in dispersion corrected density functional theory. J. Comp. Chem. 2011, 32, 1456–1465. [Google Scholar]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Paulsen, H.; Trautwein, A.X. Density functional theory calculations for spin-crossover complexes. Top. Curr. Chem. 2012, 235, 197–219. [Google Scholar]
- Davidson, E.R. Natural orbitals. Adv. Quant. Chem. 1972, 6, 235–266. [Google Scholar]
- Davidson, E.R. Properties and uses of natural orbitals. Rev. Mod. Phys. 1972, 44, 451–464. [Google Scholar] [CrossRef]
- Roos, B.O. The complete active space self-consistent field method and its applications in electronic structure calculations. Adv. Chem. Phys. 1987, 69, 399–445. [Google Scholar]
- Veryazov, V.; Malmqvist, P.A.; Roos, B.O. How to select active space for multiconfigurational quantum chemistry? Int. J. Quantum Chem. 2011, 111, 3329–3338. [Google Scholar] [CrossRef]
- Kandalam, A.K.; Blanco, M.A.; Pandey, R. Theoretical study of AlnNn, GanNn, and InnNn (n = 4, 5, 6) clusters. J. Phys. Chem. B 2002, 106, 1945–1953. [Google Scholar] [CrossRef]
- Li, M.G.; Dzubak, A.L.; Mulla, A.; Brogden, D.W.; Berry, J.F.; Gagliardi, L. Assessing metal–metal multiple bonds in Cr–Cr, Mo–Mo, and W–W compounds and a hypothetical U–U compound: A quantum chemical study comparing DFT and multireference methods. Chem. Eur. J. 2012, 18, 1737–1749. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision A.03; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Neese, F. Software update: The ORCA program system, version 4.0. WIREs Comput. Mol. Sci. 2018, 8. [Google Scholar] [CrossRef]
- Schäfer, A.; Huber, C.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr. J. Chem. Phys. 1994, 100, 5829–5835. [Google Scholar] [CrossRef]
- Neese, F. An improvement of the resolution of the identity approximation for the formation of the Coulomb matrix. J. Comp. Chem. 2003, 24, 1740–1747. [Google Scholar] [CrossRef]
- Angeli, C.; Cimiraglia, R.; Evangelisti, S.; Leininger, T.; Malrieu, J.-P. Introduction of N-electron valence states for multireference perturbation theory. J. Chem. Phys. 2001, 114, 10252–10264. [Google Scholar] [CrossRef]
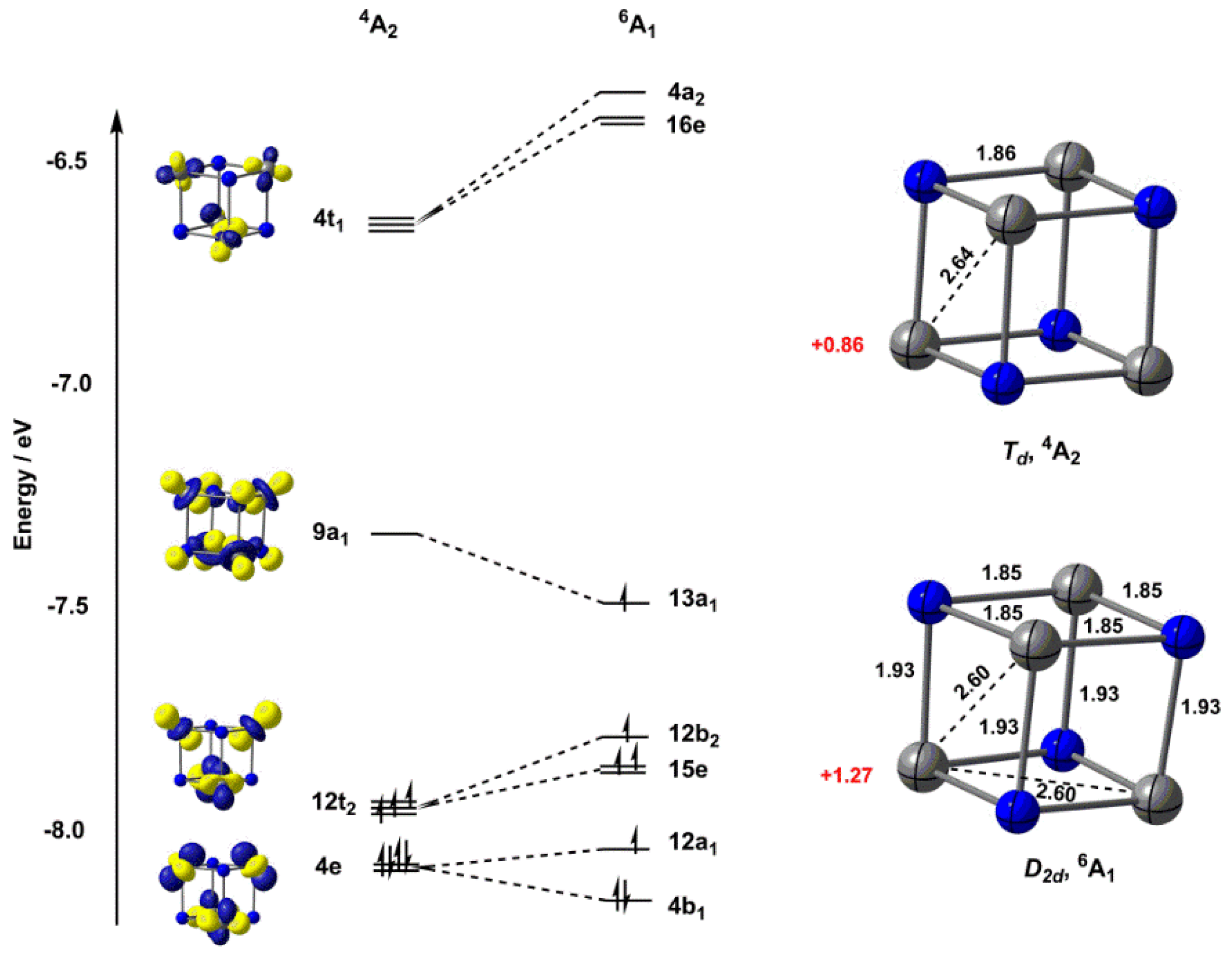
| Functional | 4A2 | 6A1 | ||||
|---|---|---|---|---|---|---|
| V–V/Å | ρ(V) | Erel/eV | V–V/Å | ρ(V) | Erel/eV | |
| TPSS | 2.64 | 0.86 | +0.19 | 2.60 | 1.27 | 0 |
| M06L | 2.62 | 0.90 | +0.38 | 2.56 | 1.29 | 0 |
| BP86 | 2.65 | 0.85 | 0 | 2.61 | 1.28 | +0.08 |
| BP86-D3 | 2.65 | 0.85 | 0 | 2.61 | 1.28 | +0.09 |
| BLYP | 2.68 | 0.85 | 0 | 2.63 | 1.28 | +0.05 |
| B3LYP | 2.62 | 0.70 | +0.65 | 2.62 | 1.36 | 0 |
| Functional | 4B3g | |
|---|---|---|
| V–V/Å 1 | ρ(V) 2 | |
| TPSS | 2.23, 2.52, 2.60 | −0.10, 0.87 |
| M06L | 2.23, 2.51, 2.58 | −0.12, 0.92 |
| BP86 | 2.24, 2.53, 2.62 | −0.03, 0.85 |
| BLYP | 2.27, 2.55, 2.64 | −0.05, 0.86 |
| B3LYP | 2.24, 2.53, 2.59 | −0.39, 1.07 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, P.; Zhang, J.-G.; McGrady, J.E. Electronic Structure of Cubane-Like Vanadium–Nitrogen Cationic Clusters [V4N4]+ and [V6N6]+. Inorganics 2019, 7, 52. https://doi.org/10.3390/inorganics7040052
He P, Zhang J-G, McGrady JE. Electronic Structure of Cubane-Like Vanadium–Nitrogen Cationic Clusters [V4N4]+ and [V6N6]+. Inorganics. 2019; 7(4):52. https://doi.org/10.3390/inorganics7040052
Chicago/Turabian StyleHe, Piao, Jian-Guo Zhang, and John E. McGrady. 2019. "Electronic Structure of Cubane-Like Vanadium–Nitrogen Cationic Clusters [V4N4]+ and [V6N6]+" Inorganics 7, no. 4: 52. https://doi.org/10.3390/inorganics7040052
APA StyleHe, P., Zhang, J.-G., & McGrady, J. E. (2019). Electronic Structure of Cubane-Like Vanadium–Nitrogen Cationic Clusters [V4N4]+ and [V6N6]+. Inorganics, 7(4), 52. https://doi.org/10.3390/inorganics7040052