Modelling the (Essential) Role of Proton Transport by Electrolyte Bases for Electrochemical Water Oxidation at Near-Neutral pH
Abstract
:1. Introduction
2. Results
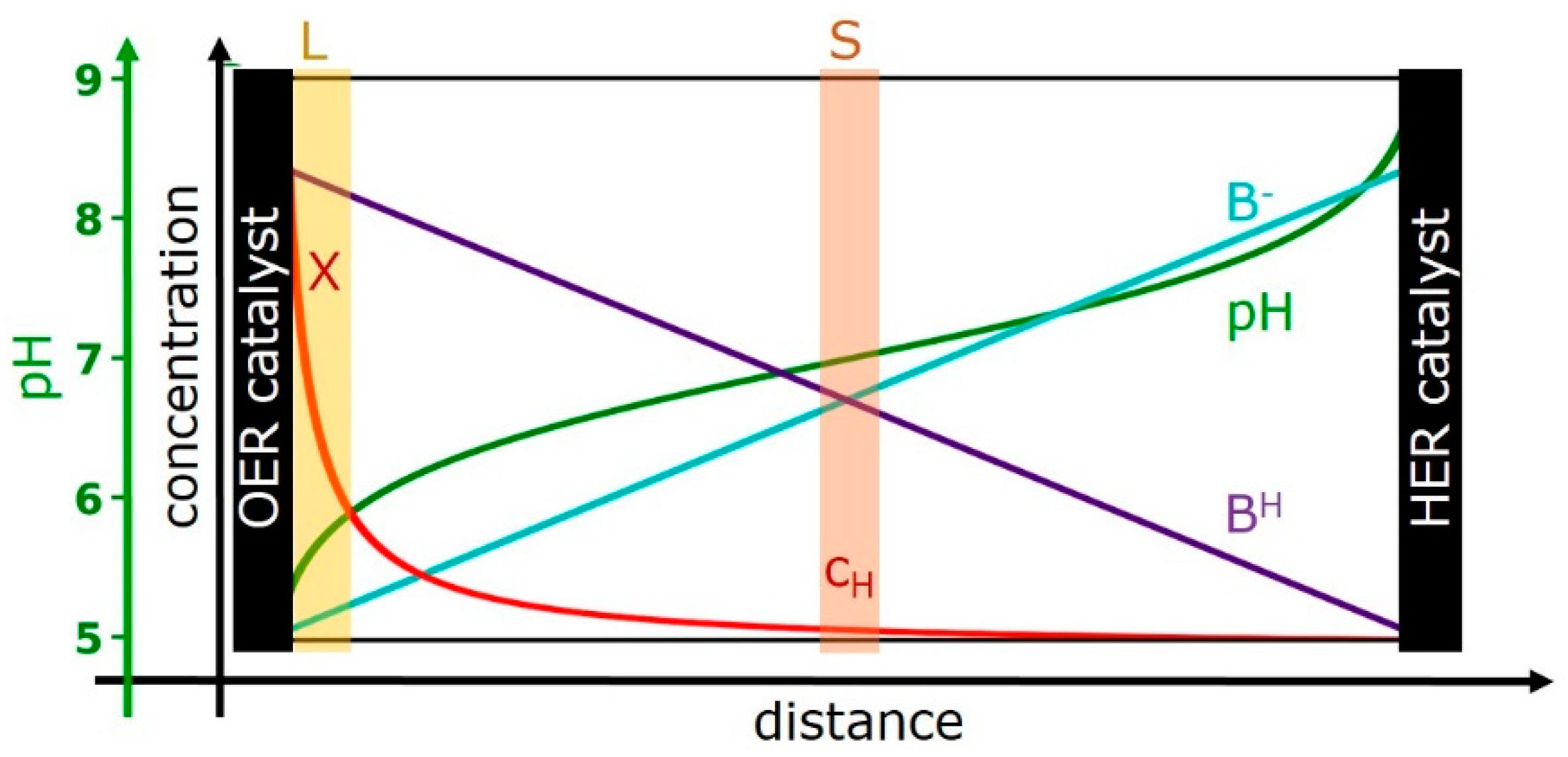
2.1. Outline of the Model
- Region A: the (volume-active) OER catalyst film (Cat)—with its proton activity, XCat, and electric overpotential, ΔV.
- Region B: a solvent layer (L) at the outer catalyst-film surface, the “buffer layer”—with its proton activity, XLayer.
- Region C: the bulk solvent (S)—with its proton concentration, cH (pH = −log cH).
2.2. Catalytic Electron Flux
2.3. Proton Flux Mediated by Buffer Molecules
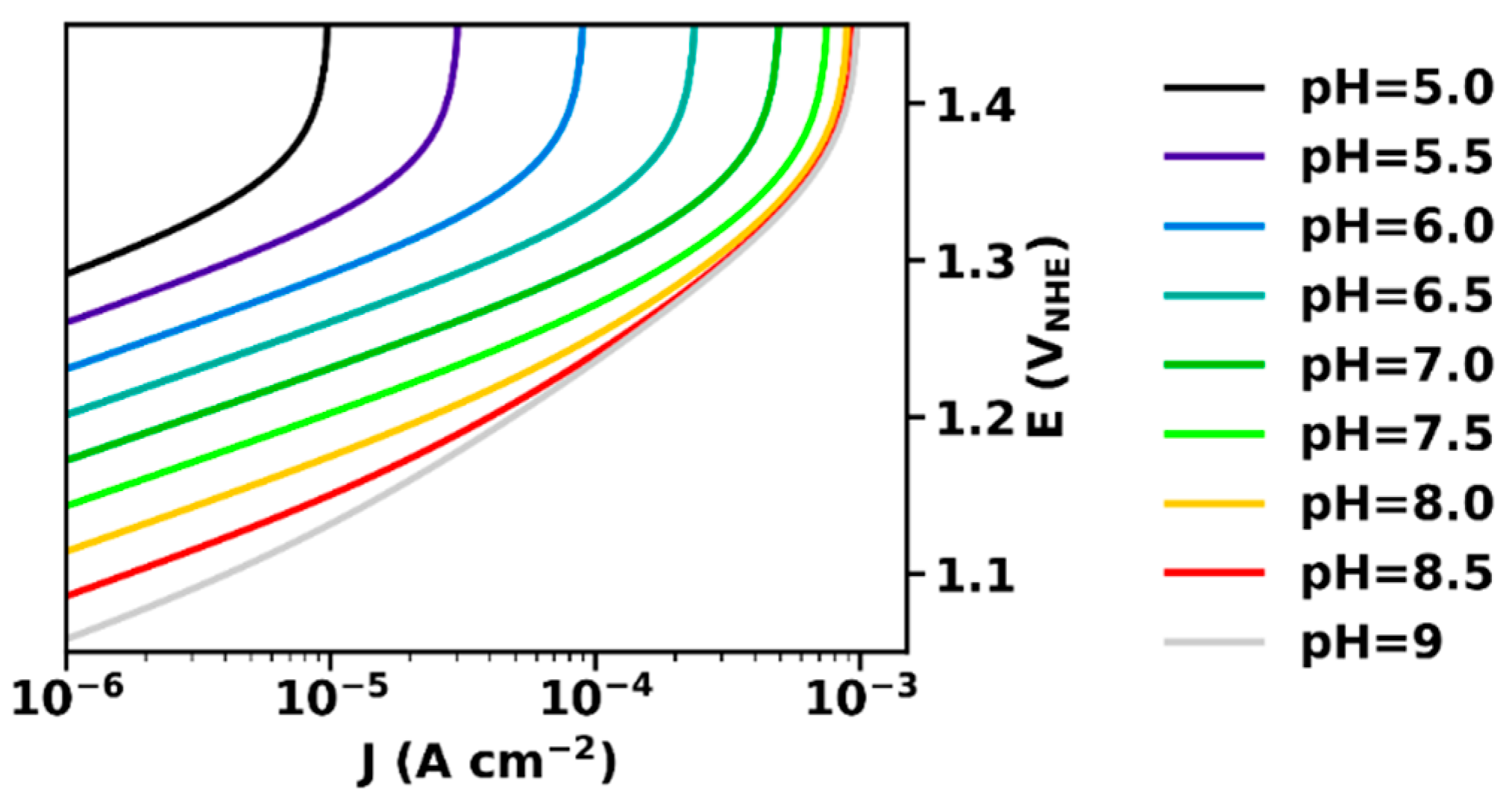
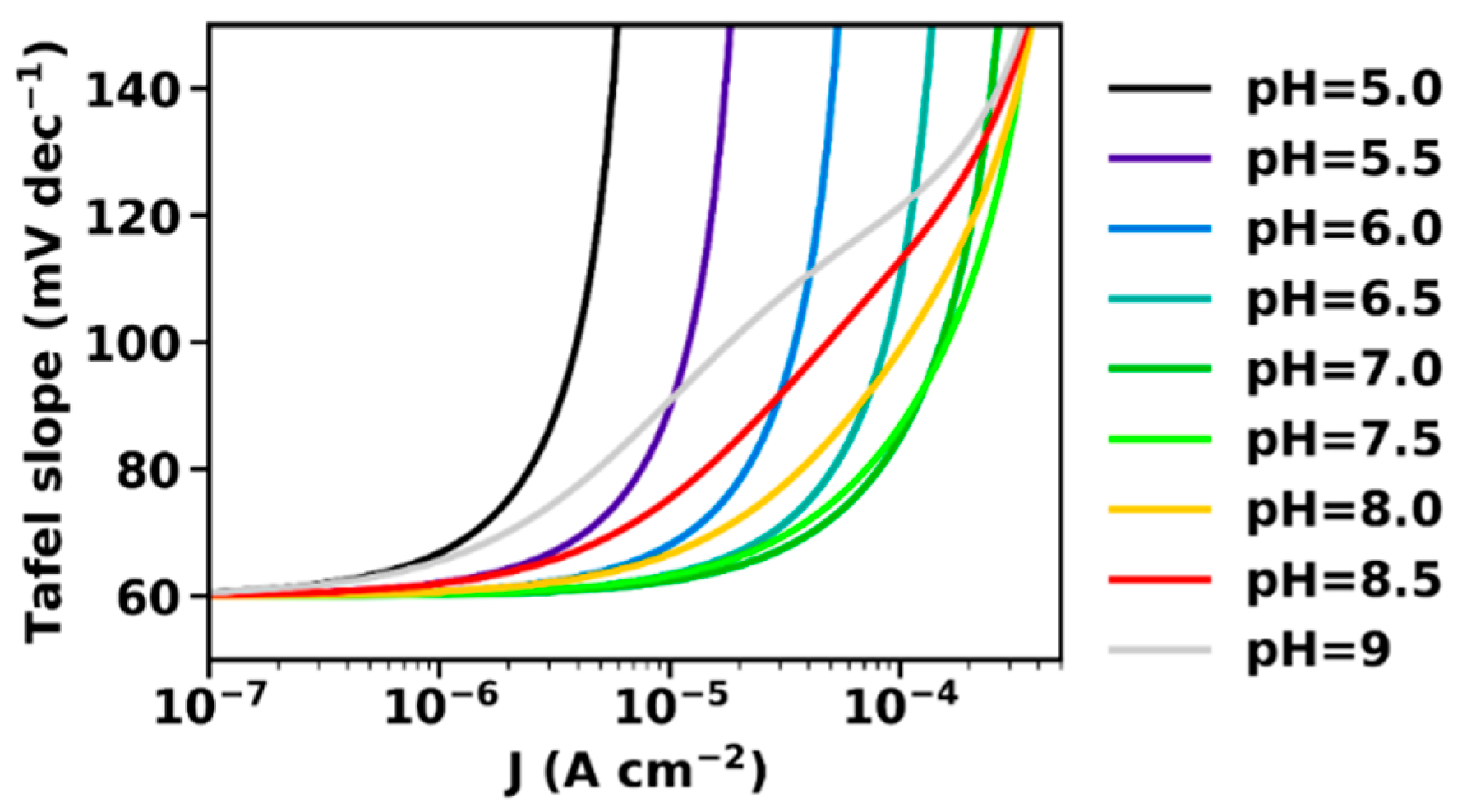
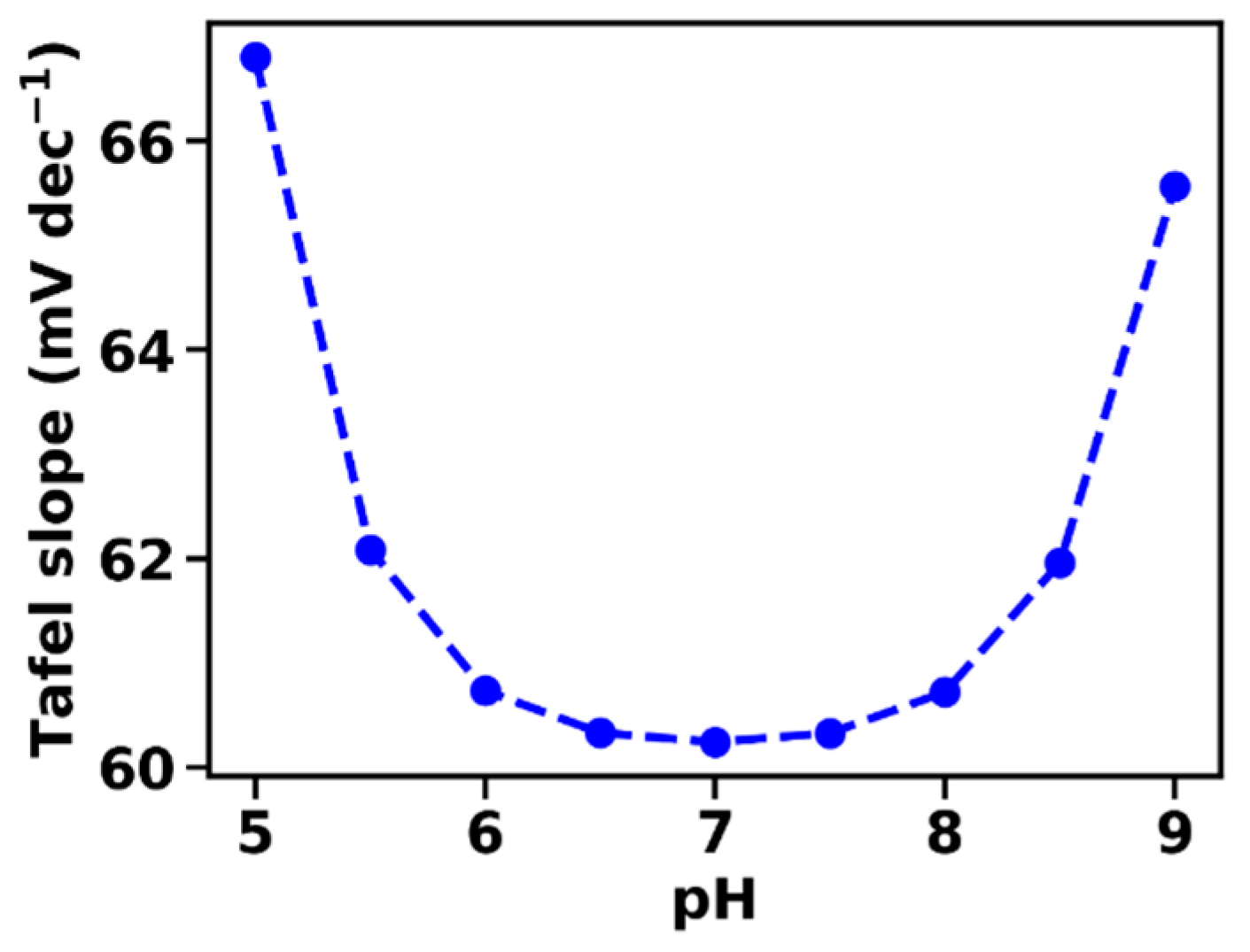
2.4. Current–Voltage Relation of OER Catalysis with Proton-Transport Limitations
3. Discussion
4. Conclusions
- For pH values ranging from about 2 to 12, the OER reaction essentially requires buffer molecules that facilitate proton transport. In the absence of an explicit buffer base, either only water molecules or hydroxide ions could serve as proton-transporting buffer bases; both cannot support significant current densities.
- In the presence of a buffer base, the maximal current density is determined by the concentration of unprotonated buffer molecules and, thus, by the solution pH and the pKa value of the used buffer, in line with experimental findings [15].
- At intermediate current densities, the Tafel slope is increased in comparison to the intrinsic Tafel slope measured at low current densities. The Tafel slope increase is avoided only when macroscopic mass transport limitations are negligible, which is achievable experimentally, e.g., by employing catalyst films deposited on rotating disc electrodes. This behavior has been observed repeatedly and is, at least, qualitatively well explained by the presented model. Whether quantitative agreement with the here described first-order model can be reached is still unclear; extension of the model to include also (e.g.,) limitations of proton transport within the catalyst or at the catalyst–solvent interface may be required.
- At intermediate current densities, the Tafel slopes reflect the buffering capacity of the BH/B− couple, a prediction that still requires experimental verification.
- The limitations by proton transport are assigned to proton transport in the electrolyte phase. This assumption predicts (macroscopic) acidification of the electrolyte near the electrode surface, a prediction that still awaits experimental verification. Additional factors may contribute to proton transport limitations, specifically rate limitations by proton transfer at the catalyst–electrolyte interface or within the catalyst film. In the present model, these are excluded by assuming equal proton activities within the catalyst film and the near-surface electrolyte.
Author Contributions
Funding
Conflicts of Interest
References
- Hunter, B.M.; Gray, H.B.; Müller, A.M. Earth-Abundant Heterogeneous Water Oxidation Catalysts. Chem. Rev. 2016, 116, 14120–14136. [Google Scholar] [CrossRef] [PubMed]
- Roger, I.; Shipman, M.A.; Symes, M.D. Earth-abundant catalysts for electrochemical and photoelectrochemical water splitting. Nat. Rev. Chem. 2017, 1, 0003. [Google Scholar] [CrossRef]
- Lewis, N.S.; Nocera, D.G. Powering the planet: Chemical challenges in solar energy utilization. Proc. Natl. Acad. Sci. USA 2006, 103, 15729–15735. [Google Scholar] [CrossRef] [PubMed]
- Gattrell, M.; Gupta, N.; Co, A. A review of the aqueous electrochemical reduction of CO2 to hydrocarbons at copper. J. Electroanal. Chem. 2006, 594, 1–19. [Google Scholar] [CrossRef]
- Jones, J.P.; Prakash, G.K.S.; Olah, G.A. Electrochemical CO2 Reduction: Recent Advances and Current Trends. Isr. J. Chem. 2014, 54, 1451–1466. [Google Scholar] [CrossRef]
- Ismail, A.A.; Bahnemann, D.W. Photochemical splitting of water for hydrogen production by photocatalysis: A review. Sol. Energy Mater. Sol. Cells 2014, 128, 85–101. [Google Scholar] [CrossRef]
- Hisatomi, T.; Kubota, J.; Domen, K. Recent advances in semiconductors for photocatalytic and photoelectrochemical water splitting. Chem. Soc. Rev. 2014, 43, 7520–7535. [Google Scholar] [CrossRef]
- Nocera, D.G. Chemistry of personalized solar energy. Inorg. Chem. 2009, 48, 10001–10017. [Google Scholar] [CrossRef]
- Nocera, D.G. The artificial leaf. Acc. Chem. Res. 2012, 45, 767–776. [Google Scholar] [CrossRef]
- Jin, J.; Walczak, K.; Singh, M.R.; Karp, C.; Lewis, N.S.; Xiang, C. An experimental and modeling/simulation-based evaluation of the efficiency and operational performance characteristics of an integrated. Energy Environ. Sci. 2014, 7, 3371–3380. [Google Scholar] [CrossRef]
- McKone, J.R.; Lewis, N.S.; Gray, H.B. Will Solar-Driven Water-Splitting Devices See the Light of Day? Chem. Mater. 2014, 26, 407–414. [Google Scholar] [CrossRef]
- Suter, S.; Cantoni, M.; Gaudy, Y.K.; Pokrant, S.; Haussener, S. Linking morphology and multi-physical transport in structured photoelectrodes. Sustain. Energy Fuels 2018, 2, 2661–2673. [Google Scholar] [CrossRef]
- Shinagawa, T.; Takanabe, K. Towards Versatile and Sustainable Hydrogen Production through Electrocatalytic Water Splitting: Electrolyte Engineering. ChemSusChem 2017, 10, 1318–1336. [Google Scholar] [CrossRef] [PubMed]
- Aiso, K.; Takeuchi, R.; Masaki, T.; Chandra, D.; Saito, K.; Yui, T. Carbonate Ions Induce Highly Efficient Electrocatalytic Water Oxidation by Cobalt Oxyhydroxide Nanoparticles. ChemSusChem 2017, 10, 687–692. [Google Scholar] [CrossRef] [PubMed]
- Klingan, K.; Ringleb, F.; Zaharieva, I.; Heidkamp, J.; Chernev, P.; Gonzalez-Flores, D.; Risch, M.; Fischer, A.; Dau, H. Water oxidation by amorphous cobalt-based oxides: Volume activity and proton transfer to electrolyte bases. ChemSusChem 2014, 7, 1301–1310. [Google Scholar] [CrossRef] [PubMed]
- Hunter, B.M.; Hieringer, W.; Winkler, J.R.; Gray, H.B.; Muller, A.M. Effect of interlayer anions on [NiFe]-LDH nanosheet water oxidation activity. Energy Environ. Sci. 2016, 9, 1734–1743. [Google Scholar] [CrossRef]
- Surendranath, Y.; Dinca, M.; Nocera, D.G. Electrolyte-dependent electrosynthesis and activity of cobalt-based water oxidation catalysts. J. Am. Chem. Soc. 2009, 131, 2615–2620. [Google Scholar] [CrossRef]
- Risch, M.; Klingan, K.; Ringleb, F.; Chernev, P.; Zaharieva, I.; Fischer, A.; Dau, H. Water oxidation by electrodeposited cobalt oxides―Role of anions and redox-inert cations in structure and function of the amorphous catalyst. ChemSusChem 2012, 5, 542–549. [Google Scholar] [CrossRef]
- Brodsky, C.N.; Bediako, D.K.; Shi, C.; Keane, T.P.; Costentin, C.; Billinge, S.J.L.; Nocera, D.G. Proton–Electron Conductivity in Thin Films of a Cobalt–Oxygen Evolving Catalyst. ACS Appl. Energy Mater. 2018, 1, 1–2. [Google Scholar] [CrossRef]
- Kanan, M.W.; Nocera, D.G. In situ formation of an oxygen-evolving catalyst in neutral water containing phosphate and Co2+. Science 2008, 321, 1072–1075. [Google Scholar] [CrossRef]
- Bergmann, A.; Zaharieva, I.; Dau, H.; Strasser, P. Electrochemical water splitting by layered and 3D cross-linked manganese oxides: Correlating structural motifs and catalytic activity. Energy Environ. Sci. 2013, 6, 2745–2755. [Google Scholar] [CrossRef]
- Yamaguchi, A.; Inuzuka, R.; Takashima, T.; Hayashi, T.; Hashimoto, K.; Nakamura, R. Regulating proton-coupled electron transfer for efficient water splitting by manganese oxides at neutral pH. Nat. Commun. 2014, 5, 4256. [Google Scholar] [CrossRef] [PubMed]
- Costentin, C.; Porter, T.R.; Saveant, J.-M. Conduction and Reactivity in Heterogeneous-Molecular Catalysis: New Insights in Water Oxidation Catalysis by Phosphate Cobalt Oxide Films. J. Am. Chem. Soc. 2016, 138, 5615–5622. [Google Scholar] [CrossRef] [PubMed]
- Bard, A.J.; Faulkner, L.R. Electrochemical Methods. Fundamentals and Application; Wiley: Hoboken, NJ, USA, 1980. [Google Scholar]
- Fletcher, S. Tafel slopes from first principles. J. Solid State Electrochem. 2009, 13, 537–549. [Google Scholar] [CrossRef]
- Bockris, J.O.; Otagawa, T. Mechanism of oxygen evolution on perovskites. J. Phys. Chem. 1983, 87, 2960–2971. [Google Scholar] [CrossRef]
- Shinagawa, T.; Garcia-esparza, A.T.; Takanabe, K. Insight on Tafel slopes from a microkinetic analysis of aqueous electrocatalysis for energy conversion. Sci. Rep. 2015, 5, 13801. [Google Scholar] [CrossRef] [PubMed]
- Bediako, D.K.; Costentin, C.; Jones, E.C.; Nocera, D.G.; Savéant, J.-M. Proton–Electron Transport and Transfer in Electrocatalytic Films. Application to a Cobalt-Based O2-Evolution Catalyst. J. Am. Chem. Soc. 2013, 135, 10492–10502. [Google Scholar] [CrossRef]
- Surendranath, Y.; Kanan, M.W.; Nocera, D.G. Mechanistic studies of the oxygen evolution reaction by a cobalt-phosphate catalyst at neutral pH. J. Am. Chem. Soc. 2010, 132, 16501–16509. [Google Scholar] [CrossRef]
- Zaharieva, I.; Chernev, P.; Risch, M.; Klingan, K.; Kohlhoff, M.; Fischer, A.; Dau, H. Electrosynthesis, functional and structural characterization of a water-oxidizing manganese oxide. Energy Environ. Sci. 2012, 5, 7081–7089. [Google Scholar] [CrossRef]
- Huynh, M.; Bediako, D.K.; Nocera, D.G. A Functionally Stable Manganese Oxide Oxygen Evolution Catalyst in Acid. J. Am. Chem. Soc. 2014, 136, 6002–6010. [Google Scholar] [CrossRef]
- Ullman, A.M.; Brodsky, C.N.; Li, N.; Zheng, S.-L.; Nocera, D.G. Probing Edge Site Reactivity of Oxidic Cobalt Water Oxidation Catalysts. J. Am. Chem. Soc. 2016, 138, 4229–4236. [Google Scholar] [CrossRef] [PubMed]
- Low, C.T.J.; Ponce de Leon, C.; Walsh, F.C. The Rotating Cylinder Electrode (RCE) and its Application to the Electrodeposition of Metals. Aust. J. Chem. 2005, 58, 246–262. [Google Scholar] [CrossRef]
- Schmidt, T.J.; Gasteiger, H.A.; Stäb, G.D.; Urban, P.M.; Kolb, D.M.; Behm, R.J. Characterization of High-Surface-Area Electrocatalysts Using a Rotating Disk Electrode Configuration. J. Electrochem. Soc. 1998, 145, 2354–2358. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dau, H.; Pasquini, C. Modelling the (Essential) Role of Proton Transport by Electrolyte Bases for Electrochemical Water Oxidation at Near-Neutral pH. Inorganics 2019, 7, 20. https://doi.org/10.3390/inorganics7020020
Dau H, Pasquini C. Modelling the (Essential) Role of Proton Transport by Electrolyte Bases for Electrochemical Water Oxidation at Near-Neutral pH. Inorganics. 2019; 7(2):20. https://doi.org/10.3390/inorganics7020020
Chicago/Turabian StyleDau, Holger, and Chiara Pasquini. 2019. "Modelling the (Essential) Role of Proton Transport by Electrolyte Bases for Electrochemical Water Oxidation at Near-Neutral pH" Inorganics 7, no. 2: 20. https://doi.org/10.3390/inorganics7020020
APA StyleDau, H., & Pasquini, C. (2019). Modelling the (Essential) Role of Proton Transport by Electrolyte Bases for Electrochemical Water Oxidation at Near-Neutral pH. Inorganics, 7(2), 20. https://doi.org/10.3390/inorganics7020020




