High-Pressure Modification of BiI3
Abstract
1. Introduction
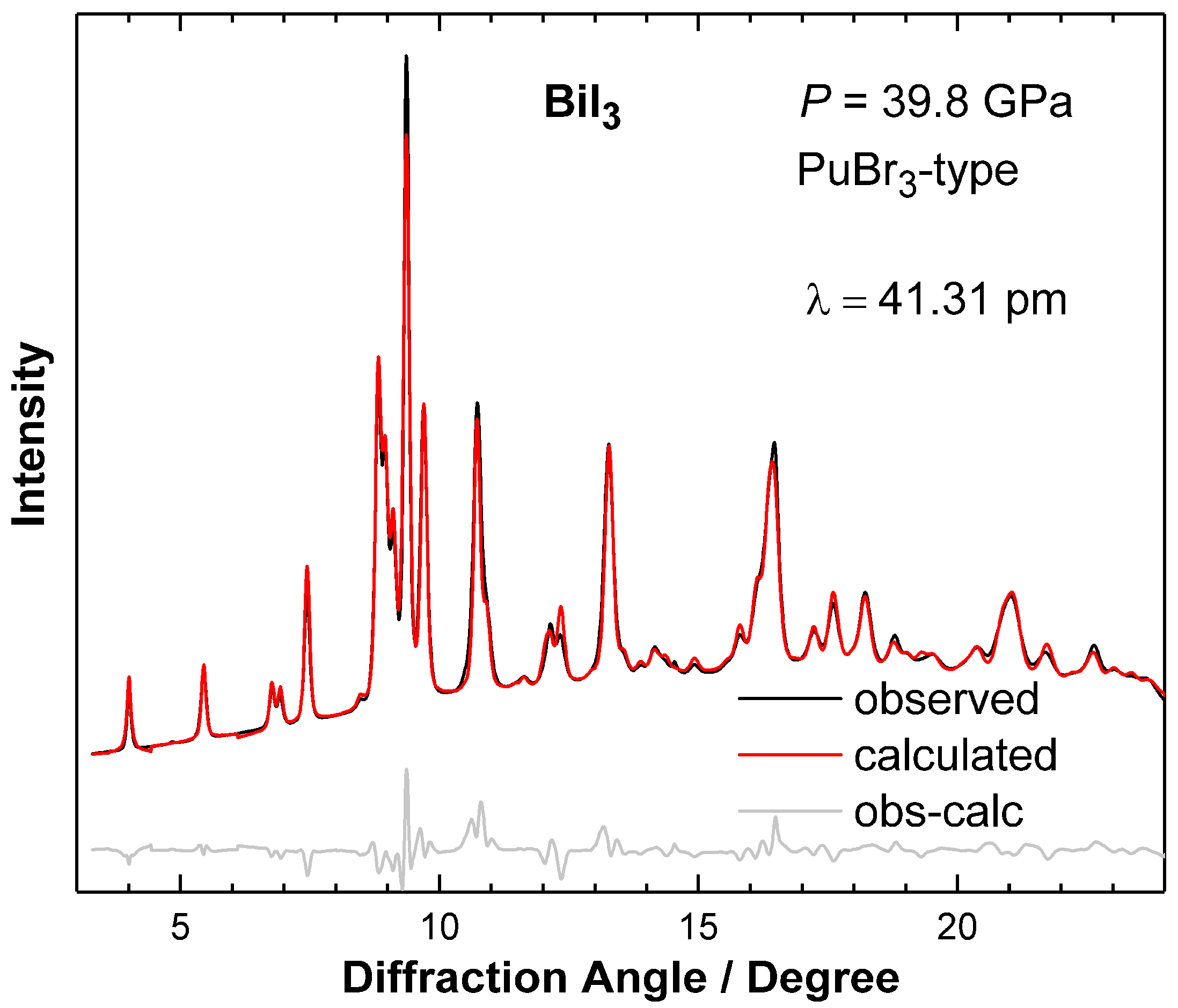
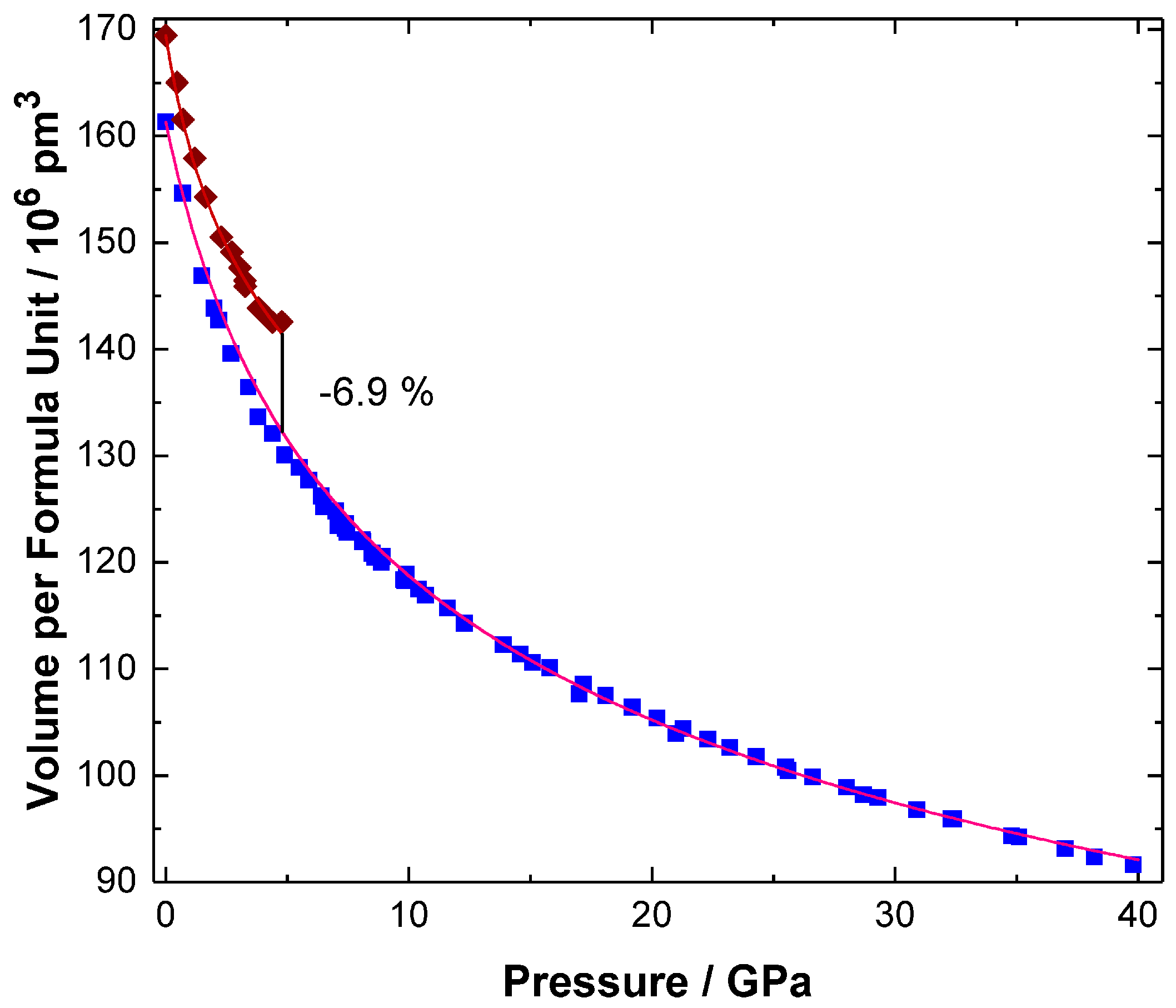
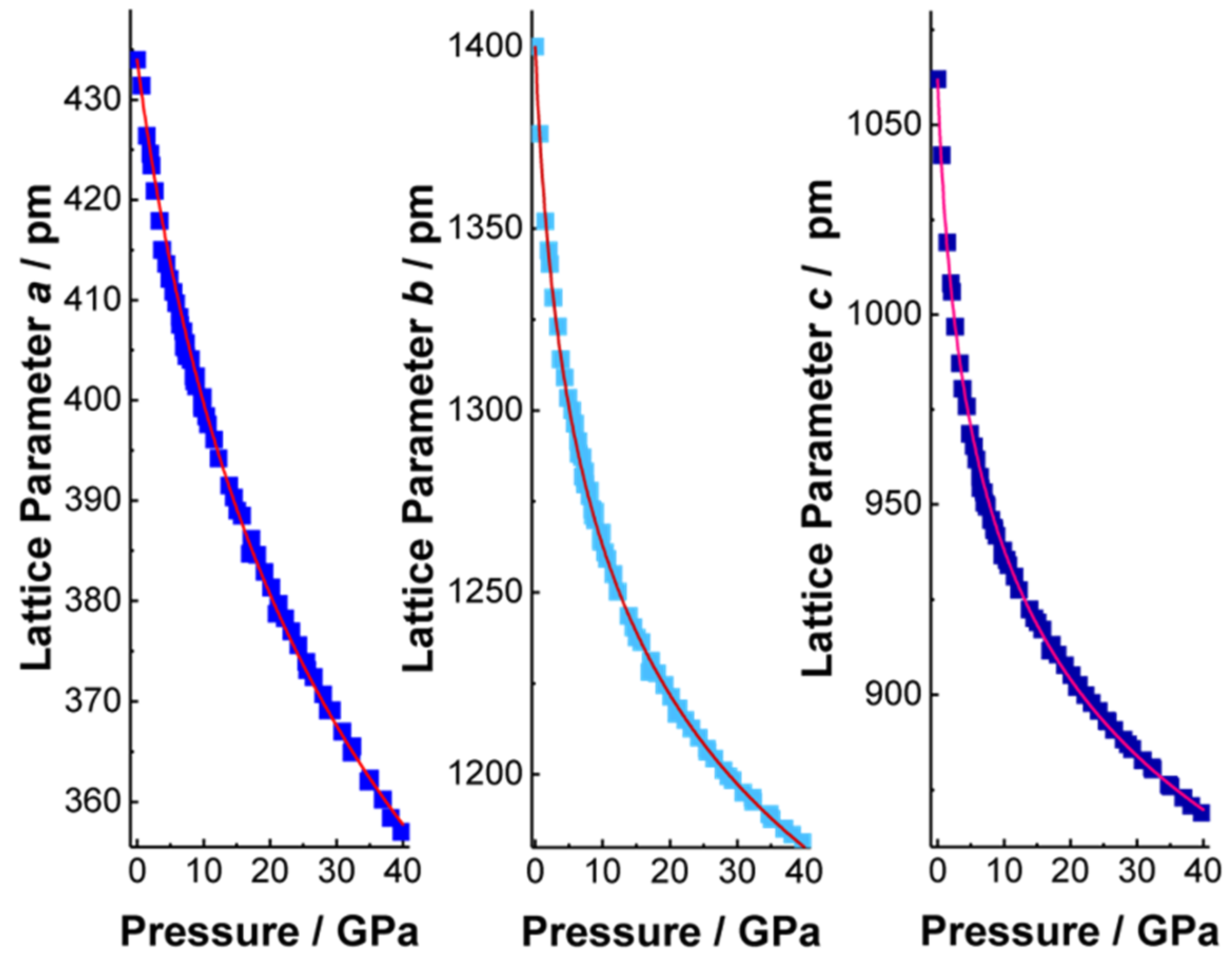
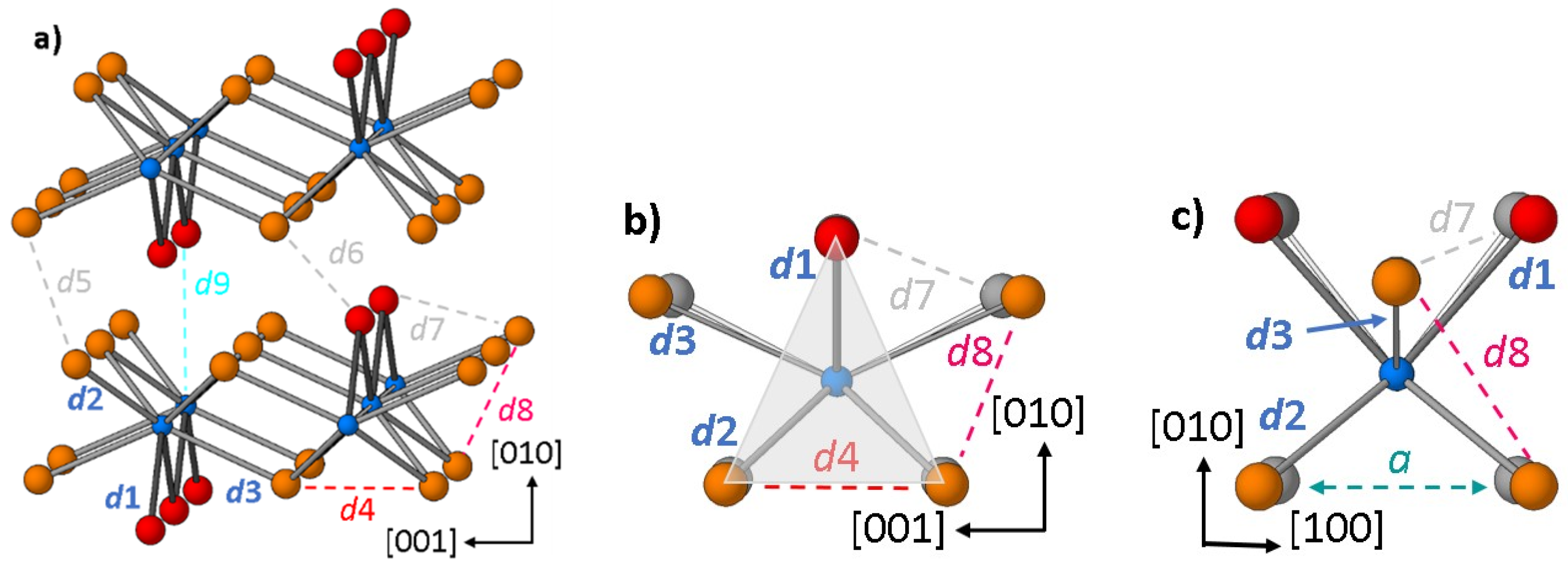
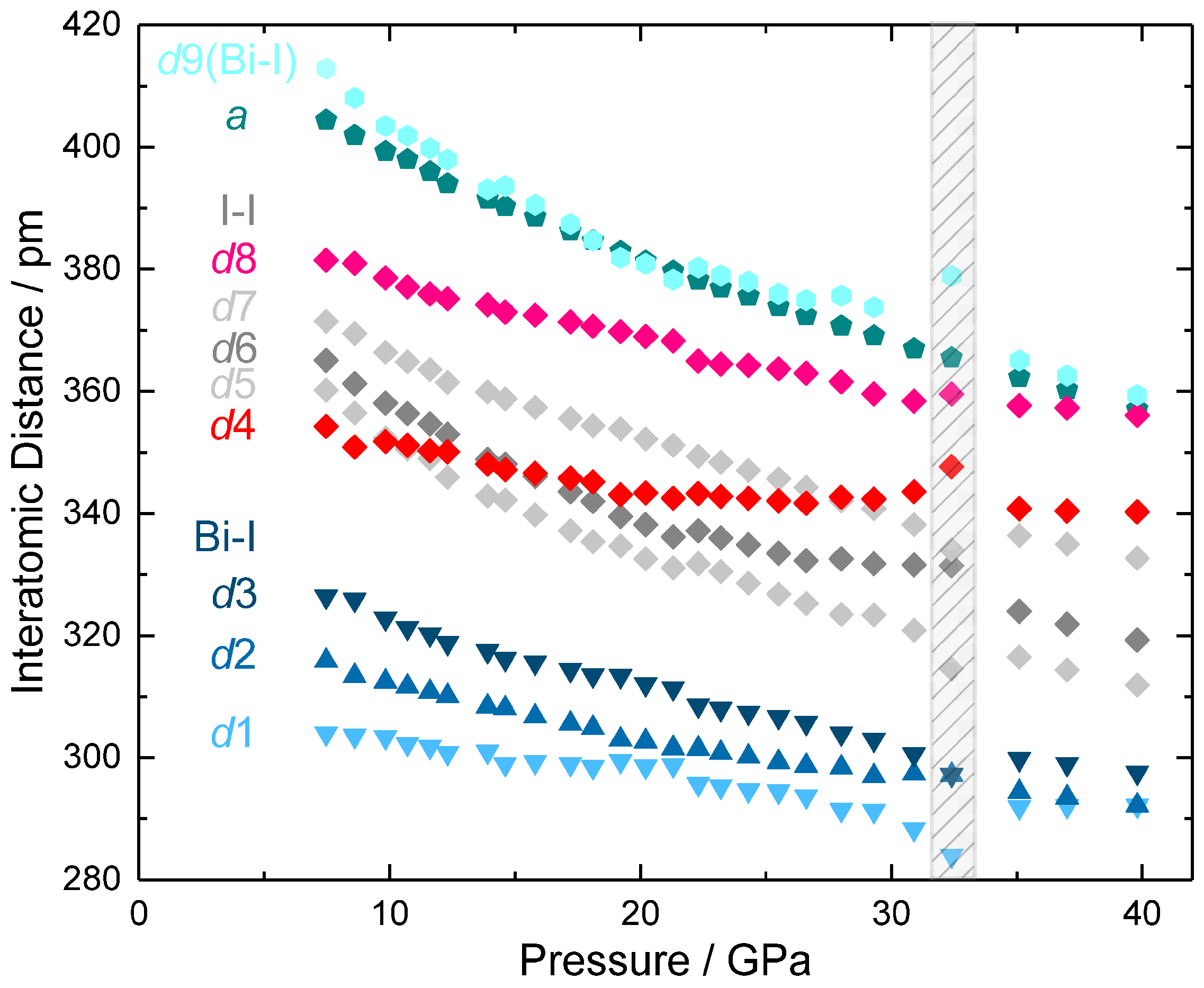
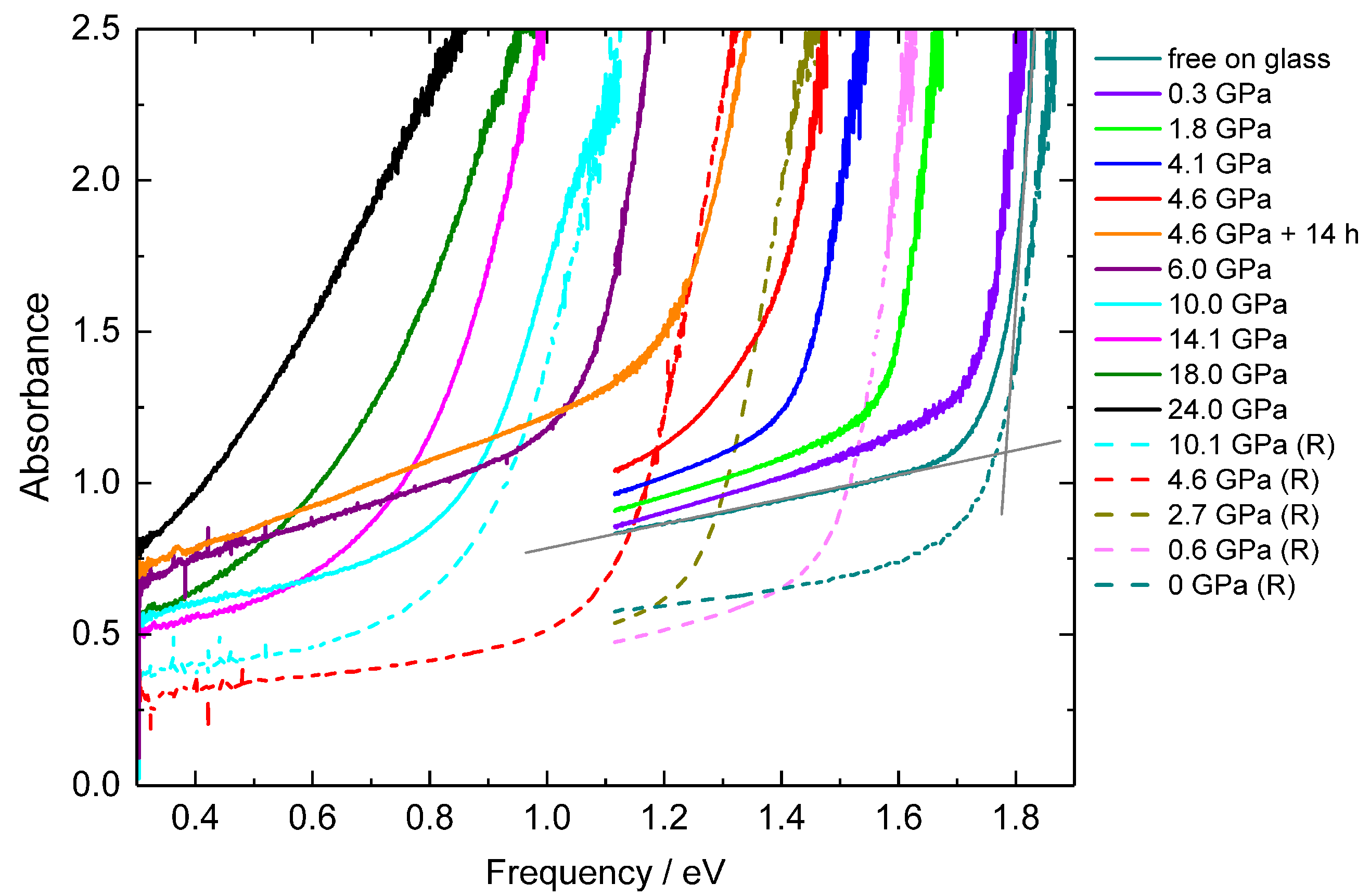
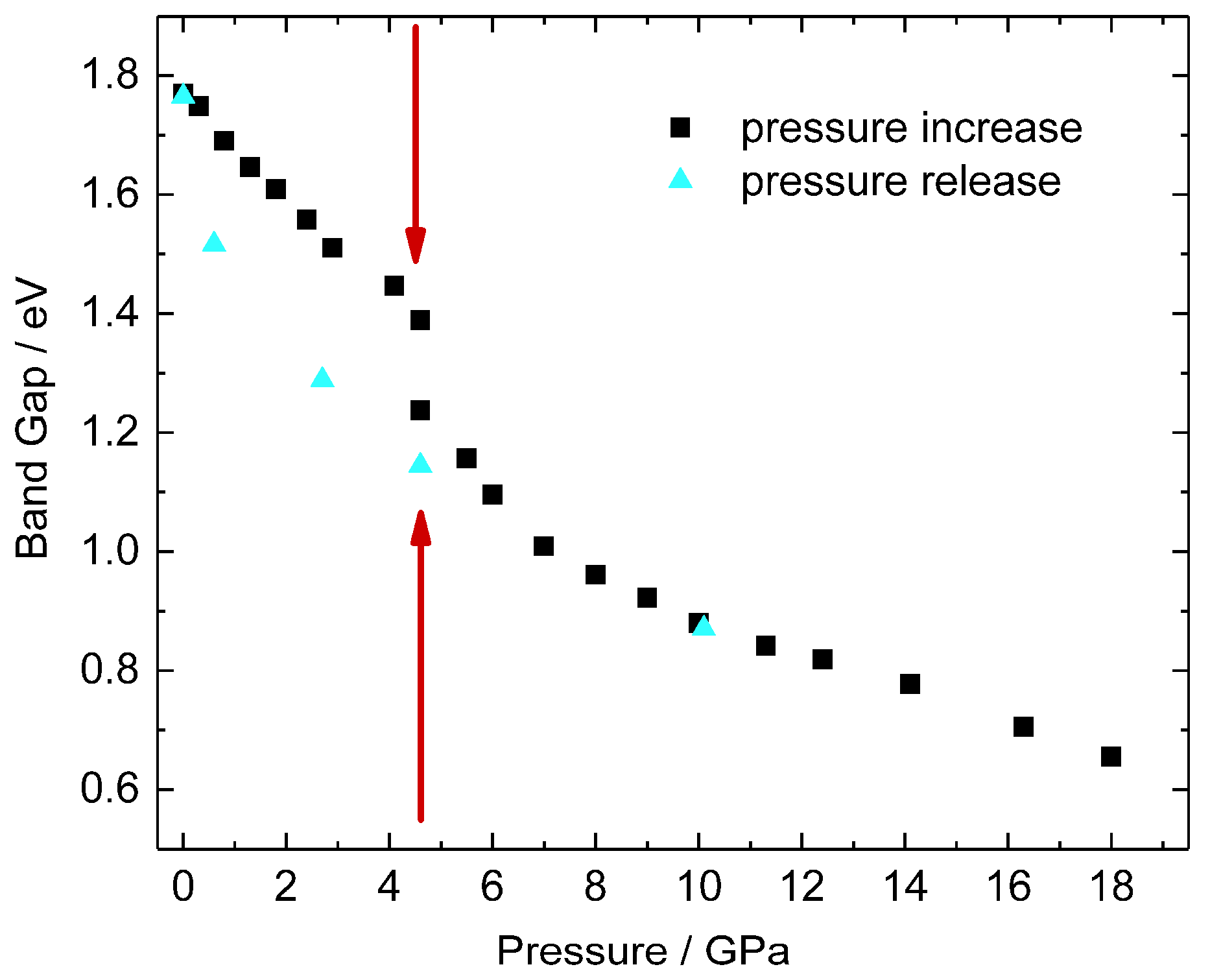
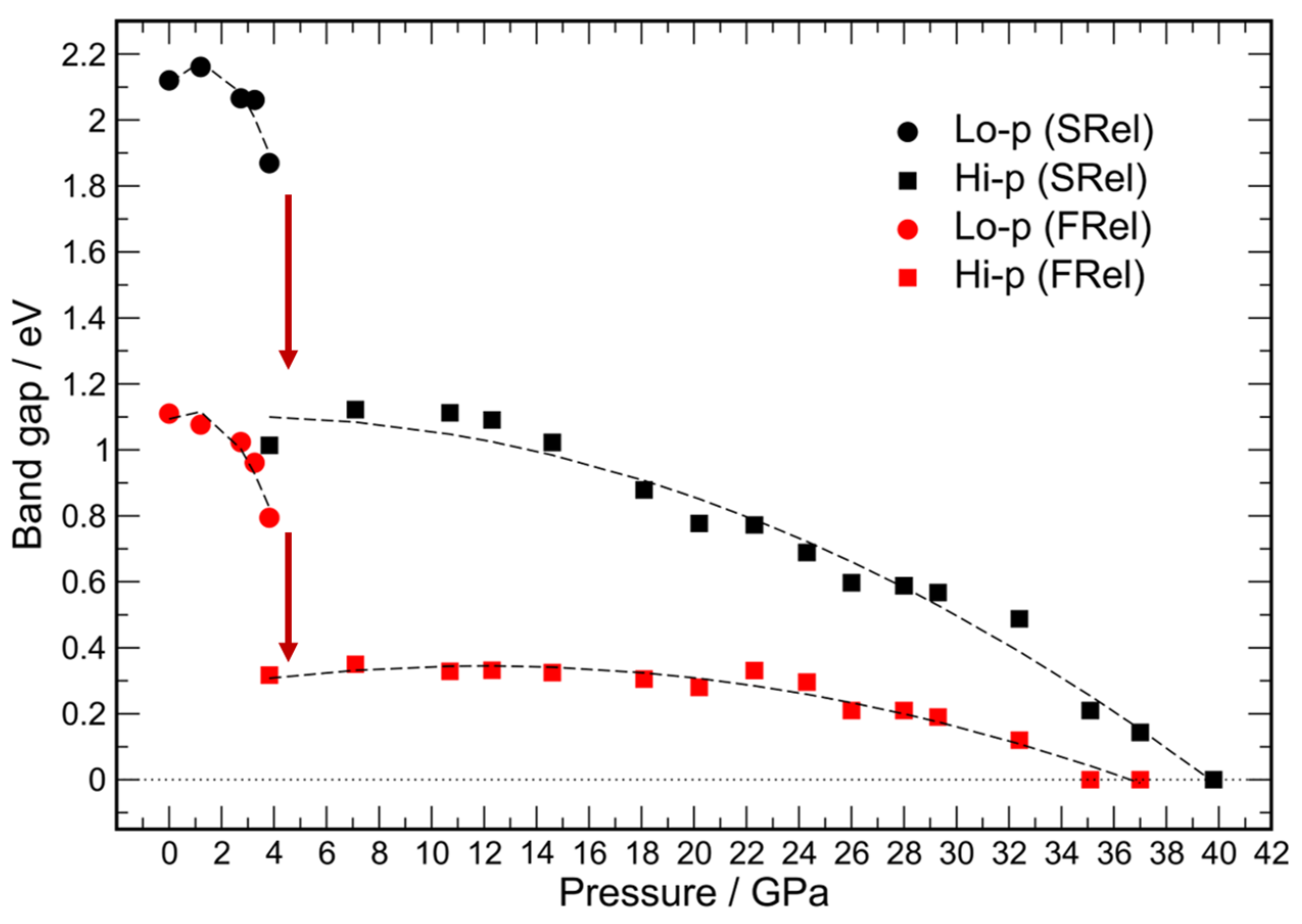
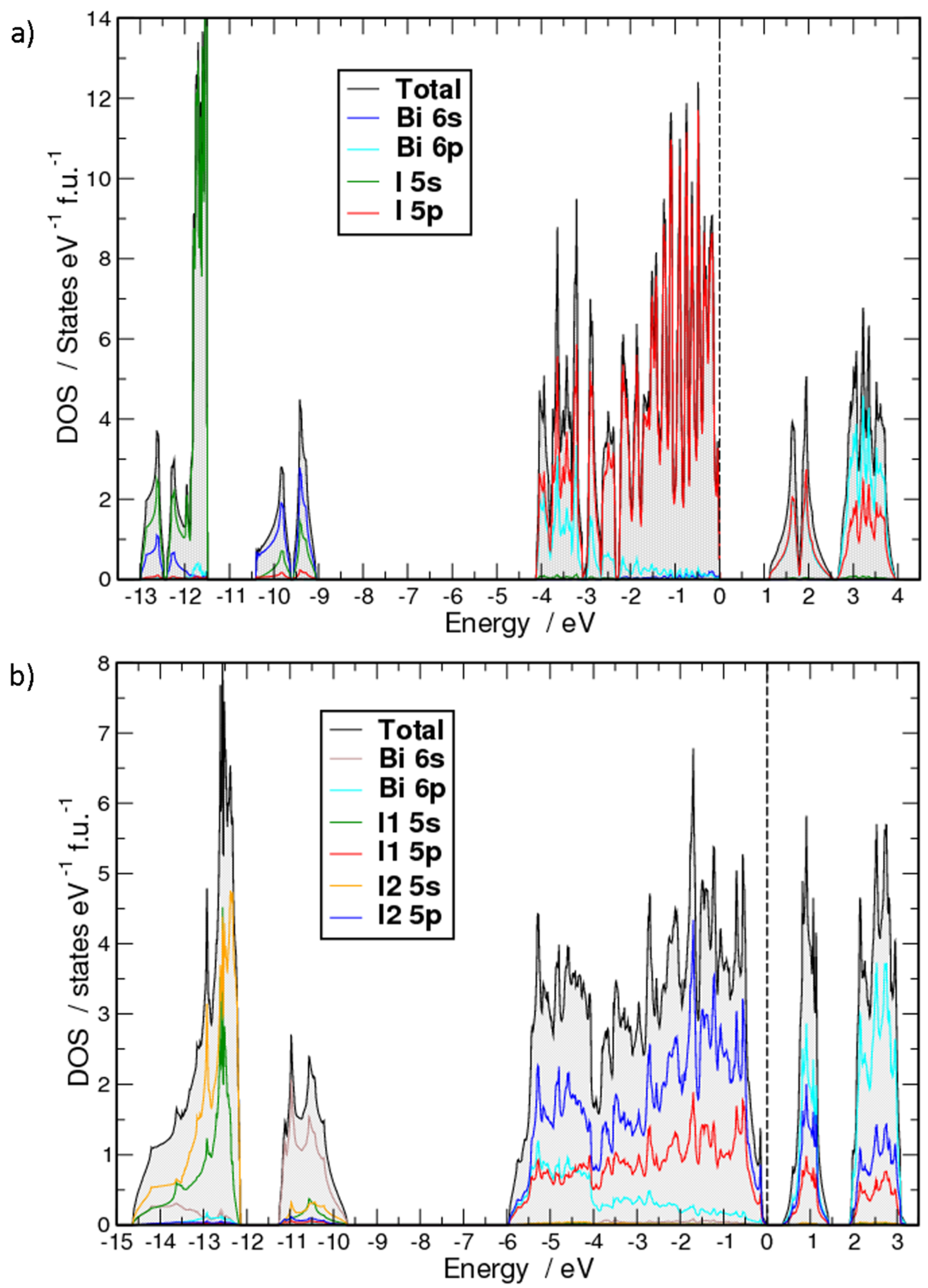
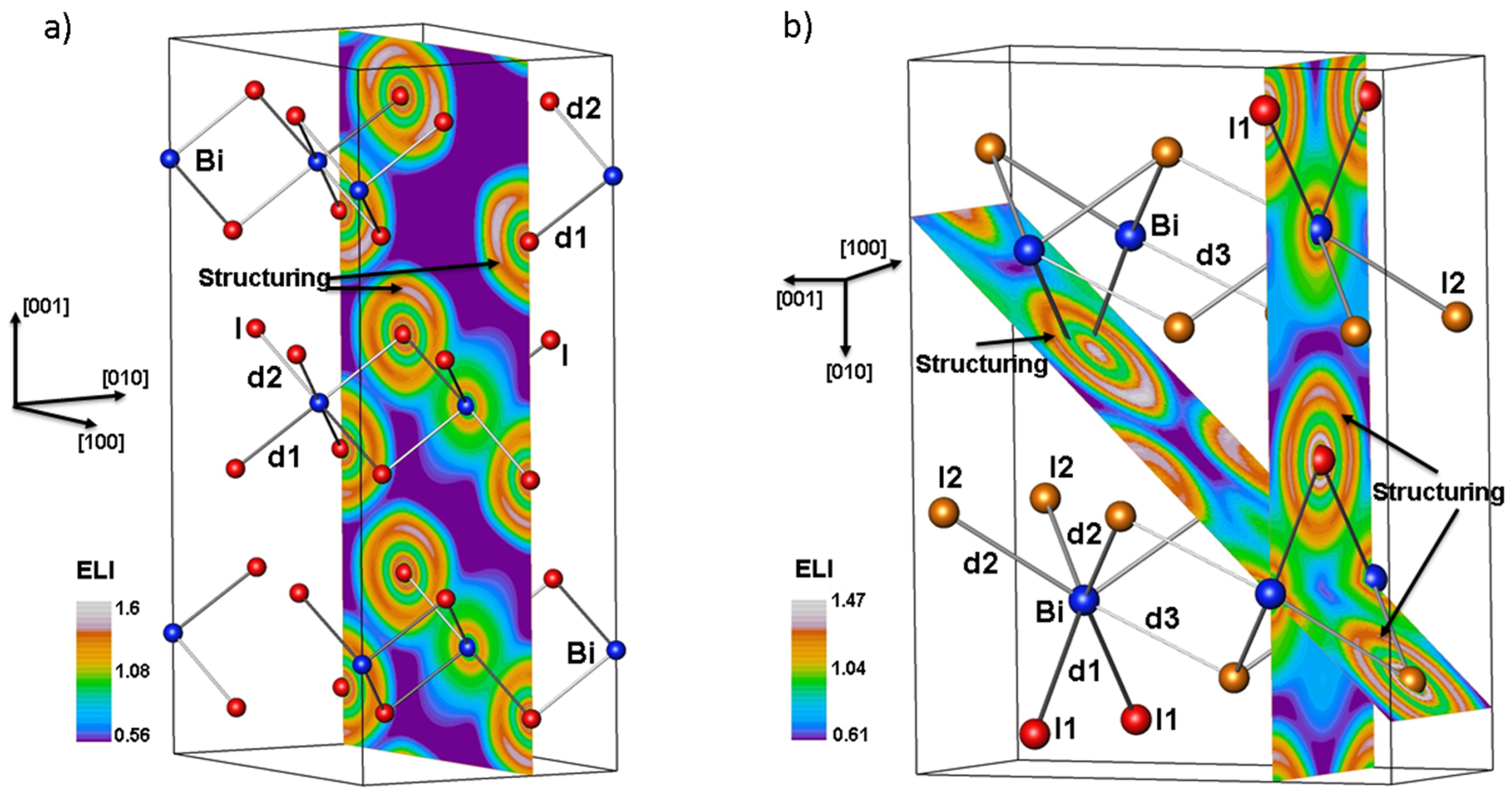
2. Results and Discussion
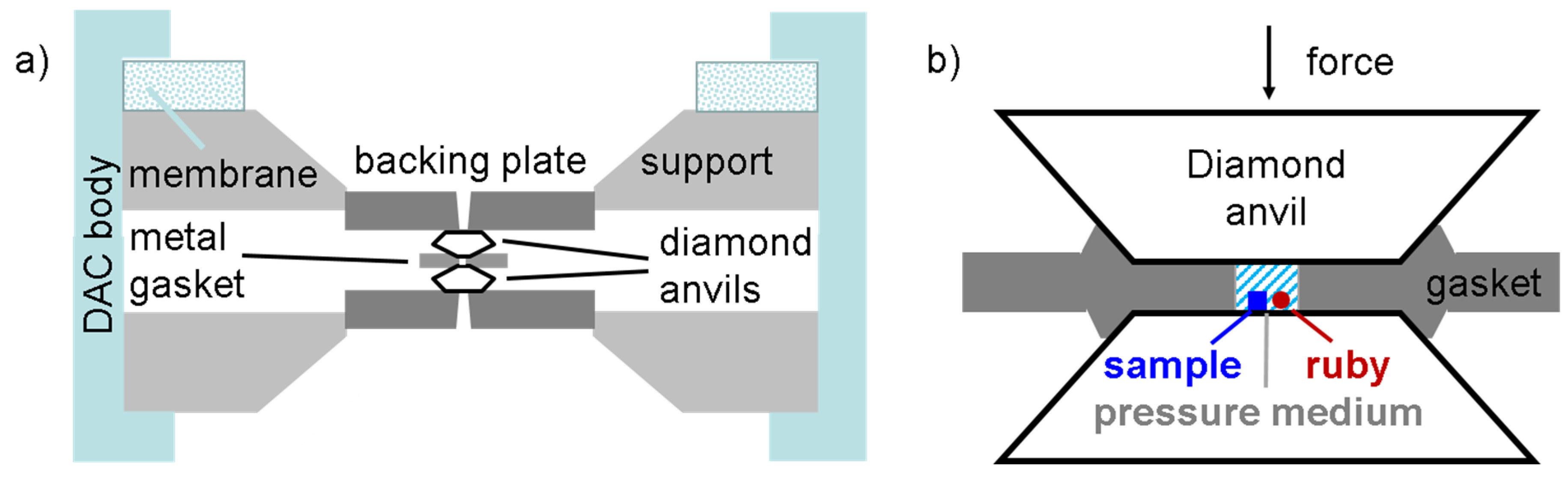
3. Materials and Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Manna, K.; Sun, Y.; Muechler, L.; Kübler, J.; Felser, C. Heusler, weyl and berry. Nat. Rev. Mater. 2018, 3, 244–256. [Google Scholar] [CrossRef]
- Schoop, L.M.; Pielnhofer, F.; Lotsch, B.V. Chemical principles of topological semimetals. Chem. Mater. 2018, 30, 3155–3176. [Google Scholar] [CrossRef]
- Von Schnering, H.G.; von Benda, H.; Kalveram, C. Wismutmonojodid bij, eine verbindung mit Bi(0) und Bi(II). ZAAC 1978, 438, 37–52. [Google Scholar] [CrossRef]
- Noguchi, R.; Takahashi, T.; Kuroda, K.; Ochi, M.; Shirasawa, T.; Sakano, M.; Bareille, C.; Nakayama, M.; Watson, M.D.; Yaji, K.; et al. A weak topological insulator state in quasi-one-dimensional bismuth iodide. Nature 2019, 566, 518–522. [Google Scholar] [CrossRef] [PubMed]
- Autes, G.; Isaeva, A.; Moreschini, L.; Johannsen, J.C.; Pisoni, A.; Mori, R.; Zhang, W.; Filatova, T.G.; Kuznetsov, A.N.; Forró, L.; et al. A novel quasi-one-dimensional topological insulator in bismuth iodide β-Bi4I4. Nat. Mater. 2016, 15, 154–158. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.-C.; Zhou, J.-J.; Yao, Y.; Zhang, F. Weak topological insulators and composite weyl semimetals: β-Bi4X4 (X=Br, I). Phys. Rev. Lett. 2016, 116, 066801. [Google Scholar] [CrossRef] [PubMed]
- Lia, X.; Chena, D.; Jinc, M.; Maa, D.; Ged, Y.; Sune, J.; Guof, W.; Suna, H.; Hana, J.; Xiaoa, W.; et al. Pressure-induced phase transitions and superconductivity in a quasi–1-dimensional topological crystalline insulator α-Bi4Br4. Proc. Natl. Acad. Sci. USA 2019, 116, 17696–17700. [Google Scholar] [CrossRef]
- Qi, Y.; Shi, W.; Werner, P.; Naumov, P.G.; Schnelle, W.; Wang, L.; Rana, K.G.; Parkin, S.; Medvedev, S.A.; Yan, B.; et al. Pressure-induced superconductivity and topological quantum phase transitions in a quasi-one-dimensional topological insulator: Bi4I4. npj Quantum Mater. 2018, 3, 4. [Google Scholar] [CrossRef]
- Pisoni, A.; Gaál, R.; Zeugner, A.; Falkowski, V.; Isaeva, A.; Huppertz, H.; Autès, G.; Yazyev, O.V.; Forró, L. Pressure effect and superconductivity in the β-Bi4I4 topological insulator. Phys. Rev. B 2017, 95, 235149. [Google Scholar] [CrossRef]
- Wang, X.; Wu, J.; Wang, J.; Chen, T.; Gao, H.; Lu, P.; Chen, Q.; Ding, C.; Wen, I.; Sun, J. Pressure-induced structural and electronic transitions in bismuth iodide. Phys. Rev. B 2018, 98, 174112. [Google Scholar] [CrossRef]
- Trotter, J.; Zobel, T. The crystal structure of SbI3 and BiI3. Zeitschrift für Kristallographie 1966, 123, 67–72. [Google Scholar] [CrossRef]
- Ruck, M. Darstellung und kristallstruktur von fehlordnungsfreiem bismuthtriiodid. Zeitschrift für Kristallographie 1995, 210, 650–655. [Google Scholar]
- Hsueh, H.C.; Chen, R.K.; Vass, H.; Clark, S.J.; Ackland, G.J.; Poon, W.C.K.; Crain, J. Compression mechanisms in quasimolecular XI3 (X = As,Sb,Bi) solids. Phys. Rev. B. 1998, 22, 14812. [Google Scholar] [CrossRef]
- Saitoh, A.; Komatsu, T.; Karasawa, T.; Ohtake, H.; Suemoto, T. Raman scattering under hydrostatic pressures in layered BiI3 and SbI3 crystals. Phys. Stat. Sol. 2001, 2, 357–367. [Google Scholar] [CrossRef]
- Saitoh, A. Raman scattering, luminescence, and absorption edge under hydrostatic pressures of layered BiI3 and SbI3. J. Raman. Spectrosc. 2007, 38, 537–542. [Google Scholar] [CrossRef]
- Hsueh, H.C.; Poon, W.C.K.; Vass, H.; Crain, J. Pressure-induced electron transfer in quasi-molecular solids. EPL 1996, 35, 689–694. [Google Scholar] [CrossRef]
- Murnaghan, F.D. The compressibility of media under extreme pressures. Proc. Natl. Acad. Sci. USA 1944, 30, 244–247. [Google Scholar] [CrossRef]
- Zachariasen, W.H. Crystal chemical studies of the 5f-series of elements. I. New structure types. Acta Crystallographica 1948, 1, 265–268. [Google Scholar] [CrossRef]
- Vergniory, M.G.; Elcoro, L.; Felser, C.; Regnault, N.; Bernevig, B.A.; Wang, Z. A complete catalogue of high-quality topological materials. Nature 2019, 566, 480–485. [Google Scholar] [CrossRef]
- Hulliger, F. Structural Chemistry of Layer-Type Phases; Lévy, F.A., Ed.; Physics and Chemistry of Materials with Layered Structures Volume 5; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1976. [Google Scholar]
- Beck, H.K.; Gladow, E. Zur hochdruckpolymorphie der seltenerd-trihalogenide. ZAAC 1979, 453, 79–92. [Google Scholar] [CrossRef]
- Beck, H.K.; Gladow, E. Der PuBr3-typ als hochdruckmodifikation bei seltenerdtrihalogeniden LnX3 (X = Cl, Br, I). ZAAC 1983, 502, 178–184. [Google Scholar]
- Kohout, M.; Wagner, F.R.; Grin, Y. Electron localization function for transition-metal compounds. Theor. Chem. Acc. 2002, 108, 150–156. [Google Scholar] [CrossRef]
- Piermarini, G.J.; Block, S.; Barnett, J.D.; Forman, R.A. Calibration of the pressure dependence of the R1 ruby fluorescence line to 195 kbar. J. Appl. Phys. 1975, 46, 2774–2780. [Google Scholar] [CrossRef]
- Hammersley, A.P.; Svensson, S.O.; Hanfland, M.; Fitch, A.N.; Häussermann, D. Two-dimensional detector software: From real detector to idealised image or two-theta scan. High Press. Res. 1996, 14, 235–248. [Google Scholar] [CrossRef]
- Akselrud, L.; Grin, Y. WinCSD: Software package for crystallographic calculations (Version 4). J. Appl. Crystallogr. 2014, 47, 803–805. [Google Scholar] [CrossRef]
- Huber, G.; Syassen, K.; Holzapfel, W.B. Pressure dependence of 4f levels in europium pentaphosphate up to 400 kbar. Phys. Rev. B 1977, 15, 5123–5128. [Google Scholar] [CrossRef]
- Blum, V.; Gehrke, R.; Hanke, F.; Havu, P.; Havu, V.; Ren, X.; Reuter, K.; Scheffler, M. Ab initio molecular simulations with numeric atom-centered orbitals. Comput. Phys. Commun. 2009, 180, 2175–2196. [Google Scholar] [CrossRef]
- Koepernik, K.; Eschrig, H. Full-potential nonorthogonal local-orbital minimum-basis band-structure scheme. Phys. Rev. B 1999, 59, 1743–1757. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef]
- Kohout, M. A measure of electron localizability. Int. J. Quantum Chem. 2004, 97, 651–658. [Google Scholar] [CrossRef]
- Kohout, M.; Wagner, F.R.; Grin, Y. Atomic shells from the electron localizability in momentum space. Int. J. Quantum Chem. 2006, 106, 1499–1507. [Google Scholar] [CrossRef]
- Kohout, M. Bonding indicators from electron pair density functionals. Faraday Discuss. 2007, 135, 43–54. [Google Scholar] [CrossRef] [PubMed]
- Villaseca, S.A.; Ormeci, A.; Levchenko, S.V.; Schlögl, R.; Grin, Y.; Armbrüster, M. CO adsorption on GaPd—Unraveling the chemical bonding in real space. Chem. Phys. Chem. 2017, 18, 334–337. [Google Scholar] [CrossRef] [PubMed]
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Clarendon Press: Oxford, UK, 1995. [Google Scholar]
- Kohout, M. Program DGrid, Version 4.6; Radebeul, Germany, 2011–2017.
- Raub, S.; Jansen, G. A quantitative measure of bond polarity from the electron localization function and the theory of atoms in molecules. Theor. Chem. Acc. 2001, 106, 223–232. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schwarz, U.; Wosylus, A.; Schmidt, M.; Akselrud, L.; Ormeci, A.; Hanfland, M.; Hermann, V.; Kuntscher, C. High-Pressure Modification of BiI3. Inorganics 2019, 7, 143. https://doi.org/10.3390/inorganics7120143
Schwarz U, Wosylus A, Schmidt M, Akselrud L, Ormeci A, Hanfland M, Hermann V, Kuntscher C. High-Pressure Modification of BiI3. Inorganics. 2019; 7(12):143. https://doi.org/10.3390/inorganics7120143
Chicago/Turabian StyleSchwarz, Ulrich, Aron Wosylus, Marcus Schmidt, Lev Akselrud, Alim Ormeci, Michael Hanfland, Volker Hermann, and Christine Kuntscher. 2019. "High-Pressure Modification of BiI3" Inorganics 7, no. 12: 143. https://doi.org/10.3390/inorganics7120143
APA StyleSchwarz, U., Wosylus, A., Schmidt, M., Akselrud, L., Ormeci, A., Hanfland, M., Hermann, V., & Kuntscher, C. (2019). High-Pressure Modification of BiI3. Inorganics, 7(12), 143. https://doi.org/10.3390/inorganics7120143





