Bond Insertion at Distorted Si(001) Subsurface Atoms
Abstract
1. Introduction
2. Computational Details
2.1. Molecules
2.2. Surfaces
2.3. Periodic Energy Decomposition Analysis
3. Results
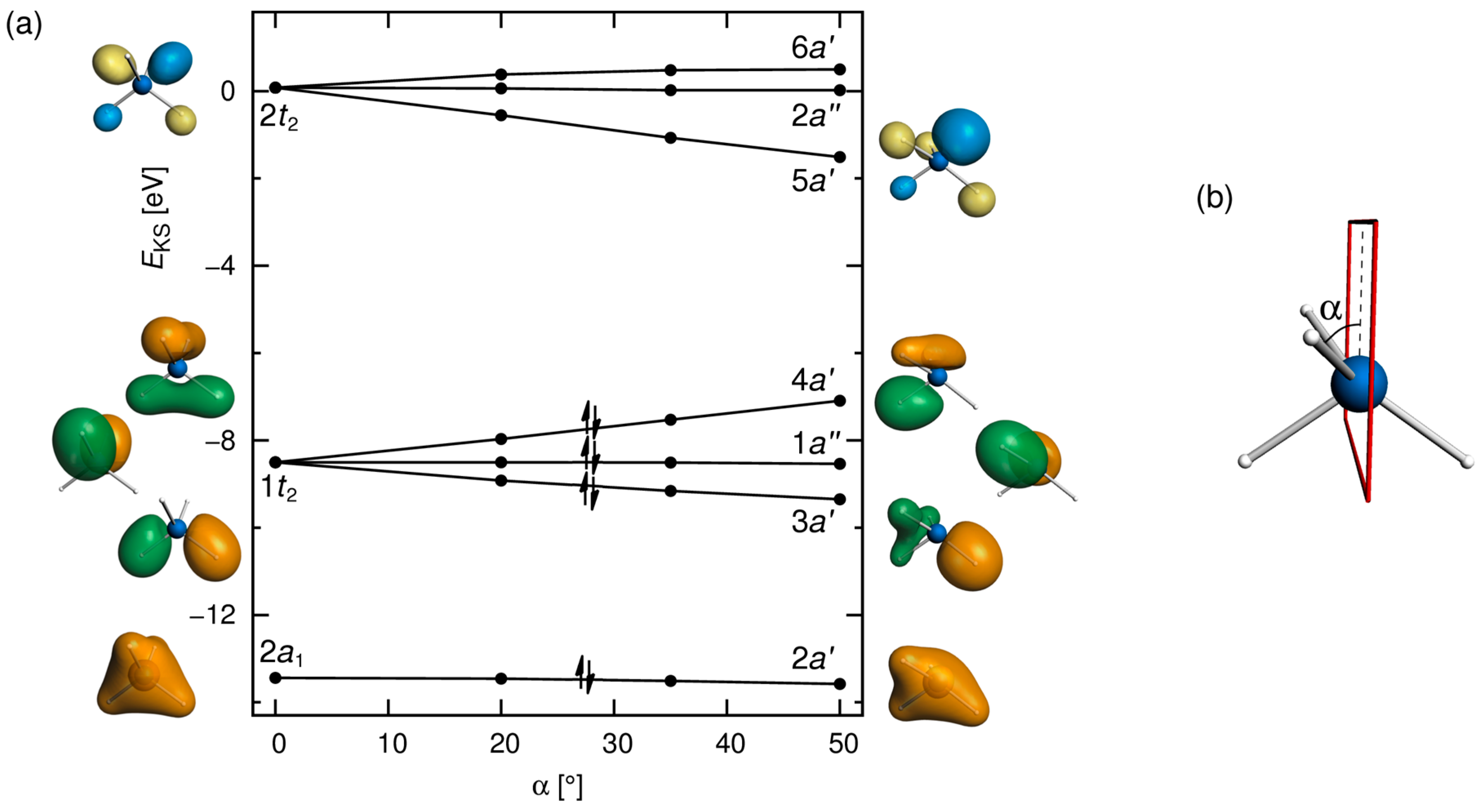
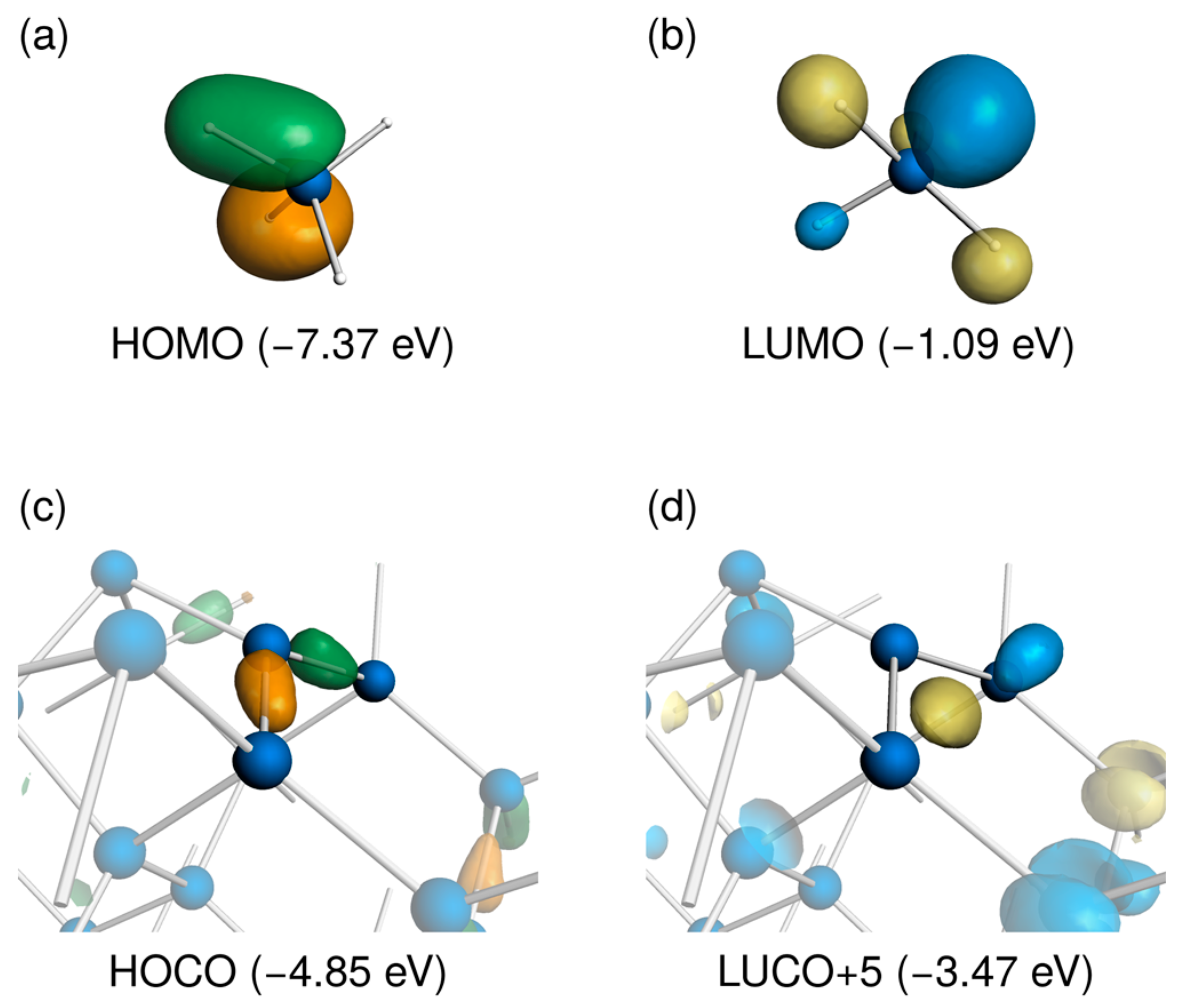
3.1. Distorted Coordination of Tetravalent Silicon
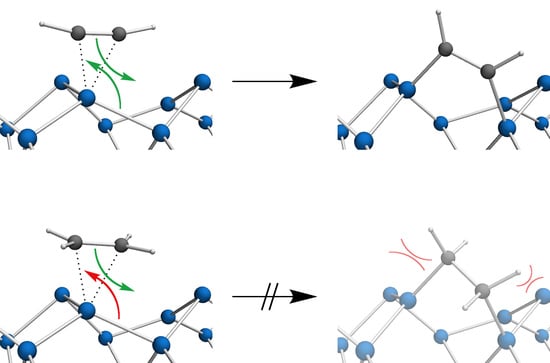
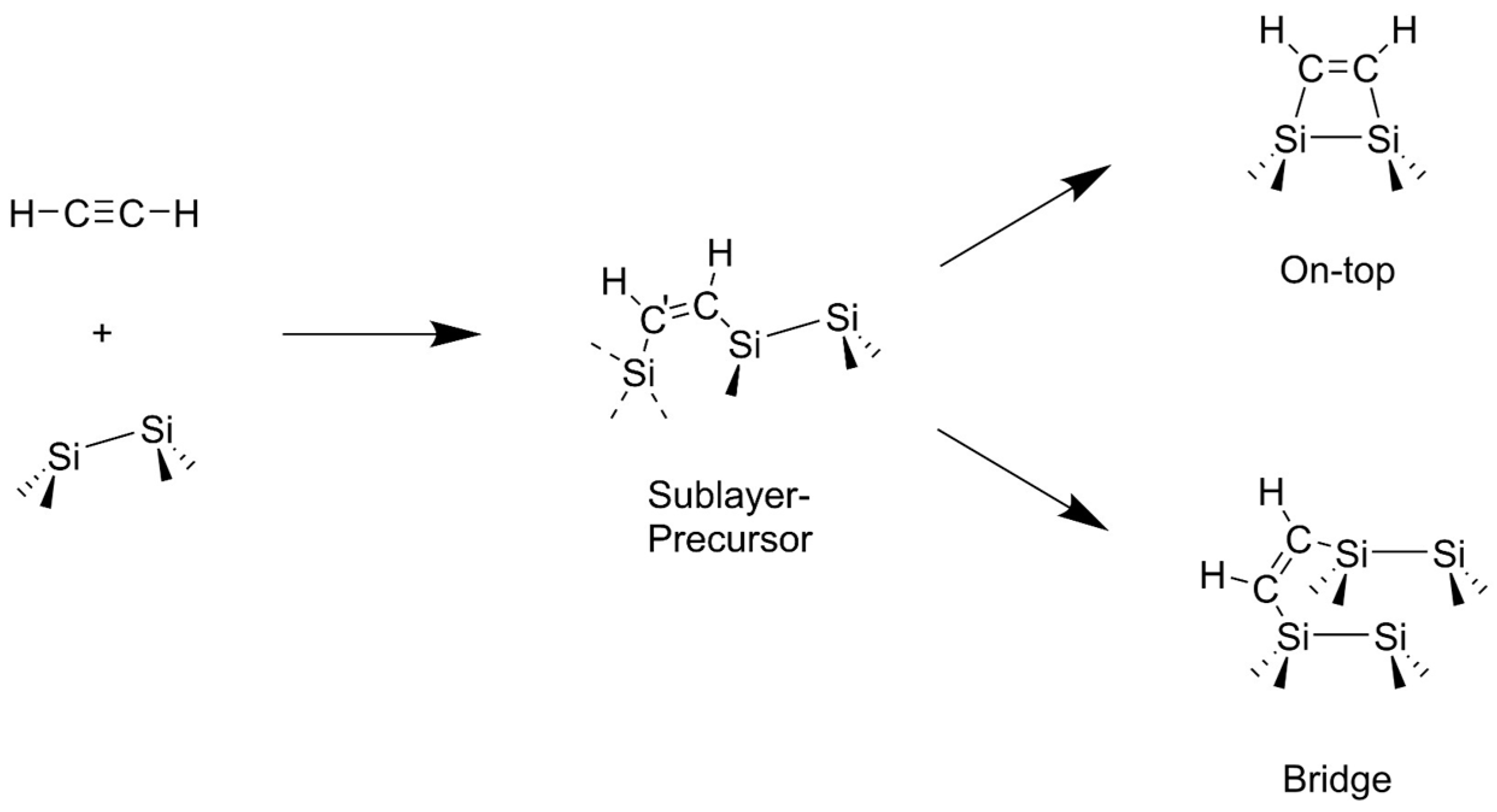
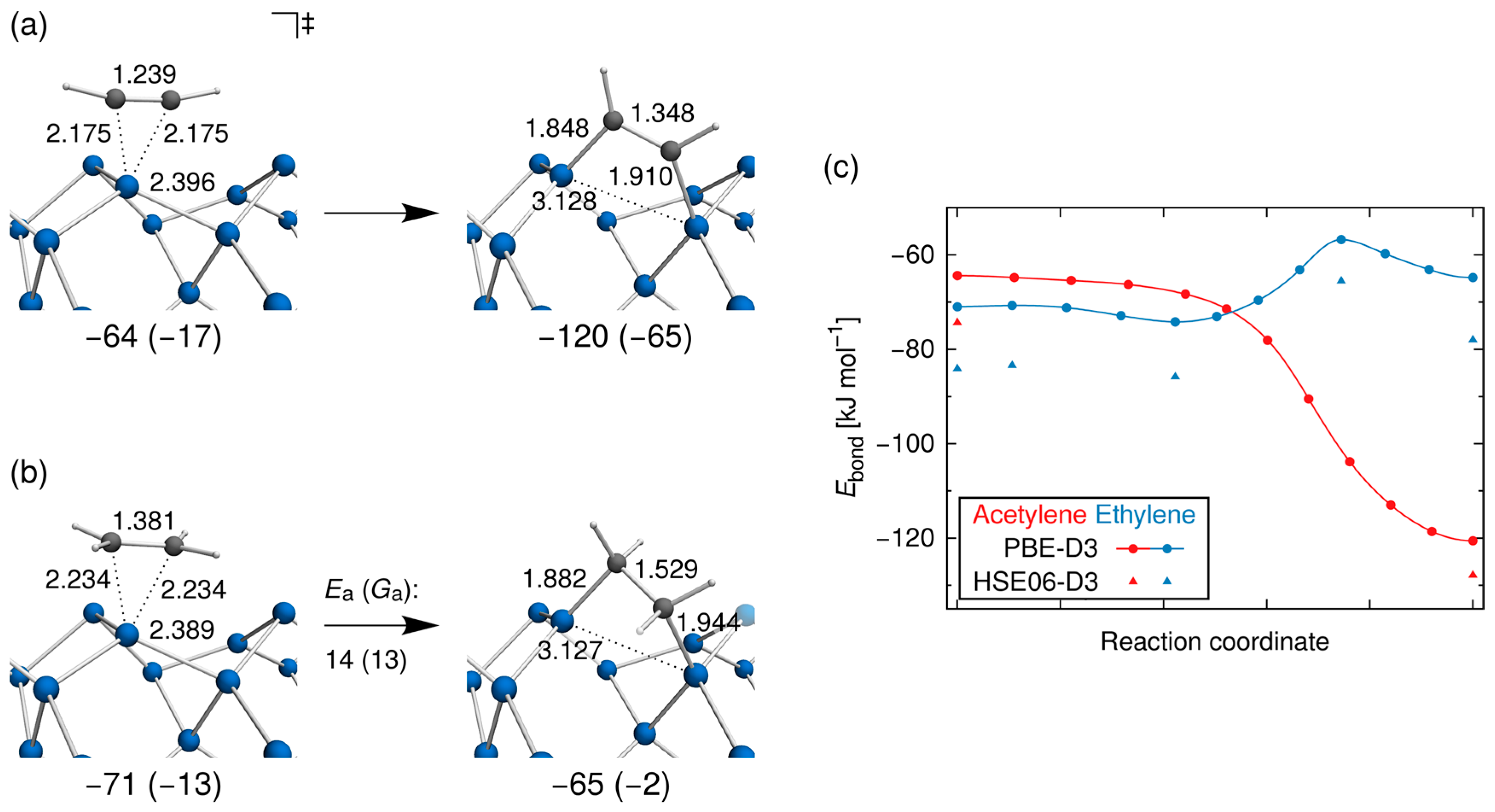
3.2. Bond Insertion of Acetylene and Ethylene on Si(001)
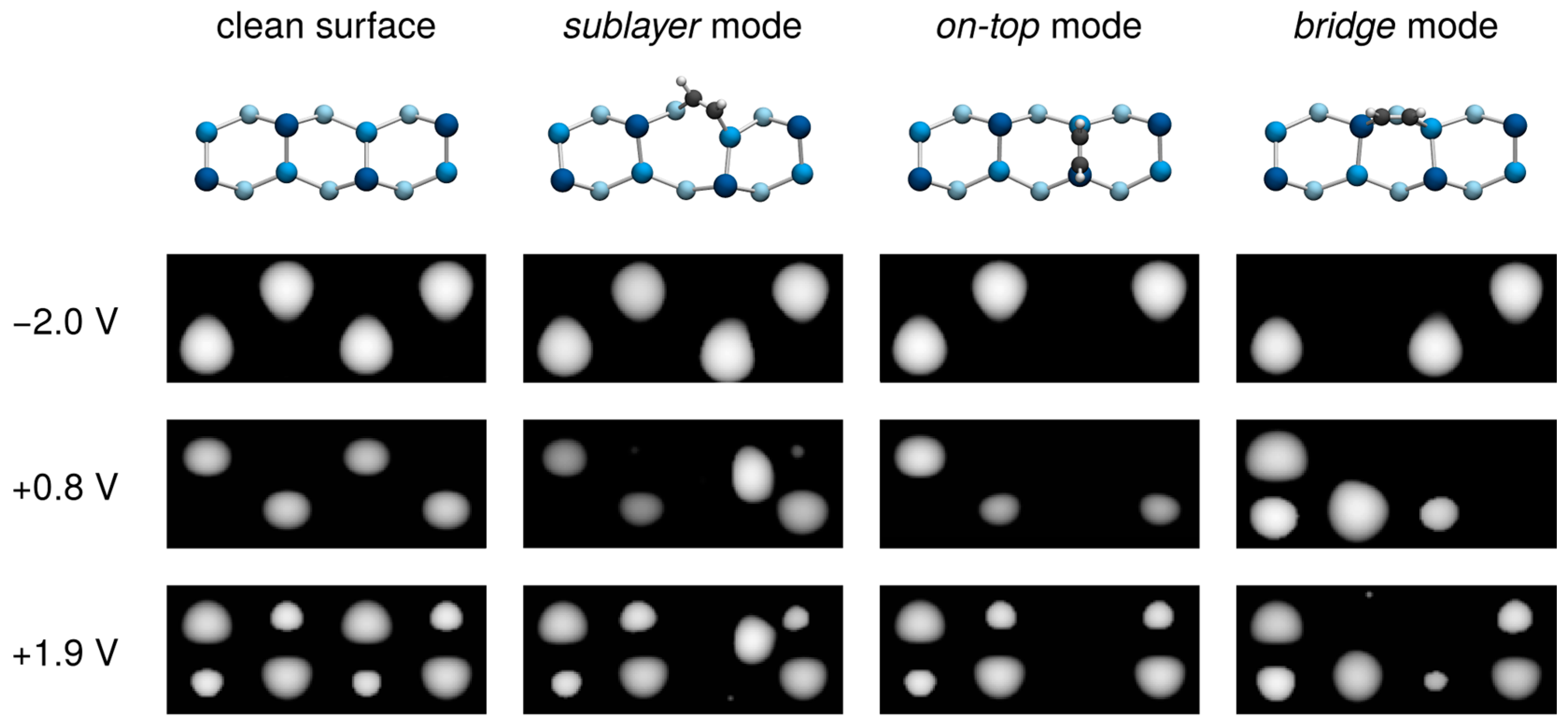
3.3. Comparison with Experiment
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- West, R.; Fink, M.J.; Michl, J. Tetramesityldisilene, a Stable Compound Containing a Silicon–Silicon Double Bond. Science 1981, 214, 1343–1344. [Google Scholar] [CrossRef] [PubMed]
- Raabe, G.; Michl, J. Multiple Bonding to Silicon. Chem. Rev. 1985, 85, 419–509. [Google Scholar] [CrossRef]
- West, R. Chemistry of the Silicon–Silicon Double Bond. Angew. Chem. Int. Ed. 1987, 26, 1201–1302. [Google Scholar] [CrossRef]
- Kira, M.; Iwamoto, T. Progress in the Chemistry of Stable Disilenes. Adv. Organomet. Chem. 2006, 54, 73–148. [Google Scholar] [CrossRef]
- Präsang, C.; Scheschkewitz, D. Reactivity in the Periphery of Functionalised Multiple Bonds of Heavier Group 14 Elements. Chem. Soc. Rev. 2016, 45, 900–921. [Google Scholar] [CrossRef] [PubMed]
- Malrieu, J.-P.; Trinquier, G. Trans-Bending at Double Bonds. Occurrence and Extent. J. Am. Chem. Soc. 1989, 111, 5916–5921. [Google Scholar] [CrossRef]
- Power, P.P. π-Bonding and the Lone Pair Effect in Multiple Bonds between Heavier Main Group Elements. Chem. Rev. 1999, 99, 3463–3504. [Google Scholar] [CrossRef] [PubMed]
- Olbrich, G. On the Structure and Stability of Si2H4. Chem. Phys. Lett. 1986, 130, 115–119. [Google Scholar] [CrossRef]
- Dolgonos, G. Relative Stability and Thermodynamic Properties of Si2H4 Isomers. Chem. Phys. Lett. 2008, 466, 11–15. [Google Scholar] [CrossRef]
- Kira, M. Bonding and Structure of Disilenes and Related Unsaturated Group-14 Element Compounds. Proc. Jpn. Acad. Ser. B 2012, 88, 167–191. [Google Scholar] [CrossRef]
- Jacobsen, H.; Ziegler, T. Nonclassical Double Bonds in Ethylene Analogues: Influence of Pauli Repulsion on Trans Bending and π–Bond Strength. A Density Functional Study. J. Am. Chem. Soc. 1994, 116, 3667–3679. [Google Scholar] [CrossRef]
- Wendel, D.; Szilvási, T.; Jandl, C.; Inoue, S.; Rieger, B. Twist of a Silicon–Silicon Double Bond: Selective Anti-Addition of Hydrogen to an Iminodisilene. J. Am. Chem. Soc. 2017, 139, 9156–9159. [Google Scholar] [CrossRef] [PubMed]
- Jemmis, E.D.; Kiran, B. Structure and Bonding in B10X2H10 (X = C and Si). The Kinky Surface of 1,2-Dehydro-o-disilaborane. J. Am. Chem. Soc. 1997, 119, 4076–4077. [Google Scholar] [CrossRef]
- Schweizer, J.I.; Scheibel, M.G.; Diefenbach, M.; Neumeyer, F.; Würtele, C.; Kulminskaya, N.; Linser, R.; Auner, N.; Schneider, S.; Holthausen, M.C. A Disilene Base Adduct with a Dative Si–Si Single Bond. Angew. Chem. Int. Ed. 2016, 55, 1782–1786. [Google Scholar] [CrossRef] [PubMed]
- Teplyakov, A.V.; Bent, S.F. Semiconductor Surface Functionalization for Advances in Electronics, Energy Conversion, and Dynamic Systems. J. Vac. Sci. Technol. A 2013, 31, 50810. [Google Scholar] [CrossRef]
- Yoshinobu, J. Physical Properties and Chemical Reactivity of the Buckled Dimer on Si(100). Prog. Surf. Sci. 2004, 77, 37–70. [Google Scholar] [CrossRef]
- Leftwich, T.R.; Teplyakov, A.V. Chemical Manipulation of Multifunctional Hydrocarbons on Silicon Surfaces. Surf. Sci. Rep. 2007, 63, 1–71. [Google Scholar] [CrossRef]
- Pecher, L.; Laref, S.; Raupach, M.; Tonner, R. Ethers on Si(001): A Prime Example for the Common Ground between Surface Science and Molecular Organic Chemistry. Angew. Chem. Int. Ed. 2017, 56, 15150–15154. [Google Scholar] [CrossRef] [PubMed]
- Filler, M.A.; Bent, S.F. The Surface as Molecular Reagent: Organic Chemistry at the Semiconductor Interface. Prog. Surf. Sci. 2003, 73, 1–56. [Google Scholar] [CrossRef]
- Zhang, Q.J.; Fan, X.L.; Lau, W.M.; Liu, Z.F. Sublayer Si Atoms as Reactive Centers in the Chemisorption on Si(100): Adsorption of C2H2 and C2H4. Phys. Rev. B 2009, 79, 195303. [Google Scholar] [CrossRef]
- Cho, J.-H.; Kleinman, L. Adsorption Kinetics of Acetylene and Ethylene on Si(001). Phys. Rev. B 2004, 69, 75303. [Google Scholar] [CrossRef]
- Nagao, M.; Umeyama, H.; Mukai, K.; Yamashita, Y.; Yoshinobu, J. Precursor Mediated Cycloaddition Reaction of Ethylene to the Si(100)c(4 × 2) Surface. J. Am. Chem. Soc. 2004, 126, 9922–9923. [Google Scholar] [CrossRef] [PubMed]
- Fan, X.L.; Zhang, Y.F.; Lau, W.M.; Liu, Z.F. Violation of the Symmetry Rule for the [2 + 2] Addition in the Chemisorption of C2H4 on Si(100). Phys. Rev. B 2005, 72, 165305. [Google Scholar] [CrossRef]
- Mette, G.; Schwalb, C.H.; Dürr, M.; Höfer, U. Site-Selective Reactivity of Ethylene on Clean and Hydrogen Precovered Si(001). Chem. Phys. Lett. 2009, 483, 209–213. [Google Scholar] [CrossRef]
- Lipponer, M.A.; Armbrust, N.; Dürr, M.; Höfer, U. Adsorption Dynamics of Ethylene on Si(001). J. Chem. Phys. 2012, 136, 144703. [Google Scholar] [CrossRef] [PubMed]
- Pecher, J.; Tonner, R. Precursor States of Organic Adsorbates on Semiconductor Surfaces are Chemisorbed and Immobile. ChemPhysChem 2017, 18, 34–38. [Google Scholar] [CrossRef] [PubMed]
- Pecher, J.; Mette, G.; Dürr, M.; Tonner, R. Site-Specific Reactivity of Ethylene at Distorted Dangling-Bond Configurations on Si(001). ChemPhysChem 2017, 18, 357–365. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Hoffmann, R. The Bare and Acetylene Chemisorbed Si(001) Surface, and the Mechanism of Acetylene Chemisorption. J. Am. Chem. Soc. 1995, 117, 4082–4092. [Google Scholar] [CrossRef]
- Matsui, F.; Yeom, H.W.; Imanishi, A.; Isawa, K.; Matsuda, I.; Ohta, T. Adsorption of Acetylene and Ethylene on the Si(001)2×1 Surface Studied by NEXAFS and UPS. Surf. Sci. 1998, 401, L413–L419. [Google Scholar] [CrossRef]
- Sorescu, D.C.; Jordan, K.D. Theoretical Study of the Adsorption of Acetylene on the Si(001) Surface. J. Phys. Chem. B 2000, 104, 8259–8267. [Google Scholar] [CrossRef]
- Mezhenny, S.; Lyubinetsky, I.; Choyke, W.J.; Wolkow, R.A.; Yates, J.T. Multiple Bonding Structures of C2H2 Chemisorbed on Si(100). Chem. Phys. Lett. 2001, 344, 7–12. [Google Scholar] [CrossRef]
- Kim, W.; Kim, H.; Lee, G.; Hong, Y.-K.; Lee, K.; Hwang, C.; Kim, D.-H.; Koo, J.-Y. Initial Adsorption Configurations of Acetylene Molecules on the Si(001) Surface. Surf. Sci. 2001, 64, 193313. [Google Scholar] [CrossRef]
- Kim, W.; Kim, H.; Lee, G.; Chung, J.; You, S.Y.; Hong, Y.K.; Koo, J.Y. Acetylene Molecules on the Si(001) Surface: Room-Temperature Adsorption and Structural Modification upon Annealing. Surf. Sci. 2002, 514, 376–382. [Google Scholar] [CrossRef]
- Silvestrelli, P.L.; Pulci, O.; Palummo, M.; Del Sole, R.; Ancilotto, F. First-Principles Study of Acetylene Adsorption on Si(100): The End-Bridge Structure. Surf. Sci. 2003, 68, 235306. [Google Scholar] [CrossRef]
- Takeuchi, N. First Principles Calculations of the Adsorption of Acetylene on the Si(001) Surface at Low and Full Coverage. Surf. Sci. 2007, 601, 3361–3365. [Google Scholar] [CrossRef]
- Czekala, P.T.; Lin, H.; Hofer, W.A.; Gulans, A. Acetylene Adsorption on Silicon (100)-(4 × 2) Revisited. Surf. Sci. 2011, 605, 1341–1346. [Google Scholar] [CrossRef]
- Taylor, P.A.; Wallace, R.M.; Cheng, C.C.; Weinberg, W.H.; Dresser, M.J.; Choyke, W.J.; Yates, J.J.T. Adsorption and Decomposition of Acetylene on Si(100)-(2 × 1). J. Am. Chem. Soc. 1992, 114, 6754–6760. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Enzerhof, M. Errata: Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1997, 78, 1396. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, S. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F.; Ahlrichs, R. Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
- Neese, F. The ORCA Program System. WIREs Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Fonseca Guerra, C.; Snijders, J.G.; te Velde, G.; Baerends, E.J. Towards an Order-N DFT Method. Theor. Chem. Acc. 1998, 99, 391–403. [Google Scholar] [CrossRef]
- Te Velde, G.; Bickelhaupt, F.M.; Baerends, E.J.; Fonseca Guerra, C.; van Gisbergen, S.J.A.; Snijders, J.G.; Ziegler, T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. [Google Scholar] [CrossRef]
- Software for Chemistry & Material (SCM). ADF2016; Theoretical Chemistry, Vrije Universiteit: Amsterdam, The Netherlands, 2016; Available online: http://www.scm.com (accessed on 21 December 2017).
- Kresse, G.; Hafner, J. Ab Initio Molecular Dynamics for Liquid Metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab Initio Molecular-Dynamics Simulation of the Liquid-Metal–Amorphous-Semiconductor Transition in Germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Krukau, A.V.; Vydrov, O.A.; Izmaylov, A.F.; Scuseria, G.E. Influence of the Exchange Screening Parameter on the Performance of Screened Hybrid Functionals. J. Chem. Phys. 2006, 125, 224106. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P. Projector Augmented-Wave Method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Henkelman, G.; Uberuaga, B.P.; Jónsson, H. A Climbing Image Nudged Elastic Band Method for Finding Saddle Points and Minimum Energy Paths. J. Chem. Phys. 2000, 113, 9901–9904. [Google Scholar] [CrossRef]
- Henkelman, G.; Jónsson, H. A Dimer Method for Finding Saddle Points on High Dimensional Potential Surfaces Using Only First Derivatives. J. Chem. Phys. 1999, 111, 7010–7022. [Google Scholar] [CrossRef]
- Boyd, D.R.J. Infrared Spectrum of Trideuterosilane and the Structure of the Silane Molecule. J. Chem. Phys. 1955, 23, 922–926. [Google Scholar] [CrossRef]
- Pecher, J.; Schober, C.; Tonner, R. Chemisorption of a Strained but Flexible Molecule: Cyclooctyne on Si(001). Chem. Eur. J. 2017, 23, 5459–5466. [Google Scholar] [CrossRef] [PubMed]
- Tersoff, J.; Hamann, D.R. Theory and Application for the Scanning Tunneling Microscope. Phys. Rev. Lett. 1983, 50, 1998–2001. [Google Scholar] [CrossRef]
- Tersoff, J.; Hamann, D.R. Theory of the Scanning Tunneling Microscope. Phys. Rev. B 1985, 31, 805–813. [Google Scholar] [CrossRef]
- Hofer, W.A. Challenges and Errors: Interpreting High Resolution Images in Scanning Tunneling Microscopy. Prog. Surf. Sci. 2003, 71, 147–183. [Google Scholar] [CrossRef]
- Palotás, K.; Hofer, W.A. Multiple Scattering in a Vacuum Barrier Obtained from Real-Space Wavefunctions. J. Phys. Condens. Matter 2005, 17, 2705–2713. [Google Scholar] [CrossRef]
- Pecher, L.; Schmidt, S.; Tonner, R. Modeling the Complex Adsorption Dynamics of Large Organic Molecules: Cyclooctyne on Si(001). J. Phys. Chem. C 2017, 121, 26840–26850. [Google Scholar] [CrossRef]
- Pecher, L.; Tonner, R. Computational analysis of the competitive bonding and reactivity pattern of a bifunctional cyclooctyne on Si(001). Theor. Chem. Acc. 2018. in print. [Google Scholar]
- Raupach, M.; Tonner, R. A Periodic Energy Decomposition Analysis (pEDA) Method for the Investigation of Chemical Bonding in Extended Systems. J. Chem. Phys. 2015, 142, 194105. [Google Scholar] [CrossRef] [PubMed]
- Te Velde, G.; Baerends, E.J. Precise Density-Functional Method for Periodic Structures. Phys. Rev. B 1991, 44, 7888–7903. [Google Scholar] [CrossRef]
- Software for Chemistry & Material (SCM). BAND2016; Theoretical Chemistry, Vrije Universiteit: Amsterdam, The Netherlands, 2016; Available online: http://www.scm.com (accessed on 21 December 2017).
- Mitoraj, M.P.; Michalak, A.; Ziegler, T. A Combined Charge and Energy Decomposition Scheme for Bond Analysis. J. Chem. Theory Comput. 2009, 5, 962–975. [Google Scholar] [CrossRef] [PubMed]
- Raupach, M. Quantum Chemical Investigation of Chemical Bonding at Surfaces—Development and Application of an Energy Decomposition Based Method. Ph.D. Thesis, Philipps-Universität Marburg, Marburg, Germany, 2015. [Google Scholar] [CrossRef]
- Walsh, A.D. The Electronic Orbitals, Shapes, and Spectra of Polyatomic Molecules. Part I. AH2 Molecules. J. Chem. Soc. 1953, 2260–2266. [Google Scholar] [CrossRef]
- Sagisaka, K.; Nara, J.; Bowler, D. Importance of Bulk States for the Electronic Structure of Semiconductor Surfaces: Implications for Finite Slabs. J. Phys. Condens. Matter 2017, 29, 145502. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.T.; Lin, J.S. Ab Initio Molecular Dynamics Study of Ethylene Adsorption onto Si(001) Surface: Short-Time Fourier Transform Analysis of Structural Coordinate Autocorrelation Function. J. Comput. Chem. 2013, 34, 2697–2706. [Google Scholar] [CrossRef] [PubMed]
- Gaberle, J.; Gao, D.Z.; Watkins, M.B.; Shluger, A.L. Calculating the Entropy Loss on Adsorption of Organic Molecules at Insulating Surfaces. J. Phys. Chem. C 2016, 120, 3913–3921. [Google Scholar] [CrossRef]
- Campbell, C.T.; Sellers, J.R.V. The Entropies of Adsorbed Molecules. J. Am. Chem. Soc. 2012, 34, 18109–18115. [Google Scholar] [CrossRef] [PubMed]
- Von Hopffgarten, M.; Frenking, G. Energy Decomposition Analysis. WIREs Comput. Mol. Sci. 2012, 2, 43–62. [Google Scholar] [CrossRef]
- Reutzel, M.; Münster, N.; Lipponer, M.A.; Länger, C.; Höfer, U.; Koert, U.; Dürr, M. Chemoselective Reactivity of Bifunctional Cyclooctynes on Si(001). J. Phys. Chem. C 2016, 120, 26284–26289. [Google Scholar] [CrossRef]

| π Complex | Sublayer | |||||||
|---|---|---|---|---|---|---|---|---|
| Acetylene (TS) | Ethylene | Acetylene | Ethylene | |||||
| ∆Eint | −105 | −106 | −656 | −583 | ||||
| ∆Eint(disp) 2 | −23 | (22%) | −27 | (25%) | −22 | (3%) | −30 | (5%) |
| ∆Eint(elec) 2 | −82 | (78%) | −79 | (75%) | −634 | (97%) | −553 | (95%) |
| ∆EPauli | 701 | 653 | 1587 | 1628 | ||||
| ∆Eelstat 3 | −367 | (47%) | −342 | (47%) | −912 | (41%) | −942 | (43%) |
| ∆Eorb 3 | −416 | (53%) | −390 | (53%) | −1310 | (59%) | −1240 | (57%) |
| ∆Eorb(M → S) 4 | −292 | (70%) | −289 | (74%) | −551 | (42%) | −536 | (43%) |
| ∆Eorb(S → M) 4 | −88 | (21%) | −76 | (19%) | −714 | (55%) | −641 | (52%) |
| ∆Eprep(M) | 15 | 10 | 364 | 341 | ||||
| ∆Eprep(S) | 17 | 16 | 156 | 161 | ||||
| Ebond 5 | −73 | (−64) | −80 | (−71) | −136 | (−120) | −81 | (−65) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pecher, L.; Tonner, R. Bond Insertion at Distorted Si(001) Subsurface Atoms. Inorganics 2018, 6, 17. https://doi.org/10.3390/inorganics6010017
Pecher L, Tonner R. Bond Insertion at Distorted Si(001) Subsurface Atoms. Inorganics. 2018; 6(1):17. https://doi.org/10.3390/inorganics6010017
Chicago/Turabian StylePecher, Lisa, and Ralf Tonner. 2018. "Bond Insertion at Distorted Si(001) Subsurface Atoms" Inorganics 6, no. 1: 17. https://doi.org/10.3390/inorganics6010017
APA StylePecher, L., & Tonner, R. (2018). Bond Insertion at Distorted Si(001) Subsurface Atoms. Inorganics, 6(1), 17. https://doi.org/10.3390/inorganics6010017