Investigation of the Structures and Energy Landscapes of Thiocyanate-Water Clusters

Abstract

The Basin Hopping search method is used to find the global minima (GM) and map the energy landscapes of thiocyanate-water clusters, (SCN⁻)(H₂O)_n with 3–50 water molecules, with empirical potentials describing the ion-water and water-water interactions. (It should be noted that beyond n = 23, the lowest energy structures were only found in 1 out of 8 searches so they are unlikely to be the true GM but are indicative low energy structures.) As for pure water clusters, the low energy isomers of thiocyanate-water clusters show a preponderance of fused water cubes and pentagonal prisms, with the weakly solvated thiocyanate ion lying on the surface, replacing two water molecules along an edge of a water polyhedron and with the sulfur atom in lower coordinated sites than nitrogen. However, by comparison with Density Functional Theory (DFT) calculations, the empirical potential is found to overestimate the strength of the thiocyanate-water interaction, especially O–H⋯S, with low energy DFT structures having lower coordinate N and (especially) S atoms than for the empirical potential. In the case of these finite ion-water clusters, the chaotropic (“disorder-making”) thiocyanate ion weakens the water cluster structure but the water molecule arrangement is not significantly changed.

1. Introduction

The Hofmeister series orders ions based on properties, such as the desolvation or “salting-out” of proteins and specific ion effects [1,2]. The Hofmeister series classifies ions as kosmotropes (order-making and increasing protein solublity) and chaotropes (disorder-making and decreasing protein solubility) [1]. Hofmeister effects can also be seen in other systems including industrial processes and atmospheric chemistry [3].

We have previously studied sulfate (SO₄²⁻) (kosmotropic) [4] and perchlorate (ClO₄⁻) (chaotropic) [5] ions solvated in finite water clusters. While in the sulfate-water clusters, the more highly charged sulfate anion was found to lie in the centre of the cluster, generating structures quite different from pure water clusters, the chlorate anion (with only a single negative charge) was found to occupy surface sites in the cluster, with overall structures similar to those of the pure water clusters [5]. This led to a greater number of dangling water O–H bonds compared to the sulfate-water case, where the suppression of dangling O–H bonds (compared to pure water clusters) has been confirmed by infra-red multiphoton dissociation (IRMPD) measurements of Williams et al [6,7]. The central location of sulfate is also consistent with tandem mass spectrometry-ion trap IR spectroscopy (in the sulfate region) of Neumark et al. [8] and photodetachment measurements by Wang et al. [9].

The thiocyanate anion (SCN⁻) is at the far chaotropic end of the Hofmeister series (beyond perchlorate). It has been suggested that a major contribution to the strong denaturing effect that thiocyanate has on proteins is the fact that it is only weakly hydrated in aqueous solution and, hence, interacts preferentially with the surface of the protein [10]. Neutron diffraction measurements of bulk aqueous solutions of thiocyanate salts show asymmetric coordination of the ends of the ion, with shorter, more directional hydrogen-bonding to the N atom and weaker coordination to S. The average coordination number of the N atom is between 2 and 3 water molecules, though there is some disagreement as to the nature of the bonding, concerning the balance of direct hydrogen-bonding and weaker Coulombic hydration interactions [10,11,12].

Lee et al. have reported DFT calculations (using the B3LYP xc functional and 6-311++G(2df,2pd) basis set) of the C–N stretching frequency of the SCN⁻ ion and changes induced by solvation in thiocyanate-water clusters with up to 16 water molecules [13], making comparisons with earlier theoretical studies of solvated CH₃–SCN molecules and making predictions for comparison with solution phase IR measurements [14]. The structures of their (SCN⁻)(H₂O)_n clusters will be compared to our results below. When writing up our research, we became aware of a recent paper by Valiev et al., in which they used DFT calculations (B3LYP/6-31++G**), combined with a genetic algorithm search method, to calculate the lowest energy structures of thiocyanate-water clusters with 1–8 water molecules [15]. Calculated vertical detachment energies (VDE) were compared with experimental photoelectron spectra (measured at 20 K) for these sizes, with generally a blue shift of the VDE observed with increasing number of water molecules.

Here, we present a study of the structures and energy landscapes of finite thiocyanate-water clusters (SCN⁻)(H₂O)_n, with 3 ≤ n ≤ 50, making comparisons with pure water clusters and comparing the results of empirical potential and DFT modelling of the thiocyanate-water clusters [16].

2. Results and Discussion

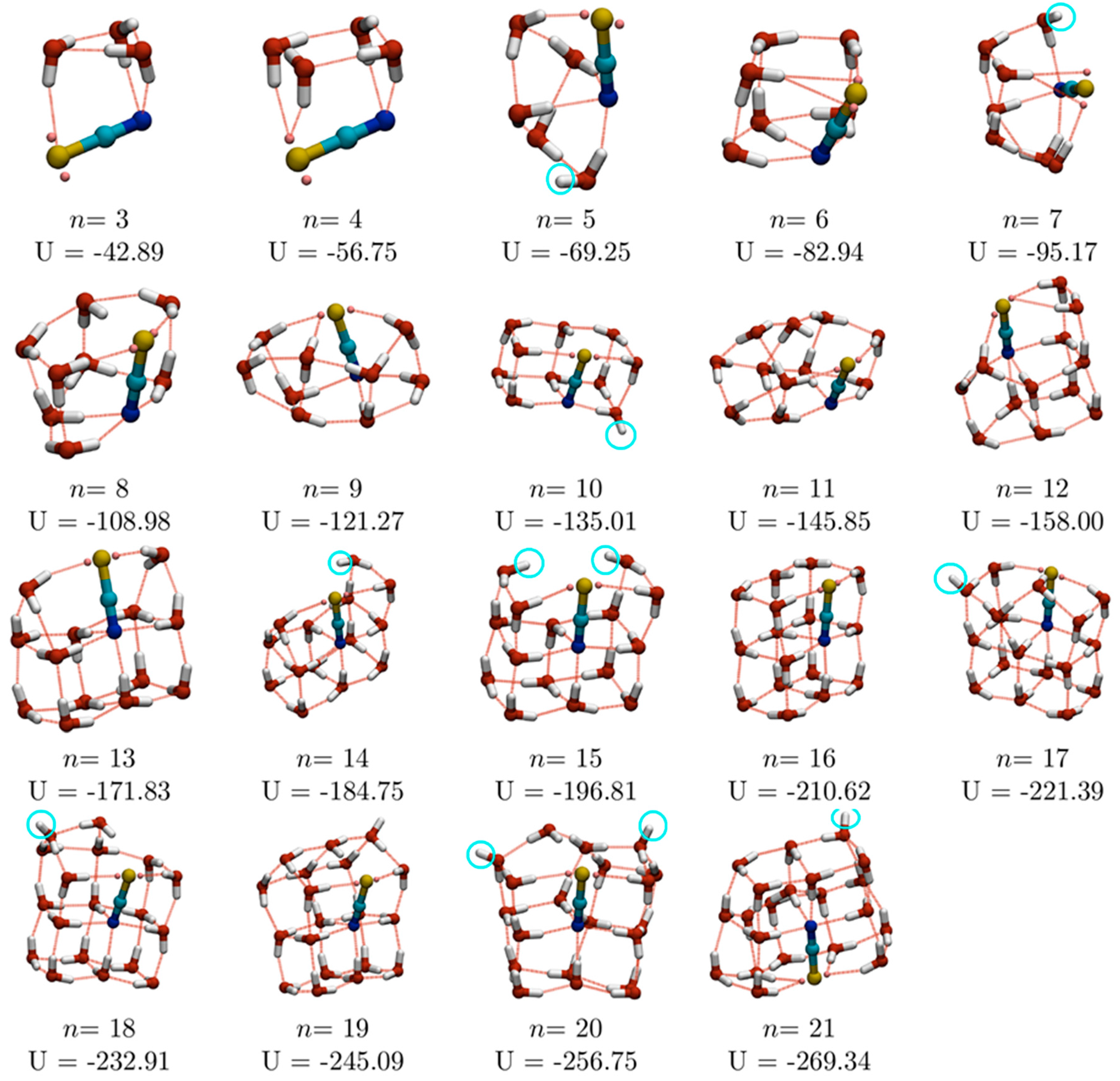
2.1. Global Minimum Structures for Hydrated Thiocyanate Clusters

Eight BH runs were performed for each hydrated thiocyanate cluster (SCN⁻)(H₂O)_n, with 3 ≤ n ≤ 50. For clusters with n ≤ 20, all eight basin-hopping runs located the same lowest energy minima, while for n = 21 and 22, five and two runs, respectively, located the same lowest energy minimum. The lowest energy isomers for 3 ≤ n ≤ 21, which are shown in Figure 1, are, therefore, good candidate global minima. 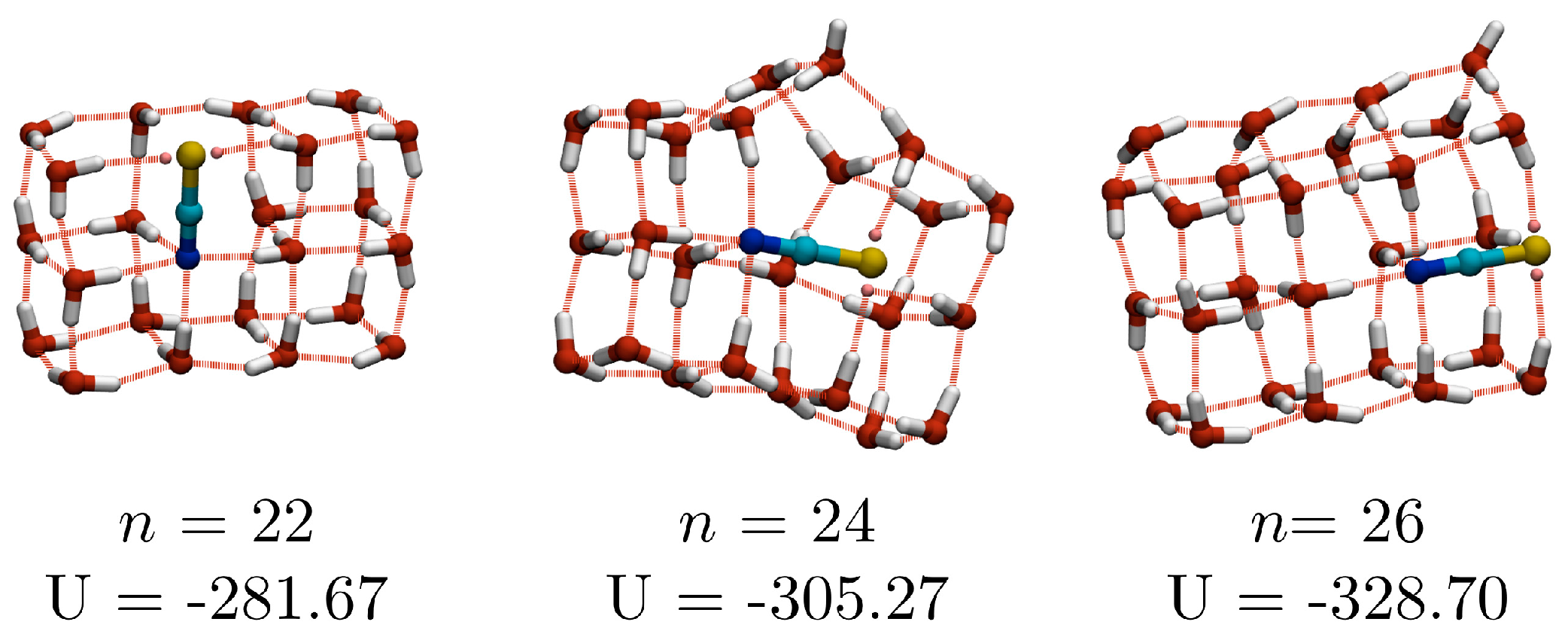However, for n ≥ 23, the lowest energy structures have been observed in only one of the independent basin-hopping searches and should be regarded as representative low-lying minima, rather than the true global minima (for the potentials used here). Three of the larger structures (with n = 22, 24 and 26), which will be discussed later, are shown in Figure 2. (Coordinates of all putative global minima and other low energy structures are listed in xyz file format in the Supplementary Materials.)

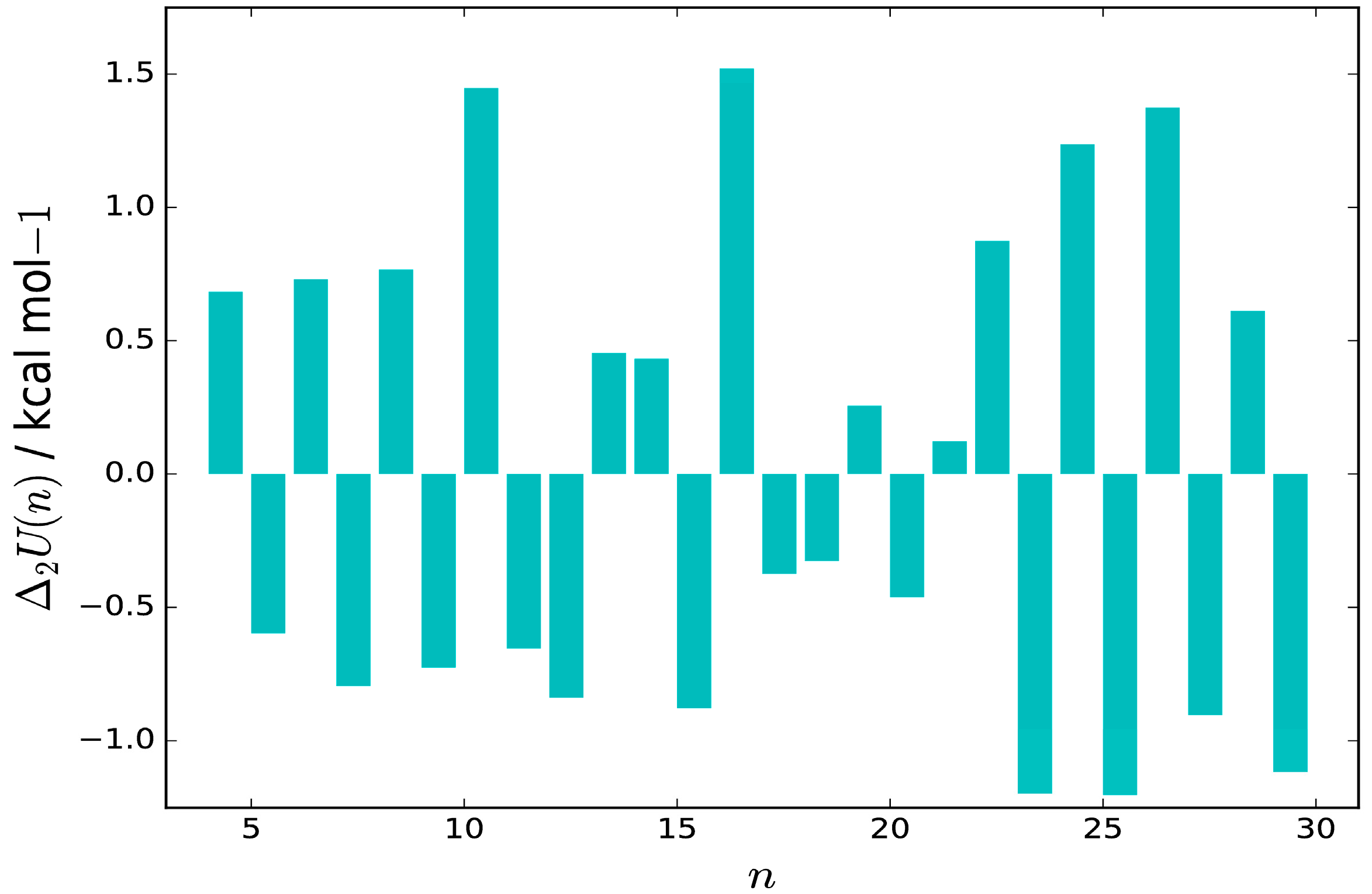
The central difference approximation to the second derivative of the energy of the putative GM for hydrated thiocyanate clusters, Δ₂U (defined in Equation (1)), is plotted as a function of n in Figure 3, for n = 4–29. The putative GM for n = 10, 16, 22, 24 and 26 can be identified as “magic number” structures, stable relative to similar-sized clusters, corresponding to positive values of Δ₂U. Figure 1 and Figure 2 reveal that these structures contain a large number of closed cube or pentagonal-prism water units, which are common motifs in pure water clusters [17], and confer stability at these sizes, with the thiocyanate ion often occupying an edge of the cluster polyhedron. We observe alternating even-odd behaviour in stability for n ≤ 10 and 22 ≤ n ≤ 34, with structures containing even numbers of water molecules being more stable.

$${\Delta }_{2}U\left(n\right)=\frac{1}{2}\left\{U\left(n+1\right)+U\left(n-1\right)-2U\left(n\right)\right\}$$

(1)

For n ≤ 10, this behaviour correlates with the number of complete four-membered rings contained within the structure. For all sizes studied, the thiocyanate ion prefers to sit on the surface of the cluster and does not become fully solvated. Common structural motifs for the structures of the global minima of (SCN⁻)(H₂O)_n are four-membered water squares and (above n = 18) five-membered water pentagons. These structures are common in the global minima of pure TIP4P water clusters, where four-membered and five-membered water rings are able to stack into cubes and pentagonal prisms of increasing length. We will use the terminology used by Wales and Hodges [17], and label three or more stacked water rings as fused cubes/fused pentagonal prisms. Structural analogies exist between the global minima of pure TIP4P clusters and hydrated thiocyanate clusters, and comparisons will be drawn throughout this analysis.

The length of the thiocyanate ion (2.84 Å) is close to the O···O distance in the water dimer (2.88 Å), which explains why SCN⁻ can replace two hydrogen-bonded water molecules along an edge of a water cluster. However, due to the asymmetry of the ion, the sulfur and nitrogen ends of the ion typically occupy different cluster sites, with the N atom preferentially occupying higher coordination sites than S (see for example the n = 13 structure, where the nitrogen atom is four-coordinated and the sulfur atom is two-coordinated). 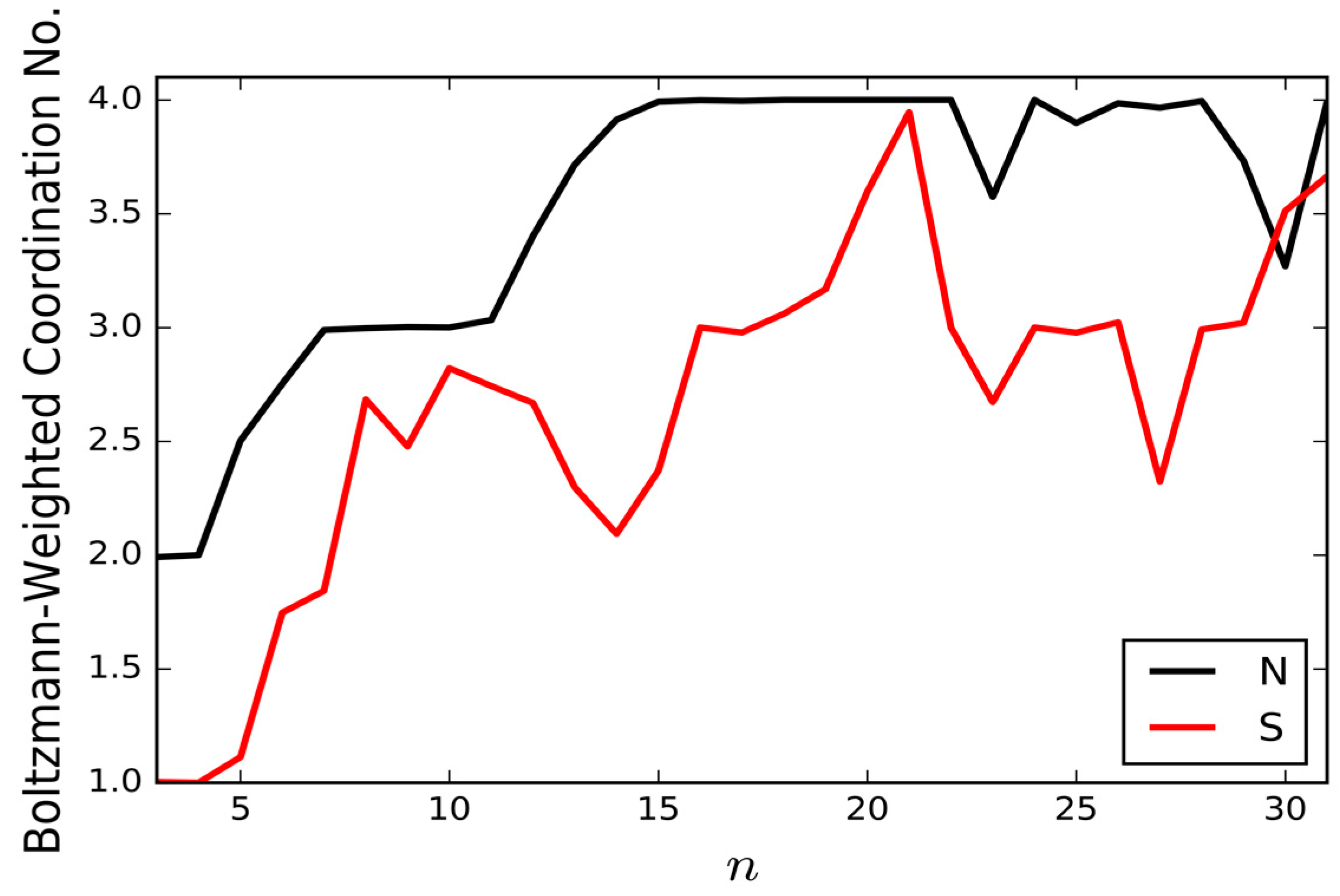Figure 4 presents the Boltzmann-weighted mean coordination numbers of the nitrogen and sulfur atoms for the thiocyanate-water clusters. To determine the coordination numbers, the H⋯X cutoff distance used for determining the presence of a hydrogen bond to the S or N end of SCN⁻ is 2.5 Å and the lower limit on the O–H⋯X angle is 130°. The Boltzmann-weighted coordination numbers are averaged over all unique isomers found for each cluster size, based on their potential energies and assuming a temperature of 130 K (this is to allow comparisons to be made with potential future IRMPD measurements) [6]. The preference for the N atom to sit at higher coordination sites is consistent with the asymmetry of coordination measured for the thiocyanate ion in bulk aqueous solution, though our coordination numbers are somewhat higher than the experimental values [10,11,12]. The higher coordination number of the N atom is due to its higher charge density: in our empirical model, both ends of the thiocyanate ion carry a charge of −0.7e, but the S atom distributes its charge between a pair of lone pair sites, lowering the charge density.

As mentioned above, water molecules are exclusively engaged in one, two, three and four water squares for n = 4, 6, 8 and 10, respectively. The increasing number of water squares culminates in a pair of fused water cubes at n = 10, with the SCN⁻ ion occupying one of the fused edges, replacing two water molecules in the double-cube TIP4P GM for (H₂O)₁₂ [17]. For n ≥ 13, fused cubes are observed in all the GM structures.

In our previous studies of water-sulfate and water-perchlorate clusters, we enumerated the number of dangling O–H bonds (i.e., those bonds which are not involved in hydrogen bonding either to other water molecules or to the anion) [4,5]. We found that, although the presence of both anions result in a reduction in the number of dangling O–H bonds, compared to pure water clusters, the effect is much more marked for the higher charged (and centrally located) SO₄²⁻ ion, which acts as a sink for hydrogen bonds. The dangling O–H bonds for the putative GM for (SCN⁻)(H₂O)_n (3 ≤ n ≤ 16) are highlighted in Figure 1 with light blue circles. Single dangling O–H bonds are seen for n = 5, 7, 10, 12, 14, 17, 18, 19 and 21, and two dangling O–H bonds for n = 15 and 20. In general, the number of dangling O–H bonds is lower than for pure water clusters: for example, 1-d linear arrangements of water cubes, such as the double cube (H₂O)₁₂, always have 4 dangling O–H bonds [17], compared to the single dangling bond found for the isostructural (SCN⁻)(H₂O)₁₂ cluster. The size-dependent mean numbers of dangling O–H bonds for thiocyanate-water clusters are similar to those for perchlorate-water, but higher than for sulfate-water clusters, showing that chaotropic anions (typically with low charge) have less of a disruptive effect on the skeletal structure of the water cluster, but cause some degree of reorganisation of the hydrogen bonding network of the water molecules, as they are hydrogen-bond acceptors but not donors. This has also been discussed by Valiev et al., who have described the thiocyanate ion as a (water) “structure weakener” rather than a “structure breaker” [15].

2.2. Energy Landscapes

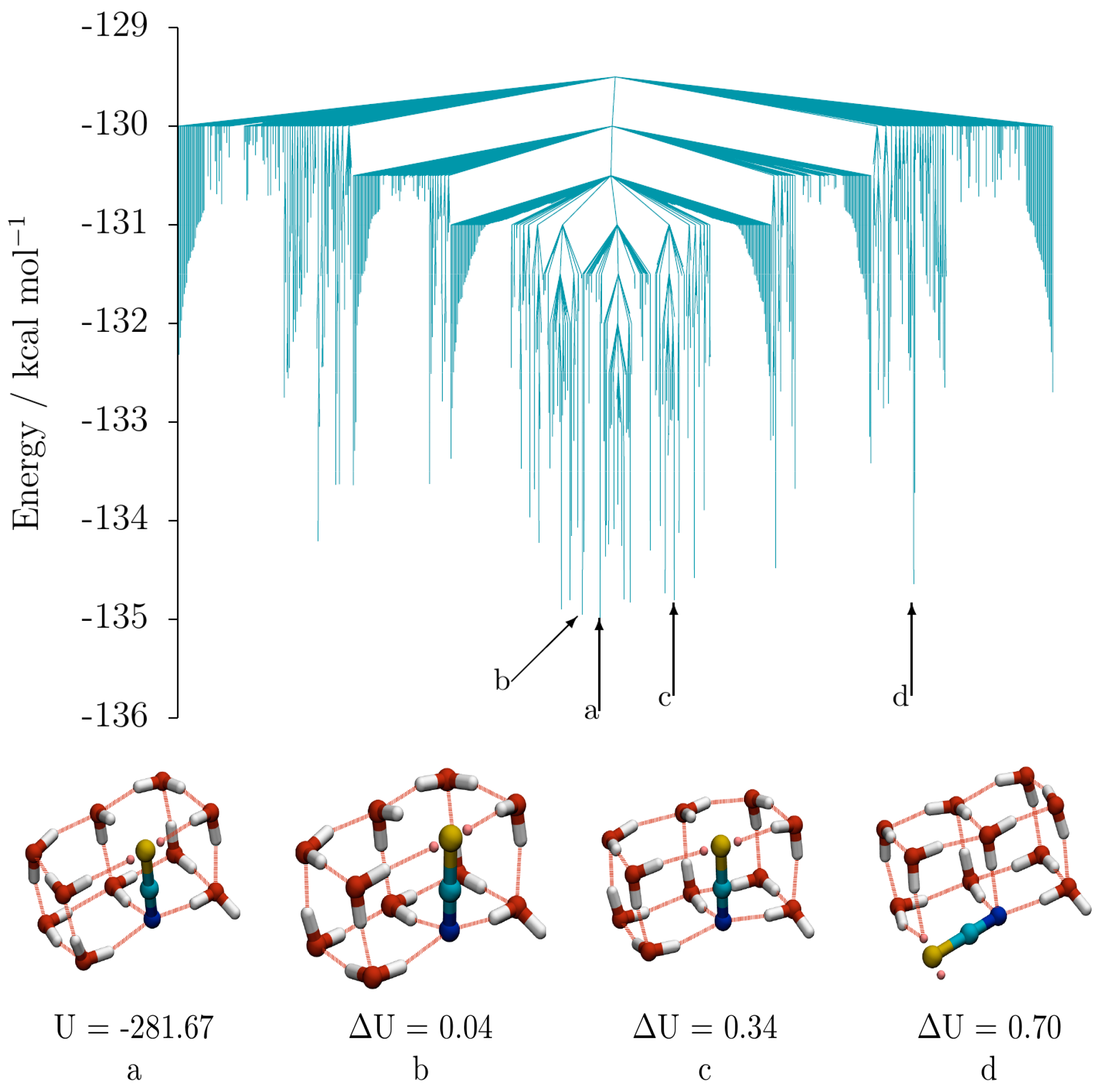
Databases of minima and transition states have been compiled for clusters in the size range 3 ≤ n ≤ 13. Figure 5 shows the low energy disconnectivity graph for (SCN⁻)(H₂O)₁₀, (taken from a database consisting of 10,136 minima and 61,436 transition states). Also shown are the global minimum (a) and the 2nd (b), 6th (c) and 9th (d) lowest energy structures, which are representative of the geometric variety observed among the low energy isomers of (SCN⁻)(H₂O)₁₀. Isomers b and c have the same double cube oxygen-thiocyanate skeleton as the GM a, and just differ by inversions of the directionality of the hydrogen bond networks (one and two inversions for b and c, respectively, relative to the GM). Isomer d is also composed of two fused cubes, but the thiocyanate ion occupies a non-shared edge, rather lying along an edge parallel to the long axis of the double cube, resulting in an S coordination of only 2.

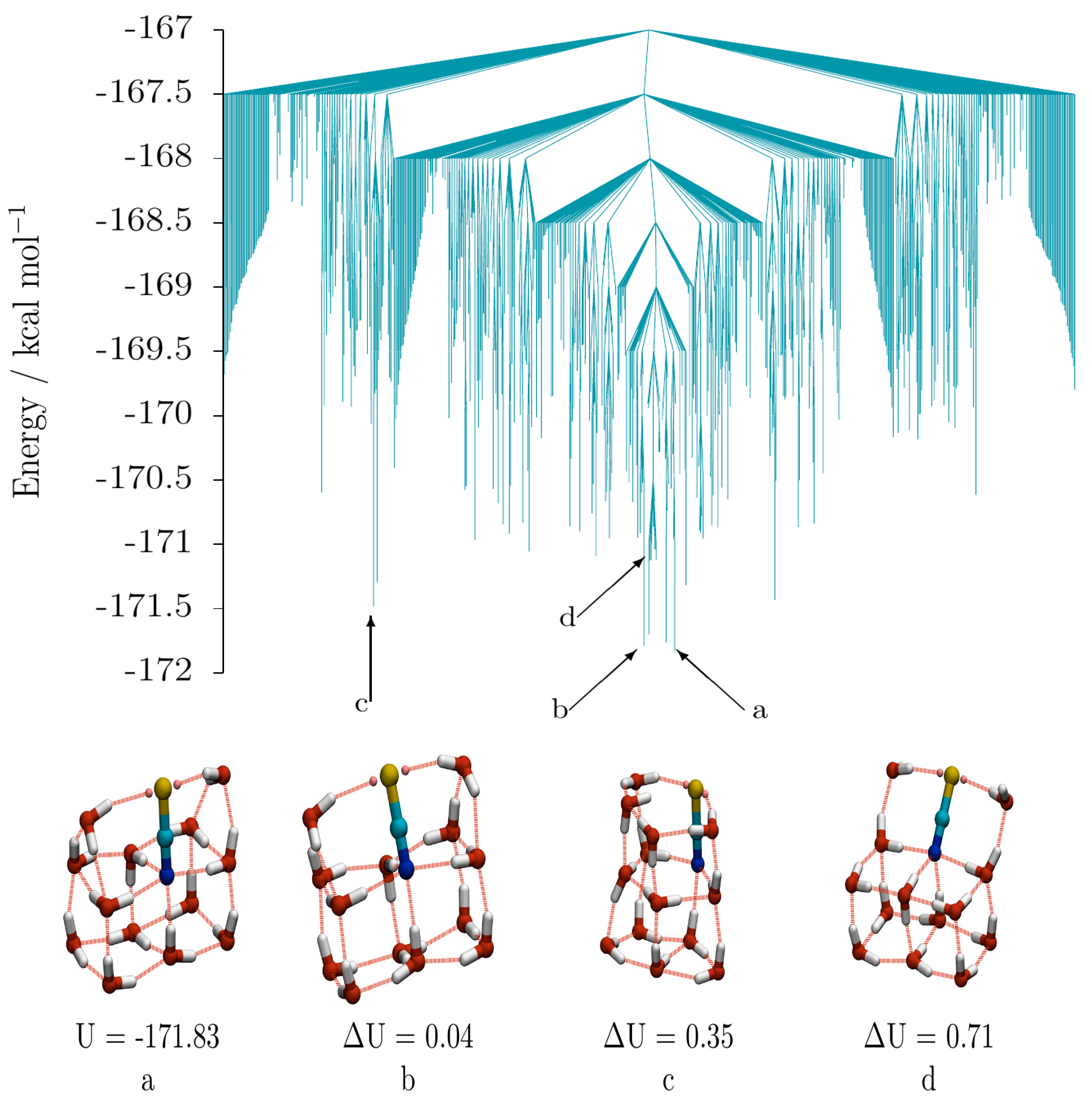
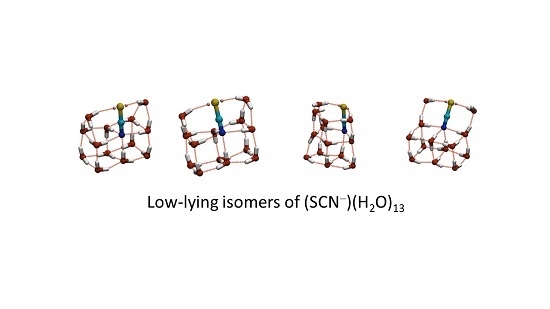
The low energy disconnectivity graph for (SCN⁻)(H₂O)₁₃ (taken from a database of 13,884 minima and 92,880 transition states) is shown in Figure 6, along with four low energy isomers. The isomers display three distinct oxygen-thiocyanate skeletons. Isomers a (GM) and b (2nd lowest-energy isomer) adopt a “house” structure, with a double cube base and double triangular prism roof, and differ from each other by a single hydrogen bond cycle inversion. Isomer d (10th lowest) is related to a and b, having an “open chest” structure, comprising a double cube and an open lid containing the thiocyanate ion. Swinging the lid over to the closed position results in a “closed chest”—corresponding to the “house”-like isomers a and b. The structure of isomer d demonstrates how an energetically stable sub-structure (in this instance the fused water cube) can stabilise a structure containing otherwise unfavourable components (such as the two under- coordinated water molecules in the lid). Other examples can be observed in the GM thiocyanate-water structures for n = 12, 14 and 15 water molecules. Isomer c, is distinct from the other isomers, as it consists of two fused pentagonal prisms (sharing a pentagonal face), though it can be derived from a “house” cluster by breaking the hydrogen bonds of the two cubes on the face closest to the roof. In isomer c (5th lowest), however, unlike in a and b, the thiocyanate ion does not occupy a fusion edge. It should also be noted that the N atom is 4-coordinate and the S atom 2-coordinate in all of these isomers.

For both the 10- and 13-water clusters, the low energy isomers share a small number of oxygen-thiocyanate skeletons, but differ by the placement of the hydrogen atoms. For example, of the lowest 40 minima on the n = 10 landscape, all but one structure has a fused cube skeleton. In spite of the structural and energetic similarity of these minima, the barriers between different hydrogen-bond cycle isomers are large (≈4 kcal·mol⁻¹ for n = 10) and barriers are larger still when the oxygen-thiocyanate skeleton is altered (≈5 kcal·mol⁻¹ to convert from isomer a to d for n = 10). Large energetic barriers imply slow relaxation times between minima, and, when coupled with energetically competitive isomers, suggest that the system will exhibit glassy or frustrated dynamics, as for pure water clusters [18]. As the number of water molecules grows, the number of possible permutations of hydrogen atoms with a given oxygen skeleton increases. Thus, it is reasonable to assume that the landscape will grow increasingly frustrated with increasing n.

The putative GM for (SCN⁻)(H₂O)₁₆ (Figure 1) has an oxygen-thiocyanate skeleton organised into a pair of fused cubes (fused along the long face of each), to form a (3 × 3 × 2) cuboid, with the N atom sitting in the central 4-coordinate site, and the S on a 3-coordinate edge site (though there are only two direct H⋯S(LP) interactions). There is little variation in the oxygen-thiocyanate skeleton amongst the other low-energy isomers (all but one of the lowest 50 energy minimum structures share an oxygen-thiocyanate skeleton).

Unlike the n = 10 system, isomers in which the thiocyanate ion sits along the edge of a cube (see isomer d in Figure 5), are not observed, nor are structures where the S atom sits in the other 4-coordinate site (opposite the N atom), which would correspond to a more solvated anion. The trend of adding additional fused cubes to a structure continues at n = 22, for which the putative GM is composed of three fused cubes. Central difference analysis (Figure 4) identifies the n = 10, 16 and 22 GM as magic number clusters, due to the stabilising effect of having all water molecules participating in a water-thiocyanate cube.

2.3. Comparison of Thiocyanate-Water Clusters with Pure TIP4P Water Clusters

The recurrent use of stable sub-units to construct larger energetically favourable superstructures is common to both hydrated thiocyanate and pure TIP4P water clusters. Examples of the structural motifs observed in both systems are shown in Figure 7 [17]. As discussed previously, 4-membered water squares (which can stack to form cubes, fused cubes etc.) and 5-membered water pentagons (which aggregate into pentagonal prisms and fused prisms) are the predominant sub-units for both, though the manner in which these units aggregate differs between the two systems. For TIP4P water, the fused-cube motif stacks into one-dimensional chains, whilst the hydrated thiocyanate global minima tend to aggregate into two dimensional structures. This difference in dimensionality is probably driven by the energetic benefit of placing the N atom in a more highly coordinated site within the water structure. Pentagons and pentagonal prisms appear in the global minima of the larger hydrated thiocyanate ions (from n = 18 onwards), either as a pentagonal face in an otherwise cubic structure (n = 18 and 21) or in a combined fused-pentagonal-prism-cube arrangement (n = 19, 24 and 26). At the empirical level, lone pentagons or pentagonal prisms (such as those found for pure TIP4P water at n = 5, 10, 15 etc.) and single cubes (as found for TIP4P (H₂O)₈) are not observed for (SCN⁻)(H₂O)_n due to the low average coordination number that the N atom would adopt. It should be noted that the GM structures for thiocyanate-water clusters with six and eight water molecules (at the EP level) are related to the pure water single cube and pentagonal prism, respectively, but with some water molecules on adjacent edges to the thiocyanate reorienting so as to donate an additional hydrogen bond to the N atom. It should be noted, however, that (as discussed in the following section) the EP over-stabilises high coordinated N relative to higher level (DFT) calculations [15,16].

Finally, it should be noted that there are far fewer homodromic hydrogen-bonded rings (cooperative hydrogen-bonded rings, with each water molecule acting as a hydrogen-bond donor and acceptor) in the thiocyanate-water clusters than in the pure water clusters. This is because the thiocyanate ion is only an H-bond acceptor. Homodromic rings can still be found for larger thiocyanate-water clusters, where such rings can form far from the thiocyanate ion.

2.4. Comparison of Empirical Potential with DFT Calculations

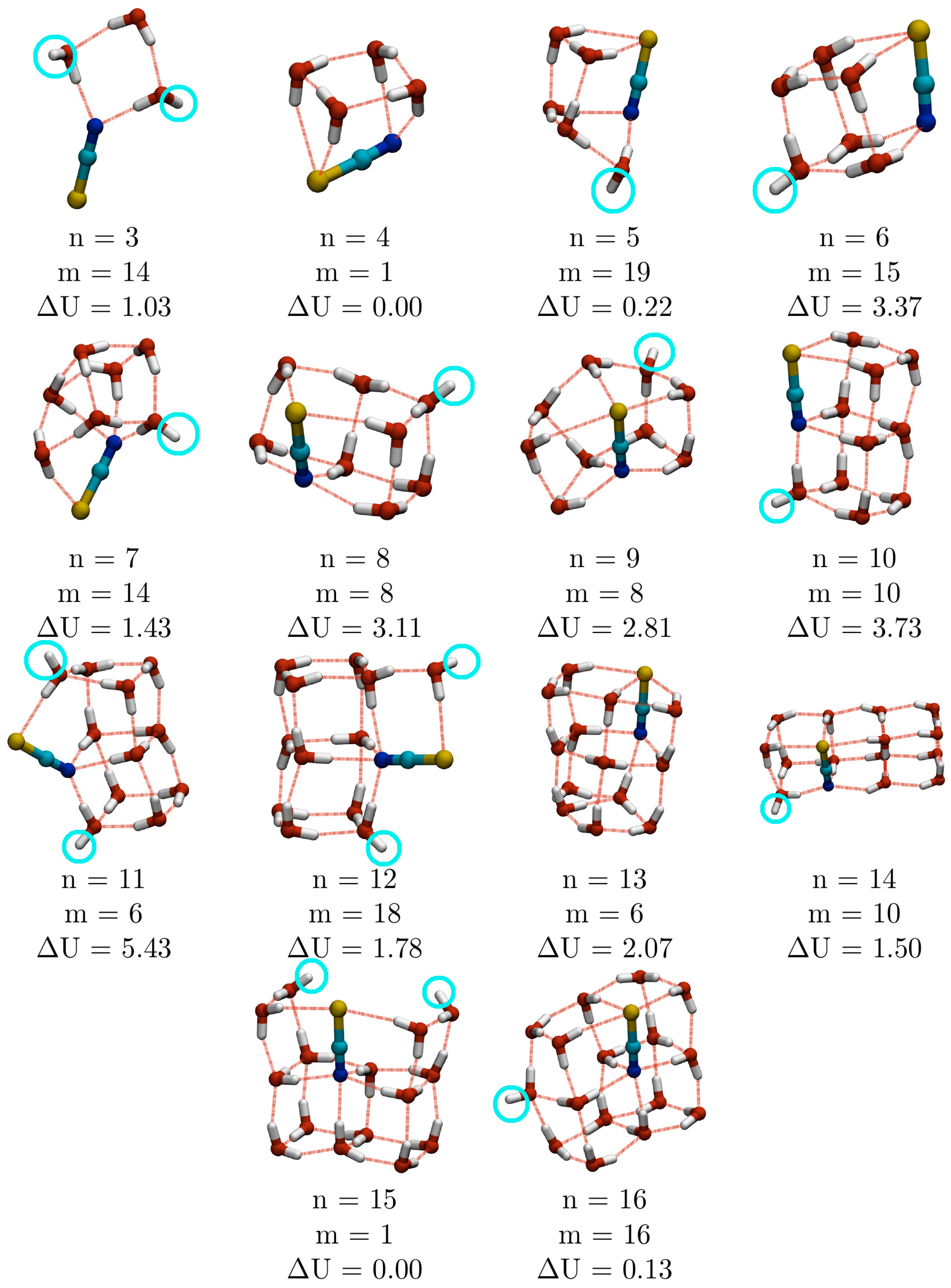
As the calculations described above were based on a simple empirical potential model, it was decided to test these against higher level DFT calculations. The twenty lowest energy EP minima for all cluster sizes in the range 3 ≤ n ≤ 16 were reoptimised at the DFT level using the B3LYP exchange-correlation functional and 6-311++G** basis set. The lowest energy isomers at the DFT level are shown in Figure 8. Each structure is assigned three labels: n (the number of water molecules); m (the energetic ranking of the empirical minimum from which it was reoptimised); and ΔU (the magnitude of the difference in DFT energy between the minimum in question and the reoptimised empirical GM). In only 2 cases (n = 4 and 15) is ΔU = 0, meaning that the EP GM gives rise to the lowest energy DFT isomer after reoptimisation (hence m = 1).

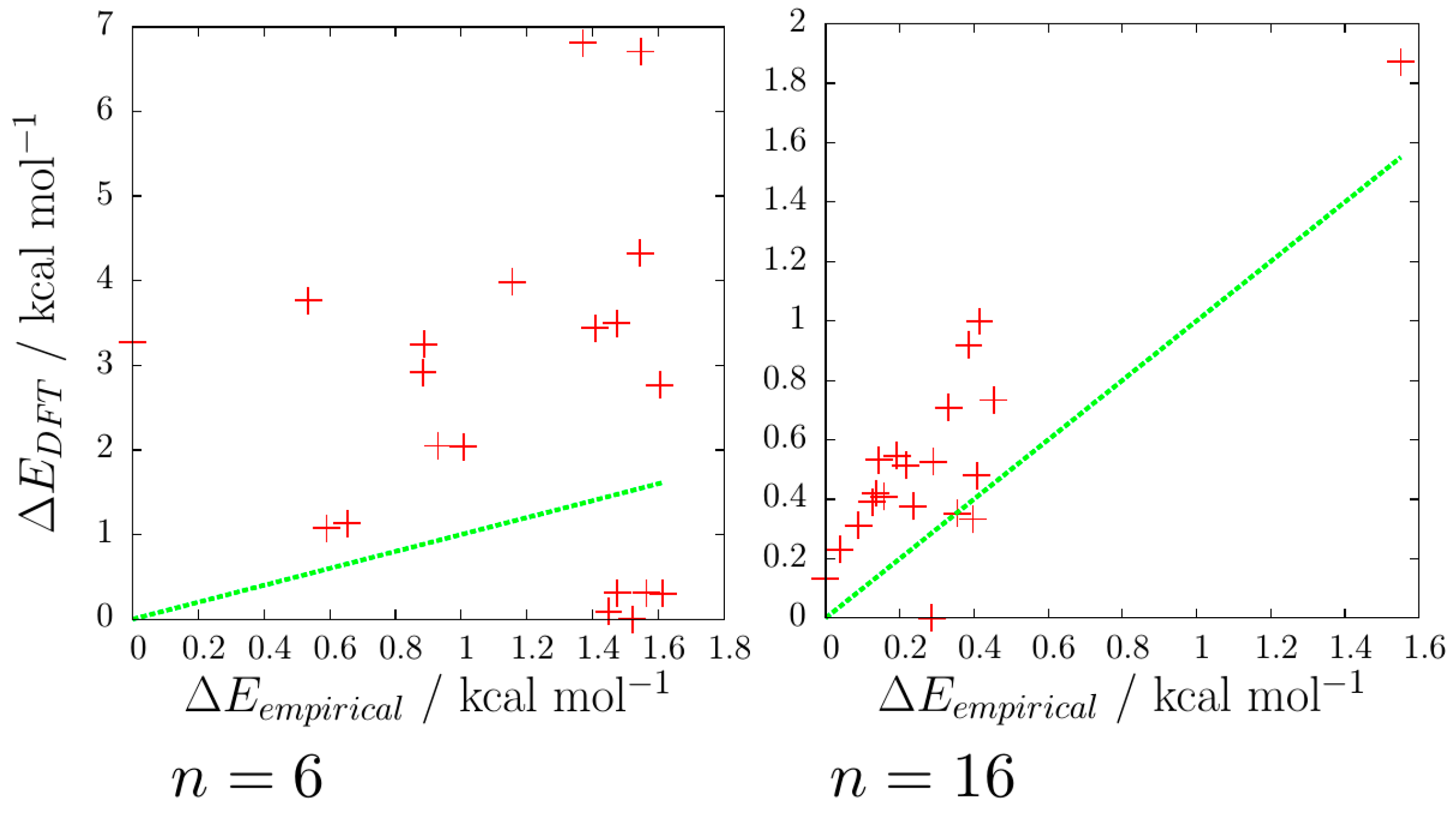
The correlation of the energies of the reoptimised DFT minima against the original EP minima has been plotted for 3 ≤ n ≤ 16 and two examples (for n = 6 and 16) are shown in Figure 9. The degree of correlation varies with n, but in general, for the 20 lowest-energy rigid-body isomers considered, it is quite poor. The correlation is particularly poor for cases where the oxygen-thiocyanate skeleton of the EP and DFT global minima differ (such as n = 6, 11 and 12). An exception is the n = 16 case, which has a good correlation between the energies of the empirical and DFT minima, which is probably due to all 20 of the lowest energy empirical isomers sharing the same oxygen-thiocyanate skeleton: the (3 × 3 × 2) cuboid, though the lowest energy DFT isomer has a different energy arrangement of hydrogen bonds than the lowest EP isomer.

Comparison of the structures of the lowest energy empirical and DFT structures reveals one general finding: the EP significantly over-estimates the strength of the water-thiocyanate interaction, particularly between water and S. This is evidenced by three factors in the DFT calculations: the tendency for the S atom to protrude from the body of the cluster (this is particularly evident for n = 3, 7 and 11) or opening out of the water-sulfur rings; the relocation of the thiocyanate ion to lower coordinated sites within the clusters; and the higher occurrence of water-thiocyanate cubes. At the DFT level, water-thiocyanate cubes begin to appear at smaller n (6 as opposed to 10 water molecules) and do so more frequently. At n = 6, 11, 12 and 14, the number of water cubes or water-thiocyanate cubes increases, which has the double benefit of increasing the number of energetically stabilising structural sub-units, whilst also reducing the co-ordination number of the thiocyanate ion. Water cubes are so stabilising that the n = 11 and 12 clusters can essentially eject the ion from the structure and still remain the most energetically favourable geometry. The lower coordination of the thiocyanate ion (particularly the S atom) is in agreement with the previously mentioned neutron diffraction studies of bulk aqueous solutions of thiocyanate salts [10,11,12]. The rigid-body model of the thiocyanate ion used in the EP approach is reasonable, as the maximum deviation from linearity of the S–C–N moiety is only 3.3° (measured in the (SCN⁻)(H₂O)₃ cluster).

The appearance of a single cube (n = 6) and one-dimensionally stacked fused cubes (double cube for n = 10, triple cube for n = 14) is reminiscent of pure TIP4P water clusters, where these motifs are observed in the GM structures for n = 8, 12 and 16 (Figure 7) [17]. It should be noted, however, that the EP GM for n = 6 (Figure 1) is a distorted cube, with an O–H⋯N hydrogen bond across one of the faces of the cube, while the lowest energy DFT isomer is a more regular cube with a dangling O–H bond on a water molecule across one of the square faces from N. In general, there is a slightly greater number of dangling O–H bonds in the lowest energy DFT minima (Figure 8) than in the EP GM (Figure 1), though they are still considerably fewer than for pure water clusters.

Though in the low energy DFT isomers the SCN⁻ ion sometimes moves to lower coordinated sites, the mean coordination number of the N atom is still greater than that of S. The lowest energy DFT structure for (SCN⁻)(H₂O)₁₆ has the same oxygen-thiocyanate skeleton as the empirical GM, but with a different hydrogen bonding network (they differ by two cycle inversions). Due to the large number of low-lying minima which share the same oxygen-thiocyanate skeleton, none of the structures which had been re-optimised had a different cage structure. Further investigation, for example coupling Basin Hopping searching with DFT energy evaluation, would be needed to determine if a more favourable heavy atom arrangement exists. However, given the propensity of the DFT calculations to favour water cubes, it is probably reasonable to assume that the skeleton is a good candidate structure (though a better hydrogen bond network may exist).

Turning to previous DFT calculations of (SCN⁻)(H₂O)_n clusters, structures presented by Lee et al. are generally quite different from those shown in Figure 8 [13], often having the thiocyanate ion in a more central, more fully solvated environment: for example, their structure for (SCN⁻)(H₂O)₁₆ consists of an SCN⁻ ion coordinated to two (H₂O)₈ cubes, one through N and the other through S. It is unlikely that these are globally optimised so they will not be discussed further here.

Comparing our results for (SCN⁻)(H₂O)_n (n = 3–8) with those presented by Valiev et al. (VDW), which were globally optimised at the DFT level using a genetic algorithm [15], we find the same lowest energy structure for n = 3 (4-membered ring with S not coordinated), n = 4 (trigonal prism, with the thiocyanate ion lying along an edge linking the two triangular faces); n = 5 (edge-bridged trigonal prism) and n = 6 (cube with thiocyanate occupying an edge). VDW showed that the calculated VDEs for these isomers are in good agreement with the PES measurements [15].

For n = 7, the lowest energy isomer of VDW is a cube, with one vertex occupied by the N atom and the rest of the thiocyanate ion sticking out of the cluster. Of the 10 metastable structures within 1.25 kcal·mol⁻¹ of the putative GM, 6 have the same skeleton, with different hydrogen-bond arrangements, while the other 4 have a distorted cube structure, with one N-water edge opened up and the S end of the ion leaning over towards the water that was formerly hydrogen-bonded to N. Our lowest energy DFT isomer (Figure 8) is a distorted version of the VDW putative GM.

The lowest energy VDW isomer for n = 8 (and for 16 other isomers up to 0.88 kcal·mol⁻¹ above the putative GM) is a pentagonal prism, with the thiocyanate ion occupying one of the edges on a pentagonal face. At an energy of 1.22 kcal·mol⁻¹ above the GM, a different cluster skeleton is found, corresponding to an open box (i.e., a cube fused with a square), with the thiocyanate ion as part of the lid (the N atom is a vertex of the cube). This structure is analogous to the “open chest” structure that we found as a metastable isomer for (SCN⁻)(H₂O)₁₃ with the EP. Our lowest energy DFT isomer (Figure 8) is a distorted pentagonal prism, with an additional water-N hydrogen-bond across one of the pentagonal faces, which may reflect the tendency of the EP (whose local minima were used as the basis for DFT reoptimisation) to form too many hydrogen bonds to the N atom.

3. Methodology

Due to the relatively large sizes of the systems under consideration, we have used an empirical potential (EP) model and rigid bodies (i.e., with fixed bond lengths and angles) to represent the thiocyanate ion and water molecules. Modelling the molecules as rigid bodies means they can be described by angle axis coordinates [19]. Rigid body modelling also reduces the computational cost, as it removes internal degrees of freedom and, hence, reduces the search space for global optimisation.

The empirical interaction energy (U) of a thiocyanate-water cluster (SCN⁻)(H₂O)_n is evaluated as the sum of Coulombic and Lennard-Jones (LJ) contributions over all pairs of interacting sites (atoms and lone pairs) for the ion-water and water-water interactions, Equation (1)):

$$U={\displaystyle \sum }_{i=1}^N{\displaystyle \sum }_{j=i+1}^N\left\{\frac{q_i{q}_j}{r_{ij}}+4{ϵ}_{ij}\left[{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^{12}-{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^6\right]\right\}$$

(2)

where σ_ij and ε_ij are the LJ parameters, r_ij is the inter-site separation, and q_i and q_j are the partial charges on sites i and j, respectively, and N is the total number of sites. For interactions between different types of sites, the LJ parameters σ_ij and ε_ij are obtained from the Lorentz–Berthelot combining rules [20].

The thiocyanate anion is modelled as a rigid ion, using the 5-site planar model of Wipf et al. [21], which includes sulfur, carbon and nitrogen atoms (arranged linearly) and two lone pair pseudoatoms orthogonal to the SCN axis, either side of the sulfur atom. The S–C, C–N and LP–S distances are 1.59 Å, 1.25 Å and 0.65 Å, respectively. The partial charges were derived from Hartree-Fock calculations on the gas phase SCN⁻ anion using a 6-31+G* basis set, with the sulfur charge split equally between the two lone pair sites. The distribution of partial charges is similar to those used in studies of thiocyanate ions at liquid-liquid interfaces [22,23]. For the LJ parameters, values from the OPLS acetonitrile force field [24] were used for N and C, and the AMBER94 force field [25] was used for the S atom and lone pair sites. The charge and LJ parameters were further optimised by fitting to calculated values of the structures and relative stabilities of [La(NCS)₆]³⁻ and [La(SCN)₆]³⁻ complexes (i.e., the experimentally observed N-bound complex, versus the hypothetical S-bound complex) in the gas phase [21]. The thiocyanate parameters are listed in

Table 1. Empirical potential parameters for SCN⁻ [21] and H₂O [26,27].

SCN−	Site	ε / kcal mol−1	σ / Å	q / e
	S	0.200	4.1426	0.00
	C	0.086	3.340	0.40
	N	0.170	3.271	−0.70
	LP (×2)	0.155	2.575	−0.35
TIP4P H2O	O	0.648	3.15	0
	H	0	0	0.52
	LP	0	0	−1.04

.

As in our previous studies [4,5], the water molecules in the thiocyanate-water clusters are modelled using the TIP4P potential (with parameters listed in Table 1), with the water molecule represented by a rigid four-body molecule with a H–O–H bond angle of 104.52° and O–H bond lengths of 0.9572 Å, and with an oxygen “lone pair” site (located 0.15 Å from the O atom along the bisector of the H–O–H angle, on the H side of the molecule) which carries the oxygen’s charge but which has no LJ interaction (the LJ interaction is centred on the O atom itself) [15,26]. The computationally inexpensive TIP4P model has been widely used to model water clusters [19,27,28], though it should be noted that the simple TIP4P model fails to reproduce some properties of bulk water and ice [29]. In future work, the effect of using polarizable ions and water molecules, as in the AMOEBA force field [30], will be investigated.

Low energy minima for the thiocyanate-water clusters were found using the Monte Carlo Basin Hopping (BH) algorithm [31,32], implemented in the pele [33] and GMIN [34] packages. For each cluster size, BH is used to obtain the lowest energy structure (the putative global minimum, GM) and to explore the potential energy landscape as efficiently as possible, for subsequent landscape mapping. Eight independent BH runs were performed (each consisting of 500,000 attempted Monte Carlo steps) for each hydrated thiocyanate cluster (SCN⁻)(H₂O)_n, with 3 ≤ n ≤ 50.

The Monte Carlo geometry moves were performed in blocks of 100 of the same type [17]. Three move-classes were employed: rigid-body rotations and translations and hydrogen-bond cycle inversions. Rotation moves: all rigid body molecules are rotated by a random angle in the range ±π radians, about the vector connecting the O atom of each TIP4P water and the central C atom of the thiocyanate ion. Translation moves: a random displacement (a uniform random unit vector times the step size of 3 Å) is applied to a randomly chosen molecule. Cycle inversion: moves the hydrogen bonding within the cluster is represented as a network graph in which each water molecule is a node and each hydrogen bond is an edge [35]. Closed cycles of hydrogen bonds within the graph are identified; one of the cycles is inverted and the graph is then projected back onto the hydrogen bonding network of the original cluster [4]. In our previous studies of sulfate- and chlorate-water clusters, these cycle inversions were found to have a greater effect on total energy for larger hydrogen bonded cycles and, hence, to be more beneficial for the global optimisation of larger clusters [4,5].

The pele software package was also used to explore the potential energy surface, constructing a data base of connected minima. The doubly-nudged elastic band method was then used to search for transition states between previously found minima [36,37]. Candidate transition states were then optimised using hybrid eigenvector-following [38,39]. The resultant energy landscapes were visualised as disconnectivity graphs [40,41,42], using the PyConnect program [42].

In order to test the applicability of the EPs, for thiocyanate-water clusters with up to 16 atoms, in each case the 20 lowest energy isomers have been reoptimized at the density functional theory (DFT) level of theory, using the NWChem package [43]. As in the work of Lee et al. [13] and Valiev et al. [15], our calculations were performed using the B3LYP exchange-correlation functional and we used the 6-311++G** basis set, which is similar to those used in the previous studies. To be consistent with the earlier work, we did not include dispersion terms. While the majority of the hydrogen-bonding energy is Coulombic in nature (which should be quite well represented by the B3LYP functional), in future work (and following detailed studies of the effect of different xc functionals and the inclusion of dispersion interactions on the structures and dynamics of pure water clusters, liquid water and ice) [44], functionals including dispersion interactions should be included to evaluate any difference in the optimal structures of ion-water clusters.