Abstract
Encapsulations of carbon dioxide into (22)- and (23)- fullerenes are evaluated. The encapsulation energy is computed with the DFT M06-2X/6-31+ approach corrected for the basis set superposition error evaluated by the counterpoise method. The resulting encapsulation energy for @(22)- and @(23)- amounts to substantial values of −14.5 and −13.9 kcal/mol, respectively. The energy gain is slightly larger than for CO@, already synthesized with a high-temperature and high-pressure treatment—so that a similar preparation of could be possible. The calculated rotational constants and IR vibrational spectra are presented for possible use in detection. The stability of is also briefly discussed.
1. Introduction
Interactions of carbon dioxide with fullerenes have been studied [1,2,3], for example, for boron-based fullerene cage [1]. Interestingly, additions of endohedral fullerenes [4,5] or carbon dioxide [6] can improve the efficiency of solar cells. Various non-metallic molecules can also be encapsulated inside fullerene cages. and were the first such non-metal endohedrals, namely prepared [7] by heating under high pressure and with a catalyst. Moreover, there is also an elegant synthetic technique that first places molecules inside open fullerene cages and then the cages are synthetically closed—for example, the preparation [8] of (O.
Such fullerene encapsulations of non-metals have also been calculated, e.g., in [9,10,11,12,13,14]. The first such calculations [9] from the year 1991 treated small molecules (, , CO, and LiH) trapped inside the cage and predicted a blue shift in the stretching frequencies. Later on, encapsulations of larger non-metal molecules into fullerene cages were also calculated [10,11,12,13,14], for example, hydrides [10] or water molecules [11,14]. Moreover, the endohedral was synthesized recently [12], and its stabilization energy was calculated [13] as −13.5 kcal/mol.
As could also be prepared [7] by the high-temperature and high-pressure treatment, there is a question regarding if may also be encapsulated in some (larger) fullerene cages. In this report, the issue is calculated for the first time—namely for the two lowest-energy and most common fullerenes (22) and (23) [15]. The pristine and isomers are produced via high-temperature synthesis [15,16] in a ratio of 2:1. The structure is located [17] only about 0.5 kcal/mol below the species. However, the chirality factor also contributes [15] to the / relative isomeric populations.
2. Calculations
The calculations are carried out with density-functional theory (DFT) treatment, namely using the DFT M06-2X functional comprehensively tested [18] for thermochemistry, kinetics, noncovalent interactions, and other applications. The M06-2X functional is employed with the standard 6-31+ basis set [19] M06-2X/6-31+( approach). The geometry optimizations are performed with the analytical first derivatives of energy. In the localized stationary points, the harmonic vibrational GF analysis is carried out using the analytical second derivatives of energy. The vibrational analysis can confirm that energy minima were indeed localized. For DFT integration, the so-called ultrafine grid is applied (and then refined with the superfine grid). For the SCF (self-consistent field) convergence, the tight criterion is used. The wavefunction stability is systematically tested in order to avoid unphysical unstable SCF solutions.
The encapsulation energy [20] is corrected for the so-called basis set superposition error (BSSE) evaluated by the approximative Boys–Bernardi counterpoise method [21] (also labeled [22] CP2). The counterpoise method guarantees that every component of a treated chemical reaction is formally described by the same number of basis-set functions so that their total energies are comparable. The BSSE correction term constitutes an important refinement of the encapsulation energy. Without the BSSE correction, the energy gain produced by encapsulation process would be overestimated (i.e., products would be over-stabilized).
The reported computations are carried out with the Gaussian program package [22]. The calculations are performed on computers operating in parallel regime, mostly with 8–24 processors (computational frequency up 3 GHz each; available operational memory up to 60 GB).
3. Results and Discussion
The calculated encapsulation energy means the potential-energy change along the studied gas-phase association process, for example for encapsulation in the (22) fullerene cage:
and similarly for the (23) cage. The M06-2X/6-31+-calculated encapsulation energy values with and without the BSSE correction are presented in Table 1.

Table 1.
The calculated encapsulation energy for @(22) and @(23).

Figure 2.
The M06-2X/6-31+-optimized structure of @(23) (the shortest contact of O with the cage carbon is indicated by dashed line).
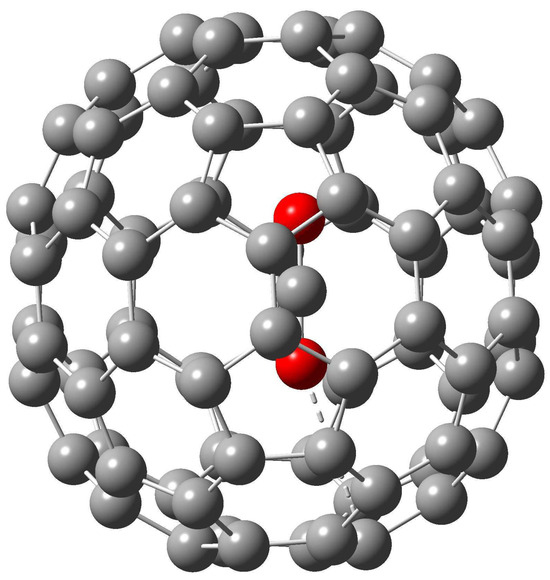
Figure 1.
The M06-2X/6-31+-optimized structure of @(22) (the shortest contact of O with the cage carbon is indicated by dashed line).
The BSSE-corrected M06-2X/6-31+ encapsulation energy for @(22) and @(23) amounts to −14.5 and −13.9 kcal/mol, respectively. At this computational level, the BSSE correction reduces the energy gain owing to the encapsulation by about 3 kcal/mol. For illustrative comparison, the encapsulation energies evaluated with smaller basis sets are also presented, i.e., for the M06-2X/6-31 computational approach but still in the same M06-2X/6-31+ optimized structures. As for the smaller basis set, the M06-2X/6-31 energy gain without the BSSE term is reduced by less than 2 kcal/mol compared to the M06-2X/6-31+ approach. On the other hand, the BSSE correction provides a larger reduction in energy gain with the smaller basis (the M06-2X/6-31 approach), namely by about 4 kcal/mol. This finding is in agreement with a general feature of the BSSE correction: the correction term would disappear in a situation of a basis set with an infinite number of basis functions (clearly enough, such an infinite computational scheme cannot practically be handled). Overall, the terms in Table 1 are somewhat more sensitive to the BSSE correction than to the basis-set choice. The calculated gain in encapsulation energy is slightly larger than in the case of , for which the encapsulation energy is calculated to be [23] about −12.5 kcal/mol. The finding suggests that could possibly be prepared by the high-temperature and high-pressure treatment [7] too.
Table 2 presents four calculated characteristics of the endohedrals—the closest contact of oxygen atoms with the cage carbons, the total charge on the cages, and the lowest and highest vibrational frequency values. The shortest distance of oxygen to the cage is, in both cases, about 3 Å. There is some small charge transfer from the unit to the cage. The Mulliken atomic charges evaluated at the M06-2X/3-21G level show negative charge transfer to the cage of −0.02 (in elementary charge units). Such rather negligible charge transfer stands in clear contrast to the substantial charge donations associated with [14] metallofullerenes. Let us mention that the Mulliken atomic charges, owing to their construction, are to be evaluated with smaller basis sets, for example, the standard 3–21G basis set applied here. The Mulliken atomic charges computed with the 3–21G basis set are known [14] to yield, for endohedral metallofullerenes, fair agreement with the available observed atomic charges [24]. Moreover, there are also deeper computational arguments [25,26] as to why larger basis sets should not be considered for the evaluation of the Mulliken charges on atoms.

Table 2.
The selected characteristics of @(22) and @(23)—the closest O-cage contact a , the total charge b on cage , the lowest vibrational frequency a, and the highest vibrational frequency a.
The harmonic vibrational analysis is considered here not only for the confirmation that energy minima were indeed found (no imaginary frequency) but also for simulations of the infrared (IR) spectra as they can be used for identification of the endohedrals when prepared. Figure 3 shows the M06-2X/6-31+G*-calculated IR vibrational spectra for @(22) and @(23). The lowest vibrational frequency belongs to a rotational motion of as a whole within the cage. The free molecule has four vibrational modes; their harmonic frequencies at the M06-2X/6-31+G* level are double-degenerated bending mode , symmetric bond stretching , and asymmetric bond stretching . After encapsulation, the frequencies are somewhat shifted (and the degeneracy removed) owing to the interactions with cages. In the case of @(22), the M06-2X/6-31+G*-calculated frequencies are 652.2, 652.8, 1404, and (i.e., in Table 2). Similarly, for @, the M06-2X/6-31+G* frequencies are 650.2, 650.4, 1408, and . The asymmetric C-O bond stretching is actually the strongest peak in the IR spectra (Figure 3).

Figure 3.
M06-2X/6-31+G*-computed IR spectra of @(22) (top) and @(23) (bottom).
Incidentally, the recent final confirmation with electron spectroscopy [27] of the presence of in the interstellar space encourages further cosmic searches [28,29,30]—even for fullerene cages with some encapsulates inside (incidentally, pressure of at Venus can reach [31] some 90 atm). As rotational spectroscopy could be used for the detection of fullerene species in interstellar space, Table 3 presents the computed rotational constants, A, B, and C, for the endohedrals (although, in interstellar space, we can rather expect the species in an ionized form).

Table 3.
The M06-2X/6-31+ rotational constants A, B, C [GHz] of the endohedrals.
Similar DFT calculations for related encapsulation in Equation (2), producing (, are now also in progress; for @(22), they concern the gas-phase process:
and similarly for the (23) cage. However, in order to compare the relative reaction populations of the related endohedrals with one and two encapsulated molecules, even the encapsulation equilibrium constants would be needed. For the process in Equation (1), the first step would be the construction of the encapsulation equilibrium constant (defined by the partial pressures p of the individual reaction components):
Then, the equilibrium constant for encapsulation in Equation (2) should also be calculated:
Equation (5) straightforwardly shows how the pressure influences the population ratio of (@(22) and @(22) endohedrals. The encapsulation equilibrium constants can be calculated using molecular partition functions supplied with rotational and vibrational parameters generated by DFT calculations.
4. Conclusions
Calculations are reported for the encapsulation of carbon dioxide into the two most common fullerenes, (22) and (23), yielding @(22) and @(23). The calculations are carried out with the DFT M06-2X/6-31+ approach. The resulting encapsulation energy for @(22) and @(23) amounts to substantial values of −14.5 and −13.9 kcal/mol, respectively. The energy gain is slightly larger than for . As was already synthesized by heating under high pressure with a catalyst, similar high-temperature and high-pressure preparation of or even ( could be possible. The computational treatment should be expanded in the future by evaluations of the related encapsulation equilibrium constants. The presented results encourage similar computational studies for still more complex [32,33,34,35,36] endohedral and other nanocarbon systems.
Author Contributions
Conceptualization, Z.S., T.A. and X.L.; methodology, Z.S. and L.A.; hardware and software, Z.S., F.U. and L.A.; models validation, Z.S., T.A., X.L. and L.A.; analysis and interpretation, Z.S., F.U., T.A. and X.L.; writing—original draft preparation, Z.S. and F.U. All authors have read and agreed to the published version of the manuscript.
Funding
The reported research has been supported by the National Natural Science Foundation of China (21925104 and 92261204), the Hubei Provincial Natural Science Foundation of China (No. 2021CFA020), and the International Cooperation Key Project of Science and Technology Department of Shaanxi; and by the Charles University Centre of Advanced Materials/CUCAM (CZ.02.1.01/0.0/0.0/15_003/0000417), the MetaCentrum (LM2010005), and CERIT-SC (CZ.1.05/3.2.00/08.0144) computing facilities.
Data Availability Statement
The data presented in this study are available in article.
Acknowledgments
A very initial phase of the research line was supported by the Alexander von Humboldt-Stiftung and the Max-Planck-Institut für Chemie (Otto-Hahn-Institut).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sun, Q.; Wang, M.; Li, Z.; Du, A.; Searles, D.J. Carbon dioxide capture and gas separation on B80 fullerene. J. Phys. Chem. C 2014, 118, 2170–2177. [Google Scholar] [CrossRef]
- Meloni, G.; Giustini, A.; Park1, H. CO2 activation within a superalkali-doped fullerene. Front. Chem. 2021, 9, 712960-1–712960-8. [Google Scholar] [CrossRef]
- Palakkal, A.S.; Pillai, R.S. Unraveling the role of fullerene encapsulation driven CO2 capture in square pillared Bio-HOF under humid condition by advanced molecular simulation. Separ. Purif. Technol. 2023, 325, 124650-1–124650-12. [Google Scholar] [CrossRef]
- Ross, R.B.; Cardona, C.M.; Guldi, D.M.; Sankaranarayanan, S.G.; Reese, M.O.; Kopidakis, N.; Peet, J.; Walker, B.; Bazan, G.C.; Van Keuren, E.; et al. Endohedral fullerenes for organic photovoltaic devices. Nature Mater. 2009, 8, 208–212. [Google Scholar] [CrossRef]
- Ye, X.; Yu, P.; Shen, W.; Hu, S.; Akasaka, T.; Lu, X. Er@C82 as a bifunctional additive to the spiro-OMeTAD hole transport layer for improving performance and stability of perovskite solar cells. Sol. RRL 2021, 5, 2100463-1–2100463-9. [Google Scholar] [CrossRef]
- Kong, J.; Shin, Y.; Röhr, J.A.; Wang, H.; Meng, J.; Wu, Y.; Katzenberg, A.; Kim, G.; Kim, D.Y.; Li, T.-D.; et al. CO2 doping of organic interlayers for perovskite solar cells. Nature 2021, 594, 51–56. [Google Scholar] [CrossRef]
- Peres, T.; Cao, B.P.; Cui, W.D.; Khong, A.; Cross, R.J.; Saunders, M.; Lifshitz, C. Some new diatomic molecule containing endohedral fullerenes. Int. J. Mass Spectr. 2001, 210/211, 241–247. [Google Scholar] [CrossRef]
- Zhang, R.; Murata, M.; Aharen, T.; Wakamiya, A.; Shimoaka, T.; Hasegawa, T.; Murata, Y. Synthesis of a distinct water dimer inside fullerene C70. Nature Chem. 2016, 8, 435–441. [Google Scholar] [CrossRef] [PubMed]
- Cioslowski, J. Endohedral chemistry: Electronic structures of molecules trapped inside the C60 cage. J. Am. Chem. Soc. 1991, 113, 4139–4141. [Google Scholar] [CrossRef]
- Charkin, O.P.; Klimenko, N.M.; Charkin, D.O.; Mebel, A.M. Theoretical study of host-guest interaction in model endohedral fullerenes with tetrahedral molecules and ions of MH4 hydrides inside the C60H36, C60H24, C84, and C60 cages. Russ. J. Inorg. Chem. 2004, 49, 868–880. [Google Scholar]
- Ramachandran, C.N.; Sathyamurthy, N. Water clusters in a confined nonpolar environment. Chem. Phys. Lett. 2005, 410, 348–351. [Google Scholar] [CrossRef]
- Bloodworth, S.; Sitinova, G.; Alom, S.; Vidal, S.; Bacanu, G.R.; Elliott, S.J.; Light, M.E.; Herniman, J.M.; Langley, G.J.; Levitt, M.H.; et al. First synthesis and characterization of CH4@C60. Angew. Chem. Int. Ed. 2019, 58, 5038–5043. [Google Scholar] [CrossRef] [PubMed]
- Jaworski, A.; Hedin, N. Local energy decomposition analysis and molecular properties of encapsulated methane in fullerene (CH4@C60). Phys. Chem. Chem. Phys. 2021, 23, 21554–21567. [Google Scholar] [CrossRef]
- Slanina, Z.; Uhlík, F.; Adamowicz, L. Theoretical predictions of fullerene stabilities. In Handbook of Fullerene Science and Technology; Lu, X., Akasaka, T., Slanina, Z., Eds.; Springer: Singapore, 2022; pp. 111–179. [Google Scholar]
- Slanina, Z.; François, J.-P.; Kolb, M.; Bakowies, D.; Thiel, W. Calculated relative stabilities of C84. Fullerene Sci. Technol. 1993, 1, 221–230. [Google Scholar] [CrossRef]
- Kikuchi, K.; Nakahara, N.; Honda, M.; Suzuki, S.; Saito, K.; Shiromaru, H.; Yamauchi, K.; Ikemoto, I.; Kuramochi, T.; Hino, S.; et al. Separation, detection and UV/Visible absorption spectra of fullerenes; C76, C78 and C84. Chem. Lett. 1991, 20, 1607–1610. [Google Scholar] [CrossRef]
- Bakowies, D.; Kolb, M.; Thiel, W.; Richard, S.; Ahlrichs, R.; Kappes, M.M. Quantum-chemical study of C84 fullerene isomers. Chem. Phys. Lett. 1992, 200, 411–417. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
- Ditchfield, R.; Hehre, W.J.; Pople, J.A. Self-consistent molecular-orbital methods. IX. An extended Gaussian-type basis for molecular-orbital studies of organic molecules. J. Chem. Phys. 1971, 54, 724–728. [Google Scholar] [CrossRef]
- Slanina, Z.; Uhlík, F.; Lee, S.-L.; Adamowicz, L.; Akasaka, T.; Nagase, S. Computed stabilities in metallofullerene series: Al@C82, Sc@C82, Y@C82, and La@C82. Int. J. Quant. Chem. 2011, 111, 2712–2718. [Google Scholar] [CrossRef]
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the difference of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. 2013, Gaussian 09, Rev. C.01, 2016, Gaussian 16, Rev. B.01,Wallingford, CT, Gaussian Inc.
- Slanina, Z.; Uhlík, F.; Nagase, S.; Akasaka, T.; Adamowicz, L.; Lu, X. A computational characterization of CO@C60. Fuller. Nanotub. Carbon Nanostructures 2017, 25, 624–629. [Google Scholar] [CrossRef]
- Takata, M.; Nishibori, E.; Sakata, M.; Shinohara, H. Charge density level structures of endohedral metallofullerenes determined by synchrotron radiation powder method. New Diam. Front. Carb. Technol. 2002, 12, 271–286. [Google Scholar]
- Hehre, W.J. A Guide to Molecular Mechanics and Quantum Chemical Calculations; Wavefunction: Irvine, CA, USA, 2003; p. 435. [Google Scholar]
- Jensen, F. Introduction to Computational Chemistry; Wiley: Chichester, UK, 2017; p. 319. [Google Scholar]
- Campbell, E.K.; Holz, M.; Gerlich, D.; Maier, J.P. Laboratory confirmation of C60+ as the carrier of two diffuse interstellar bands. Nature 2015, 523, 322–323. [Google Scholar] [CrossRef]
- Berné, O.; Tielens, A.G.G.M. Formation of buckminsterfullerene (C60) in interstellar space. Proc. Natl. Acad. Sci. USA 2012, 109, 401–406. [Google Scholar] [CrossRef] [PubMed]
- Berné, O.; Montillaud, J.; Joblin, C. Top-down formation of fullerenes in the interstellar medium. Astronom. Astrophys. 2015, 577, A133-1–A133-9. [Google Scholar] [CrossRef]
- Hansen, C.S.; Peeters, E.; Cami, J.; Schmidt, T.W. Open questions on carbon-based molecules in space. Commun. Chem. 2022, 5, 94-1–94-4. [Google Scholar] [CrossRef]
- Slanina, Z.; Fox, K.; Kim, S.J. A computational evaluation of altitude profiles of the equilibrium monomeric-dimeric CO2 fractions in the atmosphere of Venus. Thermochim. Acta 1992, 200, 33–39. [Google Scholar] [CrossRef]
- Rodríguez-Fortea, A.; Balch, A.L.; Poblet, J.M. Endohedral metallofullerenes: A unique host-guest association. Chem. Soc. Rev. 2011, 40, 3551–3563. [Google Scholar] [CrossRef]
- Basiuk, V.A.; Basiuk, E.V. Noncovalent complexes of Ih-C80 fullerene with phthalocyanines. Fuller. Nanotub. Carbon Nanostructures 2018, 26, 69–75. [Google Scholar] [CrossRef]
- Basiuk, V.A.; Tahuilan-Anguiano, D.E. Complexation of free-base and 3d transition metal(II) phthalocyanines with endohedral fullerene Sc3N@C80. Chem. Phys. Lett. 2019, 722, 146–152. [Google Scholar] [CrossRef]
- Li, M.; Zhao, R.; Dang, J.; Zhao, X. Theoretical study on the stabilities, electronic structures, and reaction and formation mechanisms of fullerenes and endohedral metallofullerenes. Coor. Chem. Rev. 2022, 471, 214762-1–214762-12. [Google Scholar] [CrossRef]
- Li, Y.B.; Biswas, R.; Kopcha, W.P.; Dubroca, T.; Abella, L.; Sun, Y.; Crichton, R.A.; Rathnam, C.; Yang, L.T.; Yeh, Y.W.; et al. Structurally defined water-soluble metallofullerene derivatives towards biomedical applications. Angew. Chem. Int. Ed. Engl. 2023, 62, e202211704-1–e202211704-10. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).