Abstract
The structure and energetics of the clusterfullerene La2C2@(450)-C100 are calculated at the B3LYP/6-31G*∼SDD level (including counterpoise correction for the basis set superposition error), and the observed features are confirmed. Its stability is explained by substantial energy gain connected with the encapsulation, viz. 140 kcal/mol per atom of the encapsulate, actually higher than previously found for comparable systems.
1. Introduction
In fullerene and metallofullerene research, calculations have from the beginning helped experimental search and understanding of new nanocarbons [1,2,3,4], more recently even with species containing around one hundred carbons [5,6,7]. In the group of such large metallofullerenes [8,9,10,11,12,13,14,15,16,17,18], another giant system has recently been characterized [14] by X-ray crystal diffraction, namely La2C2@(450)-C100. In this study, the giant clusterfullerene is calculated using the density functional theory (DFT) in order to further enhance knowledge of its structure and encapsulation energetics.
2. Calculations
The (450)-C100 fullerene is one of the 450 isolated-pentagon-rule (IPR) cages of C100 [19] (if enantiomers are considered as equivalent, 862 IPR isomers if enantiomers are regarded as distinct). Interestingly, the total number of all C100 isomeric cages (i.e., IPR and non-IPR cages) is 285,913 if enantiomers are considered equivalent [4]. The (450)-C100 fullerene exhibits topological symmetry which is however reduced owing to the Jahn-Teller distortion. At our computational level the topological symmetry is in geometry optimization lowered to the point group of symmetry (Figure 1, one can speak on a near -symmetry). Interestingly enough, there are other C100 IPR cages with a higher topological symmetry like or T.
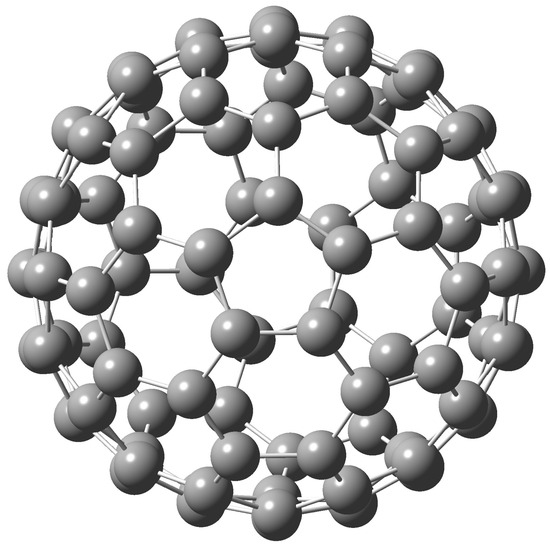
Figure 1.
The B3LYP/6-31G* optimized structure of (450)-C100.
The La2C2@(450)-C100 geometrical structure was optimized with the Becke’s three parameter DFT functional with the non-local Lee-Yang-Parr correlation functional [20,21,22], the approach is conventionally labeled as B3LYP. The DFT calculations were at first performed in a combined atomic basis set: the standard 3-21G basis for C atoms while for La atoms the SDD basis set with the SDD effective core potential [23] (B3LYP/3-21G∼SDD). The geometry optimization started from the X-ray structure [14] and was further refined with the B3LYP/6-31G*∼SDD treatment using an extended 6-31G*∼SDD basis set, followed by the GF harmonic vibrational analysis. The vibrational analysis allows for a check of the nature of the stationary points found, i.e., if local energy minima were really found (and not activated complexes or even higher types of hypersurface stationary points). Moreover, the analysis can also be used for simulations of the IR and Raman vibrational spectra. For numerical integrations with the DFT functional the so called ultrafine grid was used. Moreover, the tight SCF (self consistent field) convergency criterion was applied. Finally, the wavefunction stability was tested throughout in order to eliminate unstable SCF solutions (without a real physical significance).
The so-called basis set superposition error (BSSE) was considered accordingly, namely by application of the approximative Boys-Bernardi counterpoise method (also known as CP2, or CPn, depending on the number of the reaction components in the treated association process) [24], since recently considered [25] also with metallofullerenes. The Boys-Bernardi approach to the BSSE correction term is an approximative treatment that ensures that every reaction component of a studied chemical process is formally described by the same number of the atomic basis set functions (so that the calculated energies are directly comparable). The required basis-set consistence is realized by rather formal, artificial atoms (thus also called ghost) possessing no electrons. The BSSE problem essentially originates in the fact that the considered basis sets are always finite. In other words, the BSSE correction would disappear in a situation of a basis set with infinite number of atomic basis functions (of course, such an infinite scheme cannot practically be handled). The BSSE correction term represents an important addition also to the energetics of any encapsulation process. Without the BSSE correction the energy gain created by encapsulation would be exaggerated (so that endohedrals would artificially be over-stabilized). Thus, the BSSE consideration is needed for reliable predictions of energetics, indeed.
All the reported calculations were performed with the program package Gaussian 09 [26]. The calculations were carried out with computers operating in parallel regime, mostly with 8–24 processors (with computational frequency up 3 GHz each and with the available operational memory up to 60 GB).
3. Results and Discussion
The B3LYP/6-31G*∼SDD optimized structure of La2C2@(450)-C100 shown in Figure 2 basically agrees with the X-ray results [14]. The calculated C-C bond length in the La2C2 encapsulate is 1.26 Å while the C-La bond 2.44 Å, the La-C shortest contact with the cage 2.64 Å. The B3LYP/3-21G SDD computed Wiberg bond index for the C-C bond is 2.58 (i.e., between double and triple bond), for C-La bond 0.69 (B3LYP/6-31G*∼SDD values C-C 2.59, C-La 0.63). It should be realized that the calculated values are obtained for the gas-phase free (isolated) endohedral. Moreover, the calculated terms correspond to the equilibrium geometries with motionless nuclei. The X-ray values are however obtained for the crystal-state endohedral.
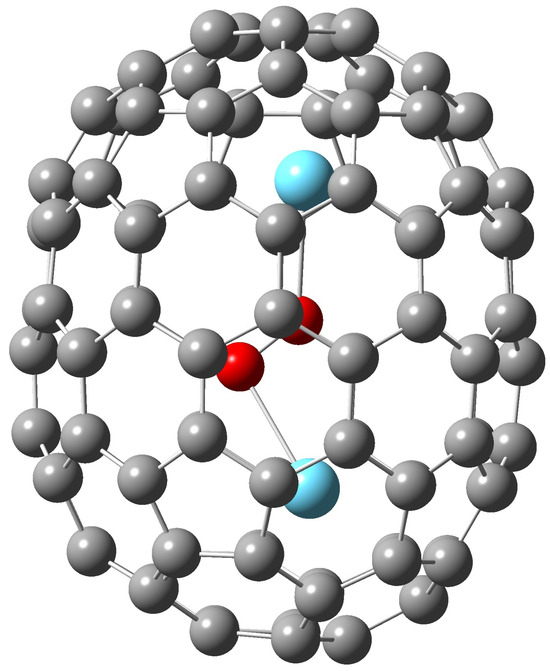
Figure 2.
The B3LYP/6-31G*∼SDD optimized structure of La2C2@(450)-C100 (carbons of La2C2 are in red).
The Mulliken atomic charges on atoms are (owing to their historical introduction) to be constructed at a simpler level, i.e., B3LYP/3-21G∼SDD. The Mulliken charges on atoms calculated with the 3-21G basis set are known [27] to produce for metallofullerenes a good agreement with the available observed charges [28]. Moreover, there are also general methodological reasons [29,30] why some larger basis sets should not be applied in the calculations of the Mulliken atomic charges on atoms—as they can sometimes produce rather unphysical values. The Mulliken charges on the La atoms are 2.41 and 2.47 (of the electron elementary charge) while on the carbons of the La2C2 encapsulate the charges are −0.32 and −0.34. Hence, the total charge on the encapsulate is 4.22. In overall, the charge transfer from the encapsulate to the cage amounts to 4.22 electrons. Thus, energetics of tetra-anions of empty cages could serve for stability estimations with encapsulations of La2C2 by other C100 cages.
Although the ground state of La2C2@(450)-C100 is singlet electronic state, the first electronic triplet state is rather low lying. At the B3LYP/6-31G*∼SDD level the triplet state is located only about 1.88 kcal/mol above the ground-state singlet.
The energy change connected with the (formal thermodynamic) gas-phase encapsulation process:
is a useful characteristics known as encapsulation energy. Calculated reaction thermodynamic changes are mostly treated as the reaction potential-energy change . However, a more adequate description refers to the enthalpy change at absolute zero temperature , i.e., the potential energy change corrected for the vibrational zero-point energies upon encapsulation :
The encapsulation potential-energy change corrected is to be refined by inclusion of the basis set superposition error [24,26] (BSSE/CP5) and so-called steric correction [25] that reflects the cage distortion upon encapsulation [31]. Table 1 presents the energy terms for reaction (1) considered as reduced or relative values, i.e., per one atom of the La2C2 encapsulate (thus in the units of kcal/mol/atom). Such reduced values are convenient for comparisons with encapsulations of species with different numbers of atoms. For example, the reduced term of −138.4 kcal/mol/atom from Table 1 represents the encapsulation-energy gain larger by 21.1 kcal/mol/atom than found [18] for Y2C2@(1660)-C108 at the same computational level. Similarly, the reduced term of −140.2 kcal/mol/atom in Table 1 gives by 3.7 kcal/mol/atom better energy gain than calculated [32] at the same level for Ti3C3@-C80. In overall, La2C2@(450)-C100 is a new interesting member of the family of metallofullerenes with relatively large energy gains upon encapsulation.

Table 1.
The B3LYP/6-31G*∼SDD computed a encapsulation energetics for La2C2@(450)-C100.
The encapsulation enthalpy (enhanced by the related entropic contributions) allows for statistical thermodynamic evaluations of the equilibrium concentrations [33,34], in our case by means of the encapsulation equilibrium constant for process (1):
defined by the partial pressures p of the individual reaction components in reaction (1). The encapsulation equilibrium constant from Equation (3) can indeed be expressed [34,35] by a compact formula using the molecular (or atomic) partition functions (the partition functions have to correspond to the selected standard state, e.g., ideal gas phase at 1 atm = 101,325 Pa pressure) and the standard encapsulation enthalpy change at the absolute zero temperature :
where symbol stands for the Avogadro number. The molecular partition functions primarily consist of the rotational-vibrational partition functions based on the molecular parameters from the GF harmonic vibrational analysis.
In principle, the encapsulation energy can also be defined [34] by a more straightforward encapsulation stoichiometry, namely:
when the basis set superposition error [24,26] is evaluated by the simpler BSSE/CP2 approach which at the B3LYP/6-31G*∼SDD level yields the reduced energy gain of −58.7 kcal/mol/atom (−62.5 kcal/mol/atom without the BSSE correction). Obviously, the energy gain must be now smaller than with the BSSE/CP5 approach as in the latter case the formation of the bonds of the encapsulate is included.
However, if one is interested in the thermodynamic-equilibrium populations of non-isomeric endohedrals [33], approach according to Equation (1) should be preferred. Incidentally, in addition to our starting system La2C2@(450)-C100 another pertinent species is known [10], viz. La2@(450)-C100. The relative populations of the two non-isomeric endohedrals can be described using the equilibrium constant defined by Equation (3) and its equivalent for parent process in Equation (6):
The population ratio of the two endohedrals is given by formula [33]:
Obviously, the relative equilibrium populations of such non-isomeric nanocarbons represent distinctly more complex problem compared to the situation of just isomeric species [34,35,36,37]. The equilibrium constant can again be evaluated by the partition functions and calculated molecular parameters as in Equation (4). The partial pressure of carbon can be approximated by the carbon saturated pressure [34]. However, the actual carbon pressure depends on particular experimental setup and thus varies from case to case. This aspect is one of the reasons why the population ratio of the two endohedrals can be different in different experiments, too. The interesting relative stability problem for non-isomeric nanocarbons should further be calculated in future.
The encapsulation of La2C2 into the (450)-C100 cage creates six new vibrational modes, actually with rather low frequencies—at the B3LYP/6-31G*∼SDD level between 24 and 73 cm−1. The low frequencies basically belong to motions of the whole La2C2 encapsulate inside the cage, they could roughly be viewed as relatively free rotations. Such low frequency motions would particularly be important for the endohedral thermodynamics [35,36]. The new vibrational frequencies created by the encapsulation also contribute to the reaction change of the vibrational zero-point energy for process (1). On the other hand, the highest computed vibrational frequency has a value of 1926 cm−1 and belongs to the bond stretching of the C-C bond in La2C2 (though the vibrational mode exhibits rather negligible IR intensity as well as Raman activity). Let us note that the gas-phase C2 molecule has [38] in the singlet ground state observed vibrational frequency of 1855 cm−1 (the C2 lowest triplet state lies higher only by 2.05 kcal/mol). For another comparison, the highest vibrational frequency of the empty (450)-C100 cage at the B3LYP/6-31G* level has value of 1615 cm−1. Figure 3 presents the B3LYP/6-31G*∼SDD calculated harmonic IR and Raman spectra of La2C2@(450)-C100. The spectra should be useful in identification of the species.
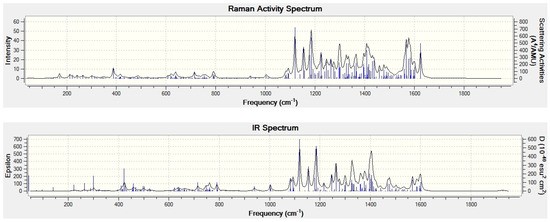
Figure 3.
The B3LYP/6-31G*∼SDD calculated IR (bottom) and Raman (top) spectra of La2C2@(450)-C100.
4. Conclusions
The structure and energetics of the metallofullerene (or clusterfullerene) La2C2@(450)-C100 are evaluated using the DFT approach at the B3LYP/6-31G*∼SDD level with inclusion of the correction for the basis set superposition error calculated by the counterpoise method. The calculated encapsulation potential-energy change amounts to a sizeable value of −140.2 kcal/mol/atom (i.e., per atom of the encapsulate), or at the level to −138.4 kcal/mol/atom. The found energy gains connected with encapsulation are larger than previously reported for other clusterfullerene systems like Y2C2@(1660)-C108 or Ti3C3@-C80. Possible descriptions of encapsulation energetics are discussed and a thermodynamically consistent evaluation of the relative equilibrium populations of non-isomeric metallofullerenes is suggested with an aim to compare the La2C2@(450)-C100 equilibrium population with that of a related observed species La2@(450)-C100. The approach can be of a use also for studies of other interesting complex nanocarbon systems [39,40,41,42,43,44,45].
Author Contributions
Conceptualization, Z.S., F.U., T.A., X.L. and L.A.; methodology, Z.S., F.U. and L.A.; hardware and software, Z.S., F.U. and L.A.; models validation, Z.S., F.U., T.A., X.L. and L.A.; analysis and interpretation, Z.S., F.U., T.A., X.L. and L.A.; writing—original draft preparation, Z.S. and F.U. All authors have read and agreed to the published version of the manuscript.
Funding
The reported research has been supported by the National Natural Science Foundation of China (21925104 and 92261204), the Hubei Provincial Natural Science Foundation of China (No. 2021CFA020), and the International Cooperation Key Project of Science and Technology Department of Shaanxi; and by the Charles University Centre of Advanced Materials/CUCAM (CZ.02.1.01/0.0/0.0/15 003/0000417), the MetaCentrum (LM2010005) and CERIT-SC (CZ.1.05/3.2.00/ 08.0144) computing facilities. A very initial phase of the research line was supported by the Alexander von Humboldt-Stiftung and the Max-Planck-Institut für Chemie (Otto-Hahn-Institut), too.
Data Availability Statement
The data presented in this study are available in article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bochvar, D.A.; Galpern, E.G. Hypothetical systems: Carbododecahedron, s-Icosahedron, and carbo-s-Icosahedron. Dokl. Akad. Nauk SSSR 1973, 209, 610–612. [Google Scholar]
- Pitzer, K.S.; Clementi, E. Large molecules in carbon vapor. J. Am. Chem. Soc. 1959, 81, 4477–4485. [Google Scholar] [CrossRef]
- Slanina, Z. Remark on the present applicability of quantum chemistry to the calculations of equilibrium and rate constants of chemical reactions. Radiochem. Radioanal. Lett. 1975, 22, 291–298. [Google Scholar]
- Slanina, Z.; Lee, S.-L.; Yu, C.-H. Computations in treating fullerenes and carbon aggregates. Rev. Comput. Chem. 1996, 8, 1–62. [Google Scholar]
- Zhao, X.; Slanina, Z.; Goto, H. Theoretical studies on the relative stabilities of C96 IPR fullerenes. J. Phys. Chem. A 2004, 108, 4479–4484. [Google Scholar] [CrossRef]
- Zhao, X.; Slanina, Z. C98 IPR isomers: Gibbs-energy based relative stabilities. J. Mol. Struct. (Theochem) 2003, 636, 195–201. [Google Scholar] [CrossRef]
- Zhao, X.; Goto, H.; Slanina, Z. C100 IPR fullerenes: Temperature-dependent relative stabilities based on the Gibbs function. Chem. Phys. 2004, 306, 93–104. [Google Scholar] [CrossRef]
- Diener, M.D.; Alford, J.M. Isolation and properties of small-bandgap fullerenes. Nature 1998, 393, 668–671. [Google Scholar] [CrossRef]
- Mercado, B.Q.; Jiang, A.; Yang, H.; Wang, Z.; Jin, H.; Liu, Z.; Olmstead, M.M.; Balch, A.L. Isolation and structural characterization of the molecular nanocapsule Sm2@D3d(822)-C104. Angew. Chem. Int. Ed. 2009, 48, 9114–9116. [Google Scholar] [CrossRef]
- Beavers, C.M.; Jin, H.; Yang, H.; Wang, Z.; Wang, X.; Ge, H.; Liu, Z.; Mercado, B.Q.; Olmstead, M.M.; Balch, A.L. La2C90 to La2C138: Isolation and crystallographic characterization of La2@D5(450)-C100. J. Am. Chem. Soc. 2011, 133, 15338–15341. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Fortea, A.; Balch, A.L.; Poblet, J.M. Endohedral metallofullerenes: A unique host-guest association. Chem. Soc. Rev. 2011, 40, 3551–3563. [Google Scholar] [CrossRef] [PubMed]
- Popov, A.A.; Yang, S.; Dunsch, L. Endohedral fullerenes. Chem. Rev. 2013, 113, 5989–6113. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Wang, S.; Troyanov, S.I. The most stable isomers of giant fullerenes C102 and C104 captured as Chlorides, C102(603)Cl18/20 and C104(234)Cl16/18/20/22. Chem. Eur. J. 2014, 20, 6875–6878. [Google Scholar] [CrossRef] [PubMed]
- Cai, W.; Bao, L.; Zhao, S.; Xie, Y.; Akasaka, T.; Lu, X. Anomalous compression of D5(450)-C100 by encapsulating La2C2 Cluster Instead of La2. J. Am. Chem. Soc. 2015, 137, 10292–10296. [Google Scholar] [CrossRef] [PubMed]
- Cai, W.; Li, F.-F.; Bao, L.; Xie, Y.; Lu, X. Isolation and crystallographic characterization of La2C2@Cs(574)-C102 and La2C2@C2(816)-C104: Evidence for the top-down formation mechanism of fullerenes. J. Am. Chem. Soc. 2016, 138, 6670–6675. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Yang, S.; Kemnitz, E.; Troyanov, S.I. New giant fullerenes identified as chloro derivatives: Isolated-pentagon-rule C108(1771)Cl12 and C106(1155)Cl24 as well as nonclassical C104Cl24. Inorg. Chem. 2016, 55, 5741–5743. [Google Scholar] [CrossRef] [PubMed]
- Pan, C.; Bao, L.; Yu, X.; Fang, H.; Xie, Y.; Akasaka, T.; Lu, X. Facile Access to Y2C2n (2n = 92–130) and crystallographic characterization of Y2C2@C1(1660)-C108: A giant nanocapsule with a linear carbide cluster. ACS Nano 2018, 12, 2065–2069. [Google Scholar] [CrossRef] [PubMed]
- Slanina, Z.; Uhlík, F.; Pan, C.; Akasaka, T.; Lu, X.; Adamowicz, L. Computed stabilization for a giant fullerene endohedral: Y2C2@C1(1660)-C108. Chem. Phys. Lett. 2018, 710, 147–149. [Google Scholar] [CrossRef]
- Shao, N.; Gao, Y.; Yoo, S.; An, W.; Zeng, X.C. Search for lowest-energy fullerenes: C98 to C110. J. Phys. Chem. A 2006, 110, 7672–7676. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Cao, X.Y.; Dolg, M. Segmented contraction scheme for small-core lanthanide pseudopotential basis sets. J. Mol. Struct. (Theochem) 2002, 581, 139–147. [Google Scholar] [CrossRef]
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the difference of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Slanina, Z.; Uhlík, F.; Lee, S.-L.; Adamowicz, L.; Akasaka, T.; Nagase, S. Computed stabilities in metallofullerene series: Al@C82, Sc@C82, Y@C82, and La@C82. Int. J. Quant. Chem. 2011, 111, 2712–2718. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Rev. D.01; Gaussian Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Slanina, Z.; Uhlík, F.; Nagase, S.; Akasaka, T.; Adamowicz, L.; Lu, X. Eu@C72: Computed Comparable Populations of Two Non-IPR Isomers. Molecules 2017, 22, 1053. [Google Scholar] [CrossRef] [PubMed]
- Okubo, S.; Kato, T.; Inakuma, M.; Shinohara, H. Separation and characterization of ESR-active lanthanum endohedral fullerenes. New Diam. Front. Carbon Technol. 2001, 11, 285–294. [Google Scholar]
- Hehre, W.J. A Guide to Molecular Mechanics and Quantum Chemical Calculations; Wavefunction: Irvine, CA, USA, 2003; p. 435. [Google Scholar]
- Jensen, F. Introduction to Computational Chemistry; Wiley: Chichester, UK, 2017; p. 319. [Google Scholar]
- Slanina, Z.; Uhlík, F.; Lu, X.; Akasaka, T.; Lemke, K.H.; Seward, T.M.; Nagase, S.; Adamowicz, L. Calculations of the water-dimer encapsulations into C84. Fullerenes Nanotub. Carbon Nanostruct. 2016, 24, 1–7. [Google Scholar] [CrossRef]
- Yu, P.; Shen, W.; Bao, L.; Pan, C.; Slanina, Z.; Lu, X. Trapping an unprecedented Ti3C3 unit inside the icosahedral C80 fullerene: A crystallographic survey. Chem. Sci. 2019, 10, 10925–10930. [Google Scholar] [CrossRef] [PubMed]
- Slanina, Z.; Uhlík, F.; Lee, S.-L.; Wang, B.-C.; Adamowicz, L.; Suzuki, M.; Haranaka, M.; Feng, L.; Lu, X.; Nagase, S.; et al. Towards relative populations of non-isomeric metallofullerenes: La@C76(Td) vs. La2@C76(Cs,17490). Fullerenes Nanotub. Carbon Nanostruct. 2014, 22, 299–306. [Google Scholar] [CrossRef]
- Slanina, Z.; Uhlík, F.; Adamowicz, L. Theoretical predictions of fullerene stabilities. In Handbook of Fullerene Science and Technology; Lu, X., Akasaka, T., Slanina, Z., Eds.; Springer: Singapore, 2022; pp. 111–179. [Google Scholar]
- Slanina, Z. Breakdown of the conventional formula for the partition function of free internal rotation. J. Phys. Chem. 1982, 86, 4782–4786. [Google Scholar] [CrossRef]
- Slanina, Z.; Zhao, X.; Kurita, N.; Gotoh, H.; Uhlík, F.; Rudziński, J.M.; Lee, K.H.; Adamowicz, L. Computing the relative gas-phase populations of C60 and C70: Beyond the traditional scale. J. Mol. Graph. Mod. 2001, 19, 216–221. [Google Scholar] [CrossRef] [PubMed]
- Slanina, Z.; Uhlík, F.; Hu, S.; Akasaka, T.; Lu, X.; Adamowicz, L. Calculated isomeric populations of Er@C82. Fullerenes Nanotub. Carbon Nanostruct. 2024, 32. [Google Scholar] [CrossRef]
- Chase, M.W., Jr.; Davies, C.A.; Downery, J.R., Jr.; Frurip, D.J.; McDonald, R.A.; Syverud, A.N. JANAF thermochemical tables, Third edition, Vols. 1,2. J. Phys. Chem. Ref. Data 1985, 14 (Suppl. 1), 646. [Google Scholar]
- Gueorguiev, G.K.; Stafström, S.; Hultman, L. Nano-wire formation by self-assembly of silicon-metal cage-like molecules. Chem. Phys. Lett. 2008, 458, 170–174. [Google Scholar] [CrossRef]
- Basiuk, V.A.; Basiuk, E.V. Noncovalent complexes of Ih-C80 fullerene with phthalocyanines. Fullerenes Nanotub. Carbon Nanostruct. 2018, 26, 69–75. [Google Scholar] [CrossRef]
- Basiuk, V.A.; Tahuilan-Anguiano, D.E. Complexation of free-base and 3d transition metal(II) phthalocyanines with endohedral fullerene Sc3N@C80. Chem. Phys. Lett. 2019, 722, 146–152. [Google Scholar] [CrossRef]
- Wang, S.; Chang, Q.; Zhang, G.; Li, F.; Wang, X.; Yang, S.; Troyanov, S.I. Structural studies of giant empty and endohedral fullerenes. Front. Chem. 2020, 8, 607712. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Zhao, R.; Dang, J.; Zhao, X. Theoretical study on the stabilities, electronic structures, and reaction and formation mechanisms of fullerenes and endohedral metallofullerenes. Coor. Chem. Rev. 2022, 471, 214762. [Google Scholar] [CrossRef]
- Li, Y.B.; Biswas, R.; Kopcha, W.P.; Dubroca, T.; Abella, L.; Sun, Y.; Crichton, R.A.; Rathnam, C.; Yang, L.T.; Yeh, Y.-W.; et al. Structurally defined water-soluble metallofullerene derivatives towards biomedical applications. Angew. Chem. Int. Ed. Engl. 2023, 62, e202211704. [Google Scholar] [CrossRef] [PubMed]
- Menon, A.; Kaur, R.; Guldi, D.M. Merging carbon nanostructures with porphyrins. In Handbook of Fullerene Science and Technology; Lu, X., Akasaka, T., Slanina, Z., Eds.; Springer: Singapore, 2022; pp. 219–264. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).