On the Structural and Vibrational Properties of Solid Endohedral Metallofullerene Li@C60
Abstract
1. Introduction
2. Results and Discussion
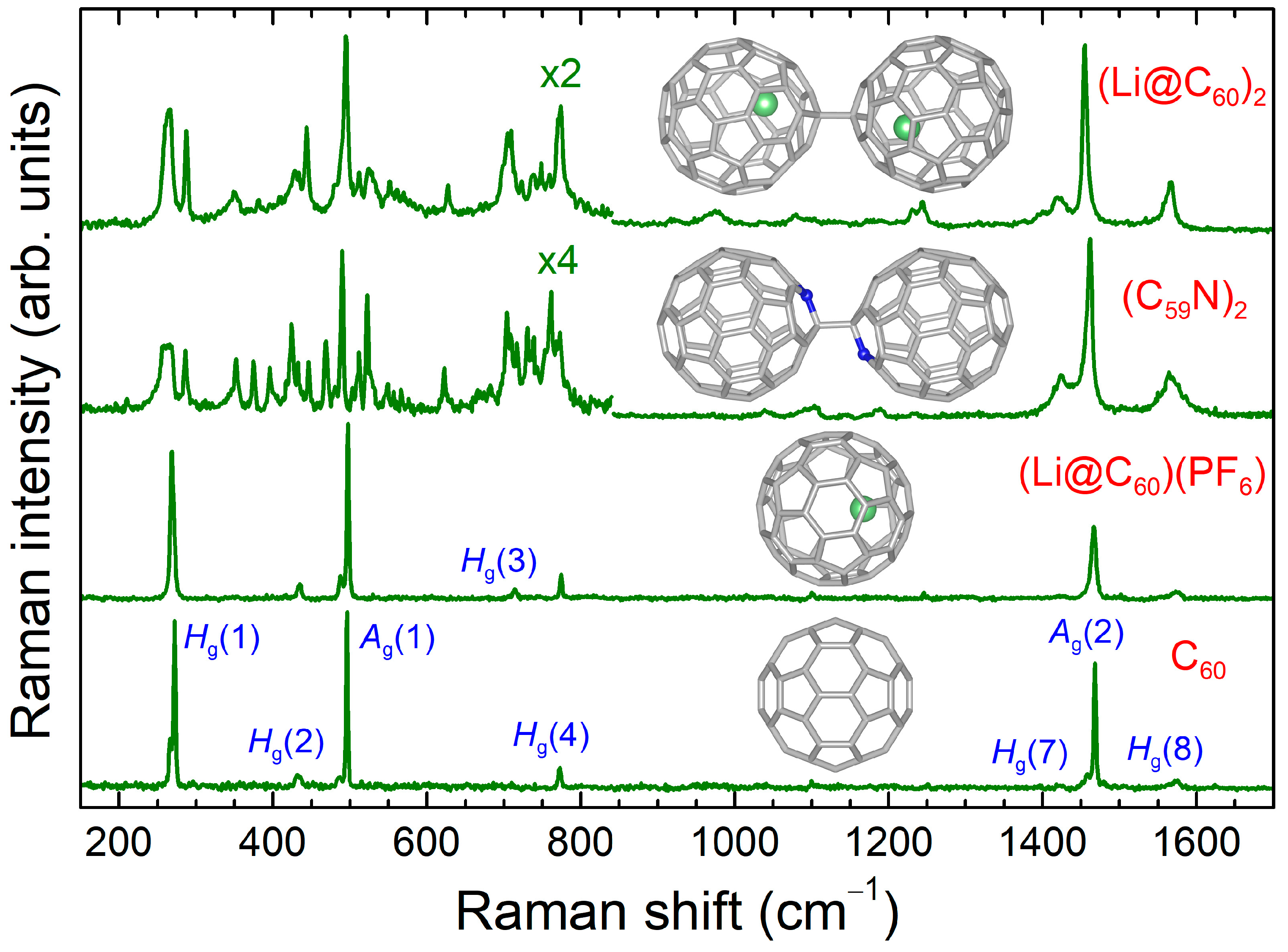
2.1. Vibrational Properties
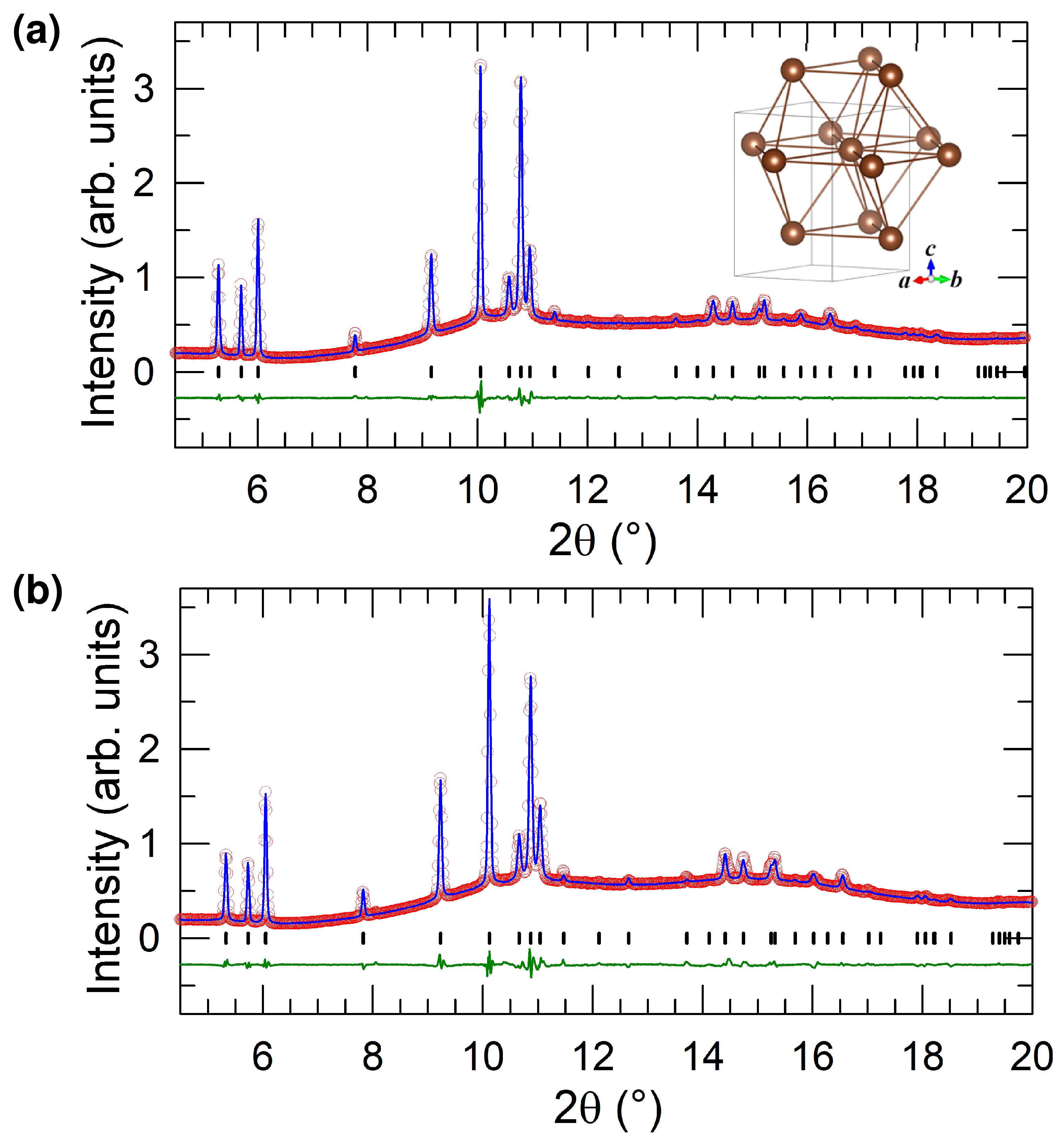
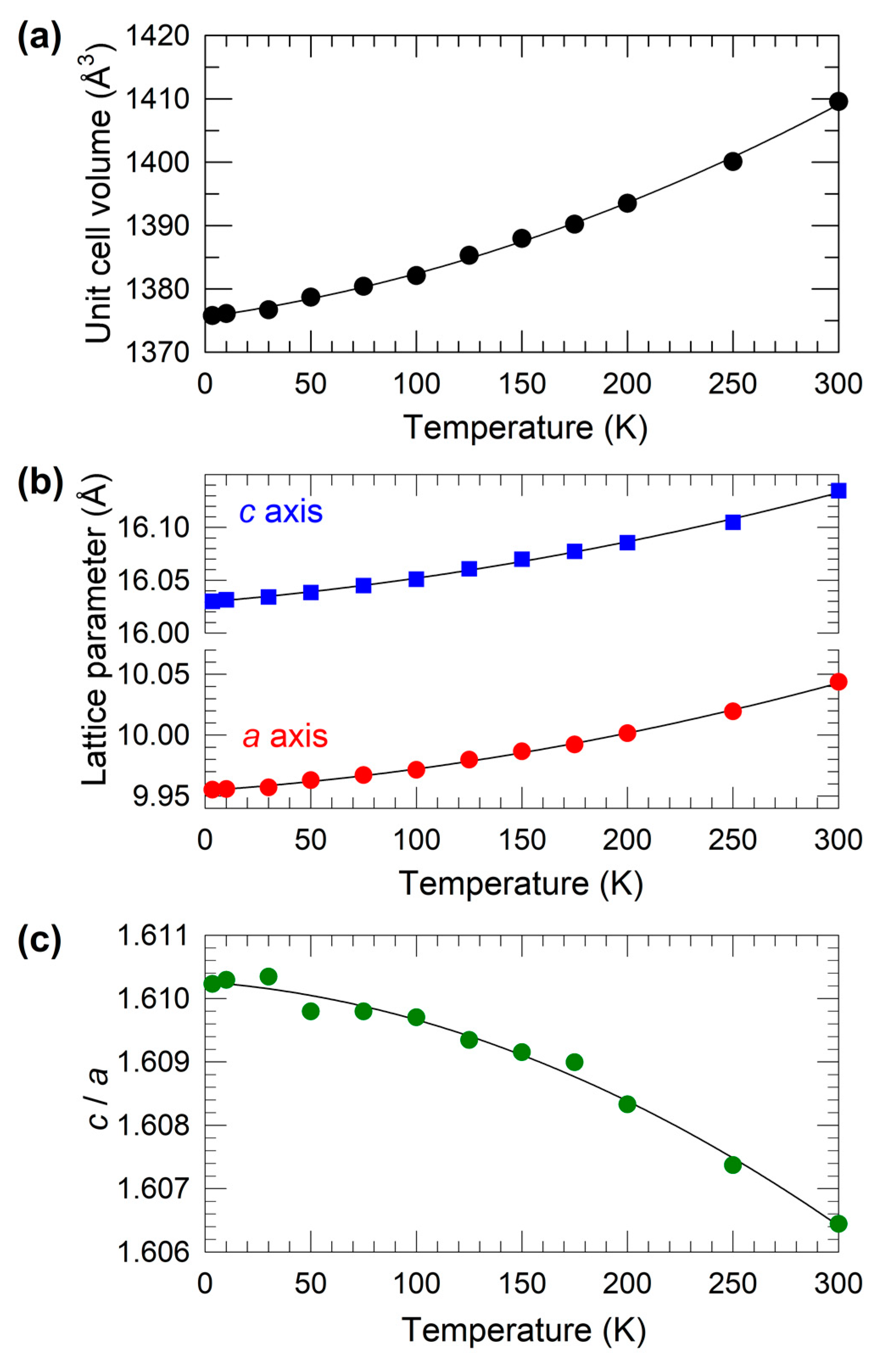
2.2. Structural Properties at Ambient Pressure
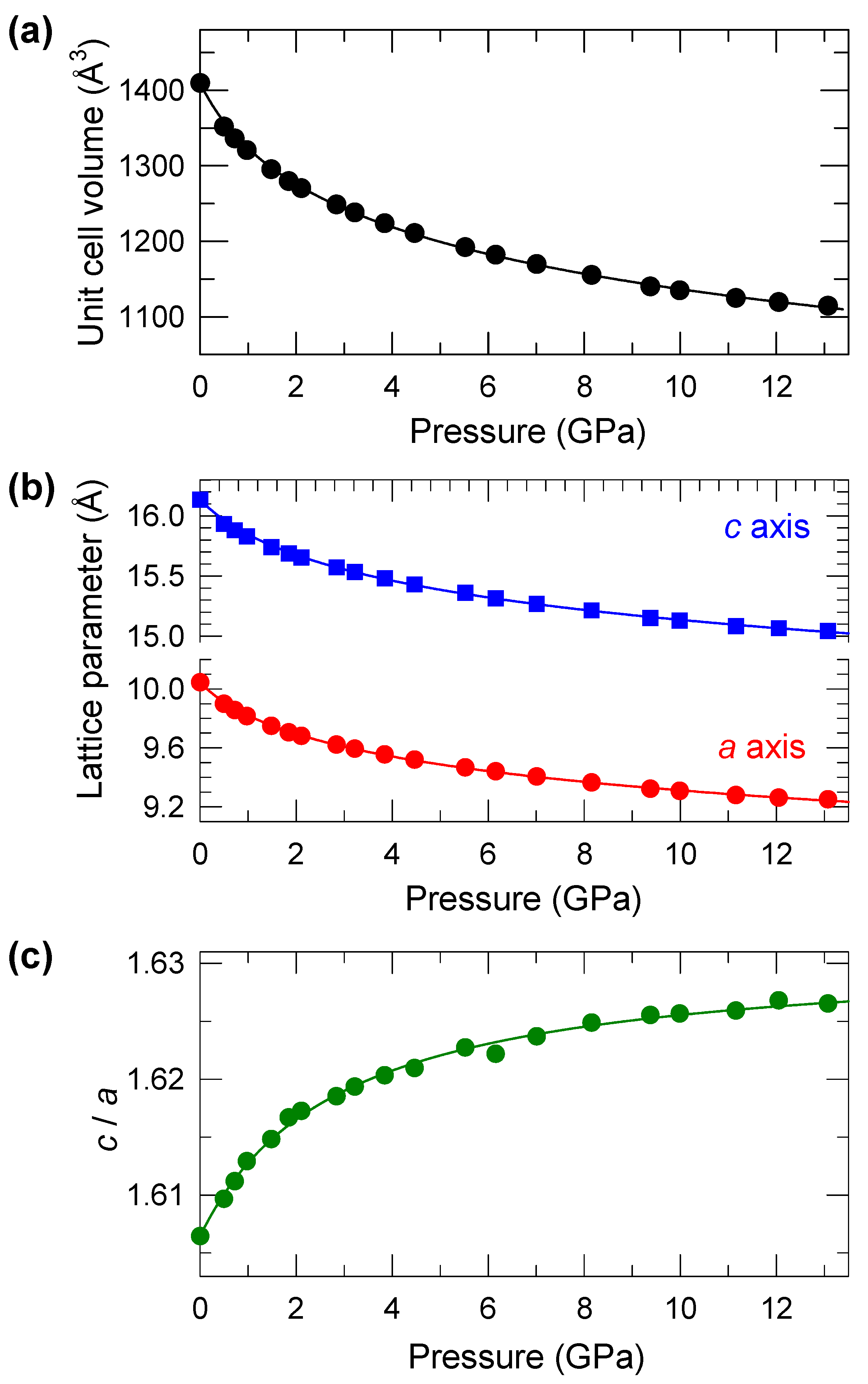
2.3. Structural Properties at High Pressure
3. Materials and Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hirsch, A.; Brettreich, M. Fullerenes: Chemistry and Reactions; Wiley-VCH, 5 Wiley-VCH Verlag GmbH & Co. KgaA: Weinheim, Germany, 2005. [Google Scholar]
- Takabayashi, Y.; Prassides, K. Unconventional high-Tc superconductivity in fullerides. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150320. [Google Scholar] [CrossRef] [PubMed]
- Zadik, R.H.; Takabayashi, Y.; Klupp, G.; Colman, R.H.; Ganin, A.Y.; Potocnik, A.; Jeglic, P.; Arcon, D.; Matus, P.; Kamaras, K.; et al. Optimized unconventional superconductivity in a molecular Jahn-Teller metal. Sci. Adv. 2015, 1, e1500059. [Google Scholar] [CrossRef]
- Nomura, Y.; Sakai, S.; Capone, M.; Arita, R. Unified understanding of superconductivity and Mott transition in alkali-doped fullerides from first principles. Sci. Adv. 2015, 1, e1500568. [Google Scholar] [CrossRef] [PubMed]
- Kasahara, Y.; Takeuchi, Y.; Zadik, R.H.; Takabayashi, Y.; Colman, R.H.; McDonald, R.D.; Rosseinsky, M.J.; Prassides, K.; Iwasa, Y. Upper critical field reaches 90 tesla near the Mott transition in fulleride superconductors. Nat. Commun. 2017, 8, 14467. [Google Scholar] [CrossRef] [PubMed]
- Hummelen, J.C.; Knight, B.; Pavlovich, J.; Gonzalez, R.; Wudl, F. Isolation of the heterofullerene C59N as its dimer (C59N)2. Science 1995, 269, 1554–1556. [Google Scholar] [CrossRef] [PubMed]
- Prassides, K.; Keshavarz-K, M.; Hummelen, J.C.; Andreoni, W.; Giannozzi, P.; Beer, E.; Bellavia, C.; Cristofolini, L.; Gonzalez, R.; Lappas, A.; et al. Isolation, structure, and electronic calculations of the heterofullerene salt K6C59N. Science 1996, 271, 1833–1835. [Google Scholar] [CrossRef]
- Shinohara, H.; Tagmatarchis, N. Endohedral Metallofullerenes: Fullereness with Metal Inside; Wiley: Chichester, UK, 2015. [Google Scholar]
- Akasaka, T.; Nagase, S. Endofullerenes: A New Family of Carbon Clusters; Springer: Dordrecht, The Netherlands, 2002. [Google Scholar]
- Komatsu, K.; Murata, M.; Murata, Y. Encapsulation of molecular hydrogen in fullerene C60 by organic synthesis. Science 2005, 307, 238–240. [Google Scholar] [CrossRef] [PubMed]
- Bloodworth, S.; Whitby, R.J. Synthesis of endohedral fullerenes by molecular surgery. Commun. Chem. 2022, 5, 121. [Google Scholar] [CrossRef] [PubMed]
- Krachmalnicoff, A.; Bounds, R.; Mamone, S.; Alom, S.; Concistrè, M.; Meier, B.; Kouřil, K.; Light, M.E.; Johnson, M.R.; Rols, S.; et al. The dipolar endofullerene HF@C60. Nat. Chem. 2016, 8, 953–957. [Google Scholar] [CrossRef]
- Aoyagi, S.; Nishibori, E.; Sawa, H.; Sugimoto, K.; Takata, M.; Miyata, Y.; Kitaura, R.; Shinohara, H.; Okada, H.; Sakai, T.; et al. A layered ionic crystal of polar Li+@C60 superatoms. Nat. Chem. 2010, 2, 678–683. [Google Scholar] [CrossRef]
- Aoyagi, S.; Sado, Y.; Nishibori, E.; Sawa, H.; Okada, H.; Tobita, H.; Kasama, Y.; Kitaura, R.; Shinohara, H. Rock-salt-type crystal of thermally contracted C60 with encapsulated lithium cation. Angew. Chem. 2012, 124, 3433–3437. [Google Scholar] [CrossRef]
- Colman, R.H.; Okur, H.E.; Garbarino, G.; Ohishi, Y.; Aoyagi, S.; Shinohara, H.; Prassides, K. Pressure effects on the crystal structure of the cubic metallofullerene salt [Li@C60][PF6] to 12 GPa. Mater. Today Commun. 2022, 31, 103275. [Google Scholar] [CrossRef]
- Ueno, H.; Aoyagi, S.; Yamazaki, Y.; Ohkubo, K.; Ikuma, N.; Okada, H.; Kato, T.; Matsuo, Y.; Fukuzumi, S.; Kokubo, K. Electrochemical Reduction of Cationic Li+@C60 to Neutral Li+@C60˙−: Isolation and Characterisation of Endohedral [60] Fulleride. Chem. Sci. 2016, 7, 5770–5774. [Google Scholar] [CrossRef] [PubMed]
- Okada, H.; Ueno, H.; Takabayashi, Y.; Nakagawa, T.; Vrankic, M.; Arvanitidis, J.; Kusamoto, T.; Prassides, K.; Matsuo, Y. Chemical reduction of Li+@C60 by decamethylferrocene to produce neutral Li+@C60•−. Carbon 2019, 153, 467–471. [Google Scholar] [CrossRef]
- Brown, C.M.; Beer, E.; Bellavia, C.; Cristofolini, L.; González, R.; Hanfland, M.; Häusermann, D.; Keshavarz-K, M.; Kordatos, K.; Prassides, K.; et al. Effects of Pressure on the Azafullerene (C59N)2 Molecular Solid to 22 GPa. J. Am. Chem. Soc. 1996, 118, 8715–8716. [Google Scholar] [CrossRef]
- Brown, C.M.; Cristofolini, L.; Kordatos, K.; Prassides, K.; Bellavia, C.; González, R.; Keshavarz-K, M.; Wudl, F.; Cheetham, A.K.; Zhang, J.P.; et al. On the Crystal Structure of Azafullerene (C59N)2. Chem. Mater. 1996, 8, 2548–2550. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Rao, A.M.; Zhou, P.; Wang, K.-A.; Hager, G.T.; Holden, J.M.; Wang, Y.; Lee, W.-T.; Bi, X.-X.; Ecklund, P.C.; Cornett, D.S.; et al. Photoinduced polymerization of solid C60 films. Science 1993, 259, 955–957. [Google Scholar] [CrossRef]
- Bethune, D.S.; Meijer, G.; Tang, W.C.; Rosen, H.J.; Golden, W.G.; Seki, H.; Brown, C.A.; de Vries, M.S. Vibrational Raman and infrared spectra of chromatographically separated C60 and C70 fullerene clusters. Chem. Phys. Lett. 1991, 179, 181–186. [Google Scholar] [CrossRef]
- Davydov, V.A.; Kashevarova, L.S.; Rakhmanina, A.V.; Senyavin, V.M.; Ceolin, R.; Szwarc, H.; Allouchi, H.; Agafonov, V. Spectroscopic study of pressure-polymerized phases of C60. Phys. Rev. B 2000, 61, 11936–11945. [Google Scholar] [CrossRef]
- Kuzmany, H.; Plank, W.; Winter, J.; Dubay, O.; Tagmatarchis, N.; Prassides, K. Raman spectrum and stability of (C59N)2. Phys. Rev. B 1999, 60, 1005–1012. [Google Scholar] [CrossRef]
- Plank, W.; Pichler, T.; Kuzmany, H.; Dubay, O.; Tagmatarchis, N.; Prassides, K. Resonance Raman excitation and electronic structure of the single bonded dimers (C60−)2 and (C59N)2. Eur. Phys. J. B 2000, 17, 33–42. [Google Scholar] [CrossRef]
- Winter, J.; Kuzmany, H. Potassium doped fullerene KxC60 with x = 0, 1, 2, 3, 4 and 6. Solid State Commun. 1992, 84, 935–938. [Google Scholar] [CrossRef]
- Kuzmany, H.; Matus, M.; Burger, B.; Winter, J. Raman scattering in C60 fullerenes and fullerides. Adv. Mater. 1994, 6, 731–745. [Google Scholar] [CrossRef]
- Kosaka, M.; Tanigaki, K.; Prassides, K.; Margadonna, S.; Lappas, A.; Brown, C.M.; Fitch, A.N. Superconductivity in LixCsC60 fullerides. Phys. Rev. B 1999, 59, R6628–R6630. [Google Scholar] [CrossRef]
- Jishi, R.A.; Dresselhaus, M.S. Mode softening and mode stiffening in C60 doped with alkali metals. Phys. Rev. B 1992, 45, 6914–6918. [Google Scholar] [CrossRef] [PubMed]
- Zhou, P.; Wang, K.A.; Wang, Y.; Eklund, P.C.; Dresselhaus, M.S.; Dresselhaus, G.; Jishi, R.A. Raman scattering in C60 and alkali-metal-saturated C60. Phys. Rev. B 1992, 46, 2595–2605. [Google Scholar] [CrossRef] [PubMed]
- Meletov, K.P.; Velkos, G.; Arvanitidis, J.; Christofilos, D.; Kourouklis, G.A. Raman study of the photopolymer formation in the {Pt(dbdtc)2}·C60 fullerene complex and the decomposition kinetics of the photo-oligomers. Chem. Phys. Lett. 2017, 68, 124–129. [Google Scholar] [CrossRef]
- Krause, M.; Dunsch, L.; Seifert, G.; Fowler, P.W.; Gromov, A.; Kratschmer, W.; Gutierrez, R.; Porezag, D.; Frauenheim, T.J. Vibrational signatures of fullerene oxides. J. Chem. Soc. Faraday Trans. 1998, 94, 2287–2294. [Google Scholar] [CrossRef]
- Krause, M.; Baes-Fischlmair, S.; Pfeiffer, R.; Plank, W.; Pichler, T.; Kuzmany, H.; Tagmatarchis, N.; Prassides, K. Thermal Stability and high temperature graphitization of bisazafullerene (C59N)2 as studied by IR and Raman spectroscopy. J. Phys. Chem. B 2001, 105, 11964–11969. [Google Scholar] [CrossRef]
- Prassides, K.; Wudl, F.; Andreoni, W. Solid Azafullerenes and Azafullerides. Fullerene Sci. Technol. 1997, 5, 801–812. [Google Scholar] [CrossRef]
- Oszlányi, G.; Bortel, G.; Faigel, G.; Gránásy, L.; Bendele, G.M.; Stephens, P.W.; Forró, L. Single C-C Bond in (C60)22−. Phys. Rev. B 1996, 54, 11849–11852. [Google Scholar] [CrossRef]
- Prassides, K.; Vavekis, K.; Kordatos, K.; Tanigaki, K.; Bendele, G.M.; Stephens, P.W. Loss of cubic symmetry in low-temperature Na2RbC60. J. Am. Chem. Soc. 1997, 119, 834–835. [Google Scholar] [CrossRef]
- Bendele, G.M.; Stephens, P.W.; Prassides, K.; Vavekis, K.; Kordatos, K.; Tanigaki, K. Effect of charge state on polymeric bonding geometry: The ground state of Na2RbC60. Phys. Rev. Lett. 1998, 80, 736–739. [Google Scholar] [CrossRef]
- Ji, C.; Li, B.; Liu, W.; Smith, J.S.; Majumdar, A.; Luo, W.; Ahuja, R.; Shu, J.; Wang, J.; Sinogeikin, S.; et al. Ultrahigh-pressure isostructural electronic transitions in hydrogen. Nature 2019, 573, 558–562. [Google Scholar] [CrossRef]
- Duclos, S.J.; Brister, K.; Haddon, R.C.; Kortan, A.R.; Thiel, F.A. Effects of Pressure and Stress on C60 Fullerite to 20 GPa. Nature 1991, 351, 380–382. [Google Scholar] [CrossRef]
- Kato, K.; Tanaka, H. Visualizing charge densities and electrostatic potentials in materials by synchrotron X-ray powder diffraction. Adv. Phys. X 2016, 1, 55–80. [Google Scholar] [CrossRef]
- Larson, A.C.; von Dreele, R.B. General Structure Analysis System (GSAS). In Los Alamos National Laboratory Report LAUR; The Regents of the University of California: Oakland, CA, USA, 2000; pp. 86–748. [Google Scholar]
- Toby, B.H. EXPGUI, a Graphical User Interface for GSAS. J. Appl. Crystallogr. 2001, 34, 210–213. [Google Scholar] [CrossRef]
- Rodríguez-Carvajal, J. Recent Advances in Magnetic Structure Determination by Neutron Powder Diffraction. Physica B Condens. Matter 1993, 192, 55–69. [Google Scholar] [CrossRef]
- Hirao, N.; Kawaguchi, S.I.; Hirose, K.; Shimizu, K.; Ohtani, E.; Ohishi, Y. New developments in high-pressure X-ray diffraction beamline for diamond anvil cell at SPring-8. Matter Radiat. Extrem. 2020, 5, 018403. [Google Scholar] [CrossRef]
- Seto, Y.; Nishio-Hamane, D.; Nagai, T.; Sata, N. Development of a software suite on X-ray diffraction experiments. Rev. High Press. Sci. Technol. 2010, 20, 269–276. [Google Scholar] [CrossRef]
- Sakai, T.; Yagi, T.; Ohfuji, H.; Irifune, T.; Ohishi, Y.; Hirao, N.; Suzuki, Y.; Kuroda, Y.; Asakawa, T.; Kanemura, T. High-pressure generation using double stage micro-paired diamond anvils shaped by focused ion beam. Rev. Sci. Instrum. 2015, 86, 033905. [Google Scholar] [CrossRef] [PubMed]
- Sakai, T.; Yagi, T.; Irifune, T.; Kadobayashi, H.; Hirao, N.; Kunimoto, T.; Ohfuji, H.; Kawaguchi-Imada, S.; Ohishi, Y.; Tateno, S.; et al. High pressure generation using double-stage diamond anvil technique: Problems and equations of state of rhenium. High Press. Res. 2018, 38, 107–119. [Google Scholar] [CrossRef]
- Zha, C.-S.; Mao, H.-K.; Hemley, R.J. Elasticity of MgO and a Primary Pressure Scale to 55 GPa. Proc. Natl. Acad. Sci. USA 2000, 97, 13494. [Google Scholar] [CrossRef]
- Klotz, S.; Chervin, J.C.; Munsch, P.; Le Marchand, G. Hydrostatic limits of 11 pressure transmitting media. J. Phys. D Appl. Phys. 2009, 42, 075413. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vrankić, M.; Nakagawa, T.; Menelaou, M.; Takabayashi, Y.; Yoshikane, N.; Matsui, K.; Kokubo, K.; Kato, K.; Kawaguchi-Imada, S.; Kadobayashi, H.; et al. On the Structural and Vibrational Properties of Solid Endohedral Metallofullerene Li@C60. Inorganics 2024, 12, 99. https://doi.org/10.3390/inorganics12040099
Vrankić M, Nakagawa T, Menelaou M, Takabayashi Y, Yoshikane N, Matsui K, Kokubo K, Kato K, Kawaguchi-Imada S, Kadobayashi H, et al. On the Structural and Vibrational Properties of Solid Endohedral Metallofullerene Li@C60. Inorganics. 2024; 12(4):99. https://doi.org/10.3390/inorganics12040099
Chicago/Turabian StyleVrankić, Martina, Takeshi Nakagawa, Melita Menelaou, Yasuhiro Takabayashi, Naoya Yoshikane, Keisuke Matsui, Ken Kokubo, Kenichi Kato, Saori Kawaguchi-Imada, Hirokazu Kadobayashi, and et al. 2024. "On the Structural and Vibrational Properties of Solid Endohedral Metallofullerene Li@C60" Inorganics 12, no. 4: 99. https://doi.org/10.3390/inorganics12040099
APA StyleVrankić, M., Nakagawa, T., Menelaou, M., Takabayashi, Y., Yoshikane, N., Matsui, K., Kokubo, K., Kato, K., Kawaguchi-Imada, S., Kadobayashi, H., Arvanitidis, J., Kubota, Y., & Prassides, K. (2024). On the Structural and Vibrational Properties of Solid Endohedral Metallofullerene Li@C60. Inorganics, 12(4), 99. https://doi.org/10.3390/inorganics12040099







