A First-Principle Study of Two-Dimensional Boron Nitride Polymorph with Tunable Magnetism
Abstract
1. Introduction
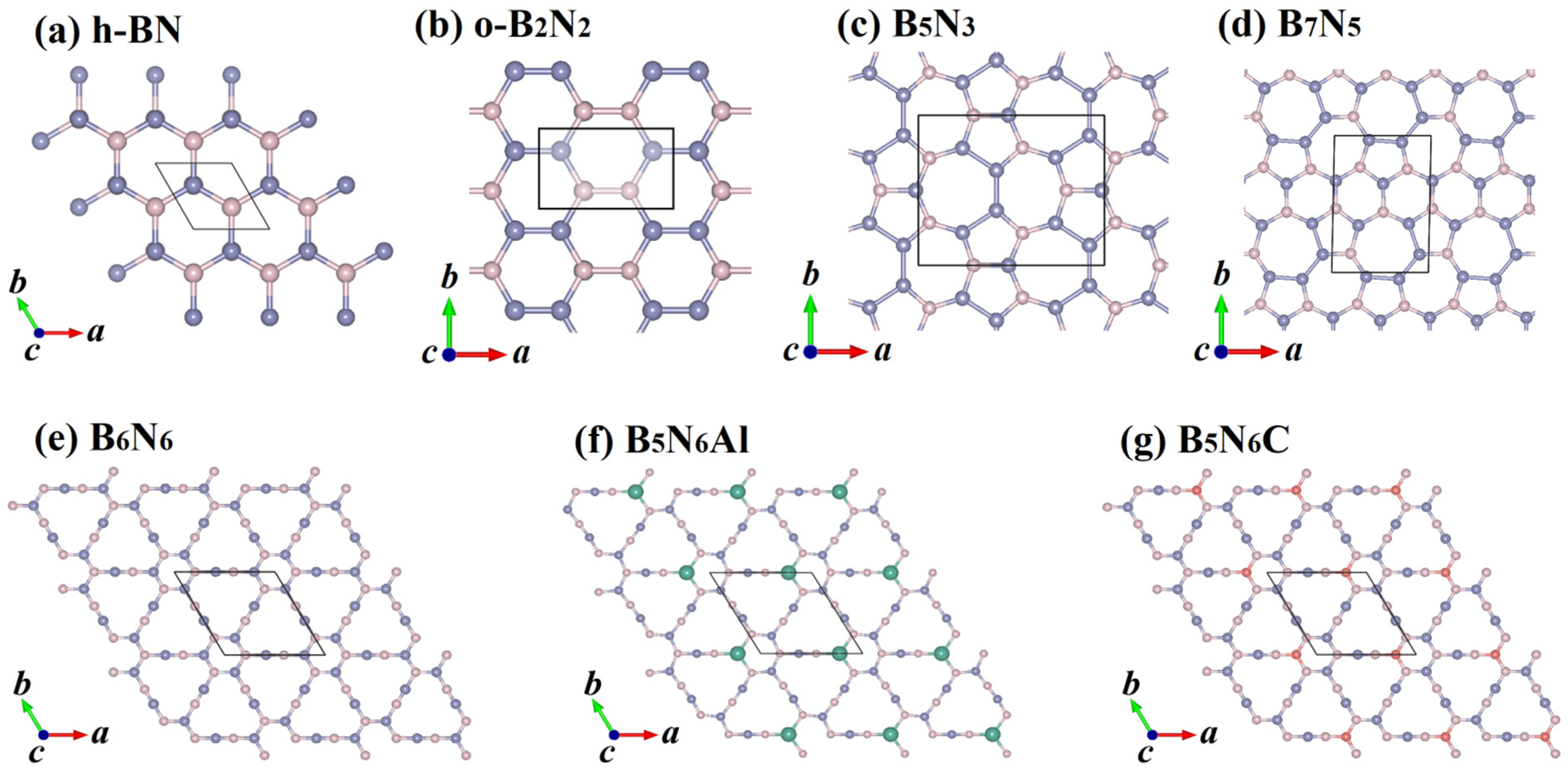
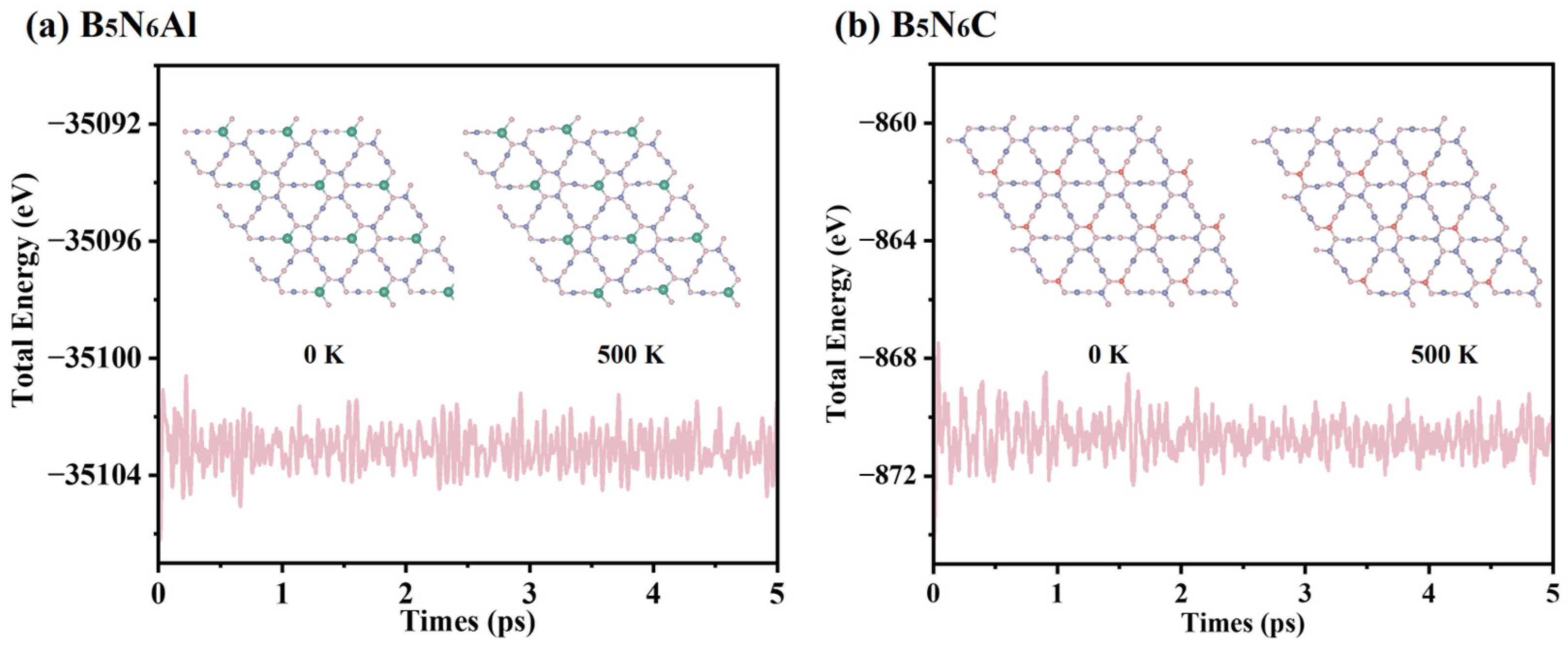
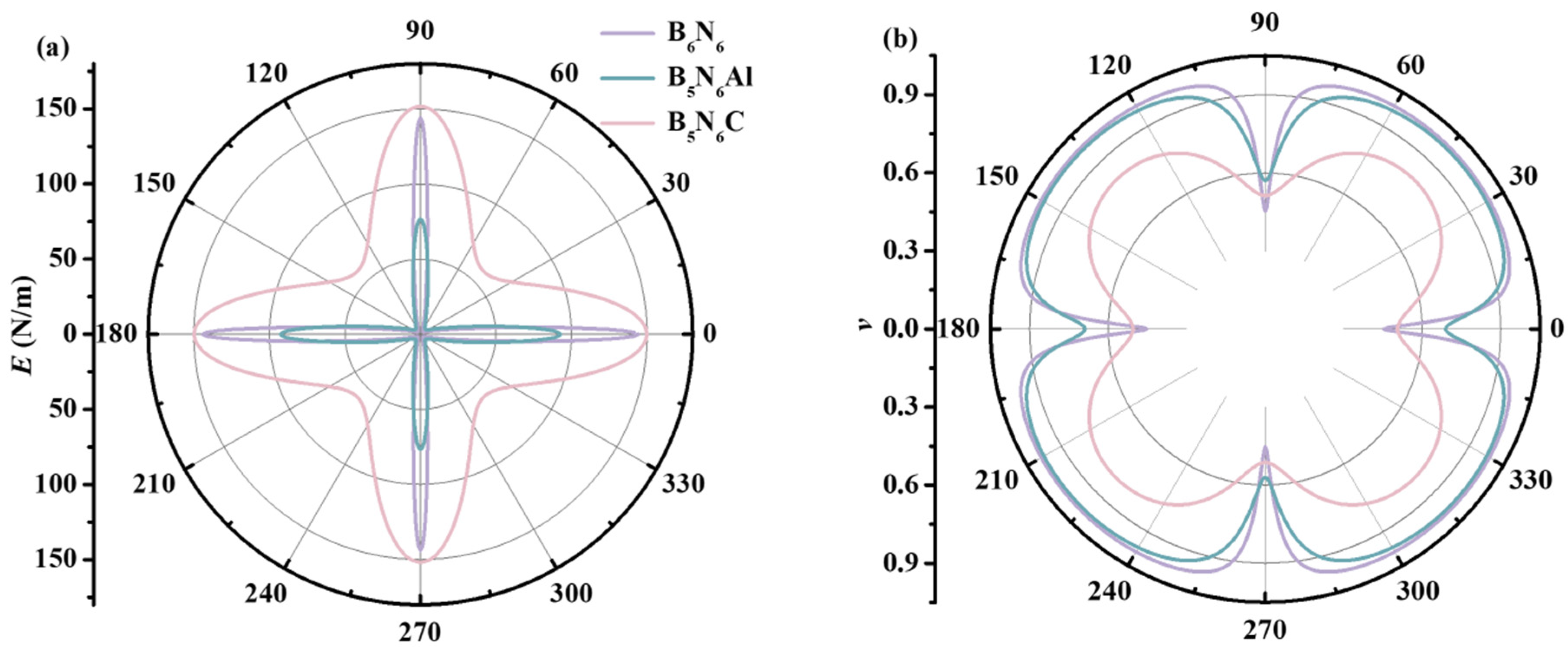
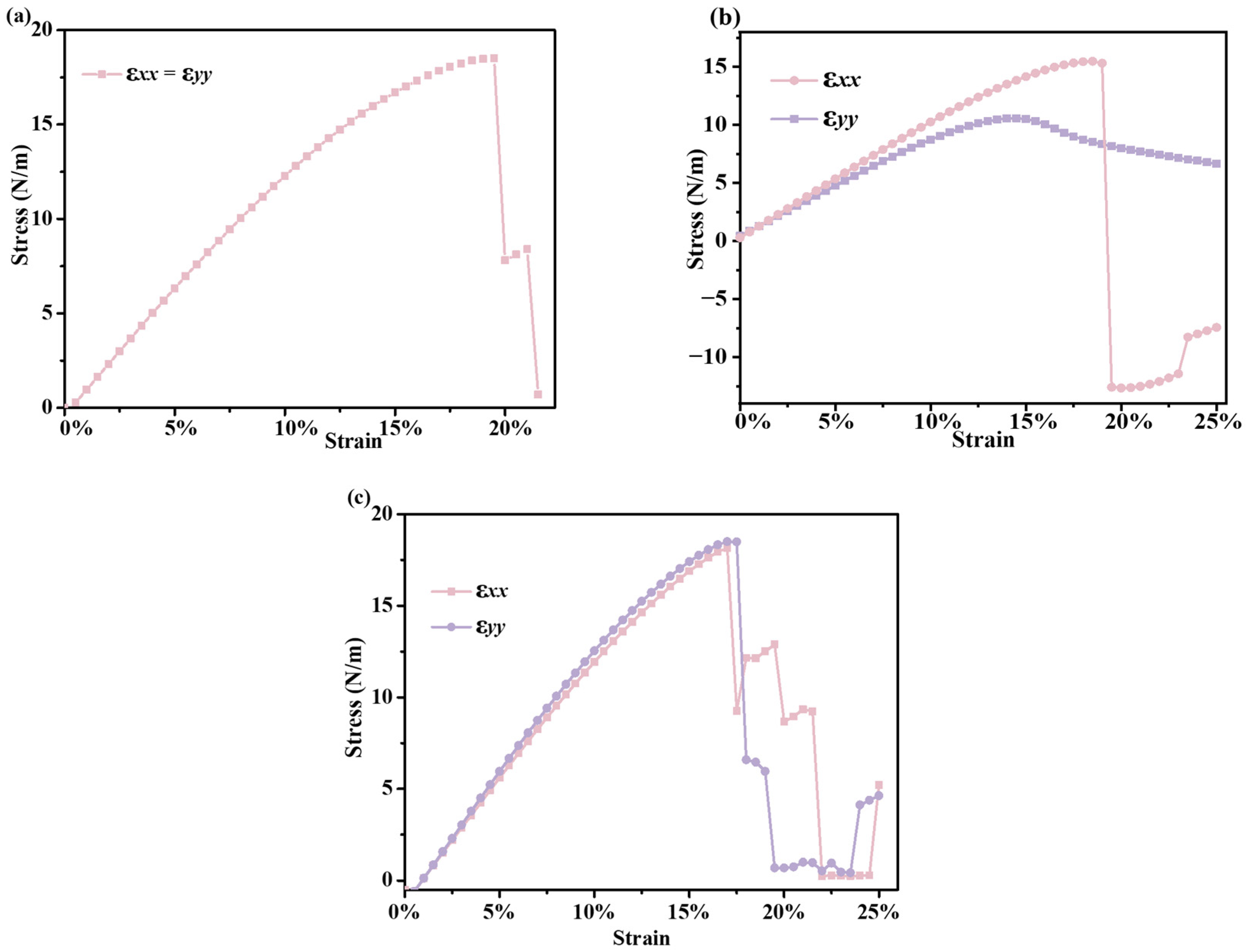
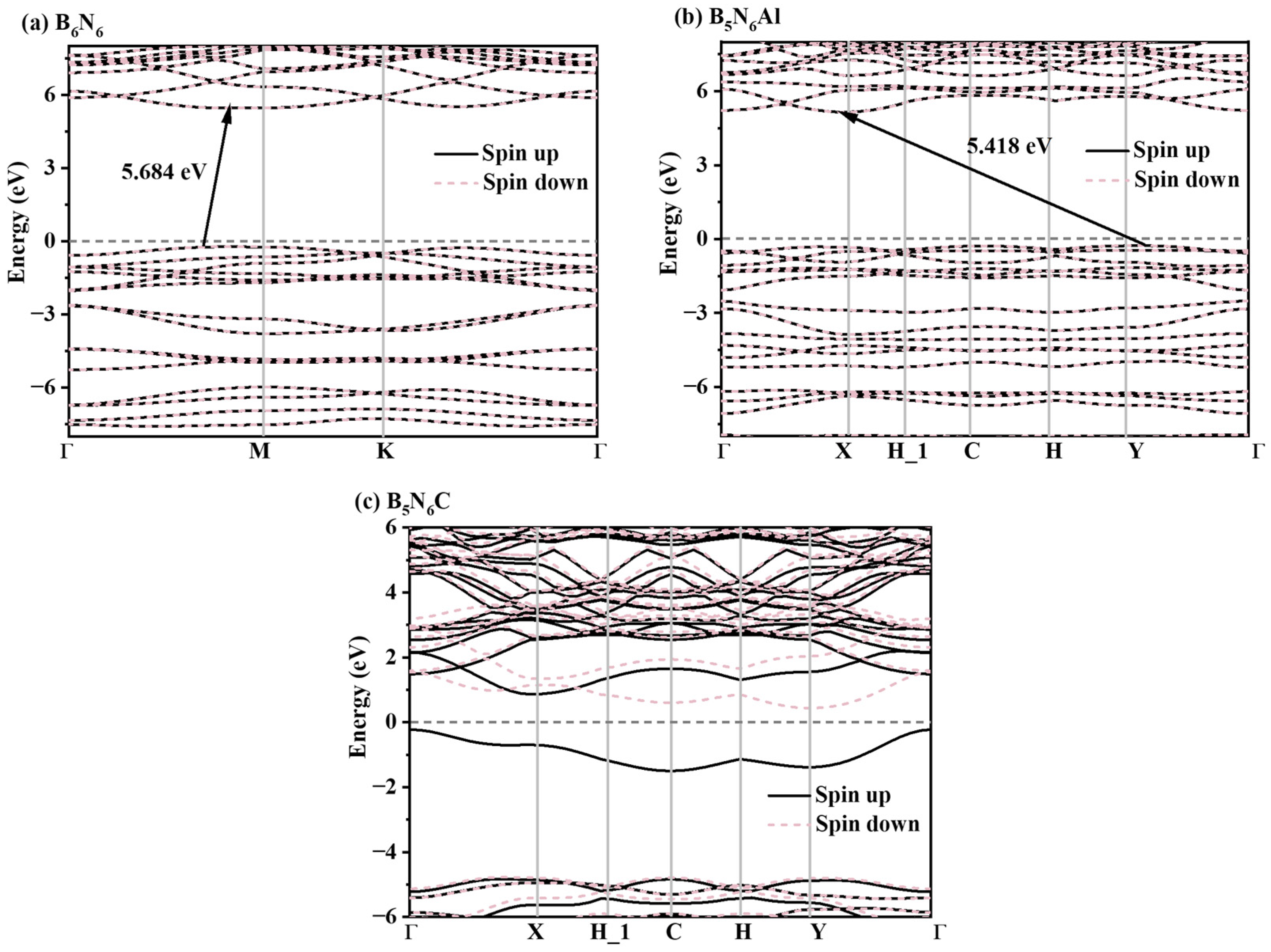
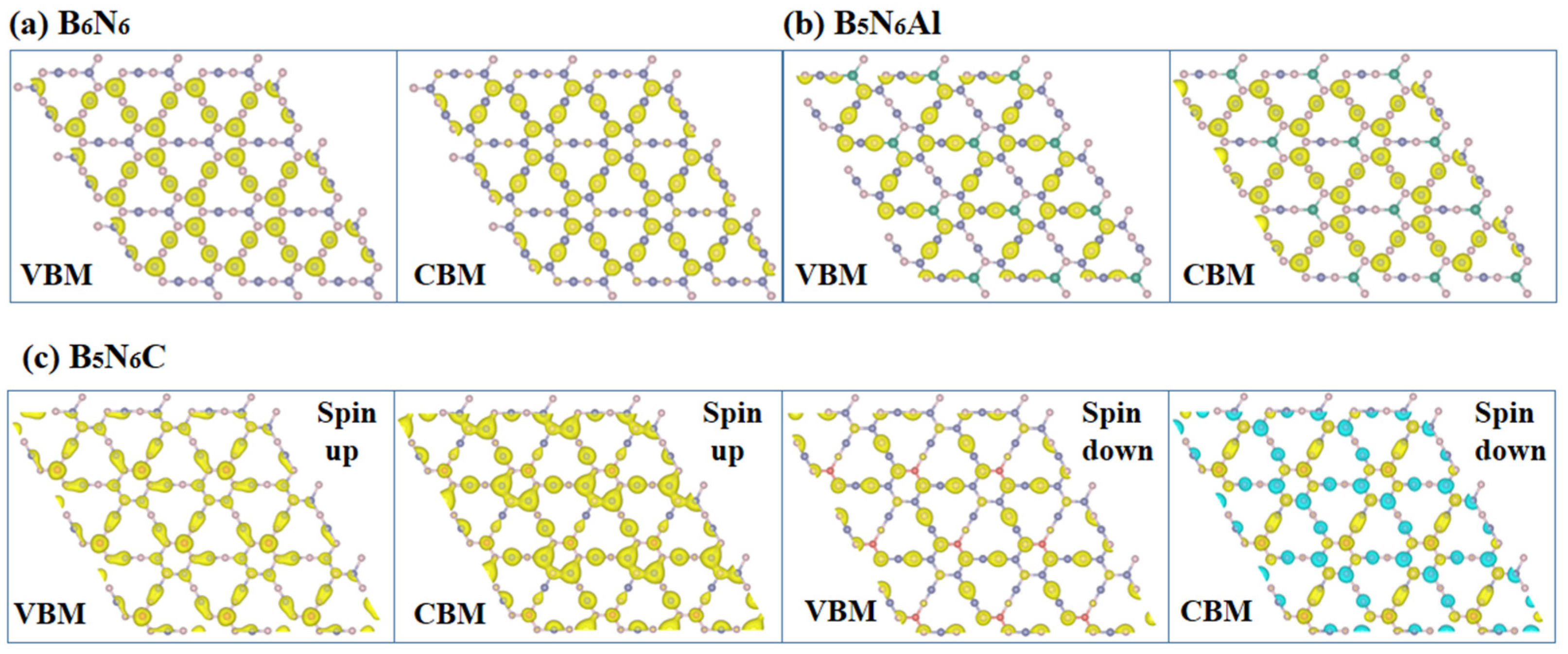
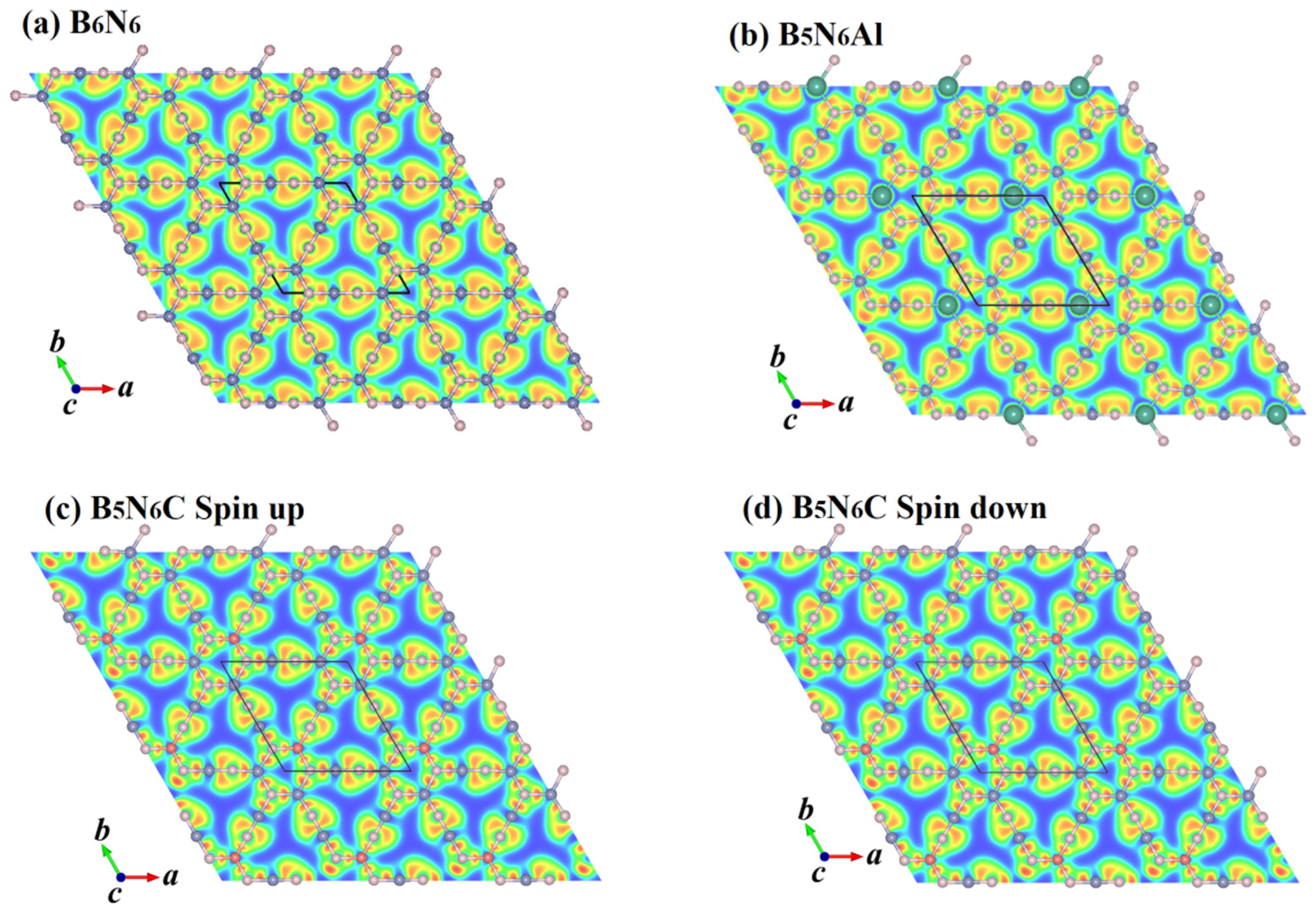
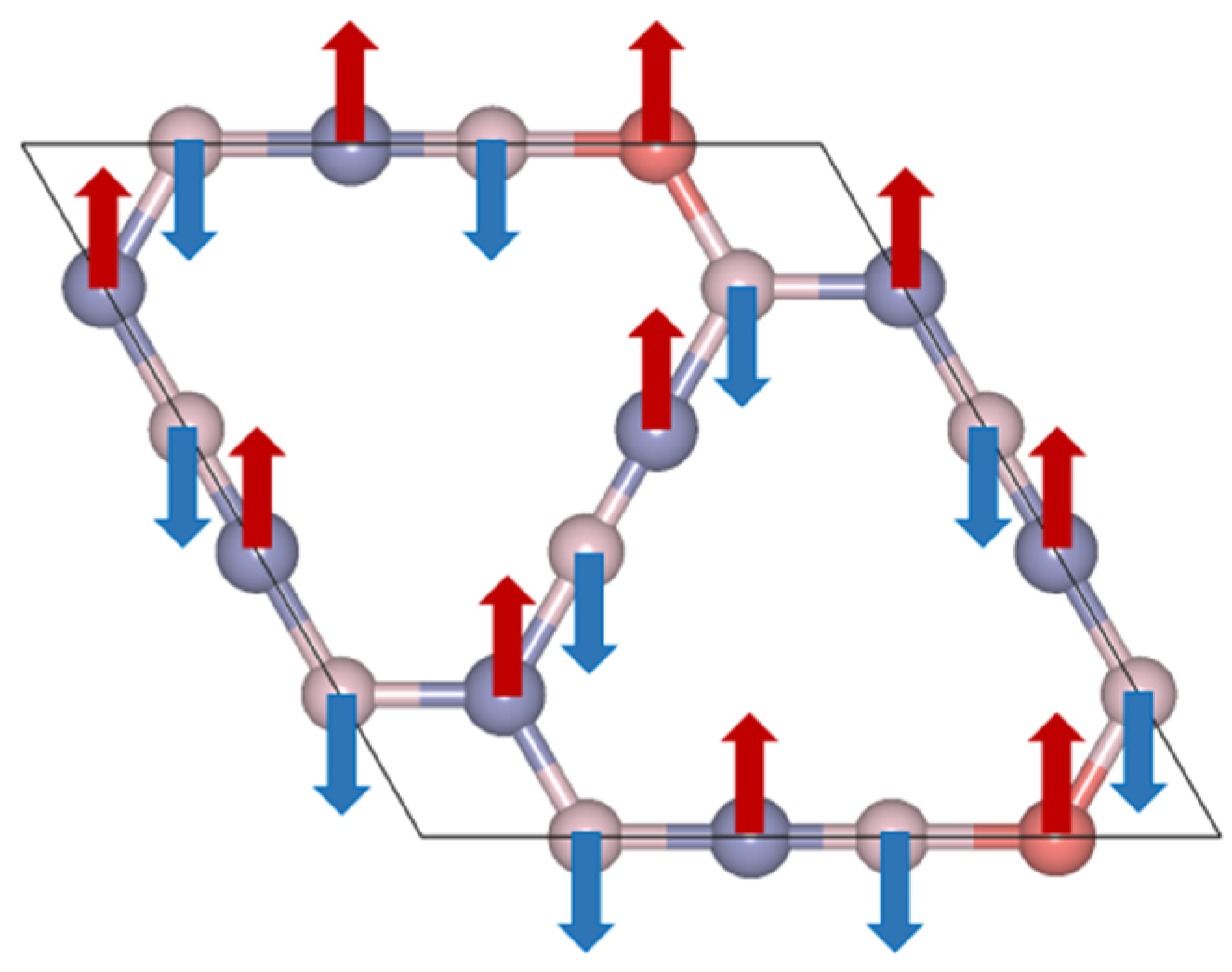
2. Results and Discussion
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bi, J.X.; Du, Z.Z.; Sun, J.M.; Liu, Y.H.; Wang, K.; Du, H.F.; Ai, W.; Huang, W. On the Road to the Frontiers of Lithium-Ion Batteries: A Review and Outlook of Graphene Anodes. Adv. Mater. 2023, 35, e2210734. [Google Scholar] [CrossRef]
- Olabi, A.G.; Abdelkareem, M.A.; Wilberforce, T.; Sayed, E.T. Application of graphene in energy storage device—A review. Renew. Sust. Energ. Rev. 2021, 135, 110026. [Google Scholar] [CrossRef]
- Xiao, Y.Q.; Pang, Y.X.; Yan, Y.X.; Qian, P.; Zhao, H.T.; Manickam, S.; Wu, T.; Pang, C.H. Synthesis and Functionalization of Graphene Materials for Biomedical Applications: Recent Advances, Challenges, and Perspectives. Adv. Sci. 2023, 10, e2205292. [Google Scholar] [CrossRef]
- Yang, H.B.; Zheng, H.J.; Duan, Y.X.; Xu, T.; Xie, H.X.; Du, H.S.; Si, C.L. Nanocellulose-graphene composites: Preparation and applications in flexible electronics. Int. J. Biol. Macromol. 2023, 253, 126903. [Google Scholar] [CrossRef]
- Ghosa, S.; Mondal, N.S.; Chowdhury, S.; Jana, D. Two novel phases of germa-graphene: Prediction, electronic and transport applications. Appl. Surf. Sci. 2023, 614, 156107. [Google Scholar] [CrossRef]
- Asim, N.; Badiei, M.; Samsudin, N.A.; Mohammad, M.; Razali, H.; Soltani, S.; Amin, N. Application of graphene-based materials in developing sustainable infrastructure: An overview. Compos. B. Eng. 2022, 245, 110188. [Google Scholar] [CrossRef]
- Sun, M.; Chou, J.P.; Hu, A.; Schwingenschlögl, U. Point Defects in Blue Phosphorene. Chem. Mater. 2019, 31, 8129–8135. [Google Scholar] [CrossRef]
- Ma, Y.; Yan, Y.; Luo, L.; Pazos, S.; Zhang, C.; Lv, X.; Chen, M.; Liu, C.; Wang, Y.; Chen, A.; et al. High-performance van der Waals antiferroelectric CuCrP2S6-based memristors. Nat. Commun. 2023, 14, 7891. [Google Scholar] [CrossRef]
- Zhang, C.; Ren, K.; Wang, S.; Luo, Y.; Tang, W.; Sun, M. Recent progress on two-dimensional van der Waals heterostructures for photocatalytic water splitting: A selective review. J. Phys. D Appl. Phys. 2023, 56, 483001. [Google Scholar] [CrossRef]
- Zhang, W.; Chai, C.; Fan, Q.; Yang, Y.; Sun, M.; Palummo, M.; Schwingenschlögl, U. Two-dimensional borocarbonitrides for photocatalysis and photovoltaics. J. Mater. Chem. C 2023, 11, 3875–3884. [Google Scholar] [CrossRef]
- Ren, K.; Yan, Y.; Zhang, Z.; Sun, M.; Schwingenschlogl, U. A family of LixBy monolayers with a wide spectrum of potential applications. Appl. Surf. Sci. 2022, 604, 154317. [Google Scholar] [CrossRef]
- Sun, M.; Re Fiorentin, M.; Schwingenschlögl, U.; Palummo, M. Excitons and light-emission in semiconducting MoSi2X4 two-dimensional materials. NPJ 2D Mater. Appl. 2022, 6, 81. [Google Scholar] [CrossRef]
- Wang, Y.; Miao, M.; Lv, J.; Zhu, L.; Yin, K.; Liu, H.; Ma, Y. An Effective Structure Prediction Method for Layered Materials Based on 2D Particle Swarm Optimization Algorithm. J. Chem. Phys. 2012, 137, 224108–224114. [Google Scholar] [CrossRef]
- Pakdel, A.; Bando, Y.; Golberg, D. Nano boron nitride flatland. Chem. Soc. Rev. 2014, 43, 934–959. [Google Scholar] [CrossRef]
- Entani, S.; Larionov, K.V.; Popov, Z.I.; Takizawa, M.; Mizuguchi, M.; Watanabe, H.; Li, S.T.; Naramoto, H.; Sorokin, P.B.; Sakai, S. Non-chemical fluorination of hexagonal boron nitride by high-energy ion irradiation. Nanotechnology 2020, 31, 125705. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.G.; Mu, X.J.; Wang, X.X.; Wang, N.; Ma, F.C.; Liang, W.J.; Sun, M.T. The thermal and thermoelectric properties of in-plane C-BN hybrid structures and graphene/h-BN van der Waals heterostructures. Mater. Today Phys. 2018, 5, 29–57. [Google Scholar] [CrossRef]
- Sun, M.; Tang, W.; Ren, Q.; Wang, S.; Yu, J.; Du, Y. A first-principles study of light non-metallic atom substituted blue phosphorene. Appl. Surf. Sci. 2015, 356, 110–114. [Google Scholar] [CrossRef]
- Wang, Z.H.; Zhou, X.F.; Zhang, X.M.; Zhu, Q.; Dong, H.F.; Zhao, M.W.; Oganov, A.R. Phagraphene: A Low-Energy Graphene Allotrope Composed of 5–6-7 Carbon Rings with Distorted Dirac Cones. Nano Lett. 2015, 15, 6182–6186. [Google Scholar] [CrossRef] [PubMed]
- Singh, N.B.; Bhattacharya, B.; Sarkar, U. A first principle study of pristine and BN-doped graphyne family. Struct. Chem. 2014, 25, 1695–1710. [Google Scholar] [CrossRef]
- Enyashin, A.N.; Ivanovskii, A.L. Graphene-like BN allotropes: Structural and electronic properties from DFTB calculations. Chem. Phys. Lett. 2011, 509, 143–147. [Google Scholar] [CrossRef]
- Bu, H.; Zhao, M.; Zhang, H.; Wang, X.; Xi, Y.; Wang, Z. Isoelectronic Doping of Graphdiyne with Boron and Nitrogen: Stable Configurations and Band Gap Modification. J. Phys. Chem. A 2012, 116, 3934–3939. [Google Scholar] [CrossRef]
- Shahrokhi, M.; Mortazavi, B.; Berdiyorov, R.G. New two-dimensional Boron Nitride allotropes with attractive electronic and optical properties. Solid State Commun. 2017, 253, 51–56. [Google Scholar] [CrossRef]
- Demirci, S.; Rad, S.E.; Kazak, S.; Nezir, S.; Jahangirov, S. Monolayer diboron dinitride: Direct band-gap semiconductor with high absorption in the visible range. Phys. Rev. B 2020, 101, 125408. [Google Scholar] [CrossRef]
- Li, X.D.; Cheng, X.L. Predicting the structural and electronic properties of two-dimensional single layer boron nitride sheets. Chem. Phys. Lett. 2018, 694, 102–106. [Google Scholar] [CrossRef]
- Chen, Y.; Zou, J.; Campbell, S.J.; Le Caer, G. Boron nitride nanotubes: Pronounced resistance to oxidation. Appl. Phys. Lett. 2004, 84, 2430–2432. [Google Scholar] [CrossRef]
- Wang, X.; Zhi, C.; Li, L.; Zeng, H.; Li, C.; Mitome, M.; Golberg, D.; Bando, Y. “Chemical Blowing” of Thin-Walled Bubbles: High-Throughput Fabrication of Large-Area, Few-Layered BN and Cx-BN Nanosheets. Adv. Mater. 2011, 23, 4072–4076. [Google Scholar] [CrossRef] [PubMed]
- Zhi, C.; Bando, Y.; Tang, C.; Kuwahara, H.; Golberg, D. Large-Scale Fabrication of Boron Nitride Nanosheets and Their Utilization in Polymeric Composites with Improved Thermal and Mechanical Properties. Adv. Mater. 2009, 21, 2889–2893. [Google Scholar] [CrossRef]
- Anota, E.C.; Hernández, A.B.; Morales, A.E.; Castro, M. Design of the magnetic homonuclear bonds boron nitride nanosheets using DFT methods. J. Mol. Graph. Model. 2017, 74, 135–142. [Google Scholar] [CrossRef]
- Cao, X.; Li, Y.; Cheng, X.; Zhang, Y. Structural analogues of graphyne family: New types of boron nitride sheets with wide band gap and strong UV absorption. Chem. Phys. Lett. 2011, 502, 217–221. [Google Scholar] [CrossRef]
- Qi, J.; Wang, S.; Wang, J.; Umezawa, N.; Blatov, V.A.; Hosono, H. B5N3 and B7N5 Monolayers with High Carrier Mobility and Excellent Optical Performance. J. Phys. Chem. Lett. 2021, 12, 4823–4832. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1956, 140, A1133. [Google Scholar] [CrossRef]
- Fan, Q.; Zhou, H.; Zhao, Y.; Yun, S. Predicting a novel two-dimensional BN material with a wide band gap. Energy Mater. 2022, 2, 200022. [Google Scholar] [CrossRef]
- Anota, E.C. 2D boron nitride incorporating homonuclear boron bonds: Stabilized in neutral, anionic and cationic charge. SN Appl. Sci. 2022, 4, 295. [Google Scholar] [CrossRef]
- Cadelano, E.; Palla, P.L.; Giordano, S.; Colombo, L. Elastic properties of hydrogenated graphene. Phys. Rev. B 2010, 82, 235414. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, Y. Density functional theory study of the silicene-like SiX and XSi3 (X = B, C, N, Al, P) honeycomb lattices: The various buckled structures and versatile electronic properties. J. Phys. Chem. C 2013, 117, 18266–18278. [Google Scholar] [CrossRef]
- Andrew, R.C.; Mapasha, R.E.; Ukpong, A.M.; Chetty, N. Mechanical properties of graphene and boronitrene. Phys. Rev. B 2012, 85, 125428. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.J.; Pack, J.D. Special points for brillouinzone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Krukau, A.V.; Vydrov, O.A.; Izmaylov, A.F.; Scuseria, G.E. Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 2006, 125, 224106. [Google Scholar] [CrossRef] [PubMed]
- Wang, V.; Liu, J.C.; Tang, G.; Geng, W.T. VASPKIT: A user-friendly interface facilitating high-throughput computing and analysis using VASP code. Comput. Phys. Commun. 2021, 267, 108033. [Google Scholar] [CrossRef]
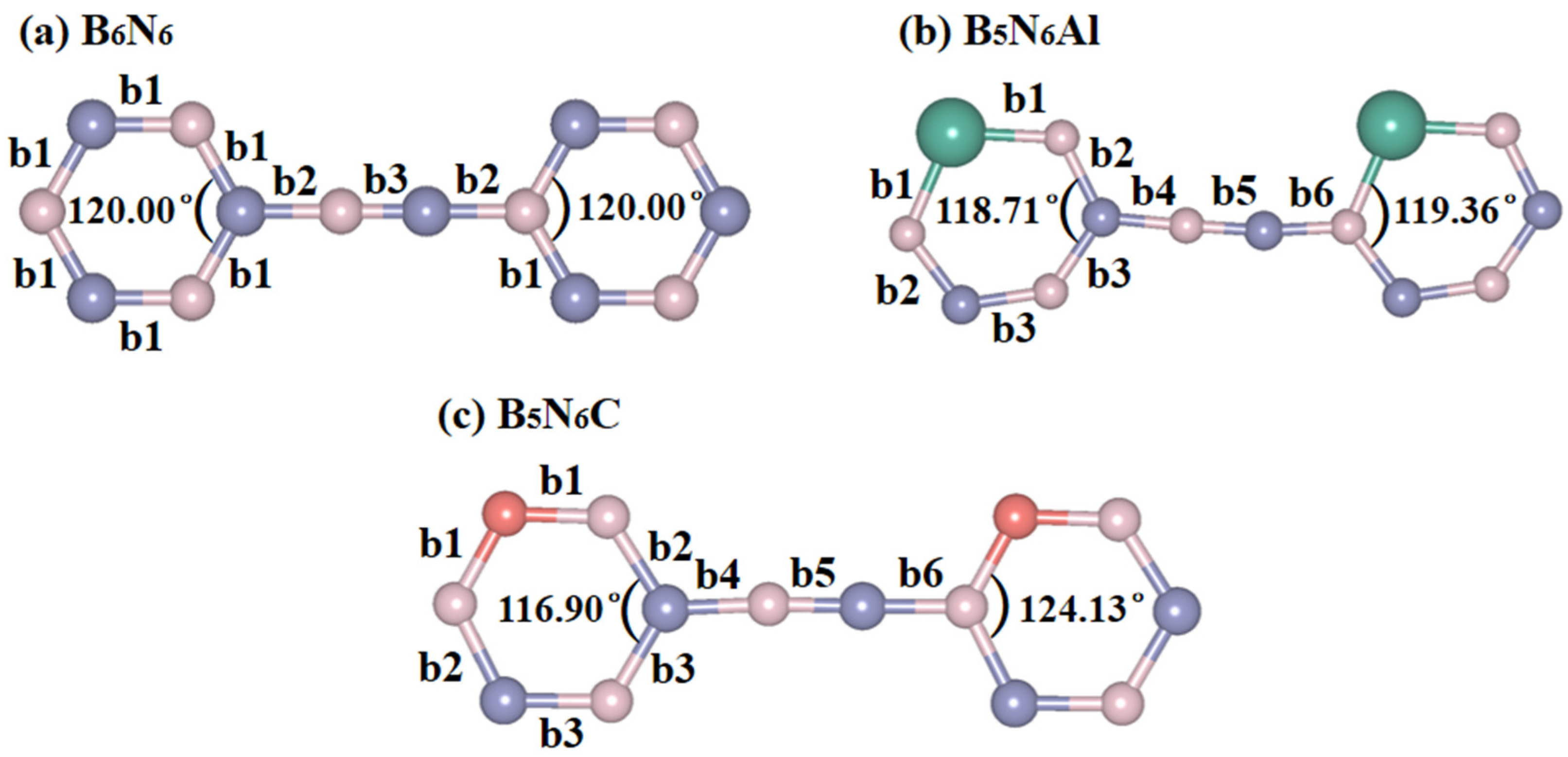

| a | b | b1 | b2 | b3 | b4 | b5 | b6 | |
|---|---|---|---|---|---|---|---|---|
| B6N6 | 6.20 | 1.275 | 1.278 | 1.094 | ||||
| B5N6Al | 7.40 | 7.18 | 1.796 | 1.451 | 1.465 | 1.390 | 1.264 | 1.374 |
| B5N6C | 6.86 | 5.93 | 1.381 | 1.451 | 1.441 | 1.380 | 1.260 | 1.391 |
| C11 | C12 | C22 | C66 | Ex | Ey | vx | vy | |
|---|---|---|---|---|---|---|---|---|
| B6N6 | 180.98 | 82.09 | 180.98 | 49.45 | 141.18 | 141.18 | 0.46 | 0.46 |
| B5N6Al | 152.14 | 86.84 | 126.11 | 44.78 | 97.83 | 76.19 | 0.69 | 0.57 |
| B5N6C | 201.78 | 103.48 | 204.66 | 53.35 | 149.46 | 151.59 | 0.50 | 0.51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiao, L.; Ma, Z.; Yan, F.; Wang, S.; Fan, Q. A First-Principle Study of Two-Dimensional Boron Nitride Polymorph with Tunable Magnetism. Inorganics 2024, 12, 59. https://doi.org/10.3390/inorganics12020059
Qiao L, Ma Z, Yan F, Wang S, Fan Q. A First-Principle Study of Two-Dimensional Boron Nitride Polymorph with Tunable Magnetism. Inorganics. 2024; 12(2):59. https://doi.org/10.3390/inorganics12020059
Chicago/Turabian StyleQiao, Liping, Zhongqi Ma, Fulong Yan, Sake Wang, and Qingyang Fan. 2024. "A First-Principle Study of Two-Dimensional Boron Nitride Polymorph with Tunable Magnetism" Inorganics 12, no. 2: 59. https://doi.org/10.3390/inorganics12020059
APA StyleQiao, L., Ma, Z., Yan, F., Wang, S., & Fan, Q. (2024). A First-Principle Study of Two-Dimensional Boron Nitride Polymorph with Tunable Magnetism. Inorganics, 12(2), 59. https://doi.org/10.3390/inorganics12020059







