Next Article in Journal
Improved Photothermal Heating of NaNdF4 Microcrystals via Low-Level Doping of Sm3+ for Thermal-Responsive Upconversion Luminescence Anti-Counterfeiting
Previous Article in Journal
Immobilization of Bromelain on Gold Nanoparticles for Comprehensive Detection of Their Antioxidant, Anti-Angiogenic, and Wound-Healing Potentials
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Inorganics
Volume 12
Issue 12
10.3390/inorganics12120326
inorganics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Perspective

Comparison of Gallium Cluster Polyhedra with Those of the Most Spherical Deltahedra: Effects of Bulky External Groups and Local Surface Curvature

by
R. Bruce King
Department of Chemistry, University of Georgia, Athens, GA 30602, USA
Inorganics 2024, 12(12), 326; https://doi.org/10.3390/inorganics12120326
Submission received: 19 November 2024 / Revised: 5 December 2024 / Accepted: 9 December 2024 / Published: 13 December 2024
Browse Figures
Versions Notes

Abstract

:
Experimentally accessible stable polyhedral clusters of gallium differ from clusters of its lighter homologue boron by having sterically demanding external groups such as tBu3Si, (Me3Si)3Si, (Me3Si)3C, (Me3Si)2N, and fluorenyl. This restricts closo deltahedral [GanRn]z gallane chemistry to octahedral derivatives such as Ga6R62− (R = SiBuPh2, SiBut3) and Ga6R6 (R = SiMe(SiMe3)2) in which the bulky external silyl groups are spread out because of the relatively high local curvature of the degree 4 vertices of the central Ga6 octahedron. The structures of larger gallium clusters are based on alternatives to closo deltahedra having exclusively high local curvature degree 4 vertices such as the 8-vertex square antiprismatic Ga8R8 (R = fluorenyl) or, more commonly, larger polyhedra or fused polyhedra with some bare gallium vertices. Some of the larger gallium clusters can be considered to be spherically aromatic systems with closed shells according to the jellium model. Examples include [Ga13(SitBu3)6]− with 8 cluster electrons corresponding to a filled 1S21P6 shell as well as [Ga@Ga18{C(SiMe3)3}6]− with 52 cluster electrons, Ga22{E(SiMe3)3]8, (E = C, Si) and Ga@Ga11{GaN(SiMe3)2}11 with 58 skeletal electrons, and [Ga26{Si(SiMe3)3}8]2− with 72 cluster electrons. The 10-vertex species Ga10{Si(SiMe3)3}6, [Ga10(SitBu3)6]−, and Ga10(SitBu3)6 have structures consisting of a fusion of two polyhedra sharing bare gallium vertices with skeletal electron counts, suggesting a multicenter core bond in each of the two polyhedral cavities.

Graphical Abstract

1. Introduction

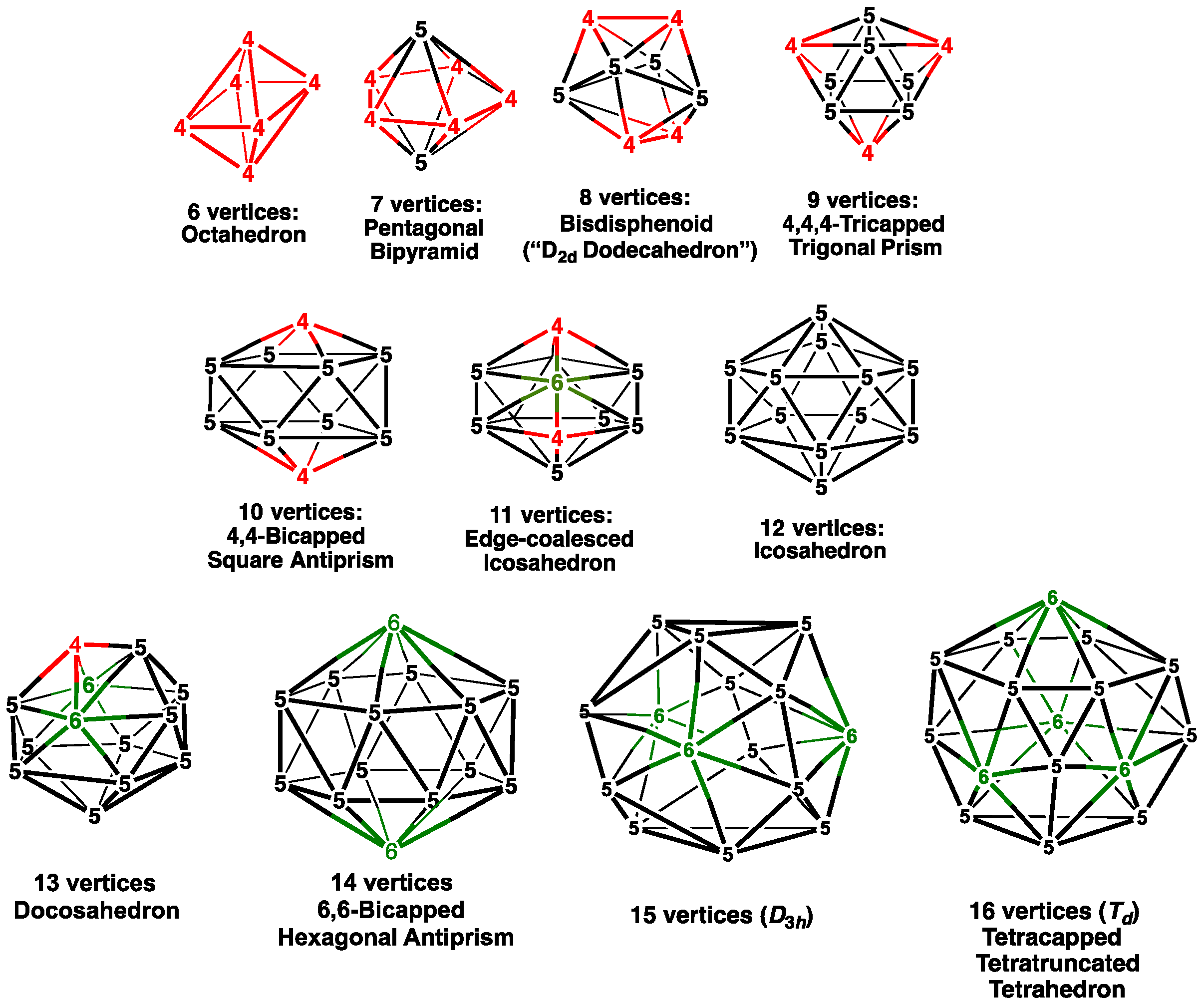
The basic building blocks for the most stable polyhedral boranes and metallaboranes are the most spherical or closo deltahedra (Figure 1) [1,2,3]. In general, such polyhedra are so-called deltahedra, having exclusively triangular faces with vertices as nearly equivalent as possible. Twelve-vertex structures, such as the dianion B12H122−, as well as the isoelectronic monoanion CB11H12− and neutral C2B10H12 and their substitution products based on a central regular icosahedron with 12 degree 5 vertices, are particularly stable. The regular octahedron with exclusively degree 4 vertices is the closo 6-vertex deltahedron. The closo deltahedra with 7 to 10 vertices have exclusively degree 4 and 5 vertices. The 11-vertex closo deltahedron necessarily has a single degree 6 vertex along with eight degree 5 vertices and two degree 4 vertices. Supraicosahedral closo deltahedra with more than 14 vertices up to the 16-vertex tetracapped tetratruncated tetrahedron are the so-called Frank–Kasper polyhedra [4], with a combination of exclusively degree 5 and 6 vertices with no adjacent pair of degree 6 vertices. Similar closo deltahedra with more than 16 vertices with no vertices of degree 7 or higher and no pair of adjacent degree 6 vertices are not possible. Thus, 16 vertices appears to be the upper size limit for closo deltahedral clusters.
A characteristic of the closo deltahedral boranes in which all vertices are group 13 or 14 atoms of the periodic table is the presence of an external hydrogen or halogen atom or an alkyl or aryl group bonded to each vertex atom. The size of these external groups must be small enough so that one such external group bonded to each vertex atom will fit around the deltahedral surface. Each vertex of the type TrR (Tr = B, Al, Ga, or In; R = hydrogen, halogen, alkyl, or aryl) is a donor of two skeletal electrons for skeletal bonding. Similarly, each vertex of the type TtR (Tt = C, Si, Ge, or Sn) is a donor of three skeletal electrons. The most stable n-vertex closo deltahedral structures have 2n + 2 skeletal electrons [5,6,7]. However, some exceptions with only 2n skeletal electrons are known experimentally, of which boron subhalides of the BnCln are among the simplest examples [8,9]. O’Neill and Wade have related the existence of stable n-vertex closo deltahedral clusters with only 2n skeletal electrons rather than the normally favored 2n + 2 skeletal electrons to the presence of non-degenerate frontier molecular orbitals in the 8- and 9-vertex closo deltahedra [10].
A topological model for the skeletal bonding in closo deltahedral boranes and related structures provides a basis for splitting the 2n + 2 skeletal electrons into 2n electrons for surface bonding leaving the remaining two electrons for an n-center core bond [11]. The surface bonding can formally be described as delocalized bonding based on canonical surface Hamiltonian circuit structures with n two-center two-electron bonds. The approximation of closo deltahedra to spheres suggests that the two electrons for the n-center core bond are effectively occupying the 1S orbital of a jellium sphere [12]. This interpretation is supported by the 2n + 8 skeletal electrons in the stable 14-vertex omnicapped cube structures (Figure 2) found in experimentally known hexacarbalanes of the types (AlMe)8(CCH2Ph)5(C≡CPh), [R4N+]2[(AlH)8(CR)6], and (AlNMe3)2(AlR)6(CR)6 [13]. If 2n of these skeletal electrons are allocated to surface bonding similar to the deltahedral boranes, then eight electrons remain for the 14-center core bond. These eight electrons are the correct number to fill the 1S and 1P orbitals of a jellium sphere. Interestingly, the Oh omnicapped cube deltahedron in these hexacarbalanes with six degree 4 carbon vertices and eight degree 6 aluminum vertices (Figure 2) is very different from the D6d bicapped hexagonal antiprism found in 14-vertex closo deltaboranes such as (µ-CH2)3C2B12H12 [14].
A major difference between experimentally known polyhedral clusters of boron and gallium is the size of the external atoms or groups bonded to the vertex atom. The boron clusters, notably the polyhedral boranes, have either single atoms, such as hydrogen or halogens, or small alkyl or aryl groups bonded to the boron vertices. Attaching such relatively small atoms or groups to each of the boron vertices in any of the closo deltahedra (Figure 1) does not create any significant steric strain between the external atoms or groups attached to adjacent boron vertices.
The situation is very different with gallium clusters, which are frequently synthesized by reactions of gallium(I) halides with lithium derivatives of the type LiR, in which R is a relatively large group, frequently a silyl group of the type SiR’3, where the R′ groups attached to the silicon atom can themselves form large groups such as trimethylsilyl [15,16,17,18]. Because of excessive steric strain between such large R groups bonded to adjacent gallium atoms, GanRn2− structures based on the closo deltahedra depicted in Figure 1 become no longer energetically feasible, except for the regular octahedron (Figure 1) with all degree 4 vertices. The greater surface curvature at each of the six degree 4 vertices of a regular octahedron has the effect of spreading rather large R groups far enough apart to reduce the steric strain in the octahedral dianions Ga6R62− (R = SiBuPh2 or SitBu3) with the favored 14 skeletal electrons (=2n+ 2 for n = 6) for a six-vertex closo deltahedron. A neutral Ga6R6 (R = SiMe(SiMe3)2) with only 12 skeletal electrons has also been synthesized and structurally characterized. However, clusters of more than six gallium atoms are found experimentally to adopt alternative structures in which steric interference between large external R groups are minimized by the presence of “bare” gallium atoms without bonds to any external groups. Such “bare” gallium atoms are “protected” by steric shielding from the large external R groups bonded to adjacent gallium atoms. Furthermore, since “bare” gallium atoms do not need to use one of their three valence electrons for a bond to an external R group, such gallium atoms can contribute all three of their valence electrons to the skeletal bonding. This leads to major differences between preferred structures for gallium clusters in the realm of experimentally accessible species relative to those in boron cluster chemistry, including, of course, the polyhedral boranes. This paper surveys the structures other than the closo deltahedra found in such gallium clusters, including interpretations of their chemical bonding. In addition, electron bookkeeping schemes incorporating a combination of bare gallium vertices contributing three skeletal electrons and RGa vertices (R = large external group) and contributing only two skeletal electrons are provided. Furthermore, larger molecular gallium clusters are discussed that are best considered as jellium spheres [12] with electron counts corresponding to filled molecular orbitals in a jellium sphere.

2. Polyhedral and Other Structures in Clusters of Six to Twelve Gallium Atoms

Gallium clusters based on simple closo deltahedra, with each gallium atom bearing a large external group, are limited to the octahedral dianions Ga6R62− (R = SiBuPh2, SitBu3) and the neutral Ga6R6 (R = SiMe(SiMe3)2), in which the bulky external silyl groups are spread out because of the relatively high local curvature of the degree 4 vertices of the central Ga6 octahedron [19,20]. 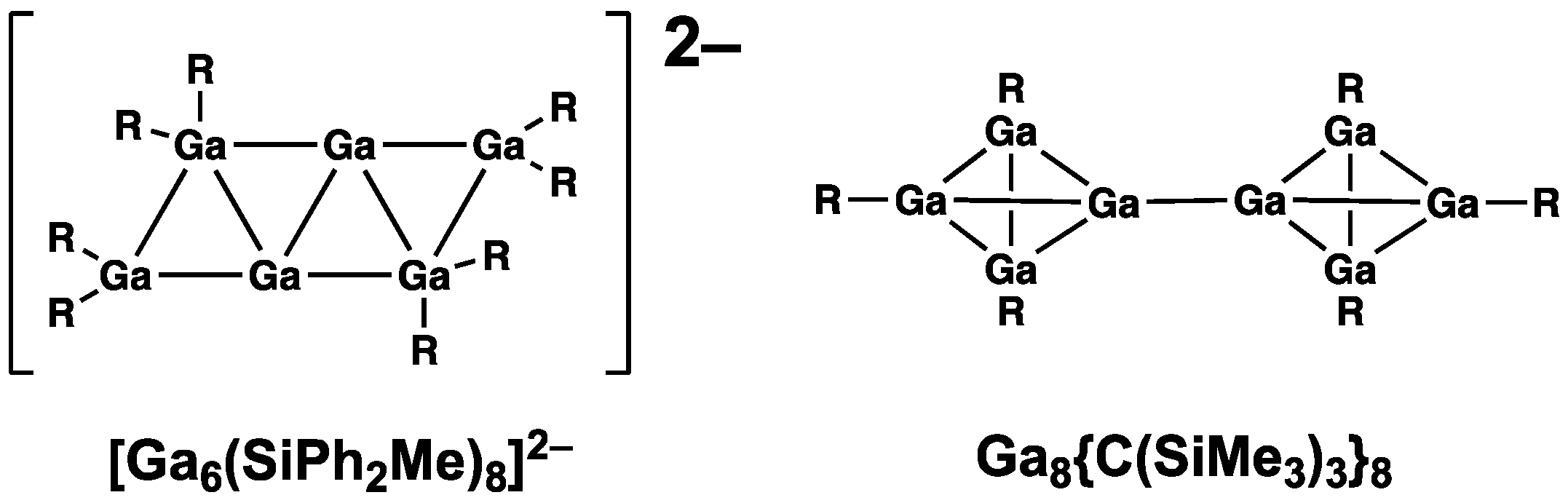In contrast to the octahedral structure of these Ga6R6 derivatives, the dianion Ga6R82− (R = SiPh2Me), with two additional large external groups, has a central planar framework consisting of four edge-sharing fused triangles with four tetracoordinate R2Ga− units bearing formal negative charges and two linear two-coordinate –Ga+– units bearing positive charges, leading to an overall dianion (Figure 3) [21].
The 8-vertex closo bisdiphenoid is found in the dianion Ga8R4I42− (R = SiMe(SiMe3)2), in which the external bulky silyl groups are attached to the four higher local curvature degree 4 vertices and the single iodine atoms are attached to the four lower local curvature degree 5 vertices [20]. The 9-vertex neutral Ga9tBu9 cluster also has a central closo deltahedron, namely the tricapped trigonal prism [22]. This corresponds to 18 skeletal electrons (=2n for n = 9). O’Neill and Wade have shown that the lack of degenerate frontier orbitals in the 8- and 9-vertex closo deltahedra leads to filled molecular orbitals and thus potentially favorable molecules having either 2n or 2n + 2 skeletal electrons [10].
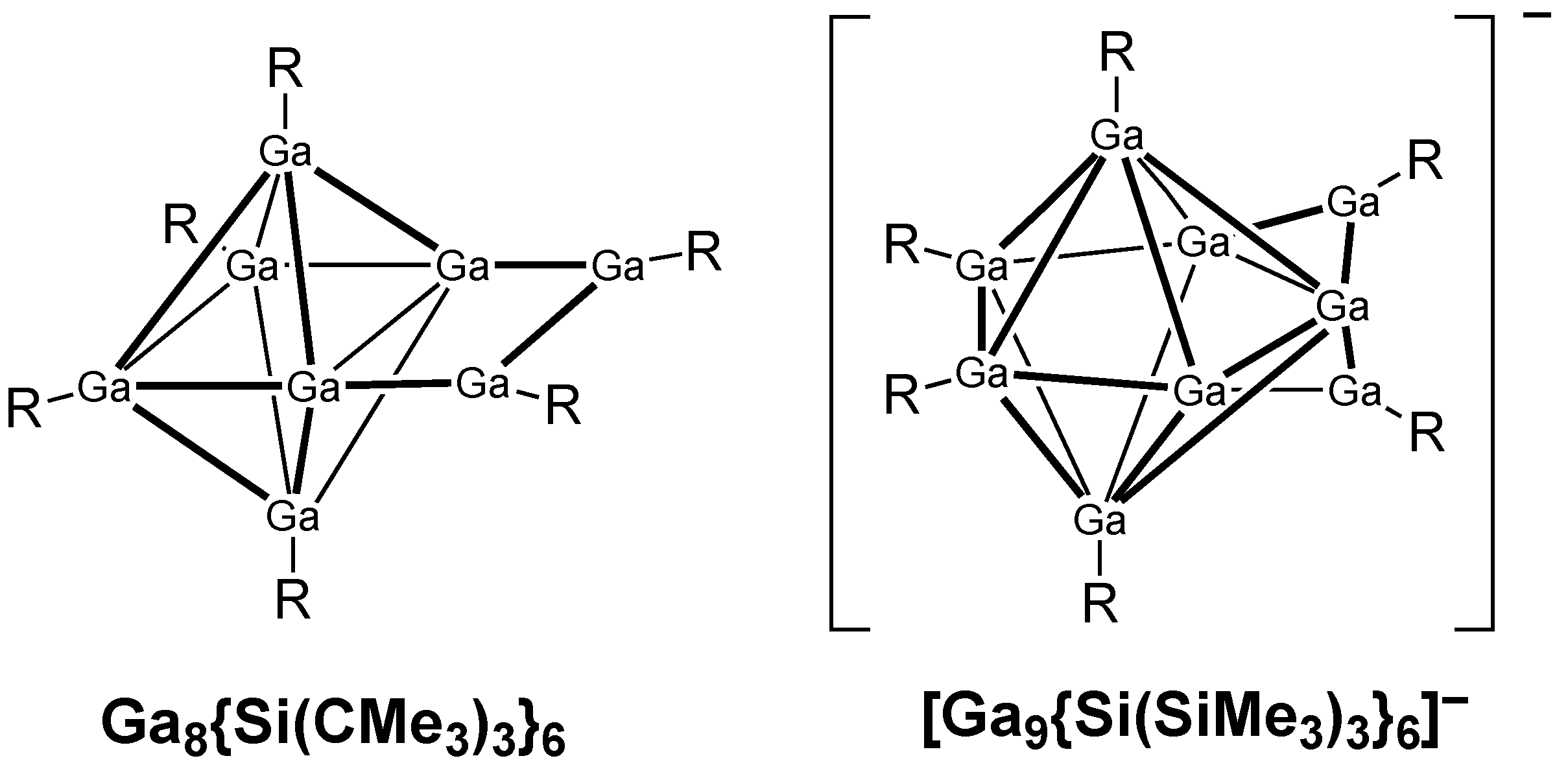
The structure of the neutral Ga8R6 (R = SitBu3) cluster with extremely bulky tri(t-butyl)silyl groups consists of a central Ga6 octahedron with four gallium atoms bonded to external R groups and the remaining two adjacent gallium atoms bridged by a RGa–GaR unit (Figure 4) [23]. It therefore more accurately can be considered to be a (µ-RGa–GaR)Ga6R4 system. Each of the six gallium atoms of the Ga6 octahedron can contribute two electrons to the skeletal bonding, whether or not they are bonded to an external R group or to one of the two external gallium atoms. The external gallium atoms do not contribute to the skeletal bonding, since the external bonding network uses all three of their valence electrons by forming a bond to the external R group, a bond to the other external gallium atom, and a bond to a gallium vertex atom of the Ga6 octahedron. Thus, this (µ-RGa-GaR)Ga6R4 structure is a 12-skeletal electron system (i.e., 2n for n =6 for the Ga6 octahedron). This can correspond to surface bonding without the multicenter core bond in the Ga6 octahedron subunit. This can relate to the deviation from sphericality of the Ga6 regular octahedron arising from the bulky RGa–GaR group bridging a pair of adjacent octahedron vertex atoms. A related Ga9R6− (R = Si(SiMe3)3) monoanion is known to have a structure consisting of a closo Ga7 deltahedron, namely the pentagonal bipyramid (Figure 1), with a Ga–Ga edge capped by an RGa–GaR unit and thus a [(µ-RGa–GaR)Ga7R4]− (Figure 4) [24]. Four of the seven pentagonal bipyramid gallium vertices bear external R groups and thus are each donors of two skeletal electrons, one gallium vertex is bare and thus is a donor of three skeletal electrons, and the remaining two gallium atoms bear the external RGa–GaR bridge and also each donate two skeletal electrons. A similar electron-bookkeeping analysis suggests that the Ga9R6− monoanion has 16 (=2n + 2 for n = 7) skeletal electrons, which is a favorable number to provide two electrons for the multicenter core bond, and 14 (=2n for n = 7) for the surface bonding in the central pentagonal bipyramid.
A clearly non-spherical structure is found in the neutral eight-vertex Ga8R6 (R = C(SiMe3)3) consisting of two Ga4 tetrahedra linked by a single Ga–Ga bond (Figure 3) [25]. The other six gallium atoms each bear a single R group. The chemical bonding in this bis(tetrahedral) Ga4–Ga4 framework consists of simple localized Ga–Ga single bonds similar to the bond connecting the two tetrahedra.
A two-dimensional planar external fluorenyl (C13H9 = Flu) group attached to a vertex gallium atom has a very different steric requirement than the large three-dimensional silyl and tert-alkyl groups in the clusters discussed above. Two neutral gallium clusters with external fluorenyl groups have been synthesized, namely the square antiprismatic Ga8Flu8 and the icosahedral Ga12Flu10 (Figure 5) [26]. A central square antiprism is effectively somewhat larger than a central bisdisphenoid because of its two square faces, and thus provides more surface area to accommodate the external fluorenyl groups. In addition, all of the vertices of a square antiprism are of degree 4 and thus have a higher local curvature than the four degree 5 vertices of the bisdisphenoid. The Ga8Flu8 cluster with each gallium vertex bonded to an external fluorenyl group is a 2n skeletal electron system, which, according to O’Neill and Wade [10], is as reasonable as 2n + 2 skeletal electrons for an 8-vertex cluster approximating a sphere. The larger 12-vertex cluster Ga12Flu10 has a central Ga12 icosahedron with two antipodally situated bare gallium vertices donating three skeletal electrons each, as well as ten FluGa vertices each donating two skeletal electrons. This makes Ga12Flu10 a 26-skeletal electron system isoelectronic with well-known very stable borane derivatives, including the dianion B12H122− and the neutral carboranes C2B10H12 [1,2,3].

3. Larger Spherical Gallium Clusters Approximated by Spherical Models

The smallest experimentally known approximately spherical gallium cluster with more than two core electrons is the 13-vertex cluster [Ga13R6]− (R = SitBu3) [27] with eight core electrons similar to hexacarbalane derivatives such as [R4N+]2[(AlH)8(CR)6] (Figure 2) [13]. The structure of [Ga13R6]− is derived from a hexacapped cube by removing one of the cube vertices with some distortion (Figure 6). The gallium vertices of the six caps of the original cube faces each bear an external SitBu3 group and are donors of two skeletal electrons each, whereas the seven remaining vertices of the underlying cube are bare gallium atoms and are donors of three skeletal electrons. The [Ga13R6]− is thus seen to be a 34-skeletal electron system corresponding to 2n + 8 for n = 13 (Table 1). Allocating 26 electrons to 13 two-electron two-center surface bonds, similar to the electron bookkeeping for deltahedral boranes, leaves 8 electrons for the core bonding, similar to the hexacarbalanes. These correspond to the filling of the 1S and 1P orbitals of a jellium sphere in a 1S21P6 configuration.
The Ga19 cluster anion [Ga@Ga18{C(SiMe3)3}6]− is known having a structure consisting of an outer 18-vertex Ga18 polyhedron with an interstitial gallium atom (Figure 6) [28]. The outer Ga18 polyhedron is clearly not a deltahedron, since it has no triangular faces at all. Instead, it has two somewhat non-planar hexagonal faces (at the top and bottom of Figure 6), as well as 12 tetragonal faces. However, the effective environment of the interstitial gallium atom (purple in Figure 6) is nearly spherical, as experimentally suggested by a sharp 71Ga NMR signal, which is otherwise rarely found in the 71Ga NMR of gallium clusters. The original report of the synthesis of this Ga19 cluster considered it to be a jellium 40-electron system arising from the valence electrons of the central [Ga@Ga12]− unit, but ignoring the additional 12 skeletal electrons contributed pairwise by the six RGa units. Since the six RGa units, as well as the 12 bare gallium atoms, are all vertices of the outer 18-vertex polyhedron, leaving their electron contributions out of the total electron count seems questionable. Including these additional 12 electrons from the six RGa units in the [Ga19R6]− jellium sphere gives a 52-electron system corresponding to filled [1S21P61D102S21F142P6]2D103S2 molecular orbitals. The portion in brackets corresponds to the 40 electrons of the Ga@Ga12 unit originally suggested by the previous authors based on the facile elimination of the six RGa units from [Ga@Ga18{C(SiMe3)3}6]− observed in gas phase collision-induced dissociation experiments.
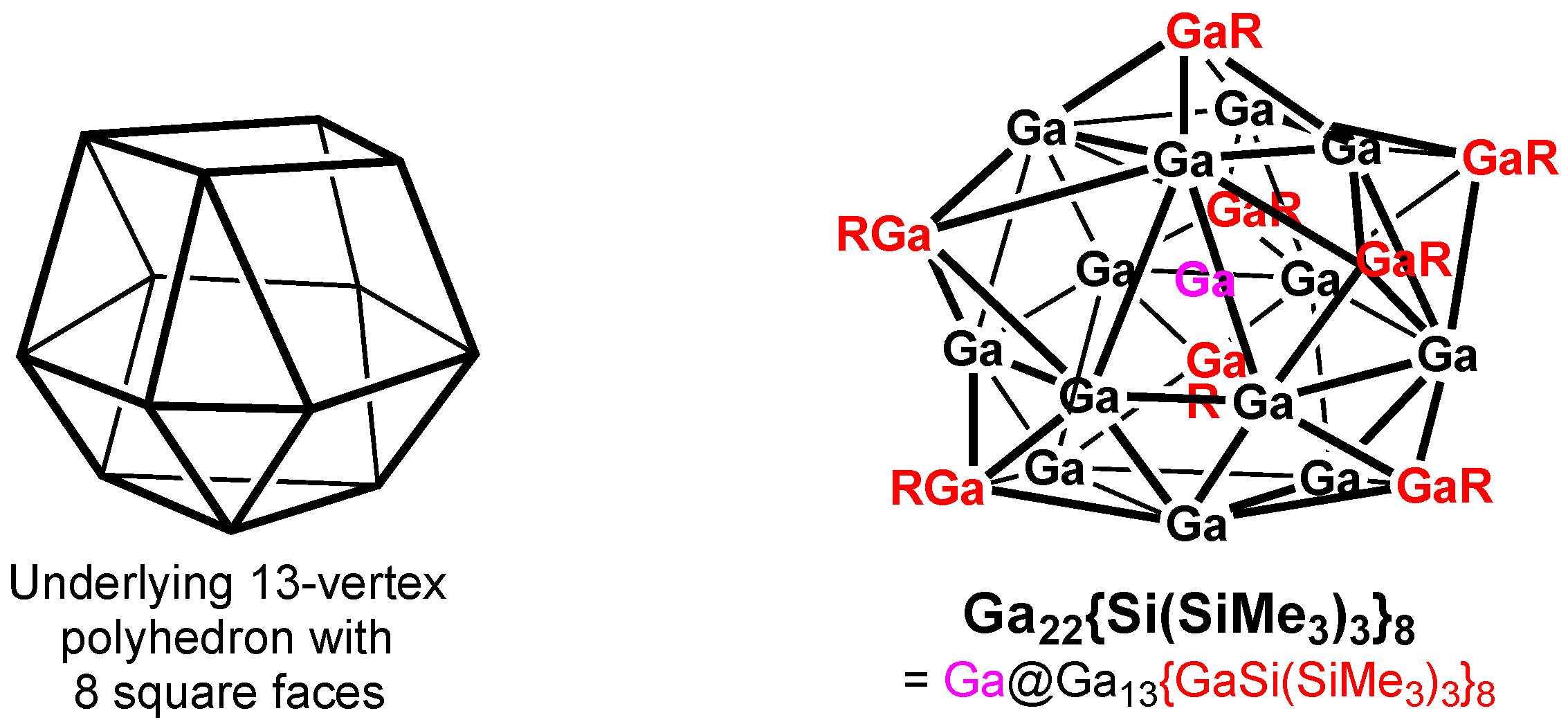
Two types of clusters with 22 gallium atoms are known to correspond to jellium spheres, with 58 electrons corresponding to filled [1S21P61D102S21F142P6]1G18 orbitals. The first such cluster, Ga22{E(SiMe3)3]8, (E = Si [29], Ge [30]), has a Ga@Ga13{GaE(SiMe3)3}8 structure based on a centered 13-vertex polyhedron with 8 tetragonal faces (Figure 7). Each of these tetragonal faces is capped by a bulky GaSi(SiMe3)3 group. The 13 bare gallium vertices in the Ga13 polyhedron and the single interstitial gallium atom each contribute all of their three valence electrons, leading to 3 × 14 = 42 electrons. The remaining 16 electrons for the 58-electron jellium sphere come from the eight capping gallium atoms in the GaSi(SiMe3)3 units, with each such unit contributing an electron pair.
The other type of Ga23 cluster with the favored 58-electrons for a jellium sphere uses slightly smaller GaN(SiMe3)2 capping units so that as many as 11 of them can fit around a centered 11-vertex polyhedron. This leads to a very unsymmetrical Ga@Ga11{GaN(SiMe3)2}11 structure [31]. The central 11-vertex polyhedron in this structure can roughly be described as deriving from a cube by removing one vertex and inserting the remaining four vertices into the resulting hole in an unsymmetrical manner. Eight of the GaN(SiMe3)2 capping units join in pairs to cap the faces of the incomplete cube as binuclear Ga2{N(SiMe3)2}2 units, whereas the other three GaN(SiMe3)2 units cap individually.

4. The Underlying “Hidden” Distorted Icosahedron in a Rather Unsymmetrical Non-Spherical 18-Vertex Gallium Cluster Structure with Surface Concavities

One of the products isolated from the reaction of GaBr with NaSitBu3 is the 18-vertex cluster Ga18(SitBu3)8 in which the gallium atoms form an 18-vertex polyhedron that is far from spherical since its surface has concavities (indentations) (Figure 8) [32]. In this Ga18(SitBu3)8 structure, there are a total of 46 electrons for cluster bonding, with 16 electrons arising from the 8 tBu3SiGa vertices and 30 electrons from the 10 bare gallium vertices. This is not a favorable number of electrons for a spherical aromatic structure, which is not surprising in view of the clearly non-spherical Ga18(SitBu3)8 structure.
The partially concave unsymmetrical Ga18 polyhedron in Ga18(SitBu3)8 has 18 triangular faces and 7 tetragonal faces, the latter of which are non-planar (Figure 8) [32]. The numbers of vertices having degrees 3, 4, 5, 6, and 7 are 4, 7, 1, 4, and 2 reflecting its low symmetry. However, removal of six of the eight tBu3SiGa vertices with central tetrahedral gallium atoms as monoanions leaves a central [Ga12(SitBu3)2]6+ formally hexacationic icosahedral core. At that point the Wade–Mingos rules [5,6,7] can be applied along with the topological aspects of the graph-theoretical model [11]. Such an analysis interprets the central [Ga12(SitBu3)2]6+ subunit of Ga18(SitBu3)8 as a 28 skeletal electron system (Table 2). This corresponds to 2n + 4 skeletal electrons for a 12-vertex deltahedral structure, such as an icosahedron with 24 electrons used for 12 formally two-center two-electron bonds in a surface canonical structure. This leaves four skeletal electrons for two core bonds. Because of the distortion of the central icosahedron from sphericality, it is reasonable for the core bonding to split into two six-center two-electron core bonds in contrast to the single twelve-center two-electron core bond in symmetrical icosahedral systems, such as B12H122− and its derivatives, with twenty-six rather than twenty-eight skeletal electrons.

5. Gallium Clusters with Fused Polyhedral Structures

In some experimentally known gallium clusters, the volume requirements of large external groups can be accommodated by structures consisting of fused polyhedra in which the gallium atoms shared by two polyhedra are bare gallium atoms. Two examples of 10-vertex gallium clusters of the type Ga10R6 are known to have structures consisting of fused octahedra sharing two vertices (Figure 9). The neutral species Ga10{Si(SiMe3)3}6 is a 24 skeletal electron system corresponding to 2n + 4 skeletal electrons for an n = 10 (Table 3) [27]. Allocating 2n = 20 skeletal electrons for the usual surface bonding in such clusters leaves four electrons for two multicenter core bonds, one in the center of each octahedron. A similar electron bookkeeping scheme for the anion [Ga10(SitBu3)6]− [27] leads to a 25 skeletal electron system. The chemical bonding topology can then be similar to Ga10{Si(SiMe3)3}6 with an extra delocalized electron. This can be considered to be a three-dimensional analog of the well-known naphthalene radical anion.
The neutral 10-vertex cluster Ga10(SitBu3)6 has a related fused polyhedral structure, but has a 7-vertex pentagonal bipyramid sharing three vertices with a fused 6-vertex polyhedron (Figure 9) [33]. The electron bookkeeping for this cluster can be similar to that for Ga10{Si(SiMe3)3}6 (Table 3) to provide electron pairs for multicenter core bonding in both the pentagonal bipyramid cavity and the 6-vertex polyhedron cavity.
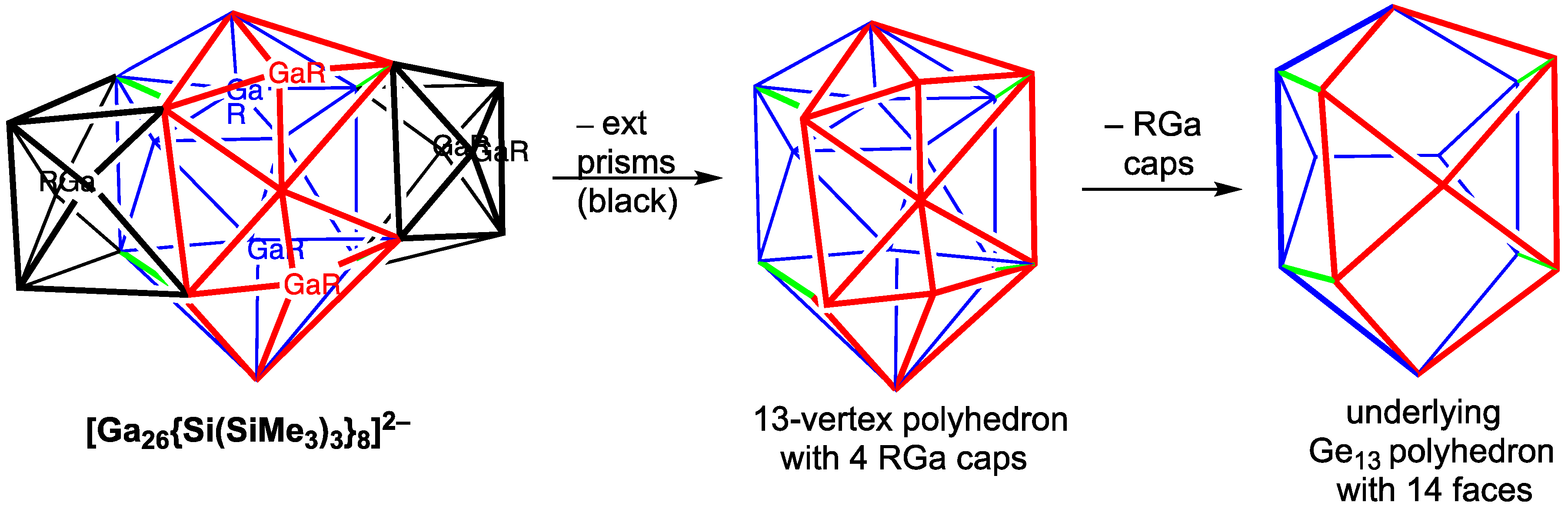
The larger cluster dianion [Ga26{Si(SiMe3)3}8]2− superficially looks like a centered 17-vertex Ga@Ga17 polyhedron having 26 triangular faces and 2 rectangular faces, in which a bicapped trigonal prism is fused to each of the rectangular faces and thus does not appear to be very spherical (Figure 10) [34]. However, the total electron count of 72 (Table 4) fits better into the consideration of [Ga26{Si(SiMe3)3}8]2− as a spherical aromatic system with 2n2 = 72 for n = 6 electrons [35]. The [Ga26{Si(SiMe3)3}8]2− structure appears more nearly spherical when its 26-vertex structure is viewed as a fusion of four 9-vertex deltahedra. In such a quadruple fusion, the interstitial gallium atom is shared between the two 9-vertex polyhedra that do not include the gallium atoms capping the two rectangular faces of the underlying 17-vertex polyhedron.

6. Conclusions

The external groups R in the experimentally known polyhedral boranes [BnRn]z− are relatively small groups such as hydrogen, halogens, or simple fairly small alkyl and aryl groups such as methyl and phenyl. The classical deltahedral structures in which each boron vertex bears such a relatively small external R group do not present any steric problems in fitting such R groups on adjacent boron atoms onto the deltahedral surface. However, presently known synthetic methods for the preparation of polyhedral gallium clusters typically use a reaction of a gallium(I) halide or similar derivative with an LiR derivative, with the R group being very sterically demanding such as tBu3Si, (Me3Si)3Si, (Me3Si)3C, (Me3Si92N), or fluorenyl. The available experimental data clearly suggest that it is impossible to fit enough of these large R groups on the surface of a closo deltahedron (Figure 1) so that each gallium vertex bears an external R group unless all of the gallium vertices are of degree 4. Such degree 4 gallium vertices have a larger local positive curvature than gallium vertices of degrees 5 or 6. Thus, octahedral clusters [Ga6R6]z (z = 0, R = Me(Me3Si)2Si; z = −2, R = tBu3Si), in which all six vertices are degree 4 vertices with high local curvature, have been synthesized and structurally characterized. The nine-vertex gallium cluster Ga9tBu9 also has the closo tricapped trigonal prismatic structure despite the six lower local curvature degree 5 vertices. However, the external nine t-butyl groups in Ga9tBu9 are not as sterically demanding as the larger external tBu3Si, (Me3Si)3Si, (Me3Si)3C, (Me3Si)2N, and fluorenyl groups found in other structures discussed in this paper. The Ga8 polyhedron in the dianion Ga8R4I42− (R = SiMe(SiMe3)2) is the closo 8-vertex deltahedron, namely the bisdisphenoid. However, in this structure, only four of the eight external groups are the bulky silyl groups; the four remaining external groups are the much smaller iodine atoms.
The two experimentally known structures with external fluorenyl C13H9 (=Flu) groups are particularly instructive. The 8-vertex Ga8Flu8 cluster has an external fluorenyl group bonded to each gallium vertex. However, the Ga8 polyhedron is not the closo bisdisphenoid with four degree 4 and four degree 5 vertices (Figure 1), but instead the square antiprism with all eight vertices of degree 4. The resulting increased local curvature over the entire polyhedral surface, because of the presence of only degree 4 vertices of Ga8Flu8, reduces the steric strain between the eight fluorenyl groups on the polyhedral surface. The larger 12-vertex Ga12Flu10 structure has a central icosahedron with all degree 5 vertices similar to the icosahedron in the numerous very stable boranes B12H122−, the isoelectronic carboranes CB11H12− and C2B10H12, and their derivatives. However, in the Ga12Flu10 structure, 2 of the 12 gallium atoms are bare so that only 10 rather than 12 external fluorenyl .groups need to be distributed onto the icosahedral surface.
The alternatives to deltahedral structures for gallium clusters with extremely bulky external groups appear to be either larger clusters or clusters considering of fused polyhedra with bare gallium atoms at the polyhedral junctions. Many of the large clusters have numbers of available gallium valence electrons corresponding to closed shells for spherical aromatic systems based on the jellium model [12]. The structure of the largest cluster discussed here, namely [Ga26{Si(SiMe3)3}8]2−, consists of an interlocking system of four 9-vertex polyhedral with a total of 72 available cluster electrons corresponding to 2n2 = 72 for n = 6 for a spherical aromatic system, as discussed by Hirsch [35]. Smaller but still large clusters exhibiting favorable numbers of electrons for closed-shell jellium structures include 23-vertex Ga@Ga13{GaE{SiMe3)3}8 (E = Si or Ge) and Ga@Ga11{GaN(SiMe3)2}11 clusters with 58 available cluster electrons corresponding to a closed-shell [1S21P61D102S21F142P6]1G18 system. A smaller 19-vertex cluster [Ga@Ga18{C(SiMe3)3}6]− has 52 available cluster electrons corresponding to a closed-shell [1S21P61D102S21F142P6]2D103S2 system.
Some of the larger gallium cluster structures not corresponding to simple closo deltahedra can be interpreted as a fusion of two such deltahedra with electron counts that can be rationalized by the Wade–Mingos rules. In such fusions of pairs of deltahedra, the vertices common to both deltahedra are bare gallium atoms so that the bulky external groups can be confined to the vertices that are unique to a single deltahedron. This provides a way of spreading out the bulky external groups. The clearest such example is the 10-vertex cluster Ga10{Si(SiMe3)3}6 with 24 (=2n + 4 for n = 10) Wadean skeletal electrons corresponding to surface bonding over the 10-vertices, leaving 4 electrons for a multicenter core bond inside each octahedral cavity. A more obscure example is the 18-vertex cluster Ga18(SitBu3)8, in which removal of six strategically placed tBu3SiGa vertices reveals a distorted Ga12(SitBu3)2 icosahedron. Electron bookkeeping suggests that 28 (=2n + 4 for n = 12) electrons are available for the skeletal bonding in this icosahedron. As in the smaller 10-vertex system, these 28 available skeletal electrons are sufficient for surface bonding over all 12 Ga12 icosahedron vertices and two multicenter core bonds inside the icosahedron.

Funding

This research received no external funding.

Data Availability Statement

Data sharing is not applicable.

Conflicts of Interest

The author has no conflicts of interest to declare.

References

  1. Muetterties, E.L. (Ed.) Boron Hydride Chemistry; Academic Press: New York, NY, USA, 1975. [Google Scholar]
  2. Grimes, R.N. Carboranes, 2nd ed.; Academic Press: New York, NY, USA, 2011. [Google Scholar]
  3. Williams, R.E. The polyborane, carborane, carbocation continuum—Architectural patterns. Chem. Rev. 1992, 92, 177–207. [Google Scholar] [CrossRef]
  4. Frank, F.C.; Kasper, J.S. Complex alloy structures regarded as sphere packings. 1. Definitions and basic principles. Acta Cryst. 1958, 11, 184–190. [Google Scholar] [CrossRef]
  5. Wade, K. The structural significance of the number of skeletal bonding electron-pairs in carboranes, the higher boranes and borane anions, and various transition-metal carbonyl cluster compounds. J. Chem. Soc. D Chem. Commun. 1971, 15, 792–793. [Google Scholar] [CrossRef]
  6. Mingos, D.M.P. A general theory for cluster and ring compounds of the main group and transition elements. Nat. Phys. Sci. 1972, 236, 99–102. [Google Scholar] [CrossRef]
  7. Mingos, D.M.P. Polyhedral skeletal electron pair approach. Acc. Chem. Res. 1984, 17, 311–319. [Google Scholar] [CrossRef]
  8. Morrison, J.A. Chemistry of the polyhedral boron halides and the diboron tetrahalides. Chem. Rev. 1991, 91, 35–48. [Google Scholar] [CrossRef]
  9. Corminboeuf, C.; Wodrich, M.W.; King, R.B.; Schleyer, P.V.R. Effects of halogen substitution on the properties of eight- and nine-vertex closo-boranes. Dalton Trans. 2008, 13, 1745–1751. [Google Scholar] [CrossRef]
  10. O’Neill, M.E.; Wade, K. Closo clusters with unusual electron numbers: The significance of frontier orbital degeneracies and bonding characteristics. J. Mol. Struct. 1983, 103, 259–268. [Google Scholar] [CrossRef]
  11. King, R.B.; Rouvray, D.H. A graph-theoretical interpretation of the bonding topology in polyhedral boranes, carboranes, and metal clusters. J. Am. Chem. Soc. 1977, 99, 7834–7840. [Google Scholar] [CrossRef]
  12. De Heer, W.A. The physics of simple metal clusters: Experimental aspects and simple models. Rev. Mod. Phys. 1993, 65, 611–676. [Google Scholar] [CrossRef]
  13. Stasch, A.; Roesky, H.W.; Schleyer, P.V.R.; Magull, J. A threefold AlH2-coordinated carbon atom as part of the first carbalanate. Angew. Chem. Int. Ed. 2003, 42, 5507–5509. [Google Scholar] [CrossRef]
  14. Deng, L.; Chan, H.-S.; Xie, Z. Synthesis, reactivity, and structural characterization of a 14-vertex carborane. Angew. Chem. Int. Ed. Engl. 2005, 44, 2128–2131. [Google Scholar] [CrossRef]
  15. Schnepf, A.; Schnöckel, H. Metalloid aluminum and gallium clusters: Element modifications on the molecular scale? Angew. Chem. Int. Ed. 2002, 41, 3532–3552. [Google Scholar] [CrossRef]
  16. Schnöckel, H. Metalloid Al- and Ga-clusters: A novel dimension in organometallic chemistry linking the molecular and solid-state areas? Dalton Trans. 2005, 19, 3131–3136. [Google Scholar] [CrossRef]
  17. Schnöckel, H. Formation, structure, and bonding of metalloid Al and Ga clusters. A challenge for chemical efforts in nanosciences. Dalton Trans. 2008, 33, 4344–4362. [Google Scholar] [CrossRef]
  18. Schnöckel, H. Structures and properties of metalloid Al and Ga clusters open our eyes to the diversity and complexity of fundamental chemical and physical processes during formation and dissolution of metals. Chem. Rev. 2010, 110, 4125–4163. [Google Scholar] [CrossRef] [PubMed]
  19. Linti, G.; Çoban, S.; Dutta, D. The hexagallane [Ga6{SiMe(SiMe3)2}6] and the closo-hexagallanate [Ga6{Si(CMe3)3}4(CH2C6H5)2]2−—The transition to an unusual precloso-cluster. Z. Anorg. Allg. Chem. 2004, 630, 319–323. [Google Scholar] [CrossRef]
  20. Gast, M.; Ejilli, B.; Wadepohl, H.; Linti, G. Synthesis and structures of polyhedral hexa- and octagallium cluster compounds. Eur. J. Inorg. Chem. 2019, 2019, 2964–2971. [Google Scholar] [CrossRef]
  21. Donchev, A.; Schnepf, A.; Baum, E.; Stößer, G.; Schnöckel, H.Z. [Ga6R8]2− (R=SiPh2Me): Eine metalloide Clusterverbindung mit einem unerwarteten Ga6-Gerüst. Allg. Chem. 2002, 628, 157–161. [Google Scholar] [CrossRef]
  22. Uhl, W.; Cuypers, L.; Harms, K.; Kaim, W.; Wagner, M.; Winter, R.; Koch, R.; Saak, W. Ga9(CMe3)9, an important new building block in the structural chemistry of the alkylelement(I) compounds EnRn(E = B–In). Angew. Chem. Int. Ed. 2001, 40, 566–568. [Google Scholar] [CrossRef]
  23. Wiberg, N.; Blank, T.; Nöth, H.; Suter, M.; Warchhold, M. Octagallane (tBu3Si)6Ga8 and its reduction to (tBu3Si)3Ga82−—On the existence of isomeric gallium clusters. Eur. J. Inorg. Chem. 2002, 4, 929–934. [Google Scholar] [CrossRef]
  24. Köstler, W.; Linti, G. Synthesis and structure of a tetragallane [R4Ga4I3]− and a polyhedral nonagallane [R6Ga9]−. Angew. Chem. Int. Ed. 1997, 36, 2644–2646. [Google Scholar] [CrossRef]
  25. Schnepf, A.; Köppe, R.; Schnöckel, H. A Ga8R6 cluster as an ideal model for a metal-metal bond? Angew. Chem. Int. Ed. 2001, 40, 1241–1243. [Google Scholar] [CrossRef]
  26. Schnepf, A.; Stößer, G.; Schnöckel, H. The first molecular square antiprismatic Ga8 cluster exhibiting a closo structure. Z. anorg. Allg. Chem. 2000, 626, 1676–1680. [Google Scholar] [CrossRef]
  27. Kehrwald, M.; Köstler, W.; Rodig, A.; Linti, G.; Blank, T.; Wiberg, N. Ga10[Si(SiMe3)3]6, [Ga19(SitBu3)6]−, and [Ga13(SitBu3)6]−—Syntheses and structural characterization of novel gallium cluster compounds. Organometallics 2001, 20, 860–867. [Google Scholar] [CrossRef]
  28. Schnepf, A.; Stößer, G.; Schnöckel, H. Synthesis, structure, and bonding of a molecular metalloid Ga19 cluster anion. J. Am. Chem. Soc. 2000, 122, 9178–9181. [Google Scholar] [CrossRef]
  29. Schnepf, A.; Weckert, E.; Linti, G.; Schnöckel, H. Ga22[Si(SiMe3)3]8: The largest atom-centered neutral main group metal cluster. Angew. Chem. Int. Ed. 1999, 38, 3381–3383. [Google Scholar] [CrossRef]
  30. Linti, G.; Rodig, A. Facile synthesis and crystal structure of a Ga22R8 cluster. Chem. Commun. 2000, 2, 127–128. [Google Scholar] [CrossRef]
  31. Hartig, J.; Stößer, A.; Hauser, P.; Schnöckel, H. A metalloid [Ga23{N(SiMe3)2}11] cluster: The jellium model put to test. Angew. Chem. Int. Ed. 2007, 46, 1658–1662. [Google Scholar] [CrossRef]
  32. Donchev, A.; Schnepf, A.; Stößer, G.; Baum, E.; Schnöckel, H.; Blank, T.; Wiberg, N. [Ga18(SitBu3)8] and [Ga22(SitBu3)8]—Syntheses and structural characterization of novel gallium cluster compounds. Chem. Eur. J. 2001, 7, 3348–3353. [Google Scholar] [CrossRef]
  33. Linti, G.; Seifert, A. A decagallane(6) cluster Ga10[Si(CMe3)3]6 with an unprecedented structure. Dalton Trans. 2008, 28, 3688–3693. [Google Scholar] [CrossRef]
  34. Rodig, A.; Linti, G. Synthesis and structure of an anionic Ga26R8 cluster with a metalloid core. Angew. Chem. Int. Ed. 2000, 39, 2952–2954. [Google Scholar] [CrossRef]
  35. Hirsch, A.; Chen, Z.; Jiao, H. Spherical aromaticity in Ih symmetrical fullerenes: The 2(N+1)2 rule. Angew. Chem. Int. Ed. 2000, 39, 3915–3917. [Google Scholar] [CrossRef]
Inorganics 12 00326 g001
Figure 1. The closo deltahedra with degree 4, 5, and 6 vertices in red, black, and green, respectively.
Figure 1. The closo deltahedra with degree 4, 5, and 6 vertices in red, black, and green, respectively.
Inorganics 12 00326 g001
Inorganics 12 00326 g002
Figure 2. The omnicapped cube found in hexacarbalane structures. In Figure 2 and Figure 6, based on omnicapped cube structures, the underlying cube vertices are in green and those of the capping vertices are in red.
Figure 2. The omnicapped cube found in hexacarbalane structures. In Figure 2 and Figure 6, based on omnicapped cube structures, the underlying cube vertices are in green and those of the capping vertices are in red.
Inorganics 12 00326 g002
Inorganics 12 00326 g003
Figure 3. Examples of clearly non-spherical gallium cluster structures.
Figure 3. Examples of clearly non-spherical gallium cluster structures.
Inorganics 12 00326 g003
Inorganics 12 00326 g004
Figure 4. Gallium clusters having central closo deltahedra with external RGa units.
Figure 4. Gallium clusters having central closo deltahedra with external RGa units.
Inorganics 12 00326 g004
Inorganics 12 00326 g005
Figure 5. Experimentally known gallium clusters with external fluorenyl groups.
Figure 5. Experimentally known gallium clusters with external fluorenyl groups.
Inorganics 12 00326 g005
Inorganics 12 00326 g006
Figure 6. The structures of the [Ga13(SitBu3)6]− and [Ga@Ga18{C(SiMe3)3}6]− cluster anions, with the interstitial gallium atom highlighted in purple.
Figure 6. The structures of the [Ga13(SitBu3)6]− and [Ga@Ga18{C(SiMe3)3}6]− cluster anions, with the interstitial gallium atom highlighted in purple.
Inorganics 12 00326 g006
Inorganics 12 00326 g007
Figure 7. The structure of the Ga22{Si(SiMe3)3}8 cluster and that of the underlying centered 13-vertex polyhedron with 8 tetragonal faces.
Figure 7. The structure of the Ga22{Si(SiMe3)3}8 cluster and that of the underlying centered 13-vertex polyhedron with 8 tetragonal faces.
Inorganics 12 00326 g007
Inorganics 12 00326 g008
Figure 8. The Ga18(SitBu3)8 polyhedron (R = tBu3Si) and its conversion to a Ga12(SitBu3)2 distorted icosahedron by removing six of the tBu3SiGa vertices and associated edges indicated in red. All of the polyhedral vertices contain gallium atoms.
Figure 8. The Ga18(SitBu3)8 polyhedron (R = tBu3Si) and its conversion to a Ga12(SitBu3)2 distorted icosahedron by removing six of the tBu3SiGa vertices and associated edges indicated in red. All of the polyhedral vertices contain gallium atoms.
Inorganics 12 00326 g008
Inorganics 12 00326 g009
Figure 9. Experimentally known 10-vertex gallium clusters having structures with two fused polyhedra, with the vertices unique to the pentagonal bipyramid or one of the octahedra depicted in red and those unique to the other octahedron depicted in black. Vertices common to both polyhedra are indicated in green.
Figure 9. Experimentally known 10-vertex gallium clusters having structures with two fused polyhedra, with the vertices unique to the pentagonal bipyramid or one of the octahedra depicted in red and those unique to the other octahedron depicted in black. Vertices common to both polyhedra are indicated in green.
Inorganics 12 00326 g009
Inorganics 12 00326 g010
Figure 10. Dissection of the [Ga26{Si(SiMe3)3}8]2− structure leading to a centered Ga@Ga13 polyhedron with 14 faces. For clarity, only the gallium atoms bearing external groups are shown in the figure of the full cluster polyhedron.
Figure 10. Dissection of the [Ga26{Si(SiMe3)3}8]2− structure leading to a centered Ga@Ga13 polyhedron with 14 faces. For clarity, only the gallium atoms bearing external groups are shown in the figure of the full cluster polyhedron.
Inorganics 12 00326 g010
Table 1. Electron bookkeeping for the 13-vertex system [Ga13(SitBu3)6]−.
Table 1. Electron bookkeeping for the 13-vertex system [Ga13(SitBu3)6]−.
6 RGa caps: 6 × 2 =12 electrons
7 bare Ga cube vertices: 7 × 3 =21 electrons
−1 charge1 electron
Total number of electrons34 electrons
Table 2. Electron bookkeeping for the 12-vertex [Ga12(SitBu3)2]6+ formal icosahedral subunit in the Ga18(SitBu3)8 structure.
Table 2. Electron bookkeeping for the 12-vertex [Ga12(SitBu3)2]6+ formal icosahedral subunit in the Ga18(SitBu3)8 structure.
2 RGa caps: 2 × 2 =4 electrons
10 bare Ga cube vertices: 10 × 3 =30 electrons
+6 charge−6 electrons
Total number of electrons28 electrons
Table 3. Electron bookkeeping for the 10-vertex cluster Ga10{Si(SiMe3)3}6.
Table 3. Electron bookkeeping for the 10-vertex cluster Ga10{Si(SiMe3)3}6.
6 RGa vertices: 6 × 2 =12 electrons
4 bare Ga vertices: 4 × 3 =12 electrons
Total number of electrons24 electrons
Table 4. Electron bookkeeping for the 26-vertex system [Ga26{Si(SiMe3)3}8]2−.
Table 4. Electron bookkeeping for the 26-vertex system [Ga26{Si(SiMe3)3}8]2−.
8 RGa caps: 8 × 2 =16 electrons
17 bare Ga vertices: 17 × 3 =51 electrons
Interstitial Ga atom3 electrons
−2 charge2 electrons
Total number of electrons72 electrons
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

King, R.B. Comparison of Gallium Cluster Polyhedra with Those of the Most Spherical Deltahedra: Effects of Bulky External Groups and Local Surface Curvature. Inorganics 2024, 12, 326. https://doi.org/10.3390/inorganics12120326

AMA Style

King RB. Comparison of Gallium Cluster Polyhedra with Those of the Most Spherical Deltahedra: Effects of Bulky External Groups and Local Surface Curvature. Inorganics. 2024; 12(12):326. https://doi.org/10.3390/inorganics12120326

Chicago/Turabian Style

King, R. Bruce. 2024. "Comparison of Gallium Cluster Polyhedra with Those of the Most Spherical Deltahedra: Effects of Bulky External Groups and Local Surface Curvature" Inorganics 12, no. 12: 326. https://doi.org/10.3390/inorganics12120326

APA Style

King, R. B. (2024). Comparison of Gallium Cluster Polyhedra with Those of the Most Spherical Deltahedra: Effects of Bulky External Groups and Local Surface Curvature. Inorganics, 12(12), 326. https://doi.org/10.3390/inorganics12120326

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop