A Structure and Magnetism Study of {MnII3MnIVLnIII3} Coordination Complexes with Ln = Dy, Yb
Abstract
1. Introduction
2. Results and Discussion
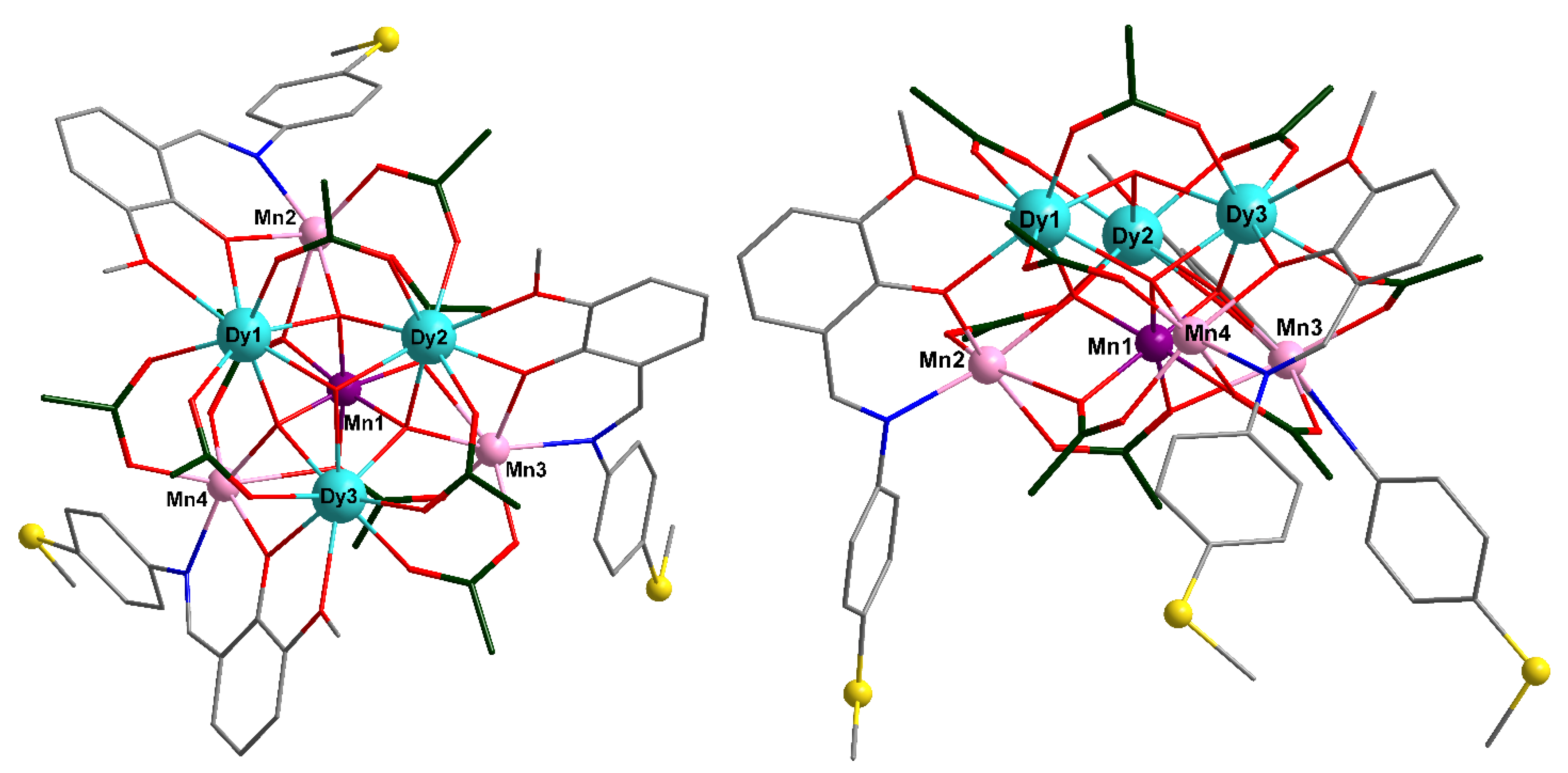
2.1. X-Ray Crystal Structure
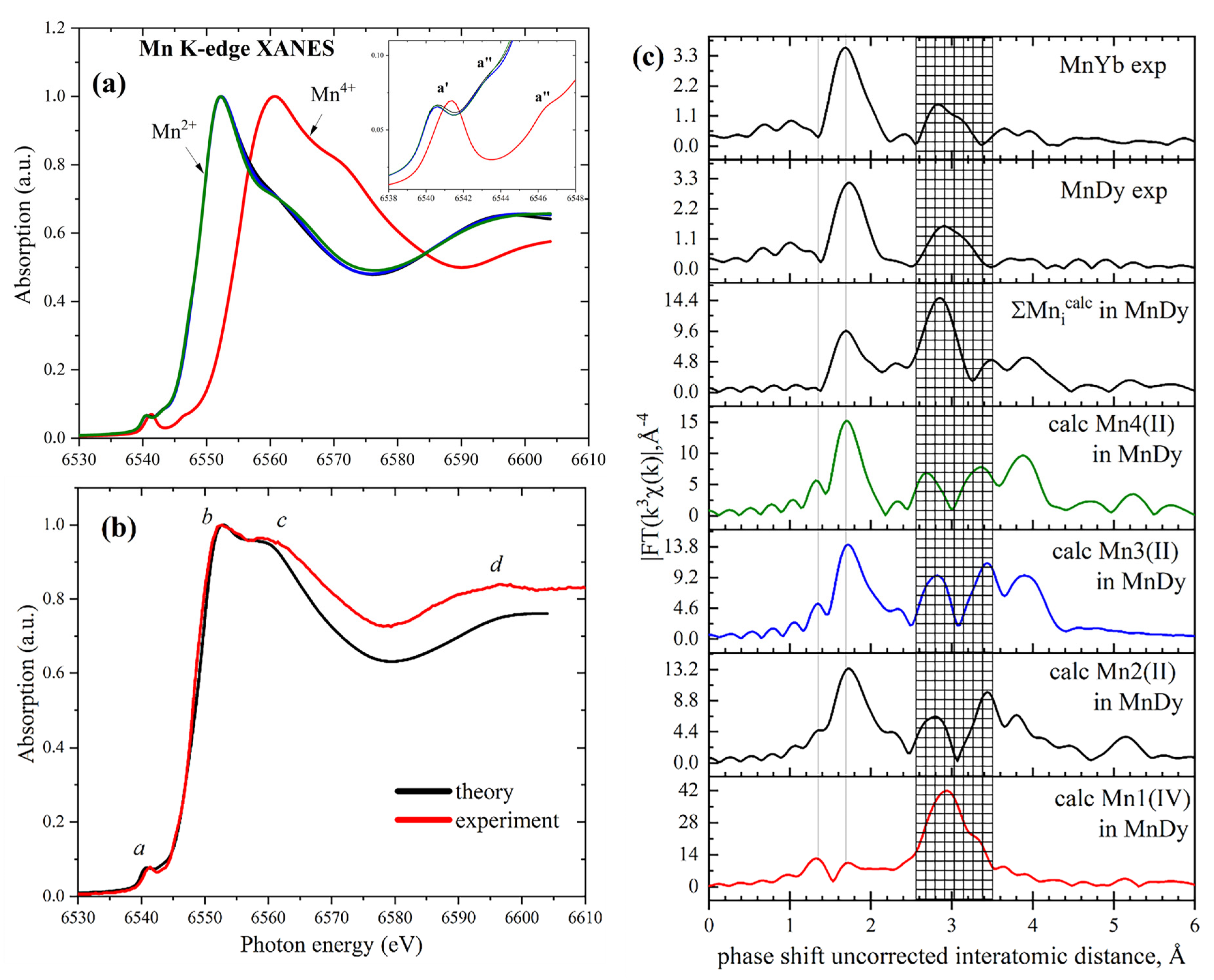
2.2. Mn K-Edge XAS
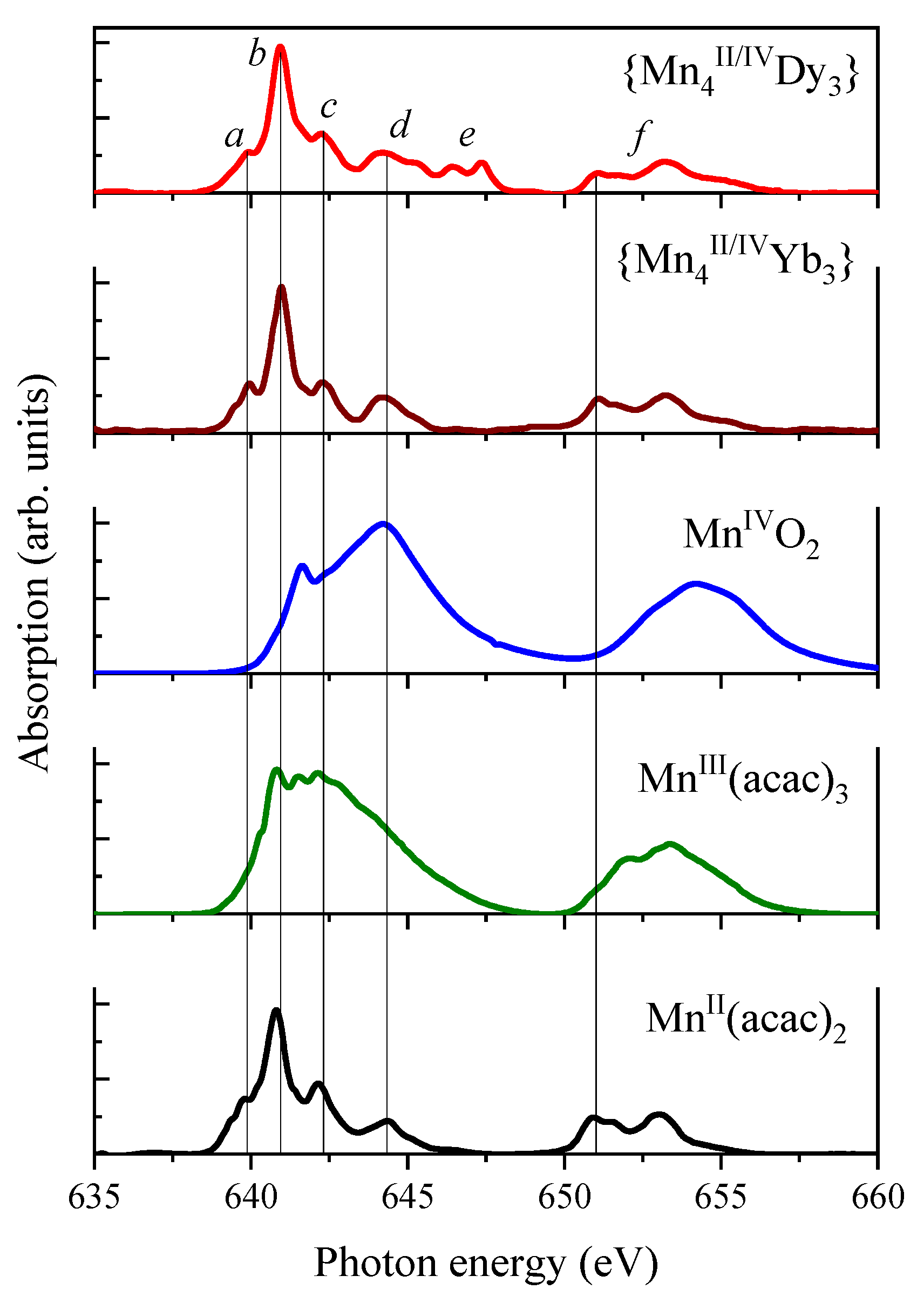
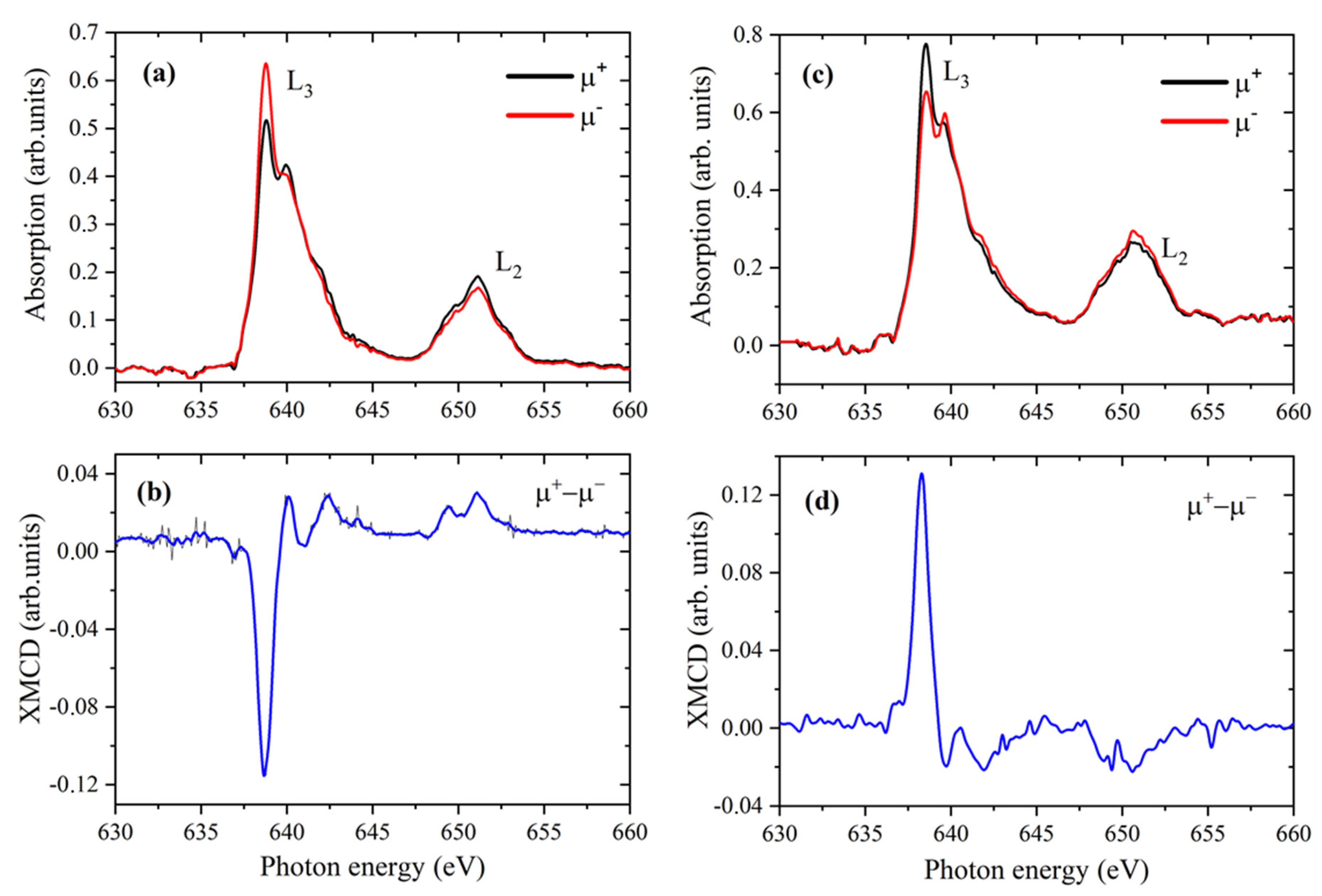
2.3. Mn L2,3—Edge XAS
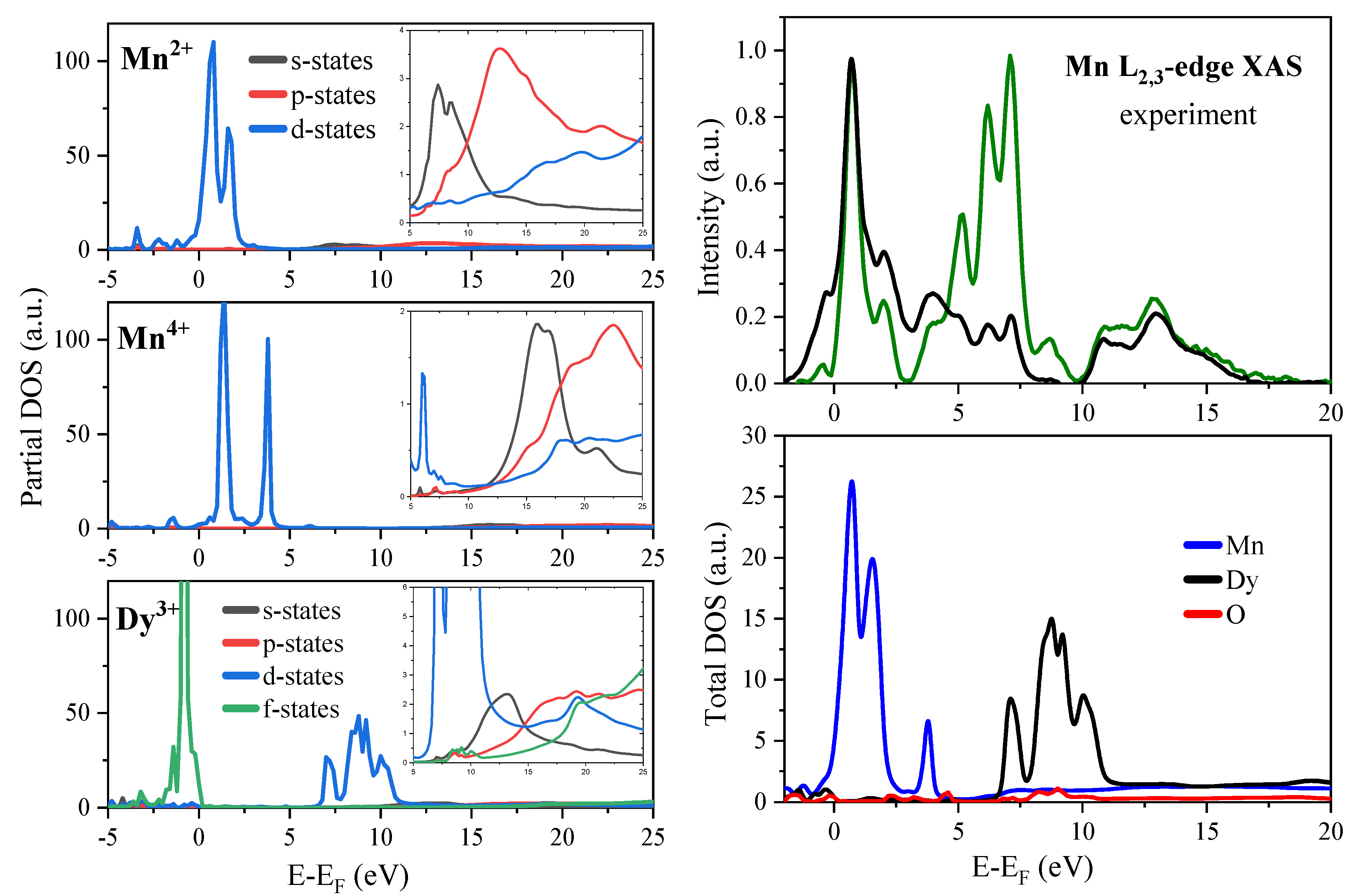
2.4. Electronic Structure
2.5. Mn RXES
2.6. Magnetochemical Properties
3. Experimental and Computational Details
3.1. X-Ray Absorption Spectroscopy
3.2. X-Ray Resonant Emission Spectroscopy
3.3. Density Functional Theory
3.4. X-Ray Magnetic Circular Dichroism
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Layfield, R.A. Organometallic single-molecule magnets. Organometallics 2014, 33, 1084–1099. [Google Scholar] [CrossRef]
- Kowalska, J.K.; Nayyar, B.; Rees, J.A.; Schiewer, C.E.; Lee, S.C.; Kovacs, J.A.; Meyer, F.; Weyhermüller, T.; Otero, E.; DeBeer, S. Iron L2,3-Edge X-ray Absorption and X-ray Magnetic Circular Dichroism Studies of Molecular Iron Complexes with Relevance to the FeMoco and FeVco Active Sites of Nitrogenase. Inorg. Chem. 2017, 56, 8147–8158. [Google Scholar] [CrossRef] [PubMed]
- Ishii, T.; Ogasawarab, K.; Sakanec, G. Exploring spin states and ligand field splitting in metal complexes: A theoretical analysis of spin–orbital interactions and magnetic properties. Dalton Trans. 2024, 53, 7175–7189. [Google Scholar] [CrossRef] [PubMed]
- Chantarangkul, C.; Patigo, A.; McMurtrie, J.C.; Clérac, R.; Rouzières, M.; Gómez-Coca, S.; Ruiz, E.; Harding, P.; Harding, D.J. Thermal Jahn–Teller Distortion Changes and Slow Relaxation of Magnetization in Mn(III) Schiff Base Complexes. Inorg. Chem. 2024, 63, 12858–12869. [Google Scholar] [CrossRef]
- Kim, H.; Yoon, G.; Park, I.; Park, K.-Y.; Lee, B.; Kim, J.; Park, Y.-U.; Jung, S.-K.; Lim, H.-D.; Ahn, D.; et al. Anomalous Jahn–Teller behavior in a manganese-based mixed-phosphate cathode for sodium ion batteries. Energy Environ. Sci. 2015, 8, 3325–3335. [Google Scholar] [CrossRef]
- Écija, D.; Urgel, J.I.; Seitsonen, A.P.; Auwärter, W.; Barth, J.V. Lanthanide-Directed Assembly of Interfacial Coordination Architectures–From Complex Networks to Functional Nanosystems. Acc. Chem. Res. 2018, 51, 365–375. [Google Scholar] [CrossRef]
- Liddle, S.T.; Mills, D.P.; Natrajan, L.S. The Lanthanides and Actinides; World Scientific Publishing Europe Ltd.: London, UK, 2021. [Google Scholar]
- Bünzli, J.-C.G. Review: Lanthanide coordination chemistry: From old concepts to coordination polymers. J. Coord. Chem. 2014, 67, 3706–3733. [Google Scholar] [CrossRef]
- Pineda, E.M.; Chilton, N.; Marx, R.; Dörfel, M.; Sells, D.O.; Neugebauer, P.; Jiang, S.-D.; Collison, D.; van Slageren, J.; McInnes, E.J.L.; et al. Direct measurement of dysprosium(III)˙˙˙dysprosium(III) interactions in a single-molecule magnet. Nat. Commun. 2014, 5, 5243. [Google Scholar] [CrossRef]
- Natterer, F.D.; Yang, K.; Paul, W.; Willke, P.; Choi, T.; Greber, T.; Heinrich, A.J.; Lutz, C.P. Reading and writing single-atom magnets. Nature 2017, 543, 226. [Google Scholar] [CrossRef]
- Guo, Y.-N.; Xu, G.-F.; Wernsdorfer, W.; Ungur, L.; Guo, Y.; Tang, J.; Zhang, H.-J.; Chibotaru, L.F.; Powell, A.K. Strong Axiality and Ising Exchange Interaction Suppress Zero-Field Tunneling of Magnetization of an Asymmetric Dy2 Single-Molecule Magnet. J. Am. Chem. Soc. 2005, 133, 11948–11951. [Google Scholar] [CrossRef]
- Woodru, D.N.; Winpenny, R.E.P.; Layfield, R.A. Lanthanide Single-Molecule Magnets. Chem. Rev. 2013, 113, 5110–5148. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, P.; Sharma, R.K.; Chouryala, Y.N.; Mudring, A.-V. Size of the rare-earth ions: A key factor in phase tuning and morphology control of binary and ternary rare-earth fluoride materials. RSC Adv. 2017, 7, 33467–33476. [Google Scholar] [CrossRef]
- Dey, A.; Acharya, J.; Chandrasekhar, V. Heterometallic 3d–4f Complexes as Single-Molecule Magnets. Chem. Asian J. 2019, 14, 4433–4453. [Google Scholar] [CrossRef] [PubMed]
- Andruh, M.; Costes, J.-P.; Diaz, C.; Gao, S. 3d#4f Combined Chemistry: Synthetic Strategies and Magnetic Properties. Inorg. Chem. 2009, 48, 3342–3359. [Google Scholar]
- Khan, A.; Lan, Y.; Kostakis, G.E.; Anson, C.E.; Powell, A.K. Using the flexible ligand bis(2-hydroxyethyl)amino–tris (hydroxymethyl)methane (“bis–tris”) to access a family of 3d–4f MnIII4Ln4 complexes. Dalton Trans. 2012, 41, 8333–8339. [Google Scholar] [CrossRef]
- Sessoli, R.; Powell, A.K. Strategies towards single molecule magnets based on lanthanide ions. Coord. Chem. Rev. 2009, 253, 2328–2341. [Google Scholar] [CrossRef]
- Glaser, T. Rational design of single-molecule magnets: A supramolecular approach. Chem. Commun. 2011, 47, 116–130. [Google Scholar] [CrossRef]
- Pointillart, F.; Bernot, K.; Sessoli, R.; Gatteschi, D. Effects of 3d–4f Magnetic Exchange Interactions on the Dynamics of the Magnetization of DyIII-MII-DyIII Trinuclear Clusters. Chem. Eur. J. 2007, 13, 1602–1609. [Google Scholar] [CrossRef]
- Bhunia, A.; Gamer, M.T.; Ungur, L.; Chibotaru, L.F.; Powell, A.K.; Lan, Y.; Roesky, P.W.; Menges, F.; Riehn, C.; Niedner-Schatteburg, G. From a Dy(III) Single Molecule Magnet (SMM) to a Ferromagnetic [Mn(II)Dy(III)Mn(II)] Trinuclear Complex. Inorg. Chem. 2012, 51, 9589–9597. [Google Scholar] [CrossRef] [PubMed]
- Ueltzen, K.; Schmitz, S.; Moors, M.; Glöß, M.; Börner, M.; Werner, I.; Warneke, Z.; Warneke, J.; Abel, B.; Monakhov, K.Y. Synthesis, Structure, and Surface Adsorption Characteristics of a Polynuclear MnII,IV–YbIII Complex. Inorg. Chem. 2021, 60, 10415–10425. [Google Scholar] [CrossRef]
- Caliebe, W.A.; Murzin, V.; Kalinko, A.; Görlitz, M. High-flux XAFS-beamline P64 at PETRA III. AIP Conf. Proc. 2019, 2054, 060031. [Google Scholar]
- Bunau, O.; Joly, Y. Self-consistent aspects of X-ray absorption calculations. J. Phys. Condens. Matter 2009, 21, 345501. [Google Scholar] [CrossRef] [PubMed]
- Fedoseenko, S.I.; Vyalikh, D.V.; Iossifov, I.F.; Follath, R.; Gorovikov, S.A.; Püttner, R.; Schmidt, J.S.; Molodtsov, S.L.; Adamchuk, V.K.; Gudat, W.; et al. Commissioning results and performance of the high-resolution Russian-German Beamline at BESSY II. Nucl. Instrum. Methods Phys. Res. A 2003, 505, 718–728. [Google Scholar] [CrossRef]
- Wang, H.-S.; Zhang, K.; Song, Y.; Pan, Z.-Q. Recent advances in 3d-4f magnetic complexes with several types of non-carboxylate organic ligands. Inorg. Chim. Acta 2021, 521, 120318. [Google Scholar] [CrossRef]
- Saha-Dasgupta, T. Double perovskites with 3d and 4d/5d transition metals: Compounds with promises. Mater. Res. Express 2020, 7, 014003. [Google Scholar] [CrossRef]
- Ikeno, H.; de Groot, F.M.F.; Stavitski, E.; Tanaka, I. Multiplet calculations of L2,3 X-ray absorption near-edge structures for 3d transition-metal compounds. J. Phys. Condens. Matter 2009, 21, 104208. [Google Scholar] [CrossRef][Green Version]
- de Groot, F. Coord. Multiplet effects in X-ray spectroscopy. Chem. Rev. 2005, 249, 31–63. [Google Scholar]
- Peng, G.; de Groot, F.M.F.; Haemaelaeinen, K.; Moore, J.A.; Wang, X.; Grush, M.M.; Hastings, J.B.; Siddons, D.P.; Armstrong, W.H.; Mullins, C.; et al. High-resolution manganese X-ray fluorescence spectroscopy. Oxidation-state and spin-state sensitivity. J. Am. Chem. Soc. 1994, 116, 2914–2920. [Google Scholar] [CrossRef]
- Coey, J.M.D. Magnetism and Magnetic Materials; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Ling, C.D.; Neumeier, J.J.; Argyriou, D.N. Observation of Antiferromagnetism in Marokite CaMn2O4. J. Solid State Chem. 2001, 160, 167–173. [Google Scholar] [CrossRef]
- Goodenough, J.B. Magnetism and The Chemical Bond; Wiley: Cambridge, MA, USA, 1963. [Google Scholar]
- Reitsma, A.J.W.; Feiner, L.F.; Oles, A.M. Orbital and spin physics in LiNiO2 and NaNiO2. New J. Phys. 2005, 7, 121. [Google Scholar] [CrossRef]
- Mostovoy, M.V.; Khomskii, D.I. Orbital Ordering in Frustrated Jahn-Teller Systems with 90° Exchange. Phys. Rev. Lett. 2002, 89, 227203. [Google Scholar] [CrossRef] [PubMed]
- Pal, S.; Lal, S. Orbital and spin ordering physics of the Mn3O4 spinel. Phys. Rev. B 2017, 96, 075139. [Google Scholar] [CrossRef]
- Blundell, S.J. Magnetism in condensed Matter. Oxford Master series. In Condensed Matter Physics; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Rawson, J.M.; Luzon, J.; Palacio, F. Magnetic exchange interactions in perfluorophenyl dithiadiazolyl radicals. Coord. Chem. Rev. 2005, 249, 2631–2641. [Google Scholar] [CrossRef]
- Schulz, C.; Lieutenant, K.; Xiao, J.; Hofmann, T.; Wong, D.; Habicht, K. Characterization of the soft X-ray spectrometer PEAXIS at BESSY II. J. Synchrotron Rad. 2020, 27, 238–249. [Google Scholar] [CrossRef]
- Butorin, S.M.; Guo, J.-H.; Magnuson, M.; Kuiper, P.; Nordgren, J. Low-energy d-d excitations in MnO studied by resonant X-ray fluorescence spectroscopy. Phys. Rev. B 1996, 54, 4405–4408. [Google Scholar] [CrossRef]
- Kuepper, K.; Klingeler, R.; Reutler, P.; Büchner, B.; Neumann, M. Excited and ground state properties of LaSrMnO4: A combined X-ray spectroscopic study. Phys. Rev. B 2006, 74, 115103. [Google Scholar] [CrossRef]
- Ebert, H. Magneto-optical effects in transition metal systems. Rep. Prog. Phys. 1996, 59, 1665. [Google Scholar] [CrossRef]
- Goering, E.; Gold, S.; Schutz, G. Ho-Fe-Garnet soft XMCD measurements below and above the compensation temperature. J. Sync. Rad. 2001, 8, 422–424. [Google Scholar] [CrossRef]
- Brice-Profeta, S.; Arrio, M.A.; Tronc, E.; Menguy, N.; Letard, I.; Cartier dit Moulin, C.; Noguès, M.; Chanéac, C.; Jolivet, J.-P.; Sainctavit, P. Magnetic order in γ-Fe2O3 nanoparticles: A XMCD study. J. Magn. Magn. Mater. 2005, 288, 354–365. [Google Scholar] [CrossRef]
- Goedkoop, J.B.; Thole, B.T.; van der Laan, G.; Sawatzky, G.A.; de Groot, F.M.F.; Fuggle, J.C. Calculations of magnetic X-ray dichroism in the 3d absorption spectra of rare-earth compounds. Phys. Rev. B 1988, 37, 2086–2093. [Google Scholar] [CrossRef]
- Thole, B.T.; van der Laan, G.; Fuggle, J.C.; Sawatzky, G.A.; Karnatak, R.C.; Esteva, J.M. 3d X-ray-absorption lines and the 3d94fn+1 multiplets of the lanthanides. Phys. Rev. B 1985, 32, 5107–5118. [Google Scholar] [CrossRef] [PubMed]
- Tripathi, S. XMCD Investigation at M4,5 Edges of the Rare Earth Elements in High-Performance Permanent Magnet. PhD Thesis, Universität Stuttgart, Stuttgart, Germany, 2018. [Google Scholar]
- Thole, B.T.; Carra, P.; Sette, F.; van der Laan, G. X-Ray circular dichroism as a probe of orbital magnetization. Phys. Rev. Lett. 1992, 68, 1943. [Google Scholar] [CrossRef] [PubMed]
- Carra, P.; Thole, B.T.; Altarelli, M.; Wang, X. X-Ray circular dichroism and local magnetic fields. Phys. Rev. Lett. 1993, 70, 694. [Google Scholar] [CrossRef]
- Chen, C.T.; Idzerda, Y.U.; Lin, H.J.; Smith, N.V.; Meigs, G.; Chaban, E.; Ho, G.H.; Pellegrin, E.; Sette, F. Experimental Confirmation of the X-Ray Magnetic Circular Dichroism Sum Rules for Iron and Cobalt. Phys. Rev. Lett. 1995, 75, 152–155. [Google Scholar] [CrossRef]
- Piamonteze, C.; Miedema, P.; de Groot, F.M.F. Accuracy of the spin sum rule in XMCD for the transition-metal L edges from manganese to copper. Phys. Rev. B 2009, 80, 184410. [Google Scholar] [CrossRef]
- Edmonds, K.W.; Farley, N.R.S.; Johal, T.K.; van der Laan, G.; Campion, R.P.; Gallagher, B.L.; Foxon, C.T. Ferromagnetic moment and antiferromagnetic coupling in (Ga,Mn)As thin films. Phys. Rev. B 2005, 71, 064418. [Google Scholar] [CrossRef]
- O’Brien, W.L.; Tonner, B.P. Oxygen-induced exchange-coupling reversal at the Mn-Co interface. Phys. Rev. B 1998, 58, 3191. [Google Scholar] [CrossRef]
- Yonamoto, Y.; Yokoyama, T.; Amemiya, K.; Matsumura, D.; Ohta, T. Magnetism of an ultrathin Mn Film on Co(100) and the effect of oxidation studied by X-ray magnetic circular dichroism. Phys. Rev. B 2001, 63, 214406. [Google Scholar] [CrossRef]
- Bannerjee, S.; O’Brien, W.L.; Tonner, B.P. Unusual magnetic phases in MnCo ultrathin alloy films. J. Magn. Magn. Mater. 1999, 267, 198–199. [Google Scholar] [CrossRef]
- Tanemura, Y.; Tanaka, A.; Jo, T. Effect of Coulomb Interaction on the X-Ray Magnetic Circular Dichroism Spin Sum Rule in 3 d Transition Elements. J. Phys. Soc. Jpn. 1996, 65, 1053. [Google Scholar]
- Duerr, H.A.; van der Laan, G.; Spanke, D.; Hillebrecht, F.U.; Brookes, N.B. Electron-correlation-induced magnetic order of ultrathin Mn films. Phys. Rev. B 1997, 56, 8156. [Google Scholar] [CrossRef]
- Schütz, G.; Goering, E.; Stoll, H. Synchrotron Radiation Techniques Based on X-ray Magnetic Circular Dichroism. In Handbook of Magnetism and Advanced Magnetic Materials; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Galanakis, I.; Alouani, M.; Oppeneer, P.M.; Dreyssé, H.; Eriksson, O. Tuning the orbital moment in transition metal compounds using ligand states. J. Phys. Condens. Matter 2001, 13, 4553. [Google Scholar] [CrossRef]
- Galanakis, I.; Oppeneer, P.M.; Ravindran, P.; Nordström, L.; James, P.; Alouani, M.; Dreysse, H.; Eriksson, O. Sign reversal of the orbital moment via ligand states. Phys. Rev. B 2001, 63, 172405. [Google Scholar] [CrossRef]
- Oppeneer, P.M.; Galanakis, I.; Grechnev, A.; Eriksson, O. Unusual magnetism and magnetocrystalline anisotropy of CrPt3. J. Magn. Magn. Mater. 2002, 240, 371–373. [Google Scholar] [CrossRef]
- Tyer, R.; van der Laan, G.; Temmerman, W.M.; Szotek, Z.; Ebert, H. Systematic theoretical study of the spin and orbital magnetic moments of 4d and 5d interfaces with Fe films. Phys. Rev. B 2003, 67, 104409. [Google Scholar] [CrossRef]
- Levy, P.M. Rare-Earth-Iron Exchange Interaction in the Garnets. I. Hamiltonian for Anisotropic Exchange Interaction. Phys. Rev. 1964, 135, A155. [Google Scholar] [CrossRef]
- de Groot, F.; Kotani, A. Core Level Spectroscopy of Solids; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Kubin, M.; Guo, M.; Kroll, T.; Loechel, H.; Kaellman, E.; Baker, M.L.; Mitzner, R.; Gul, S.; Kern, J.; Foehlisch, A.; et al. Probing the oxidation state of transition metal complexes: A case study on how charge and spin densities determine Mn L-edge X-Ray absorption energies. Chem. Sci. 2018, 9, 6813–6829. [Google Scholar] [CrossRef]
- Ament, L.J.P.; van Veenendaal, M.; Devereaux, T.P.; Hill, J.P.; van den Brink, J. Resonant inelastic X-ray scattering studies of elementary excitations. Rev. Mod. Phys. 2011, 83, 705–767. [Google Scholar] [CrossRef]
- Ghiringhelli, G.; Matsubara, M.; Dallera, C.; Fracassi, F.; Tagliaferri, A.; Brookes, N.B.; Kotani, A.; Braicovich, L. Resonant inelastic X-Ray scattering of MnO: L2,3 edge measurements and assessment of their interpretation. Phys. Rev. B 2006, 73, 035111. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef] [PubMed]
- ADF 2020, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands. Available online: http://www.scm.com (accessed on 14 July 2020).
- te Velde, G.; Bickelhaupt, F.M.; Baerends, E.J.; Fonseca Guerra, C.; van Gisbergen, S.J.A.; Snijders, J.G.; Ziegler, T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. [Google Scholar] [CrossRef]
- Fonseca Guerra, C.; Snijders, J.G.; te Velde, G.; Baerends, E.J. Towards an order-N DFT method. Theor. Chem. Acc. 1998, 99, 391–403. [Google Scholar] [CrossRef]
- van Lenthe, E.; Baerends, E.J. Optimized Slater-type basis sets for the elements 1–118. J. Comput. Chem. 2003, 24, 1142–1156. [Google Scholar] [CrossRef]
- van Lenthe, E.; Baerends, E.J.; Snijders, J.G. Relativistic regular two-component Hamiltonians. J. Chem. Phys. 1993, 99, 4597–4610. [Google Scholar] [CrossRef]
- McConnell, H.M. Ferromagnetism in Solid Free Radicals. J. Chem. Phys. 1963, 39, 1910. [Google Scholar] [CrossRef]
- Yoshizawa, K.; Hoffman, R. The role of orbital interactions in determining ferromagnetic coupling in organic molecular assemblies. J. Am. Chem. Soc. 1995, 117, 6921–6926. [Google Scholar] [CrossRef]
- Crocombette, J.P.; Thole, B.T.; Jollet, F. The importance of the magnetic dipole term in magneto-circular X-ray absorption dichroism for 3d transition metal compounds. J. Phys. Condens. Matter 1996, 8, 4095. [Google Scholar] [CrossRef]
- Krishnamurthy, V.V.; Keavney, D.J.; Haskel, D.; Lang, J.C.; Srajer, G.; Sales, B.C.; Mandrus, D.G.; Robertson, J.L. Temperature dependence of Eu 4f and Eu 5d magnetizations in the filled skutterudite EuFe4Sb12. Phys. Rev. B 2009, 79, 014426. [Google Scholar] [CrossRef]

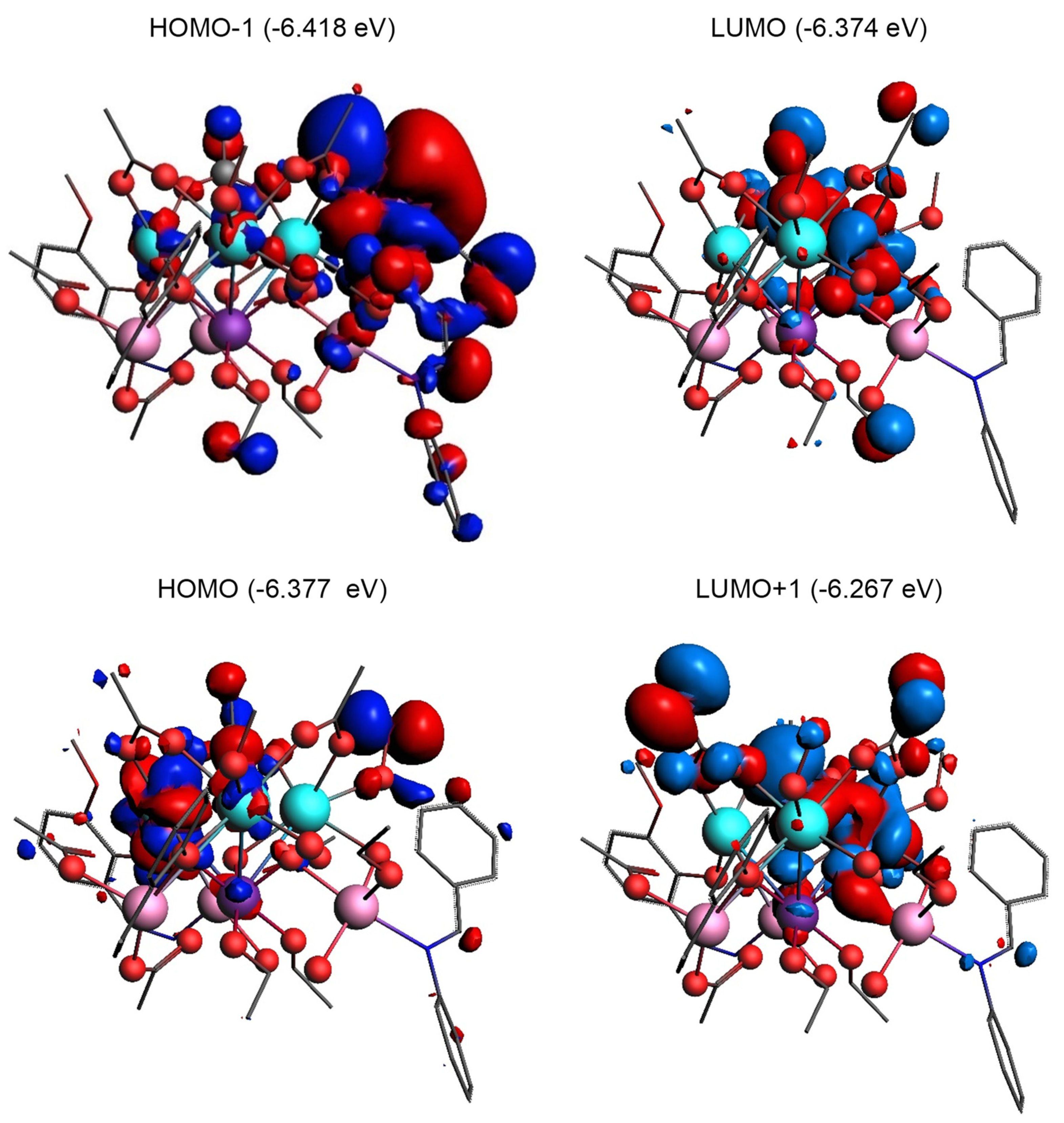

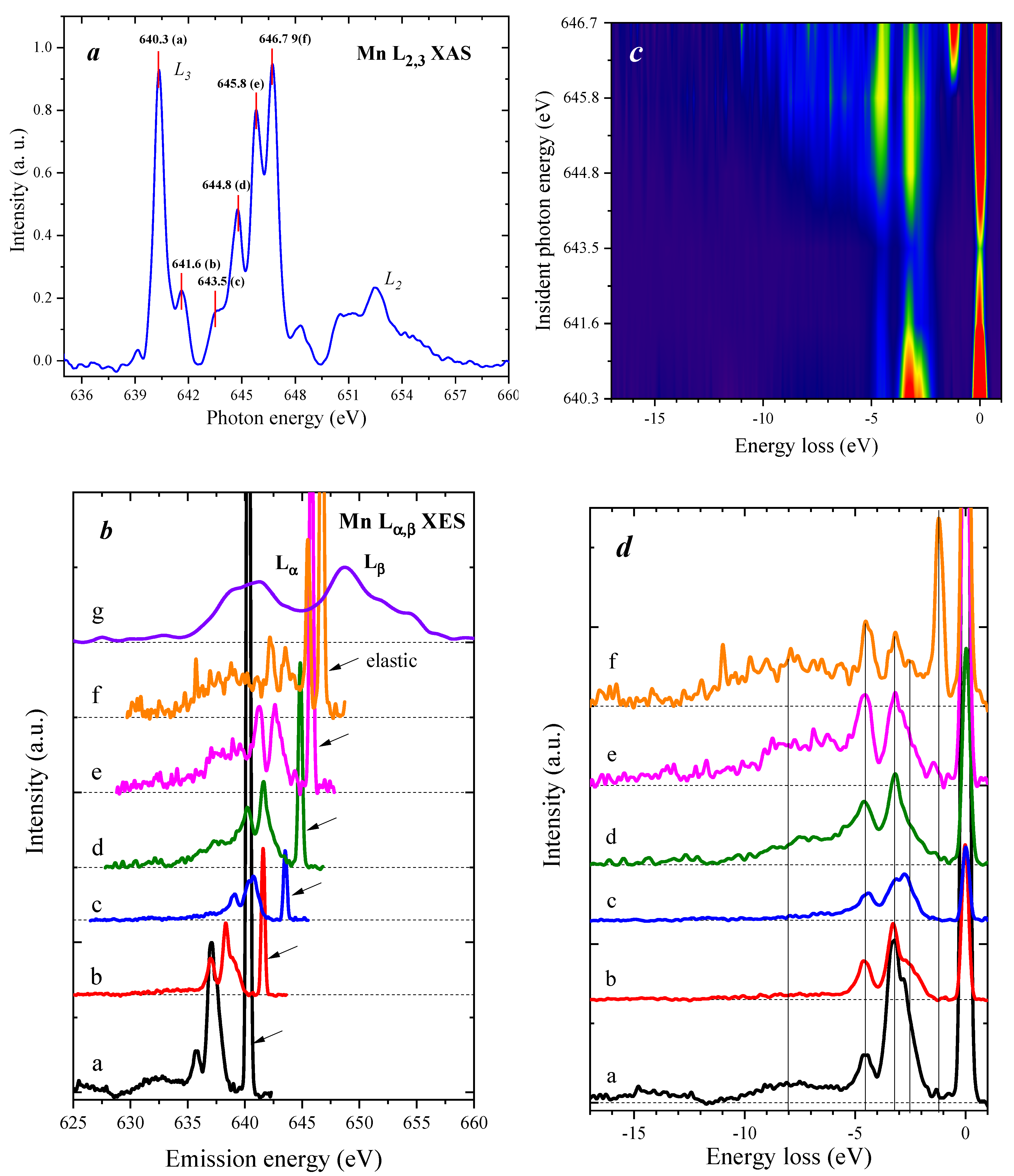
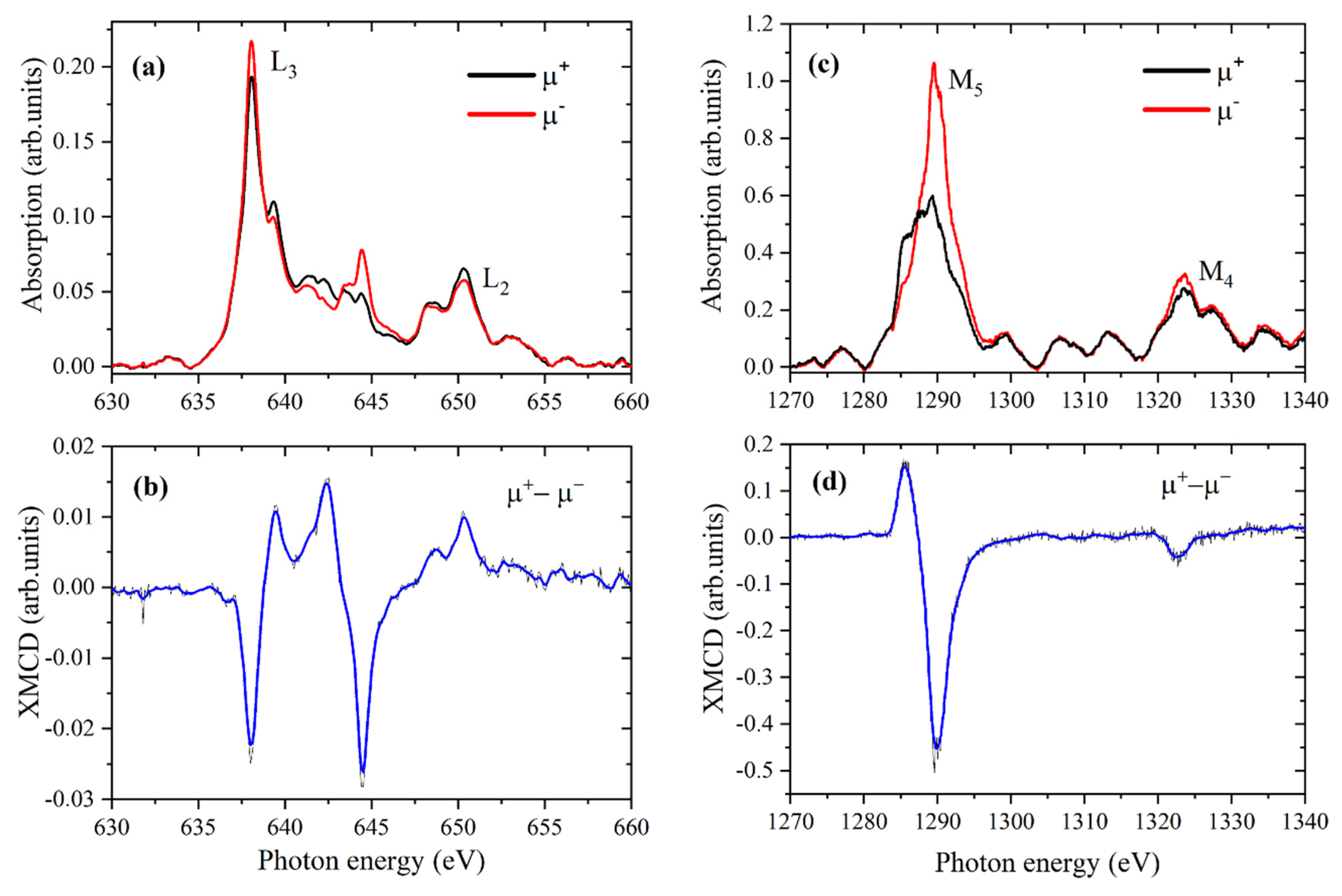

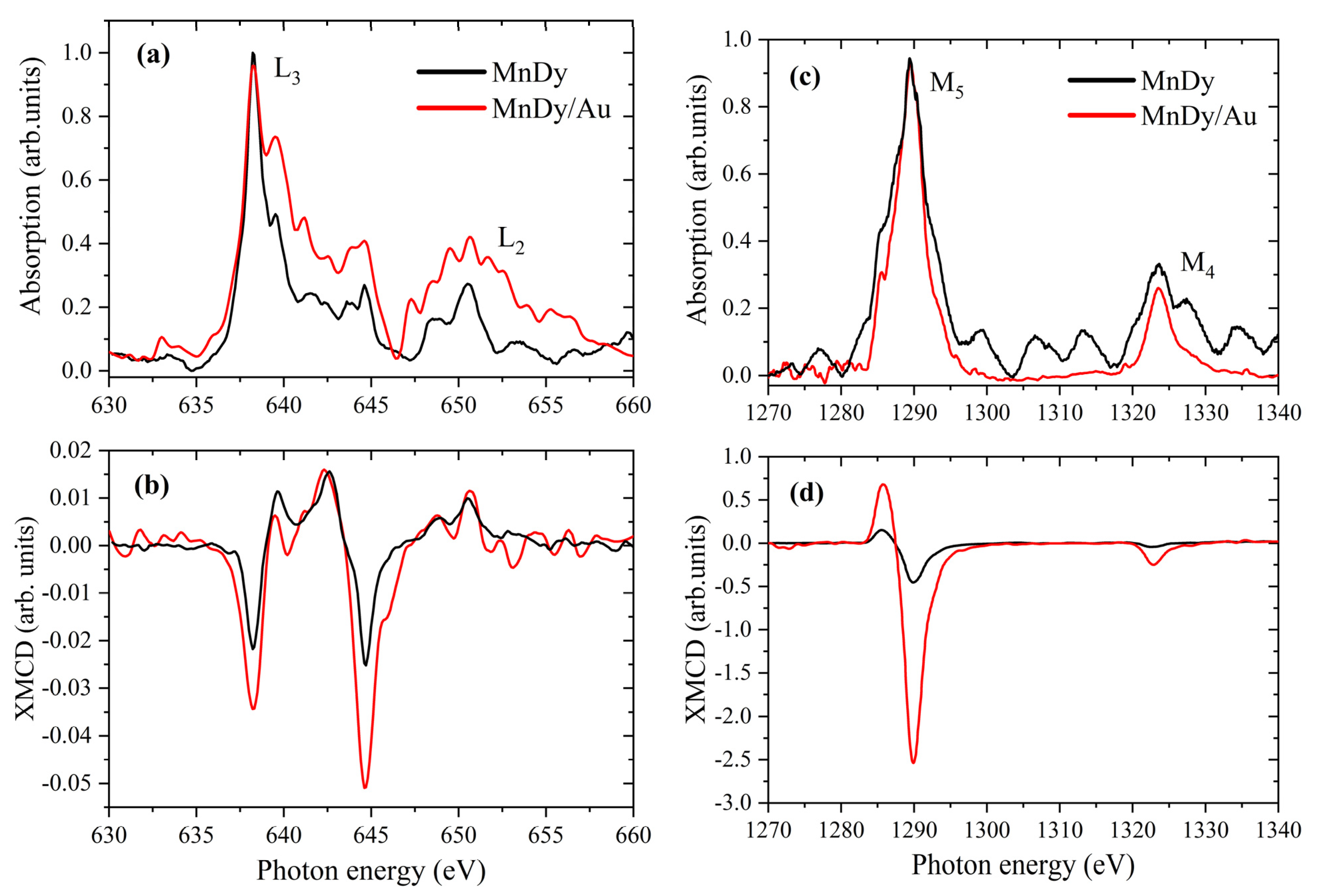

| Atom | Charge | Spin Density | Spin Direction | S | P | D | F |
|---|---|---|---|---|---|---|---|
| Dy1 | 1.9847 | 4.9380 | ↑ | 1.0542 | 2.9784 | 0.4149 | 7.0291 |
| ↓ | 1.0491 | 2.9698 | 0.3872 | 2.1327 | |||
| Dy2 | 1.9749 | −4.8851 | ↑ | 1.0459 | 2.9727 | 0.3619 | 2.1895 |
| ↓ | 1.0557 | 2.9809 | 0.3942 | 7.0244 | |||
| Dy3 | 1.9668 | −4.8873 | ↑ | 1.0459 | 2.9723 | 0.3694 | 2.1853 |
| ↓ | 1.0552 | 2.9777 | 0.4039 | 7.0235 | |||
| Mn1 | 1.4304 | −2.5910 | ↑ | 0.9594 | 3.1509 | 1.3790 | 0.0000 |
| ↓ | 1.0036 | 3.2101 | 3.8666 | 0.0000 | |||
| Mn2 | 1.1655 | 4.4922 | ↑ | 1.0886 | 3.2329 | 4.8418 | 0.0000 |
| ↓ | 1.0425 | 3.1603 | 0.4683 | 0.0000 | |||
| Mn3 | 1.1547 | 4.5739 | ↑ | 1.0894 | 3.2407 | 4.8795 | 0.0000 |
| ↓ | 1.0377 | 3.1648 | 0.4332 | 0.0000 | |||
| Mn4 | 1.1513 | 4.6054 | ↑ | 1.0934 | 3.2412 | 4.8925 | 0.0000 |
| ↓ | 1.0388 | 3.1617 | 0.4212 | 0.0000 | |||
| O1 | −1.0543 | −0.0253 | ↑ | 1.9539 | 2.5444 | 0.0163 | 0.0000 |
| ↓ | 1.9510 | 2.5735 | 0.0153 | 0.0000 | |||
| O2 | −1.0545 | −0.0520 | ↑ | 1.9540 | 2.5305 | 0.0168 | 0.0000 |
| ↓ | 1.9509 | 2.5867 | 0.0157 | 0.0000 | |||
| O3 | −1.0597 | −0.0194 | ↑ | 1.9538 | 2.5495 | 0.0168 | 0.0000 |
| ↓ | 1.9502 | 2.5739 | 0.0155 | 0.0000 |
| Orbital mL (μB/atom) | Spin mS (μB/atom) | Total (mL + mS) (μB/atom) | Ratio mL/mS | |
|---|---|---|---|---|
| Mn | −0.18 | 1.57 | 1.39 | −0.12 |
| Dy | 2.15 | −1.47 | 0.68 | −1.46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mazalova, V.; Asanova, T.; Asanov, I.; Fromme, P. A Structure and Magnetism Study of {MnII3MnIVLnIII3} Coordination Complexes with Ln = Dy, Yb. Inorganics 2024, 12, 286. https://doi.org/10.3390/inorganics12110286
Mazalova V, Asanova T, Asanov I, Fromme P. A Structure and Magnetism Study of {MnII3MnIVLnIII3} Coordination Complexes with Ln = Dy, Yb. Inorganics. 2024; 12(11):286. https://doi.org/10.3390/inorganics12110286
Chicago/Turabian StyleMazalova, Victoria, Tatiana Asanova, Igor Asanov, and Petra Fromme. 2024. "A Structure and Magnetism Study of {MnII3MnIVLnIII3} Coordination Complexes with Ln = Dy, Yb" Inorganics 12, no. 11: 286. https://doi.org/10.3390/inorganics12110286
APA StyleMazalova, V., Asanova, T., Asanov, I., & Fromme, P. (2024). A Structure and Magnetism Study of {MnII3MnIVLnIII3} Coordination Complexes with Ln = Dy, Yb. Inorganics, 12(11), 286. https://doi.org/10.3390/inorganics12110286







