Fabrication of a Laminated Actuator with Excellent Linearity Using Ground Potassium Sodium Niobate-Based Ceramic Sheets
Abstract
:1. Introduction
2. Results and Discussion
2.1. Phase Observation and Analysis of Piezoelectric Ceramics
2.2. Surface Morphology Observations and Grinding Force Analysis
2.3. Physical Properties of the Piezoelectric Ceramics
2.4. P−E Loops
2.5. S−E Curves
2.6. Actuator Manufacture, Displacement Test, and Linear Regression
2.6.1. Manufacture of the Actuator
2.6.2. Linear Regression Analysis of the Displacement–Voltage Relationship of the Actuator
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kang, W.S.; Koh, J.H. (1−x)Bi0.5Na0.5TiO3-xBaTiO3 lead-free piezoelectric ceramics for energy-harvesting applications. J. Eur. Ceram. Soc. 2015, 35, 2057–2064. [Google Scholar] [CrossRef]
- Mayamae, J.; Sukkha, U.; Niemchareon, S.; Muanghlua, R.; Vittayakorn, N. Ferroelectric and Piezoelectric Properties of the Lead Free 0.9BaTiO3-(0.1−x)Bi0.5Na0.5TiO3-xBi(Mg0.5Ti0.5)O3 Solid Solution. Ferroelectrics 2016, 490, 23–35. [Google Scholar] [CrossRef]
- Maiwa, H. Dielectric and Electromechanical Properties of BatiO3 Ceramics Prepared by HotIsostatic Pressing. Ferroelectrics 2014, 463, 15–24. [Google Scholar] [CrossRef]
- Fu, F.; Zhai, J.; Xu, Z.; Shen, B.; Yao, X. Grain growth kinetics of textured- Batioceramics. Bull. Mater. Sci. 2014, 37, 779–787. [Google Scholar] [CrossRef]
- Kimura, M.; Minamikawa, T.; Ando, A.; Sakabe, Y. Temperature characteristics of (ba1-xsrx)2nanb5o15 ceramics. J. Appl. Phys. 1997, 36, 6051–6054. [Google Scholar] [CrossRef]
- Kumar, N.; Ionin, A.; Ansell, T.; Kwon, S.; Hackenberger, W.; Cann, D. Multilayer ceramic capacitors based on relaxor BaTiO3-Bi(Zn1/2Ti1/2)O3 for temperature stable and high energy density capacitor applications. Appl. Phys. Lett. 2015, 106, 549. [Google Scholar] [CrossRef]
- Kumar, N.; Cann, D.P. Resistivity Enhancement and Transport Mechanisms in (1x)BaTiO3-xBi(Zn1/2Ti1/2)O3 and (1x)SrTiO3-xBi(Zn1/2Ti1/2)O3. J. Am. Ceram. Soc. 2015, 98, 2548–2555. [Google Scholar] [CrossRef]
- Huang, S.; Kim, T.; Hou, D.; Cann, D.; Jones, J.L.; Jiang, X. Flexoelectric characterization of BaTiO3-0.08Bi(Zn1/2Ti1/2)O3. Appl. Phys. Lett. 2017, 110, 1–4. [Google Scholar] [CrossRef]
- Hou, D.; Usher, T.M.; Zhou, H.; Raengthon, N.; Triamnak, N.; Cann, D.P.; Forrester, J.S.; Jones, J.L. Temperature-induced local and average structural changes in BaTiO3xBi(Zn1/2Ti1/2)O3 solid solutions: The origin of high temperature dielectric permittivity. J. Appl. Phys. 2017, 122, 064103. [Google Scholar] [CrossRef]
- Yu, L.; Deng, H.; Zhou, W.; Yang, P.; Chu, J. Structural characteristics and optical properties of lead-free Bi(Zn1/2Ti1/2)O3-BaTiO3 ceramics. Ceram. Int. 2017, 43, 6175–6179. [Google Scholar] [CrossRef]
- Saito, Y.; Takao, H.; Tani, T.; Nonoyama, T.; Takatori, K.; Homma, T.; Nagaya, T.; Nakamura, M. Lead-Free Piezoceramics. Nature 2004, 432, 84–87. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Zhang, X.; Su, W.; Wang, X.; Yao, W.; Zhou, C.; Zhang, J. Outstanding piezoelectric properties, phase transitions and domain configurations of 0.963(K0.48Na0.52)(Nb0.955Sb0.045)O3−0.037(Bi0.50Na0.50)HfO3 ceramics. J. Alloys Compd. 2019, 779, 800–804. [Google Scholar] [CrossRef]
- Jiang, M.; Zhang, J.; Rao, G.; Li, D.; Randall, C.A.; Li, T.; Peng, B.; Li, L.; Gu, Z.; Liu, X.; et al. Ultrahigh piezoelectric coefficient of a lead -free K0.5Na0.5NbO3-based single crystal fabricated by a simple seed- free solid state growth method. J. Mater. Chem. C 2019, 7, 14845–14854. [Google Scholar] [CrossRef]
- Shrout, T.R.; Zhang, S.J. Lead-free piezoelectric ceramics: Alternatives for PZT? J. Electroceramics 2007, 19, 113–126. [Google Scholar] [CrossRef]
- Wu, J.; Xiao, D.; Zhu, J. Potassium-sodium niobate lead-free piezoelectric materials: Past, present, and future of phase boundaries. Chem. Rev. 2015, 115, 2559–2595. [Google Scholar] [CrossRef] [PubMed]
- Malič, B.; Koruza, J.; Hreščak, J.; Bernard, J.; Wang, K.; Fisher, J.G.; Benčan, A. Sintering of Lead-Free Piezoelectric Sodium Potassium Niobate Ceramics. Materials 2015, 8, 8117–8146. [Google Scholar] [CrossRef] [PubMed]
- Jiang, L.; Tan, Z.; Xing, J.; Wu, J.; Chen, Q.; Zhang, W.; Xiao, D.; Zhu, J. New potassium–sodium niobate ternary system with large piezoelectric coefficient and high Curie temperature. J. Mater. Sci. Mater. Electron. 2016, 27, 9812–9820. [Google Scholar] [CrossRef]
- Kong, Z.; Bai, W.; Zheng, P.; Zhang, J.; Wen, F.; Chen, D.; Shen, B.; Zhai, J. Enhanced electromechanical properties of CaZrO3-modified (K0.5Na0.5)NbO3-based lead-free ceramics. Ceram. Int. 2017, 43, 7237–7242. [Google Scholar] [CrossRef]
- Fang, X.; Jian, C.; Lu, Y.; Zhang, Q.; Qi, Z.; Zhou, T.; He, Y. Exploration on the origin of enhanced piezoelectric properties in transition-metal ion doped KNN based lead-free ceramics. Ceram. Int. 2018, 44, 16745–16750. [Google Scholar]
- Gongora-Rubio, M.R.; Espinoza-Vallejos, P.; Sola-Laguna, L.; Santiago-Aviles, J.J. Overview of low temperature co-fired ceramics tape technology for meso-system technology (MsST). Sens. Actuators 2001, A89, 222–241. [Google Scholar] [CrossRef]
- Park, H.Y.; Seo, I.T.; Choi, J.H.; Nahm, S.; Lee, H.G. Low-Temperature Sintering and Piezoelectric Properties of (Na0.5K0.5)NbO3 Lead-Free Piezoelectric Ceramics. J. Am. Ceram. Soc. 2010, 93, 36–39. [Google Scholar] [CrossRef]
- Liu, J.; Jia, P.; Zhang, H.; Tian, X.; Liang, H.; Hong, Y.; Liang, T.; Liu, W.; Xiong, J. Fiber-optic Fabry-Perot pressure sensor based on low-temperature co-fired ceramic technology for high-temperature applications. Appl. Opt. 2018, 57, 4211. [Google Scholar] [CrossRef] [PubMed]
- Qu, Z.Q. An efficient modelling method for laminated composite plates with piezoelectric sensors and actuators. Smart Mater. Struct. 2001, 10, 807. [Google Scholar] [CrossRef]
- Lin, J.C.; Nien, M.H. Adaptive modeling and shape control of laminated plates using piezoelectric actuators. J. Mater. Process. Technol. 2007, 189, 231–236. [Google Scholar] [CrossRef]
- Talebitooti, R.; Daneshjoo, K.; Jafari, S.A.M. Optimal control of laminated plate integrated with piezoelectric sensor and actuator considering TSDT and mesh free method. Eur. J. Mech.—A/Solids 2016, 55, 199–211. [Google Scholar] [CrossRef]
- Guo, Y.; Zhu, Y. Modeling and Analysis on Hysteresis Nonlinear Characteristics of the Piezoelectric Stack Actuators. Piezoelectrics Acoustooptics 2017, 39, 520–524. [Google Scholar]
- Kakimoto, K.I.; Sumi, T.; Kagomiya, I. Pressure-dependent raman scattering spectrum of piezoelectric (Li,Na,K)NbO3 lead-free ceramics. Jpn. J. Appl. Phys. 2010, 49, 09MD10. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, Y.; Zhang, X.; Huang, R.; Liu, R.; Zhou, H. The effect of sintering and poling processing on the phase structure of Li0.058(Na0.51K0.49)0.942NbO3 lead-free ceramics. Scr. Mater. 2012, 66, 97–100. [Google Scholar] [CrossRef]
- Zhou, J.J.; Li, J.F.; Zhang, X.W. Orthorhombic to tetragonal phase transition due to stress release in (Li,Ta)-doped(K,Na)NbO3 lead-free piezoceramics. J. Eur. Ceram. Soc. 2012, 32, 267–270. [Google Scholar] [CrossRef]
- Wu, C.; Duan, W.; Zhang, X.W.; Liu, Z. Effects of hydrostatic pressure on Pb(Zr1−xTix)O3 near the morphotropic phase boundary. J. Appl. Phys. 2010, 108, 124102. [Google Scholar] [CrossRef]
- Malkin, S.; Hwang, T.W. Grinding Mechanisms for Ceramics. CIRP Ann.—Manuf. Technol. 1996, 45, 569–580. [Google Scholar] [CrossRef]
- Denkena, B.; Busemann, S.; Gottwik, L.; Grove, T.; Wippermann, A. Material Removal Mechanisms in Grinding of Mixed Oxide Ceramics. Procedia Cirp 2017, 65, 70–77. [Google Scholar] [CrossRef]
- Hessert, R.; Eigenmann, B.; Vöhringer, O.; Löhe, D. Fracture mechanical evaluation of the effects of grinding residual stresses on bending strength of ceramics. Mater. Sci. Eng. 1997, 234–236, 1126–1129. [Google Scholar] [CrossRef]
- Pfeiffer, W.; Hollstein, T. Damage determination and strength prediction of machined ceramics by X-ray diffraction techniques. Mach. Adv. Mater. 1993, 45, 235–245. [Google Scholar]
- Bifano, T.G.; Dow, T.A.; Scattergood, R.O. Ductile-Regime Grinding: A New Technology for Machining Brittle Materials. ASME J. Eng. Ind. 1991, 113, 184–189. [Google Scholar] [CrossRef]
- Damjanovic, D. Ferroelectric, dielectric and piezoelectric properties of ferroelectric thin films and ceramics. Rep. Prog. Phys. 1999, 61, 1267–1324. [Google Scholar] [CrossRef]
- Li, J.; Fei, L.; Zhang, S. Decoding the Fingerprint of Ferroelectric Loops: Comprehension of the Material Properties and Structures. J. Am. Ceram. Soc. 2014, 97, 1–27. [Google Scholar]
- Qin, Y.; Zhang, J.; Tan, Y.; Yao, W.; Wang, C.; Zhang, S. Domain configuration and piezoelectric properties of (K0.50Na0.50)1−xLix(Nb0.80Ta0.20)O3 ceramics. J. Eur. Ceram. Soc. 2014, 34, 4177–4184. [Google Scholar] [CrossRef]
- Kungl, H.; Fett, T.; Wagner, S.; Hoffmann, M.J. Nonlinearity of strain and strain hysteresis in morphotropic LaSr-doped lead zirconate titanate under unipolar cycling with high electric fields. J. Appl. Phys. 2007, 101, 29. [Google Scholar] [CrossRef]
- Hua, T.; Zhang, S.; Feng, Y.; Fei, L.; Shrout, T.R.; Johnson, D. Piezoelectric Property and Strain Behavior of Pb(Yb0.5Nb0.5)O3–PbHfO3–PbTiO3 Polycrystalline Ceramics. J. Am. Ceram. Soc. 2013, 96, 2857–2863. [Google Scholar]
- Trzepieciński, T.; Ryzińska, G.; Biglar, M.; Gromada, M. Modelling of multilayer actuator layers by homogenisation technique using Digimat software. Ceram. Int. 2016, 43, 3259–3266. [Google Scholar] [CrossRef]
- Yan, S.; Sun, C.; Cui, Q.; He, M.; Wang, R.; Hao, J.; Chu, X. Dielectric, piezoelectric and dc bias characteristics of Bi-doped PZT multilayer ceramic actuator. Mater. Chem. Phys. 2020, 255, 123605. [Google Scholar] [CrossRef]
- Raghu, N.; Kumar, V.; Dayas, K.R.; Rao, I.C. Overview of multilayer ceramic actuator program at C-MET. Proc. SPIE—Int. Soc. Opt. Eng. 2003, 5062, 473–480. [Google Scholar]
- Chen, J.; Du, Z.Z.; Yang, Y.T.; Hu, H. The electrical properties of low-temperature sintered 0.07Pb(Sb1/2Nb1/2)O3-0.93Pb(ZrTi1)O3 multilayer piezoceramic actuator. Ceram. Int. 2021, 47, 15195–15201. [Google Scholar] [CrossRef]
- Koo, B.K.; Saleem, M.; Lim, D.H.; Kim, M.S.; Kim, I.S.; Jeong, S.J. Fabrication of borosilicate-glass-coated CuAg inner electrode for multilayer ceramic actuator. Sens. Actuators A Phys. 2018, 277, 8–17. [Google Scholar] [CrossRef]
- Jeong, S.J.; Lim, D.H.; Saleem, M.; Koo, B.G.; Kim, M.S. Properties of CuAg/(BiNaSr)TiO3 multilayer ceramic actuator. Ceram. Int. 2018, 44, S112–S116. [Google Scholar] [CrossRef]
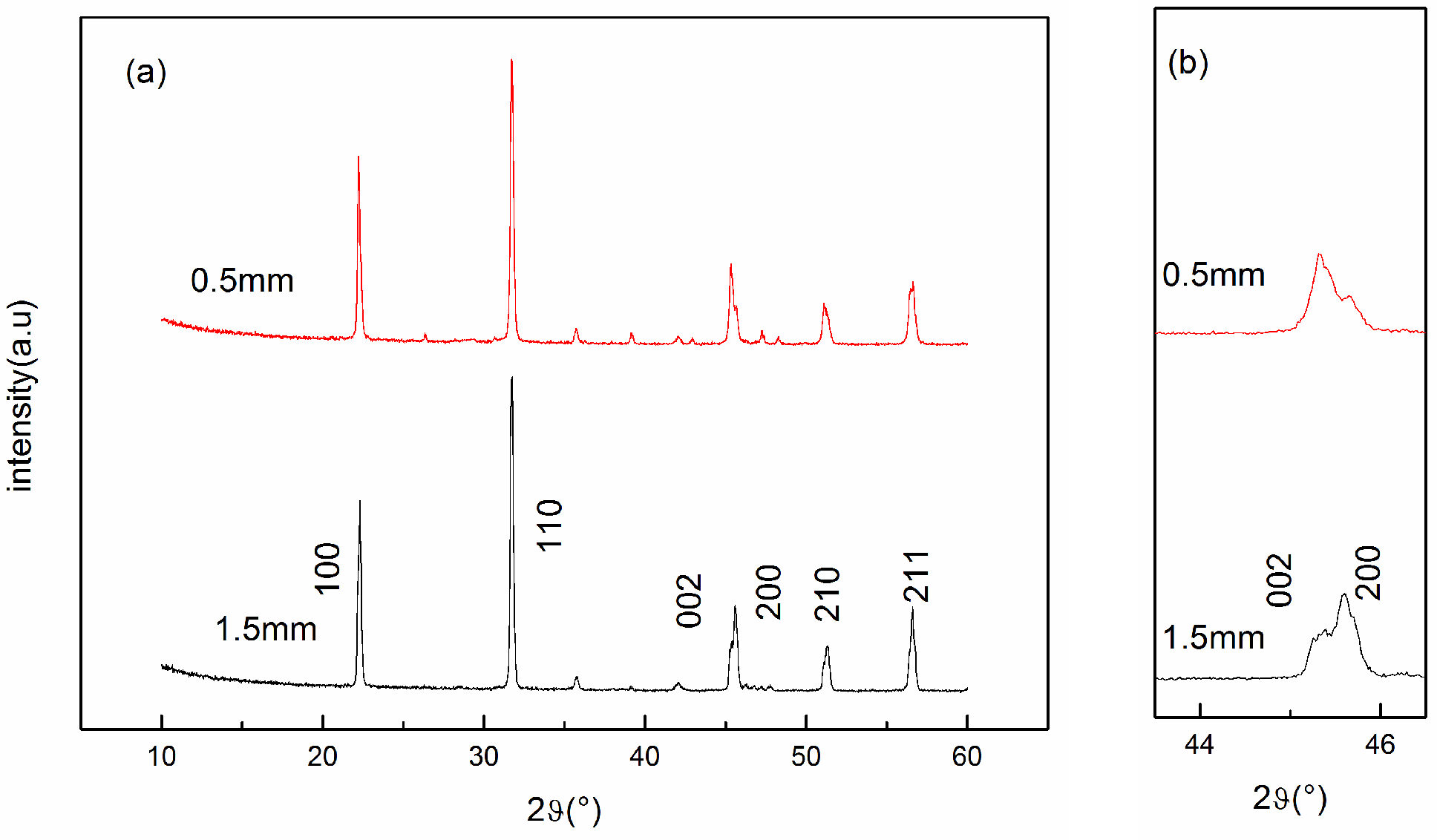

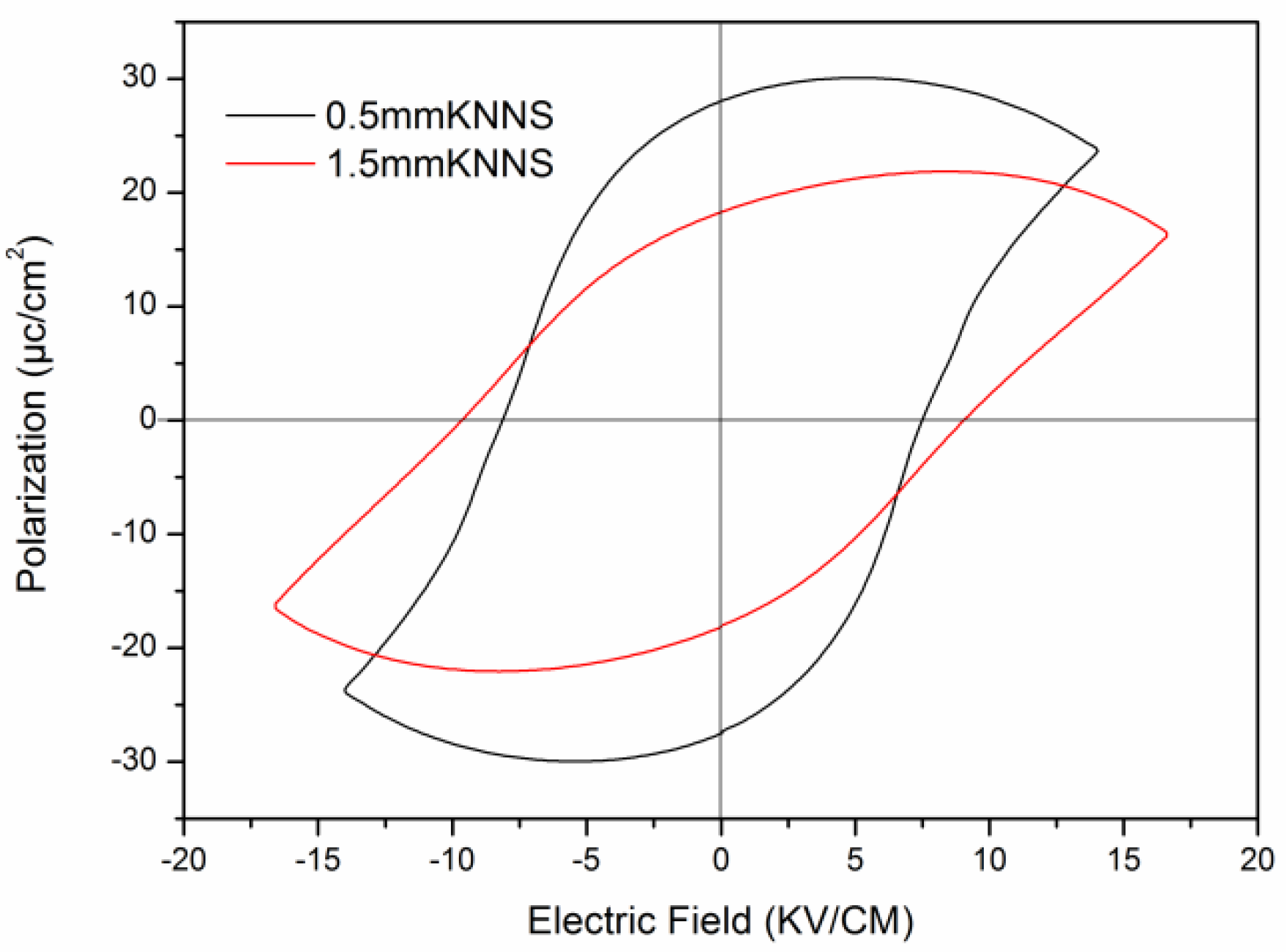
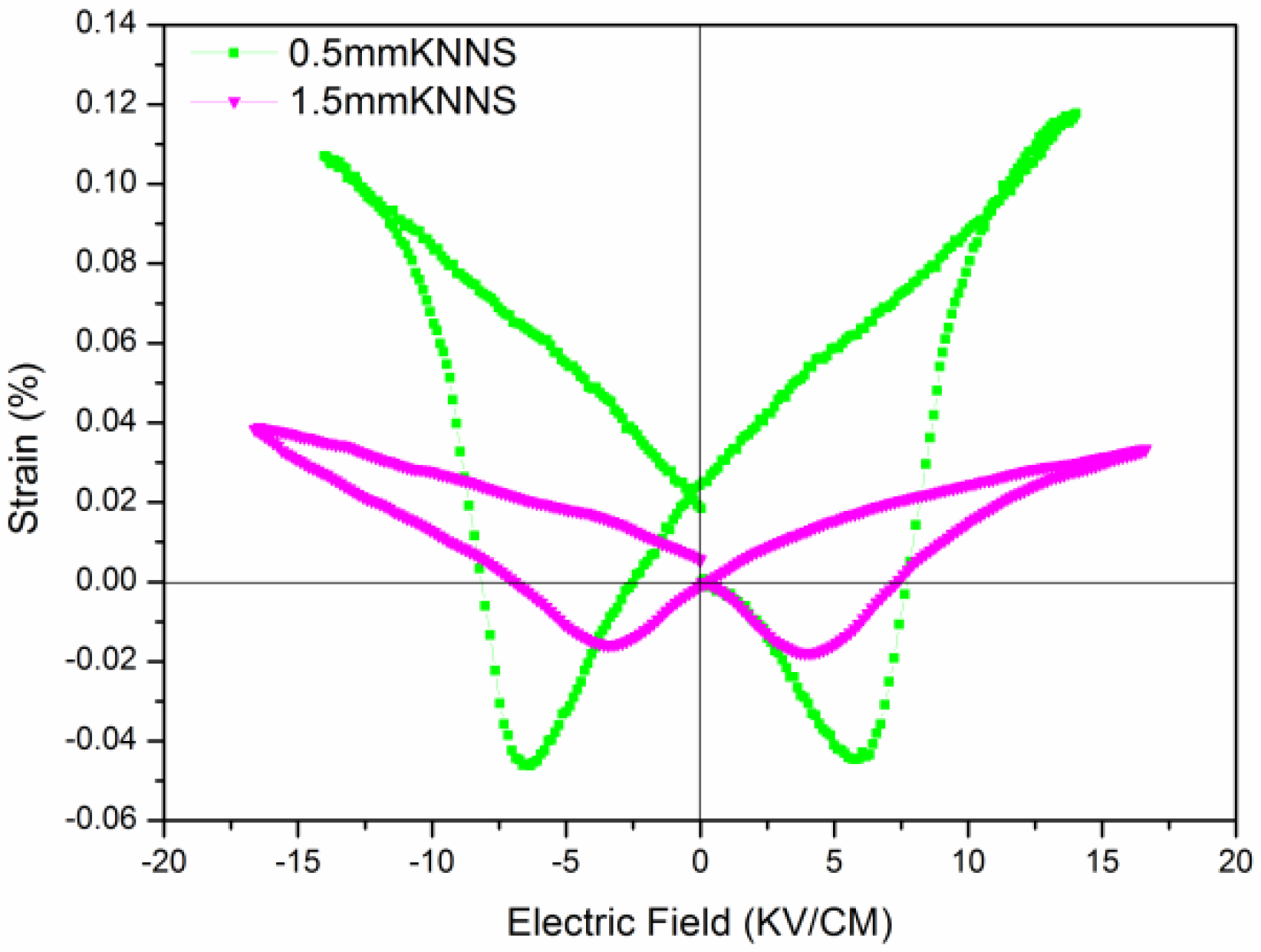
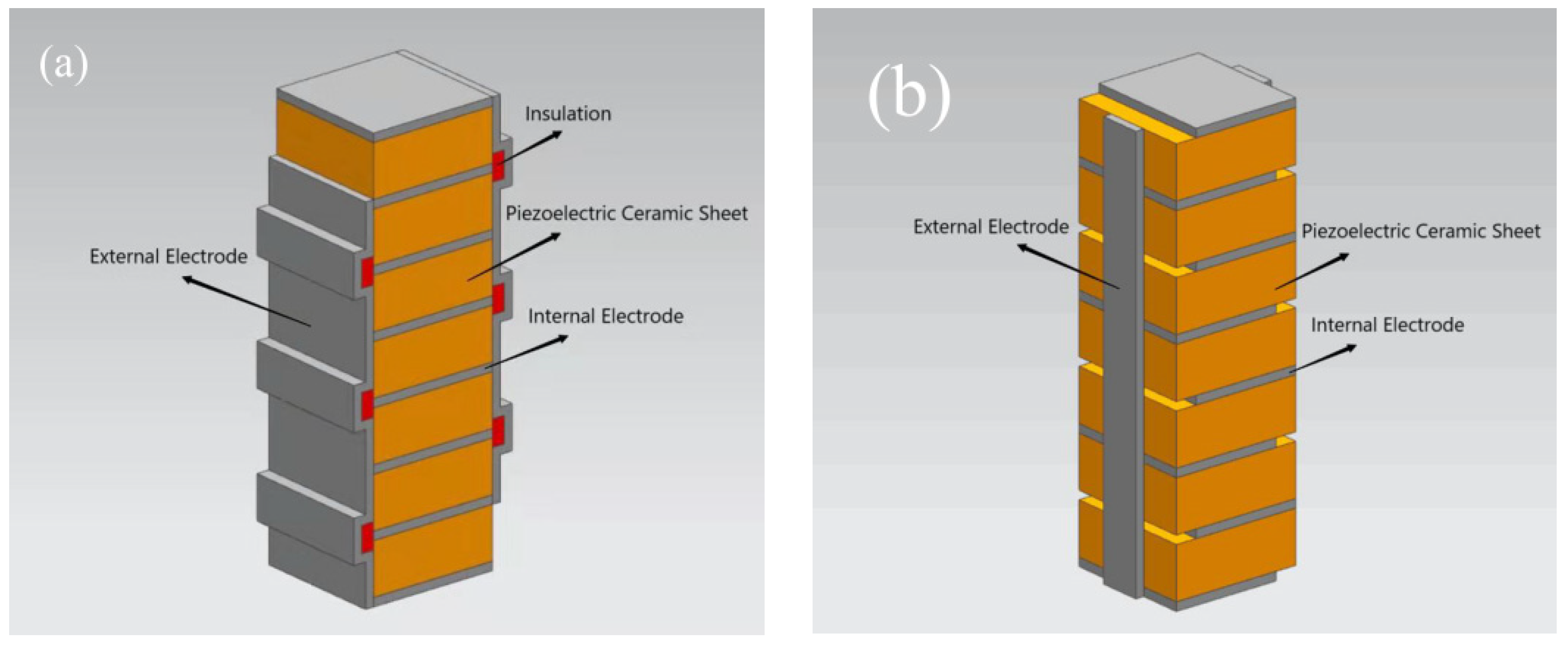


| Thickness | a(Å) | b(Å) | c(Å) | c/a |
|---|---|---|---|---|
| 1.5 mm | 7.9496 | 7.9496 | 7.9947 | 1.0057 |
| 0.5 mm | 8.0025 | 7.8802 | 7.9395 | 0.9921 |
| Samples | d33 (pC/N) | εr | Density (g/cm3) |
|---|---|---|---|
| 1.5 mm-thick | 198 | 1299.5 | 4.56 |
| 0.5 mm-thick | 268 | 1393.4 | 4.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Hang, Q.; Zheng, D.; Lin, F.; Chen, C. Fabrication of a Laminated Actuator with Excellent Linearity Using Ground Potassium Sodium Niobate-Based Ceramic Sheets. Inorganics 2024, 12, 18. https://doi.org/10.3390/inorganics12010018
Zhang Y, Hang Q, Zheng D, Lin F, Chen C. Fabrication of a Laminated Actuator with Excellent Linearity Using Ground Potassium Sodium Niobate-Based Ceramic Sheets. Inorganics. 2024; 12(1):18. https://doi.org/10.3390/inorganics12010018
Chicago/Turabian StyleZhang, Youming, Qiang Hang, Dongxi Zheng, Fei Lin, and Caifeng Chen. 2024. "Fabrication of a Laminated Actuator with Excellent Linearity Using Ground Potassium Sodium Niobate-Based Ceramic Sheets" Inorganics 12, no. 1: 18. https://doi.org/10.3390/inorganics12010018
APA StyleZhang, Y., Hang, Q., Zheng, D., Lin, F., & Chen, C. (2024). Fabrication of a Laminated Actuator with Excellent Linearity Using Ground Potassium Sodium Niobate-Based Ceramic Sheets. Inorganics, 12(1), 18. https://doi.org/10.3390/inorganics12010018








