Next Article in Journal
Methods for Obtaining Phosphorus-Containing Fertilizers Based on Industrial Waste
Next Article in Special Issue
Lu-Lu Bond in Lu2@C60 Metallofullerenes
Previous Article in Journal
Synthesis, X-ray Structure of Two Hexa-Coordinated Ni(II) Complexes with s-Triazine Hydrazine Schiff Base Ligand
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Inorganics
Volume 11
Issue 5
10.3390/inorganics11050223
inorganics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

DFT Analysis of the Electronic and Structural Properties of Lanthanide Nitride Cluster Fullerenes Ln3N@C80

by
César Martínez-Flores
and
Vladimir A. Basiuk
*
Instituto de Ciencias Nucleares, Universidad Nacional Autónoma de México, Circuito Exterior C.U., Ciudad de México 04510, Mexico
*
Author to whom correspondence should be addressed.
Inorganics 2023, 11(5), 223; https://doi.org/10.3390/inorganics11050223
Submission received: 19 April 2023 / Revised: 8 May 2023 / Accepted: 17 May 2023 / Published: 22 May 2023
(This article belongs to the Special Issue Research on Metallofullerenes)
Browse Figures
Versions Notes

Abstract

:
We have undertaken a DFT study of the nitride cluster fullerenes (NCFs) Ln3N@C80 for the complete series of fourteen lanthanides plus lanthanum by using the PBE functional with the Grimme’s dispersion correction (PBE-D2). We tested the DN and DND basis sets, which are equivalent to 6-31G and 6-31G(d) Pople-type basis sets, respectively. Due to the known convergence problems when treating lanthanide-containing systems, only with the DN basis set was it possible to complete the calculations (geometry optimization and analysis of selected electronic parameters) for all the fifteen NCFs. We found that the bending of the Ln3N cluster increases as the ionic radius increases, in general agreement with the available X-ray diffraction data. The Ln3N cluster becomes more planar as the Ln–N bond length is contracted, and the C80 cavity slightly deforms. The HOMO-LUMO energies and distribution, as well as the charge and spin of the encapsulated metal ions, are analyzed.

Graphical Abstract

1. Introduction

At the end of the last century, it was discovered experimentally that it was possible trap atoms or molecules (A) inside fullerene cages (Cn): the resulting complexes are referred to as endohedral fullerenes (EFs or endohedral metallofullerenes, EMFs, when A species contains metals) of the general formula A@Cn. The new structures were related to promises of application in many areas of medicine as magnetic resonance imaging contrast agents, single-molecule magnets, electron-spin quantum computing, etc. [1,2,3]. This was the logical next step in the chemistry of carbon nanoclusters after the experimental discovery of the C60 molecule via mass spectrometry in 1985 [4,5], when the efforts to obtain new related systems with unique geometrical and electronic properties dramatically increased [6,7]. The A@Cn structures described until present are based on the combination of different atoms/molecules and fullerenes of variable size. In 1999, Dorn and collaborators [8] reported on the synthesis of Sc3N@Ih(7)-C80, a member of a new family of EFs named nitride clusterfullerenes (NCFs). The NCFs encapsulate an M3N cluster where M usually is a rare-earth metal (Sc, Y or lanthanide), and the fullerene C2n cage comprises different sizes (60 < 2n < 88) [9]. The M3N cluster is made up of M3+ ions located at the vertices of a triangle, with the nitride N3− in its center. Neither the M3N cluster nor the C2n–Ih cage can be synthesized separately due to their lability, whereas their combination leads to the stabilization of NCF via the electron transfer of six electrons from the cluster to the carbon cage as it is suggested by experimental and theoretical data [10,11,12].
One of the most interesting NCF types is the one where the lanthanide (Ln) species are present in the internal cluster (Ln3N) due to the presence of 4f-electrons in their electronic configuration. The Ln-based combinations exhibit long spin relaxation lifetimes [13,14,15] and intriguing geometrical characteristics [16,17,18]. In some cases, the encapsulated Ln3N cluster suffers deformation from planar topology, depending on the Ln metal and cavity size. In addition, changes can be observed in the Ln–N bond length, the Ln–N–Ln angle between Ln and N species, as well as the C2n cage geometry. Such changes have been reported for a broad variety of cavity sizes and species [2,3,9].
A particularly interesting and important family is Ln3N@C80 NCFs. Here, one should emphasize that the previous experimental and theoretical research reports were limited to consideration of a few selected members of this family. The topology of the inner cluster has been analyzed both experimentally and theoretically. For example, this is the case for X-ray studies of Ln3N bending in Gd3N@C80 [19], Tb3N@C80 [20], Ho3N@C80 [21] and Er3N@C80 [21,22]. For Lu3N@C80 [23], the encapsulated species has a planar structure, explained by the fact that Lu has the smallest ionic radius of all lanthanides. Interestingly, the X-ray structural analysis turns out to be a very challenging task, since until now it has been impossible to crystallize pure Ln3N@C80 NCFs; the ‘trick’ which is used to obtain experimental geometries is to co-crystallize NCF with nickel (II) octaethylporphyrin [19,20,21,22,23]. The interaction between the two interacting units is very strong, so one cannot be totally sure whether it does not alter the Ln3N@C80 geometry. In this regard, theoretical calculations within the framework of density functional theory (DFT) on isolated NCFs have an evident advantage in terms of excluding the external influence of the above sort. Within this area, one should mention several efforts to characterize the geometrical and electronic properties of NCFs. For example, Aparicio-Anglès et al. [16] showed for M3N@C80 (where M = Sc, Y, La-Nd, Gd, Tb, Er, Tm and Lu), as well as for some other NCFs, that the bending of the M3N cluster increases as the atomic radius increases. Additionally, Schlesier et al. [24] used DFT calculations to analyze the geometrical features of some M3N@C80 members (namely, mixed dysprosium–lanthanide DyM2N@C80 and Dy2MN@C80, where M = Gd, Er, Tm and Lu), with a similar conclusion that the N atom is pushed out of the plane of Ln ions. On the other hand, to the best of our knowledge, the information on the frontier molecular orbital and spin density distribution in NCFs is rather scarce [7,25,26], with no published information on how they change during the step-by-step adding of 4f-electrons from La to Lu.
The changes in Ln–N bond lengths were analyzed previously both experimentally [21,27,28] and theoretically [16,24,29,30] for several NCFs. In particular, Olmstead et al. [21], Yang et al. [27] and Zuo et al. [28] reported the relevant experimental data for the Ho, Er, Dy and Tm NCFs. Aparicio-Anglès et al. [16] presented the DFT-calculated values for the Ln–N bond length for selected lanthanides including La-Nd, Gd, Tb and Er-Lu, and found it shortened as the ionic radius decreased. Both the above values and the ones reported by Schlesier et al. [24] and Gan et al. [29] for Gd, Dy, Er and Lu NCFs are in good agreement with the experimental parameters. On the other hand, again, there are no published DFT-calculated values comprising the complete lanthanide series.
In the present work we made an attempt to trace how the main geometrical and electronic properties of Ln3N@C80 NCFs change for the complete series from lanthanum to lutetium, that is, during the step-by-step addition of 4f-electrons. The DFT functional of choice was PBE, same as in the most systematic related study by Aparicio-Anglès et al. [16] (though, periodic plane wave calculations instead of cluster calculations were employed in their work). Nevertheless, our approach has an important difference from the latter, where for Tb, Er, Tm and Lu ions, having very deep 4f orbitals, the f electrons were considered for simplicity to be in the core (that is, included in the pseudopotential); in our case, to fulfill our goal, all the 4f electrons had to be included explicitly.

2. Results and Discussion

Selected geometrical parameters, orbital energies and other electronic properties for Ln3N@C80 NCFs were calculated by using the DN and DND basis sets (Table 1, Table 2, Table 3 and Table 4 and Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7). We considered the complete series of lanthanides with the purpose of tracing the effect of a step-by-step adding of 4f-electrons on the selected geometrical and electronic parameters of NCFs. It was also important to verify to what degree the results can vary when using the basis sets of different sizes.
Table
Table 1. Three Ln–N bond lengths (in Å), Ln–N–Ln angles (in °), the pyramidalization (θ) angle of the Ln3N cluster (in °), Ln⋯Ln distances (in Å), and the N⋯CC80 distance between N and the nearest C80 aromatic ring (in Å) were calculated by using the DN basis set.
Table 1. Three Ln–N bond lengths (in Å), Ln–N–Ln angles (in °), the pyramidalization (θ) angle of the Ln3N cluster (in °), Ln⋯Ln distances (in Å), and the N⋯CC80 distance between N and the nearest C80 aromatic ring (in Å) were calculated by using the DN basis set.
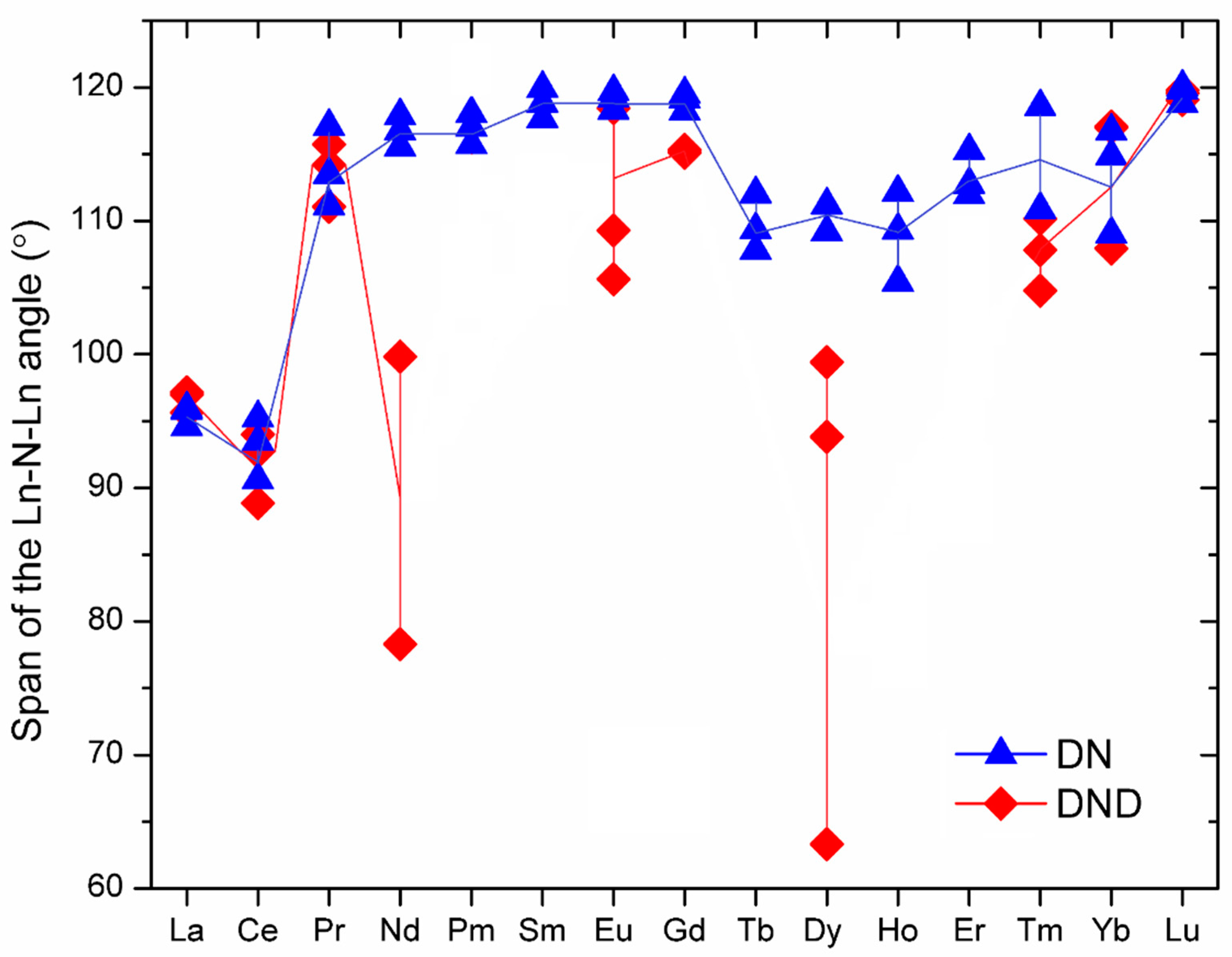
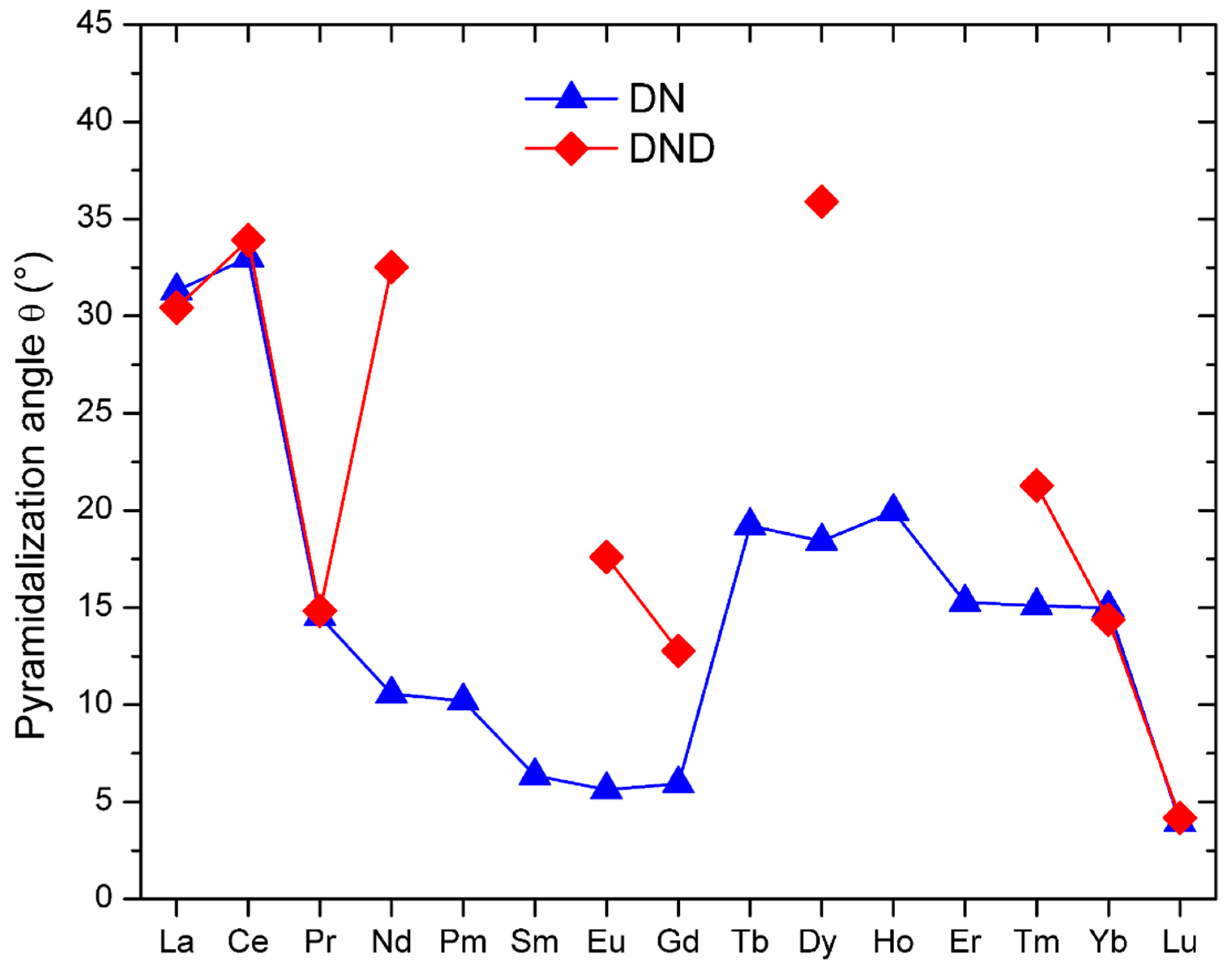
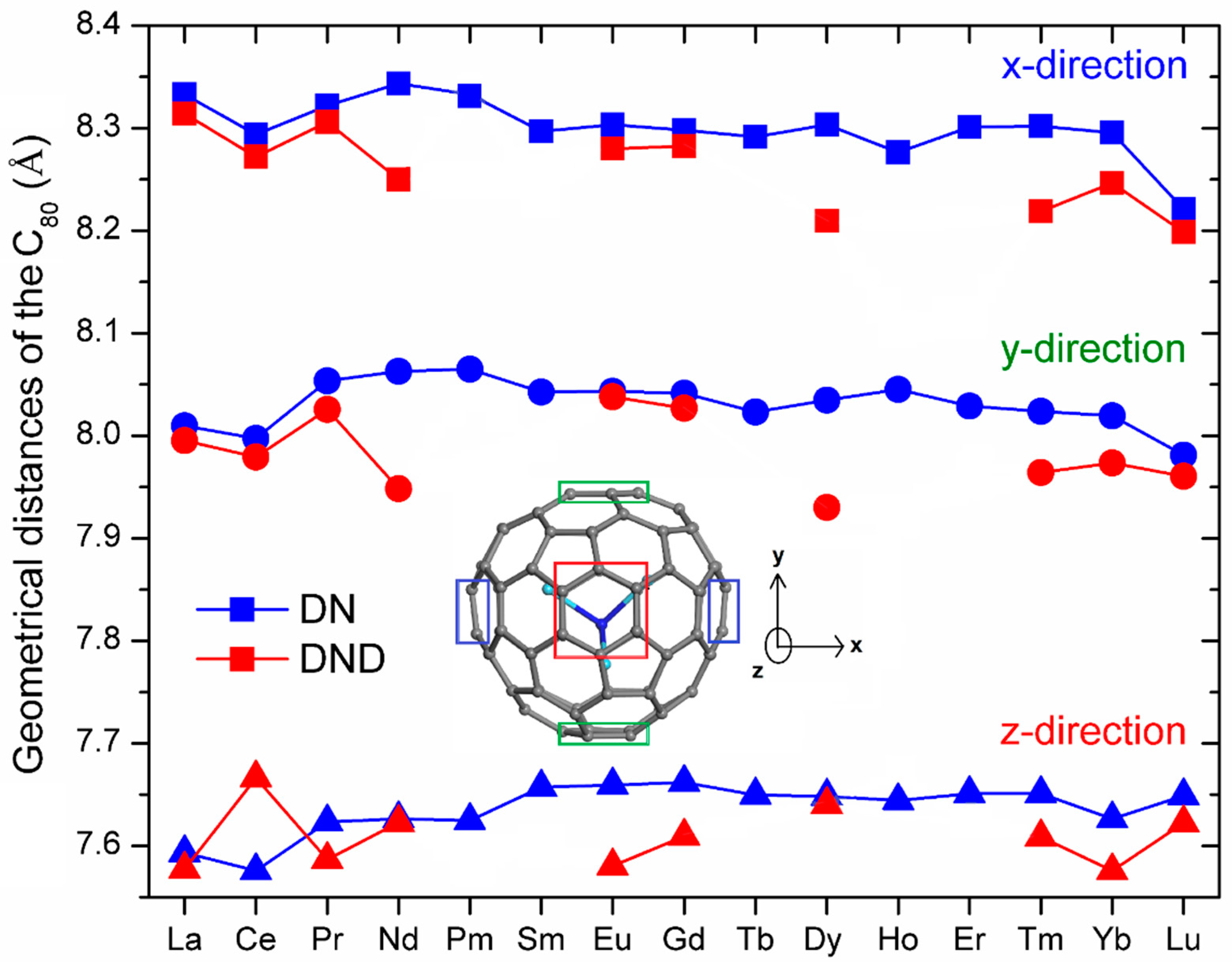
NFCLn–N (Å)Ln–N–Ln (°)θ (°)Ln⋯Ln (Å)N⋯CC80 (Å)
La3N@C802.247, 2.260, 2.26594.6, 95.8, 96.031.33.325, 3.345, 3.3522.949
Ce3N@C802.179, 2.223, 2.24290.6, 93.5, 95.233.03.174, 3.206, 3.2662.962
Pr3N@C802.068, 2.082, 2.165111.1, 113.5, 117.114.53.503, 3.540, 3.5403.597
Nd3N@C802.079, 2.086, 2.090115.5, 116.7, 117.910.63.533, 3.550, 3.5683.758
Pm3N@C802.076, 2.085, 2.086115.7, 117.0, 118.010.23.532, 3.550, 3.5683.770
Sm3N@C802.058, 2.059, 2.084117.7, 118.8, 119.96.43.543, 3.564, 3.5663.925
Eu3N@C802.064, 2.065, 2.068118.3, 119.2, 119.75.63.548, 3.564, 3.5693.948
Gd3N@C802.064, 2.065, 2.066118.2, 119.1, 119.55.93.546, 3.56, 3.5673.957
Tb3N@C802.090, 2.108, 2.126107.8, 109.4, 112.019.23.422, 3.441, 3.4813.443
Dy3N@C802.097, 2.112, 2.116109.2, 109.2, 111.218.43.431, 3.446, 3.4773.461
Ho3N@C802.081, 2.128, 2.132105.4, 109.3, 112.220.03.433, 3.496, 3.8893.423
Er3N@C802.069, 2.084, 2.086112.0, 112.7, 115.315.33.444, 3.472, 3.5083.617
Tm3N@C802.056, 2.065, 2.092110.8, 110.9, 118.615.13.415, 3.423, 3.5433.593
Yb3N@C802.022, 2.086, 2.088109.0, 114.9, 116.715.03.398, 3.464, 3.4973.543
Lu3N@C802.047, 2.049, 2.050118.8, 119.8, 120.03.93.528, 3.545, 3.5483.985
Table
Table 2. Three Ln–N bond lengths (in Å), Ln–N–Ln angles (in °), the pyramidalization (θ) angle of the Ln3N cluster (in °), Ln⋯Ln distances (in Å), and the N⋯CC80 distance between N and the nearest C80 aromatic ring (in Å) were calculated by using the DND basis set.
Table 2. Three Ln–N bond lengths (in Å), Ln–N–Ln angles (in °), the pyramidalization (θ) angle of the Ln3N cluster (in °), Ln⋯Ln distances (in Å), and the N⋯CC80 distance between N and the nearest C80 aromatic ring (in Å) were calculated by using the DND basis set.
NFCLn–N (Å)Ln–N–Ln (°)θ (°)Ln⋯Ln (Å)N⋯CC80 (Å)
La3N@C802.236, 2.251, 2.25295.6, 97.0, 97.230.43.360, 3.366, 3.3372.983
Ce3N@C802.177, 2.223, 2.24688.9, 92.7, 94.033.93.126, 3.184, 3.2352.933
Pr3N@C802.048, 2.120, 2.129111.1, 114.2, 115.714.83.503, 3.508, 3.5303.563
Nd3N@C802.054, 2.310, 2.31078.3, 99.8, 99.832.52.917, 3.343, 3.3432.998
Eu3N@C802.039, 2.090, 2.223105.6, 109.3, 118.417.63.446, 3.487, 3.5483.462
Gd3N@C802.078, 2.093, 2.096115.1, 115.3, 115.312.83.520, 3.526, 3.5393.692
Dy3N@C801.984, 2.304, 2.47763.3, 93.8, 99.435.93.275, 3.277, 2.5132.935
Tm3N@C802.060, 2.123, 2.132104.8, 107.8, 110.221.33.370, 3.388, 3.4293.366
Yb3N@C802.014, 2.084, 2.086117.0, 117.1, 108.014.43.373, 3.494, 3.4973.551
Lu3N@C802.054, 2.054, 2.054119.1, 119.6, 119.84.23.541, 3.550, 3.5543.994
From La to Lu, the Ln3N cluster shows geometrical changes in Ln–N bond lengths, Ln–N–Ln angles, Ln⋯Ln distances, N⋯CC80 distances (between N and the nearest C80 ring), and the bending degree. These changes are due to the electrostatic repulsion between the fullerene cage and the Ln3N unit, which depends on the size of the metal ion (Table 1 and Table 2; Figure 1 and Figure 2). In the case of Ln–N bond lengths, the DN results are close to the ones obtained previously experimentally [19,20,21,22,27,28,31] and theoretically [22,23,24,29,32,33], with the present DFT values tending to be slightly higher (except for Nd [16], Gd and Lu [16,24,33] NCFs). The average calculated values for La and Ho NCFs reach a maximum discrepancy of 4.4% and 3.7% in comparison with the computational results of Gan et al. [29] and experimental values of Olmstead et al. [21], respectively. In general, the trend in Ln–N bond length changes can be described as follows: a notable contraction is observed from La3N@C80 (2.247–2.265 Å; Table 1 and Figure 1) to Gd3N@C80 (2.064–2.066 Å), then an increase for Tb3N@C80 (2.090–2.126 Å), followed by a gradual decrease until the end of the series, that is, Lu3N@C80 (2.047–2.05 Å). The largest span of Ln–N bond lengths was found for Pr (0.097 Å). The experimental values by Olmstead et al. [21], Yang et al. [27] and Zuo et al. [28] showed a similar reduction in Ln–N bond length in the series of Dy-Tm NCFs, as with the DFT-computed data reported previously [22,23,24,29,32,33]. In the present study, with the DN basis set, within the entire series two general situations can be observed: in most cases, only two Ln–N bonds have the same (or almost the same) length (La, Pr-Sm and Dy-Yb), whereas for the Eu, Gd and Lu NCFs, all three bond lengths are almost exactly equal.
Inorganics 11 00223 g001 550
Figure 1. Comparison of the three Ln–N bond lengths in Ln3N@C80 NCFs calculated by using the DN and DND basis sets.
Figure 1. Comparison of the three Ln–N bond lengths in Ln3N@C80 NCFs calculated by using the DN and DND basis sets.
Inorganics 11 00223 g001
Regarding the geometries obtained with the DND basis sets (Table 2 and Figure 1), the general trend of Ln–N bond contraction can be seen in two (incomplete) series: La-Gd and especially Dy-Lu. However, this conclusion is not as straightforward as the one made for the DN basis set. The reason is that the use of the DND basis set results in too-rampant differences between the three Ln–N bond lengths, which are supposed to be more uniform, according to the experimental geometries ([21] and references therein). An especially ‘conflictive’ case is Dy3N@C80, for which the difference span reaches 0.493 Å, with the Dy–N bond lengths being 1.984, 2.304 and 2.477 Å; whereas the experimental ones are 2.017, 2.087 and 2.059 Å [21]; and the ones obtained with the DN basis set are 2.097, 2.112 and 2.116 Å (Table 1). The comparison of the two sets of results leads to a clear conclusion that, despite the prevailing idea that the use of a larger basis guarantees more realistic geometries (among other computed parameters), in the present case the smaller DN basis set is preferred to DND. In other words, for Ln3N@C80 NCFs we observe the same tendency as in the case of lanthanide ‘double-decker’ bisphthalocyanines that have been reported recently [34]. Taken together with the results of another study on Ln@C60 endohedral fullerenes [35], where no substantial effect of the basis set (DN vs. DND) on the calculated parameters was found, one can strongly suggest the use of DN for further theoretical investigations of lanthanide-containing NCFs, polyazamacrocyclic and probably some other classes of Ln compounds (at least when using the DMol3 module). Hereafter in this section we will place emphasis on the parameters obtained with the DN basis set for the same reasons. Coming back to the Ln–N bond lengths (Figure 1), one final observation to mention is that a reasonably good match between the DN and DND-computed values was obtained only for five lanthanides: La, Ce, Gd, Yb and Lu.
Inorganics 11 00223 g002 550
Figure 2. Comparison of the three Ln–N–Ln angles in Ln3N@C80 NCFs calculated by using the DN and DND basis sets.
Figure 2. Comparison of the three Ln–N–Ln angles in Ln3N@C80 NCFs calculated by using the DN and DND basis sets.
Inorganics 11 00223 g002
Another important and closely related geometric parameter is the Ln–N–Ln angle (Table 1 and Table 2; Figure 2), which directly reflects the effect of Ln3N confinement within the C80 cage. In the case of the DN basis set, the NCFs studied can be classified into two groups (though the difference between them is rather subtle): the three Ln–N–Ln values are notably different for Ce-Sm, Tb, Ho, Er and Yb; whereas for La, Eu, Gd, Dy, Tm and Lu, one value is different from the other two. The phenomenon of lanthanide contraction manifests itself in the general trend of increasing Ln–N–Ln angles in two separate series: Pr-Gd and Tb-Lu; in other words, the effect is not continuous from Pr to Lu. In addition, with the values for La and Ce NCFs, which have the largest Ln3+ ionic radii, the angles are much smaller than for all other Ln3N@C80 species, due to the strongest confinement. As a whole, this behavior correlates with the trends in the changes of Ln–N bond length; the larger Ln–N–Ln angles match the smaller Ln–N values. In the case of the DND basis set (Table 2; Figure 2), the changes in Ln–N–Ln angles from La to Lu are much more rampant, with very big differences between the three values for most NCFs, which is no surprise considering the results of the Ln–N bond length analysis presented above.
When comparing our results (obtained with the more reliable DN basis set) with that reported by other authors, for Er3N@C80 we found an average Er-N-Er angle of 113.3°, which differs from the experimental value [22] by 6%. In the case of Tb3N@C80 and Tm3N@C80, we obtained the average angles of 109.7° and 113.4°, respectively, which are up to 7% smaller than the values calculated by Aparicio-Anglès et al. [16], who used a very different theoretical approach (periodic calculations without inclusion of a dispersion correction and explicit consideration of the 4f-electrons).
Inorganics 11 00223 g003 550
Figure 3. Pyramidalization (θ) angle in Ln3N endohedral species calculated by using the DN and DND basis sets.
Figure 3. Pyramidalization (θ) angle in Ln3N endohedral species calculated by using the DN and DND basis sets.
Inorganics 11 00223 g003
The bending of the Ln3N cluster caused by the confinement within the C80 cage can also be characterized by the pyramidalization angle θ, which is referred to as one of the most important geometric parameters for NCFs [36]. Several experimental [19,20,21,23,37] and theoretical [6,16,24,33] reports showed that the Ln3N cluster can acquire a planar or bent shape depending on the Ln metal and the size of the C2n cavity. In most cases, large fullerene cages favor planar geometry [24]. The θ values obtained are summarized in Table 1 and Table 2 and Figure 3. The ones obtained with the DN basis set exhibit more uniform behavior compared to the rampant ones calculated with DND, in particular, a more uniform decrease, which is split into two series of Ce-Gd and Tb-Lu. Only for La, Ce, Yb and Lu did the DN and DND values approximately coincide, with the lowest θ values of 3.9 and 4.2°, respectively, found for the Lu3N cluster. As a whole, the θ angles presented here are larger compared to the experimental [19,20,21,28] and DFT-calculated ones [16,17,18,19,20,28] reported by other authors, and again, the DN basis set yields more realistic results. On the other hand, it is difficult to explain why the experimental θ values for the central lanthanides Gd, Tb and Dy uniformly decrease (14.6, 12.6 and 7.4°, respectively; [21] and references therein), but the DN-computed angles jump from 5.9° for Gd to 19.2° and to 18.4° for Tb and Dy, respectively. One should remember, however, that the experimental values were obtained for NCF–Ni(II) octaethylporphyrin co-crystals (where solvent molecules are present as well), and it remains unclear how the solid-state environment can influence the geometry of encapsulated Ln3N species.
Inorganics 11 00223 g004 550
Figure 4. Average distances between opposite aromatic rings of fullerene cage in Ln3N@C80 NCFs calculated by using the DN and DND basis sets. The x- (horizontal), y- (vertical) and z-directions (into the plain of view) are considered, as explained by the inset.
Figure 4. Average distances between opposite aromatic rings of fullerene cage in Ln3N@C80 NCFs calculated by using the DN and DND basis sets. The x- (horizontal), y- (vertical) and z-directions (into the plain of view) are considered, as explained by the inset.
Inorganics 11 00223 g004
Other geometric parameters of interest are the Ln⋯Ln and N⋯CC80 distances (between the N atom and the nearest hexagon/pentagon ring of C80 cage) [16,29], which directly depend on the bending of the Ln3N cluster (Table 1 and Table 2; Figures S1 and S2 of the Electronic Supplementary Information). For example, the N⋯CC80 distances exhibit behavior opposite to the behavior of the θ values, since the increase in pyramidalization results in a closer approach of the N atom to the fullerene cage.
The presence of encapsulated bulky Ln3N clusters leads to slight geometrical changes in the geometry of the C80 cage. It can be expressed in different ways. As Figure 4 explains, the way we did it is to measure average distances between two opposite C–C bonds in the x-direction, between two opposite pentagonal rings in the y-direction, and between two opposite hexagons in the z-direction. As calculated with the DN basis set, the C80 cage exhibits relatively stable geometry with variations of 0.12 (x-direction), 0.08 (y-direction) and 0.09 Å (z-direction) between the maximum (La and Nd for x-; Pm for y-; Sm-Gd for z-direction) and minimum (Lu for x- and y-directions; Ce for z-direction) distances. As a general trend, the cage is compressed in the x- and y-directions, and at the same time slightly elongates in the z-direction, as the atomic number of lanthanides increases. Like for all the above parameters analyzed, the use of the DND basis sets yields very rampant values without clear trends.
Table
Table 3. HOMO, LUMO and HOMO-LUMO gap energies (in eV), as well as the charge and spin values (in e; formal spin of Ln atom in parenthesis) for Ln3N@C80 NCFs calculated by using the DN basis set.
Table 3. HOMO, LUMO and HOMO-LUMO gap energies (in eV), as well as the charge and spin values (in e; formal spin of Ln atom in parenthesis) for Ln3N@C80 NCFs calculated by using the DN basis set.
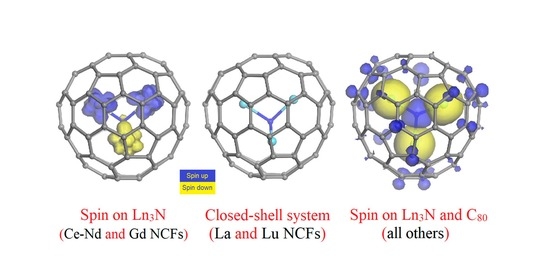
NFCEHOMO (eV)ELUMO (eV)Egap (eV)Charge (e)Spin (e) a
LnNLnN
La3N@C80−6.012−4.6401.3710.447, 0.467, 0.486−0.9250, 0, 0 (0)0
Ce3N@C80−5.818−4.9560.8620.397, 0.415, 0.439−0.8090.948, 0.992, 1.044 (1)0.042
Pr3N@C80−5.500−4.7980.7020.303, 0.352, 0.353−0.4532.063, 2.072, 2.103 (2)0.051
Nd3N@C80−5.923−4.9830.9410.160, 0.178, 0.180−0.6343.147, 3.162, 3.179 (3)0.179
Pm3N@C80−5.976−5.2480.7280.054, 0.070, 0.080−0.6964.223, 4.256, 4.268 (4)0.066
Sm3N@C80−5.956−5.6600.2960.424, 0.434, 0.463−0.8375.441, 5.446, 5.474 (5)0.446
Eu3N@C80−5.940−5.8680.0720.426, 0.441, 0.469−0.8576.646, 6.649, 6.661 (6)0.627
Gd3N@C80−6.046−4.5891.4570.496, 0.512, 0.527−0.9926.899, 6.934, 6.935 (7)0.028
Tb3N@C80−5.979−5.7910.1890.409, 0.430, 0.454−0.8275.519, 5.520, 5.530 (6)0.198
Dy3N@C80−5.974−5.9000.0740.412, 0.412, 0.435−0.8244.338, 4.387, 4.409 (5)0.109
Ho3N@C80−5.952−5.8820.0700.457, 0.499, 0.505−0.8623.350, 3.360, 3.384 (4)0.058
Er3N@C80−5.961−5.8720.0890.467, 0.487, 0.542−0.8782.377, 2.393, 2.421 (3)0.083
Tm3N@C80−5.960−5.8350.1250.368, 0.375, 0.420−0.8221.263, 1.268, 1.273 (2)0.005
Yb3N@C80−5.942−5.8590.0830.417, 0.420, 0.445−0.8550.012, 0.099, 0.110, (1)0.053
Lu3N@C80−6.034−4.5061.5280.557, 0.584, 0.595−1.0740, 0, 0 (0)0
a Absolute values.
Table 3 and Table 4 summarize the calculated HOMO, LUMO and HOMO-LUMO gap (Egap) energies, as well as the charge and spin (from Mulliken population analysis) of Ln and N atoms as calculated with the DN and DND basis sets. For the frontier orbital energies, obtained with either the DN or DND basis set, no clear trend is observed (Table 3 and Table 4), with La, Gd and Lu NCFs having similar values for LUMO energies with both basis sets. The DN-calculated Egap energies (Table 3) tend to decrease in the entire NCF series, with the exception of the ‘jumping-back’ values for Nd, Gd and Lu derivatives. These species with totally empty (La), half-filled (Gd) and totally filled (Lu) 4f orbitals exhibit the highest gap values of 1.371, 1.457 and 1.528 eV, respectively; these results are in good agreement with the DFT-calculated values by Zhu et al. [38]. As a whole, Egap spans from 0.070 (Ho3N@C80) to 1.528 eV (Lu3N@C80) with DN, and from 0.084 (Dy3N@C80) to 1.485 eV (La and Lu3N@C80), with no clear trend, when the DND basis set is used (Table 4). Here, it is appropriate to mention that the GGA functionals (including PBE) tend to underestimate HOMO-LUMO gap energies, and we present the values obtained simply to illustrate their relative behavior from La to Lu.
Table
Table 4. HOMO, LUMO and HOMO-LUMO gap energies (in eV), as well as the charge and spin values (in e; formal spin of Ln atom in parenthesis) for Ln3N@C80 NCFs calculated by using the DND basis set.
Table 4. HOMO, LUMO and HOMO-LUMO gap energies (in eV), as well as the charge and spin values (in e; formal spin of Ln atom in parenthesis) for Ln3N@C80 NCFs calculated by using the DND basis set.
NFCEHOMO (eV)ELUMO (eV)Egap (eV)Charge (e)Spin (e) a
LnNLnN
La3N@C80−5.769−4.2841.4850.962, 0.962, 0.962−1.0210, 0, 0 (0)0
Ce3N@C80−5.459−4.6950.7640.829, 0.837, 0.838−0.8891.052, 1.079, 1.101 (1)0.116
Pr3N@C80−5.214−4.5370.6770.050, 0.082, 0.086−0.7582.047, 2.047, 2.065 (2)0.051
Nd3N@C80−5.579−5.1400.4380.060, 0.164, 0.174−0.5453.185, 3.220, 3.297 (3)0.127
Eu3N@C80−5.649−5.5580.0900.888, 0.907, 0.907−0.9336.567, 6.608, 6.703 (6)0.243
Gd3N@C80−5.739−4.3651.3730.854, 0.857, 0.857−1.1366.866, 6.910, 6.913 (7)0.031
Dy3N@C80−5.634−5.5500.0840.696, 0.867, 0.901−0.7424.175, 4.159, 4.446 (5)0.261
Tm3N@C80−5.673−5.5730.1000.819, 0.823, 0.832−0.9641.266, 1.282, 1.288 (2)0.114
Yb3N@C80−5.650−5.5630.0880.845, 0.862, 0.862−1.0120.014, 0.114, 0.122 (1)0.085
Lu3N@C80−5.758−4.2721.4850.882, 0.884, 0.884−1.2150, 0, 0 (0)0
a Absolute values.
As we mentioned in Introduction, the Ih-C80 fullerene is a very reactive molecule per se [1,3], but its combination with some other species (M3N, M2, etc.) gives stable complexes [1,2,9,10,39,40]; this stabilizing effect is due to electron transfer from the encapsulated species to the carbon cage. Formally, in the case of rare-earth derivatives M3N@C80, the M3N cluster is supposed to donate six electrons to C80. Nevertheless, it turns out that the “actual” charges are very different from “formal” charges, which are integers and imply that the cluster−cage bonding is purely ionic. This aspect was addressed in several theoretical studies (on representative Sc3N@C80), which found that the calculated net Sc3N charges are also much smaller than the values expected for the purely ionic bonding [41,42]; for example, around +1, either from the Mulliken or Hirshfeld population analysis [42]. This effect is referred to as “back-donation” [43,44]. Additionally, in our calculations, the actual positive charge on Ln atoms (Table 3 and Table 4; from the Mulliken population analysis) was much lower than the “formal” charge of +3; in particular, it spans from 0.054–0.080 e (Pm3N) to 0.557–0.595 e (Lu3N) with the DN basis set, and from 0.050–0.086 e (Pr3N) to 0.962 e (La3N) with DND. For the N atom, the values vary from −0.453 e (Pr3N) to −1.074 e (Lu3N) with DN, and from −0.545 e (Nd3N) to −1.215 e (Lu3N) with DND. The DN-calculated absolute values are generally lower than the DND ones. It is interesting and important to mention the observation that the use of a smaller basis set produces more reliable results for the Mulliken population analysis [45,46,47].
Inorganics 11 00223 g005 550
Figure 5. Selected patterns of HOMO-LUMO distributions (isosurfaces at 0.03 a.u.) in Ln3N@C80 NCFs calculated by using the DN basis set.
Figure 5. Selected patterns of HOMO-LUMO distributions (isosurfaces at 0.03 a.u.) in Ln3N@C80 NCFs calculated by using the DN basis set.
Inorganics 11 00223 g005
Figure 5 shows the selected patterns of the HOMO and LUMO distribution obtained with the DN basis set. After analyzing these plots for the complete NCF series, it was not possible to classify them in a simple way due to a large variability in the results (with both basis sets). Here, we show the four most distinctive cases (La, Pr, Gd and Ho NCFs) obtained with the DN basis set (the reader can find all the plots for the fifteen NCFs in Electronic Supplementary Information, in Figures S3–S6; with the aim of completeness of the graphical presentation, both the front and the side views are included.) As can be seen in Figure 5, the HOMO lobes in the case of La and Gd NFCs are very similar: they are localized on the C80 cage, with no apparent contribution from the Ln3N cluster. In the case of Ho NCF, the HOMO distribution on fullerene cage is rather similar to the one found for La and Gd complexes, but a minor contribution from the Ho3N cluster can be observed as well. For Pr3N@C80, the HOMO lobes are localized mostly on two Pr atoms, whereas the contribution from the C80 cage is minimal. For the LUMO density, the lobes on Ln and N atoms are of highly variable size; of the ones presented in Figure 5, the largest ones can be seen for the La3N cluster. The LUMO lobes on the fullerene cage almost vanish for La, Ce, Nd, Pm, Sm and Tb NCFs. The results obtained with DND (Figures S5–S6) only partially match the ones calculated by using the DN basis set.
As compared to the formal spin for isolated Ln3+ ions, the results obtained with the DN and DND basis sets (Table 3 and Table 4; Figure 6) show the possibility of spin transfer both to and from lanthanide species. In the DN data set (Table 3), spin depletion from Ln can be observed for Ce (but from two cerium atoms only) and the late lanthanides Gd-Yb (by up to 0.890–0.988 e for Yb, compared to to the formal spin of 1 e for isolated Yb3+); this can be also seen from Figure 6 (here we plotted the average values for simplicity). The early lanthanides Pr-Eu tend to acquire additional spin, with the strongest increase by 0.646–0.661 e observed for Eu (compared to the formal spin of 6 e for isolated Eu3+). For La and Lu ions with totally empty and totally filled 4f orbitals, respectively, the spin remains to be zero. The limited available values calculated by using the DND basis set (Table 4 and Figure 6) follow a similar trend.
Inorganics 11 00223 g006 550
Figure 6. Comparison of the average spin of three Ln ions in Ln3N@C80 NCFs calculated by using the DN and DND basis sets with the formal spin of isolated Ln3+ ions.
Figure 6. Comparison of the average spin of three Ln ions in Ln3N@C80 NCFs calculated by using the DN and DND basis sets with the formal spin of isolated Ln3+ ions.
Inorganics 11 00223 g006
The spin density plots for Ln3N@C80 NCFs presented in Figure 7 (the DN data set) cannot serve as a similar quantitative measure of spin transfer, but instead are more illustrative, especially in order to show variability in spin alignment. In the most simplistic terms of spin distribution, they can be classified into three general cases. The first one includes La and Lu NCFs (with the closed-shell electronic configuration of Ln species), where no unpaired electrons can be found on either the Ln3N cluster or C80 cage (the corresponding side views are shown in Figure S7). In the case of Ce-Nd and Gd NCFs, the main contribution comes from the Ln3N cluster, where the largest lobes are localized on metal species. For the remaining NCFs (Pm-Eu, Tb-Yb), spin density can be found on both the cluster and fullerene cage. In the calculations with the DND basis set, qualitatively similar spin density plots were obtained (Figures S8 and S9 of the Electronic Supplementary Information).
Inorganics 11 00223 g007 550
Figure 7. Spin density plots (isosurfaces at 0.02 a.u.) for Ln3N@C80 complexes as calculated by using the DN basis set. Blue and yellow lobes correspond to spin-up and spin-down electrons, respectively.
Figure 7. Spin density plots (isosurfaces at 0.02 a.u.) for Ln3N@C80 complexes as calculated by using the DN basis set. Blue and yellow lobes correspond to spin-up and spin-down electrons, respectively.
Inorganics 11 00223 g007
As regards the spin-up and spin-down directions, they turned out to be broadly variable as well. When considering Ln3N cluster only, all the NCFs can be classified into the following groups: (1) the spin directions of all four atoms coincide (spin-up) for Tb, Dy and Yb; (2) the spin directions of three Ln atoms coincide, but for the N atom it is the opposite, which is observed for Nd, Sm and Eu; (3) the spin directions of Ln atoms differ (2 + 1) for all the remaining NCFs (Ce, Pr, Pm, Gd, Ho, Er and Tm). One should also note that in three cases of Tb, Dy and Yb derivatives, the spin directions of Ln3N atoms (spin-up) are the same as those of the small lobes found on the carbon atoms of the C80 cage.

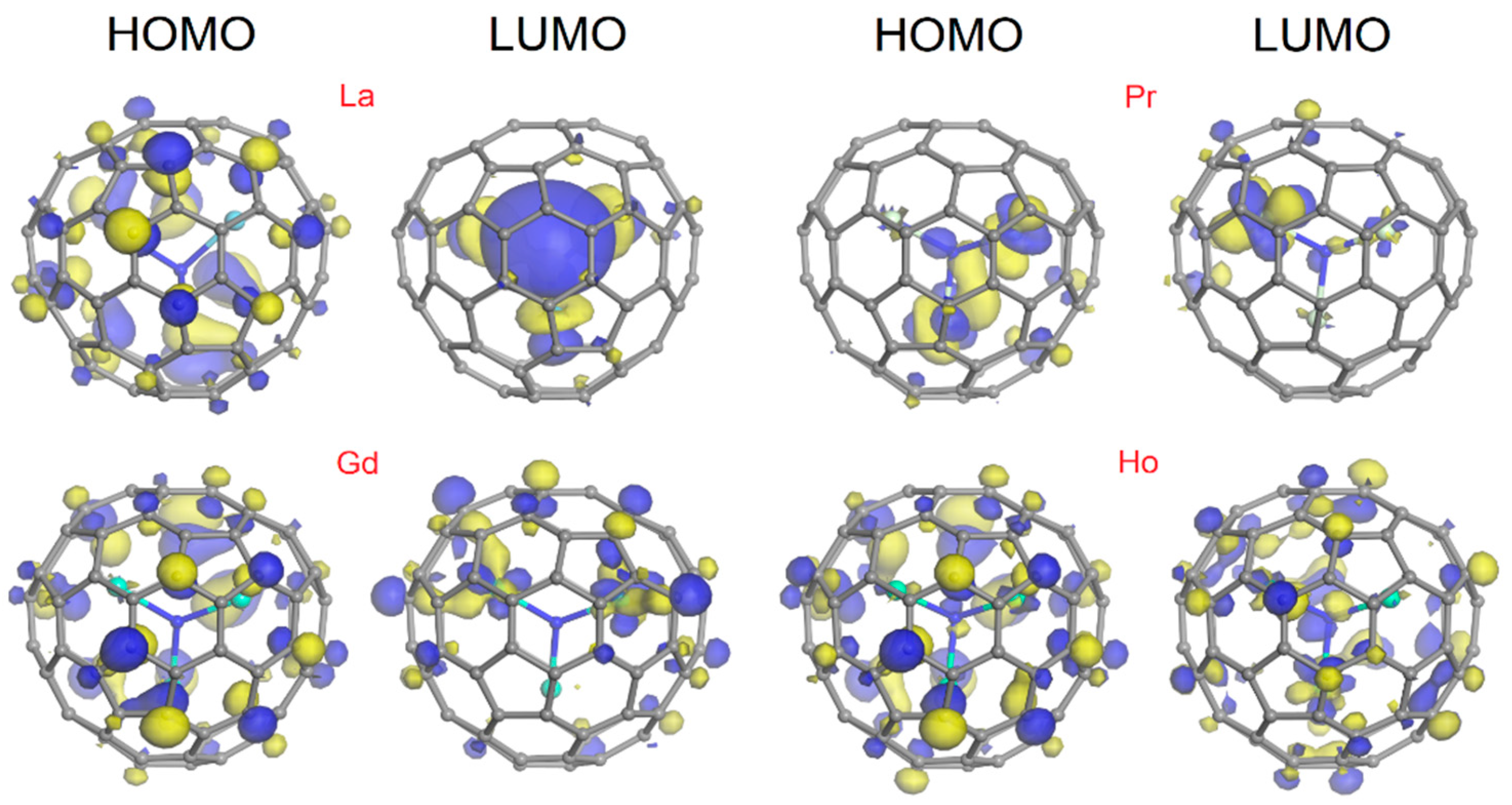
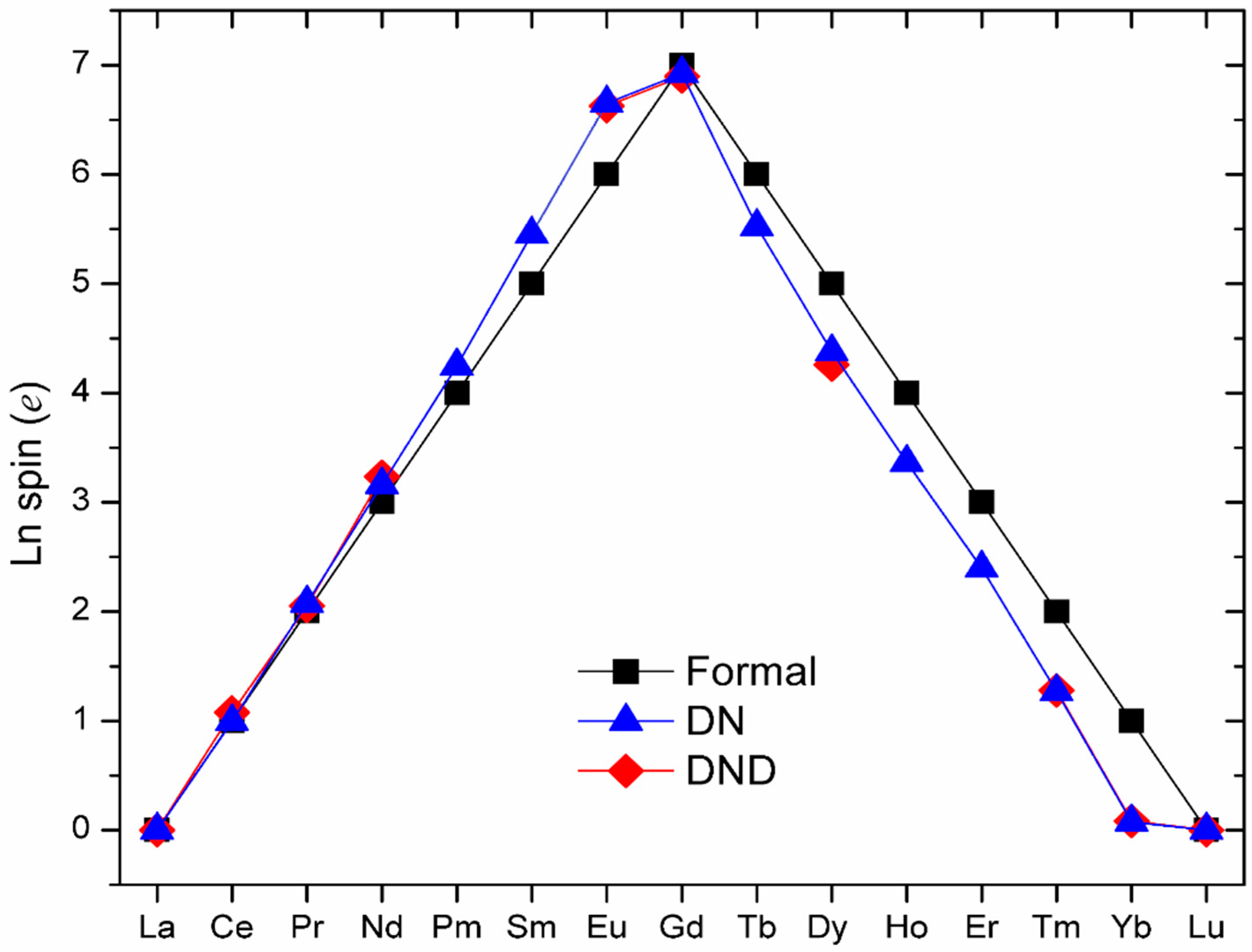
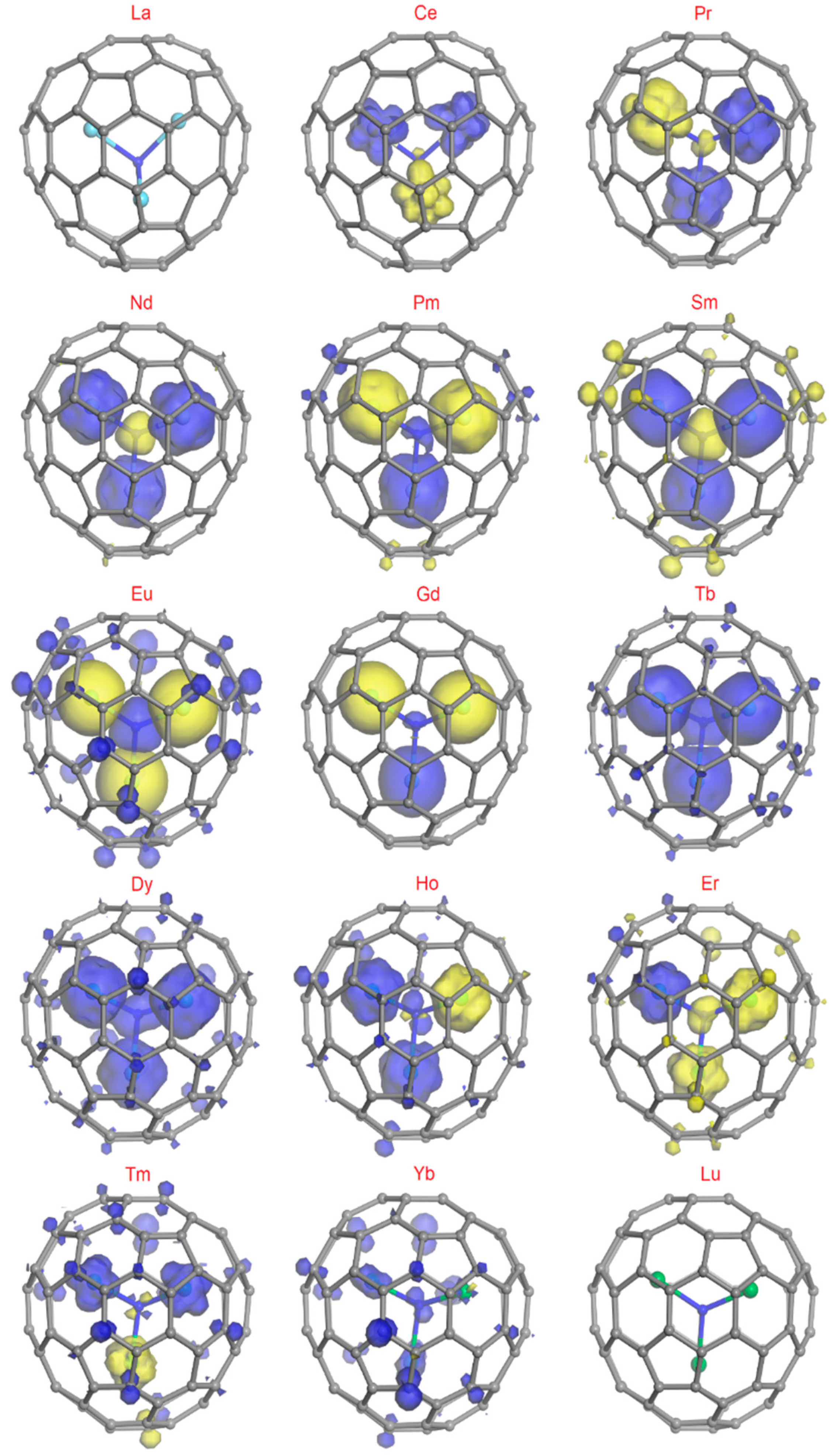
3. Computational Methods

The theoretical analysis of the geometries and electronic properties of Ln3N@C80 NCFs was performed by using the numerical-based DFT module DMol3, which is a part of the Materials Studio 8.0 software package [48,49,50,51]. The Perdew–Burke–Ernzerhof (PBE) general gradient approximation functional [52] was employed in combination with the empirical dispersion correction developed by Grimme [53], usually referred to as PBE-D (or PBE-D2). The previous computational method was successfully used in our previous studies involving C80-based dyads [25,54], as well as in numerous studies by other research groups on systems that include metal species and carbon nanoclusters.
The DN (with no polarization functions added) and DND (with a polarization d-function added on all non-hydrogen atoms) double-numerical basis sets were employed, which are equivalent to the 6-31G and 6-31G(d) Pople-type basis sets. The full geometry optimization and the calculation of the electronic parameters were performed with the DFT semi-core pseudopotentials (DSPPs), including relativistic and spin-orbit coupling effects, whose account is important due to the presence of the lanthanide species. In the calculations with the DN basis set, the real space cutoff (defined by the presence of lanthanide species) was 4.3 Å and a DND of 5.0 Å. The convergence criteria were as follows: For the DN basis set, an energy gradient of 10−4 Ha/Å, maximum force of 0.02 Ha/Å, maximum displacement of 0.05 Å, and SCF tolerance of 10−4 Ha; for the DND basis set, an energy gradient of 2∙10−5 Ha/Å, maximum force of 0.004 Ha/Å, maximum displacement of 0.005 Å, and SCF tolerance of 10−5 Ha.
The existence of 4f orbitals results in a high number of degenerate states near the Fermi level, which has a serious negative impact on the self-consistent field (SCF) convergence. Thermal smearing was employed as an indispensable tool to solve the (almost always inevitable) SCF convergence problems according to the general protocol explained in the previous studies [55,56]. It was found that the use of a very low value of 0.0001 Ha (equivalent temperature of 31.6 K) yields stable and consistent results. At the same time, even with the use of thermal smearing tools, only for the DN basis set was a successful convergence afforded for all Ln3N@C80 NCFs. With DND, we were unable to finish the calculations for Pm-, Sm-, Tb-, Ho- and Er-containing systems.

4. Conclusions

The most important results can be summarized as follows.
(1) The geometry optimization and electronic parameter calculation for the series of fifteen Ln3N@C80 NCFs (Ln = La-Lu) was possible to complete only with the DN basis set. The use of DND basis sets leads to SCF convergence problems, due to which it was impossible to obtain the results for Pm-, Sm-, Tb-, Ho- and Er-containing systems. Furthermore, within the NCFs for which the computations seemed to be successful, too-rampant behavior was observed for most important geometric parameters (including the Ln–N bond lengths, Ln–N–Ln angles, and pyramidalization angle θ), which is supposed to be more uniform and logical.
(2) For the frontier orbital energies, obtained with either the DN or DND basis set, no clear trend is observed. The DN-calculated Egap energies tend to decrease in the entire NCF series, with the exception of the ‘jumping-back’ values for Nd, Gd and Lu derivatives. These species with totally empty (La), half-filled (Gd) and totally filled (Lu) 4f orbitals exhibit the highest gap values of 1.371, 1.457 and 1.528 eV, respectively, which are in good agreement with the DFT results reported elsewhere. The corresponding HOMO and LUMO distribution patterns are highly variable.
(3) The calculated “actual” positive charge on Ln atoms, as estimated from the Mulliken population analysis, is much lower than the “formal” charge of +3; it spans from 0.054–0.080 e (Pm3N) to 0.557–0.595 e (Lu3N) with the DN basis set, and from 0.050–0.086 e (Pr3N) to 0.962 e (La3N) with DND. Similarly, for the N atom, the values vary from −0.453 e (Pr3N) to −1.074 e (Lu3N) with DN, and from −0.545 e (Nd3N) to −1.215 e (Lu3N) with DND. These results are in good agreement with the known effect of “back-donation”.
(4) As compared to the formal spin for isolated Ln3+ ions, the results obtained show the possibility of spin transfer both to and from lanthanide species. In the DN data set, spin depletion from Ln can be observed for Ce (but from two cerium atoms only) and the late lanthanides Gd-Yb, with it being up to 0.890–0.988 e for Yb. The early lanthanides Pr-Eu tend to acquire additional spin, with the strongest increase by 0.646–0.661 e observed for Eu. For La and Lu ions with totally empty and totally filled 4f orbitals, respectively, the spin remains to be zero. The spin density plots reveal interesting features in terms of localization of unpaired electrons, as well as spin alignment.

Supplementary Materials

Supplementary data associated with this article can be found in the online version at https://www.mdpi.com/article/10.3390/inorganics11050223/s1. Figure S1: Comparison of the Ln⋯Ln distance (Å) in Ln3N@C80 NCFs calculated by using the DN and DND basis sets; Figure S2: Comparison of the N⋯CC80 distance (Å) of the Ln3N@C80 complexes calculated by using the DN and DND basis sets; Figure S3: Complete patterns of HOMO-LUMO distribution (front views with isosurfaces at 0.03 a.u.) in Ln3N@C80 NCFs calculated by using the DN basis set; Figure S4: Complete patterns of HOMO-LUMO distribution (isosurfaces at 0.03 a.u.) in Ln3N@C80 NCFs but rotated at an angle of 90° to the left (side view) with respect to Figure S3; Figure S5: Patterns of HOMO-LUMO distribution (front views with isosurfaces at 0.03 a.u.) in Ln3N@C80 NCFs calculated by using the DND basis set; Figure S6: Patterns of HOMO-LUMO distribution (isosurfaces at 0.03 a.u.) in Ln3N@C80 NCFs but rotated at an angle of 90° to the left (side views) with respect to Figure S5; Figure S7: Spin density plots (isosurfaces at 0.02 a.u.) for Ln3N@C80 NCFs calculated by using the DN basis set but rotated an angle of 90° to the left (side views) with respect to Figure 7. Blue and yellow lobes correspond to spin-up and spin-down electrons, respectively; Figure S8: Spin density plots (isosurfaces at 0.02 a.u.) for Ln3N@C80 NCFs were calculated by using the DND basis set. Blue and yellow lobes correspond to spin-up and spin-down electrons, respectively; Figure S9: Spin density plots (isosurfaces at 0.02 a.u.) for Ln3N@C80 NCFs calculated by using the DND basis set but rotated an angle of 90° to the left (side views) with respect to Figure S8.

Author Contributions

Conceptualization, V.A.B.; methodology, V.A.B.; validation, C.M.-F.; formal analysis, C.M.-F.; investigation, C.M.-F.; data curation, C.M.-F.; writing—original draft preparation, C.M.-F.; writing—review and editing, V.A.B.; visualization, C.M.-F.; supervision, V.A.B.; funding acquisition, V.A.B. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Autonomous University of Mexico (UNAM), grant DGAPA-IN103622.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The raw/processed data required to reproduce these findings cannot be shared at this time due to technical limitations (their total size of a few GB).

Acknowledgments

C.M.-F. thanks to DGAPA-UNAM for the postdoctoral fellowship.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Chaur, M.N.; Melin, F.; Ortiz, A.L.; Echegoyen, L. Chemical, Electrochemical, and Structural Properties of Endohedral Metallofullerenes. Angew. Chem. Int. Ed. 2009, 48, 7514–7538. [Google Scholar] [CrossRef] [PubMed]
  2. Popov, A.A.; Yang, S.; Dunsch, L. Endohedral fullerenes. Chem. Rev. 2013, 113, 5989–6113. [Google Scholar] [CrossRef] [PubMed]
  3. Yang, S.; Wei, T.; Jin, F. When metal clusters meet carbon cages: Endohedral clusterfullerenes. Chem. Soc. Rev. 2017, 46, 5005–5058. [Google Scholar] [CrossRef] [PubMed]
  4. Heath, J.R.; O’Brien, S.C.; Zhang, Q.; Liu, Y.; Curl, R.F.; Tittel, F.K.; Smalley, R.E. Lanthanum complexes of spheroidal carbon shells. J. Am. Chem. Soc. 1985, 107, 7779–7780. [Google Scholar] [CrossRef]
  5. Kroto, H.; Heath, J.; O’Brien, S.; Curl, R.F.; Smalley, R.E. C60: Buckminsterfullerene. Nature 1985, 318, 162–163. [Google Scholar] [CrossRef]
  6. Shen, W.; Hu, S.; Lu, X. Endohedral Metallofullerenes: New Structures and Unseen Phenomena. Chem. Eur. J. 2020, 26, 5748–5757. [Google Scholar] [CrossRef]
  7. Miyazaki, T.; Hino, S. Electronic and Geometric Structures of Cluster Encapsulated Fullerenes. In Physics and Chemistry of Carbon-Based Materials; Kubozono, Y., Ed.; Springer: Singapore, 2019. [Google Scholar] [CrossRef]
  8. Stevenson, S.; Rice, G.; Glass, T.; Harich, K.; Cromer, F.; Jordan, M.R.; Craft, J.; Hadju, E.; Bible, R.; Olmstead, M.M.; et al. Small-bandgap endohedral metallofullerenes in high yield and purity. Nature 1999, 401, 55–57. [Google Scholar] [CrossRef]
  9. Dunsch, L.; Yang, S. Metal Nitride Cluster Fullerenes: Their Current State and Future Prospects. Small 2007, 3, 1298–1320. [Google Scholar] [CrossRef]
  10. Popov, A.A. (Ed.) Endohedral Fullerenes: Electron Transfer and Spin; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
  11. Campanera, J.M.; Bo, C.; Poblet, J.M. General Rule for the Stabilization of Fullerene Cages Encapsulating Trimetallic Nitride Templates. Angew. Chem. Int. Ed. 2005, 44, 7230–7233. [Google Scholar] [CrossRef]
  12. Jiang, Y.; Li, Z.; Wu, Y.; Wang, Z. Ln3@C80+ (Ln = lanthanide): A new class of stable metallofullerene cations with multicenter metal-metal bonding in the sub-nanometer confined space. Inorg. Chem. Front. 2022, 9, 2173–2181. [Google Scholar] [CrossRef]
  13. Bunzli, J.-C.G. Rising Stars in Science and Technology: Luminescent Lanthanide Materials. Eur. J. Inorg. Chem. 2017, 2017, 5058–5063. [Google Scholar] [CrossRef]
  14. Gaita-Ariño, A.; Luis, F.; Hill, S.; Coronado, E. Molecular spins for quantum computation. Nat. Chem. 2019, 11, 301–309. [Google Scholar] [CrossRef] [PubMed]
  15. Westerström, R.; Dreiser, J.; Piamonteze, C.; Muntwiler, M.; Weyeneth, S.; Brune, H.; Rusponi, S.; Nolting, F.; Popov, A.; Yang, S.; et al. An Endohedral Single-Molecule Magnet with Long Relaxation Times: DySc2N@C80. J. Am. Chem. Soc. 2012, 134, 9840–9843. [Google Scholar] [CrossRef] [PubMed]
  16. Aparicio-Anglès, X.; Alegret, N.; Clotet, A.; Rodríguez-Fortea, A.; Poblet, J.M. Endohedral Metallofullerenes Containing Lanthanides: A Robust Yet Simple Computational Approach. J. Phys. Chem. C 2013, 117, 12916–12921. [Google Scholar] [CrossRef]
  17. Nakanishi, R.; Satoh, J.; Katoh, K.; Zhang, H.; Breedlove, B.K.; Nishijima, M.; Nakanishi, Y.; Omachi, H.; Shinohara, H.; Yamashita, M. DySc2N@C80 Single-Molecule Magnetic Metallofullerene Encapsulated in a Single-Walled Carbon Nanotube. J. Am. Chem. Soc. 2018, 140, 10955–10959. [Google Scholar] [CrossRef] [PubMed]
  18. Li, B.; Gu, X.; Jin, P. Overlooked Effects of La-4f Orbitals in Endohedral Metallofullerenes. Inorg. Chem. 2022, 61, 5891–5902. [Google Scholar] [CrossRef]
  19. Stevenson, S.; Phillips, J.P.; Reid, J.E.; Olmstead, M.M.; Rath, S.P.; Balch, A.L. Pyramidalization of Gd3N inside a C80 cage. The synthesis and structure of Gd3N@C80. Chem. Commun. 2004, 2814–2815. [Google Scholar] [CrossRef]
  20. Zuo, T.; Beavers, C.M.; Duchamp, J.C.; Campbell, A.; Dorn, H.C.; Olmstead, M.M.; Balch, A.L. Isolation and structural characterization of a family of endohedral fullerenes including the large, chiral cage fullerenes Tb3N@C88 and Tb3N@C86 as well as the Ih and D5h isomers of Tb3N@C80. J. Am. Chem. Soc. 2007, 129, 2035–2043. [Google Scholar] [CrossRef]
  21. Olmstead, M.M.; Zuo, T.; Dorn, H.C.; Li, T.; Balch, A.L. Metal ion size and the pyramidalization of trimetallic nitride units inside a fullerene cage: Comparisons of the crystal structures of M3N@Ih-C80 (M = Gd, Tb, Dy, Ho, Er, Tm, Lu, and Sc) and some mixed metal counterparts. Inorg. Chim. Acta 2017, 1, 321–326. [Google Scholar] [CrossRef]
  22. Hu, S.; Zhao, P.; Shen, W.; Yu, P.; Huang, W.; Ehara, M.; Xie, Y.; Akasaka, T.; Lu, X. Crystallographic characterization of Er3N@C2n (2n = 80, 82, 84, 88): The importance of a planar Er3N cluster. Nanoscale 2019, 11, 13415–13422. [Google Scholar] [CrossRef]
  23. Shen, W.-Q.; Bao, L.-P.; Hu, S.-F.; Gao, X.-J.; Xie, Y.-P.; Gao, X.-F.; Huang, W.-H.; Lu, X. Isolation and crystallographic characterization of Lu3N@C2n (2n = 80 − 88): Cage selection by cluster size. Chem. Eur. J. 2018, 24, 16692–16698. [Google Scholar] [CrossRef] [PubMed]
  24. Schlesier, C.; Liu, F.; Dubrovin, V.; Spree, L.; Büchner, B.; Avdoshenko, S.M.; Popov, A.A. Mixed dysprosium-lanthanide nitride clusterfullerenes DyM2N@C80-Ih and Dy2MN@C80-Ih (M = Gd, Er, Tm, and Lu): Synthesis, molecular structure, and quantum motion of the endohedral nitrogen atom. Nanoscale 2019, 11, 13139–13153. [Google Scholar] [CrossRef] [PubMed]
  25. Basiuk, V.A.; Tahuilan-Anguiano, D.E. Complexation of free-base an 3d transition metal(II) phthalocyanines with endohedral fullerene Sc3N@C80. Chem. Phys. Lett. 2019, 722, 146–152. [Google Scholar] [CrossRef]
  26. Yamada, M.; Liu, M.T.H.; Nagase, S.; Akasaka, T. New Horizons in Chemical Functionalization of Endohedral Metallofullerenes. Molecules 2020, 25, 3626. [Google Scholar] [CrossRef] [PubMed]
  27. Yang, S.; Troyanov, S.I.; Popov, A.A.; Krause, M.; Dunsch, L. Deviation from the Planarity-a Large Dy3N Cluster Encapsulated in an Ih-C80 Cage:  An X-ray Crystallographic and Vibrational Spectroscopic Study. J. Am. Chem. Soc. 2006, 128, 16733–16739. [Google Scholar] [CrossRef]
  28. Zuo, T.; Olmstead, M.M.; Beavers, C.M.; Balch, A.L.; Wang, G.; Yee, G.T.; Shu, C.; Xu, L.; Elliott, B.; Echegoyen, L.; et al. Preparation and structural characterization of the Ih and the D5h isomers of the endohedral fullerenes Tm3N@C80: Icosahedral C80 cage encapsulation of a trimetallic nitride magnetic cluster with three uncoupled Tm3+ ions. Inorg. Chem. 2008, 47, 5234–5244. [Google Scholar] [CrossRef]
  29. Gan, L.-H.; Yuan, R. Influence of cluster size on the structures and stability of trimetallic nitride fullerenes M3N@C80. ChemPhysChem 2006, 7, 1306–1310. [Google Scholar] [CrossRef]
  30. Slanina, Z.; Uhlík, F.; Feng, L.; Akasaka, T.; Lu, X.; Adamowicz, L. Calculations of the Lu3N@C80 two-isomer equilibrium. Fuller. Nanotub. Carbon Nanostruct. 2019, 27, 382–386. [Google Scholar] [CrossRef]
  31. Krause, M.; Dunsch, L. Gadolinium nitride Gd3N in carbon cages. The influence of cluster size and bond strength. Angew. Chem. Int. Ed. 2005, 44, 1557–1560. [Google Scholar] [CrossRef]
  32. Lu, J.; Sabirianov, R.F.; Mei, W.N.; Gao, Y.; Duan, C.G.; Zeng, X.C. Structural and magnetic properties of Gd3N@C80. J. Phys. Chem. B 2006, 110, 23637–23640. [Google Scholar] [CrossRef]
  33. Zhang, Z.X.; Liu, Y.; Han, P.D.; Zhuang, S.Y.; Wang, T.S.; Luo, S.C.; Xum, B.S. Metallofullerenes encaging mixed-metal clusters: Synthesis and structural studies of GdxHo3−xN@C80 and GdxLu3−xN@C80. ChemPhysChem 2015, 16, 295–298. [Google Scholar] [CrossRef] [PubMed]
  34. Martínez-Flores, C.; Bolivar-Pineda, L.M.; Basiuk, V.A. Lanthanide bisphthalocyanine single-molecule magnets: A DFT survey of their geometries and electronic properties from lanthanum to lutetium. Mater. Chem. Phys. 2022, 287, 126271. [Google Scholar] [CrossRef]
  35. Martínez-Flores, C.; Basiuk, V.A. Ln@C60 endohedral fullerenes: A DFT analysis for the complete series from lanthanum to lutetium. Comp. Theor. Chem. 2022, 1217, 113878. [Google Scholar] [CrossRef]
  36. Thomsen, C.; Reich, S. Raman Scattering in Carbon Nanotubes. In Light Scattering in Solid IX. Topics in Applied Physics; Cardona, M., Merlin, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; Volume 108. [Google Scholar] [CrossRef]
  37. Stevenson, S.; Lee, H.M.; Olmstead, M.M.; Kozikowski, C.; Stevenson, P.; Balch, A.L. Preparation and crystallographic characterization of a new endohedral, Lu3N@C80∙5 (o-xylene), and comparison with Sc3N@C80∙5 (o-xylene). Eur. J. Chem. 2002, 8, 4528–4535. [Google Scholar] [CrossRef]
  38. Zhu, Y.; Li, Y.; Yang, Z.Q. First-principles investigation on the electronic structures of intercalated fullerenes M3N@C80 (M = Sc, Y, and lanthanides). Chem. Phys. Lett. 2008, 4614, 285–289. [Google Scholar] [CrossRef]
  39. Koltover, V.K.; Bubnov, V.P.; Estrin, Y.I.; Lodygina, V.P.; Davydov, R.M.; Subramoni, M.; Manoharan, P.T. Spin-transfer complexes of endohedral metallofullerenes: ENDOR and NMR evidences. Phys. Chem. Chem. Phys. 2003, 5, 2774–2777. [Google Scholar] [CrossRef]
  40. Dunsch, L.; Krause, M.; Noack, J.; Georgi, P. Endohedral nitride cluster fullerenes: Formation and spectroscopic analysis of L3−xMxN@C2n (0 ≤ x ≤ 3; N = 39, 40). J. Phys. Chem. Solids 2004, 65, 309–315. [Google Scholar] [CrossRef]
  41. Popov, A.A.; Dunsch, L. Hindered cluster rotation and 45Sc hyperfine splitting constant in distonoid anion radical Sc3N@C80−, spatial spin−charge separation as a general principle for anions of endohedral fullerenes with metal-localized lowest unoccupied molecular orbitals. J. Am. Chem. Soc. 2008, 130, 17726–17742. [Google Scholar] [CrossRef]
  42. Valencia, R.; Rodríguez-Fortea, A.; Poblet, J.M. Understanding the stabilization of metal carbide endohedral fullerenes M2C2@C82 and related systems. J. Phys. Chem. A 2008, 112, 4550–4555. [Google Scholar] [CrossRef]
  43. Liu, D.; Hagelberg, F.; Park, S.S. Charge transfer and electron backdonation in metallofullerenes encapsulating NSc3. Chem. Phys. 2006, 330, 380–386. [Google Scholar] [CrossRef]
  44. Wu, J.; Hagelberg, F. Computational study on C80 enclosing mixed trimetallic nitride clusters of the form GdxM3−xN (M = Sc, Sm, Lu). J. Phys. Chem. C 2008, 112, 5770–5777. [Google Scholar] [CrossRef]
  45. Lu, J.; Zhang, X.; Zhao, X. Relativistic electronic structure calculations on endohedral Gd@C60, La@C60, Gd@C74, and La@C74. App. Phys. A 2000, 70, 461–464. [Google Scholar] [CrossRef]
  46. Slanina, Z.; Uhlík, F.; Akasaka, T.; Lu, X.; Adamowicz, L. Computational modeling of the Ce@C82 metallofullerene isomeric composition. ECS J. Solid State Sci. Technol. 2019, 8, M118–M121. [Google Scholar] [CrossRef]
  47. Slanina, Z.; Uhlík, F.; Akasaka, T.; Lu, X.; Adamowicz, L. Calculated relative thermodynamic stabilities of the Gd@C82 isomers. ECS J. Solid State Sci. Technol. 2021, 10, 071013. [Google Scholar] [CrossRef]
  48. Delley, B. An all-electron numerical method for solving the local density functional for polyatomic molecules. J. Chem. Phys. 1990, 92, 508–517. [Google Scholar] [CrossRef]
  49. Delley, B. Fast calculation of electrostatics in crystals and large molecules. J. Phys. Chem. 1996, 100, 6107–6110. [Google Scholar] [CrossRef]
  50. Delley, B. From molecules to solids with the DMol3 approach. J. Chem. Phys. 2000, 113, 7756–7764. [Google Scholar] [CrossRef]
  51. Delley, B.; Ellis, D.; Freeman, A.; Baerends, E.; Post, D. Binding energy and electronic structure of small copper particles. Phys. Rev. B 1983, 27, 2132–2144. [Google Scholar] [CrossRef]
  52. Perdew, J.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
  53. Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
  54. Basiuk, V.A.; Basiuk, E.V. Noncovalent complexes of Ih-C80 fullerene with phthalocyanines. Fuller. Nanotub. Carbon Nanostruct. 2018, 26, 69–75. [Google Scholar] [CrossRef]
  55. Basiuk, V.A. Electron smearing in DFT calculations: A case study of doxorubicin interaction with single-walled carbon nanotubes. Int. J. Quantum Chem. 2011, 111, 4197–4205. [Google Scholar] [CrossRef]
  56. Basiuk, V.A.; Prezhdo, O.V.; Basiuk, E.V. Thermal smearing in DFT calculations: How small is really small? A case of La and Lu atoms adsorbed on graphene. Mater. Today Commun. 2020, 25, 101595. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Martínez-Flores, C.; Basiuk, V.A. DFT Analysis of the Electronic and Structural Properties of Lanthanide Nitride Cluster Fullerenes Ln3N@C80. Inorganics 2023, 11, 223. https://doi.org/10.3390/inorganics11050223

AMA Style

Martínez-Flores C, Basiuk VA. DFT Analysis of the Electronic and Structural Properties of Lanthanide Nitride Cluster Fullerenes Ln3N@C80. Inorganics. 2023; 11(5):223. https://doi.org/10.3390/inorganics11050223

Chicago/Turabian Style

Martínez-Flores, César, and Vladimir A. Basiuk. 2023. "DFT Analysis of the Electronic and Structural Properties of Lanthanide Nitride Cluster Fullerenes Ln3N@C80" Inorganics 11, no. 5: 223. https://doi.org/10.3390/inorganics11050223

APA Style

Martínez-Flores, C., & Basiuk, V. A. (2023). DFT Analysis of the Electronic and Structural Properties of Lanthanide Nitride Cluster Fullerenes Ln3N@C80. Inorganics, 11(5), 223. https://doi.org/10.3390/inorganics11050223

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop