Abstract
The progress of modern electronics largely depends on the possible emergence of previously unknown materials in electronic technology. The search for and combination of new materials with extraordinary properties used for the production of new small-sized electronic devices and the improvement of the properties of existing materials due to improved technology for their manufacture and processing, in general, will determine the progress of highly promising electronics. In order to solve the problematic tasks of the miniaturization of electronic components with an increase in the level of connection of integrated circuits, new forms of electronic devices are being created using nanomaterials with controlled electrophysical characteristics. One of the unique properties of fullerene structures is that they can enclose one or several atoms inside their carbon framework. Such structures are usually called endohedral fullerenes. The electronic characteristics of endohedral fullerenes significantly depend on the properties of the encapsulated atom, which makes it possible to control them by choosing the encapsulated atom required by the property. Within the framework of the density functional theory in combination with the method of the nonequilibrium Green’s functions, the features of electron transport in fullerene nanojunctions were considered, which demonstrate “core–shell” nanoobjects, the “core” of which is an alkali halide crystal—KI—and the “shell” of which is an endohedral fullerene C180 located between the gold electrodes (in the nanogap). The values of the total energy and the stability diagram of a single-electron transistor based on endohedral fullerene (KI)@C180 were determined. The dependence of the total energy of fullerene molecules on the charge state is presented. The ranges of the Coulomb blockade, as well as their areas associated with the central Coulomb diamond were calculated.
1. Introduction
Presently, it has become clear that the possibilities of silicon-based semiconductor electronics are limited. It turned out to be impossible to increase the speed of electronic systems and, at the same time, reduce the size and energy expended [1,2]. However, this problem can be solved by creating new materials for electronic technology. In this case, it is natural to first carry out the computer simulation and calculation of various electrophysical properties of new materials before starting their synthesis. To solve the problems of the miniaturization of electronic components with an increase in the degree of integration of circuits, new types of electronic devices are being developed using nanomaterials with controlled electrophysical properties [3,4,5].
At present, the use of different types of carbon nanostructures in various areas of life, from the biomedical domain to solar energy, is widely known [6,7,8,9,10,11,12,13,14,15,16,17]. There are several works, both experimental [18,19,20,21] and using computer simulations [22,23], on the study of the crystallography of various alkali iodides grown in single-walled carbon nanotubes. Since single-walled carbon nanotubes have a relatively simple atomic structure with well-defined dimensions, they can be considered as test objects for testing theoretical hypotheses in the field of materials science of low-dimensional systems. In [18], the growth of MI (M = Li, Na, K, Rb, Cs) inside SWNTs was studied by visualization using high-resolution transmission electron microscopy. It was found that, inside SWNTs with diameters of 1.4 nm and 1.6 nm, encapsulated KI nanocrystals with the structures (2 × 2 × ∞) and (3 × 3 × ∞), respectively, are effectively formed. In this case, for all iodides from Li to Rb, the structure corresponded to fcc, and only for CsI to bcc. In crystals whose thickness did not exceed 2–6 atomic layers, an increase in the lattice constant up to 12% was recorded, which was interpreted as a decrease in the coordination at the crystal–carbon interface. It is noted that defects in nanotubes and tube bending can significantly cause changes in the crystal growth behavior and even block it completely in some cases. The possibility of growing various low-dimensional objects (CdCl2, TbCl3, BaI2, ZrCl4) inside a carbon nanotube was shown in [20]. In [22,23], an attempt was made to explain the previously recorded experimental results from encapsulated KI and CsI nanocrystals using computer simulation using the GULP program. It has been found that the electronic properties of empty nanotubes, as well as the charge transfer in encapsulated materials play essential roles in determining their crystal structures and electrical properties. Therefore, this may extend to most “guest–host” systems.
Another type of low-dimensional system consisting of carbon atoms is fullerene—a convex, closed polyhedron. As in SWNTs, other chemical elements (atoms, small molecules) can be located inside the carbon cage. In this case, the fullerene is endohedral [24,25,26]. A distinctive feature of endohedral fullerenes is their unusual electronic properties [26,27]. In [25], the synthesis, isolation, and electrochemical properties of endohedral fullerenes of metal nitrides Gd3N@C82 and Gd3N@C86 were demonstrated.
There are several experimental works [25] in which it was demonstrated that fullerenes could be used to create single-electron transistors (SETs), since this is resistant to changes in electric charge. At present, SETs are promising devices in nanoelectronics, the mechanism of action of which is realized based on the phenomenon of correlated electron tunneling and Coulomb blockade. The main elements of the SET are the island and the control electrode. The island must be necessarily separated by the tunnel transitions of the electrodes, the so-called “drain+source”. The control electrode solely affects this island due to capacitive coupling, which is a “gate”. At present, works are known in which the realized possibility of using single molecules or atoms as single-electron devices is indicated [28,29].
The uniqueness of the endohedral fullerene lies in the fact that the carbon shell can be considered negatively charged, while the object placed inside the carbon frame is like a positively charged core.
Due to the fact that there were works on the introduction of alkali metal iodides into carbon nanostructures, in order to create a single-electron transistor, the authors of the work placed an alkali halide KI crystal inside the C180 endohedral fullerene. In this paper, an attempt was made, within the framework of density functional theory and the method of the nonequilibrium Green’s functions, to determine the values of the total energy and the stability diagrams of the MEP based on endohedral fullerene (KI)@C180.
2. Geometry
It is known that one of the unique properties of fullerene structures is that they can enclose one or more atoms inside their carbon framework. The electronic properties of endohedral fullerenes essentially depend on the properties of the encapsulated atom, which makes it possible to control them by selecting the encapsulated atom with the desired property. The work [30] showed the effect of encapsulated alkali metals Li, Na, and K on the electrical transport characteristics of a single-electron transistor based on Me@C60 (Me = Li, Na, K). The geometry of nanodevices in the form of models of single-electron transistors, the conduction channels of which are C180 fullerene and an encapsulated KI alkali halide crystal, are located between two gold source–sink electrodes. Based on the parameters of the encapsulated crystal, fullerene C180 was chosen, which was previously considered in models of nanodevices forming a nanojunction of the “core–shell” type and is more optimal for the introduction of an alkali halide crystal. The crystal embedded in C180 fullerene has a cubic structure with the chemical formula K4I4. The structure places two ions along each edge for a total of eight ions. In Figure 1b shows, the purple spheres are K+ ions and the dark pink spheres are I- halide ions. The source located on the right side of the entire structure with a size of ~24.47 Å and the drain of a similar size located on the left consisted of 460 gold atoms. The size of the quasiparticle scattering region was commensurate with the size of the C180 molecules (with a diameter of ~11.97 Å). The nanodevice models under consideration were placed in a nanogap ~17.13 Å in size. They were nanoobjects in the form of endofullerenes. The distance from the fullerene surface to the electrodes was ~2.58 Å. The primary geometric parameters of the considered nanodevices are shown in Figure 1.
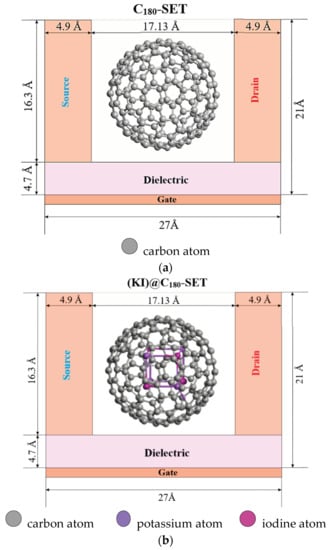
Figure 1.
SET geometry: (a) C180-SET; (b) (KI)@C180-SET.
The computer simulation of the electrical characteristics of the nanojunction was carried out within the framework of density functional theory in combination with the nonequilibrium Green’s functions method and local density approximation. In the process of modelling, the charges (Q = −2, −1, 0, 1, 2) were chosen as electric charges for each molecule. In addition, the quantum–chemical properties of the geometric structure of the molecule were calculated, which corresponded to the stable ground state of the molecule at each value of the selected charge [28]. The choice of the charge values from −2e to 2e was due to the fact that the state of small molecules with more than two additional electrons becomes unstable. Geometry optimization was implemented in the Atomistix ToolKit Virtual NanoLab 15.1 (Denmark, Syn-opsis) (ATK VNL) [29,31], which has already been successfully tested in a series of computational works [32,33,34,35,36,37,38,39,40,41]. ATK VNL is the leading, industry-proven platform for modeling materials, nanostructures, and nanoelectronic devices at the atomic scale. It includes quantum mechanical methods such as density functional theory (DFT) with LCAO or plane wave basis sets and semiempirical models, a simulation engine for atomic-scale simulations using classical potentials, and a module for simulating nanoscale devices and transport using the nonequilibrium method Green’s functions (NEGFs).
Within the framework of DFT, the process of optimizing the geometry of fullerene nanodevices and mapping the interatomic interaction was carried out; the generalized gradient approximation of Perdew–Burke–Ernzerhof was used as the exchange–correlation functional, which allows describing such nanostructures with accuracy. The PBE functional is the default exchange–correlation functional. It is recommended, in particular, for studying molecules interacting with metal surfaces, although it is also reliable enough for volumetric calculations. The generalized gradient approximation in the PBE and BLYP forms was used in all the calculations. When optimizing nanostructures in the PBE functional, the parameters of the atomic configuration were relaxed until the forces on all the atoms of the molecule became less than the specified threshold value of 0.05 eV/Å. To confirm that the stationary points corresponded to the minima, the vibrational frequencies were computed. To check the reliability of the parameters used in the calculations, we performed a geometry optimization using a larger dnp basis. Despite the long computational time, as a result, the energy changes were less than 0.05 eV, and the shifts of the atomic coordinates were less than 10−3 Å.
The computer simulation of the electrical characteristics of the nanojunction was carried out within the framework of the density functional theory in combination with the NEGF method and local density approximation.
To calculate the nonequilibrium electron density, ATK uses the NEGF method. The electron density is given in terms of the electron density matrix, which is divided into left and right contributions:
The contribution of the left density matrix is now determined by the NEGF theory:
where
Is the spectral density matrix. Note that, while there is a nonequilibrium electron distribution in the central region, the electron distribution in the electrode is described by a Fermi function ƒ with an electron temperature TL.
Furthermore, in this equation, G is the retarded Green’s function, and
is the broadening function of the left electrode, given in terms of the left electrode self-energy, ΣL. A similar equation exists for the right density matrix contribution.
When optimizing the C180 fullerene, the bond length between neighboring C—C carbon atoms was 2.049 Å, and the fullerene diameter was 11.97 Å. The distance from the fullerene to the electrodes was 2.603 Å. In endohedral fullerene (KI)@C180, the C—C bond length ranged from 2.049 to 2.02 Å, and the distance between the K—C and K—I atoms was 3.35 Å and 2.88 Å, respectively. When KI was introduced into the C180 cavity, a slight change in its geometry was observed. The diameter of the fullerene (KI)@C180 was 11.964 Å, and the distance from the endohedral fullerene to the electrodes was 2.58 Å.
3. Results
3.1. Dependence of the Total Energy on the Charge State
Figure 2 shows the dependence of the total energy of the fullerene molecules on the charge state. Based on the results of the total energy calculations, it is shown that, with a negative value of the charge, the total energy was higher than with a positive one. The total energy of fullerene with a neutral charge was −28,383.99233 eV, and for endohedral fullerene (KI)@C180-SET, −31,556.29148 eV. Table 1 shows the numerical data on the dependence of the total energy on the state of charges.
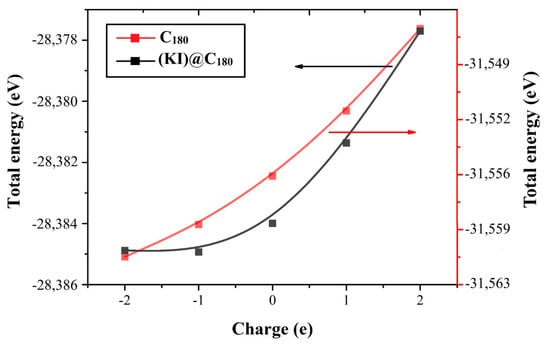
Figure 2.
The dependency of the total energy of molecules C180-SET and (KI)@C180-SET on their total charge.

Table 1.
Dependence of the total energy of fullerene molecules on the charge state.
3.2. The Dependence of Total Energy on Voltage
Figure 3 shows the dependence of the total energy on the gate voltage (VG) for the C180- and (KI)@C180-based SETs for different charge states. As can be seen, at VG > 0, the state of negative charge (Q = −1, −2) showed a significant decrease in the total energy of the SET, making it stable at positive values of VG. From Figure 3a for C180, we observe that, when the voltage reached 8 V, the graphs related to the negative charges Q = −1, −2 practically connect. However, when the fullerene KI was included in the cavity, the electrical properties changed, and the graphs characterizing the negative charges Q = −1 and −2 intersect already at a voltage of ~2.5 V and E ≈ −15 eV (Figure 3b). At VG < 0, the positive state of charge (Q = 1, 2) was more stable relative to the negative state due to the shift in the levels of the highest free and lowest free molecular orbitals with the gate voltage. In C180 fullerene, the graphs characterizing states with Q = 1 and 2 have an intersection point at V ≈ −2.8 V and E ≈ −13 eV. In the (KI)@C180 system, states with positive charges Q = 1 and 2 have intersections at the points V ≈ −7.3 V and E ≈ −17 eV. We also observed significant differences when comparing Figure 3a,b in systems with zero charge. Thus, the energy maximum in C180 was fixed at ≈ −12 eV and in (KI)@C180, ≈ −14 eV.
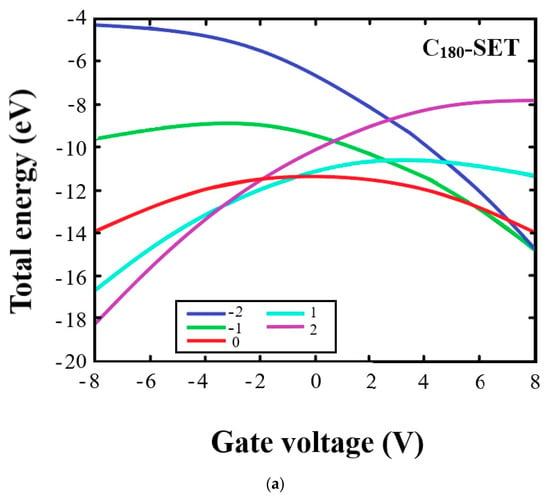
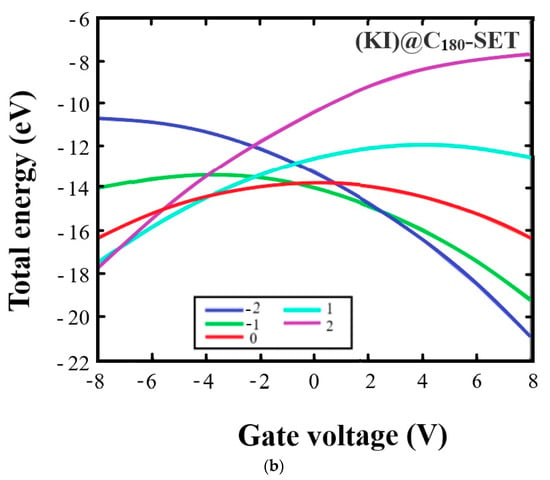
Figure 3.
Dependence of total energy from the gate voltage for SETs based on: (a) C180; (b) (KI)@C180. Different charged states of the molecule are shown with different colored curves: blue (−2), green (−1), red (0), turquoise (1), and violet (2).
The above data allowed us to conclude that (KI)@C180 can be used as an SET in another energy area.
3.3. Coulomb Blockade in SET C180 and (KI)@C180
The Coulomb blockade of tunneling is a phenomenon that makes it possible to study the electronic states in quantum dots and the transport effects associated with them [42,43,44]. Coulomb blockade blocks the passage of electrons through a quantum dot connected between two tunnel contacts. The electron located at the point creates an additional Coulomb potential barrier and is also repelled by the contacts’ electrons. By preventing an electron from leaving a point, the Coulomb barrier prevents other electrons from reaching it. The phenomenon of Coulomb blockade is observed when the Coulomb energy of a quantum dot is much greater than the temperature and the distance between the quantum dot levels [45].
In applied science, a single-electron transistor operating based on the Coulomb blockade effect is of great interest. A single-electron transistor consists of tunnel barriers separating the quantum dot from the source and drain regions. The effect of Coulomb blockade was studied in single-electron transistors C180 and (KI)@C180—quantum dots separated by tunnel barriers from the source and drain regions.
When the charge of the Coulomb blockade is overcome, it is transferred from to the SET. To overcome it, it is necessary to apply sufficient charge energy by adjusting the gate potential and the electrode voltage. For given values of the gate voltage and bias voltage (VSD), the number of molecular energy levels within the bias window is given by the color codes in Figure 4a,b.
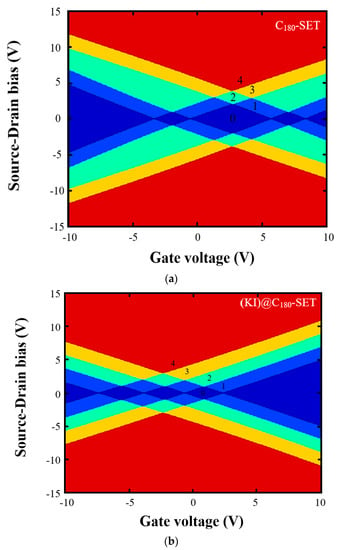
Figure 4.
Charge stability diagrams for SETs—(a) C180; (b) (KI)@C180. The number of charge states for given bias potentials are represented by the following colors: blue (0), light blue (1), green (2), yellow (3), and red (4).
In Figure 4, the control gate electrode can be used to transfer the Coulomb island from the conducting mode to the tunneling current blocking mode. In the bias voltage range −1.926 V ≤ VSD ≤ 1.926 V, by selecting the gate voltage in the interval −0.591 V ≤ VG ≤ 5.685 V, one can put the C180-SET into blockade mode. In the absence of voltage on the substrate (VG = 0 V), the Coulomb blockade occurs at a bias voltage equal to −0.941 V ≤ VSD ≤ 0.941 V. To switch to the turn-on mode (KI)@C180-SET, it is necessary to apply a gate voltage in the range from VGmin = −0.658 V to VGmax = 2.379 V at a set bias voltage of −0.858 V ≤ VSD ≤ 0.934 V. At bias voltage values equal to VSDmin = −0.643 V and VSDmax = 0.737 V, there is no voltage on the substrate (VG = 0 V), and no electric current passes.
Inside each Coulomb diamond, the equilibrium value of the number of excess electrons ΔN is indicated. The area of the Coulomb blockade is shown in dark blue and is indicated by the number 0. If the operating point of the SET is inside this Coulomb diamond, where there is no energy level to support electron transport, then the electron transport through the transistor is not possible. Single-electron tunneling in transistors occurs in the area represented by light blue and marked with the number 1.
The area of the Coulomb rhombus in fullerene with potassium iodide is significantly smaller than in “pure” fullerene (see Table 2). The change in the diamond area of the Coulomb blockade is related to the electronic structure of the encapsulated molecule. These results can be useful in the design of the SET, since reducing the area of the Coulomb diamond in the stability diagram can lead to fewer fluctuations, so the current fluctuation as a trip limiter of the SET is reduced, and therefore, the SET can operate at higher speeds.

Table 2.
The main parameters of the central Coulomb diamond according to stability diagrams.
4. Conclusions
In this work, the electronic properties of the model fullerene C180 and endohedral fullerene (KI)@C180 were studied within the framework of DFT + NEGF. Based on the optimized geometric structures of these fullerenes, the dependences of the total energy of the C180-SET and (KI)@C180-SET molecules on their total charge, the dependence of the total energy on the gate voltage, and the stability diagram of a single-electron transistor were determined. It was shown that the encapsulation of an alkali halide KI crystal in C180 fullerene led to a significant change in its electrical properties. It was shown that a large source–drain voltage was required to bring the C180-SET out of the Coulomb blockade mode compared to a transistor based on (KI)@C180. Due to the decrease in the area of the Coulomb diamond on the charge stability diagram (KI)@C180-SET, it becomes possible to increase the speed of integrated circuits based on them. The simulation results obtained in this work can be useful in the creation of single-electron nanodevices.
Author Contributions
Conceptualization, L.M. and D.S.; methodology, A.I. and L.M.; software, D.S.; validation, L.M. and A.I.P.; formal analysis, A.D.; investigation, A.I.; resources, D.S.; data curation, A.I.P.; writing—original draft preparation, L.M. and A.I.; writing—review and editing, L.M. and A.I.; visualization, A.I. and A.D.; supervision, L.M.; project administration, A.I.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Science and Higher Education of the Republic of Kazakhstan by Project No. AP09057911 “Experimental studies of the mechanisms of luminescence of KI, RbI and CsI crystals at the activation by cations-homologues and low temperature deformation”. In addition, the research of A.I.P. was partly supported by the RADON project (GA 872494) within the H2020-MSCA-RISE-2019 call and COST Action CA20129 “Multiscale Irradiation and Chemistry Driven Processes and Related Technologies” (MultIChem). A.I.P. thanks the Institute of Solid-State Physics, University of Latvia. ISSP UL as the Center of Excellence is supported through the Framework Program for European universities, Union Horizon 2020, H2020-WIDESPREAD-01–2016–2017-TeamingPhase2, under Grant Agreement No. 739508, CAMART2 project.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cuevas, J.C.; Scheer, E. Molecular Electronics (An Introduction to Theory and Experiment), 2nd ed.; World Scientific Publishing Co. Pte. Ltd.: Hackensack, NJ, USA, 2017. [Google Scholar]
- Xiang, R.; Inoue, T.; Zheng, Y.; Kumamoto, A.; Qian, Y.; Sato, Y.; Liu, M.; Tang, D.; Gokhale, D.; Guo, J.; et al. One-dimensional van der Waals heterostructures. Science 2020, 367, 6477. [Google Scholar] [CrossRef] [PubMed]
- Sergeyev, D. One-dimensional Schottky nanodiode based on telescoping polyprismanes. Adv. Nano Reseach 2021, 10, 339. [Google Scholar]
- Chuan, M.W.; Lau, J.Y.; Wong, K.L.; Hamzah, A.; Alias, N.E.; Lim, C.S.; Tan, M.L.P. Low-dimensional modelling of n-type doped silicene and its carrier transport properties for nanoelectronic applications. Adv. Nano Reseach 2021, 10, 415. [Google Scholar]
- Montanaro, A.; Wei, W.; De Fazio, D.; Sassi, U.; Soavi, G.; Aversa, P.; Ferrari, A.C.; Happy, H.; Legagneux, P.; Pallecchi, E. Optoelectronic mixing with high-frequency graphene transistors. Nat. Commun. 2021, 12, 2728. [Google Scholar] [CrossRef] [PubMed]
- Gaur, M.; Misra, C.; Yadav, A.B.; Swaroop, S.; Maolmhuaidh, F.O.; Bechelany, M.; Barhoum, A. Biomedical applications of carbon nanomaterials: Fullerenes, quantum dots, nanotubes, nanofibers, and graphene. Materials 2021, 14, 5978. [Google Scholar] [CrossRef]
- Yao, S.; Yuan, X.; Jiang, L.; Xiong, T.; Zhang, J. Recent progress on fullerene-based materials: Synthesis, properties, modifications, and photocatalytic applications. Materials 2020, 13, 2924. [Google Scholar] [CrossRef]
- Bellucci, S.; Saharian, A.A. Fermionic Casimir densities in toroidally compactified spacetimes with applications to nanotubes. Phys. Rev. D 2009, 79, 085019. [Google Scholar]
- Bleija, M.; Platnieks, O.; Macutkevič, J.; Starkova, O.; Gaidukovs, S. Comparison of Carbon-Nanoparticle-Filled Poly(Butylene Succinate-co-Adipate) Nanocomposites for Electromagnetic Applications. Nanomaterials 2022, 12, 3671. [Google Scholar] [CrossRef]
- Vanskevičė, I.; Kazakova, M.A.; Macutkevic, J.; Semikolenova, N.V.; Banys, J. Dielectric Properties of Hybrid Polyethylene Composites Containing Cobalt Nanoparticles and Carbon Nanotubes. Materials 2022, 15, 1876. [Google Scholar] [CrossRef]
- Latko-Durałek, P.; Bertasius, P.; Macutkevic, J.; Banys, J.; Boczkowska, A. Fibers of Thermoplastic Copolyamides with Carbon Nanotubes for Electromagnetic Shielding Applications. Materials 2021, 14, 5699. [Google Scholar] [CrossRef]
- Karbovnyk, I.; Klym, H.; Piskunov, S.; Popov, A.A.; Chalyy, D.; Zhydenko, I.; Lukashevych, D. The impact of temperature on electrical properties of polymer-based nanocomposites. Low Temp. Phys. 2020, 46, 1231–1234. [Google Scholar] [CrossRef]
- Kazerovskis, J.; Piskunov, S.; Zhukovskii, Y.F.; D’yachkov, P.N.; Bellucci, S. Formation of linear Ni nanochains inside carbon nanotubes: Prediction from density functional theory. Chem. Phys. Lett. 2013, 577, 92–95. [Google Scholar] [CrossRef]
- Zhukovskii, Y.F.; Piskunov, S.; Bellucci, S. Double-wall carbon nanotubes of different morphology: Electronic structure simulations. Nanosci. Nanotechnol. Lett. 2012, 4, 1074–1081. [Google Scholar] [CrossRef]
- Bellucci, S.; Balasubramanian, C.; Grilli, A.; Micciulla, F.; Raco, A.; Popov, A.; Baranov, V.; Biryukov, V.; Chesnokov, Y.; Maisheev, V. Using a deformed crystal for bending a sub-GeV positron beam. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2006, 252, 3–6. [Google Scholar] [CrossRef]
- Kozlovskiy, A.L.; Zhumatayeva, I.Z.; Mustahieva, D.; Zdorovets, M.V. Phase Transformations and Photocatalytic Activity of Nanostructured Y2O3/TiO2-Y2TiO5 Ceramic Such as Doped with Carbon Nanotubes. Molecules 2020, 25, 1943. [Google Scholar] [CrossRef] [PubMed]
- Shmatko, V.; Yalovega, G.E.; Ulyankina, A.; Kuriganova, A.; Bogoslavskaja, E.; Smirnova, N.V. Investigation of the morphological, atomic and electronic structural changes CuOx nanoparticles and CNT in a nanocomposite CuOx/CNT: SEM and X-ray spectroscopic studies. Key Eng. Mater. 2016, 683, 215–220. [Google Scholar] [CrossRef]
- Sloan, J.; Kirkland, A.I.; Hutchison, J.L.; Green, M.L.H. Aspects of crystal growth within carbon nanotubes. C. R. Physique. 2003, 4, 1063–1074. [Google Scholar] [CrossRef]
- Meyer, R.R.; Sloan, J.; Dunin-Borkowski, R.E.; Kirkland, A.I.; Novotny, M.C.; Bailey, S.R.; Hutchison, J.L.; Green, M.L.H. Discrete atom imaging of one-dimensional crystals formed within single-walled carbon nanotubes. Science. 2000, 289, 1324–1326. [Google Scholar] [CrossRef]
- Sloan, J.; Kirkland, A.I.; Hutchison, J.L.; Green, M.L.H. Integral atomic layer architectures of 1D crystals inserted into single walled carbon nanotubes. Chem. Commun. 2002, 13, 1319–1332. [Google Scholar] [CrossRef]
- Sloan, J.; Novotny, M.C.; Bailey, S.R.; Brown, G.; Xu, C.; Williams, V.C.; Friedrichs, S.; Flahaut, E.; Callender, R.L.; York, A.P.E.; et al. Two layer 4:4 co-ordinated KI crystals grown within single walled carbon nanotubes. Chem. Phys. Lett. 2000, 329, 61–65. [Google Scholar] [CrossRef]
- Bichoutskaia, E.; Pyper, N.C. Theoretical study of the structures and electronic properties of all-surface KI and CsI nanocrystals encapsulated in single walled carbon nanotubes. J. Chem. Phys. 2008, 129, 154701. [Google Scholar] [CrossRef] [PubMed]
- Sleats, E.L.; Green, M.L.H.; Kirkland, A.I.; Green, J.C. DFT calculations of KI crystals formed within single-walled carbon nanotubes. Chem. Phys. Lett. 2008, 466, 76–78. [Google Scholar]
- Bethune, D.S.; Johnson, R.D.; Salem, J.R.; de Vries, M.S.; Yannoni, C.S. Atoms in carbon cages: The structure and properties of endohedral fullerenes. Nature 1993, 366, 123–128. [Google Scholar] [CrossRef]
- Chaur, M.N.; Athans, A.J.; Echegoyen, L. Metallic nitride endohedral fullerenes: Synthesis and electrochemical properties. Tetrahedron 2008, 64, 11387–11393. [Google Scholar] [CrossRef]
- Li, M.; Zhao, R.; Dang, J.; Zhao, X. Theoretical study on the stabilities, electronic structures, and reaction and formation mechanisms of fullerenes and endohedral metallofullerenes. Coord. Chem. Rev. 2022, 471, 214762. [Google Scholar] [CrossRef]
- Mohajeri, R.; Jahanshahi, M.; Ghorbanzadeh Ahangari, M. Methane storage capacity of carbon fullerenes and their mechanical and electronic properties: Experimental and theoretical study. Mater. Chem. Phys. 2018, 211, 192–199. [Google Scholar] [CrossRef]
- Xing-Xing, Y.; Bairu, L.; Hao-Sheng, L.; Fei, J.; Chuang, N.; Kai-Qing, L.; Guan-Wu, W.; Shangfeng, Y. Successively Regioselective Electrosynthesis and Electron Transport Property of Stable Multiply Functionalized [60] Fullerene Derivatives. Research 2020, 21, 2059190. [Google Scholar]
- Brandbyge, M.; Mozos, J.L.; Ordejon, P.; Taylor, J.; Stokbro, K. Density-functional method for nonequilibrium electron transport. Phys. Rev. 2002, 65, 165401. [Google Scholar] [CrossRef]
- Sergeyev, D. Single Electron Transistor Based on Endohedral Metallofullerenes Me@C60 (Me = Li, Na, K). J. Nano-Electron. Phys 2020, 12, 03017. [Google Scholar] [CrossRef]
- Stradi, D.; Martinez, U.; Blom, A.; Brandbyge, M.; Stokbro, K. General atomistic approach for modeling metal-semiconductor interfaces using density functional theory and nonequilibrium Green’s function. Phys. Rev. 2016, 93, 155302. [Google Scholar] [CrossRef]
- Myasnikova, L.; Istlyaup, A.; Sergeyev, D.; Zhanturina, N.; Shunkeyev, K.; Popov, A.I. Computer Simulations of the Band Structure and Density of States of the Linear Chains of NaCl Ions. Latv. J. Phys. Tech. Sci. 2019, 56, 49–56. [Google Scholar] [CrossRef]
- Wasfi, A.; Awwad, F.; Gelovani, J.G.; Qamhieh, N.; Ayesh, A.I. COVID-19 Detection via Silicon Nanowire Field-Effect Transistor: Setup and Modeling of Its Function. Nanomaterials 2022, 12, 2638. [Google Scholar] [CrossRef] [PubMed]
- Sergeyev, D.; Zhanturina, N.; Aizharikov, A.; Popov, A.I. Influence of “Productive” Impurities (Cd, Na, O) on the Properties of the CuZnSnS Absorber of Model Solar Cells. Latv. J. Phys. Tech. Sci. 2021, 58, 13–23. [Google Scholar]
- Zhanturina, N.; Sergeyev, D.; Aimaganbetova, Z.; Zhubaev, A.; Bizhanova, K. Structural Properties of Yttrium Aluminum Garnet, Doped with Lanthanum. Crystals 2022, 12, 1132. [Google Scholar] [CrossRef]
- Vemuri, S.K.; Chaliyawala, H.; Ray, A.; Mukhopadhyay, I. A powerful approach to develop nitrogen-doped graphene sheets: Theoretical and experimental framework. J. Mater. Sci. 2022, 57, 10714–10723. [Google Scholar] [CrossRef]
- Salih, E.; Ayesh, A.I. Enhancing the Sensing Performance of Zigzag Graphene Nanoribbon to Detect NO, NO2, and NH3 Gases. Sensors 2020, 20, 3932. [Google Scholar] [CrossRef] [PubMed]
- Salih, E.; Ayesh, A.I. Pt-doped armchair graphene nanoribbon as a promising gas sensor for CO and CO2: DFT study. Phys. E Low-Dimens. Syst. Nanostructures 2021, 125, 114418. [Google Scholar] [CrossRef]
- Vohra, R.; Kaur, H.; Kaur, J.; Kumar, R. Investigation of transport behavior in borospherene-based molecular wire for rectification applications. J. Mater. Res. 2022, 37, 360–368. [Google Scholar] [CrossRef]
- Chen, Y.; Nie, W.; Peng, Z.; Yu, F.; Yang, J.; Li, Y. Strontium oxides with enzyme-like activity: A colorimetric sensor array for highly sensitive discrimination of bisphenols. Sens. Actuators B Chem. 2022, 364, 131869. [Google Scholar] [CrossRef]
- Ayesh, A.I. The effect of ZrOx modification of graphene nanoribbon on its adsorption for NOx: A DFT investigation. Mater. Chem. Phys. 2022, 291, 126693. [Google Scholar] [CrossRef]
- Koenraad, P.M.; Flatte, M.E. Single dopants in semiconductors. Nat. Mater. 2011, 10, 91–100. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Li, W.; Feng, L.; Chen, X.; Hansen, A.; Grimme, S.; Fortier, S.; Sergentu, D.-C.; Duignan, T.J.; Autschbach, J.; et al. A diuranium carbide cluster stabilized inside a C80 fullerene cage. Nat. Commun. 2018, 1, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Pogosov, A.G.; Budantsev, M.V.; Shevyrin, A.A.; Plotnikov, A.E.; Bakarov, A.K.; Toropov, A.I. High-Temperature Coulomb Blockade. Pis’ma v Zh. Èksper. Teoret. Fiz. 2006, 83, 152–156. [Google Scholar] [CrossRef]
- Wunderlich, J.; Jungwirth, T.; Kaestner, B.; Irvine, A.C.; Shick, A.B.; Stone, N.; Wang, K.-Y.; Rana, U.; Giddings, A.D.; Foxon, C.T.; et al. Coulomb Blockade Anisotropic Magnetoresistance Effect in a (Ga, Mn) As Single-Electron Transistor. Phys. Rev. Lett. 2006, 97, 077201. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).