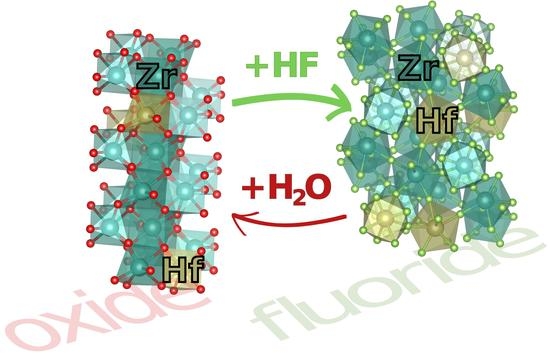
Stability of Hydroxo/Oxo/Fluoro Zirconates vs. Hafniates—A DFT Study
Abstract
1. Introduction
1.1. Motivation
1.2. Known Crystal Structures
2. Computational Details
3. Results and Discussion
3.1. Oxo/Oxofluoro/Fluoro Crystals of Zr vs. Hf
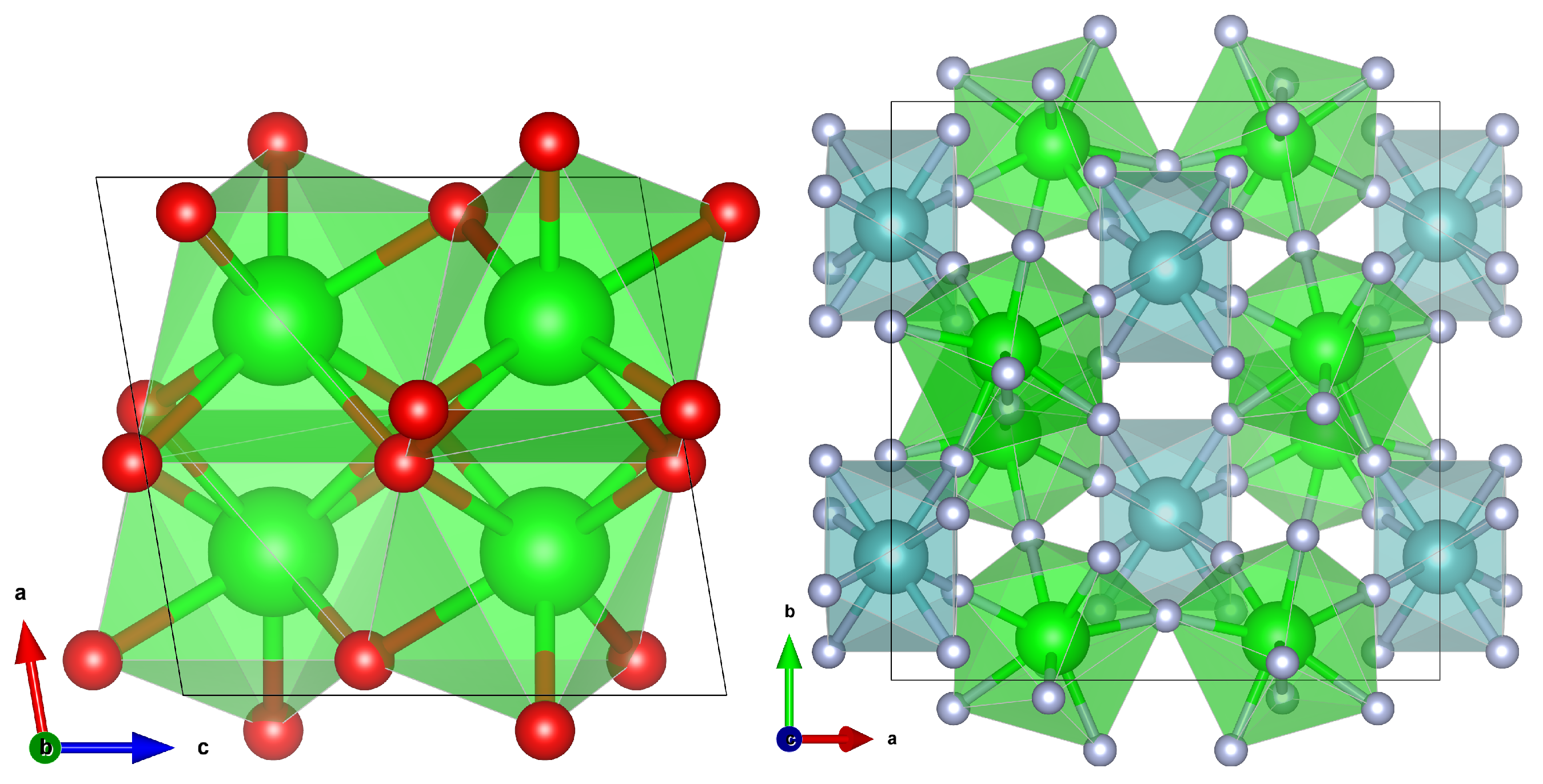
3.1.1. Crystal Structures
3.1.2. Reaction Energies
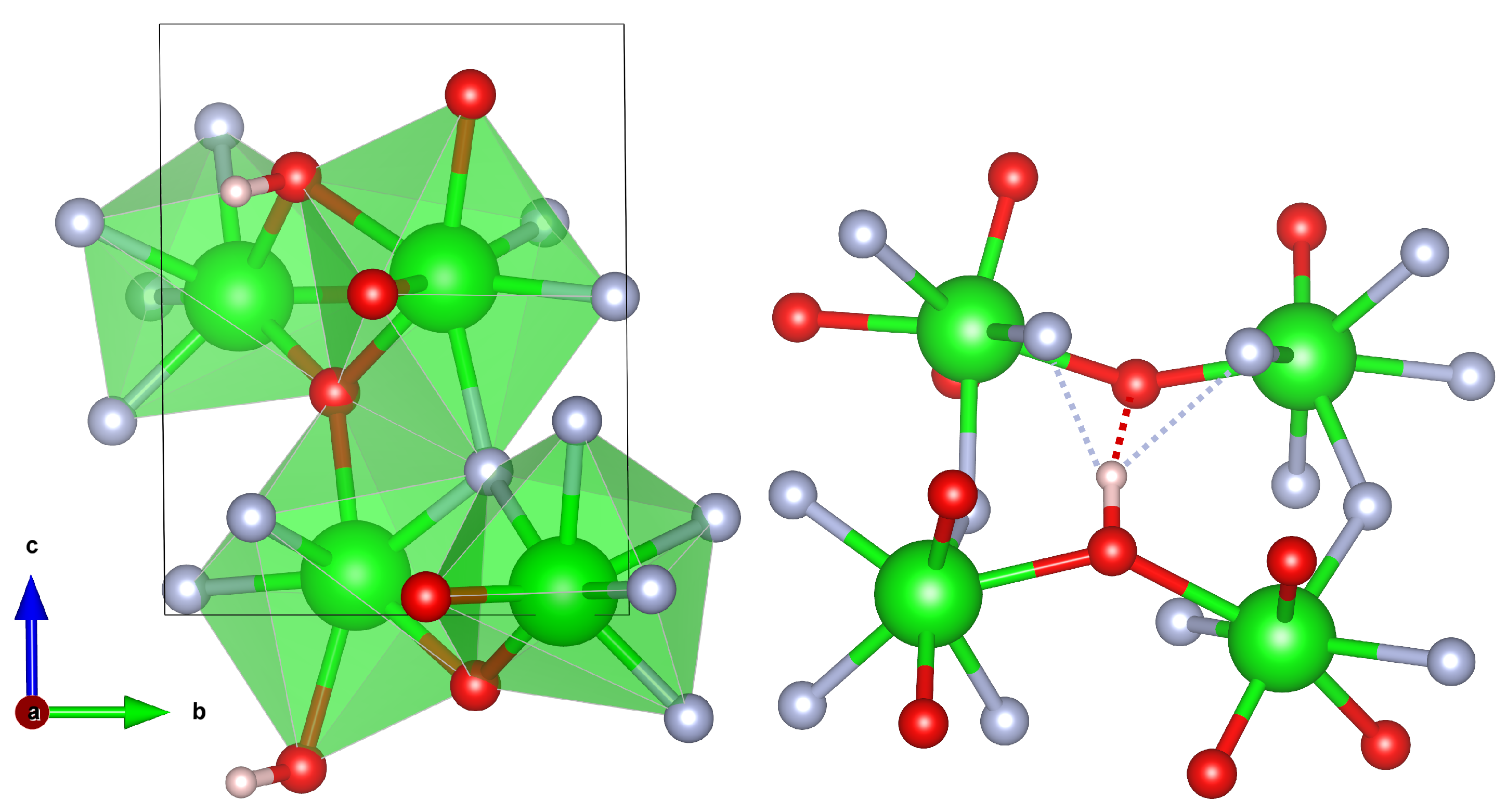
3.2. Mono-Hydroxylated Oxofluoro/Fluoro Crystals of Zr vs. Hf
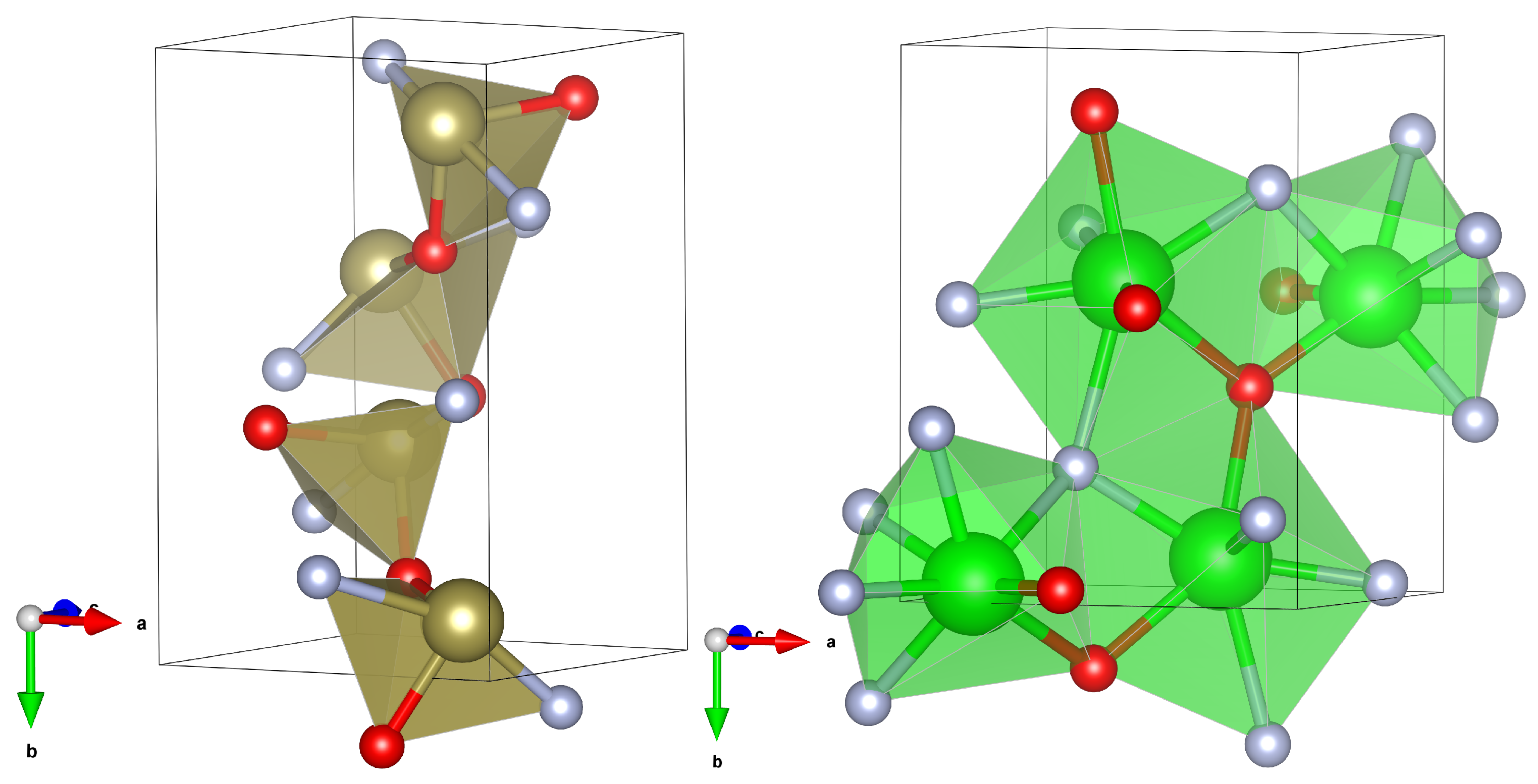
3.2.1. Crystal Structures
3.2.2. Reaction Energies and H-Bond Patterns
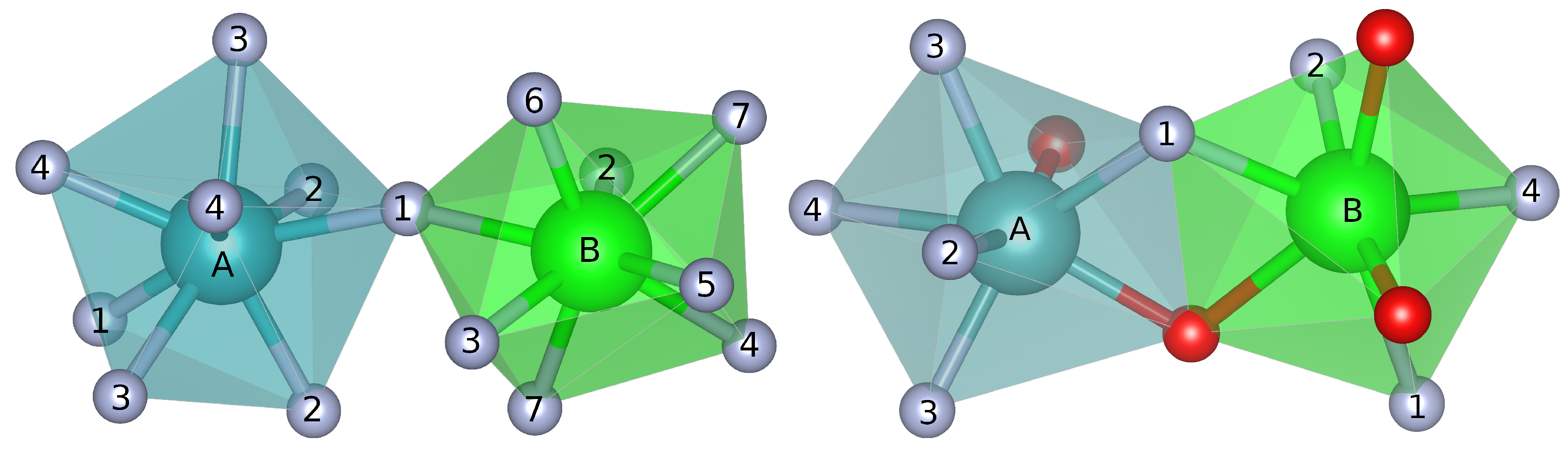
3.3. Partial Charges
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shannon, R.D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Cryst. A 1976, 32, 751–767. [Google Scholar] [CrossRef]
- Park, M.H.; Lee, Y.H.; Mikolajick, T.; Schroeder, U.; Hwang, C.S. Review and perspective on ferroelectric HfO2-based thin films for memory applications. MRS Commun. 2018, 8, 795–808. [Google Scholar] [CrossRef]
- Cozmuta, I.; Cozic, S.; Poulain, M.; Poulain, S.; Martini, J.R.L. Breaking the Silica Ceiling: ZBLAN-Based Opportunities for Photonics Applications. In Proceedings of the SPIE OPTO, San Francisco, CA, USA, 1–6 February 2020; Volume 11276, p. 112760R. [Google Scholar] [CrossRef]
- He, Z.; Li, W.; Yu, A.; Wu, Y.; Cai, Z. Efficient UV-visible emission enabled by 532 nm CW excitation in an Ho3+-doped ZBLAN fiber. Opt. Express 2022, 30, 10414. [Google Scholar] [CrossRef] [PubMed]
- Hasz, W.C.; Whang, J.H.; Moynihan, C.T. Comparison of physical properties of ZrF4- and HfF4 based melts and glasses. J. Non Cryst. Solids 1993, 161, 127–132. [Google Scholar] [CrossRef]
- Dmitruk, L.; Vinogradova, N.; Kozlov, V.; Machov, V.; Devitsin, E.; Fyodorov, V. Scintillating HfF4-based glasses doped cerium chloride and cerium oxide compounds. J. Non Cryst. Solids 1997, 213–214, 311–314. [Google Scholar] [CrossRef]
- Brekhovskikh, M.; Sukhoverkhov, V.; Fedorov, V.; Batygov, S.; Dmitruk, L.; Vinogradova, N.; Devitsin, E.; Kozlov, V.; Provorova, A. Influence of fluorooxidizers on scintillation properties of fluorohafnate glass doped with Ce3+. J. Non Cryst. Solids 2000, 277, 68–71. [Google Scholar] [CrossRef]
- Jones, J.V., III; Piatak, N.M.; Bedinger, G.M. Zirconium and Hafnium, Professional Paper 1802-V; Technical report; US Geological Survey: Reston, VA, USA, 2017. [Google Scholar] [CrossRef]
- Bau, M. Controls on the fractionation of isovalent trace elements in magmatic and aqueous systems: Evidence from Y/Ho, Zr/Hf, and lanthanide tetrad effect. Contrib. Mineral. Petrol. 1996, 123, 323–333. [Google Scholar] [CrossRef]
- Ellison, A.J.; Hess, P.C. Solution behavior of +4 cations in high silica melts: Petrologic and geochemical implications. Contrib. Mineral. Petrol. 1986, 94, 343–351. [Google Scholar] [CrossRef]
- Linnen, R.L.; Keppler, H. Melt composition control of Zr/Hf fractionation in magmatic processes. Geochim. Cosmochim. Act 2002, 66, 3293–3301. [Google Scholar] [CrossRef]
- Neves, J.M.C.; Nunes, J.E.L.; Sahama, T.G. High hafnium members of the zircon-hafnon series from the granite pegmatites of Zambézia, Mozambique. Contrib. Mineral. Petrol. 1974, 48, 73–80. [Google Scholar] [CrossRef]
- Yin, R.; Wang, R.C.; Zhang, A.C.; Hu, H.; Zhu, J.C.; Rao, C.; Zhang, H. Extreme fractionation from zircon to hafnon in the Koktokay No. 1 granitic pegmatite, Altai, northwestern China. Am. Mineral. 2013, 98, 1714–1724. [Google Scholar] [CrossRef]
- Kudryashov, N.M.; Skublov, S.G.; Galankina, O.L.; Udoratina, O.V.; Voloshin, A.V. Abnormally high-hafnium zircon from rare-metal pegmatites of the Vasin-Mylk deposit (the northeastern part of the Kola Peninsula). Geochemistry 2020, 80, 125489. [Google Scholar] [CrossRef]
- Loges, A.; Migdisov, A.A.; Wagner, T.; Williams-Jones, A.E.; Markl, G. Fluoride complexation of hafnium under hydrothermal conditions. Mineral. Mag. 2012, 76, 2030. [Google Scholar]
- Haynes, W.M. (Ed.) CRC Handbook of Chemistry and Physics, 97th ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Luo, Y.R. Comprehensive Handbook of Chemical Bond Energies, 1st ed.; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Mullins, R.; Kondati Natarajan, S.; Elliott, S.D.; Nolan, M. Self-Limiting Temperature Window for Thermal Atomic Layer Etching of HfO2 and ZrO2 Based on the Atomic-Scale Mechanism. Chem. Mater. 2020, 32, 3414–3426. [Google Scholar] [CrossRef]
- Skaggs, R.L.; Rogers, D.T.; Hunter, D.B. Review of Anhydrous Zirconium-Hafnium Separation Techniques; Technical report; US Department of the Interior, Bureau of Mines: Washington, DC, USA, 1984. [Google Scholar]
- Vilakazi, B.M.; Monnahela, O.S.; Wagener, J.B.; Carstens, P.A.B.; Ntsoane, T. A thermogravimetric study of the fluorination of zirconium and hafnium oxides with anhydrous hydrogen fluoride gas. J. Fluor. Chem. 2012, 141, 64–68. [Google Scholar] [CrossRef]
- Migdisov, A.; Williams-Jones, A.E.; van Hinsberg, V.; Salvi, S. An experimental study of the solubility of baddeleyite (ZrO2) in fluoride-bearing solutions at elevated temperature. Geochim. Cosmochim. Acta 2011, 75, 7426–7434. [Google Scholar] [CrossRef]
- Loges, A.; Louvel, M.; Wilke, M.; Jahn, S.; Klemme, S.; Welter, E.; Borchert, M.; Qiao, S.; Manni, M.; Keller, B.; et al. Fluoride Complexation of Zr and Hf in Hydrothermal Aqueous Fluids. Online Resource on ResearchGate. 2022. Available online: https://www.researchgate.net/publication/359514094_Fluoride_complexation_of_Zr_and_Hf_in_hydrothermal_aqueous_fluids?channel=doi&linkId=62421da67931cc7ccf00a78c&showFulltext=true (accessed on 30 October 2022).
- Ryzhenko, B.N.; Kovalenko, N.I.; Prisyagina, N.I.; Starshinova, N.P.; Krupskaya, V.V. Experimental determination of zirconium speciation in hydrothermal solutions. Geochem. Int. 2008, 46, 328–339. [Google Scholar] [CrossRef]
- Boysen, H.; Frey, F.; Vogt, T. Neutron powder investigation of the tetragonal to monoclinic phase transformation in undoped zirconia. Acta Crystallogr. B 1991, 47, 881–886. [Google Scholar] [CrossRef]
- Block, S.; Da Jornada, J.A.H.; Piermarini, G.J. Pressure-Temperature Phase Diagram of Zirconia. J. Am. Ceram. Soc. 1985, 68, 497–499. [Google Scholar] [CrossRef]
- Shin, D.; Arroyave, R.; Liu, Z.k. Thermodynamic modeling of the Hf–Si–O system. Calphad 2006, 30, 375–386. [Google Scholar] [CrossRef]
- Al-Khatatbeh, Y.; Lee, K.K.M.; Kiefer, B. Phase diagram up to 105 GPa and mechanical strength of HfO2. Phys. Rev. B 2010, 82, 144106. [Google Scholar] [CrossRef]
- Králik, B.; Chang, E.K.; Louie, S.G. Structural properties and quasiparticle band structure of zirconia. Phys. Rev. B 1998, 57, 7027–7036. [Google Scholar] [CrossRef]
- Demkov, A.A. Investigating Alternative Gate Dielectrics: A Theoretical Approach. Phys. Status Solidi B 2001, 226, 57–67. [Google Scholar] [CrossRef]
- Zhao, X.; Vanderbilt, D. First-principles study of structural, vibrational, and lattice dielectric properties of hafnium oxide. Phys. Rev. B 2002, 65, 233106. [Google Scholar] [CrossRef]
- Zhao, X.; Vanderbilt, D. Phonons and lattice dielectric properties of zirconia. Phys. Rev. B 2002, 65, 75105. [Google Scholar] [CrossRef]
- Debernardi, A.; Fanciulli, M. Structural and vibrational properties of high-dielectric oxides, HfO2 and TiO2: A comparative study. Mater. Sci. Semicond. Process. 2006, 9, 1014–1019. [Google Scholar] [CrossRef]
- Luo, X.; Zhou, W.; Ushakov, S.V.; Navrotsky, A.; Demkov, A.A. Monoclinic to tetragonal transformations in hafnia and zirconia: A combined calorimetric and density functional study. Phys. Rev. B 2009, 80, 134119. [Google Scholar] [CrossRef]
- Li, J.; Meng, S.; Niu, J.; Lu, H. Electronic structures and optical properties of monoclinic ZrO2 studied by first-principles local density approximation + U approach. J. Adv. Ceram. 2017, 6, 43–49. [Google Scholar] [CrossRef]
- Li, J.; Han, J.; Meng, S.; Lu, H.; Tohyama, T. Optical properties of monoclinic HfO2 studied by first-principles local density approximation + U approach. Appl. Phys. Lett. 2013, 103, 071916. [Google Scholar] [CrossRef]
- Jomard, G.; Petit, T.; Pasturel, A.; Magaud, L.; Kresse, G.; Hafner, J. First-principles calculations to describe zirconia pseudopolymorphs. Phys. Rev. B 1999, 59, 4044–4052. [Google Scholar] [CrossRef]
- Kuwabara, A.; Tohei, T.; Yamamoto, T.; Tanaka, I. Ab initio lattice dynamics and phase transformations of ZrO2. Phys. Rev. B 2005, 71, 64301. [Google Scholar] [CrossRef]
- Fadda, G.; Colombo, L.; Zanzotto, G. First-principles study of the structural and elastic properties of zirconia. Phys. Rev. B 2009, 79, 214102. [Google Scholar] [CrossRef]
- Fadda, G.; Zanzotto, G.; Colombo, L. First-principles study of the effect of pressure on the five zirconia polymorphs. II. Static dielectric properties and Raman spectra. Phys. Rev. B 2010, 82, 64106. [Google Scholar] [CrossRef]
- Delarmelina, M.; Quesne, M.G.; Catlow, C.R.A. Modelling the bulk properties of ambient pressure polymorphs of zirconia. Phys. Chem. Chem. Phys. 2020, 22, 6660–6676. [Google Scholar] [CrossRef]
- Jaffe, J.E.; Bachorz, R.A.; Gutowski, M. Low-temperature polymorphs of ZrO2 and HfO2: A density-functional theory study. Phys. Rev. B 2005, 72, 144107. [Google Scholar] [CrossRef]
- Laudadio, E.; Stipa, P.; Pierantoni, L.; Mencarelli, D. Phase Properties of Different HfO2 Polymorphs: A DFT-Based Study. Crystals 2022, 12, 90. [Google Scholar] [CrossRef]
- Low, J.J.; Paulson, N.H.; D’Mello, M.; Stan, M. Thermodynamics of monoclinic and tetragonal hafnium dioxide (HfO2) at ambient pressure. Calphad 2021, 72, 102210. [Google Scholar] [CrossRef]
- Rivas-Silva, J.F.; Flores-Riveros, A.; Durand-Niconoff, J.S.; Aquino, N. Ab initio analysis of some fluoride and oxide structures doped with Pr and Yb. Int. J. Quantum Chem. 2004, 97, 815–825. [Google Scholar] [CrossRef]
- Legein, C.; Fayon, F.; Martineau, C.; Body, M.; Buzaré, J.Y.; Massiot, D.; Durand, E.; Tressaud, A.; Demourgues, A.; Péron, O.; et al. 19F High Magnetic Field NMR Study of β-ZrF4 and CeF4: From Spectra Reconstruction to Correlation between Fluorine Sites and 19F Isotropic Chemical Shifts. Inorg. Chem. 2006, 45, 10636–10641. [Google Scholar] [CrossRef]
- Benner, G.; Müller, B.G. Zur Kenntnis binärer Fluoride des ZrF4-Typs: HfF4 und ThF4. Z. Anorg. Allg. Chem. 1990, 588, 33–42. [Google Scholar] [CrossRef]
- McDonald, R.A.; Sinke, G.C.; Stull, D.R. High Temperature Enthalpy, Heat Capacity, Heat of Fusion, and Melting Point of Zirconium Tetrafluoride. J. Chem. Eng. Data 1962, 7, 83. [Google Scholar] [CrossRef]
- Sicius, H. (Ed.) Titangruppe: Elemente der vierten Nebengruppe. In Handbuch der chemischen Elemente; Springer: Berlin/Heidelberg, Germany, 2021; pp. 483–529. [Google Scholar] [CrossRef]
- Joubert, P.; Gaudreau, B. Sur quelques oxyfluorures de zirconium tetravalent. Rev. Chim. Mine. 1975, 12, 289–302. [Google Scholar]
- Papiernik, R.; Frit, B. Structure cristalline d’une phase cubique desordonnee de type ReO3 excedentaire en anions: ZrF2.67O0.67. Mater. Res. Bull. 1984, 19, 509–516. [Google Scholar] [CrossRef]
- Holmberg, B. The crystal structure of Zr7O9F10. Acta Crystallogr. B 1970, 26, 830–835. [Google Scholar] [CrossRef]
- Flynn, S.; Zhang, C.; Griffith, K.J.; Shen, J.; Wolverton, C.; Dravid, V.P.; Poeppelmeier, K.R. Fluoridation of HfO2. Inorg. Chem. 2021, 60, 4463–4474. [Google Scholar] [CrossRef] [PubMed]
- Rickard, C.E.F.; Waters, T.N. The hafnium tetrafluoride-water system. J. Inorg. Nucl. Chem. 1964, 26, 925–930. [Google Scholar] [CrossRef]
- Jain, A.; Ong, S.P.; Hautier, G.; Chen, W.; Richards, W.D.; Dacek, S.; Cholia, S.; Gunter, D.; Skinner, D.; Ceder, G.; et al. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 11002. [Google Scholar] [CrossRef]
- Clearfield, A.; Vaughan, P.A. The crystal structure of zirconyl chloride octahydrate and zirconyl bromide octahydrate. Acta Crystallogr. 1956, 9, 555–558. [Google Scholar] [CrossRef]
- Scholz, J.; Scholz (nee Böhme), K.; McQuillan, A.J. In Situ Infrared Spectroscopic Analysis of the Water Modes of [Zr4(OH)8(H2O)16]8+ during the Thermal Dehydration of ZrOCl2·8H2O. J. Phys. Chem. A 2010, 114, 7733–7741. [Google Scholar] [CrossRef]
- Zhukov, A.V.; Chizhevskaya, S.V.; Phyo, P.; Panov, V.A. Heterophase Synthesis of Zirconium Hydroxide from Zirconium Oxychloride. Inorg. Mater. 2019, 55, 994–1000. [Google Scholar] [CrossRef]
- Bergerhoff, G.; Brown, I. Crystallographic Databases; International Union of Crystallography: Chester, UK, 1987. [Google Scholar]
- Gabela, F.; Kojić-Prodić, B.; Šljukić, M.; Rużić-Toroš, Z. Refinement of the crystal structure of di-μ-fluoro-hexafluorohexaaquadizirconium(IV), Zr2F8(H2O)6. Acta Crystallogr. B 1977, 33, 3733–3736. [Google Scholar] [CrossRef]
- Kojić-Prodić, B.; Gabela, F.; Rużić-Toroš, Z.; Šljukić, M. Structure of aquatetrafluorozirconium(IV). Acta Crystallogr. B 1981, 37, 1963–1965. [Google Scholar] [CrossRef]
- Davidovich, R.; Gerasimenko, A.; Bukvetskii, B.; Logvinova, V.; Buslaev, Y. Crystal structure of hydroxonium hexafluorozirconate. Russ. J. Coord. Chem./Koord. Khimiya 1987, 13, 706–709. [Google Scholar]
- Charpin, P.; Lance, M.; Nierlich, M.; Vigner, J.; Lambard, J. Structures of oxonium pentafluorozirconate mono- and dihydrates. Acta Crystallogr. C 1988, 44, 1698–1701. [Google Scholar] [CrossRef]
- Marsh, R.E. Structure of oxonium pentafluorozirconate dihydrate. Corrigendum. Acta Crystallogr. C 1989, 45, 980. [Google Scholar] [CrossRef]
- Davidovich, R.L.; Pushilin, M.A.; Logvinova, V.B.; Gerasimenko, A.V. Crystal structure of monoclinic modifications of zirconium and hafnium tetrafluoride trihydrates. J. Struct. Chem. 2013, 54, 541–546. [Google Scholar] [CrossRef]
- Guillet, L.; Ider, A.; Laval, J.P.; Frit, B. Crystal structure of TeOF2. J. Fluor. Chem. 1999, 93, 33–38. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Norm-conserving and ultrasoft pseudopotentials for first-row and transition elements. J. Phys. Condens. Matter 1994, 6, 8245–8257. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Balog, M.; Schieber, M.; Michman, M.; Patai, S. Chemical vapor deposition and characterization of HfO2 films from organo-hafnium compounds. Thin Solid Films 1977, 41, 247–259. [Google Scholar] [CrossRef]
- Lucovsky, G.; Fulton, C.C.; Zhang, Y.; Zou, Y.; Luning, J.; Edge, L.F.; Whitten, J.L.; Nemanich, R.J.; Ade, H.; Schlom, D.G.; et al. Conduction band-edge States associated with the removal of d-state degeneracies by the Jahn-Teller effect. IEEE Trans. Device Mater. Reliab. 2005, 5, 65–83. [Google Scholar] [CrossRef]
- French, R.H.; Glass, S.J.; Ohuchi, F.S.; Xu, Y.N.; Ching, W.Y. Experimental and theoretical determination of the electronic structure and optical properties of three phases of ZrO2. Phys. Rev. B 1994, 49, 5133–5142. [Google Scholar] [CrossRef]
- Smith, D.K.; Newkirk, W. The crystal structure of baddeleyite (monoclinic ZrO2) and its relation to the polymorphism of ZrO2. Acta Cryst. 1965, 18, 983–991. [Google Scholar] [CrossRef]
- Tkatchenko, A.; Scheffler, M. Accurate Molecular Van Der Waals Interactions from Ground-State Electron Density and Free-Atom Reference Data. Phys. Rev. Lett. 2009, 102, 73005. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Maimaitiyili, T.; Steuwer, A.; Blomqvist, J.; Bjerkén, C.; Blackmur, M.S.; Zanellato, O.; Andrieux, J.; Ribeiro, F. Observation of the δ to ϵ Zr-hydride transition by in-situ synchrotron X-ray diffraction. Cryst. Res. Technol. 2016, 51, 663–670. [Google Scholar] [CrossRef]
- Romans, P.A.; Paasche, O.G.; Kato, H. The transformation temperature of hafnium. J. Less-Common Met. 1965, 8, 213–215. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in molecules. Acc. Chem. Res. 1985, 18, 9–15. [Google Scholar] [CrossRef]
- Henkelman, G.; Arnaldsson, A.; Jónsson, H. A fast and robust algorithm for Bader decomposition of charge density. Comp. Mat. Sci. 2006, 36, 354–360. [Google Scholar] [CrossRef]
- Sanville, E.; Kenny, S.D.; Smith, R.; Henkelman, G. Improved grid-based algorithm for Bader charge allocation. J. Comput. Chem. 2007, 28, 899–908. [Google Scholar] [CrossRef] [PubMed]
- Tang, W.; Sanville, E.; Henkelman, G. A grid-based Bader analysis algorithm without lattice bias. J. Phys. Condens. Matter 2009, 21, 84204. [Google Scholar] [CrossRef] [PubMed]
- Yu, M.; Trinkle, D.R. Accurate and efficient algorithm for Bader charge integration. J. Chem. Phys. 2011, 134, 64111. [Google Scholar] [CrossRef]
- Tran, R.; Xu, Z.; Radhakrishnan, B.; Winston, D.; Sun, W.; Persson, K.A.; Ong, S.P. Surface energies of elemental crystals. Sci. Data 2016, 3, 160080. [Google Scholar] [CrossRef] [PubMed]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Howard, C.J.; Hill, R.J.; Reichert, B.E. Structures of ZrO2 polymorphs at room temperature by high-resolution neutron powder diffraction. Acta Crystallogr. B 1988, 44, 116–120. [Google Scholar] [CrossRef]
- Pathak, S.; Das, P.; Das, T.; Mandal, G.; Joseph, B.; Sahu, M.; Kaushik, S.D.; Siruguri, V. Crystal structure of monoclinic hafnia (HfO2) revisited with synchrotron X-ray, neutron diffraction and first-principles calculations. Acta Crystallogr. C 2020, 76, 1034–1042. [Google Scholar] [CrossRef]
- Quintard, P.E.; Barbéris, P.; Mirgorodsky, A.P.; Merle-Méjean, T. Comparative Lattice-Dynamical Study of the Raman Spectra of Monoclinic and Tetragonal Phases of Zirconia and Hafnia. J. Am. Ceram. Soc. 2002, 85, 1745–1749. [Google Scholar] [CrossRef]
- Goldstein, M.; Hughes, R.J.; Unsworth, W.D. Vibrational spectra of some heavy metal teftafluorides in the solid state. Spectrochim. Acta A 1975, 31, 621–624. [Google Scholar] [CrossRef]
- Neese, F. Software update: The ORCA program system—Version 5.0. WIREs Comput Mol Sci. 2022, 12, e1606. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
- Andrae, D.; Häußermann, U.; Dolg, M.; Stoll, H.; Preuß, H. Energy-adjusted ab initio pseudopotentials for the second and third row transition elements. Theoret. Chim. Acta 1990, 77, 123–141. [Google Scholar] [CrossRef]
- van Wüllen, C. Molecular density functional calculations in the regular relativistic approximation: Method, application to coinage metal diatomics, hydrides, fluorides and chlorides, and comparison with first-order relativistic calculations. J. Chem. Phys. 1998, 109, 392–399. [Google Scholar] [CrossRef]
- Pantazis, D.A.; Chen, X.Y.; Landis, C.R.; Neese, F. All-Electron Scalar Relativistic Basis Sets for Third-Row Transition Metal Atoms. J. Chem. Theory Comput. 2008, 4, 908–919. [Google Scholar] [CrossRef]
- Steiner, T. The Hydrogen Bond in the Solid State. Angew. Chem. Int. Ed. 2002, 41, 48–76. [Google Scholar] [CrossRef]
- Jeffrey, G. An Introduction to Hydrogen Bonding; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Brammer, L.; Bruton, E.A.; Sherwood, P. Fluoride ligands exhibit marked departures from the hydrogen bond acceptor behavior of their heavier halogen congeners. New J. Chem. 1999, 23, 965–968. [Google Scholar] [CrossRef]
- Hirata, S.; Iwata, S. Ab Initio Hartree—Fock and Density Functional Studies on the Structures and Vibrations of an Infinite Hydrogen Fluoride Polymer. J. Phys. Chem. A 1998, 102, 8426–8436. [Google Scholar] [CrossRef]
- Johnson, M.W.; Sándor, E.; Arzi, E. The crystal structure of deuterium fluoride. Acta Crystallogr. B 1975, 31, 1998–2003. [Google Scholar] [CrossRef]

| Compound | a (Å) | b (Å) | c (Å) | V (Å) | (Å) | () | |
|---|---|---|---|---|---|---|---|
| ZrO2 | 4 | 5.154 | 5.224 | 5.332 | 141.56 | 35.39 | 99.55 |
| lit. PB91 [41] | 4 | 5.197 | 5.279 | 5.349 | 144.74 | 36.18 | 99.53 |
| lit. exp. [86] | 4 | 5.150 | 5.212 | 5.317 | 140.88 | 35.22 | 99.23 |
| HfO2 | 4 | 5.105 | 5.182 | 5.277 | 137.64 | 34.41 | 99.54 |
| lit. PB91 [41] | 4 | 5.128 | 5.191 | 5.297 | 139.25 | 34.81 | 99.71 |
| lit. exp. [87] | 4 | 5.114 | 5.168 | 5.290 | 138.03 | 34.51 | 99.21 |
| TeOF2 | 4 | 5.212 | 8.025 | 5.485 | 227.81 | 56.95 | 96.82 |
| lit. exp. [65] | 4 | 5.307 | 8.289 | 5.513 | 241.09 | 60.27 | 96.22 |
| ZrOF2 | 4 | 5.305 | 6.879 | 5.318 | 193.88 | 48.47 | 92.63 |
| HfOF2 | 4 | 5.265 | 6.982 | 5.388 | 197.74 | 49.44 | 93.22 |
| ZrF4 | 12 | 11.694 | 9.889 | 7.660 | 710.40 | 59.20 | 126.68 |
| lit. exp. [45] | 12 | 11.845 | 9.930 | 7.730 | 732.53 | 61.04 | 126.32 |
| HfF4 | 12 | 11.609 | 9.816 | 7.600 | 694.85 | 57.90 | 126.65 |
| lit. exp. [46] | 12 | 11.725 | 9.869 | 7.636 | 713.48 | 59.46 | 126.15 |
| Solid-State Reactions | (eV/f.u.) | ||||
|---|---|---|---|---|---|
| Nr. | M = Zr | M = Hf | |||
| (I) | M(s) + O2(g) | → | MO2(s) | −19.279 | −19.545 |
| (I) | M(s) + 2H2O(g) | → | MO2(s) + 2 H2(g) | −5.274 | −5.540 |
| (II) | M(s) + 2 F2(g) | → | MF4(s) | −18.439 | −18.718 |
| (II) | M(s) + 4 HF(g) | → | MF4(s) + 2 H2(g) | −7.448 | −7.727 |
| (II) | MO2(s) + 4 HF(g) | → | MF4(s) + 2 H2O(g) | −2.174 | −2.188 |
| (II) | MOF2(s) + 2 HF(g) | → | MF4(s) + H2O(g) | −1.283 | −1.302 |
| (III) | M(s) + H2O(g) + 2HF(g) | → | MOF2(s) + 2 H2(g) | −6.165 | −6.425 |
| (III) | MO2(s) + F2(g) | → | MOF2(s) + O2(g) | +0.616 | +0.622 |
| (III) | MO2(s) + 2HF(g) | → | MOF2(s) + H2O(g) | −0.891 | −0.885 |
| lit. PBE solid to gas reactions [18] | |||||
| (II) | MO2(s) + 4 HF(g) | → | MF4(g) + 2 H2O(g) | −1.14 | −0.91 |
| (III) | MO2(s) + 2 HF(g) | → | MOF2(g) + H2O(g) | +2.96 | +3.87 |
| Compound | “” | a (Å) | b (Å) | c (Å) | V (Å) | “” (Å) | () | () | () |
|---|---|---|---|---|---|---|---|---|---|
| Zr6F23OH | 6 | 7.649 | 7.666 | 7.681 | 355.54 | 59.26 | 117.43 | 80.48 | 117.02 |
| Hf6F23OH | 6 | 7.591 | 7.610 | 7.626 | 347.97 | 58.00 | 117.41 | 80.40 | 117.01 |
| Zr4O4F7OH | 4 | 5.257 | 5.371 | 6.830 | 192.67 | 48.17 | 90.49 | 90.22 | 92.24 |
| Hf4O4F7OH | 4 | 5.289 | 5.372 | 6.830 | 193.84 | 48.46 | 90.23 | 90.37 | 92.71 |
| Solid-State Reactions | (eV/U.C.) | ||||
|---|---|---|---|---|---|
| Nr. | M = Zr | M = Hf | |||
| (2) | M6F24(s) + H2O | → | M6F23OH(s) + HF | ||
| (3) | M4O4F8(s) + H2O | → | M4O4F7OH(s) + HF | ||
| Zr6F23OH | ||||
|---|---|---|---|---|
| OH Pos. | (eV/U.C.) | (Å) | (Å) | (°) |
| 1 | 0.168 | 0.97 | (2.53), (2.17), (2.05) | (164), (101), (107) |
| 2 | 0 | 0.98 | 2.09, (2.07), (2.11) | 178, (104), (107) |
| 3 | 0.091 | 0.98 | 2.11, (2.16), (2.14) | 154, (106), (103) |
| 4 | 0.137 | 0.98 | (2.46), (1.92), (1.86) | (176), (112), (110) |
| 5 | 0.050 | 0.98 | 2.17, (2.04), (2.18) | 167, (107), (106) |
| 6 | 0.227 | 0.98 | (2.59), (2.02), (1.84) | (169), (110), (116) |
| 7 | 0.188 | 0.97 | (2.46), (2.04), (1.98) | (143), (99), (107) |
| Hf6F23OH | ||||
| OH Pos. | (eV/U.C.) | (Å) | (Å) | (°) |
| 1 | 0.174 | 0.97 | 2.20, (2.01), (2.18) | 170, (109), (99) |
| 2 | 0 | 0.97 | 2.10, (2.12), (2.04) | 174, (106), (104) |
| 3 | 0.091 | 0.97 | 2.11, (2.15), (2.13) | 153, (106), (103) |
| 4 | 0.156 | 0.97 | (2.44), (1.91), (1.82) | (178), (112), (111) |
| 5 | 0.049 | 0.98 | 2.17, (2.04), (2.17) | 164, (107), (106) |
| 6 | 0.273 | 0.98 | (2.38), (2.07), (1.76) | (168), (104), (119) |
| 7 | 0.093 | 0.97 | 2.11, (2.12), (2.15) | 154, (104), (106) |
| Zr4O4F7OH | ||||||
|---|---|---|---|---|---|---|
| OH Pos. | (eV/U.C.) | (Å) | (Å) | (°) | (Å) | (°) |
| 1 | 0 | 0.99 | 1.82, (2.21) | 147.88, (130.59) | (2.98) | (137.81) |
| 2 | 0.215 | 0.98 | 1.80, (2.29) | 147.70, (99.21) | (2.20), (2.66) | (111.38), (100.00) |
| 3 | 0.024 | 1.00 | — | — | 1.72, (2.50) | 166.17, (115.74) |
| 4 | 0.251 | 0.97 | 1.90, (2.33) | 155.97, (98.93) | (2.78) | (95.05) |
| Hf4O4F7OH | ||||||
| OH Pos. | (eV/U.C.) | (Å) | (Å) | (°) | (Å) | (°) |
| 1 | 0 | 0.99 | 1.87, (2.37) | 147.41, (131.32) | (2.91) | (140.75) |
| 2 | 0.248 | 0.98 | 1.87, (2.32) | 150.33, (96.44) | (2.21), (2.61) | (112.13), (107.42) |
| 3 | 0.022 | 1.00 | — | — | 1.71, (2.56) | 165.59, (116.82) |
| 4 | 0.284 | 0.97 | 1.95, (2.28) | 162.72, (98.86) | (2.46) | (91.40) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anders, J.; Göritz, F.; Loges, A.; John, T.; Paulus, B. Stability of Hydroxo/Oxo/Fluoro Zirconates vs. Hafniates—A DFT Study. Inorganics 2022, 10, 259. https://doi.org/10.3390/inorganics10120259
Anders J, Göritz F, Loges A, John T, Paulus B. Stability of Hydroxo/Oxo/Fluoro Zirconates vs. Hafniates—A DFT Study. Inorganics. 2022; 10(12):259. https://doi.org/10.3390/inorganics10120259
Chicago/Turabian StyleAnders, Jennifer, Fabian Göritz, Anselm Loges, Timm John, and Beate Paulus. 2022. "Stability of Hydroxo/Oxo/Fluoro Zirconates vs. Hafniates—A DFT Study" Inorganics 10, no. 12: 259. https://doi.org/10.3390/inorganics10120259
APA StyleAnders, J., Göritz, F., Loges, A., John, T., & Paulus, B. (2022). Stability of Hydroxo/Oxo/Fluoro Zirconates vs. Hafniates—A DFT Study. Inorganics, 10(12), 259. https://doi.org/10.3390/inorganics10120259