Abstract
The conditions for achieving the maximal unquenched orbital angular momentum L = 3 and the highest magnetic anisotropy in mononuclear 3d complexes with axial coordination symmetry are examined in terms of the ligand field theory. It is shown that, apart from the known linear two-coordinate 3d7 complex CoII(C(SiMe2ONaph)3)2 characterized by record magnetic anisotropy and single-molecule magnet (SMM) performance (with the largest known spin-reversal barrier Ueff = 450 cm−1), the maximal orbital angular momentum L = 3 can also be obtained in linear two-coordinate 3d2 complexes (V3+, Cr4+) and in trigonal-prismatic 3d3 (Cr3+, Mn4+) and 3d8 (Co+, Ni2+) complexes. A comparative assessment of the SMM performance of the 3d2, 3d3 and 3d8 complexes indicates that they are unlikely to compete with the record linear complex CoII(C(SiMe2ONaph)3)2, whose magnetic anisotropy is close to the physical limit for a 3d metal.
1. Introduction
Mononuclear paramagnetic metal complexes with high magnetic anisotropy are of great interest in recent years, largely due to the development of low-dimensional molecule-based magnetically bistable materials featuring slow magnetic relaxation and blocking of magnetization at low temperature—single-molecule magnets (0D, SMMs) [1,2,3,4,5,6,7,8,9] and single-chain magnets (1D, SCMs) [10,11,12]. The overall performance of SMMs and SCMs is quantified by two key parameters, the effective energy barrier to magnetization reversal (Ueff) and the blocking temperature (TB), below which the magnetization persists in zero external fields [6,7,8,9,10,11,12]. The Ueff and TB values depend strongly on the magnetic anisotropy of spin carriers incorporated in the high-spin molecule. The early research was mainly focused on polynuclear transition-metal complexes based on high-spin 3d-ions with enhanced single-ion magnetic anisotropy arising from the zero-field splitting (ZFS) of the ground spin state, such as Mn3+ and Ni2+ [1,2,3]. Then, after the discovery of slow magnetic relaxation in mononuclear lanthanide complexes (2003) [13] and later in mononuclear transition metal compounds (2010) [14,15], research interest has turned to SMMs involving single paramagnetic ion with high magnetic anisotropy due to the first-order unquenched orbital angular momentum, 4f-complexes [16,17,18,19,20,21,22,23,24] and special orbitally degenerate 3d-complexes with high axial symmetry [25,26]. These mononuclear 4f- and 3d-SMMs are known as single-ion magnets (SIMs).
At present, it is generally recognized that the unquenched orbital angular momentum of the magnetic metal ions is the most important factor governing large magnetic anisotropy and high SMM characteristics [8]. In this respect, lanthanide ions are especially attractive. In fact, all Ln3+ ions with open 4fN-shell exhibit large unquenched orbital angular momentum L (ranging from 3 to 6, except Gd3+ with L = 0) due to very weak ligand-field (LF) splitting energy and strong spin-orbit coupling (SOC) of 4f-electrons; the maximal orbital momentum L = 6 occurs in Nd3+ (4f3, 4I9/2), Pm3+ (4f4, 5I4), Ho3+ (4f10, 5I8) and Er3+ (4f11, 4I15/2) ions. Due to the strong SOC of 4f electrons, the orbital momentum L and spin S are coupled into the total angular momentum J; the ground state of free Ln3+(4fN) ions corresponds to the 2S+1LJ multiplet with J = L − S (N < 7) and J = L + S (N > 7). For Ln3+ ions in a ligands coordination environment, the ground J-multiplet undergoes LF splitting into 2J + 1 sublevels (called Stark sublevels) creating a highly anisotropic ground state [8,20]. In particular, pure Ising-type uniaxial magnetic anisotropy occurs in monometallic lanthanide complexes with distinct axial symmetry, in which axial LF lifts the (2J + 1)-fold degeneracy of the ground multiplet into ±MJ microstates with a definite projection of the total angular momentum [16,17,18,19,20,21,22,23,24]. The energy splitting diagram of ±MJ states (E vs. MJ) depends on both the strength and the intrinsic structure of the axial LF, which is specified by three axial LF parameters B20, B40, B60 [27]. In the optimal case, the strong field stabilizes the doubly degenerate ground state with maximal MJ projection (MJ = ±J) and with large energy separation from excited LF states thereby resulting in a double-well potential with the high-energy barrier Ueff inherent to high-performance SMMs. In particular, such LF-splitting pattern is observed in square antiprismatic [13], pentagonal-bipyramidal [28,29] and quasi-linear metallocene lanthanide complexes [30,31], many of which exhibit exceptionally high Ueff and TB values, including a record-setting dysprosium metallocene SMM with Ueff = 1541 cm−1 and TB = 80 K [31]. Recent trends in high-performance 4f SIM are reviewed in ref. [32].
Later on, since the report on the first mononuclear trigonal pyramidal FeII complexes with SMM behavior (2010) [14,15], extensive efforts have been taken to the development of 3d SIMs using diverse approaches to increase magnetic anisotropy and energy barrier; numerous 3d SIMs were reported in the past decade [8,25,26]. However, in contrast to f-block element complexes, in transition metal complexes the orbital angular momentum is commonly quenched (L = 0) by a strong LF to produce the spin-only ground state with low second-order magnetic anisotropy [33]. In the majority of high-spin 3d complexes, magnetic anisotropy is typically due to zero-field splitting (ZFS) of the ground spin multiplet 2S + 1, which is generally a weak effect resulting from second-order SOC [34]. Hence, the barriers Ueff of 3d SIMs are mostly low, within a few tens of cm−1 [8,25,26,33]. The most efficient strategy toward high-performance 3d SIMs takes advantage of unquenched orbital angular momentum (L ≠ 0) giving rise to the first-order spin-orbit splitting of the ground spin stated with L ≠ 0, which provides considerably stronger magnetic anisotropy and high energy barriers [16,17,18,19,20,21,22,23,24]. Unquenched first-order orbital angular momentum can only appear in orbitally degenerate transition metal complexes with high symmetry, such as octahedral CoII and [FeIII(CN)6]3 complexes (Oh) [33,34], trigonal-pyramidal (C3v), [14,15] trigonal-bipyramidal (D3h), [35] trigonal-prismatic (D3h) [36,37], pentagonal-bipyramidal (D5h) [38] and linear (D∞h) two-coordinate complexes [39,40,41,42,43].
However, apart from unquenched orbital angular momentum, another important condition for the highest SMM performance of mononuclear 3d complexes is the axial limit of the magnetic anisotropy, which has a purely Ising-type nature, with zero transverse components. This case occurs in the LF of axial symmetry, which is produced by tuning the geometric axiality of the ligand environment of the 3d-ion. Depending on the specific type of the coordination polyhedron and electronic configuration of the 3d ion, the axial LF may stabilize the ground orbital doublet with the projection of the orbital angular momentum ML = 0, ±1, ±2, or ±3. The latter is further split by the first-order SOC into energy levels ±MJ with definite projection MJ of the total angular momentum J along the magnetic axis, which ranges from L + S to |L − S|. In this regime, spin energy levels are represented by pure |±MJ> spin wave functions, in which quantum tunneling of magnetization (QTM) is suppressed both in the ground and exited spin states. In these systems the barrier Ueff is controlled by the first-order SOC energy ζ3dLS, which is proportional to the value of the ground-state orbital angular momentum ML; approximately, Ueff is specified by ζ3dML/2S, which is the energy separation between the ground ±MJ and first exited ±(MJ −1) states [42]. This leads to a pure Ising magnetic anisotropy and double-well potential with two lowest MJ = ±J states similar to those in 4f SIMs [16,17,18,19,20,21,22,23,24]. Accordingly, the highest barriers Ueff are observed in 3d SIMs with large orbital momentum ML, namely, in linear 3d7 complexes [FeI(C(SiMe3)3)2]− (226 cm−1) [40] and [(sIPr)CoIINDmp] (413 cm−1) [41] and also in trigonal-prismatic CoII complex (152 cm−1) [36] featuring L = 2, S = 3/2 and MJ = ±7/2 in the ground state. The record barrier belongs to linear two-coordinate cobalt complex, CoII(C(SiMe2ONaph)3)2 (Ueff = 450 cm−1) [42] and for the monocoordinated cobalt(II) adatom on a MgO surface (Ueff = 468 cm−1) [43] which have L = 3, S = 3/2 and MJ = ±9/2 in the ground state.
Considering that a large unquenched orbital angular momentum is extremely important for attaining the highest SMM performance in 3d-SIMs, the relevant question is in which mononuclear 3d complexes, besides the already known record-breaking linear two-coordinate 3d7 complexes [42,43], the maximum orbital angular momentum L = 3 (represented by the ground orbital doublet ML = ±3) is feasible. In this paper, general conditions for the appearance of the maximum orbital angular momentum L = 3 in mononuclear 3d complexes are analyzed in terms of the LF theory. We show that, apart from the linear two-coordinate 3d7 complex CoII(C(SiMe2ONaph)3)2 [42], the ground-state orbital doublet ML = ±3 can occur in linear 3d2 complexes and in trigonal-prismatic 3d3 and 3d8 complexes. Specific conditions for the LF splitting pattern of 3d orbitals leading to L = 3 are established.
2. Results
Below, the basic conditions for the realization of the maximal orbital angular momentum ML = ±3 in mononuclear 3d complexes with the axial LF are analyzed. First of all, it is clear that the ground orbital doublet ML = ±3 can only occur in 3d ions, which in the free-ion state have a 2S+1F ground atomic term featuring the maximum orbital angular momentum L = 3 for 3d ions, i.e., 3d2, 3d3, 3d7 and 3d8 ions. In transition–metal complexes with the LF of axial symmetry, the lowest 2S+1F term splits into four orbital components 2S+1F(ML) with a projection of orbital momentum ML = 0, ±1, ±2, ±3 (Figure 1). The objective of the present study is to establish conditions for the ML = ±3 orbital doublet to be the ground state.
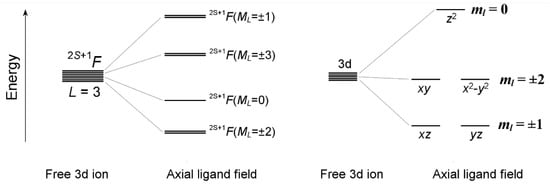
Figure 1.
Energy splitting of the ground-state atomic term 2S+1F(L = 3) and 3d orbitals in a ligand field of axial symmetry. The orbital composition of the 2S+1F(ML = ±3) states is shown below in the insets to the corresponding figures.
In an axial LF, five 3d orbitals are split into three groups of orbitals with a definite projection of the one-electron orbital angular momentum ml on the anisotropy axis z, 3dz2 (ml = 0), (3dxz, 3dyz) (ml = ±1) and 3dxy, 3dx2 − y2 (ml = ±2) (Figure 1). A necessary (but not sufficient) condition for the ML = ±3 ground state is the presence of one unpaired electron in each of the two doubly degenerate 3d orbitals with magnetic numbers ml = ±1, and ml = ±2, i.e., (xz, yz)1(xy, x2 − y2)1 or (xz, yz)3(xy, x2 − y2)3. For each of the 3d ions selected above, the LF splitting pattern of 3d-orbitals leading to the 2S+1F(ML = ±3) ground state is examined in terms of the conventional LF theory, which takes into account the interelectron repulsion (quantified in terms of the Racah parameters B and C) and SOC, ζ3dΣilisi. LF calculations are performed with the full basis set of 3dN configurations involving 45 (3d2, 3d8) and 120 (3d3, 3d7) |LMLSMS> microstates. Details of LF calculations are available in the Supplementary Materials.
2.1. 3d2 Complexes (V3+, Cr4+)
The necessary condition for the 3F(ML = ±3) orbital doublet to be the ground state is to have the LF spitting pattern E(z2) > E(xz, yz) > E(xy, x2 − y2). Such an orbital energy scheme can occur in complexes with linear or quasi-linear two-coordinate complexes [44] similar to the quasi-linear FeII [39] and CoII complexes [42]. For a quantitative evaluation, LF calculations for the energy levels of the 3d2 configuration were performed using the Racah parameters B = 600, C = 2900 cm−1 and SOC constant ζ = 150 cm−1, which are typical for V3+ ion [45]. The calculations were performed with fixed orbital energies E(z2) = 10,000 cm−1, E(xy, x2 − y2) = 0 and variable orbital energy E(xz, yz) = Δ (see inset in Figure 2a). The orbital doublet 3F(ML = ±3) (shown in the solid red line in Figure 2a) is found to be the ground state in the energy range 0 ≤ Δ ≤ 5400 cm−1; at larger energies, the ground state is the orbital singlet 3F(ML = 0), whose wave function Det||xy↑, x2 − y2↑|| corresponds to two singly occupied xy and x2 − y2 orbitals with parallel electron spins (Figure 2a). From the point of view of coordination geometry, the only suitable case for the 3F(ML = ±3) ground state is a linear two-coordination of 3d2 ion. Numerous 3d complexes of this type were reported in the literature, as outlined in a review article [44].
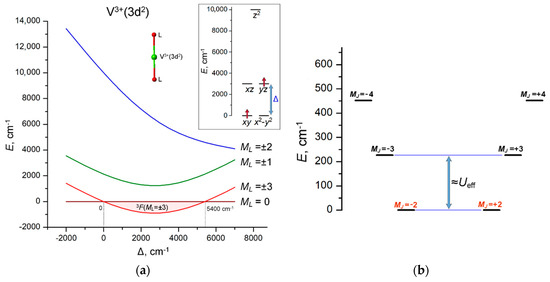
Figure 2.
(a) Variation of the energies of the 3F(ML) LF states of V3+(3d2) ion in linear coordination with increasing energy separation Δ = E(xz, yz) − E(xy, x2 − y2) between the lowest and first excited sets of 3d orbitals. The range of the stabilization of the 3F(ML = ±3) ground state (0 ≤ Δ ≤ 5400 cm−1) is marked with light pink. Inset: the LF splitting pattern of 3d orbitals in a linear two-coordination, E(xy, x2 − y2) = 0, E(z2) = 10,000 cm−1 (fixed) and E(xz, yz) = Δ (variable); (b) E vs. MJ diagram calculated at Δ = 3000 cm−1. The spin-reversal barrier Ueff ≈ 200 cm−1 is approximately estimated by the energy separation between the ground MJ = ±2 and the first excited MJ = ±3 states.
The calculated E vs. MJ diagram indicates that such a 3d2 complex may be a SMM with a barrier Ueff of about 200 cm−1, as estimated from the energy gap between ground MJ = ±2 and first excited MJ = ±3 states (Figure 2b). Remarkably, the E vs. MJ diagram has an inverse order of ±MJ levels compared to the usual double-well spin energy profile (with the maximum MJ at the bottom and the minimum MJ at the top) due to the antiparallel coupling of the orbital momentum L = 3 and spin S = 1 of V3+(3d2) ion. However, the actual SMM performance of the linear two-coordinate complex of V3+ is expected to be much lower due to the non-Kramers nature of the ground doublet MJ = ±2, which is subject to splitting due to possible deviations from the axiality of the molecular structure, leading to fast under-barrier quantum tunneling of magnetization (QTM) that shortcuts the energy barrier. Hence, in terms of SMM performance, the situation with the linear two-coordinate 3d2 complex is much less favorable compared to the record cobalt 3d7 complex CoII(C(SiMe2ONaph)3)2 [42].
2.2. 3d3 Complexes (Cr3+, Mn4+)
The ground state of a free 3d3 ion is a 4F atomic term, which is split by the axial LF into four orbital components, 4F(ML = ±3), 4F(ML = ±2), 4F(ML = ±1) and 4F(ML = 0). The 4F(ML = ±3) state originates from the (xy, x2 − y2)1(xz, yz)1(z2)1 electronic configuration. LF analysis indicates that this configuration can only occur at the E(xy, x2 − y2) > E(xz, yz) > E(z2) LF splitting pattern of 3d orbitals. Comparative LF calculations with atomic parameters B = 650, C = 3000 cm−1 and ζ = 250 cm−1 for Cr3+ ion reveal that the orbital doublet 4F(ML = ±3) is the ground state when the energy difference Δ = E(xy, x2 − y2) − E(xz, yz) between the energy levels of the (xy, x2 − y2) and (xz, yz) orbitals is within the range 0 ≤ Δ ≤ 5850 cm−1. Beyond this range, the ground state turns to the 4F(ML = 0) orbital singlet, which is represented by a mixture of the (xy)1(x2 − y2)1(z2)1 and (xz)1(yz)1(z2)1 electronic configurations (Figure 3).
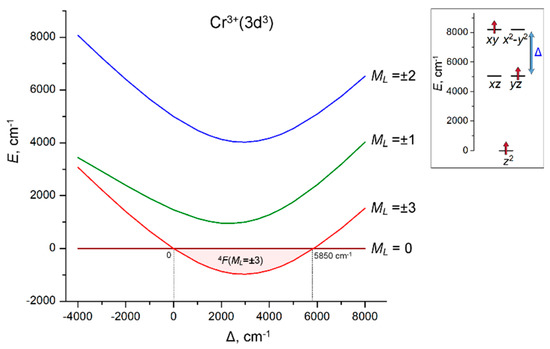
Figure 3.
Dependence of the energies of the 4F(ML) LF states of Cr3+(3d3) ion on the energy separation Δ = E(xy, x2 − y2) − E(xz, yz) between the (xy, x2 − y2) and (xz, yz) sets of 3d orbitals. The range of the stabilization of the 4F(ML = ±3) ground state (0 ≤ Δ ≤ 5850 cm−1) is marked with light pink. Inset: the LF splitting pattern of 3d orbitals, E(z2) = 0, E(xz, yz) = 5000 cm−1 (fixed) and E(xy, x2 − y2) = 5000 cm−1 + Δ (variable). LF calculations were done with atomic parameters B = 650, C = 3000 and ζ = 250 cm−1.
Evidently, the linear two-coordinate geometry of 3d3 complexes cannot provide the required orbital pattern E(xy, x2 − y2) > E(xz, yz) > E(z2) since linear coordination is characterized by another order of orbital energies, E(z2) > E(xz, yz) > E(xy, x2 − y2), which can result in ML = ±1 or ML = ±2 ground state. Therefore, unlike the record linear two-coordinate Co2+(3d7) complexes with the ML = ±3 ground state, linear 3d3 complexes have a maximum achievable orbital angular momentum of only ML = ±2.
Among a variety of axial symmetry coordination geometries, the necessary orbital splitting pattern E(xy, x2 − y2) > E(xz, yz) > E(z2) can be obtained in the trigonal-prismatic coordination of the 3d3 ion. However, in trigonal-prismatic complexes, the energy order of 3d orbital strongly depends on the polar angle θ of the trigonal prism. In order to evaluate the conditions for stabilization of the ML = ±3 ground state, LF calculations are performed in combination with the angular overlap model (AOM) [46,47,48,49,50,51] using the AOM parameters eσ = 9000 cm−1 and eσ/eπ = 4 for Cr3+ ions. These calculations show that the ground state 4F(ML = ±3) with the maximal orbital momentum ML = ±3 stabilizes in a compressed trigonal prism with a polar angle θ ranging between 61° and 66.5° (Figure 4a).
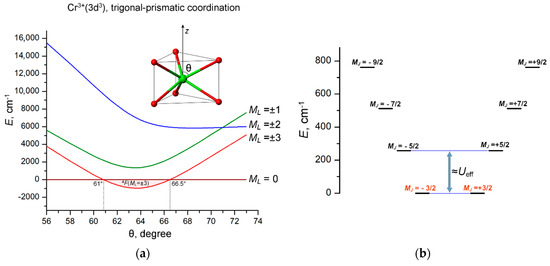
Figure 4.
(a) Variation of the energies of the 4F(ML) LF states of Cr3+(3d3) ion with increasing polar angle θ in a trigonal-prismatic coordination polyhedron. The range of the stabilization of the 4F(ML = ±3) ground state (61° ≤ θ ≤ 66.5°) is marked with light pink; (b) E vs. MJ diagram calculated at θ = 64°. The spin-reversal barrier Ueff ≈ 200 = 250 cm−1 is approximately estimated by the energy separation between the ground MJ = ±3/2 and the first excited MJ = ±5/2 states.
SOC splits the ground orbital doublet ML = ±3 into four Kramer doublets with the projection of the total angular momentum MJ = ±3/2, ±5/2, ±7/2 and ±9/2, listed in order of increasing energy; their energy diagram with the total splitting energy of 762 cm−1 is shown in Figure 4b. These results indicate that such a complex should have a SMM behavior with a barrier of about 250 cm−1, corresponding to the energy separation between the ground MJ = ±3/2 and first excited MJ = ±5/2 states. However, as opposed to linear two-coordinate CoII complexes [42,43], the trigonal-prismatic 3d3 complexes with doubly degenerate ground state ML = ±3 is Jahn–Teller active, subject to distortions that remove orbital degeneracy and thereby reduce the magnetic anisotropy of the complex. Nevertheless, LF/AOM calculations indicate that with moderate departures from the regular D3h geometry, the overall energy pattern of the JM states (Figure 4b) does not change much, so the trigonal-prismatic 3d3 complex behaves as an SMM with an estimated barrier of about 150–200 cm−1.
2.3. 3d7 Complexes (Fe+,Co2+)
Linear two-coordinate 3d7 cobalt complex CoII(C(SiMe2ONaph)3)2 [42] is currently the only known individual mononuclear 3d complex featuring the maximal orbital angular momentum L = 3. From the point of view of the LF theory, in the 3d7 configuration the orbital LF splitting pattern E(z2) > E(xz, yz) > E(xy, x2 − y2) is a necessary condition for the stabilization of the ML = ±3 ground state. Note that the order of the 3d orbitals in the 3d7 configuration is opposite to that in the 3d3 configuration because of the electron–hole symmetry. As in the case of 3d2 and 3d3 complexes, the additional condition is the restriction on the energy separation between the ml = ±1 and ml = ±2 orbitals, Δ = E(xz, yz) − E(xy, x2 − y2), which is 0 ≤ Δ ≤ 6750 cm−1 (Figure 5). Outside this range, the ground state is the orbital singlet 4F(ML = 0). Formally, an extra condition is a limitation on the total LF splitting energy ΔLF = E(z2) − E(xy, x2 − y2) < 22,000 cm−1, which is, however, too large to occur in a linear two-coordinate 3d7 complex exhibiting much lower total LF splitting energy, around 6000 cm−1 [42].
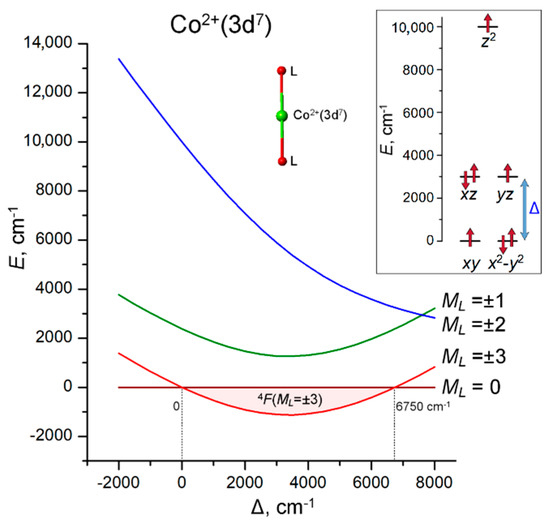
Figure 5.
Energies of the 4F(ML) LF states of Co2+(3d7) ion in a linear coordination as a function of the energy gap Δ = E(xz, yz) − E(xy, x2 − y2). The range of the stabilization of the 4F(ML = ±3) ground state (0 ≤ Δ ≤ 6750 cm−1) is marked with light pink. Inset: the LF splitting pattern of 3d orbitals, E(xy, x2 − y2) = 0, E(z2) = 10,000 cm−1 (fixed) and E(xz, yz) = Δ (variable). LF calculations are performed with atomic parameters B = 750, C = 3800 and ζ = 480 cm−1.
In light of these results, it is interesting to consider the difference in the nature of the ground state of the isoelectronic linear two-coordinate 3d7 complexes [FeI(C(SiMe3)3)2]− (ML = ±2) [40] and CoII(C(SiMe2ONaph)3)2 (ML = ±3) [42]. The underlying reason is the different order of the actual 3d orbitals, which is E(xz, yz) > E(xy, x2 − y2) > E(z2) (ca. 5200, 3200 and 0 cm−1, respectively) in the FeI complex [40] and E(z2) > E(xz, yz) > E(xy, x2 − y2) ((ca. 5700, 3000 and 0 cm−1) in CoII complex [42]. A significant decrease in the energy of the 3dz2 orbital in FeI(C(SiMe3)3)2]− is caused by a very strong 4s–3dz2 mixing [40]. The combination of the ground orbital state ML = ±3, the parallel coupling of the orbital momentum L = 3 and spin S = 3/2 and a sufficiently strong SOC leads to the most favorable conditions for obtaining a record spin-reversal barrier Ueff = 450 cm−1 of CoII(C(SiMe2ONaph)3)2 [42].
2.4. 3d8 Complexes (Ni2+, Co1+)
As in the case of 3d2 complexes with L = 3, the necessary condition for the occurrence of the ML = ±3 ground state in a 3d8 complex is the presence of one unpaired electron on the doubly degenerate 3d orbitals with magnetic quantum numbers ml = ±1 and ml = ±2, i.e., (x2 − y2, xy)3(xz, yz)3(z2)2. For this, the order of the 3d orbitals should be the same as in 3d3 complexes, i.e., E(xy, x2 − y2) > E(xz, yz) > E(z2). Therefore, this LF splitting pattern can occur in trigonal-prismatic complexes (see Figure 4a), but not in linear two-coordinate complexes (Figure 5). As in the case of other above 3d complexes, there is an additional condition that constrains the energy separation between ml = ±1 and ml = ±2 orbitals, Δ = E(xy, x2 − y2) − E(xz, yz), which is 0 ≤ Δ ≤ 7200 cm−1.(Figure 6). LF/AOM calculations for a trigonal-prismatic 3d8 complex with variable polar angle θ indicate that the ML = ±3 ground state stabilizes at 61° ≤ θ ≤ 74.2°, corresponding to a compressed trigonal prism (Figure 7a). Several trigonal-prismatic cage complexes of NiII were recently reported in [52]. In these complexes, the Ni2+ ion is encapsulated in a frame-type clathrochelate cage, that forces robust trigonal-prismatic coordination. However, in these complexes, the polar angle θ is about 52°, which is well below the critical angle θ > 61° (Figure 7a). Accordingly, the ground state of these complexes was found to be orbital singlet 3F(ML = 0) with a second-order magnetic anisotropy due to ZFS [48], which agrees well with the results of LF/AOM calculations indicating the ML = 0 ground state at θ ≈ 52° (Figure 7a). One more example of a trigonal-prismatic 3d8 complex is given by similar clathrochelate complexes CoI(GmCl2)3(BPh)2 reported in ref. [53]. Unfortunately, these complexes also do not fall into the range of existence of the ground state ML = ±3 due to violation of the Δ > 0 criterion (which is actually Δ ≈ −4500 cm−1), resulting in the ground state being the orbital singlet 3F(ML = 0).
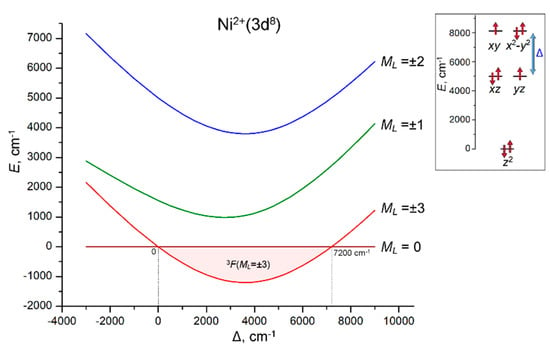
Figure 6.
Variation of the energies of the 3F(ML) LF states of Ni2+(3d8) ion with increasing energy gap Δ = E(xy, x2 − y2) − E(xz, yz). The range of the stabilization of the 3F(ML = ±3) ground state (0 ≤ Δ ≤ 7200 cm−1) is marked with light pink. Inset: the LF splitting pattern of 3d orbitals, E(z2) = 0, E(xz, yz) = 5000 cm−1 (fixed) and E(xy, x2 − y2) = 5000 cm−1 + Δ (variable). LF calculations are performed with atomic parameters B = 800, C = 3200 and ζ = 600 cm−1.
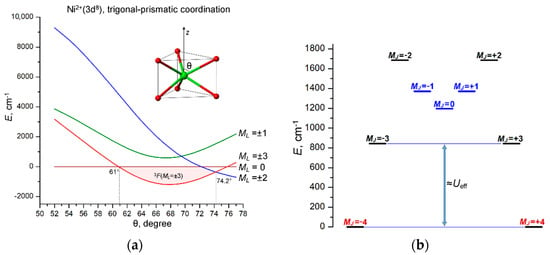
Figure 7.
(a) Variation of the energies of the 3F(ML) LF states of Ni2+(3d8) ion with increasing polar angle θ in trigonal-prismatic coordination, as obtained from LF/AOM calculations. The range of the stabilization of the 3F(ML = ±3) ground state (61° ≤ θ ≤ 74.2°) is marked with light pink; (b) E vs. MJ diagram calculated at θ = 64°. The spin-reversal barrier Ueff ≈ 850 cm−1 is approximately estimated by the energy separation between the ground MJ = ±3/2 and the first excited MJ = ±5/2 states; the MJ = 0 and MJ = ±1 states (marked in blue) originate from 2S+1L atomic terms other than 3F. LF/AOM calculations were performed with eσ = 5000 cm−1, eσ/eπ = 4 AOM parameters and atomic parameters B = 800, C = 3200 and ζ = 600 cm−1.
The calculated E vs. MJ diagram suggests potentially high SMM characteristics of the compressed (θ > 61°) trigonal-prismatic Ni2+ complex with a perfect D3h symmetry. In particular, the spin-reversal barrier Ueff, assigned to the energy separation between the ground state JM = ±4 and the first excited state JM = ±3, is as high as 857 cm−1 (Figure 7b), which is significantly larger than in the record cobalt complex CoII(C(SiMe2ONaph)3)2 (450 cm−1) [42]. However, it should be considered that, similarly to the trigonal-prismatic 3d3 complex, this complex is Jahn–Teller active and is subject to significant distortions that tend to reduce magnetic anisotropy. In fact, LF/AOM calculations for distorted complexes show that even subtle departures from the regular trigonal-prismatic geometry (D3h) of the complex cause noticeable splitting of the ground non-Kramers doublet JM = ±4 (tens of cm−1), which should lead to complete suppression of the SMM behavior due to fast QTM processes in the split ground state JM = ±4 (Figure 7b).
3. Materials and Methods
Ligand Field and Angular Overlap Model Calculations
Ligand-field calculations for many-electron 3dN ions (3d2, 3d3, 3d7 and 3d8) were performed in terms of the conventional LF theory involving the one-electron LF operator (specified by the set of energies of 3d orbitals in an axial LF, E(xy, x2 − y2), E(xz, yz) and E(z2)), interelectron Coulomb repulsion (treated in terms of the Racah parameters B and C) and the spin-orbit coupling ζ3dΣilisi. Angular-overlap model calculations [46,47,48] for trigonal-prismatic complexes were carried out with the AOM parameters eσ = 5000 cm−1 (for Ni2+) and 9000 cm−1 (Cr3+) at a fixed ratio of eσ/eπ = 4. Details of LF and AOM calculations are available in the Supplementary Materials.
4. Discussion and Conclusions
This study has established that the maximum orbital angular momentum L = 3 observed in the linear two-coordinate 3d7 complex CoII(C(SiMe2ONaph)3)2 [42] (as well as in the monocoordinated Co adatom on a MgO surface [43]) is not a unique single phenomenon, but under specific conditions, it can also be obtained in some complexes of 3d2, 3d3 and 3d8 transition metal ions. The basic point is that in the free-ion state these ions have the ground-state atomic term 2S+1F with maximal orbital angular momentum L = 3, which, when split in the ligand field of axial symmetry, can produce the ground orbital doublet 2S+1F(ML = ±3) with a maximum projection ML = ±3 of the orbital momentum L = 3. For each of these electronic configurations, the LF splitting pattern of 3d orbitals leading to the ground orbital doublet 2S+1F(ML = ±3) has been established. Then, with the help of LF and AOM calculations, it was shown that the maximal orbital angular moment L = 3 is realized in the linear two-coordinate geometry for the 3d2 and 3d7 ions and in the compressed trigonal-prismatic coordination (with polar angle θ > 61°) for the 3d3 and 3d8 ions. In this regard, it is worth noting that the linear two-coordinate geometry, which intuitively appears to be the most preferable for obtaining maximum magnetic anisotropy, in the case of 3d3 and 3d8 ions yields only an orbital momentum L = 2, not L = 3.
These results can be used to assess the prospects for improving the SMM performance of single-ion 3d SMMs. The calculated E vs. MJ spin energy diagrams show that the SMM performance of the linear 3d2 complex and the trigonal-prismatic 3d3 complex is significantly lower than that of the linear cobalt complex due to weaker spin-orbit coupling and antiparallel coupling of L and S. On the other hand, although the calculated spin energy diagram for the trigonal-prismatic Ni2+(3d8) complex formally indicates a higher barrier (Ueff ≈ 850 cm−1) than for the record linear cobalt complex (450 cm−1) [42], in reality, this complex is unlikely to be a good SMM because of the Jahn–Teller distortions resulting in the significant splitting of the ground non-Kramer doublet MJ = ±4 (Figure 7b), that causes fast QTM processes bypassing the barrier. Thus, despite the possible presence of maximum orbital momentum L = 3 in the aforementioned 3d2, 3d3 and 3d8 complexes, they cannot compete as SMMs with linear two-coordinate 3d7 cobalt complex CoII(C(SiMe2ONaph)3)2 [42].
In summary, this study has shown that the maximal orbital angular momentum L = 3 can occur only in 3d2, 3d3, 3d7 and 3d8 complexes with axial symmetry of the ligand field. However, the SMM performance of 3d2, 3d3 and 3d8 complexes appeared significantly lower than that of the linear two-coordinate 3d7 complex CoII(C(SiMe2ONaph)3)2 with L = 3. Thus, these results confirm the earlier conclusion [42] that linear two-coordinate 3d7 complexes provide the maximal SMM performance of mononuclear 3d complexes (Ueff = 450 cm−1), which is apparently near the physical limit for a single 3d metal ion.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/inorganics10120227/s1, details of LF and AOM calculations.
Author Contributions
Conceptualization, validation, methodology, writing—original draft preparation, writing—review and editing, supervision, V.S.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Russian Science Foundation, project No. 18-13-00264.
Data Availability Statement
The data presented in this study are available in this article and in the Supplementary Materials.
Acknowledgments
V.S.M. acknowledges support by the Ministry of Science and Higher Education within the State assignment FSRC ‘Crystallography and Photonics’ RAS in part of the development of computational approaches for analysis of extreme magnetic anisotropy in transition-metal complexes.
Conflicts of Interest
The author declares no conflict of interest.
References
- Sessoli, R.; Gatteschi, D.; Caneschi, A.; Novak, M.A. Magnetic bistability in a metal-ion cluster. Nature 1993, 365, 141–143. [Google Scholar] [CrossRef]
- Gatteschi, D.; Sessoli, R. Quantum tunneling of magnetization and related phenomena in molecular materials. Angew. Chem. Int. Ed. 2003, 42, 268–297. [Google Scholar] [CrossRef] [PubMed]
- Gatteschi, D.; Sessoli, R.; Villain, J. Molecular Nanomagnets; Oxford University Press: Oxford, UK, 2006. [Google Scholar] [CrossRef]
- Leuenberger, M.N.; Loss, D. Quantum computing in molecular magnets. Nature 2001, 410, 789–793. [Google Scholar] [CrossRef] [PubMed]
- Bogani, L.; Wernsdorfer, W. Molecular spintronics using single-molecule magnets. Nat. Mater. 2008, 7, 179. [Google Scholar] [CrossRef] [PubMed]
- Bartolomé, J.; Luis, F.; Fernández, J.F. (Eds.) Molecular Magnets: Physics and Applications; NanoScience and Technology; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1–395. ISBN 1010:9783642406089. [Google Scholar]
- McInnes, E.J.L.; Winpenny, R.E.P. 4.14—Molecular Magnets. Comprehensive Inorganic Chemistry II; Elsevier: Edinburgh, UK, 2013; Volume 4, pp. 371–396. [Google Scholar] [CrossRef]
- Feng, M.; Tong, M.-L. Single Ion Magnets from 3d to 5f: Developments and Strategies. Chem.—Eur. J. 2018, 24, 7574–7594. [Google Scholar] [CrossRef]
- Coronado, E. Molecular magnetism: From chemical design to spin control in molecules, materials and devices. Nat. Rev. Mat. 2020, 5, 87–104. [Google Scholar] [CrossRef]
- Caneschi, A.; Gatteschi, D.; Lalioti, N.; Sangregorio, C.; Sessoli, R.; Venturi, G.; Vindigni, A.; Rettori, A.; Pini, M.G.; Novak, M.A. Cobalt(II)-Nitronyl Nitroxide Chains as Molecular Magnetic Nanowires. Angew. Chem. Int. Ed. 2001, 40, 1760–1763. [Google Scholar] [CrossRef]
- Coulon, C.; Miyasaka, H.; Clérac, R. Single-Chain Magnets: Theoretical Approach and Experimental Systems. In Single-Molecule Magnets and Related Phenomena. Structure and Bonding; Winpenny, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2006; Volume 122, pp. 163–206. [Google Scholar] [CrossRef]
- Sun, H.-L.; Wang, Z.-M.; Gao, S. Strategies towards Single-Chain Magnets. Coord. Chem. Rev. 2010, 254, 1081–1100. [Google Scholar] [CrossRef]
- Ishikawa, N.; Sugita, M.; Ishikawa, T.; Koshihara, S.-Y.; Kaizu, Y. Lanthanide Double-Decker Complexes Functioning as Magnets at the Single-Molecular Level. J. Am. Chem. Soc. 2003, 125, 8694–8695. [Google Scholar] [CrossRef]
- Freedman, D.E.; Harman, W.H.; Harris, T.D.; Long, G.J.; Chang, C.J.; Long, J.R. Slow magnetic relaxation in a high-spin iron(II) complex. J. Am. Chem. Soc. 2010, 132, 1224–1225. [Google Scholar] [CrossRef]
- Harman, W.H.; Harris, T.D.; Freedman, D.E.; Fong, H.; Chang, A.; Rinehart, J.D.; Ozarowski, A.; Sougrati, M.T.; Grandjean, F.; Long, G.J.; et al. Slow magnetic relaxation in a family of trigonal pyramidal iron(II) pyrrolide complexes. J. Am. Chem. Soc. 2010, 132, 18115–18126. [Google Scholar] [CrossRef]
- Rinehart, J.D.; Long, J.R. Exploiting Single-Ion Anisotropy in the Design of f-Element Single-Molecule Magnets. Chem. Sci. 2011, 2, 2078–2085. [Google Scholar] [CrossRef]
- Woodruff, D.N.; Winpenny, R.E.P.; Layfield, R.A. Lanthanide Single-Molecule Magnets. Chem. Rev. 2013, 113, 5110–5148. [Google Scholar] [CrossRef]
- Liddle, S.T.; van Slageren, J. Improving f-Element Single Molecule Magnets. Chem. Soc. Rev. 2015, 44, 6655–6669. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, L.; Tang, J. Lanthanide single molecule magnets: Progress and perspective. Dalton Trans. 2015, 44, 3923–3929. [Google Scholar] [CrossRef]
- Layfield, R.; Murugesu, M. Lanthanides and Actinides in Molecular Magnetism; John Wiley & Sons: New York, NY, USA, 2015; pp. 1–368. ISBN 978-3-527-33526-8. [Google Scholar]
- Lu, J.; Guo, M.; Tang, J. Recent Developments in Lanthanide Single-Molecule Magnets. Chem.—Asian J. 2017, 12, 2772–2779. [Google Scholar] [CrossRef]
- Liu, J.-L.; Chen, Y.-C.; Tong, M.-L. Symmetry Strategies for High Performance Lanthanide-Based Single-Molecule Magnets. Chem. Soc. Rev. 2018, 47, 2431–2453. [Google Scholar] [CrossRef]
- Feltham, H.L.C.; Brooker, S. Review of Purely 4f and Mixed-Metal nd-4f Single-Molecule Magnets Containing only One Lanthanide Ion. Coord. Chem. Rev. 2014, 276, 1–33. [Google Scholar] [CrossRef]
- Layfield, R.A. Organometallic Single-Molecule Magnets. Organometallics 2014, 33, 1084–1099. [Google Scholar] [CrossRef]
- Craig, G.A.; Murrie, M. 3d single-ion magnets. Chem. Soc. Rev. 2015, 44, 2135–2147. [Google Scholar] [CrossRef]
- Frost, J.M.; Harriman, K.L.M.; Murugesu, M. The rise of 3-d single-ion magnets in molecular magnetism: Towards materials from molecules? Chem. Sci. 2016, 7, 2470–2491. [Google Scholar] [CrossRef] [PubMed]
- Wyborne, B.G. Spectroscopic Properties of Rare Earths; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1965; pp. 1–241. ISBN 978-0470965078. [Google Scholar]
- Liu, J.; Chen, Y.-C.; Liu, J.-L.; Vieru, V.; Ungur, L.; Jia, J.-H.; Chibotaru, L.F.; Lan, Y.; Wernsdorfer, W.; Gao, S.; et al. A stable pentagonal bipyramidal Dy(III) single-ion magnet with a record magnetization reversal barrier over 1000 K. J. Am. Chem. Soc. 2016, 138, 5441–5450. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.-S.; Chilton, N.F.; Winpenny, R.E.P.; Zheng, Y.-Z. On approaching the limit of molecular magnetic anisotropy: A near-perfect pentagonal bipyramidal dysprosium(III) single-molecule magnet. Angew. Chem. Int. Ed. 2016, 55, 16071–16074. [Google Scholar] [CrossRef] [PubMed]
- Goodwin, C.A.P.; Ortu, F.; Reta, D.; Chilton, N.F.; Mills, D.P. Molecular magnetic hysteresis at 60 kelvin in dysprosocenium. Nature 2017, 548, 439–442. [Google Scholar] [CrossRef] [PubMed]
- Guo, F.-S.; Day, B.M.; Chen, Y.-C.; Tong, M.-L.; Mansikkamäki, A.; Layfield, R.A. Magnetic Hysteresis up to 80 Kelvin in a Dysprosium Metallocene Single-Molecule Magnet. Science 2018, 362, 1400–1403. [Google Scholar] [CrossRef]
- Zhu, Z.; Tang, J. Lanthanide single-molecule magnets with high anisotropy barrier: Where to from here? Natl. Sci. Rev. 2022, nwac194. [Google Scholar] [CrossRef]
- Bar, A.K.; Pichon, C.; Sutter, J.-P. Magnetic Anisotropy in Two- to Eight-Coordinated Transition–Metal Complexes: Recent Developments in Molecular Magnetism. Coord. Chem. Rev. 2016, 308, 346–380. [Google Scholar] [CrossRef]
- Boca, R. Zero-field splitting in metal complexes. Coord. Chem. Rev. 2004, 248, 757–815. [Google Scholar] [CrossRef]
- Marriott, K.E.R.; Bhaskaran, L.; Wilson, C.; Medarde, M.; Ochsenbein, S.T.; Hill, S.; Murrie, M. Pushing the limits of magneticanisotropy in trigonal bipyramidal Ni(II). Chem. Sci. 2015, 6, 6823–6828. [Google Scholar] [CrossRef]
- Novikov, V.V.; Pavlov, A.A.; Nelyubina, Y.V.; Boulon, M.-E.; Varzatskii, O.; Voloshin, Y.Z.; Winpenny, R.E.P. A Trigonal Prismatic Mononuclear Cobalt(II) Complex Showing Single-Molecule Magnet Behavior. J. Am. Chem. Soc. 2015, 137, 9792–9795. [Google Scholar] [CrossRef]
- Yao, B.; Singh, M.K.; Deng, Y.-F.; Wang, Y.-N.; Dunbar, K.R.; Zhang, Y.-Z. Trigonal Prismatic Cobalt(II) Single-Ion Magnets: Manipulating the Magnetic Relaxation Through Symmetry Control. Inorg. Chem. 2020, 59, 8505–8513. [Google Scholar] [CrossRef]
- Sutter, J.P.; Béreau, V.; Jubault, V.; Bretosh, K.; Pichon, C.; Duhayon, C. Magnetic anisotropy of transition metal and lanthanide ions in pentagonal bipyramidal geometry. Chem. Soc. Rev. 2022, 51, 3280–3313. [Google Scholar] [CrossRef]
- Zadrozny, J.M.; Atanasov, M.; Bryan, A.M.; Lin, C.-Y.; Rekken, B.D.; Power, P.P.; Neese, F.; Long, J.R. Slow magnetization dynamics in a series of two-coordinate iron(II) complexes. Chem. Sci. 2013, 4, 125–138. [Google Scholar] [CrossRef]
- Zadrozny, J.M.; Xiao, D.J.; Atanasov, M.; Long, G.J.; Grandjean, F.; Neese, F.; Long, J.R. Magnetic blocking in a linear iron(I) complex. Nat. Chem. 2013, 5, 577–581. [Google Scholar] [CrossRef]
- Yao, X.-N.; Du, J.-Z.; Zhang, Y.-Q.; Leng, X.-B.; Yang, M.-W.; Jiang, S.-D.; Wang, Z.-X.; Ouyang, Z.-W.; Deng, L.; Wang, B.-W.; et al. Two-Coordinate Co(II) Imido Complexes as Outstanding Single-Molecule Magnets. J. Am. Chem. Soc. 2017, 139, 373–380. [Google Scholar] [CrossRef]
- Bunting, P.C.; Atanasov, M.; Damgaard-Møller, E.; Perfetti, M.; Crassee, I.; Orlita, M.; Overgaard, J.; van Slageren, J.; Neese, F.; Long, J.R. A linear cobalt(II) complex with maximal orbital angular momentum from a non-Aufbau ground state. Science 2018, 362, eaat7319. [Google Scholar] [CrossRef]
- Rau, G.; Baumann, S.; Rusponi, S.; Donati, F.; Stepanow, S.; Gragnaniello, L.; Dreiser, J.; Piamonteze, C.; Nolting, F.; Gangopadhyay, S.; et al. Reaching the magnetic anisotropy limit of a 3d metal atom. Science 2014, 344, 988–992. [Google Scholar] [CrossRef] [PubMed]
- Powell, P.P. Stable Two-Coordinate, Open-Shell (d1–d9) Transition Metal Complexes. Chem. Rev. 2012, 112, 3482–3507. [Google Scholar] [CrossRef]
- Reber, C.; Güdel, H.U. Near-infrared luminescence spectroscopy of Al2O3:V3+ and YP3O9:V3+. Chem. Phys. Lett. 1989, 154, 425–431. [Google Scholar] [CrossRef]
- Schaeffer, C.E.; Jorgensen, C.K. The angular overlap model, an attempt to revive the ligand field approaches. Mol. Phys. 1965, 9, 401–412. [Google Scholar] [CrossRef]
- Schäffer, C.E. A perturbation representation of weak covalent bonding. Struct. Bonding. 1968, 5, 68–95. [Google Scholar] [CrossRef]
- Jorgensen, C.K. The Nephelauxetic Series. Prog. Inorg. Chem. 1962, 4, 73–124. [Google Scholar] [CrossRef]
- Mironov, V.S.; Bazhenova, T.A.; Manakin, Y.V.; Lyssenko, K.A.; Talantsev, A.D.; Yagubskii, E.B. A new Mo(IV) complex with the pentadentate (N3O2) Schiff-base ligand: The first non-cyanide pentagonal–bipyramidal paramagnetic 4d complex. Dalton Trans. 2017, 46, 14083–14087. [Google Scholar] [CrossRef] [PubMed]
- Manakin, Y.V.; Mironov, V.S.; Bazhenova, T.A.; Lyssenko, K.A.; Gilmutdinov, I.F.; Bikbaev, K.S.; Masitov, A.A.; Yagubskii, E.B. (Et4N)[MoIII(DAPBH)Cl2], the first pentagonal-bipyramidal Mo(III) complex with a N3O2-type Schiff-base ligand: Manifestation of unquenched orbital momentum and Ising-type magnetic anisotropy. Chem. Commun. 2018, 54, 10084–10087. [Google Scholar] [CrossRef]
- Bazhenova, T.A.; Zorina, L.V.; Simonov, S.V.; Mironov, V.S.; Maximova, O.V.; Spillecke, L.; Koo, C.; Klingeler, R.; Manakin, Y.V.; Vasiliev, A.N.; et al. The first pentagonal-bipyramidal vanadium(iii) complexes with a Schiff-base N3O2 pentadentate ligand: Synthesis, structure and magnetic properties. Dalton Trans. 2020, 49, 15287–15298. [Google Scholar] [CrossRef]
- Campanella, A.J.; Ozvat, T.M.; Zadrozny, J.M. Ligand design of zero-field splitting in trigonal prismatic Ni(ii) cage complexes. Dalton Trans. 2022, 51, 3341–3348. [Google Scholar] [CrossRef]
- Nehrkorn, J.; Veber, S.L.; Zhukas, L.A.; Novikov, V.V.; Nelyubina, Y.V.; Voloshin, Y.Z.; Holldack, K.; Stoll, S.; Schnegg, A. Determination of Large Zero-Field Splitting in High-Spin Co(I) Clathrochelates. Inorg. Chem. 2018, 57, 15330–15340. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).