Influence of the Width of Launch Beam Distribution on the Transmission Performance of Seven-Core Polymer-Clad Silica Fibers

Abstract

We propose a space division multiplexing (SDM) in a newly constructed multicore polymer-clad silica fiber (PCSF) with seven cores arrayed in a hexagonal array, each carrying a centrally launched beam. This enables a higher SDM capacity at longer fiber lengths in the proposed seven-core PCSF if compared with previously proposed angular division multiplexing (ADM) in single-core (SC) PCSF. As a result, the SDM is not limited to short fiber lengths in the proposed seven-core PCSF, as it is in the case of the ADM channels due to mode coupling in the SC PCSF. In addition, the time-independent power flow equation (TI PFE) is used to analyze the effect of the width of the launch beam distribution on the equilibrium mode distribution (EMD) and steady state distribution (SSD) in each of the seven cores of the investigated PCSF. The width of the launch beam distribution has a considerable impact on the fiber length at which the EMD and SSD are attained, according to our numerical results. Thus, by decreasing the full width at half maximum (FWHM) of the launch beam distribution from 20 to 2°, the length at which EMD is established increases from L_c = 1020 to 1250 m, and the length at which SSD is attained increases from z_s = 2650 to 3250 m. A narrow launch beam distribution leads to higher bandwidth at small and intermediate fiber lengths. On the other hand, at shorter fiber lengths, a wider launch beam distribution induces a bandwidth change from 1/z proportional to 1/z^1/2 proportional curve, e.g., a slower bandwidth reduction. When building a multicore optical fiber transmission system for SDM, such characterization of multicore PCSFs under various launch conditions should be taken into account.

1. Introduction

The growing need for digital data bandwidth in access and backbone networks is driving the development of new technologies to boost network capacity, particularly in optical fiber networks. Optical fiber systems’ capacity has increased as a result of technological advancements such as low-loss single-mode fibers, fiber amplifiers, multiplexing, and high-efficiency spectral coding [1]. Optical data multiplexing is realized in wavelength [2], polarization, time, phase, and space [1]. Wavelength-division multiplexed (WDM) systems based on single-mode (SM) SC fibers are rapidly nearing their Shannon capacity limit [3]. SDM, which includes mode division multiplexing using multimode or few-mode fibers and/or core multiplexing using multicore (MC) fibers [4], has received a lot of attention in the last decade as a way to overcome the Shannon capacity limit of WDM networks using SM-SCFs [1,5,6,7,8]. SDMs can operate at the same or separate wavelengths [9]. Every SDM channel inside the carrier SC fiber is provided radially distributed, dedicated spatial positions as these channels transit the length of the carrier in the case of SDM at the same wavelength. The launch angle and mode coupling strength dictate where each channel is located within the single-core fiber. We earlier demonstrated a three-, four-, and five-channel SDMs in SC plastic optical fibers [10].

PCSFs are multimode optical fibers with several uses in optical telecommunications and sensors [11,12]. The simplicity with which the cladding can be removed makes them particularly handy for sensors that require access to evanescent wave. The differential mode attenuation and rate of mode coupling affect the transmission characteristics of multimode optical fibers [13,14,15,16,17,18]. Mode coupling in SC PCSFs has been shown to dramatically reduce the fiber length at which the SDM may be implemented with low crosstalk between neighboring optical channels [19]. In SC PCSF, an SDM with three ADM channels can be produced with low crosstalk between three ADM channels only at short fiber lengths of up to 55 m, and with two ADM channels at fiber lengths of up to 200 m [19]. It is obvious that such an ADM in SC PCSF is limited to short fiber lengths. One should also note here that more details regarding the manufacturing and fabrication of MC fibers can be found in Ref. [20].

In this paper, in order to increase the capacity and the transmission lengths for SDM in PCSF systems, we propose the SDM in a newly built MC PCSF with seven cores arrayed in a hexagonal array, each carrying a centrally launched beam. By numerically solving the TI PFE, the effect of the width of the launch beam distribution on the state of mode coupling, e.g., EMD and SSD, in each of the proposed multimode MC PCSF’s seven cores is explored. In the core-cladding interface, the refractive index profile of all homogenous cores has a step between two constant values. The effect of mode coupling changes the angular input optical power distribution that comes from a specific launch as the distance from the input fiber end increases. As a result, the far-field radiation patterns are changed [21]. For example, a ring can be imaged behind the output end of a short fiber if we arrange a centrally symmetric launch at a fixed angle θ = θ₀ to the fiber axis, the ring diameter is proportional to that initial launch angle θ₀. The boundaries of this ring blur when the fiber is “lengthened”, and the ring progressively morphs into a disk. This is owing to the effects of mode coupling accumulating with distance from the input end, causing the angular power distribution to gradually widen and shift towards θ = 0°, which was initially narrowly centered around θ = θ₀. The distribution even of the highest order guiding mode shifted its midpoint to zero degrees at the coupling length L_c, when EMD is attained. The angular light distribution becomes fixed and centered when the fiber is lengthened beyond the value known as z_s (the disk is brightest in its center). Except for the overall brightness, this is an SSD that is unaffected by launch conditions: when normalized to its highest value, SSD is the same regardless of launch angle(s).

In order to achieve a higher SDM capacity at longer fiber lengths, we propose a seven-core PCSF. Compared with previously proposed ADM in SC PCSF, we show that this multicore fiber demonstrates a higher SDM capacity. By numerically solving the TI PFE for varying widths of the launch beam distribution, we determine the length at which the EMD as well as an SSD is attained in each of the seven cores of the MC PCSF.

This paper is organized in the following manner: the second chapter describes the TI PFE; the third chapter presents results obtained by numerically solving the TI PFE, i.e., the influence of the FWHM of the launch beam distribution on the length at which EMD and SSD are achieved; the improvement of the SDM capacity of PCSF is also discussed.

2. Time-Independent Power Flow Equation

Gloge’s TI PFE for power distribution inside a multimode step-index fiber, assuming that mode coupling in multimode optical fibers occurs primarily between neighbor modes, is provided as [22]:

$$\frac{\partial P(\theta ,z)}{\partial z}=-\alpha (\theta )P(\theta ,z)+\frac{D}{\theta }\frac{\partial }{\partial \theta }\left(\theta \frac{\partial P(\theta ,z)}{\partial \theta }\right)$$

(1)

where P(θ,z) is the angular power distribution, z is distance from the input end of the fiber, θ is the propagation angle with respect to the core axis, D is the coupling coefficient assumed constant [20,21,22,23] and $\alpha (\theta )$ is the modal attenuation. Except near the cutoff, the attenuation is constant α(θ) = α₀ throughout the region of guided modes $0\le \theta \le {\theta }_c$ [23]. Therefore, α(θ) need not be accounted for when solving (1) for mode coupling and this equation reduces to [17]:

$$\frac{\partial P(\theta ,z)}{\partial z}=\frac{D}{\theta }\frac{\partial P(\theta ,z)}{\partial \theta }+D\frac{{\partial }^{2}P(\theta ,z)}{\partial {\theta }^2}$$

(2)

The explicit finite-difference approach [17] was used to produce a numerical solution of the TI PFE (2) for a Gaussian launch-beam distribution of the form:

$$P(\theta ,z=0)=\frac{1}{\sigma \sqrt{2\pi }}\exp \left[-\frac{{(\theta -{\theta }_0)}^2}{2{\sigma }^2}\right]$$

(3)

with $0\le \theta \le {\theta }_c$, where θ₀ is the mean value of the incidence angle distribution, with FWHM = $2\sigma \sqrt{2\ln 2}=2.355\sigma$ (σ is standard deviation).

3. Results and Discussion

The transmission characteristics of the proposed MC PCSF with seven cores, which is designed from the SC PCSF experimentally examined by Kagami et al. [24], are explored in this article. Figure 1 shows the MC PCSF with seven cores placed in a hexagonal array. Individual cores and cladding for the MC PCSF are proposed to be composed of the same material as the core and cladding for the SC PCSF. The core diameter of this fiber is d = 400 μm and NA = 0.37. The inner critical angle of this fiber is ${\theta }_c$ = 14.75° (measured in air θ_c = 21.7°), where it is assumed in the calculations that n₁ = 1.4535 is the refractive index of the silica core at λ = 790 nm [24]. In order to avoid core-to-core mode coupling, the MC PCSF with fiber diameter d = 400 μm is designed from this SC PCSF in such a manner that seven cores with radius a = 20 µm, arranged in a hexagonal geometry, have inter-core distance Λ = 150 µm (the cores are uncoupled for Λ ≥ 7a) [3]. The coupling coefficient for the SC PCSF investigated by Kagami et al. [24] is D = 6.4 × 10⁻⁶ rad²/m [19], which we adopted in this work. Using the following equation:

$$N=\frac{2{\pi }^2{a}^2{\mathrm{NA}}^2}{{\lambda }^2}$$

(4)

we obtain a number of modes N = 1732 in each of the seven cores of the proposed MC PCSF. A large number of modes can be seen as a modal continuum, which is necessary for the employment of Equation (2).

To make comparisons easier, we numerically solved the TI PFE and calculated the lengths at which the EMD and SSD are attained in each of the seven cores of the MC PCSF for various launch beam widths. The TI PFE (2) was solved using the explicit finite difference approach [17]. For z in the range of zero to z_s, the development of the normalized output power distribution with fiber length z was found (z_s is fiber length where SSD is achieved).

Figure 2 depicts a situation in which a beam with Gaussian distribution and (FWHM)_z=0 = 10° was launched at four different input angles of θ₀ = 0, 8, and 16° (measured outside the fiber).

When the launch distribution at the input end of the fiber is centered at θ₀ = 0°, the power distribution remains at the same angle as the distance from the input fiber end rises, but its width grows owing to mode coupling, as shown in Figure 2. Figure 2a shows radiation patterns of non-centrally launched beams in short fibers that are centered at values near to their initial values. Figure 2b demonstrates that coupling is stronger for low-order modes when fiber length is increased: their distributions migrated further towards θ = 0°. Higher-order mode coupling can only be noticed after longer fiber lengths. All the mode distributions move their midpoints to zero degrees (from the initial value of θ₀ at the input fiber end) only after the fiber’s coupling length L_c is reached, producing the EMD at L_c = 1140 m in Figure 2c. At z_s = 2940 m, an SSD is established (Figure 2d).

Table 1. Coupling length L_c for obtaining the EMD and length z_s for establishing an SSD in each of seven cores of MC PCSF for varying FWHM of the launch beam distribution. The case of SC PCSF previously investigated in Ref. [19] is included for comparison.

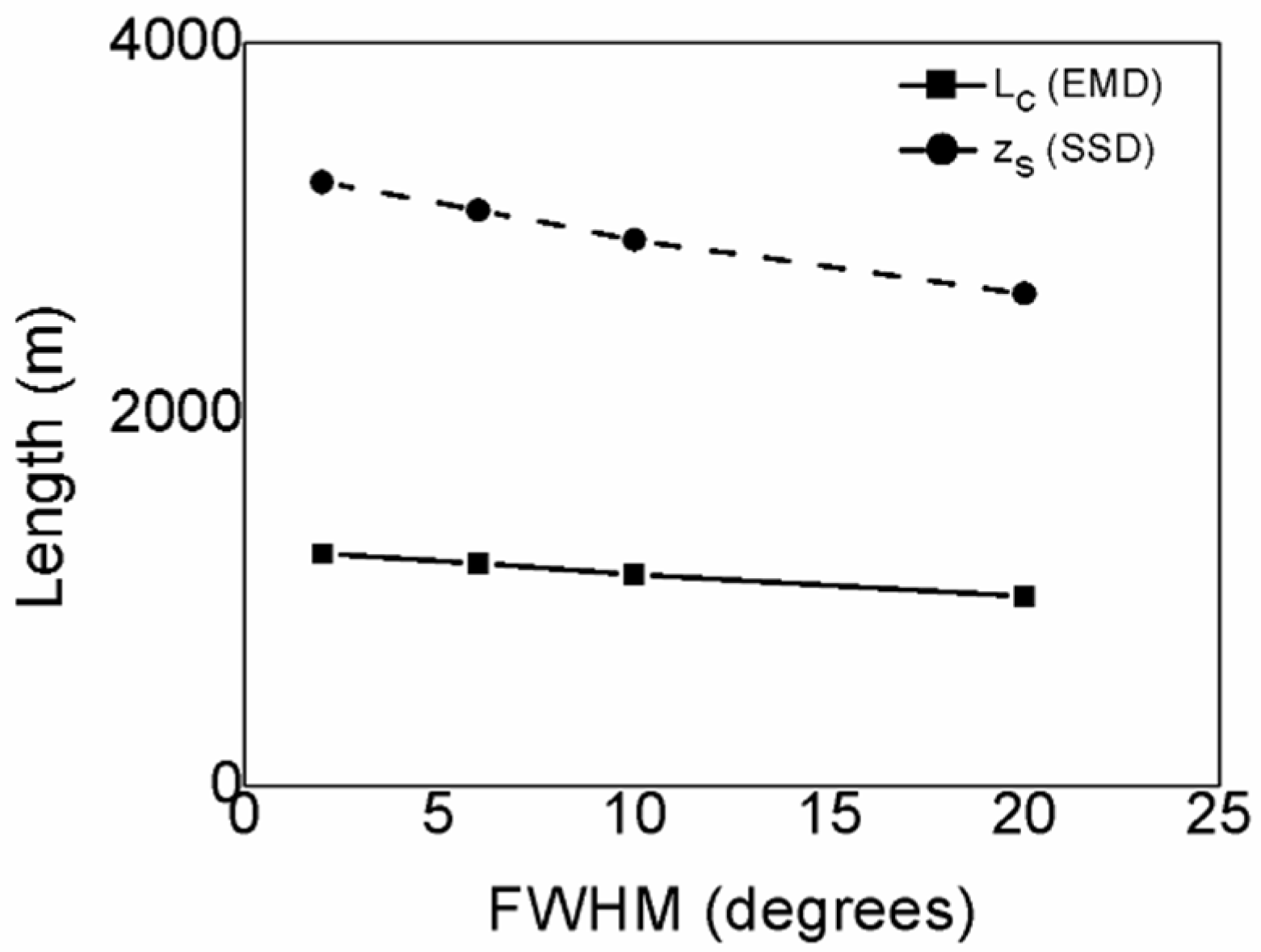
Optical Fiber Type	FWHM (°)	Lc (m)	zs (m)
MC PCSF (this work)	2	1250	3250
SC PCSF (Ref. [19])	6	1200	3100
MC PCSF (this work)	10	1140	2940
MC PCSF (this work)	20	1020	2650

shows that as the width of the launch beam distribution is increased, the length L_c, which is required for obtaining the EMD, and the length z_s, which is required for establishing the SSD, decreases.

Since the energy of a wide launch beam is divided more evenly to the guided modes in the fiber, the EMD and SSD are forced to be established at shorter distances than with a narrow launch beam (Figure 3).

This information is important for realization of SDM in the proposed PCSF with seven cores, each carrying a centrally launched beam. Namely, at shorter fiber lengths, a wider launch beam distribution induces a bandwidth change from 1/z proportional to 1/z^1/2 proportional curve (a slower bandwidth decrease). Compared with a wide launch beam distribution, a narrow launch beam distribution leads to higher bandwidth at small and intermediate fiber lengths [25]. Therefore, a narrower launch beam is a better choice for short and intermediate lengths of fiber optic communication links. One should note that in practice an optical lens can be used for realization of narrow launch beams. The bandwidth converges to a launch independent behavior at a specific fiber length where SSD is attained. Furthermore, it is worth noting that a trench-assisted core in multicore fiber can further minimize dispersion and crosstalk between cores [26]. Moreover, besides dispersion, the fiber nonlinearities must be considered in the case of large transmission bandwidth and rate [27,28].

Finally, because mode coupling in SC PCSFs limits the fiber length at which the SDM can be realized with minimal crosstalk between two and three neighbor angular optical channels [19], we proposed in this article an SDM in a new designed MC PCSF with seven cores arranged in a hexagonal array, each carrying a centrally launched beam (θ₀ = 0°). This enables a higher SDM capacity at longer fiber lengths in the proposed seven-core PCSF compared with ADM in SC PCSF. As a result, the proposed SDM in the MC PCSF with seven cores is not limited to short fiber lengths, as for the ADM channels due to mode coupling in the SC PCSF [19].

4. Conclusions

A novel MC PCSF design with seven cores arranged in a hexagonal array is proposed, with small inter-core crosstalk. By numerically solving the TI PFE, the effect of the width of the launch beam distribution on EMD and SSD in each carrier seven core is examined. Our numerical results demonstrate that as the width of the launch beam dispersion is increased, the length L_c, which is required for accomplishing the EMD, and the length z_s, which is required for establishing the SSD, decreases. Because the energy of a wide launch beam is divided more evenly among guided modes in the fiber, the EMD and SSD are forced to be established at shorter distances than with a narrow launch beam. Thus, by decreasing the FWHM of the launch beam distribution from 20 to 2°, the length at which EMD is established increases from L_c = 1020 to 1250 m, and the length at which SSD is attained increases from z_s = 2650 to 3250 m. Due to the fact that a narrow launch beam distribution leads to a higher bandwidth than a wide launch beam distribution at shorter fiber lengths, while a wider launch beam distribution forces bandwidth shift from 1/z proportional to 1/z^1/2 proportional curve (slower bandwidth decrease) to occur at shorter fiber lengths, the results reported in this work should be taken into account when designing an MC PCSF transmission system. Finally, unlike the angular optical channels in the SC PCSF, the proposed SDM in the MC PCSF with seven cores, each carrying a centrally launched beam, is not limited to short fiber lengths.