Abstract
Recently, optical coordinate transformation has garnered considerable research interest for manipulating structured light in emerging optical communication applications. Herein, we propose a circle-Cassinian optical coordinate transformation based on polarization invariance to generate an elliptical-symmetry radially polarized (ESRP) optical beam. Accordingly, we designed three isotropic phase plates for placement in the 4f optical system. The numerical simulations demonstrated accurate generation of the ESRP beam with specified intensity, including an overall intensity adjustment applied in the input plane. Therefore, the proposed method can aid in designing vector light fields, and the ESRP beam can be applied to optical tweezers and surface plasmonic-field generation.
1. Introduction
Structured light is referred to as the optical field modulated in amplitude, phase, and polarization, and it is emerging as a predominant aspect in various research fields such as optical tweezers, optical communication, quantum entanglement, nonlinear optics, microscopy, and imaging [1]. In the expanding zoology of structure light, the optical beam with elliptic-symmetry provides interesting insights [1,2,3], as it is slightly beyond the conventional cylindrical-symmetry beam. An appealing application of the optical beam with elliptic-symmetry, such as Mathieu–Gaussian beam and Ince–Gaussian, has been demonstrated in optical trapping [4].
More recently, systematic studies have been conducted on the complex vector beam with Ince–Gaussian and Mathieu–Gaussian modes [5,6]. However, the production of an elliptic-symmetry radially polarized (ESRP) beam, which is defined as a beam with its linear polarization perpendicular to the confocal ellipses at all locations, still remains a challenge. As reported in a prior study aiming to produce elliptic-symmetry vector beams [7], the ESRP beam is not associated with the no-diffraction eigenmodes of the wave equation; therefore, it cannot be simply produced using the Ince–Gaussian or Mathieu–Gaussian modes.
Although the ESRP beam proposed in this study can be deemed similar to the two kinds of elliptic-symmetry vector beams developed previously—one in [7] and another in [8,9,10], the internal structure of the proposed ESRP beam is apparently distinct from the existing beams. In particular, the vector beam in [7] has been developed based on a confocal elliptic coordinate system, but its linear polarization remains in the same direction when tracing along each confocal hyperbola, which indicates that the polarization was not perpendicular to the confocal ellipses at all locations. In contrast, the vector beam in [8,9,10] has been designed to ensure the perpendicular alignment of its polarization with respect to a set of ellipses at all locations, and thus, it exhibits a radial distribution. Nonetheless, these ellipses are concentric ellipses and not confocal ellipses. Although the vector beam in [8,9,10] can be used to optimize the surface plasmon generation for an elliptical plasmonic structure, such as an elliptic slit [10], it cannot be defined under the conventional elliptic coordinate system. Therefore, the ESRP beam should be more precisely designed based on the elliptical coordinate system to achieve a radial polarization distribution.
In this study, we propose a method to generate the introduced ESRP beam using the optical coordinate transformation [11,12]. Recently, the optical coordinate transformation has attracted renewed interest in the research of orbital angular momentum (OAM) optical beam separation and detection [13,14,15,16,17,18,19,20], especially the multiplication and division of OAM optical beams [21,22,23,24,25]. However, control of the polarization property has seldom been discussed in research related to optical coordinate transformation, but it is crucial if the input beam is a vector beam. The basic principle of polarization is straightforward: upon applying the phase plane based on the isotropic refractive index during the optical coordinate transformation, the coordinate transformation does not alter the polarization state on a point-to-point basis. Herein, we introduced a circle-Cassinian conformal transformation to employ this principle and subsequently demonstrated that the ESRP beam can be produced by considering the cylindrical-symmetric radially polarized beam as an input because the produced ESRP beam is capable of independently adjusting the amplitude as well as the linear polarization direction of the electrical field.
The remainder of the paper is structured as follows. In Section 2, the polarization structure of the ESRP beam is discussed in detail. Thereafter, in Section 3, the principle of applying the circle-Cassinian transformation for obtaining the ESRP beam is introduced, followed by Section 4, which presents the mathematical equations for the phase plate design with correlation to the optical system. All of the numerical simulation results are elaborated in Section 5, and lastly, the discussion on the obtained findings along with the conclusive remarks of this study are noted in Section 6.
2. Polarization Structure of ESRP Beam
To clarify the distinction between the ESRP and two other elliptic-symmetry vector beams reported earlier [7,8], we compare their polarization structures and mathematical descriptions herein. As depicted in Figure 1, the polarization structures are plotted along with their respective coordinates: the vector beams demonstrated in [7,8] are presented in Figure 1a,b, whereas the ESRP beam proposed in this research is portrayed in Figure 1c.
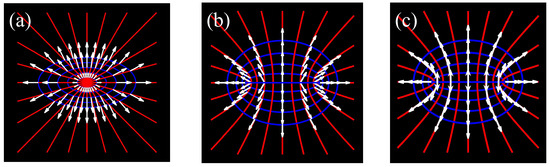
Figure 1.
Polarization structure of the three elliptic-symmetry vector beams. (a,b) are the elliptic-symmetry vector beams reported in [7,8], respectively. (c) is the ESRP beam reported in this paper.
For the vector beam in Figure 1a, its normalized electric field Jones vector (for simplified comparison, we eliminated the possible variation in the intensity distribution) can be expressed as [8]
where denotes the eccentricity to define all of the concentric ellipses. In principle, this vector beam can be considered a consequence of stretching along a single coordinate direction (here, the x direction) from the traditional cylinder-symmetric radially polarized beam (RPB) with the final polarization perpendicular to the concentric ellipses at all locations (as depicted in Figure 1a. As determined from Equation (1), the polarization angle remains the same in the case when a radial line passing through the origin is observed. Based on this perspective, this polarization pattern is similar to that of the first-order cylinder vector beam (CVB). However, there is a prominent difference: the deviation angle of the polarization off the radial line varies upon moving on to another radial line, whereas the deviation angle remains unchanged for the first-order CVB.
For the vector beam displayed in Figure 1b, its normalized electric field Jones vector can be expressed based on the elliptic coordinates as follows [7]:
where denotes the azimuthal elliptic coordinate (: radial elliptic coordinate). As can be derived from Equation (2), the polarization direction depends only on the value of , and thus, it remains the same in the case where a hyperbolic coordinate curve is traced. As depicted in Figure 1b, the polarization will be eventually perpendicular to the ellipse with , but it cannot be perpendicular to all other confocal ellipses.
In contrast to Figure 1b, the proposed ESRP beam shown in Figure 1c was constructed based on the elliptic coordinates but with distinguished internal polarization structures to ensure that the polarization is perpendicular to each confocal ellipse at all locations. The variations in the polarization distribution between the ESRP and vector beam in Figure 1a were apparent. Moreover, in terms of optical intensity singular points, both vector beams (Figure 1a,b) contained only a singular point at the center, whereas the proposed ESRP beam contained a short line connecting the two foci as the singular points.
In this study, we derived the mathematic expression for the ESRP beam (with normalized Jones vectors) as follows:
Interestingly, we observed that the curves on which the polarization remained were related to the Cassinian oval coordinates plotted in Figure 2a as well as the hyperbolic curves (red curve). For a more prominent illustration, the confocal ellipses sharing the same foci with the Cassinian ovals—to which the polarization is perpendicular at all locations—are plotted in Figure 2b instead of the Cassinian curves. (Proof for both Equation (3) and the relationship presented in Figure 2b are detailed in Appendix A).
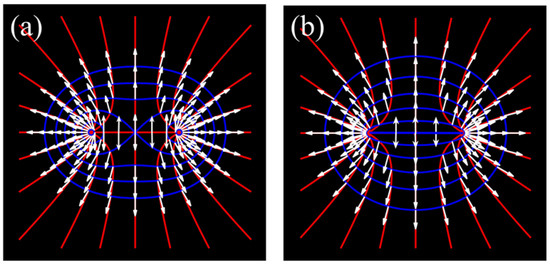
Figure 2.
Geometric representation of the polarization distribution of an ESRP beam with respect to various background curves. In (a), blue curves represent Cassinian ovals, whereas red curves represent the hyperbolic curves perpendicular to the Cassinian ovals. In (b), the blue curves were replaced with confocal ellipses sharing the same foci with the Cassinian ovals.
3. Principle of Using Circle-Cassinian Transformation to Obtain ESRP Beam
First, let us consider a general geometric coordinate transformation performed using a single lens, as displayed in Figure 3, where the input field at the front-focal-plane was set as and the output field at the back-focal-plane was . Based on the paraxial approximation supporting the Fourier transform between the two focal planes and the stationary phase principle (as the considered spatial scale is much larger than the wavelength), the point-to-point corresponding field map can be fulfilled with the application of two specific phase plates and (though an amplitude adjustment term is required owing to the conservation of light energy ) [12]. Herein, was determined by the requested coordinate transformation as
where k represents the wavenumber and f denotes the focal length of the lens, whereas is required for phase correction, as follows:
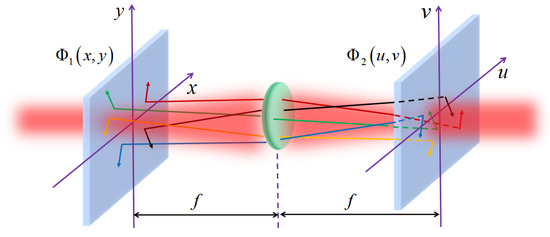
Figure 3.
Illustration of optical coordinate transformation based on a single lens (transformation leaves the polarization state unchanged with point-to-point basis).
Let us thoroughly examine the polarization property of the coordinate transformation, which has been previously overlooked. As illustrated in Figure 3, by considering the locally linearly polarized input beam, the two phase plates are generally polarization isotropic, the polarization state after the transformation is essentially unchanged according to the point-to-point basis. Therefore, the coordinate transformation can establish a simple method to reorganize the polarization distribution from the input field, thereby producing new kinds of vector beams.
Regardless, an issue should be addressed prior to detailing the desired coordinate transformation for obtaining the ESRP beam. The coordinate transformation can be designed based on conformal mapping transformation if the coordinates are combined as a complex unit (e.g., and ). Although the coordinate transformation performed using only a single lens Equation (4) fails to satisfy the conformal mapping condition, it is still consistent with anti-conformal mapping [23]. Favorably, this problem can be circumvented by connecting two such consequential transformations using two lenses, i.e., the 4f optical system [23].
Let us define the current research problem: production of the ESRP beam based on conformal mapping using the radially polarized light (that can be conveniently obtained) as the input field and the 4f optical system. The reformation of the problem in the mathematical description can be stated as follows. Let us use the retracing method, considering a point in the output plane as , and thereafter, its corresponding point in the input plane will be determined using the inverse conformal mapping, such as
As the polarization direction remains unchanged at points W and Z, its mathematical relation can be derived. At point Z, the polarization can be predetermined from the radially polarized input beam as
at point W, according to the proposed ESRP beam, the polarization direction should satisfy the requirement of being perpendicular to one of the confocal ellipses containing W. The point W can be defined using elliptic coordinates and expressed as
where c denotes half of the focal length of the ellipses. Evidently, the polarization direction at W should be
Therefore, from
where the axes of the Z-plane are parallel to that of the W-plane. From Equations (6) and (7), we can derive
Thus, we need to determine the conformal mapping that can satisfy Equation (11). Inspired by the elegant approach of using complex analysis to describe the electrical field distribution produced by two nearby, infinitely long, thin wires with identical charges [26], we derived that the so-called circle-Cassinian conformal mapping
is exactly a solution of Equation (11). For a rapid analysis, we can further rewrite the right-hand side of Equation (11) and apply Equation (12) as
Note that the relation expressed in Equation (11) can be simply proved by substituting Equation (8) into Equation (13). (For detailed proof, please refer to Appendix A, and for further geometric explanation, please refer to Appendix B).
The Cassinian ovals (as displayed in Figure 2a) constitute a family of curves that are defined based on the following condition: multiplication of the distances of a point from the two foci equals a constant (rather than the sum of the distances from two foci equals a constant for the ellipses). With reference to Equation (12) for transforming circles to Cassinian ovals, we set (i.e., ) and replaced Z with W to obtain correspondence . However, our concern is not regarding the Cassinian ovals transformed from the circles but rather the accompanying orthogonal curves transformed from the radial lines. As illustrated in Figure 4, two sets of hyperbolas cross the two foci.
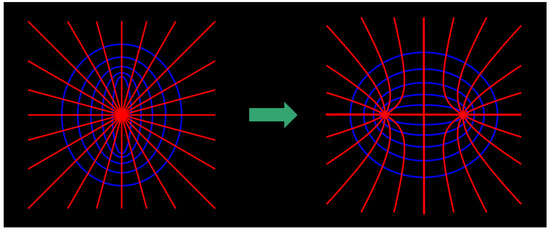
Figure 4.
Illustration of circle-Cassinian transformation that converts radial lines into hyperbolas that are orthogonal to the Cassinian ovals and converts vertical confocal ellipses into horizontal confocal ellipses.
Notably, the confocal mapping expressed in Equation (12) contains the rotational transformation of the vertical confocal ellipses by with respect to the horizontal confocal ellipses, as depicted in Figure 4 (the derivation is presented in Appendix A). This fact will majorly aid in designing the correction for light beam intensity.
4. Phase Plate Design and Related Optical System
As discussed earlier, to achieve a conformal mapping, two sequential anti-conformal coordinated transformation based on a single lens (Figure 3) are required to be sequentially connected. Therefore, the circle-Cassinian transformation in Equation (12) can be realized by categorizing the relationship of Equation (12) into the composition of two cascade anti-conformal mappings. The manner of classifying this composition is a choice. Herein, we selected the most straightforward one, i.e.,
as illustrated in Figure 5, the symbol Q represents the spatial points in the intermit plane, expressed as . Note that the square-root algorithm in Equation (14) is limited in the first and fourth quadrants of the Q-plane and that the function of can thus be applied to ensure complete coverage of the transformation across the entire Q-plane.
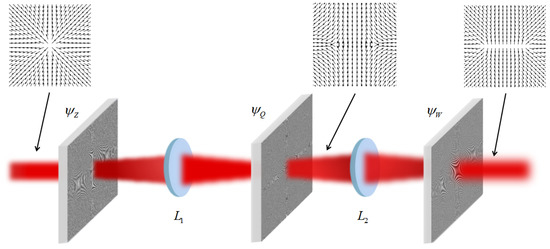
Figure 5.
Schematic of 4f optical system for generating ESRP beam. The three inlets show, respectively, the polarization distribution patterns right before the phase plate , and right after the phase plates and .
Upon determining the transformation in Equations (14) and (15), the two phase plates should be derived based on Equations (4) and (5) to satisfy the transformation in Equation (14) (with the phase distribution defined as and ) as well as that for fulfilling the transformation of Equation (15) (with the phase distribution defined as and ). As the correction phase plate and the transforming phase plate is located at the same plane (at Q-plane), we can combine them into a single phase plate. More importantly, the finalized three phase plates (, , and ) should be arranged into the 4f optical system, as illustrated in Figure 5, which included the illustrated polarization patterns of the three light beams: incident beam before , light beam in the intermit plane after , and output beam after .
According to Equations (4) and (5), the following expressions (their derivation are detailed in Appendix C) can be derived:
As illustrated in Figure 5, the input optical beam of radial polarization can be transformed into the output beam with the required polarization of an ESRP beam with the equipment of these three phase plates.
5. Numerical Simulation Results
First, the phase distribution patterns of the three phase plates , , and , and the two phase functions and are exhibited in Figure 6, which were evaluated from Equations (16)–(20) by setting the following parameters: wavelength was , focus radius of the confocal ellipses was , focal lengths of lenses and were both (referring to Figure 5), and the phase plate size was .
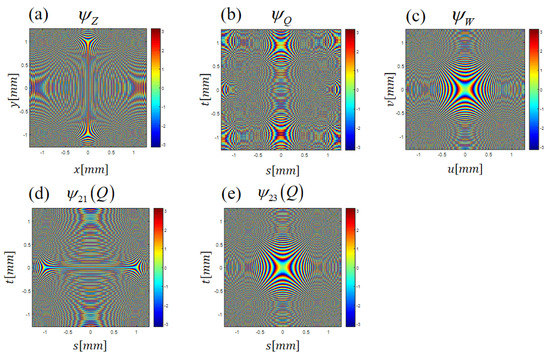
Figure 6.
Phase distributions of three phase plates (a), (b) and (c), and the two phase functions (d) and (e).
Thereafter, before working on the ESRP beam, we initially studied the property of the circle-Cassinian transformation of the 4f optical system illustrated in Figure 5 by simply setting the input beam as a linearly polarized beam (essentially the scalar case) with its amplitude pattern composed of several rings (with inner radii of 0.5, 0.9, 1.5, and 2 mm and a thickness of 0.2 mm), as illustrated in Figure 7. The major purpose of such a study is to verify the developed MATLAB program that was adapted from the program reported in [27]. This program could derive the light field distribution at any vertical plane by calculating the Fresnel diffraction integral based on the fast-Fourier transformation (FFT) algorithm. The intensity distributions at several representative planes are presented in Figure 7. As observed, after the first transformation according to Equation (14), the set of rings has transformed into a set of Cassinian ovals at the 2f plane, and the second transformation according to Equation (15) maintains the Cassinian oval patterns.
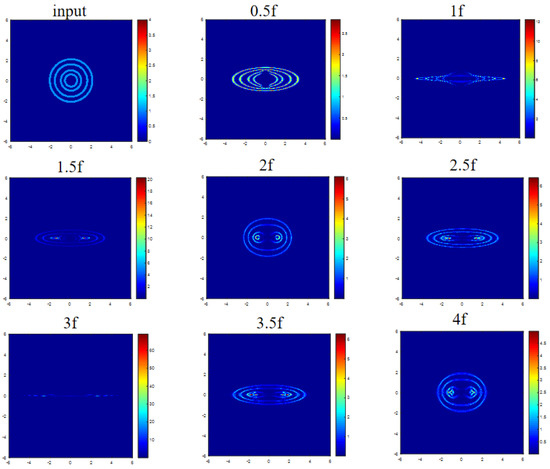
Figure 7.
Simulated intensity pattern at 0.5f, 1f, 1.5f, 2f, 2.5f, 3f, 3.5f, and 4f in the 4f optical system to display the progress of circle-Cassinian transformation.
Finally, we focused on the procedure for obtaining the ESRP beams. Overall, the optical system including all three phase plates did not require any modification as that for obtaining patterns displayed in Figure 7. Instead, the input optical beam was required to be reset. As discussed, a natural choice is to simply set the radially polarized light beam as the input beam that can be easily produced (e.g., with a vortex half-wave retarder). Thereafter, the simulation can be independently conducted on two orthogonal optical field components using the same program for calculation of Figure 7. However, to obtain the ESRP beam with the required polarization distribution along with an appropriately defined intensity, the distortion of the intensity distribution induced by the circle-Cassinian transformation should be analyzed and compensated.
Owing to the local energy conservation, the transformed amplitude underwent an adjustment based on the Hessian determinant of the transformation [12,23,28], and in the circle-Cassinian case, the adjustments of the two steps (refer to Appendix D for the derivation) can be respectively expressed as follows:
In principle, in addition to the phase plate , we can add an amplitude adjustment of at the plane Q-plane. However, we can equally achieve this compensation by applying the following amplitude adjustment onto the input beam:
Thus, we set the input beam pattern as
whereas
which follows the vertical ellipse distribution displayed in Figure 4. As described, the circle-Cassinian transformation transforms these vertical ellipses into the horizontal ellipses with the same focal radius. Herein, we set an inner dark region of size defined by to avoid the singularity problem that can arise according to Equation (21) (because the area in the neighborhood of the origin in the input plane Z will be transformed to that in the vicinity of the two foci in the Q-plane). Accordingly, the parameters for the calculation in Equation (25) were set as , and . There are many methods to generate this intensity pattern such as using an amplitude spatial light modulator, or the combination of a polarizer, a quarter-wave plate, and a LC-SLM [29] or double-phase hologram technique [30].
In the simulation results presented in Figure 8, the input beam pattern obtained according to the amplitude of Equation (24) along with its polarization along the radial direction at all locations are depicted in Figure 8d. The resulting beam pattern in the Q-plane along with the final output in the W-plane are portrayed in Figure 8e,f, respectively. To prominently illustrate the variations in the polarization distribution, the polarization angle distribution (in radian) was illustrated with the same color map, as depicted on the right-hand side in Figure 8a–c. Upon comparing Figure 8c with Figure 8a, the colored section boundaries indicate the alteration in the polarization direction from along the radial lines to along the hyperbola curves. Incidentally, a close examination of Figure 8b revealed that the polarization did not attain the final form at the Q-plane, although the intensity was achieved (Figure 8e,f).
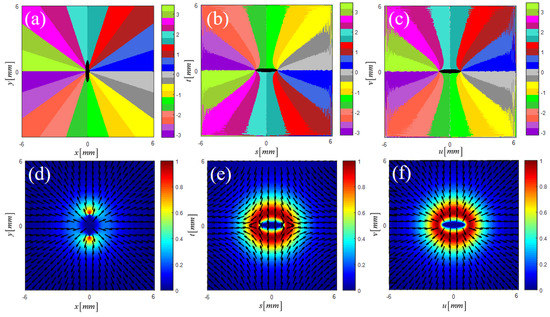
Figure 8.
Simulation results displaying the generation of ESRP beam. (a–c) Polarization-angle color map on the Z−, Q−, and W−planes, respectively; (d) depicts the input beam; (e) depicts the beam in the intermediate plane Q; (f) depicts the ESRP beam.
Notably, the polarization directions in Figure 8a–c display a narrow distribution in each color region. The number of plotted region was merely limited by that of the color map. Moreover, owing to the noise induced by the FFT calculation, especially for the high-frequency components, the polarization in certain places displayed a low degree of elliptical polarization (e.g., in the vicinity of the edge in Figure 8c). Thus, in this case, only the long axis component of the elliptical polarization was maintained as the local linear polarization field.
6. Discussion and Conclusions
The simulation results in Figure 7 proved that the 4f optical system illustrated in Figure 5 can accomplish the circle-Cassinian conformal mapping. This step of the simulation still pertains to the scalar type of the optical coordinate transformation without involving the polarization. To consider the circle-Cassinian transformation for the input vector field, we initially decomposed the vector field into two orthogonal components and, thereafter, independently applied the same transformation for them. This signified the initial recognition of the inherent polarization-maintaining principle for its subsequent application. Note that this principle can be strictly true only in the paraxial optics that has been generally assumed in the optical coordinate transformation.
To obtain the ESRP beam (Figure 8), we enforced a small dark-area mask in the input beam to avoid the divergence of the output beam, as implied in Equation (21). Consequently, each polarization-angle color map illustrated in Figure 8 displays a dark region at the beam center, i.e., the polarization state at that location is simply indeterminate. Notwithstanding, this should not impact the potential practical application of the ESRP beam, as the dark region occupies only a very small proportion. There are some other issues to be considered for the experimental study. The phase plates designed according to a specific laser wavelength can be manufactured with the PMMA (poly methyl methacrylate) material with the low combination loss about [14]. The accuracy of processing the phase plates and the accuracy of aligning them will unavoidably affect the quality of the ESRP beam. Additionally, the possible aberration of the lenses may need to be compensated.
In summary, we proposed a new kind of optical beam called the ESRP beam and numerically demonstrated the generation of this beam using the optical coordinate transformation method, where the RPB served as the input and the circle-Cassinian conformal mapping enacted the coordinate transformation. All of the phase plates for achieving this transformation have been mathematically detailed and the experiment realization should be straightforward. We believe that the approach exploiting the inherent polarization property of the optical coordinate transformation can provide a useful route for designing and producing various forms of structured light. Furthermore, the ESRP beam can be employed in certain applications for optical tweezing, surface plasmons, and light–matter interaction. For example, the ESRP beam can be used to selectively excite some surface plasmon resonant modes of a metal elliptical nanodisk and to actively rotate the elliptical nanodisk.
Author Contributions
Conceptualization, H.W. and H.F.; methodology, H.W.; software, H.W.; validation, H.W. and H.F.; formal analysis, H.W. and H.F.; investigation, H.F. and H.W.; resources, H.F.; original draft preparation, H.W.; writing—review and editing, H.F. and H.W.; visualization, H.W.; supervision, H.F.; funding acquisition, H.F. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (12074268), the Natural Science Foundation of Guangdong Province (2018B030311048), and the Natural Science Foundation of Shenzhen City (the Stable Support Plan Program: 20200814164819001).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Circle-Cassinian Transformation and Its Properties
First, the derivation of the normalized electric field Jones vector of the ESRP beam on the W-plane, i.e., Equation (3) in the main text, is detailed herein. Given that and and expressed in the elliptic coordinate , the equation for the confocal ellipses can be written as
With the definition of , as the local polarization of the ESRP beam should be perpendicular to the ellipse, the Jones vector of the ESRP beam should satisfy
where and . The evaluation of the derivatives result in
which reflects Equation (3) in the main text.
To determine the conformal mapping that can transform the radially polarized light beam into the ESRP beam, we need to apply the principle that the optical coordinate transformation is based on paraxial optics and it will not alter the polarization state at the point-to-point basis. Therefore, we can obtain
As we can write , the right-hand side of Equation (A4) can be further expressed as
where the relation of has been applied.
The left-hand side of Equation (A4) can be further expressed as
Thus, the following requirement can be achieved
By observing and comparing the two sides of Equation (A7), we can determine that the transformation is the solution, which is the so-called circle-Cassinian transformation that transforms the circles to the Cassinian curves. Note that the above derivation provides the proof for Equations (11)–(13) in the main text.
In the following segment, we provide proofs of the two transformation properties (of the circle-Cassinian transformation ) illustrated as Figure 4 in the main text, namely, (1) the set of vertical confocal ellipses with foci at will be converted to the set of horizontal confocal ellipses with foci at ; (2) the set of radial lines passing through the origin will be converted to the set of hyperbolas passing through the points .
To prove the first property, we first express a vertical ellipse with the foci at
Upon squaring both sides of Equation (A8) and substituting the relation of , we can derive the following:
Therefore,
For the proof of the second property, was substituted into to obtain
By eliminating , we can further obtain
Comprehensively, Equation (A13) describes the hyperbolas determined by the parameter (i.e., each hyperbola correlates to a radial line), and for any , the points reflect the solution at all instances.
Appendix B. Geometric Proof of Vector Property of Circle-Cassinian Transformation
In Appendix A, we elaborated the derivation and confirmed that the circle-Cassinian transformation represents the conformal mapping to convert the radially polarized light beam into the ESRP light beam. However, this analytical derivation still did not provide an intuitive explanation. Thus, herein, we provide further derivation based on pure geometrical interpretation, especially the geometry property related to the reflection of the light beam onto a parabola or an ellipse.
Based on the geometry from a radial line in the Z-plane that will be transformed to a curve in the W-plane using the circle-Cassinian transformation , as denoted by the red line in Figure A1a and the red curve in Figure A1b. In particular, the angle of line is denoted as , and can be described as
Correspondingly, the curve bears the form of
Evidently, passes through the point . In addition, the infinite is asymptotically approaching , and therefore, in Figure A1b, we added the green line :
which represents the tangential line of at infinity.
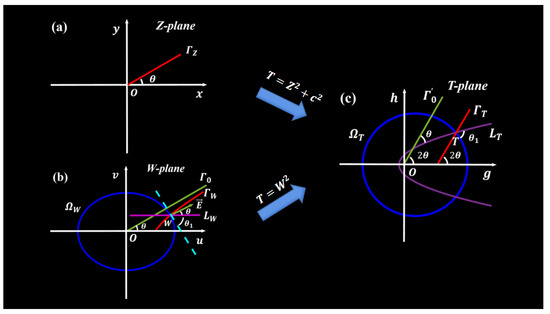
Figure A1.
Conformal mapping between any two of Z-plane (a), W-plane (b), and T-planes (c).
Continuing in Figure A1b, we selected an arbitrary point on and denoted it as W. Moreover, the ellipse has two foci at , and it was drawn in blue. In addition, we draw the horizontal line (with the violet color) passing the point W. Apparently, the intersection angle between and equals , as marked in the figure. More importantly, starting from the point W, we draw a vector as the green arrow to present the resulting ESRP polarization direction. The vector is parallel to the line owing to the optical principle discussed already (geometrical coordinate transformation does not alter the polarization direction). Therefore, along the curve , the polarization direction is consistent as is transformed from on which the polarization direction at every point is set as being in the direction of .
Currently, the problem requiring proof has become geometrically clear—denoting the intersection angle at point W between and ellipse as , we require to prove the following relationship:
i.e., vector is perpendicular to at W.
Interestingly, we detected that the proof for this hard-looking problem can be geometrically visualized with the aid of an assistant intermediate complex plane denoted by T, which is related to the Z- and W-planes, respectively, as
As depicted in Figure A1c, we detected several interesting observations on T-plane, stated as follows.
(1) : (including ) was transformed into the line . This is much more convenient for observations from the perspective of transforming from the line into : the transformation will initially rotate with respect to a line with the intersection angle and, thereafter, shift the line toward .
(2) : was transformed into another line owing to . Moreover, is parallel to , but it passes the origin point.
(3) : was transformed into a horizontal parabola that presumes the origin point as its focal point. This can be conveniently reviewed: denote the point W as and , and from , we can derive .
(4) : the ellipse was transformed into another ellipse , as observed from the following derivation.
Moreover, can be expressed as
and its transformation in T-plane is
which represents an ellipse with two foci at and . As depicted in Figure A1c, the two foci passed by the lines and , respectively.
As the transformation between T and W were conformal (Figure A1c), the intersection angle at line and parabola was still , and the intersection angle between the ellipse and parabola was still .
Thus, the problem for proving Equation (A17) on Figure A1b can be altered to proving Equation (A17) on Figure A1c. Let us redraw Figure A1c on Figure A2 by adding several assistant lines: at point T, tangle line of parabola , tangle line of ellipse , and the directional horizontal line M. As represented in the Figure A2, consider the line M as an incident light path, and then, it will be reflected at T by the parabola and pass straight through point O. Based on this geometric optics property of the parabola, we can immediately derive the angular equivalent relationship of
Similarly, the geometry optics property of the ellipse can be applied at point T or the directional lines of and ((i.e., light path will be reflected from the ellipse to the light path , because F and O belong to the two foci), thereby deriving another angular equivalent relationship such as
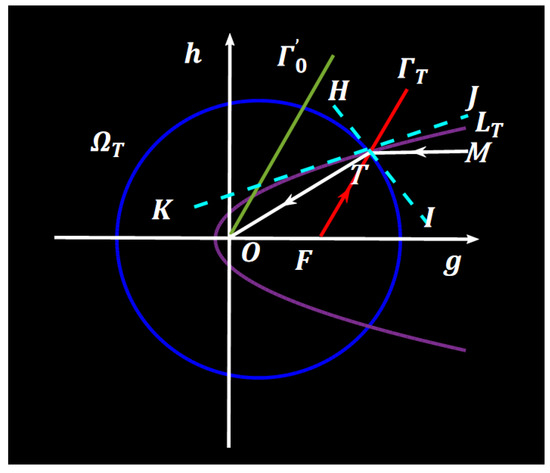
Figure A2.
Geometrical analysis on T-plane based on geometry of light beam reflection onto the parabola and ellipse.
Finally, let us focus on the relationship (as is parallel to the g-axis):
We already know that
However, based on the relationship stated in Equations (A21) and (A22), we can further derive the following:
Therefore, Equation (A23) can be rewritten as
thereby accomplishing the proof in Equation (A17).
Appendix C. Calculation of Phase Profiles for Circle-Cassinian Transformation
The phase profiles can be more conveniently calculated based on the recently reported complex analysis [23]. For phase on the Z-plane,
For the phase corrector on the Q-plane, it can be computed as
For the second coordinate transformation, the transforming phase on the Q-plane can be expressed as
Finally, for the phase corrector on the W-plane,
Appendix D. Calculation of Amplitude Correction Factor
The Wirtinger operator is defined as
Moreover, Equations (A31) and (A32) derive into
For the complex variable , consider Q as only a complex function of , and accordingly, the differential forms of x and y can be written as follows [23]:
where and , according to the Cauchy–Riemann equation [26].
Then, the additional amplitude factors and can be calculated in a complex form. From the Z- to Q-planes,
Similarly, from the Q- to W-planes, the additional amplitude factor was expressed as follows:
References
- Shen, Y.; Wang, X.; Xie, Z.; Min, C.; Fu, X.; Liu, Q.; Gong, M.; Yuan, X. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light Sci. Appl. 2019, 8, 90. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Forbes, A.; de Oliveira, M.; Dennis, M.R. Structured light. Nat. Photonics 2021, 15, 253–262. [Google Scholar] [CrossRef]
- Forbes, A. Structured light from lasers. Laser Photonics Rev. 2019, 13, 1900140. [Google Scholar] [CrossRef]
- Yang, Y.; Ren, Y.; Chen, M.; Arita, Y.; Rosales-Guzmán, C. Optical trapping with structured light: A review. Adv. Photonics 2021, 3, 034001. [Google Scholar] [CrossRef]
- Li, Y.; Hu, X.; Perez-Garcia, B.; Zhao, B.; Gao, W.; Zhu, Z.; Rosales-Guzmán, C. Classically entangled Ince–Gaussian modes. Appl. Phys. Lett. 2020, 116, 221105. [Google Scholar] [CrossRef]
- Rosales-Guzmán, C.; Hu, X.; Rodríguez-Fajardo, V.; Hernandez-Aranda, R.I.; Forbes, A.; Perez-Garcia, B. Experimental generation of helical Mathieu–Gauss vector modes. J. Opt. 2021, 23, 034004. [Google Scholar] [CrossRef]
- Pan, Y.; Li, Y.; Li, S.-M.; Ren, Z.-C.; Kong, L.-J.; Tu, C.; Wang, H.-T. Elliptic-symmetry vector optical fields. Opt. Express 2014, 22, 19302–19313. [Google Scholar] [CrossRef] [PubMed]
- Lerman, G.M.; Levy, U. Tight focusing of spatially variant vector optical fields with elliptical symmetry of linear polarization. Opt. Lett. 2007, 32, 2194–2196. [Google Scholar] [CrossRef]
- Lerman, G.M.; Lilach, Y.; Levy, U. Demonstration of spatially inhomogeneous vector beams with elliptical symmetry. Opt. Lett. 2009, 34, 1669–1671. [Google Scholar] [CrossRef]
- Lerman, G.M.; Yanai, A.; Ben-Yosef, N.; Levy, U. Demonstration of an elliptical plasmonic lens illuminated with radially–like polarized field. Opt. Express 2010, 18, 10871–10877. [Google Scholar] [CrossRef]
- Bryngdahl, O. Geometrical transformations in optics. J. Opt. Soc. Am. 1974, 64, 1092–1099. [Google Scholar] [CrossRef]
- Hossack, W.; Darling, A.; Dahdouh, A. Coordinate transformations with multiple computer-generated optical elements. J. Mod. Opt. 1987, 34, 1235–1250. [Google Scholar] [CrossRef]
- Berkhout, G.C.; Lavery, M.P.; Courtial, J.; Beijersbergen, M.W.; Padgett, M.J. Efficient sorting of orbital angular momentum states of light. Phys. Rev. Lett. 2010, 105, 153601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lavery, M.P.; Robertson, D.J.; Berkhout, G.C.; Love, G.D.; Padgett, M.J.; Courtial, J. Refractive elements for the measurement of the orbital angular momentum of a single photon. Opt. Express 2012, 20, 2110–2115. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mirhosseini, M.; Malik, M.; Shi, Z.; Boyd, R.W. Efficient separation of the orbital angular momentum eigenstates of light. Nat. Commun. 2013, 4, 2781. [Google Scholar] [CrossRef] [PubMed]
- Wan, C.; Chen, J.; Zhan, Q. Compact and high-resolution optical orbital angular momentum sorter. APL Photonics 2017, 2, 031302. [Google Scholar] [CrossRef] [Green Version]
- Ruffato, G.; Girardi, M.; Massari, M.; Mafakheri, E.; Sephton, B.; Capaldo, P.; Forbes, A.; Romanato, F. A compact diffractive sorter for high-resolution demultiplexing of orbital angular momentum beams. Sci. Rep. 2018, 8, 10248. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Liu, Z.; Gao, S.; Huang, X.; Feng, Y.; Liu, W.; Li, Z. Two-dimension and high-resolution demultiplexing of coaxial multiple orbital angular momentum beams. Opt. Express 2019, 27, 4338–4345. [Google Scholar] [CrossRef]
- Malik, M.; Mirhosseini, M.; Lavery, M.P.; Leach, J.; Padgett, M.J.; Boyd, R.W. Direct measurement of a 27-dimensional orbital-angular-momentum state vector. Nat. Commun. 2014, 5, 3115. [Google Scholar] [CrossRef] [Green Version]
- Cheng, J.; Wan, C.; Zhan, Q. High-resolution optical orbital angular momentum sorter based on Archimedean spiral mapping. Opt. Express 2022, 30, 16330–16339. [Google Scholar] [CrossRef]
- Zhou, H.; Dong, J.; Wang, J.; Li, S.; Cai, X.; Yu, S.; Zhang, X. Orbital angular momentum divider of light. IEEE Photonics J. 2016, 9, 6500208. [Google Scholar] [CrossRef]
- Zhao, Z.; Ren, Y.; Xie, G.; Li, L.; Yan, Y.; Ahmed, N.; Wang, Z.; Liu, C.; Willner, A.J.; Ashrafi, S.; et al. Invited Article: Division and multiplication of the state order for data-carrying orbital angular momentum beams. APL Photonics 2016, 1, 090802. [Google Scholar] [CrossRef]
- Takashima, S.; Kobayashi, H.; Iwashita, K. Integer multiplier for the orbital angular momentum of light using a circular-sector transformation. Phys. Rev. A 2019, 100, 063822. [Google Scholar] [CrossRef] [Green Version]
- Ruffato, G.; Massari, M.; Romanato, F. Multiplication and division of the orbital angular momentum of light with diffractive transformation optics. Light Sci. Appl. 2019, 8, 113. [Google Scholar] [CrossRef] [Green Version]
- Wen, Y.; Chremmos, I.; Chen, Y.; Zhang, Y.; Yu, S. Arbitrary multiplication and Division of the Orbital Angular Momentum of Light. Phys. Rev. Lett. 2020, 124, 213901. [Google Scholar] [CrossRef]
- Needham, T. Visual Complex Analysis; Oxford University Press: New York, NY, USA, 1998; pp. 532–538. [Google Scholar]
- Qian, X. Digital Lab of Information Optics; Science Press: Beijing, China, 2015; pp. 35–39. [Google Scholar]
- Ruffato, G.; Kobayashi, H. Roulette caustics in transformation optics of structured light beams. Opt. Commun. 2021, 490, 126893. [Google Scholar] [CrossRef]
- Han, W.; Yang, Y.; Cheng, W.; Zhan, Q. Vectorial optical field generator for the creation of arbitrarily complex fields. Opt. Express 2013, 21, 20692–20706. [Google Scholar] [CrossRef]
- Mendoza-Yero, O.; Mínguez-Vega, G.; Lancis, J. Encoding complex fields by using a phase-only optical element. Opt. Lett. 2014, 39, 1740–1743. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).