All-Fiber Photoacoustic Gas Sensing with Interferometric Location
Abstract
:1. Introduction
2. Methodology
2.1. PAS Gas Sensing
2.2. FMCW Laser Ranging
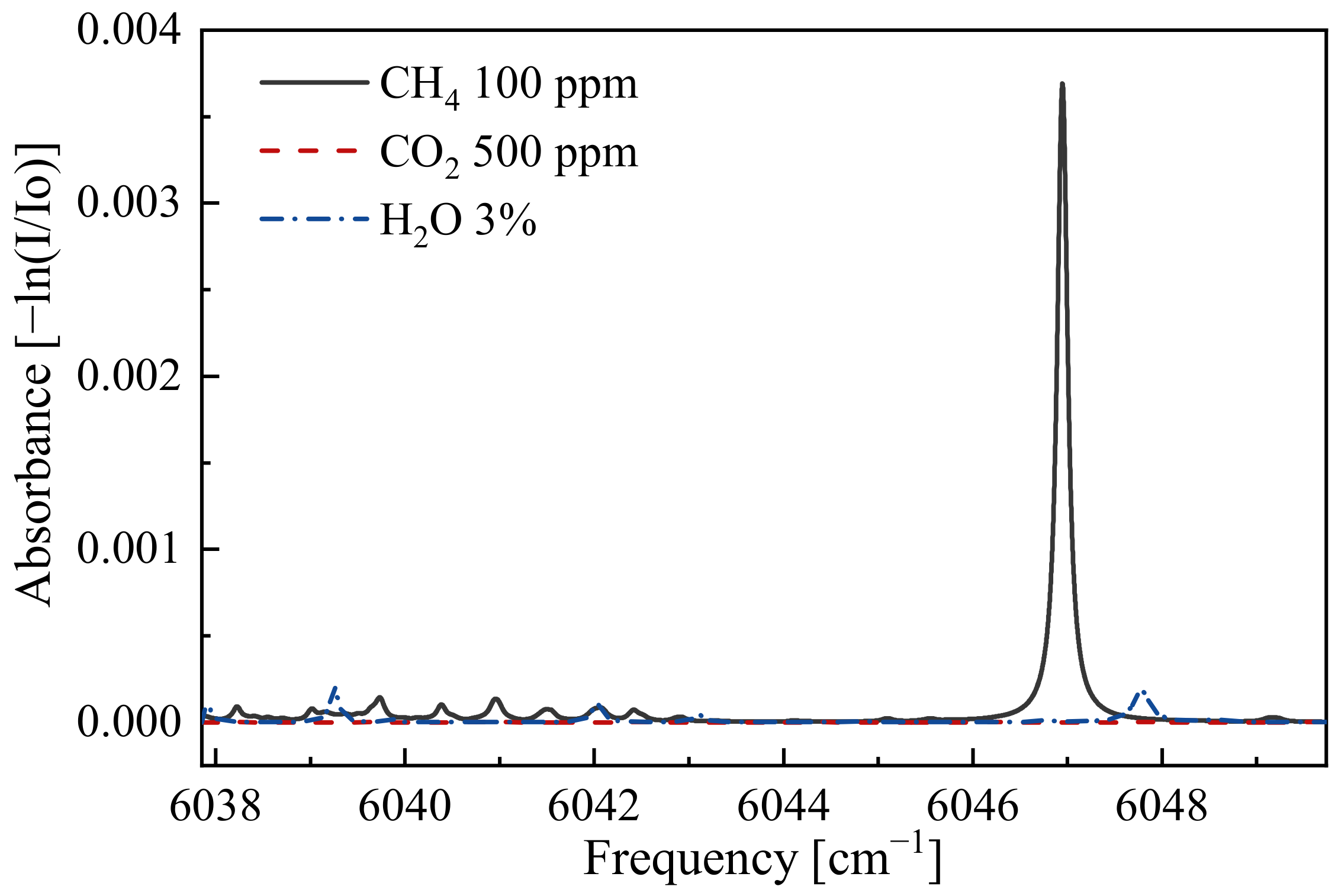
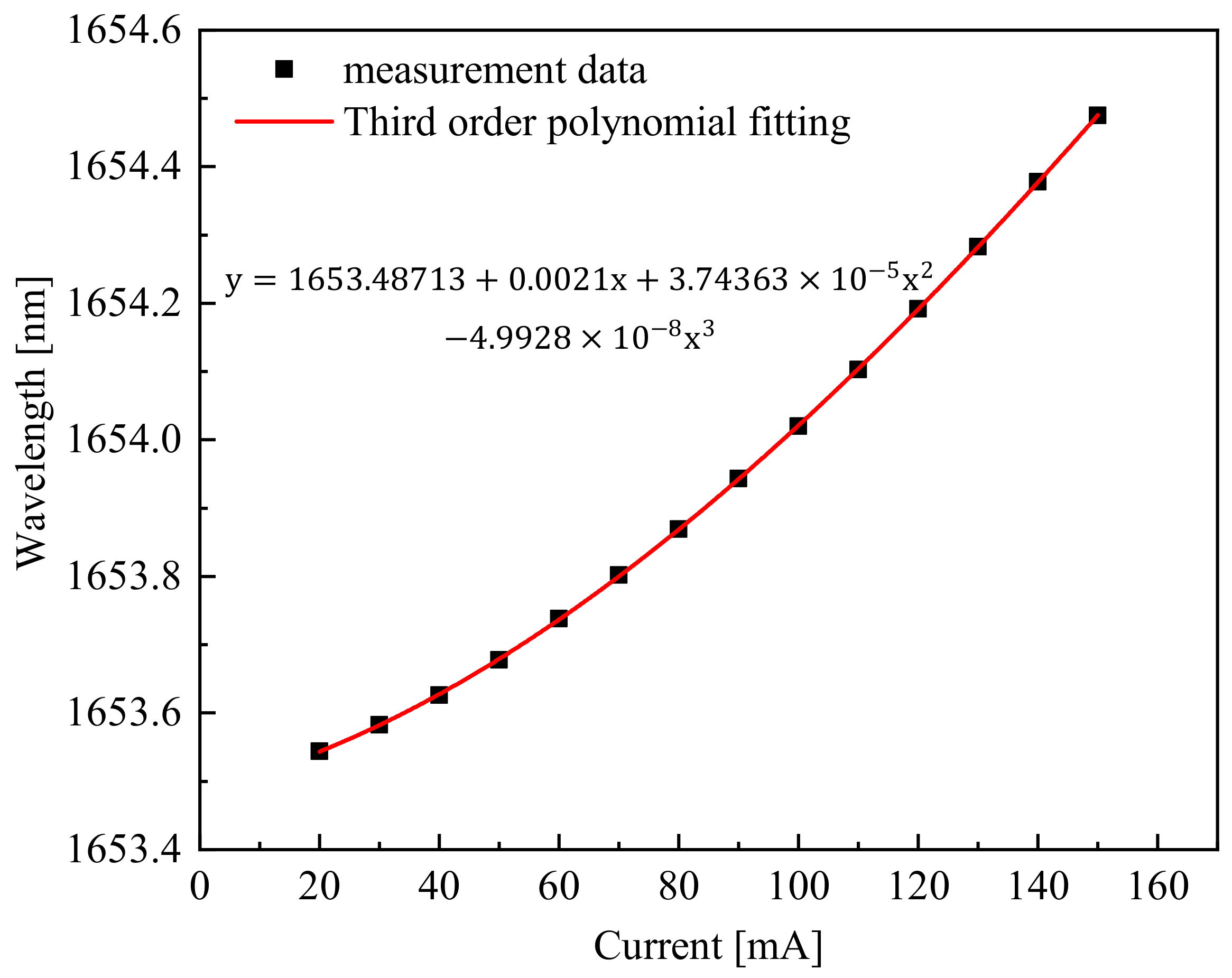
2.3. Absorption Line Selection and Laser Characterization
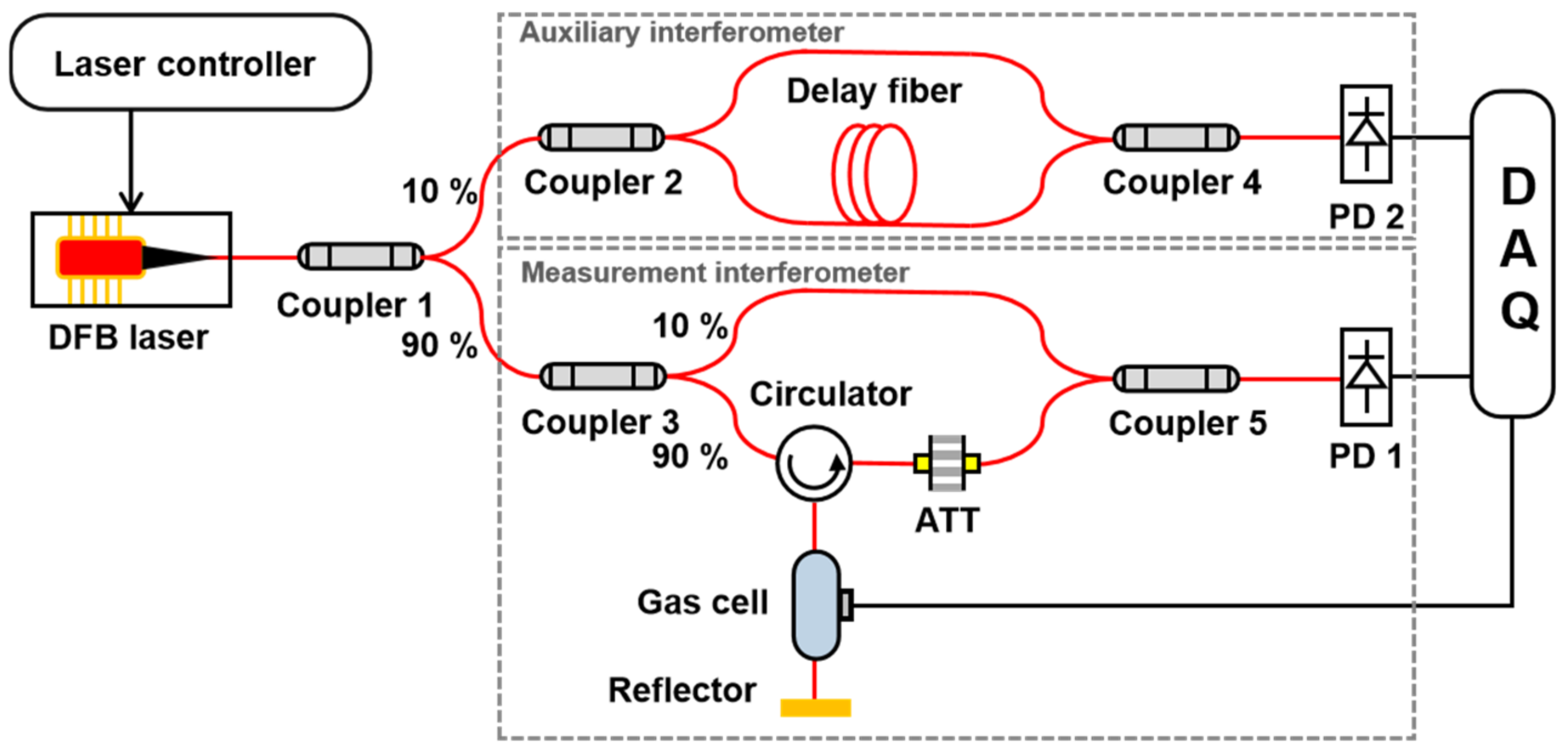
3. Experimental Setup
4. Experimental Results
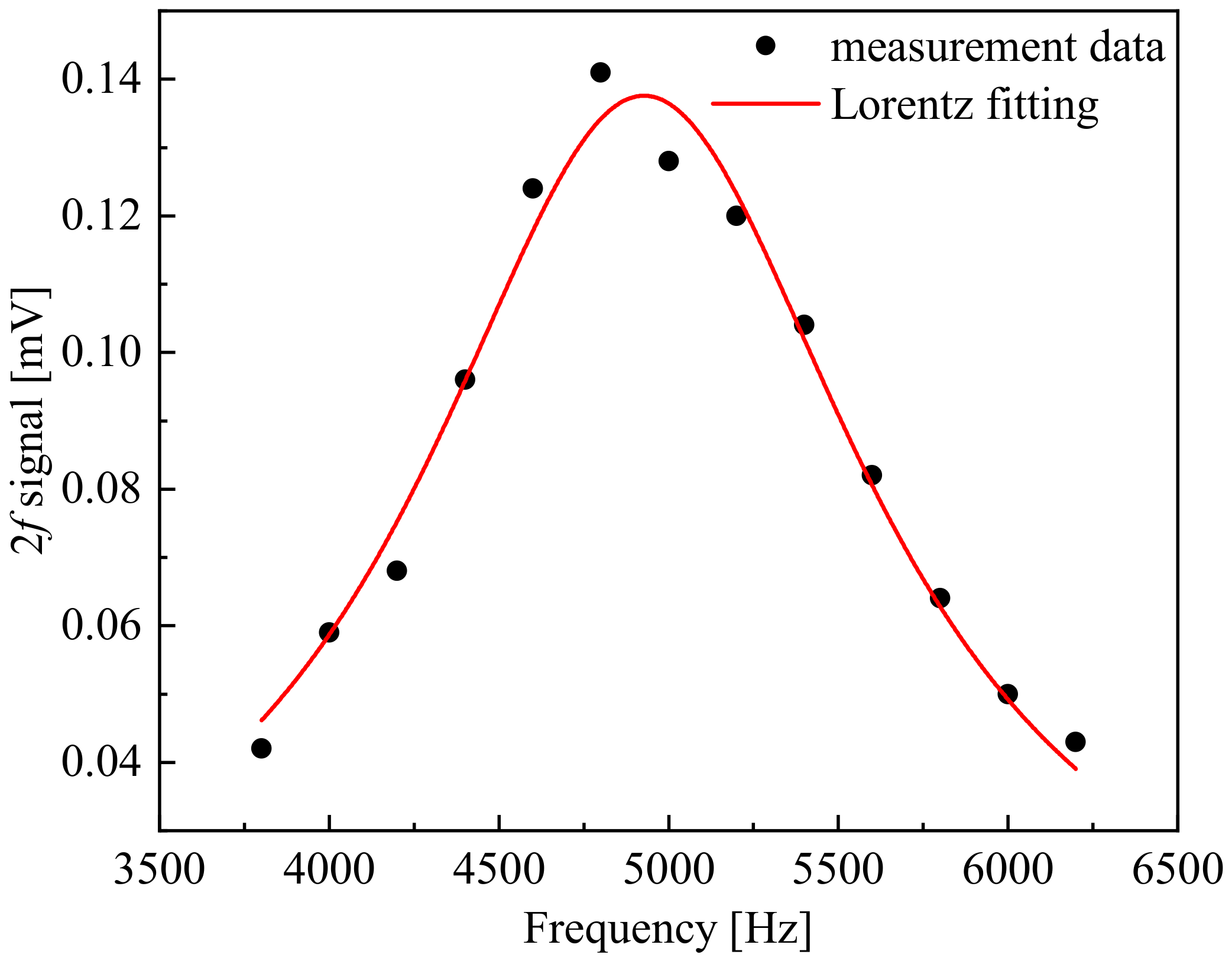
4.1. Optimization of Experimental Parameters
4.2. Gas Concentration Sensing
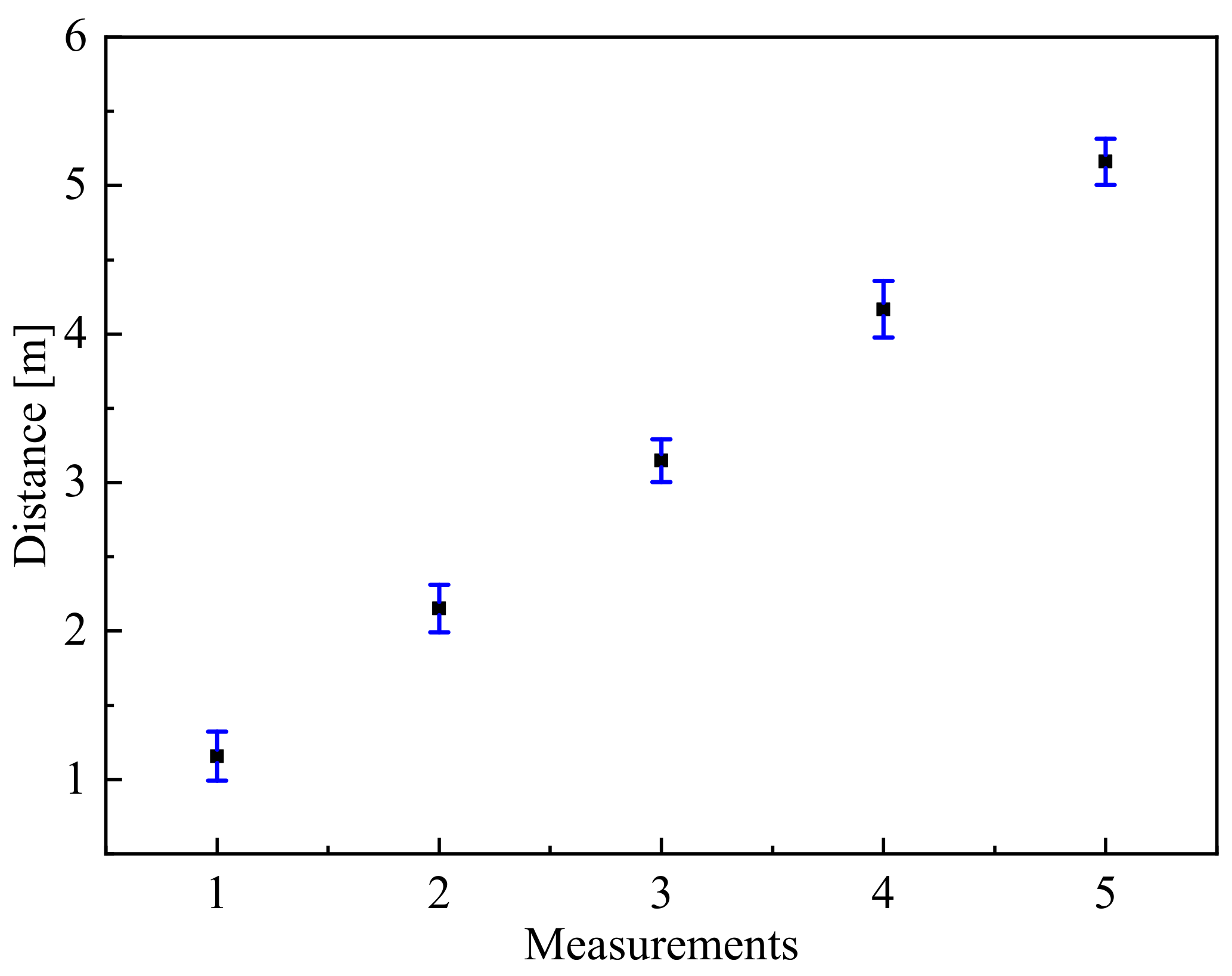
4.3. Laser Ranging
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Borri, S.; Patimisco, P.; Galli, I.; Mazzotti, D.; Giusfredi, G.; Akikusa, N.; Yamanishi, M.; Scamarcio, G.; De Natale, P.; Spagnolo, V. Intracavity quartz-enhanced photoacoustic sensor. Appl. Phys. Lett. 2014, 104, 091114. [Google Scholar] [CrossRef]
- Ma, Y.; He, Y.; Zhang, L.; Yu, X.; Zhang, J.; Sun, R.; Tittel, F.K. Ultra-high sensitive acetylene detection using quartz-enhanced photoacoustic spectroscopy with a fiber amplified diode laser and a 30.72 kHz quartz tuning fork. Appl. Phys. Lett. 2017, 110, 031107. [Google Scholar] [CrossRef] [Green Version]
- Lv, H.; Zheng, H.; Liu, Y.; Yang, Z.; Wu, Q.; Lin, H.; Montano, B.A.Z.; Zhu, W.; Yu, J.; Kan, R.; et al. Radial-cavity quartz-enhanced photoacoustic spectroscopy. Opt. Lett. 2021, 46, 3917–3920. [Google Scholar] [CrossRef]
- Yin, X.; Dong, L.; Wu, H.; Gao, M.; Zhang, L.; Zhang, X.; Liu, L.; Shao, X.; Tittel, F.K. Compact QEPAS humidity sensor in SF6 buffer gas for high-voltage gas power systems. Photoacoustics 2022, 25, 100319. [Google Scholar] [CrossRef]
- Chen, K.; Zhang, B.; Liu, S.; Yu, Q. Parts-per-billion-level detection of hydrogen sulfide based on near-infrared all-optical photoacoustic spectroscopy. Sens. Actuators B Chem. 2019, 283, 1–5. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Q.; Zhang, H.; Borri, S.; Galli, I.; Sampaolo, A.; Patimisco, P.; Spagnolo, V.L.; De Natale, P.; Ren, W. Doubly resonant photoacoustic spectroscopy: Ultra-high sensitivity meets ultra-wide dynamic range. Photoacoustics 2022, 27, 100387. [Google Scholar] [CrossRef]
- Gong, Z.; Wu, G.; Jiang, X.; Li, H.; Gao, T.; Guo, M.; Ma, F.; Chen, K.; Mei, L.; Peng, W.; et al. All-optical high-sensitivity resonant photoacoustic sensor for remote CH4 gas detection. Opt. Express 2021, 29, 13600–13609. [Google Scholar] [CrossRef]
- He, Y.; Ma, Y.; Tong, Y.; Yu, X.; Peng, Z.; Gao, J.; Tittel, F.K. Long distance, distributed gas sensing based on micro-nano fiber evanescent wave quartz-enhanced photoacoustic spectroscopy. Appl. Phys. Lett. 2017, 111, 241102. [Google Scholar] [CrossRef]
- Wei, T.; Zifarelli, A.; Dello Russo, S.; Wu, H.; Menduni, G.; Patimisco, P.; Sampaolo, A.; Spagnolo, V.; Dong, L. High and flat spectral responsivity of quartz tuning fork used as infrared photodetector in tunable diode laser spectroscopy. Appl. Phys. Rev. 2021, 8, 041409. [Google Scholar] [CrossRef]
- Wu, H.; Dong, L.; Zheng, H.; Yu, Y.; Ma, W.; Zhang, L.; Yin, W.; Xiao, L.; Jia, S.; Tittel, F.K. Beat frequency quartz-enhanced photoacoustic spectroscopy for fast and calibration-free continuous trace-gas monitoring. Nat. Commun. 2017, 8, 15331. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Q.; Wang, Z.; Ren, W. Wavelength-stabilization-based photoacoustic spectroscopy for methane detection. Meas. Sci. Technol. 2017, 28, 065102. [Google Scholar] [CrossRef]
- Zhang, H.; Jin, W.; Hu, M.; Hu, M.; Liang, J.; Wang, Q. Investigation and Optimization of a Line-Locked Quartz Enhanced Spectrophone for Rapid Carbon Dioxide Measurement. Sensors 2021, 21, 5225. [Google Scholar] [CrossRef]
- Yin, X.; Gao, M.; Miao, R.; Zhang, L.; Zhang, X.; Liu, L.; Shao, X.; Tittel, F.K. Near-infrared laser photoacoustic gas sensor for simultaneous detection of CO and H2S. Opt. Express 2021, 29, 34258–34268. [Google Scholar] [CrossRef]
- Aoyama, K.-I.; Nakagawa, K.; Itoh, T. Optical time domain reflectometry in a single-mode fiber. IEEE J. Quantum Electron. 1981, 17, 862–868. [Google Scholar] [CrossRef]
- Eickhoff, W.; Ulrich, R. Optical frequency domain reflectometry in single-mode fiber. Appl. Phys. Lett. 1981, 39, 693–695. [Google Scholar] [CrossRef]
- Sumida, S.; Okazaki, S.; Asakura, S.; Nakagawa, H.; Murayama, H.; Hasegawa, T. Distributed hydrogen determination with fiber-optic sensor. Sens. Actuators B Chem. 2005, 108, 508–514. [Google Scholar] [CrossRef]
- Floridia, C.; Salgado, F.; Rosolem, J.; Bassan, F.; Fracarolli, J.; Penze, R.; Pereira, L. Methane leak detection and spectral analysis by using only optical time domain reflectrometry in semidistributed remote optical sensors. In Proceedings of the 2016 IEEE SENSORS, Orlando, FL, USA, 30 October–3 November 2016; pp. 1–3. [Google Scholar] [CrossRef]
- Jin, W.; Ho, H.; Cao, Y.; Ju, J.; Qi, L. Gas detection with micro-and nano-engineered optical fibers. Opt. Fiber Technol. 2013, 19, 741–759. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.; Liu, F.; He, X.; Jin, W.; Zhang, M.; Yang, F.; Ho, H.L.; Tan, Y.; Gu, L. Distributed gas sensing with optical fibre photothermal interferometry. Opt. Express 2017, 25, 31568–31585. [Google Scholar] [CrossRef]
- Stove, A.G. Linear FMCW radar techniques. In IEE Proceedings F (Radar and Signal Processing); IET Digital Library: London, UK, 1992; Volume 139, pp. 343–350. [Google Scholar] [CrossRef]
- Zavrsnik, M.; Stewart, G. Coherence addressing of quasi-distributed absorption sensors by the FMCW method. J. Light. Technol. 2000, 18, 57–65. [Google Scholar] [CrossRef]
- Ye, F.; Qian, L.; Qi, B. Multipoint chemical gas sensing using frequency-shifted interferometry. J. Light. Technol. 2009, 27, 5356–5364. [Google Scholar] [CrossRef]
- Lou, X.; Chen, C.; Feng, Y.; Dong, Y. Simultaneous measurement of gas absorption spectra and optical path lengths in a multipass cell by FMCW interferometry. Opt. Lett. 2018, 43, 2872–2875. [Google Scholar] [CrossRef]
- Lou, X.; Feng, Y.; Chen, C.; Dong, Y. Multi-point spectroscopic gas sensing based on coherent FMCW interferometry. Opt. Express 2020, 28, 9014–9026. [Google Scholar] [CrossRef]
- Miklós, A. Acoustic aspects of photoacoustic signal generation and detection in gases. Int. J. Thermophys. 2015, 36, 2285–2317. [Google Scholar] [CrossRef]
- Dumitras, D.; Dutu, D.; Matei, C.; Magureanu, A.; Petrus, M.; Popa, C. Laser photoacoustic spectroscopy: Principles, instrumentation, and characterization. J. Optoelectron. Adv. Mater. 2007, 9, 3655. Available online: https://www.webofscience.com/wos/WOSCC/full-record/000251768700001 (accessed on 31 March 2022).
- Glombitza, U.; Brinkmeyer, E. Coherent frequency-domain reflectometry for characterization of single-mode integrated-optical waveguides. J. Light. Technol. 1993, 11, 1377–1384. [Google Scholar] [CrossRef]
- Moore, E.D.; McLeod, R.R. Correction of sampling errors due to laser tuning rate fluctuations in swept-wavelength interferometry. Opt. Express 2008, 16, 13139–13149. [Google Scholar] [CrossRef]
- Shi, G.; Zhang, F.; Qu, X.-H.; Meng, X. High-resolution frequency-modulated continuous-wave laser ranging for precision distance metrology applications. Opt. Eng. 2014, 53, 122402. [Google Scholar] [CrossRef]
- Ahn, T.-J.; Kim, D.Y. Analysis of nonlinear frequency sweep in high-speed tunable laser sources using a self-homodyne measurement and Hilbert transformation. Appl. Opt. 2007, 46, 2394–2400. [Google Scholar] [CrossRef]
- Shi, G.; Wang, W.; Zhang, F. Precision improvement of frequency-modulated continuous-wave laser ranging system with two auxiliary interferometers. Opt. Commun. 2018, 411, 152–157. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, Z.; Chang, J.; Ren, W. Fiber-ring laser-based intracavity photoacoustic spectroscopy for trace gas sensing. Opt. Lett. 2017, 42, 2114–2117. [Google Scholar] [CrossRef]
- Xuan, H.; Jin, W.; Liu, S. Long-period gratings in wavelength-scale microfibers. Opt. Lett. 2010, 35, 85–87. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stone, J.A.; Stejskal, A.; Howard, L. Absolute interferometry with a 670-nm external cavity diode laser. Appl. Opt. 1999, 38, 5981–5994. [Google Scholar] [CrossRef]
- Baumann, E.; Deschênes, J.-D.; Giorgetta, F.R.; Swann, W.C.; Coddington, I.; Newbury, N.R. Speckle phase noise in coherent laser ranging: Fundamental precision limitations. Opt. Lett. 2014, 39, 4776–4779. [Google Scholar] [CrossRef] [PubMed]
- Scherr, S.; Ayhan, S.; Fischbach, B.; Bhutani, A.; Pauli, M.; Zwick, T. Measurement. An efficient frequency and phase estimation algorithm with CRB performance for FMCW radar applications. IEEE Trans. Instrum. Meas. 2014, 64, 1868–1875. [Google Scholar] [CrossRef]
- Wu, H.; Dong, L.; Zheng, H.; Liu, X.; Yin, X.; Ma, W.; Zhang, L.; Yin, W.; Jia, S.; Tittel, F.K. Enhanced near-infrared QEPAS sensor for sub-ppm level H2S detection by means of a fiber amplified 1582 nm DFB laser. Sens. Actuators B Chem. 2015, 221, 666–672. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Wang, Q.; Zhang, W.; Wei, H.; Li, Y.; Ren, W.J.O.L. Ultrasensitive photoacoustic detection in a high-finesse cavity with Pound–Drever–Hall locking. Opt. Lett. 2019, 44, 1924–1927. [Google Scholar] [CrossRef] [PubMed]
- Mao, X.; Zheng, P.; Wang, X.; Yuan, S. Breath methane detection based on all-optical photoacoustic spectrometer. Sens. Actuators B Chem. 2017, 239, 1257–1260. [Google Scholar] [CrossRef]
- Cao, Y.; Jin, W.; Ho, H.L.; Ma, J. Miniature fiber-tip photoacoustic spectrometer for trace gas detection. Opt. Lett. 2013, 38, 434–436. [Google Scholar] [CrossRef] [Green Version]
- Hu, Y.; Qiao, S.; He, Y.; Lang, Z.; Ma, Y. Quartz-enhanced photoacoustic-photothermal spectroscopy for trace gas sensing. Opt. Express 2021, 29, 5121–5127. [Google Scholar] [CrossRef]
- Wolf, E. Introduction to the Theory of Coherence and Polarization of Light; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Schibli, T.; Hartl, I.; Yost, D.; Martin, M.; Marcinkevičius, A.; Fermann, M.; Ye, J. Optical frequency comb with submillihertz linewidth and more than 10 W average power. Nat. Photonics 2008, 2, 355–359. [Google Scholar] [CrossRef]
- Li, F.; Lan, T.; Huang, L.; Ikechukwu, I.P.; Liu, W.; Zhu, T. Spectrum evolution of Rayleigh backscattering in one-dimensional waveguide. Opto-Electron. Adv. 2019, 2, 19001201–19001207. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Hu, M.; Zhang, H.; Wang, J.; Tang, T.; Hu, M.; Wang, Q. All-Fiber Photoacoustic Gas Sensing with Interferometric Location. Photonics 2022, 9, 546. https://doi.org/10.3390/photonics9080546
Li M, Hu M, Zhang H, Wang J, Tang T, Hu M, Wang Q. All-Fiber Photoacoustic Gas Sensing with Interferometric Location. Photonics. 2022; 9(8):546. https://doi.org/10.3390/photonics9080546
Chicago/Turabian StyleLi, Meng, Mengpeng Hu, Hui Zhang, Jianing Wang, Tongyu Tang, Mai Hu, and Qiang Wang. 2022. "All-Fiber Photoacoustic Gas Sensing with Interferometric Location" Photonics 9, no. 8: 546. https://doi.org/10.3390/photonics9080546
APA StyleLi, M., Hu, M., Zhang, H., Wang, J., Tang, T., Hu, M., & Wang, Q. (2022). All-Fiber Photoacoustic Gas Sensing with Interferometric Location. Photonics, 9(8), 546. https://doi.org/10.3390/photonics9080546





