Optical System Design of Oblique Airborne-Mapping Camera with Focusing Function
Abstract
:1. Introduction
2. Main Technical Indicators and Decomposition of Airborne-Mapping Cameras
2.1. Technical Requirements of Airborne Mapping Cameras
2.2. Requirements of Mapping Scale for the Ground Sample Distance (GSD)
2.3. Requirements of Mapping Scale for the Interior Orientation Element Accuracy
3. Optical System Design of the Oblique Airborne-Mapping Camera
3.1. Optical System Parameters
3.2. Configuration Design of the Optical System
3.3. Environmental Adaptability
4. Analysis of the Influence of System Focusing on Mapping Accuracy
4.1. Analysis of the Influence of System Focusing on Image Quality
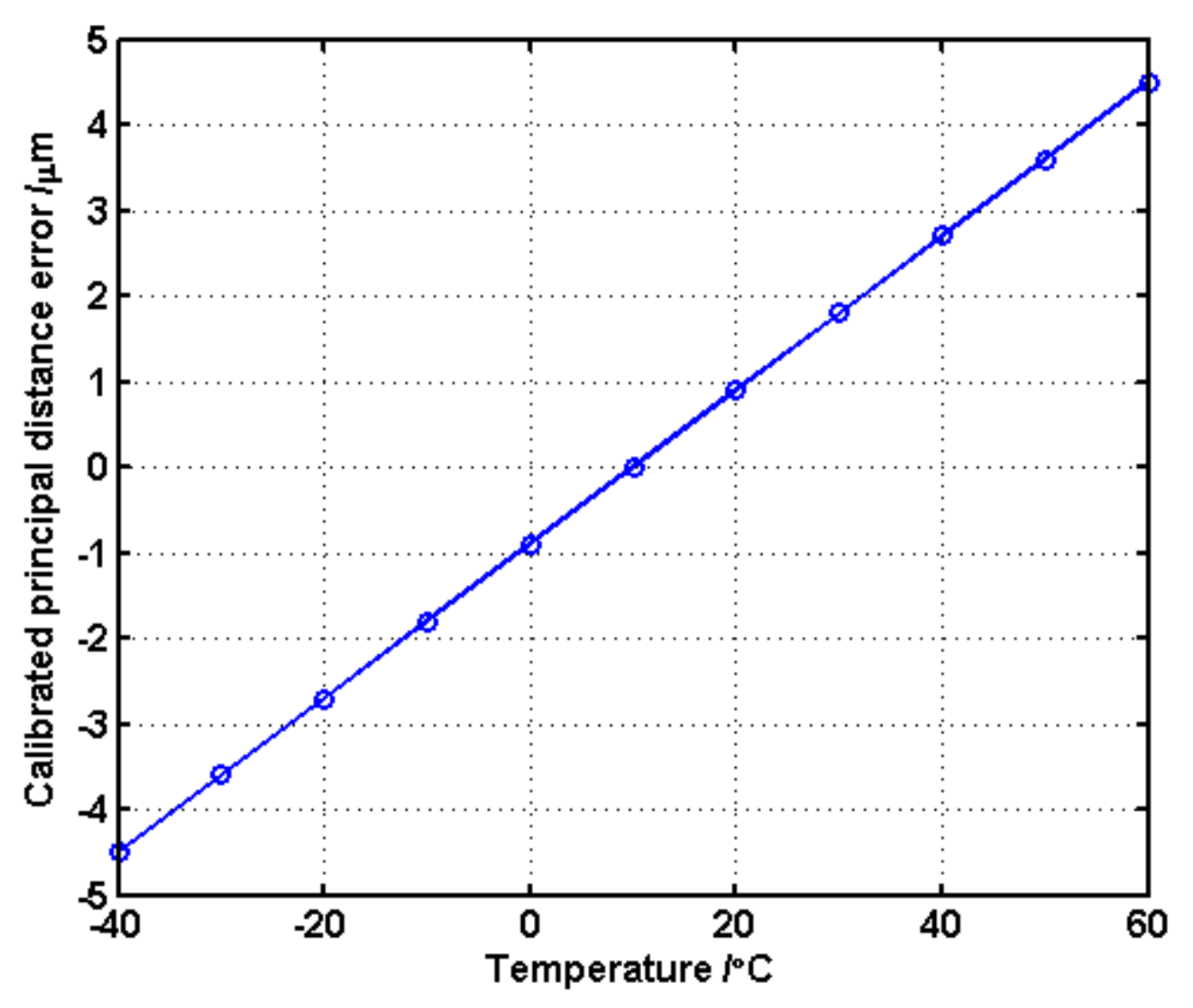
4.2. Analysis of the Influence of System Focusing on Interior Orientation Elements
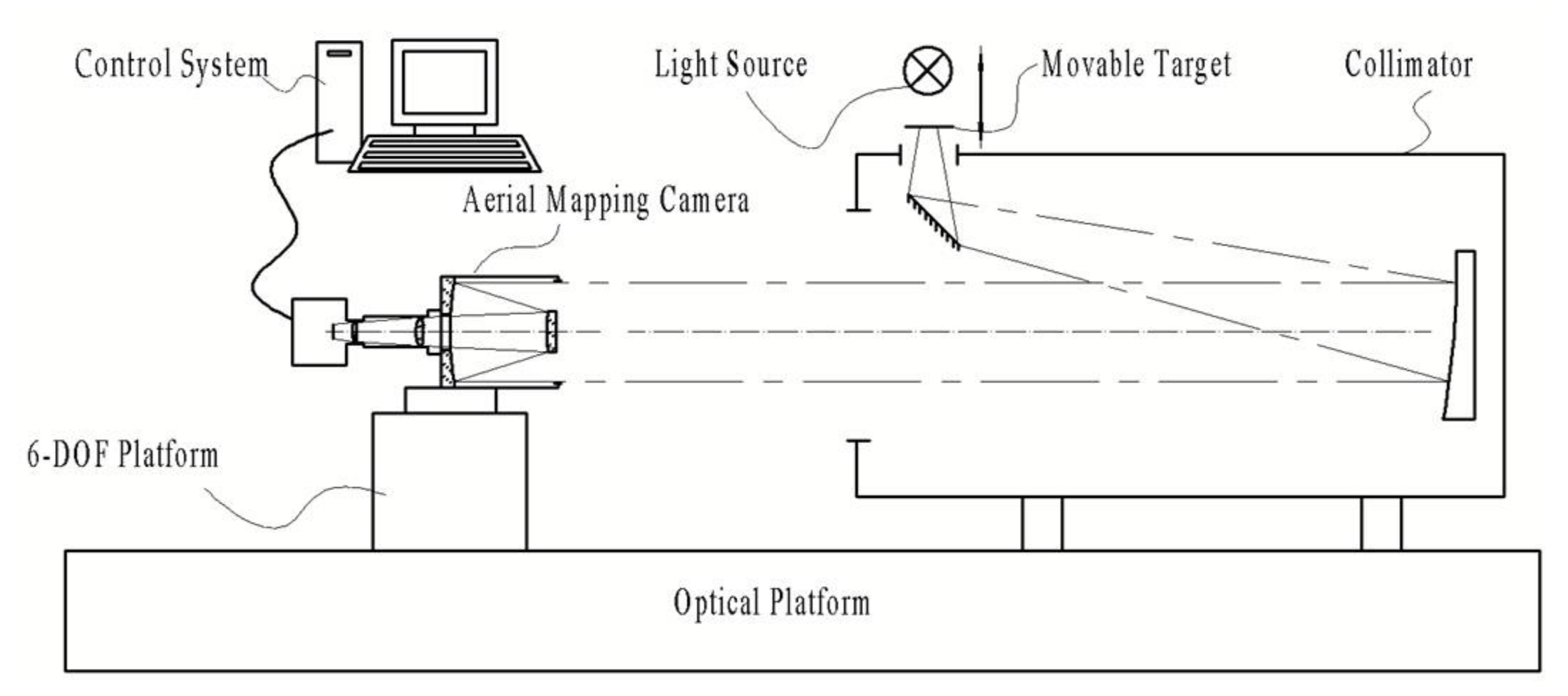
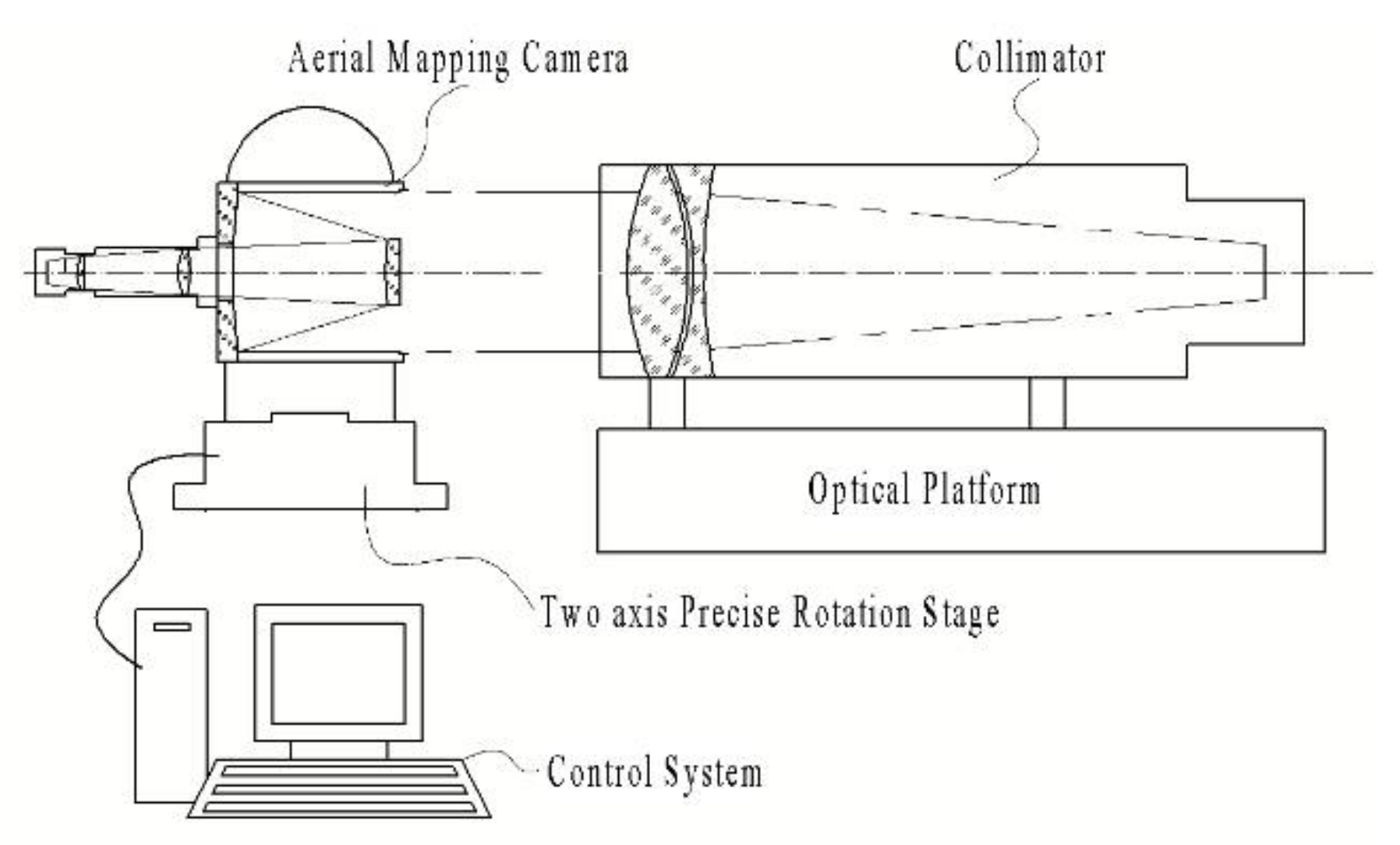
5. Real Experiment
5.1. Pixel Resolution Experiment in Laboratory
5.2. Interior Orientation Element Calibration Experiment in Laboratory
5.3. Flight Experiment with Real Data
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ahmad, M.J.; Ahmad, A.; Kanniah, K.D. Large scale topographic mapping based on unmanned aerial vehicle and aerial photogrammetric technique. In Proceedings of the 9th IGRSM International Conference and Exhibition on Geospatial & Remote Sensing (IGRSM 2018), Kuala Lumpur, Malaysia, 24 April 2018; IOP Conference Series: Earth and Environmental Science. IOP Publishing: Bristol, UK, 2018. [Google Scholar]
- Hugenholtz, C.H.; Whitehead, K.; Brown, O.W.; Barchyn, T.E.; Moorman, B.J.; LeClair, A.; Riddell, K.; Hamilton, T. Geomorphological mapping with a small unmanned aircraft system (sUAS): Feature detection and accuracy assessment of a photogrammetrically-derived digital terrain model. Geomorphology 2013, 194, 16–24. [Google Scholar] [CrossRef]
- Yalcin, G.; Selcuk, O. 3D city modelling with Oblique Photogrammetry Method. Procedia Technol. 2015, 19, 424–431. [Google Scholar] [CrossRef]
- Yang, B.; Ali, F.; Yin, P.; Yang, T.; Yu, Y.; Li, S.; Liu, X. Approaches for exploration of improving multi-slice mapping via forwarding intersection based on images of UAV oblique photogrammetry. Comput. Electr. Eng. 2021, 92, 107135. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, P.; Hu, Q.; Ai, M.; Hu, D.; Li, J. A UAV-based panoramic oblique photogrammetry (POP) approach using spherical projection. ISPRS J. Photogramm. Remote Sens. 2020, 159, 198–219. [Google Scholar] [CrossRef]
- Svennevig, K.; Guarnieri, P.; Stemmerik, L. From oblique photogrammetry to a 3D model–Structural modeling of Kilen, eastern North Greenland. Comput. Geosci. 2015, 83, 120–126. [Google Scholar] [CrossRef]
- Li, W.; Leng, X.; Chen, X.; Li, Q. Development Situation and Trend of Domestic and International Aerial Mapping Camera. In Proceedings of the 2011 International Conference on Mechatronic Science, Electric Engineering and Computer, Jilin, China, 19 August 2011. [Google Scholar]
- Udin, W.S.; Ahmad, A. Assessment of Photogrammetric Mapping Accuracy Based on Variation Flying Altitude Using Unmanned Aerial Vehicle. In Proceedings of the 8th International Symposium of the Digital Earth (ISDE8), Kuching Sarawak, Malaysia, 26 August 2013; IOP Conference Series: Earth and Environmental Science. IOP Publishing: Bristol, UK, 2013. [Google Scholar]
- Wang, X. Research on Technologies of Stability and Calibration Precision of Mapping Camera. Phys. Procedia 2011, 22, 512–516. [Google Scholar]
- Guerrero, J.; Gutiérrez, F.; Carbonel, D.; Bonachea, J.; Garcia-Ruiz, J.M.; Galve, J.P.; Lucha, P. 1:5000 Landslide map of the upper Gállego Valley (central Spanish Pyrenees). J. Maps 2012, 8, 484–491. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, A. Method and precision analysis of multi-baseline photogrammetry. Geomat. Inf. Sci. Wuhan Univ. 2007, 32, 847–851. [Google Scholar]
- Yu, J.; Sun, S. Error Propagation of Interior Orientation Elements of Surveying Camera in Ground Positioning. Spacecr. Recovery Remote Sens. 2010, 31, 16–22. [Google Scholar]
- Zhou, P.; Tang, X.; Wang, X.; Liu, C.; Wang, Z. Geometric accuracy evaluation model of domestic push-broom mapping satellite image. Geomat. Inf. Sci. Wuhan Univ. 2018, 43, 1628–1634. [Google Scholar]
- Bodrov, S.V.; Kachurin, Y.Y.; Kryukov, A.V.; Batshev, V.I. Compact long-focus catadioptric objective. In Proceedings of the 25th International Symposium on Atmospheric and Ocean Optics: Atmospheric Physics, Novosibirsk, Russia, 18 December 2019; Volume 11208. [Google Scholar]
- Galan, M.; Strojnik, M.; Wang, Y. Design method for compact, achromatic, high-performance, solid catadioptric system (SoCatS), from visible to IR. Opt. Express 2019, 27, 142–149. [Google Scholar] [CrossRef] [PubMed]
- Laikin, M. Lens Design, 4th ed.; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Shen, Y.; Wang, H.; Xue, Y.; Xie, Y.; Lin, S.; Liu, J.; Liu, M. Compact catadioptric optical system with long focal length large relative aperture and large field of view. In Proceedings of the AOPC 2020: Telescopes, Space Optics, and Instrumentation, Beijing, China, 5 November 2020; Volume 11570. [Google Scholar]
- Lim, T.-Y.; Park, S.-C. Design of a Catadioptric System with Corrected Color Aberration and Flat Petzval Curvature Using a Graphically Symmetric Method. Curr. Opt. Photonics 2018, 2, 324–331. [Google Scholar]
- Liu, Y.; Yang, B.; Gu, P.; Wang, X.; Zong, H. 50X five-group inner-focus zoom lens design with focus tunable lens using Gaussian brackets and lens modules. Opt. Express 2020, 28, 29098–29111. [Google Scholar] [CrossRef]
- Qu, R.; Duan, J.; Liu, K.; Cao, J.; Yang, J. Optical Design of a 4× Zoom Lens with a Stable External Entrance Pupil and Internal Stop. Photonics 2022, 9, 191. [Google Scholar] [CrossRef]
- Xie, N.; Cui, Q.; Sun, L.; Wang, J. Optical athermalization in the visible waveband using the 1+∑ method. Appl. Opt. 2019, 58, 635–641. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Shen, W. Analytical design of athermal ultra-compact concentric catadioptric imaging spectrometer. Opt. Express 2019, 27, 31094–31109. [Google Scholar] [CrossRef]
- Zhu, Y.; Cheng, J.; Liu, Y. Multiple lenses athermalization and achromatization by the quantitative replacement method of combined glasses on athermal visible glass map. Opt. Express 2021, 29, 34707–34722. [Google Scholar] [CrossRef] [PubMed]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light, 6th ed.; Pergamon Press: Oxford, UK, 1980. [Google Scholar]
- Yuan, G.; Zheng, L.; Sun, J.; Liu, X.; Wang, X.; Zhang, Z. Practical Calibration Method for Aerial Mapping Camera Based on Multiple Pinhole Collimator. IEEE Access 2019, 8, 39725–39733. [Google Scholar] [CrossRef]
- Zhang, G.; Zhao, H.; Zhang, G.; Chen, Y. Improved genetic algorithm for intrinsic parameters estimation of on-orbit space cameras. Opt. Commun. 2020, 475, 126235. [Google Scholar] [CrossRef]
- Zhang, H.; Yuan, G.; Liu, X. Precise calibration of dynamic geometric parameters cameras for aerial mapping. Opt. Lasers Eng. 2022, 149, 106816. [Google Scholar] [CrossRef]
- Teppati Losè, L.; Chiabrando, F.; Giulio Tonolo, F. Boosting the Timeliness of UAV Large Scale Mapping. Direct Georeferencing Approaches: Operational Strategies and Best Practices. ISPRS Int. J. Geo-Inf. 2020, 9, 578. [Google Scholar] [CrossRef]



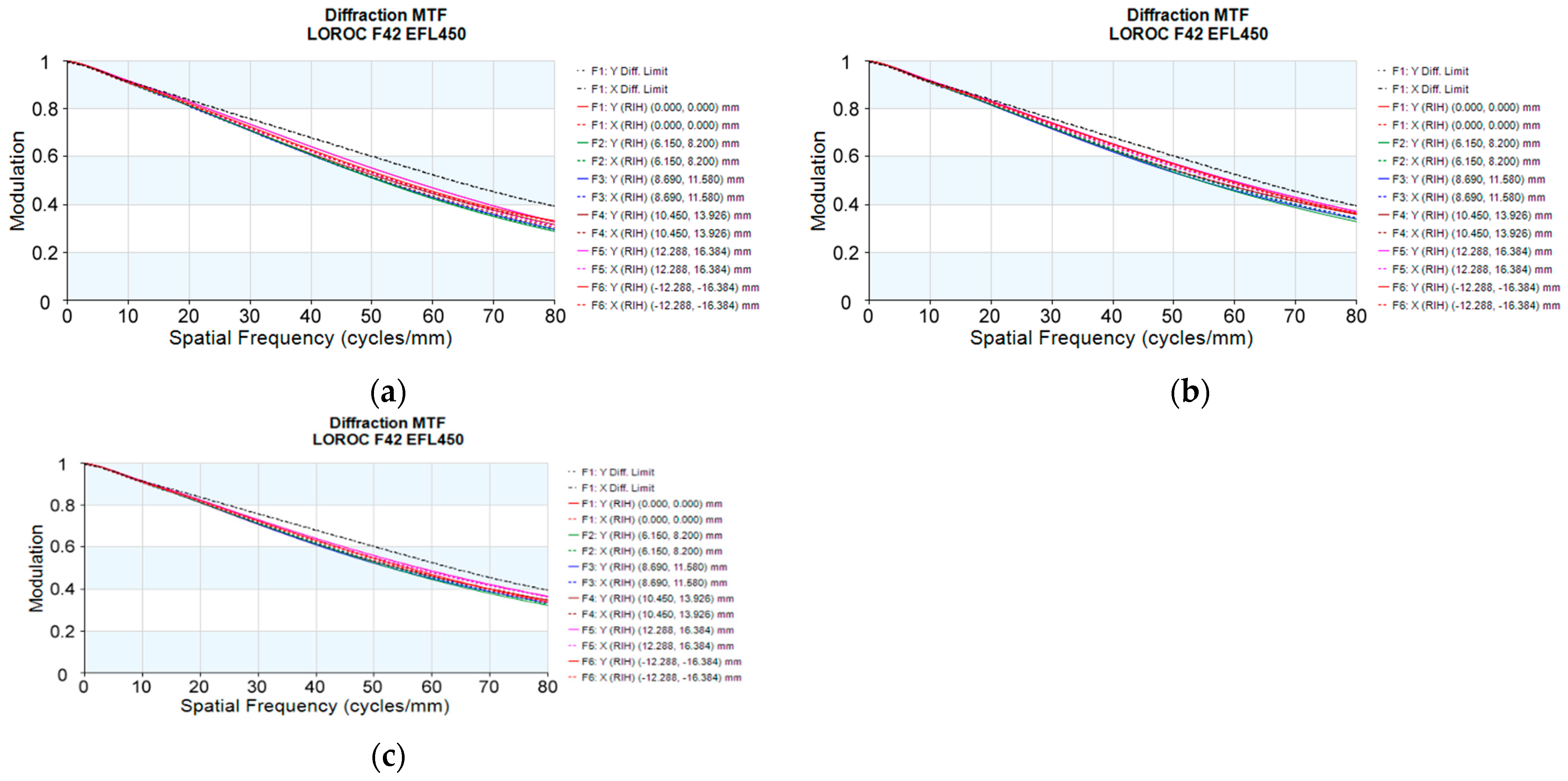
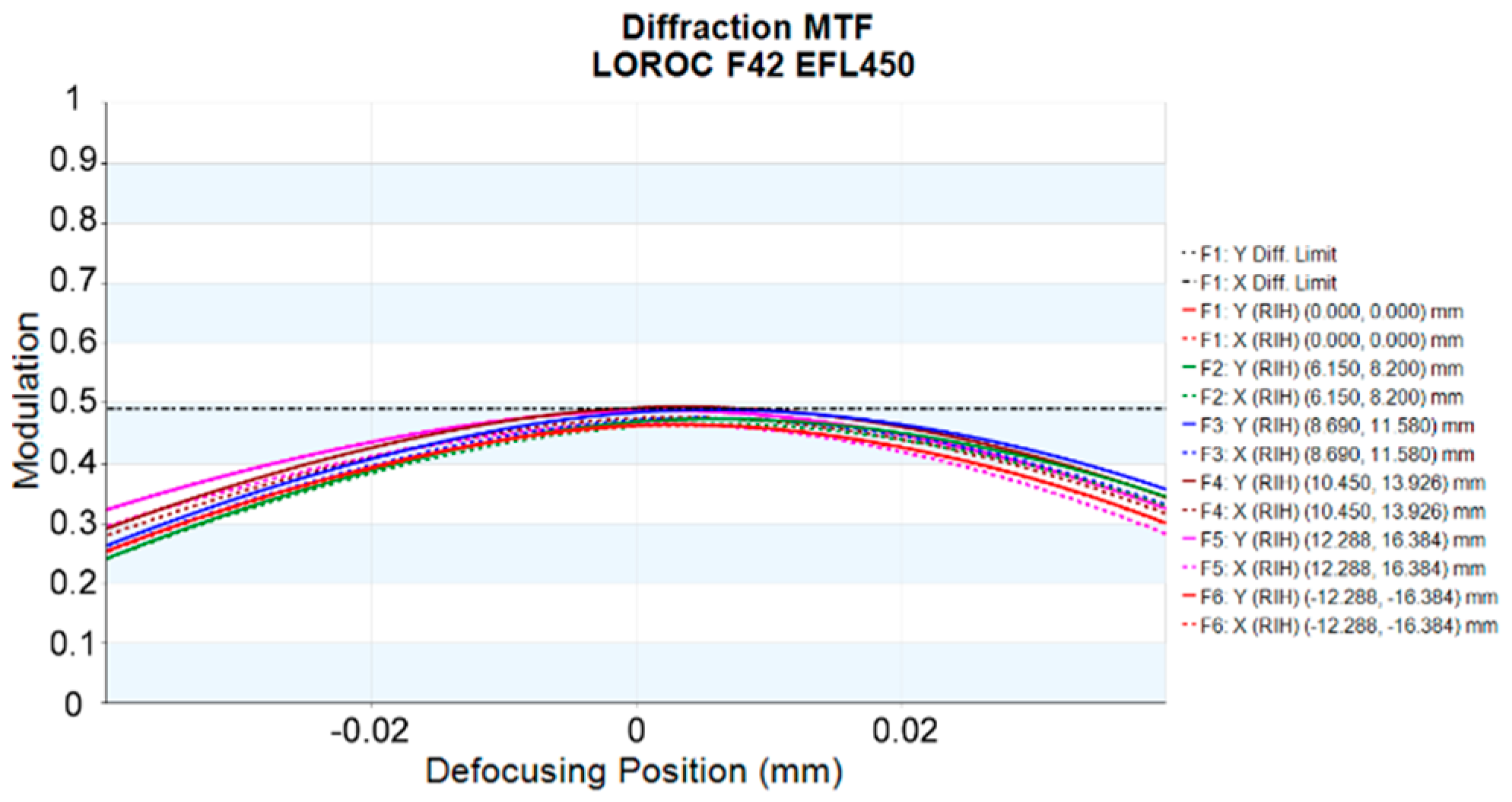
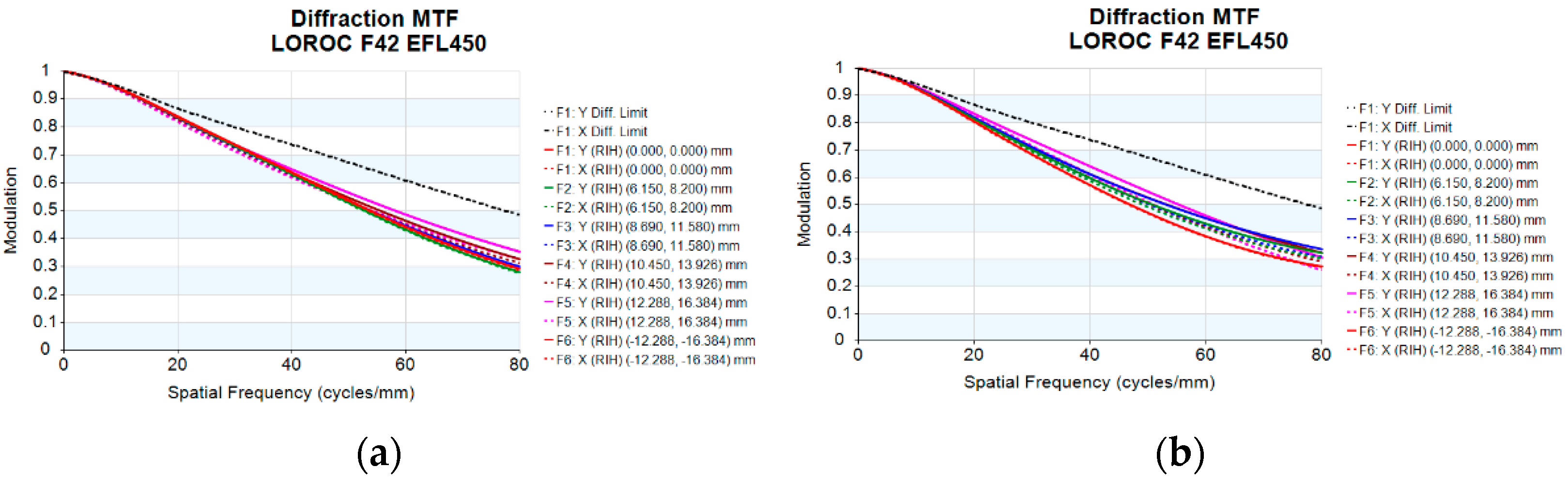






| Parameters | Values |
|---|---|
| Wavelength | 435–900 nm |
| Flight altitude | 1–7.5 km |
| Scanning range | ±60° |
| Modulation transfer function (MTF) | ≥0.2 (80 lp/mm at whole field of view (fov)) |
| Mapping scale | 1:5000 |
| Scale Imaging Accuracy | GSD/m |
|---|---|
| 1:2000 | ≤0.20 |
| 1:5000 | ≤0.50 |
| Scale-Imaging Accuracy | Terrain Category | Plane Accuracy/m | Elevation Accuracy/m |
|---|---|---|---|
| 1:2000 | Flat grounds | 1.2 | 0.40 |
| Hills | 1.2 | 0.50 | |
| Mountains | 1.6 | 1.20 | |
| High mountains | 1.6 | 1.50 | |
| 1:5000 | Flat grounds | 2.5 | 0.50 |
| Hills | 2.5 | 1.20 | |
| Mountains | 3.75 | 2.50 | |
| High mountains | 3.75 | 4.00 |
| Interior Orientation Elements | Composition | Value/μm |
|---|---|---|
| Calibrated principal distance measurement error | 3 | |
| ≤8 | ||
| ≤10 | ||
| Principle point measurement error | 3 | |
| ≤2 | ||
| ≤2 |
| Parameters | Values |
|---|---|
| Wavelength | 435–900 nm |
| Focal length | 450 mm |
| Diagonal image size | 40.96 mm |
| F-number | 4.2 |
| Maximum relative distortion | ≤0.1% |
| MTF | ≥0.2 (80 lp/mm at whole fov and different focusing positions) |
| Pixel size | 6.4 μm |
| Telecentric angle | ≤0.1° |
| Back focal length | ≥12 mm |
| Total length | ≤265 mm |
| Focusing Position | Object Distance/km | Imaging Range/km | Scanning Range/° |
|---|---|---|---|
| 1 | Inf | 4.5 km~inf | ±60 |
| 2 | 3 | 2–9 | ±60 |
| 3 | 2.5 | 1.8–5.5 | ±60 |
| 4 | 2 | 1.5–4.2 | ±60 |
| 5 | 1.5 | 1–2.5 | ±53 |
| 6 | 1 | 0.8–1.3 | ±39 |
| Focusing Position | |||||
|---|---|---|---|---|---|
| 1 | 15 × 15 | 16.395 | 12.276 | 450.145 | 0.02% |
| 2 | 15 × 15 | 16.388 | 12.278 | 449.064 | 0.04% |
| 3 | 15 × 15 | 16.383 | 12.291 | 448.828 | 0.03% |
| 4 | 15 × 15 | 16.389 | 12.295 | 448.536 | 0.05% |
| 5 | 15 × 15 | 16.393 | 12.283 | 447.944 | 0.04% |
| 6 | 15 × 15 | 16.386 | 12.279 | 446.937 | 0.06% |
| Parameters | Values |
|---|---|
| Flight altitude | 3.17 km |
| Flight speed | 242 km/h |
| Scanning range | ±60° |
| Typical exposure time | 0.5 ms |
| Accuracy of the stable platform | <35 urad (PV-value) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Chen, W.; Ding, Y.; Qu, R.; Chang, S. Optical System Design of Oblique Airborne-Mapping Camera with Focusing Function. Photonics 2022, 9, 537. https://doi.org/10.3390/photonics9080537
Zhang H, Chen W, Ding Y, Qu R, Chang S. Optical System Design of Oblique Airborne-Mapping Camera with Focusing Function. Photonics. 2022; 9(8):537. https://doi.org/10.3390/photonics9080537
Chicago/Turabian StyleZhang, Hongwei, Weining Chen, Yalin Ding, Rui Qu, and Sansan Chang. 2022. "Optical System Design of Oblique Airborne-Mapping Camera with Focusing Function" Photonics 9, no. 8: 537. https://doi.org/10.3390/photonics9080537
APA StyleZhang, H., Chen, W., Ding, Y., Qu, R., & Chang, S. (2022). Optical System Design of Oblique Airborne-Mapping Camera with Focusing Function. Photonics, 9(8), 537. https://doi.org/10.3390/photonics9080537




