Abstract
Signal recognition accuracy and recognition time are the two most important parameters of pattern recognition in a fiber optic vibration sensing system. To obtain high recognition accuracy and short recognition time, this paper optimized the VGG16 algorithm and carried out VGG16-1D and VGG16-2D recognition on big data signals generated by a Michelson–Sagnac interferometric vibration sensor system. The results indicate that VGG16-1D has a higher accuracy of 98.44% and a shorter recognition time of 0.03 s. The proposed method is a more accurate and faster pattern recognition method for big data signals from optical fiber vibration sensing systems, which is helpful in promoting further applications of optical fiber sensing systems.
1. Introduction
Although much research has been performed on the signal recognition accuracy of optical fiber vibration sensor systems, the recognition accuracy rate remains between 90% and 98% [1,2], and they are unable to reach 100% accuracy. A distributed optical fiber sensing system has many advantages, such as all-optical signal, sensitive sensing, and long sensing distance. It is widely used in oil and gas pipeline detection, high-speed rail intrusion, perimeter security, and other fields. Among many optical fiber sensing technologies, Sagnac-based optical fiber sensing technology is widely used in intrusion detection [3,4] because of its simple implementation, long sensing distance, and low cost. For a fiber optic sensor system, after accurate demodulation of the signal and feature extraction, the subsequent pattern recognition step will be entered. The accuracy of the results of this part directly determines the final result of the system. Bingjie Wang used wavelet decomposition and the radial basis role neural network classification method, which reached 85% recognition accuracy of the vibration signal [5]. Zhixian Ma proposed extracting the MFCC of the vibration signal as a feature vector and using GMM HMMs to detect intrusion signals. The false alarm rate and missed detection rate were reduced to 4% and 3%, respectively [6]. Wang Ning used the echo state network to identify the vibration event of the sensing fiber hanging on the fence, achieving an accuracy rate of 98.75% [7]. Bao Jiye decomposed the vibration signal using variable modal decomposition and extracted the spectral entropy, energy ratio, and kurtosis of the eigenmode function as the eigenvectors. The SVM method was used for pattern recognition of the eigenvector, which reached 98% recognition accuracy [8]. Qiushi Mi proposed the multilayer perceptron neural network (MLP NNs) to detect the enclosure of the substation, with a recognition accuracy of 97.6% [9].
In addition to recognition accuracy, recognition time is another important parameter. This parameter determines the recognition speed and whether the method can be used for real-time monitoring, especially in cases with large amounts of signal data. In current research of optical fiber vibration sensing signals, the attention paid to the identification time is generally insufficient. Many pattern recognition studies have provided accuracy data, but they have not provided recognition time data. Generally speaking, the recognition method with higher accuracy will result in higher processing time. In existing reports for ANN, RVFL, SCN, and dropout SCN, the time are 0.8754, 0.2064, 0.3257, and 0.3411 s, respectively, and the corresponding accuracy rates are 80%, 85.33%, 90.67%, and 94.67%, respectively [10]. In Chengang Lyu’s work, the time delay was 0.58 s, and the accuracy was 97.67% [11]. In this present study, the VGG16 algorithm is used to study the pattern recognition method with high accuracy and fast recognition speed for large amounts of signals generated by the Michelson–Sagnac interference vibration sensor system.
2. VGG Theory and Optimization
VGG is a convolutional neural network developed by the visual geometry group laboratory and Google’s DeepMind. The VGG model, using a very small (3 × 3) convolution kernel, constructs a deeper convolution neural network structure [12]. The basic mechanism consists of a convolution layer (five layers), a full connection layer (three layers), and a softmax output layer. The interval between layers is Max pooling. VGG uses several very small (3 × 3) convolution kernel layers instead of large convolution kernel layers. Thus, the parameters are reduced, and the fitting ability of the network is increased [13].
Two models, VGG16-2D and VGG16-1D, are used to process the data. VGG16-2D is a two-dimensional convolution neural network model, and VGG16-1D is a one-dimensional convolutional neural network with reference to VGG16-2D structure optimization. The model consists of eight convolution layers, four maximum pooling layers, one global average pooling layer, one linear layer, and one softmax layer. The model’s learning ability is enhanced by adding small convolution kernels.
To achieve better results, the above typical VGG16-1D network structure has undergone a number of innovations, as follows, and as Figure 1 shows:
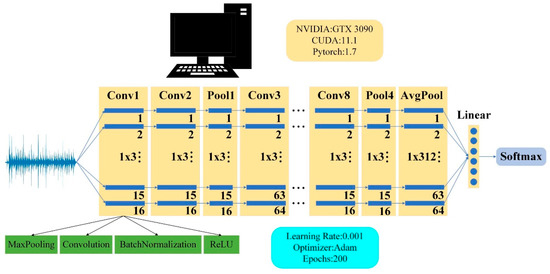
Figure 1.
VGG16 network structure model.
(1) A maximum pooling layer is added to the first layer of the network. Considering the large signal length and dimension of the Michelson–Sagnac interferometric vibration sensor system is not conducive to model training and convergence, the maximum pooling layer is added in the first layer of the model to rapidly reduce the signal length for subsequent convolution operations.
(2) To prevent the model from overfitting, the original full connection layer is removed. The convolution layer uses (1,3) small convolution kernel. To prevent the model from overfitting, the batch norm is performed after the convolution operation of each layer. The activation function is ReLU. To prevent the training process from over training, the ADAM optimizer is added to the training process.
In this experiment, the computer environment configuration for deep learning is as follows: Windows 10 platform, NVIDIA GTX 3090 GPU, and python deep learning framework.
3. Experimental System and Signal Preprocessing
3.1. Experimental System
The optical fiber vibration sensing experimental system is the Michelson–Sagnac interference type sensing system, with the structure diagram presented in Figure 2. This type of system has the advantages of high sensitivity and positioning accuracy and is suitable for applications in the external field environment [14]. The system uses a super light emitting diode (SLD) and a distributed feedback laser (DFB) as the light sources of the system. SLD and DFB lasers are, respectively, connected to the reflection port and through port of WDM1. Two beams of light from the DFB laser are emitted into Faraday rotating mirror 1 (FRM1) and FRM2 from WDM2 and WDM3 through the through ports and then return through the optical coupler (OC). Photodetectors (PD1, PD2, PD3, PD4) are used to receive the returned optical signal. An optical isolator (OI) is used to prevent the backward returning laser from entering the laser, which affects the performance of the laser. There is a time delay fiber (TDF) in the center of the optical loop, which is used to ensure that the system can make a high response to the interference signal. The length difference between sensing optical fiber 1 (SOF1) and sensing optical fiber 2 (SOF2) should not exceed 50 cm to ensure good interference visibility. In the system, the propagation paths M1 and M2 of the Michelson interferometer pass through components and ports, and two beam propagation paths S1 and S2 of the Sagnac interferometer passing through components and ports were illustrated clearly in our early work [14]. When the optical fiber coupler (OC) is combined, two light waves will interfere due to the coherence, and the interference intensity changes with the change of optical phase difference. The MI signals output from the through ports of WDM4 and WDM5 are received by PD1 and PD3, respectively. The SI signals output from the reflection ports of WDM4 and WDM5 are received by PD2 and PD4, respectively.
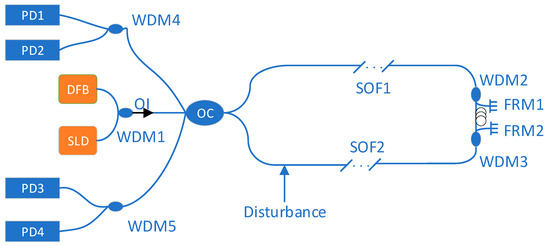
Figure 2.
Michelson–Sagnac interferometric sensing system.
The interference signal can be expressed as follows [14]:
Among them, E01 and E03 represent the amplitude of the light intensity detected by the detectors PD1 and PD3. E02 and E04 represent the amplitude of the light intensity detected by the detectors PD2 and PD4.
In this system, optical fiber vibration is caused by external disturbance, and the output optical phase change signals of different interferometers in the optical fiber are ΔφMI(t) and ΔφSI(t), respectively. The different working principles of different interferometers will produce different phase difference signals. The system finally obtains the phase information through the joint solution of ΔφMI(t) and ΔφSI(t). Similarly, if the optical fiber phase change is caused by external disturbance, then the phase information demodulated by the system is proportional to [14], as follows:
3.2. Data Segmentation
Six types of vibration signals are collected by the Michelson–Sagnac optical fiber sensing system, including “climbing”, “shearing”, “wind blowing”, “sawing”, “pushing-pulling”, and “walking” signals. The sampling frequency of signals is 500,000. The collected signals are divided into single samples with a length of 500,000, corresponding to the information collected by a 1 s signal. The segmentation method is shown in Figure 3.
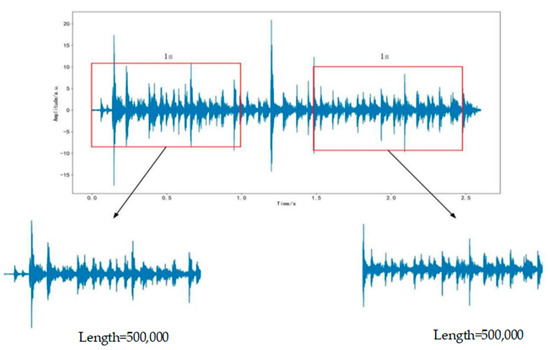
Figure 3.
Segmentation of six signal types.
As can be seen from Figure 3, each sample is divided into a single sample signal with a length of 500,000. The amplitude diagram of the six types of segmented signals is shown in Figure 4.
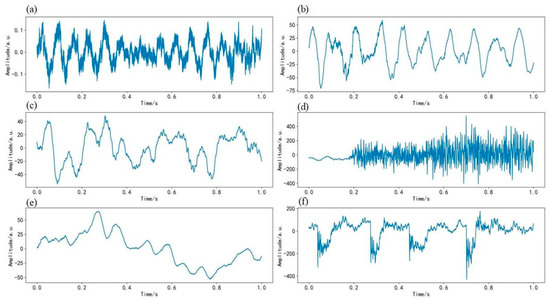
Figure 4.
Amplitude diagram of six signals: (a) climbing, (b) shearing, (c) wind blowing, (d) sawing, (e) pushing and pulling, and (f) walking.
From Figure 4, the vibration signals of the six optical fiber sensing systems are quite different. Among them, the vibration signals of wind blowing are very regular. For other vibration signals such as (d) “sawing”, there is no vibration in the front of the signals, and the high-frequency signals appear at the back. The regularity of the whole system is not as good as that of (c) wind-induced vibration.
3.3. Data Set Division
After data segmentation, a total of 1080 data samples were obtained, and each fiber vibration signal had 180 samples. The 1080 sample sets were then divided into a training set and a test set, as shown in Table 1. The VGG16 model consists of small convolution kernels and a special model structure. Even in the case of few samples, it has a strong learning ability.

Table 1.
Data set partition.
The VGG16-1D method is used to identify vibration signals. The loss function used by VGG1D is the cross-entropy loss function. At the same time, to highlight the processing time advantages of VGG16-1D, this paper also used the VGG16-2D method to analyze and identify the gray signal image and compare the advantages and disadvantages of the two methods. The signal collected by the optical fiber sensing system must first be segmented. After the original data is segmented, many sample sets are obtained, and then these sample sets are preprocessed. If the VGG16-1D model is used, the one-dimensional signal is directly input for training. If the VGG16-2D model is used, the one-dimensional signal needs to be converted into a single channel gray image, then input into the model for training, and finally output the signal category. Figure 5 shows the flow chart of the algorithm.
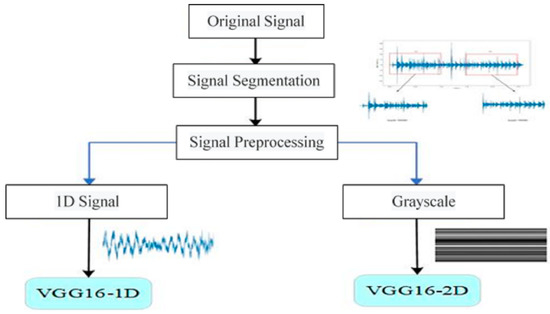
Figure 5.
Algorithm flow chart.
3.4. Grayscale Image Conversion
For the same experimental data, the VGG16-2D algorithm and the optimized VGG16-1D algorithm are compared. The VGG16-2D input is a two-dimensional matrix, so it is necessary to convert it to a one-dimensional signal. After the one-dimensional vibration signal is normalized, it is converted from one-dimensional to a two-dimensional matrix. This matrix is the corresponding grayscale image after signal conversion. The shape of the segmented signal (1, 500,000) is converted into a gray image (1, 500, 1000). The gray images of the six signals after conversion are shown in Figure 6.

Figure 6.
Grayscale image of six signals: (a) climbing, (b) shearing, (c) wind blowing, (d) sawing, (e) pushing and pulling, and (f) walking.
4. Experimental Results and Analysis
4.1. Recognition Rate Analysis
Table 2 lists the identification results of the VGG16-1D and VGG16-2D models for fiber vibration signals. It is evident that the accuracy of VGG16-1D is 98.44%, which is 2.09% higher than that of VGG16-2D. The VGG16-1D model has the best recognition effect for walking, pushing and pulling, and wind blowing vibration signals. The accuracy, recall rate, and F number of the VGG16-2D model are both 100%. However, the accuracy rate is only 90%, the recall rate is 93%, and the F number is 92%. The recall rate and F number of the two models are not high, and the accuracy rate and recall rate are the same as the F number. A potential explanation for the poor recognition effect of the two models for the sawing vibration signal is that the regularity of the lifting action is not strong, which leads to the models having a poor recognition effect. In addition, the climbing accuracy of VGG16-1D is 3% lower than that of VGG16-2D, while other indicators of VGG16-1D are better than VGG16-2D.

Table 2.
Model identification results.
Figure 7 presents the confusion matrix of the two models, and Figure 7a illustrates the identification results of VGG16-1D. The correct recognition rate of VGG16-1D for climbing, wind blowing, and walking is all 100%, and the correct detection rate for shearing is 97%. There is a 3% probability that it will be mistakenly detected as climbing. VGG16-1D has the lowest recognition accuracy of this type of signal at only 90%. It has a 6% probability of being mistakenly detected as a climbing signal and a 3% probability of being mistakenly detected as a push-pull signal. For push-pull signals, the correct detection rate is 98%, and there is a 2% probability of false detection as climbing. Overall, most signals are mistakenly detected as climbing signals. As shown in Figure 7b, the recognition result of VGG16-2D is shown. It can be seen that only the correct detection rate of the wind blowing signal reaches 100% in the recognition results of VGG16-2D. The correct detection rates of climbing, shearing, sawing, pushing and pulling, and walking is 91%, 97%, 87%, 93%, and 98%, respectively. Among them, VGG16-2D has the lowest correct detection rate for this kind of signal, and a 12% probability is detected as the other four vibration signals. Moreover, from the first column of the confusion matrix, most signals will be mistakenly detected as climbing signals. For climbing signals, the correct detection rate is 91%, and the probability of false detection is 9%. According to the two confusion matrix diagrams, VGG16-1D is better than VGG-2D for the recognition of five signal types. This is mainly because VGG16-1D directly processes vibration signals instead of binary images, thus avoiding information loss and distortion in the process of image processing. In addition, the structure optimization of VGG16-1D improves the recognition rate to a certain extent.
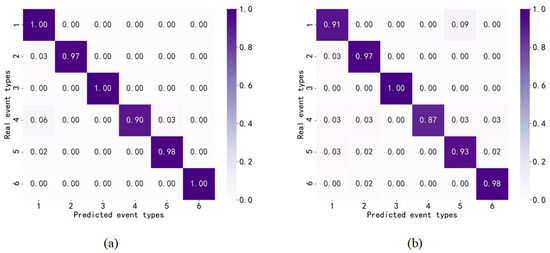
Figure 7.
Confusion matrix of the two models, (a) VGG16-1D, (b) VGG16-2D.
4.2. Processing Time Analysis
In Chengang Lyu’s work, the data processing time is 0.58 s (the sum of preprocessing time and reasoning time) [11]. For comparison, we give the preprocessing time, CPU inference time, and GPU inference time. As shown in Table 3, the CPU inference time of VGG16-1D is 0.026686 s, and the data processing time is 0.032893 s, which is an order of magnitude faster than Chengang Lyu. If it is processed by GPU, the reasoning time of GPU is 0.005616 s, and the processing time of data is 0.011823 s. The CPU inference time of VGG16-2D is 1.090148 s. The data processing time is 1.096217 s. If it is processed by GPU, the reasoning time of GPU is 0.021798 s and the processing time of data is 0.027867 s. From the above data, it is clear that the processing time of the VGG16-1D sample only needs 0.03 s, which fully meets the requirements of real-time processing. The processing time of VGG16-2D is longer than that reported in the previous literature because of the large amount of data in this work. A volume of a single sample reaches 500,000 sampling points, while Chengang Lyu had only 2000 sampling points in a single sample. In addition, the number of parameters of VGG16-1D is 85 times less than that of the parameters of VGG16-2D. Therefore, the processing speed of VGG16-1D is much faster than that of VGG16-2D. In one of our works on the dual-model hybrid pattern recognition method, the average recognition accuracy was 97.1% and time was 0.589 s [15]. Obviously, the method presented in this paper has higher accuracy and faster processing speed.

Table 3.
Processing time of different models and processors.
In this paper, the processing time of VGG16-1D on CPU and GPU is found to be much faster than that of VGG16-2D. In addition, the accuracy rate of VGG11D-1D is about 2% higher than that of VGG16-2D. Generally speaking, VGG16-1D is more suitable for Michelson–Sagnac fiber vibration signal identification and is also more suitable for mobile devices with low configuration and power consumption.
5. Conclusions
In this paper, the VGG16 method was used to analyze the signal of the Michelson–Sagnac optical fiber vibration sensor system. By adding a maximum pooling layer to the first layer of the VGG16-1D network and removing the original full connection layer, the structure of the VGG16-1D method is optimized. The main innovations of this paper are as follows:
(1) Using the VGG16-1D method, high accuracy of pattern recognition is obtained. Based on the data of “climbing”, “shearing”, “wind blowing”, “sawing”, “push-pull”, and “walking” signals obtained by the Michelson–Sagnac interferometer sensor system, the VGG convolution neural network model analysis was conducted. The results show that the accuracy of VGG16-1D is 98.44%, which is 2.09% higher than that of VGG16-2D. The recognition rate of VGG16-2D for “wind blowing” and “shearing” signals is only 93%, while the recognition rate of VGG16-1D is 100%. The accuracy rate of VGG16-1D is higher than that of VGG16-2D, which is largely because VGG16-1D is optimized on the basis of the VGG16-2D structure, absorbing the reasonable parts of the VGG16-2D structure and removing the unreasonable parts. In addition, the information loss caused by the two-dimensional image of a one-dimensional signal is avoided.
(2) Using the VGG16 method, a fast pattern recognition speed is obtained. In terms of processing time, using CPU processing, the single sample processing of VGG16-1D requires only 0.03 s. Under the condition of a high accuracy rate (98.44%), the speed is much better than other methods, which fully meets the requirements of real-time processing.
With widespread applications in oil and gas pipeline monitoring and intrusion alarms, the application scenarios of the optical fiber vibration sensor system are increasing. However, more accurate and faster pattern recognition methods are bottleneck problems that limit the wider applications of optical fiber vibration sensor systems. The work of this paper is helpful in solving this bottleneck problem.
Author Contributions
Conceptualization, J.C. and H.W.; methodology, J.C.; software, Q.S. and H.P.; validation, J.H.; formal analysis, H.W.; investigation, B.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sun, Q.; Li, Q.; Chen, L.; Quan, J.; Li, L. Pattern recognition based on pulse scanning imaging and convolutional neural network for vibrational events in Φ-OTDR. Optik 2020, 219, 165205. [Google Scholar] [CrossRef]
- Pan, Y.; Wen, T.; Ye, W. Time attention analysis method for vibration pattern recognition of distributed optic fiber sensor. Optik 2022, 251, 168127. [Google Scholar] [CrossRef]
- Allwood, G.; Wild, G.; Hinckley, S. Optical Fiber sensors in physical intrusion detection systems: A review. IEEE Sens. J. 2016, 16, 5497–5509. [Google Scholar] [CrossRef]
- Juarez, J.C.; Maier, E.W.; Choi, K.N.; Taylor, H.F. Distributed fiber-optic intrusion sensor system. J. Lightwave Technol. 2005, 23, 2081–2087. [Google Scholar] [CrossRef]
- Wang, B.; Pi, S.; Sun, Q.; Jia, B. Improved wavelet packet classification algorithm for vibrational intrusions in distributed fiber-optic monitoring systems. Opt. Eng. 2015, 54, 1–6. [Google Scholar] [CrossRef]
- Ma, Z.; Yao, L.; Jie, Z. An optic-fiber fence intrusion recognition system using mixture Gaussian hidden Markov models. Ieice Electron. Expr. 2017, 14, 23–26. [Google Scholar] [CrossRef][Green Version]
- Wang, N.; Fang, N.; Wang, L. Intrusion recognition method based on echo state network for optical fiber perimeter security systems. Opt. Commun. 2019, 451, 301–306. [Google Scholar] [CrossRef]
- Bao, J.; Mo, J.; Xu, L.; Liu, Y.; Lv, X. VMD-based vibrating fiber system intrusion signal recognition. Optik 2019, 205, 163753. [Google Scholar] [CrossRef]
- Mi, Q.; Yu, H.; Xiao, Q.; Wu, H. Intrusion behavior classification method applied in a perimeter security monitoring system. Opt. Express 2021, 29, 8592–8605. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Zeng, Z.; Qu, H.; Sun, C. A Novel Fiber Intrusion Signal Recognition Method for OFPS Based on SCN with Dropout. J. Lightwave Technol. 2019, 37, 5221–5230. [Google Scholar] [CrossRef]
- Lyu, C.; Huo, Z.; Cheng, X.; Jiang, J.; Alimasi, A.; Liu, H. Distributed optical fiber sensing intrusion pattern recognition based on GAF and CNN. J. Lightwave Technol. 2020, 38, 4174–4182. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. In Proceedings of the 3rd International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015; pp. 1–14. [Google Scholar]
- Tabi Fouda, B.M.; Han, D.; An, B.; Lu, X.; Tian, Q. Events detection and recognition by the fiber vibration system based on power spectrum estimation. Adv. Mech. Eng. 2018, 10, 1–9. [Google Scholar] [CrossRef]
- Song, Q.; Zhou, P.; Peng, H.; Hu, Y.; Xiao, Q.; Wu, H.; Jia, B. Improved localization algorithm for distributed fiber-Optic sensor based on merged Michelson-Sagnac interferometer. Opt. Express 2020, 28, 7207–7220. [Google Scholar] [CrossRef] [PubMed]
- Cheng, J.; Song, Q.; Peng, H.; Huang, J.; Wu, H.; Jia, B. Dual-model hybrid pattern recognition method based on fiber optic line-based sensor with a large amount of data. Opt. Express 2022, 30, 1818–1828. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).