Scintillation Index for Spherical Wave Propagation in Anisotropic Weak Oceanic Turbulence with Aperture Averaging under the Effect of Inner Scale and Outer Scale

Abstract

Due to the advantages of high transmission rate, lower power consumption, high security, etc., underwater wireless optical communication (UWOC) has been widely studied and considered as a potential technique for underwater communication. However, its performance is severely degraded by oceanic turbulence due to refractive index fluctuations, which is caused by the change of inhomogeneous ocean environment. Within our derived spatial power spectrum model under anisotropic oceanic turbulence, we conducted a detailed investigation for a spherical wave propagating in weak anisotropic turbulence in this paper. Based on the derived oceanic spectrum, we proposed a scintillation index model for spherical wave in anisotropic oceanic turbulence considering the aperture averaging effect at non-zero inner scale and limited outer scale. Besides, we analyze the aperture averaging scintillation index under the influence of channel parameters such as inner and outer scales. Simulation results reveal that the scintillation index increases with the increase of the outer scale, while the inner scale induces an opposite trend on the scintillation index. Moreover, the inner scale exhibits a larger impact than the outer scale on the UWOC system over weak oceanic turbulence.

1. Introduction

With the help of acoustic and radio frequency (RF) communication, which have metrics in long-distance transmission and high tolerance to water turbidity effects, respectively, underwater communication has broad prospects in scientific research and military fields, such as navigation and control, underwater ecological protection monitoring, environmental protection and so on [1,2]. However, these communication schemes encouter a bottleneck in transmission rate due to the ever-increasing demand for underwater communication. For instance, the transmission of an underwater sensor network requires an even higher transmission rate than before. Although the transmission rate of RF communication is faster than that of acoustic communication, it is far from sufficient due to the increasing requirements of the underwater Internet of Things [3,4]. Therefore, the need for a solution on how to prompt the transmission speed of underwater wireless communication is urgent and remains a challenging topic.

Benefiting from its lower power consumption, low-cost deployment, high security and transmission rate, underwater wireless optical communication (UWOC) has become an alternative method for ocean communication. Significant attention has been devoted to UWOC systems and fruitful achievements have proved their potential application in disaster prevention, environmental monitoring, offshore oil field exploration and so on [5,6]. Although UWOC systems are widely employed, they are seriously interfered by the underwater environment, which restrict them to a certain extent. The performance of UWOC can be severely damaged by absorption, scattering and underwater turbulence. Therefore, photons inevitably interact with water molecules and other particulate matter in the water, leading to absorption and scattering.

In addition, many undesired effects, such as beam expansion, jitter and intensity fluctuations, can result in a severe drop in beam quality due to the influence of oceanic turbulence when the wave propagates in seawater [7,8]. The statistical characteristics of the rectangular cusped random beams, which maintain the rectangular tip profile under the weak load, propagating in oceanic turbulence were studied by Lu and Zhao [9]. It was proved that the spectral density and the degree of spectral consistency are significantly affected by various turbulence parameters. A more realistic environment where the eddy diffusivity of temperature and salt were not equal was futher considered by Elamassie et al. [10]. The scintillation index of both plane and spherical waves under weak oceanic turbulence was obtained. Li et al. proposed a new ocean spectrum to study the influence of oceanic turbulence in the unstable stratification on the Gaussian beam scintillation index [11]. The results show that the fluctuation of temperature and salinity in ocean turbulence significantly impacts the scintillation index, and weak ocean turbulence with larger kinematic viscosity can obtain a smaller scintillation index. Moreover, the asymmetric oceanic turbulence will affect the pluse broadening and the received probability of the OAM modes in the Lommel–Gaussian pulsed beams [12].

Most studies described above treated the seawater as isotropic turbulence while ignoring its anisotropic property. The difference from isotropic is that the physical properties of anisotropic turbulence are closely related to the orientation. In addition, the measurement results of various orientations are very different. The turbulence vortex is isotropic only in the inertial sub-interval [13]. In reality, oceanic turbulence exhibits asymmetric spatial frequencies in various directions, resulting in an anisotropic spatial power spectral density due to the rotation of the Earth [14]. The effect of anisotropic oceanic turbulence on the intensity fluctuations was discussed by Baykal [15,16]. Thereafter, the effect of anisotropic turbulence on the average bit error rate (BER) was further investigated when an asymmetrical Gaussian beam propagates in anisotropic turbulence [17]. The BER decreased in response to increased anisotropy levels in various directions. Moreover, the performance of an optical wireless communication system operating in anisotropic oceanic turbulence is better than that when operating in isotropic oceanic turbulence.

Due to the numerous effects of beam propagation in the ocean, many techniques are used to improve the efficiency of the entire UWOC system. To compensate for the effect of alignment error on the coupling efficiency of single-mode fiber, Wu et al. designed a fiber coupler with a degree of freedom coupling structure and used a variable-gain stochastic parallel gradient descent algorithm to find the optimal alignment attitude [18]. Ma et al. used the intermediate frequency signal as the feedback control signal, which improved the mixing efficiency of the system [19]. The corner detection method and the optical flow method were used by Wang et al. to calculate the optical flow displacement based on two consecutive frames. The results show that the method is feasible and can eliminate noise accurately [20]. Considering the impact of oceanic turbulence on UWOC, some excellent schemes have been employed to decrease the scintillation index.

Considering the impact of oceanic turbulence on UWOC, some excellent schemes have been employed to decrease the scintillation index, including the utilization of multiple-input and multiple-output [21,22,23], different beam types at the transmitter [24,25] and larger aperture diameters [26]. Aperture averaging, i.e., expanding the aperture diameter of the receiver, has proven to be a useful method for enhancing the communication performance of optical beams propagating in turbulence. Approximate expressions for the aperture averaging of scintillation in atmosphere environment were derived by Churnside [27]. It was concluded that if the aperture diameter is larger than the spatial size that produces irradiance fluctuations, the receiver will average the fluctuations, thereby reducing the scintillation index. Khalighi et al. [28] compared the performance of wireless optical communication systems with single-aperture and multi-aperture receivers under different turbulent conditions. The conclusion is drawn that under moderate turbulence, a single large aperture diameter is more conducive to obtaining good performance than multiple aperture diameters, while using multiple aperture diameters is more advantageous than using a single large aperture diameter under strong turbulence. Furthermore, increasing the aperture diameter is also a good way to improve communication performance in oceanic turbulence. The averaging aperture effect has a significant impact on the UWOC system, which has been studied in detail in [29]. In [30,31], the scintillation index of an optical wave in both anisotropic and isotropic turbulence was greatly decreased with the aperture averaging effect.

Although the influence of wave shapes, aperture averaging and turbulence parameters on UWOC systems has been extensively studied, the impact of the inner and outer scales of turbulence has not been well examined. Motivated by this, Yang et al. analyzed the scintillation index of a Gaussian laser beam containing both inner and outer scales effects on a ground-space slant path under moderate-to-strong atmospheric turbulence [32]. A theoretical irradiance fluctuation expression based on new spectra of plane and spherical waves in weak turbulence was derived in [33], which proved that the scintillation expression in atmospheric turbulence can fit well for oceanic turbulence under a small inner scale. Chen et al. further studied the scintillation index of a Gaussian beam through a non-Kolmogorov maritime atmospheric turbulence channel with the aperture averaging effect and discussed the influence of the inner scale of the maritime turbulence [34]. It was revealed that the scintillation index of the Gaussian beam increased with increasing inner scale and decreasing receiver aperture diameters. Though some studies have revealed that the inner scale has a more significant impact on the scintillation index than the outer scale when an optical wave propagates though the moderate-to-strong turbulence [35], this conclusion has not been certified under a weak turbulence, to the best of our knowledge.

According to the above analysis, the individual influences of the inner and outer scales on UWOC system were studied, while their comprehensive impacts on this system under anisotropic weak oceanic turbulence have not been simultaneously studied yet. To fill this gap, we focus on revealing the effect of inner and outer scales on a spherical wave’s scintillation index under weak anisotropic oceanic turbulence. The major contributions of this study are summarized as follows. The aperture averaging technique is used to alleviate the fluctuation of the intensity. Specifically, the channel and system parameters are considered, such as inner and outer scales, anisotropic factors, structure parameters, aperture diameters and wavelengths. Moreover, the influence of the system and channel parameters on the scintillation index is scrutinized in detail.

The rest of this study is structured as follows. In Section 2, we introduce a modified anisotropic spatial power spectrum model that takes the inner and outer scales into account. Considering the effects of both the inner and outer scales, the scintillation index model of a spherical wave propagating in the weak oceanic turbulence with the aperture average effect is derived in Section 3. The simulation results are presented and evaluated in Section 4. Finally, concluding remarks are given in Section 5.

2. Spectrum of Anisotropic Oceanic Turbulence

Plenty of turbulence models, such as Kolmogorov spectrum, Tatarskii spectrum and von Kármán spectrum, have been used to characterize the turbulent environment. Considering the effects of both the inner and outer scales of oceanic turbulence, the modified Kolmogorov spectrum of refractive-index fluctuations is empolyed in this study and is expressed as [33].

$${\Phi }_n\left(\kappa \right)=0.033C_n^2\left[1+a_1\left(\frac{\kappa }{{\kappa }_i}\right)+a_2{\left(\frac{\kappa }{{\kappa }_i}\right)}^{7/6}\right]\frac{exp\left(-{\kappa }^2/{\kappa }_i^2\right)}{{\left({\kappa }^2+{\kappa }_o^2\right)}^{11/6}}.$$

(1)

Note that we mainly consider the temperature-induced fluctuation in this study. Therefore, only the seawater temperature-induced spectrum model is employed here. Where $C_n^2$ represents the refractive-index structure parameter for Kolmogorov turbulence and has units of m${}^{-2/3}$, ${\kappa }_i=3.3/L_i$ and ${\kappa }_o=2\pi /L_o$, where $L_i$ and $L_o$ are the inner and outer scales, respectively. Note that $a_1=-0.061$ and $a_2=2.836$ in a maritime turbulent environment according to [34]. $\kappa =\sqrt{{\kappa }_x^2+{\kappa }_y^2+{\kappa }_z^2}$ is the spatial frequency of the oceanic turbulence fluctuations. This spectral model is extensively used for theoretical calculations over both atmosphere and ocean environment [36]. The accuracy of this model has been well confirmed with the experimental data under oceanic turbulence [37].

According to the anisotropic property of oceanic turbulence, as discussed in Section 1, we use the concept of anisotropy in atmospheric turbulence [38] together with the spectral density index of refraction fluctuations under isotropic oceanic turbulence in this study [39]. Therefore, the spectral density index of refraction fluctuations under the anisotropic oceanic turbulence can be written as

$$\begin{array}{cc}\hfill {\Phi }_n\left(\kappa \right)=& 0.033C_n^2{\mu }_x{\mu }_y\left[1+a_1\left(\frac{{\kappa }^{\prime }}{{\kappa }_i}\right)+a_2{\left(\frac{{\kappa }^{\prime }}{{\kappa }_i}\right)}^{7/6}\right]\frac{exp\left(-{\kappa }^2/{\kappa }_i^2\right)}{{\left({\kappa }^{{}^{\prime }2}+{\kappa }_o^2\right)}^{11/6}}\hfill \end{array}.$$

(2)

In this paper, only the anisotropy turbulence along the propagation direction is considered for simplicity, i.e., the z direction of the beam, and is accounted for by the influential anisotropic factors ${\mu }_x$ and ${\mu }_y$, which are in the x and y directions, respectively. Note that this model can be recast to an isotropic case when ${\mu }_x={\mu }_y=1$. We also have ${\mathit{\kappa }}_x^{\prime }={\mu }_x{\mathit{\kappa }}_x$, ${\mathit{\kappa }}_y^{\prime }={\mu }_y{\mathit{\kappa }}_y$, ${\mathit{\kappa }}_z^{\prime }={\mathit{\kappa }}_z$, and ${\mathit{\kappa }}^{\prime }=\sqrt{{\mathit{\kappa }}_x^{{}^{\prime }2}+{\mathit{\kappa }}_y^{{}^{\prime }2}+{\mathit{\kappa }}_z^{{}^{\prime }2}}=\sqrt{{\mu }_x^2{\mathit{\kappa }}_x^2+{\mu }_y^2{\mathit{\kappa }}_y^2+{\mathit{\kappa }}_z^2}$, where ${\kappa }_x$, ${\kappa }_y$ and ${\kappa }_z$ are the x, y and z components of the spatial frequency, respectively.

For simplification, we use the Markov approximation [40], which is usually used in the theory of wave propagation in random media, with the assumption that the refractive index is delta-correlated at any pair of points located along the direction of propagation. By invoking the Markov approximation, we ignore ${\kappa }_z$, i.e., the spatial wavenumber component along the direction of propagation. Therefore, Equation (2) can be further rewritten as

$$\begin{array}{cc}\hfill {\Phi }_n\left({\mu }_x,{\mu }_y,{\kappa }_x,{\kappa }_y\right)& =0.033C_n^2{\mu }_x{\mu }_y\left[1+a_1\left(\frac{\sqrt{{\mu }_x^2{\kappa }_x^2+{\mu }_y^2{\kappa }_y^2}}{{\kappa }_i}\right)\right.\hfill \\ & \left.+a_2{\left(\frac{\sqrt{{\mu }_x^2{\kappa }_x^2+{\mu }_y^2{\kappa }_y^2}}{{\kappa }_i}\right)}^{7/6}\right]\frac{exp\left[-\left({\mu }_x^2{\kappa }_x^2+{\mu }_y^2{\kappa }_y^2\right)/{\kappa }_i^2\right]}{{\left({\mu }_x^2{\kappa }_x^2+{\mu }_y^2{\kappa }_y^2+{\kappa }_o^2\right)}^{11/6}}\hfill \end{array}.$$

(3)

3. Scintillation Index for Spherical Wave with Aperture Average Effect

In the anisotropic ocean turbulence, the scintillation index is usually used to measure the performance level of the UWOC systems under intensity fluctuations. Under weak fluctuation conditions, the scintillation index is approximately equal to the log-irradiance variance, i.e., $m^2={\sigma }_{lnI}^2$ [37]. Previous studies [15,41] show that the scintillation index ${\sigma }_{lnI}^2$ is strongly related to the log-amplitude variance ${\sigma }_{\chi }^2$. The log-irradiance variance can be expressed as [42] ${\sigma }_{lnI}^2=〈{\left(ln\frac{I}{\langle I\rangle }\right)}^2〉$, where $\langle I\rangle$ is the statistical mean of the optical intensity. The log-amplitude variance is used to describe the strength of amplitude fluctuation and is defined as [43] ${\sigma }_{\chi }^2=〈{\left(ln\frac{A}{\langle A\rangle }\right)}^2〉$, where A is the amplitude of an optical wave and $\langle A\rangle$ is the statistical average of the amplitudes. The relationship between the logarithmic intensity fluctuation variance and the logarithmic amplitude fluctuation variance can be derived as ${\sigma }_{lnI}^2=4{\sigma }_{\chi }^2$. Therefore, the scintillation index can be obtained

$$m^2=4{\sigma }_{\chi }^2.$$

(4)

By using the Rytov method, the variance of the log-amplitude for a spherical wave propagating in the anisotropic turbulent medium is derived as [44]

$$\begin{array}{cc}\hfill {\sigma }_{\chi }^2=& \pi Re\left\{{\int }_0^{L}dz{\int }_{-\infty }^{+\infty }d{\kappa }_x{\int }_{-\infty }^{+\infty }d{\kappa }_y\right.\left[P\left(z,{\kappa }_x,{\kappa }_y\right)P\left(z,-{\kappa }_x,-{\kappa }_y\right)\right.\hfill \\ & \left.\left.+{\left|P\left(z,{\kappa }_x,{\kappa }_y\right)\right|}^2\right]·{\Phi }_n\left({\mu }_x,{\mu }_y,{\kappa }_x,{\kappa }_y\right)\right\}\hfill \end{array},$$

(5)

It should be noted that only the radial component is considered and used for the point-like scintillation case, that is, the normalized variance amount of scintillation at a specific position (normally on-axis) of the transverse receiver plane. In addition, the symbol Re in Equation (5) denotes the real part, z is the distance along the propagation axis, and L is the wave propagation distance. In addition, we have

$$P\left(z,{\kappa }_x,{\kappa }_y\right)=jkexp\left[-0.5{\left(kL\right)}^{-1}jz(L-z)\left({\kappa }_x^2+{\kappa }_y^2\right)\right],$$

(6)

which is the propagation expression in Equation (5), $j=\sqrt{-1}$, $k=2\pi /\lambda$ and is the number of the wave and $\lambda$ is the wavelength.

In addition, according to the previous study [33], the logarithmic amplitude variance of the spherical wave over a circular aperture, which is over a certain area of the receiver aperture and sometimes called “power scintillation” can be obtained by

$$\begin{array}{cc}\hfill & {\sigma }_{\chi D}^2=\pi Re\left\{{\int }_0^{L}dz\left\{{\int }_{-\infty }^{+\infty }d{\kappa }_x{\int }_{-\infty }^{+\infty }d{\kappa }_y\right.\right.\left[P\left(z,{\kappa }_x,{\kappa }_y\right)·P\left(z,-{\kappa }_x,-{\kappa }_y\right)\right.\hfill \\ \hfill & \left.\left.\left.+{\left|P\left(z,{\kappa }_x,{\kappa }_y\right)\right|}^2\right]·{\Phi }_n\left({\mu }_x,{\mu }_y,{\kappa }_x,{\kappa }_y\right)·exp\left[-D^2\left({\mu }_x^2{\kappa }_x^2+{\mu }_y^2{\kappa }_y^2\right)z^2/16\right]\right\}\right\},\hfill \end{array}$$

(7)

where D denotes the diameter of the receiver aperture. It is noted that anisotropy also affects the beam vector, which is denoted by $\kappa$ in the aperture averaging effect. In addition, the aperture averaging effect can be expressed by the integral of the radial parameters ${\kappa }_x$ and ${\kappa }_y$.

Finally, the intensity fluctuations of a spherical optical beam in an anisotropic oceanic medium are quantified by the scintillation index by inserting Equation (7) into Equation (4). Note that we mainly focus on the effect of oceanic turbulence on the scintillation index, thus the closed-form expression of the scintillation index is ignored in this study.

4. Results and Discussion

The numerical results for the scintillation index of an UWOC system with spherical wave propagation in weak anisotropic turbulence are discussed in this section. The key parameters used in the simulation are listed in

Table 1. Key parameters used in calculations.

Figure	λ (nm)	L (m)	D (cm)	${\mathit{L}}_{\mathit{i}}$ (mm)	${\mathit{L}}_{\mathit{o}}$	${\mathit{\mu }}_{\mathit{x}}$	${\mathit{\mu }}_{\mathit{y}}$
Figure 1	532	10	1	10	[0.5, 3]	1, 1.01, 1.02	1, 1.03, 1.04
Figure 2	532	10	1, 2, 3	10	[0.5, 3]	1	1.2
Figure 3	532, 1064, 1550	10	1	10	[0.5, 3]	1	1.2
Figure 4	532	10	1	[2, 10]	10	1, 1.6, 1.8	1, 1.2, 1.4
Figure 5	532	10	1, 2, 3	[2, 10]	10	1	1.2
Figure 6	532, 1064, 1550	10	1	[2, 10]	10	1	1.2
Figure 7	532	10	1, 1.1, 1.2, 1.28, 1.29, 1.3, 2	[2, 10]	10	1	1,2
Figure 8	532	10	1	[2, 10]	10	1, 1.4	1, 1.2
Figure 9	532	10	[1, 5]	10	10	1, 1.4, 1.5, 1.6	1, 1.1, 1.2, 1.3
Figure 10	532	[10, 20]	1	10, 15, 20	1, 5, 10	1	1.2
Figure 11	532	10	1	[2, 10]	[10, 30]	1	1.2
Figure 12	532	[10, 30]	1	10	10	1	1.2

, and according to [45,46,47], the structure parameter $C_n^2$ is $7\times {10}^{-17}$, unless special instructions are given. In addition, the unit of the aperture diameter is in millimeters [29,48].

The influence of the outer scale on the scintillation index of a spherical wave under the conditions of different anisotropic factors is depicted in Figure 1. As we can see from this figure, the scintillation index of a spherical optical beam increases as the outer scale $L_o$ increases. For instance, when ${\mu }_x$ = 1.01 and ${\mu }_y$ = 1, the scintillation index with an outer scale of 0.5 m is 0.0291 and when the outer scale becomes 3 m, the scintillation index increases to 0.0295. This phenomenon can be explained by the fact that the outer scale is the upper limit of the inertial zone and the refracting power of turbulence is directly limited by the outer scale. Therefore, a larger outer scale results in more severe scintillation.

Figure 1. Scintillation index of a spherical wave versus the outer scale for different anisotropic factors.

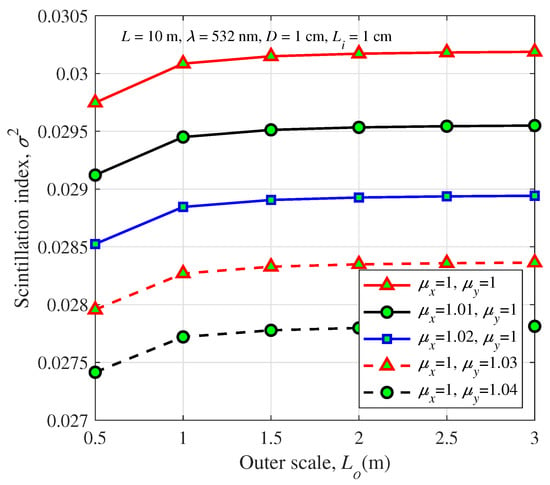
Figure 1. Scintillation index of a spherical wave versus the outer scale for different anisotropic factors.

In addition, from Figure 1 we obtain that the scintillation index of the beam propagating in isotropic turbulence is more significant than that in anisotropic turbulence. Note that this conclusion has also been obtained in previous studies [44,49]. For a fixed anisotropic factor in the x-direction, the larger anisotropic factor in the y-direction induces a smaller scintillation index. This phenomenon is also suitable for the anisotropic factor in the x-direction. Therefore, we conclude that anisotropic turbulence is helpful for spherical wave propagation in seawater. The reason for this phenomenon is that anisotropy changes the focusing properties of oceanic turbulence.

Figure 2 and Figure 3 show the relationship between the outer scale $L_o$ and the scintillation index under different aperture diameters and wavelengths, respectively. Obviously, the scintillation index increases with increasing outer scale, as shown in Figure 1. Note that this trend is subdued due to the specific parameter values. Furthermore, the aperture averaging has a mitigating effect on the scintillation index, as shown in Figure 2. The larger aperture diameter decreases the scintillation index significantly. The scintillation index for the 532, 1064 and 1550 nm wavelengths are depicted in Figure 3, showing that the scintillation index decreases as the wavelength increases. This phenomenon is because shorter optical wavelengths are more susceptible to oceanic turbulence than longer optical wavelengths. The longer the optical wavelength, the smaller the fluctuation of the overall variance of the wavefront, and the more stable it is in spatial frequency, while the shorter the optical wavelength, the greater the fluctuation of the wavefront, and the more sensitive it is to the influence of turbulence. Therefore, we conclude that increasing the aperture diameter and the optical wavelength is an alternative method to mitigate the influence of oceanic turbulence on the UWOC system. In addtion, it can be concluded from Figure 1, Figure 2 and Figure 3 that the outer scale has a small effect on the scintillation even neglected, which is similar to the previous studies [35,50].

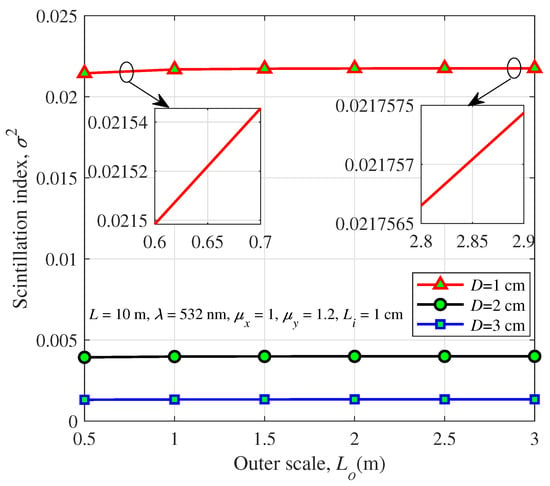
Figure 2. Scintillation index of a spherical wave versus the outer scale for different aperture diameters.

Figure 2. Scintillation index of a spherical wave versus the outer scale for different aperture diameters.

Figure 3. Scintillation index of a spherical wave versus the outer scale for different wavelengths.

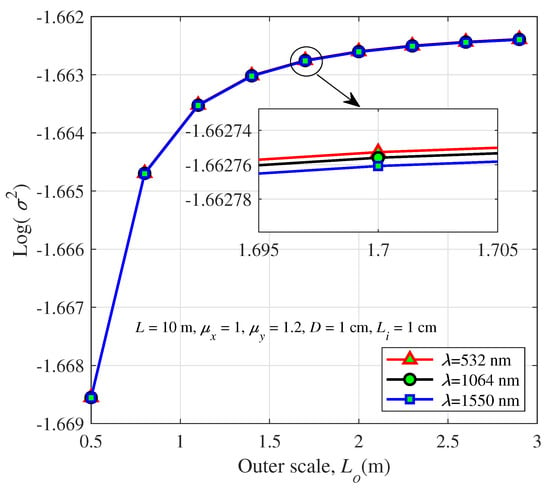
Figure 3. Scintillation index of a spherical wave versus the outer scale for different wavelengths.

To further investigate the influence of the inner scale on the scintillation, we plot the curve of the inner scale $L_i$ versus the scintillation index under different anisotropic factors, as shown in Figure 4. Different from the influence of the outer scale, the inner scale shows the opposite trend, i.e., the scintillation index decreases as the inner scale increases. In addition, this declining trend levels off as the inner scale continue to increase. This can be explained by the fact that when the inner scale is non-zero, it serves as the lower limit of the inertial zone and governs the diffraction ability of turbulence. As the inner scale becomes larger, the diffraction distortion caused by the small vortices is weakened. In addition, both in the x-direction and in the y-direction, a spherical wave has a lower scintillation index when propagates in higher anisotropic oceanic turbulence. Moreover, the scintillation index of the beam propagating in anisotropic turbulence is always lower than its propagation in isotropic turbulence (${\mu }_x$ = ${\mu }_y$ = 1). This phenomenon is because anisotropy changes the focusing properties of oceanic turbulence. Anisotropic turbulence vortices act as lenses with a longer radius of curvature than isotropic turbulence vortices. The higher the anisotropy, the longer the radius of curvature, resulting in reduced amplitude fluctuations and thus lower scintillation index.

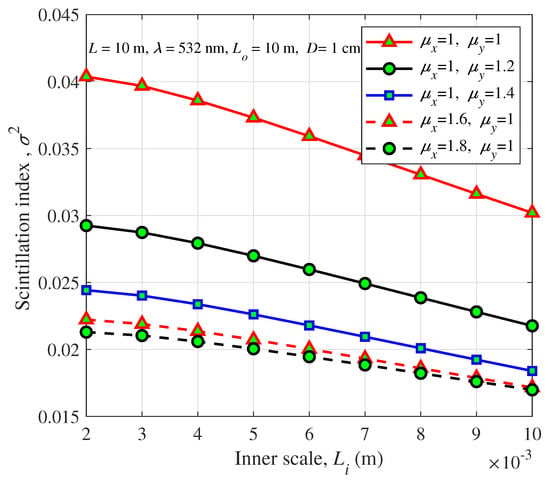
Figure 4. Scintillation index of a spherical wave versus the inner scale for different anisotropic factors.

Figure 4. Scintillation index of a spherical wave versus the inner scale for different anisotropic factors.

The impact of the aperture diameter and optical wavelength on the scintillation index as a function of the inner scale is also demonstrated in Figure 5 and Figure 6, respectively. Obviously, the scintillation index decreases along with the increase of the aperture diameter and wavelength, which further confirms our simulations in Figure 2 and Figure 3. Note that the decreasing trend of scintillation index under different wavelengths is valid for a smaller value of the inner scale. However, this trend slows down when the inner scale is more prominent, since a coherence length change is mitigated.

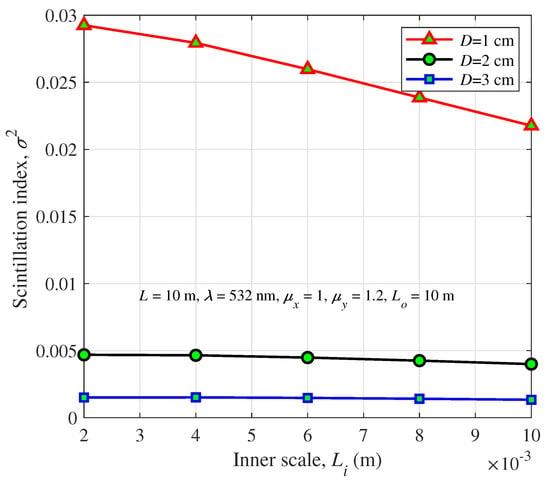
Figure 5. Scintillation index of a spherical wave versus the inner scale for different aperture diameters.

Figure 5. Scintillation index of a spherical wave versus the inner scale for different aperture diameters.

Figure 6. Scintillation index of a spherical wave versus the inner scale for different wavelengths.

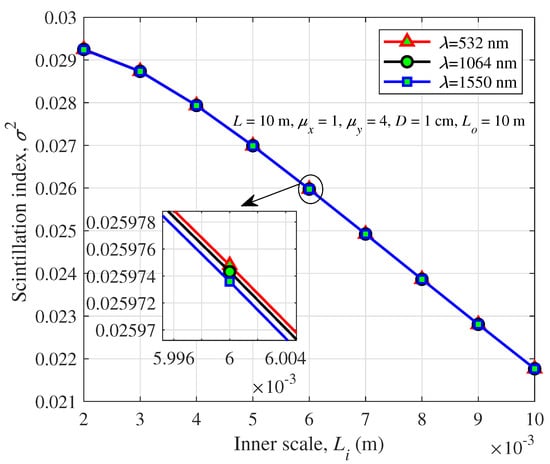
Figure 6. Scintillation index of a spherical wave versus the inner scale for different wavelengths.

Increasing the aperture parameter significantly reduce the scintillation index shown in Figure 5. Moreover, the beam of smaller wavelength has better performance, as is shown in Figure 6. The above two figures are all conducted under anisotropic turbulence. To further consider the aperture averaging effect under isotropic turbulence (${\mu }_x$ = ${\mu }_y$ = 1), we studied the scintillation index after changing the aperture diameters under isotropic conditions, as shown in Figure 7. It is observed that the scintillation index under anisotropic oceanic turbulence is much smaller than that under isotropic turbulence, which is consistent with Figure 1 and Figure 4. With the increase of the aperture diameters, the scintillation index of the beam propagating in isotropic decreases gradually and approaches that in anisotropic turbulence. In Figure 7, when aperture diameter D = 1 cm, the scintillation index at ${\mu }_x$ = 1, ${\mu }_y$ = 2 is lower than the scintillation index in isotropic. When the aperture diameter is 1.29 cm, the two curves almost coincide. Therefore, we can reduce the scintillation index by changing the aperture size in isotropic oceanic turbulence.

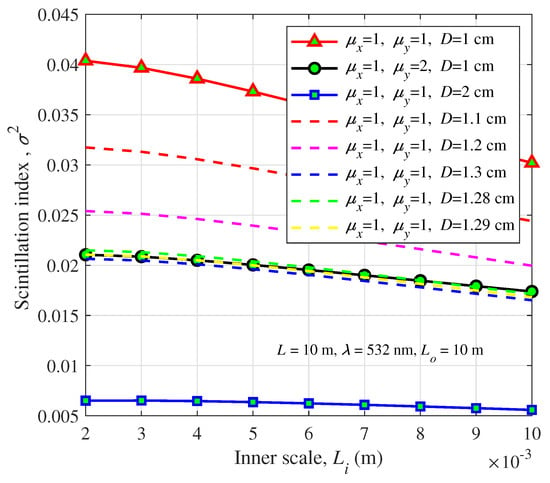
Figure 7. Scintillation index of a spherical wave versus the inner scale under isotropic turbulence for different aperture diameters.

Figure 7. Scintillation index of a spherical wave versus the inner scale under isotropic turbulence for different aperture diameters.

The influence of the aperture averaging effect and anisotropic turbulence on the scintillation index is presented in Figure 8. Note that with or without aperture averaging in Figure 8 means whether the aperture averaging effect is used in the UWOC system or not. Obviously, the scintillation index decreases more sharply with the aperture averaging effect than that without the aperture averaging effect. This phenomenon is apparent when the inner scale is small. Furthermore, for a fixed value of ${\mu }_x$ or ${\mu }_y$, the anisotropic turbulence factor in the y or x axis contributes to the decrease of the scintillation index. The detailed variation of the scintillation index under various anisotropic turbulence factors with the aperture averaging effect is also given in the embedded subfigure, which further confirms our conclusions in Figure 4 and Figure 5.

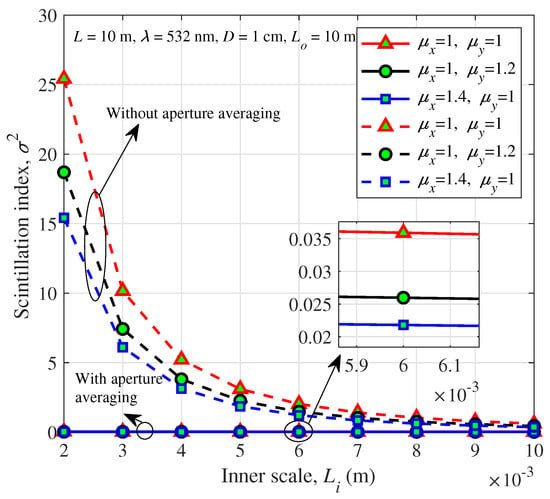
Figure 8. Scintillation index of a spherical wave versus the inner scale with and without the aperture averaging effect for different anisotropic factors.

Figure 8. Scintillation index of a spherical wave versus the inner scale with and without the aperture averaging effect for different anisotropic factors.

Figure 9 demonstrates the effect of aperture diameter on the scintillation index under different anisotropic factors. The scintillation index decreases with increasing ${\mu }_x$ or ${\mu }_y$. In addition, the scintillation index decreases gradually as the aperture diameter increases, which is similar to Figure 8. Note that the scintillation index tends to be consistent when the aperture diameter is larger enough.

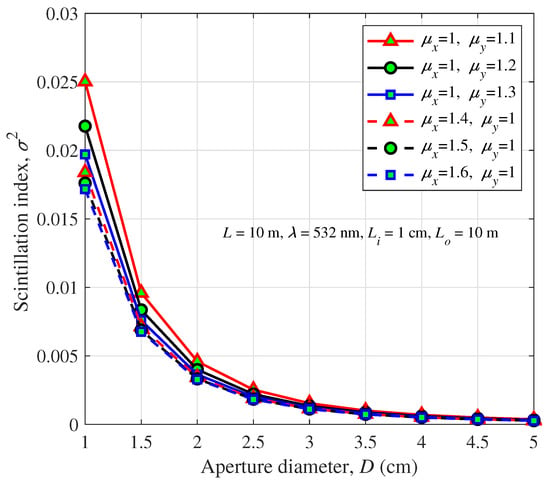
Figure 9. Scintillation index of a spherical wave versus the receiver aperture diameter for different anisotropic factors.

Figure 9. Scintillation index of a spherical wave versus the receiver aperture diameter for different anisotropic factors.

Figure 10 depicts the influence of the inner scale $L_i$ and outer scale $L_o$ as a function of propagation distance L in anisotropic ocean turbulence. As shown in Figure 10, the scintillation index increases with increasing propagation distance, since the intensity fluctuations of the beam propagation in weak anisotropic turbulence increase and become increasingly more unstable. It can be seen from Figure 10 that there is a minimal effect of the outer scale on the scintillation index for a fixed inner scale when the propagation distance is considerable. However, there is a contrary trend for the inner scale, i.e., a larger inner scale leads to a smaller scintillation index. This phenomenon can be explained from a physical point of view: the outer scale of turbulence is much larger than the spot radius of the beam. The outer scale is a relatively uniform and stable medium for small beams. The inner scale of turbulence is smaller, and the change of the inner scale of turbulence per unit area is larger. Therefore, we conclude that the inner scale of the oceanic turbulence plays a more significant role than the outer scale in affecting the scintillation index in weak turbulent conditions.

Figure 10. Scintillation index of a spherical wave versus the propagation distance for different inner and outer scales.

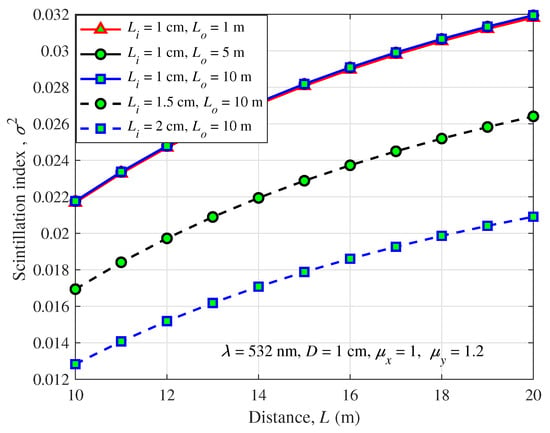
Figure 10. Scintillation index of a spherical wave versus the propagation distance for different inner and outer scales.

The effect of both inner and outer scales on the scintillation index is shown in Figure 11. It can be seen from this figure that in the case of weak turbulence, the outer scale has little effect on the scintillation index compared to the inner scale, which is similar to the previous conclusions [35,50].

Figure 11. Scintillation index of a spherical wave versus the inner and outer scales.

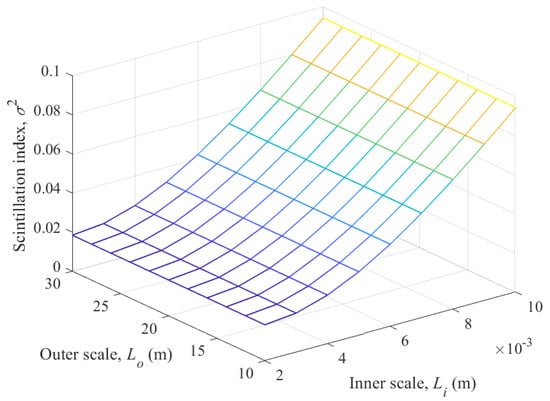
Figure 11. Scintillation index of a spherical wave versus the inner and outer scales.

The turbulence structure parameter is an influencing factor that affects the intensity of turbulence. Figure 12 analyzes the influence of the turbulence structure parameters, $C_n^2$, on the scintillation index with aperture averaging of a spherical wave in the marine environment. The results show that the scintillation index increases with the increase of $C_n^2$. This phenomenon is more obvious with the increase of the communication distance.

Figure 12. Scintillation index of a spherical wave versus the propagation distance for different structure parameters.

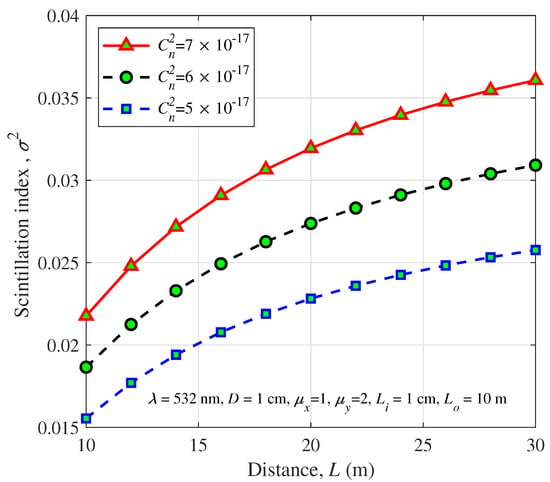
Figure 12. Scintillation index of a spherical wave versus the propagation distance for different structure parameters.

5. Conclusions

This study adopted a spatial power spectrum model that considers both the inner and outer scales. The scintillation index of a spherical wave propagating in weak anisotropic ocean turbulence was derived. Simulation results show that the inner scale, outer scale, aperture diameter, optical wavelength and propagation distance significantly influence the scintillation index under weak anisotropic turbulence. More specifically, the scintillation index decreases with increasing inner scale while increases subdued with the increase of the outer scale. For spherical waves, the effect of the inner scale on the scintillation index is obvious, while the effect of the outer scale on it can be negligible. In addition, anisotropic oceanic turbulence is helpful for spherical waves propagating in the ocean. Moreover, we further reveal that increasing the aperture diameter and optical wavelength is an alternative method of improving the performance of UWOC systems in oceanic turbulence. The presented results can be beneficial in designing optical wireless communication systems for ocean environments.