Abstract
Recently, atmospheric-turbulence-induced fading in free-space optical (FSO) communication with pointing error impairment was modeled and studied using the Fisher–Snedecor distribution with a good fit to experimental data. In this letter, we investigate the end-to-end performance of dual-hop FSO fixed-gain relaying systems operating over turbulence channels. More specifically, we present closed-form expressions for the cumulative distribution function and the probability density function of the end-to-end signal-to-noise (SNR) ratio of the proposed system. Consequently, the outage probability, ergodic capacity, and average bit error rate performance are derived with tight asymptotic results in high-SNR regimes to gain more insight into the impacts of system parameters and channel turbulence conditions. Finally, Monte Carlo simulations are provided to validate the analytical results, revealing a significant performance gain compared to a single FSO link in the medium- to high-SNR range by using dual-hop FSO relaying.
1. Introduction
Free-space optical (FSO) communication systems with high achievable data rates have gained considerable attention as a promising candidate for transmission techniques in the next generation of wireless communication systems. Moreover, they utilize a large bandwidth spectrum at a low cost with a better level of security than the unlicensed optical spectrum [1]. Despite the aforementioned advantages, FSO communication requires beam paths throughout the environment, and the optical beams used in transmission are significantly impacted by various atmospheric turbulence conditions [2].
Numerous irradiance models have been proposed in the literature with different mathematical representations. More specifically, some well-known distributions that characterize atmospheric turbulence are gamma-gamma (GG) [3,4], log-normal [1], and Málaga [5]. The log-normal distribution fits experimental data well under conditions of low irradiance fluctuations. In contrast, under a wide range of turbulence conditions, the GG turbulence model fits experimental data exceptionally well, making it the most commonly used model for the FSO channel. Recently, the authors of [6] proposed a new model using the Fisher–Snedecor , which provides a good fit to characterize the atmospheric turbulence over FSO links while also requiring simpler mathematical representations than for GG. Consequently, the performance of an FSO communication system operating over turbulence with pointing error was investigated in [7]. More specifically, the results in [6] showed that, when compared to the well-known GG distribution [8], the recently proposed distribution always provides at least the same or even a better fit to experimental results. The same conclusion was mentioned when considering the pointing error in the model [7].
On the other hand, FSO provides high data rates only for short-range communication. In long-range transmission, the performance is significantly degraded by the effects of atmospheric-turbulence-induced fading, fog attenuation, and pointing errors, which lead to frequent link outages. To address various turbulence issues with other limitations of long-range communication, relaying techniques have been employed as an efficient alternative. Various relaying-assisted systems have proposed integrating FSO into outdoor and indoor broadcasting systems. A mixed FSO–radio-frequency relaying system was considered in [3] with the GG turbulence channel and Rayleigh fading RF channel. In [9], the authors presented a comprehensive outage performance analysis of a mixed RF–FSO communication system, where the RF link was distributed over the Nakagami-m channel, while the FSO link followed GG turbulence. Additionally, the performance of a cooperative power-line communication–FSO communication system was analyzed in terms of the outage probability and average bit error rate (BER) in [10]. However, dual-hop FSO systems have attracted little attention in the literature when considering the impact of the distribution, which is the primary purpose of this letter.
In this letter, with the great modeling performance and low computational cost of the distribution, we extend previous studies on cooperative communication by considering the statistical model for the FSO link and presenting an exact closed-form analysis of the end-to-end performance of dual-hop FSO systems. Although the proposed system enables optical wireless connectivity to reach remote areas via the open nature of optical wireless communication, the use of amplify-and-forward (AF) relays complicates the expression of the end-to-end signal-to-noise ratio (SNR) and requires the manipulation of special mathematical functions. More precisely, we present an analytical framework that takes into account the impacts of both pointing errors and various types of turbulence to analyze the performance of the proposed systems with both heterodyne detection (HD) and intensity modulation/direct detection (IM/DD) techniques. More specifically, the probability density function (PDF) and cumulative distribution function (CDF) of the proposed system’s end-to-end SNR are derived. As a consequence, the statistical characterization of the SNR is then used to develop tractable closed-form expressions for the outage probability (OP), ergodic capacity (EC), and average bit error rate (BER). Additionally, we provide asymptotic expressions for the achievable diversity gain to obtain important insights into the impacts of system parameters. The results show that the analytical derivation is completely consistent with the Monte Carlo simulations, demonstrating its advantages under various channel conditions.
2. Proposed System Model
In Figure 1, we consider a cooperative transmission from a source node (S) to a destination node (D) via a relay node (R) that amplifies the received signal using AF relaying and retransmits the data to the final destination. Let be the SNR of the first FSO hop from S to R, while denotes the signal-to-noise ratio (SNR) of the second FSO hop from R to D. Then, the end-to-end SNR can be given as , where C is a fixed relay gain. Moreover, both links are assumed to follow turbulence, where the channel gain for the i-th link is modeled as , where , , and are the deterministic propagation loss, atmospheric turbulence attenuation, and pointing error attenuation, respectively. More precisely, the PDF of the irradiance [6] can be represented as
where and are two key factors affecting the optical propagation parameters of the i-th link, such as the atmospheric refractive-index structure parameter, propagation path length, and inner and outer scales of turbulence. Then, and [6] can be expressed as
where and are the small-scale and large-scale log-irradiance variances, respectively. More specifically, the small-scale log-irradiance variance [6], , can be expressed as
where is the spherical wave scintillation index [11], is the equivalent aperture diameter, and represents the strength of irradiance fluctuations, such as turbulence. Moreover, the large-scale log-irradiance variance [6], , can be expressed as
where and denote the large-scale log irradiance variances that consider inner-scale and outer-scale effects, respectively. In addition, the PDF of the pointing error impairment [7] is
where represents the fraction of the received power. Here, , where and are the beam-width and the pointing error displacement standard deviation, respectively.
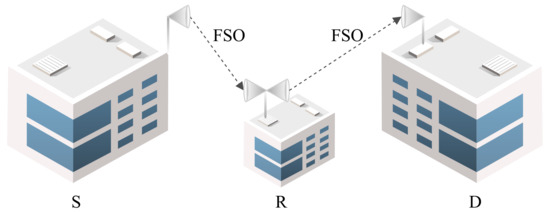
Figure 1.
System model.
3. Statistics of the SNR of an Equivalent End-to-End Communication Link
3.1. CDF of the End-to-End SNR
From Equation (12) in [7] and the definition of the Fox-H function in Equation (1.1) in [12], the PDF of the received SNRs for both detection techniques can be expressed by
where , , and denotes the Fox-H function. Here, represents HD and represents IM/DD. Furthermore, is the average electrical SNR of the i-th link, which can be defined as for . For , , where the average SNR is and is the expectation operator. Moreover, by integrating (6), the CDF of SNR of the i-th FSO link can be expressed by
For the proposed AF relaying dual-hop system, the CDF of the end-to-end SNR, , can be calculated as
By using the definition of the univariate Fox-H function Equation (1.1) in [12], we can write the integral in (8) as
where and represent the -plane and -plane contours, respectively. Moreover, by integrating , changing the integral variable , utilizing Equation (A.1) in [12], and performing some manipulations, we can obtain the CDF of the end-to-end SNR, , as
where , ,
, , , and is the bivariate Fox-H function [12].
3.2. PDF of the End-to-End SNR
The closed-form analytic expression of the PDF of the end-to-end SNR can be derived by differentiating (6) with respect to . Using Equation (1.69) in [12], can be given as
where .
3.3. Asymptotic Analysis
Assuming and applying the same method as in Section IV in [13], the asymptotic CDF is derived as
where and . By applying Equation (1.5.9) in [14] to (12) and using elementary functions, the OP in the asymptotic regime can be expressed as
where for are constants that can be easily obtained from Equation (1.5.10) in [14]. Consequently, when goes to infinity, the diversity order can be expressed as
Remark 1.
We can observe from (14) that the diversity order is a function of the FSO turbulence parameters , pointing error , and detection mode , but not the turbulence parameter . This is consistent with the conclusion for the single link in [7].
4. Performance Analysis
4.1. Outage Probability Analysis
The OP is related to the probability that the end-to-end SNR is below a specified threshold value [15]. For the proposed system with AF relaying, an exact closed-form analytic expression for the OP can be given as
4.2. Ergodic Capacity Analysis
The EC is defined as , where for and for . More specifically, the EC can be expressed in terms of by using integration by parts as follows:
4.3. Bit Error Rate Analysis
For various binary and non-binary modulation schemes, the expression of the average BER can be given as
where , and are used to denote the parameters for different modulation schemes [7]. Specifically, for binary phase-shift keying (BPSK), we have and , while for on–off keying (OOK), and , and for M-ary pulse position modulation, and . By substituting (7) into (19) and using Equation (3.381/4) in [16], Equation (1.1) in [12], the average BER of the proposed system can be derived as
Replacing (10) into (19) and employing Equation (3.381/4) in [16], Equation (A.1) in [12], after some algebraic manipulations, we have
where . Similarly to (13), the asymptotic BER can be formulated as
where are constants that can be obtained from Equation (1.5.10) in [14]. Moreover, the diversity order from (22) is still , agreeing with the results in (14) obtained using the CDF derivation.
5. Simulation Results
The numerical results from Monte Carlo simulations are presented in this section to demonstrate the correctness of the analytical derivations and provide insights into how various link parameters affect the performance. All parameters of FSO links utilized here are obtained from [7]; the FSO link distance is 3500 m, and the wavelength is nm. The parameters a and b for various turbulence conditions can be obtained using (2–4), as in [7]. More specifically, we consider three sets of the FSO link, , , and , which correspond to the weak, medium, and strong turbulence conditions, respectively. Additionally, unless otherwise specified, the average SNRs of the two hops are equal in all circumstances (i.e., ).
Figure 2 shows the OP versus for both and under weak, moderate, and strong turbulence conditions to illustrate the consistency between the simulation and analytical results. As can be observed, the OP of the proposed system is higher when the IM/DD is used instead of HD. Additionally, increasing the turbulence degree results in higher OP.
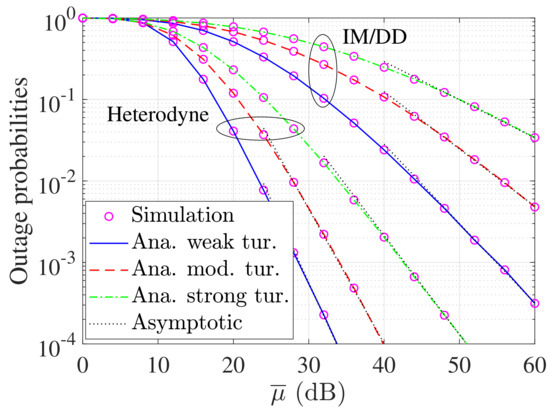
Figure 2.
OP versus with different turbulence conditions.
Figure 3 shows the OP performance of the dual-hop and single-link scenarios where the single link is split into two equal-distance links. As can be seen, due to the minimized pointing error impairments, using dual-hop FSO transmission links can greatly enhance system performance compared to a single FSO link in the medium- to high-SNR range.
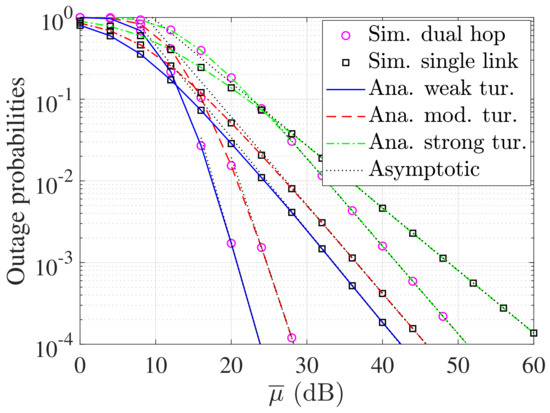
Figure 3.
OP versus for single FSO and dual-hop FSO links.
Figure 4 illustrates the performance of the proposed system with HD under moderate turbulence conditions for the pointing error conditions of , , and , which are 1.1, 1.8, and 4.4. Additionally, the average SNR of the first hop is fixed at two different values of 20 and 36 dB. As expected, the OP performance improves when increases. Furthermore, the OP performance at low dB can be observed differently in two SNR regimes. When is lower than 30 dB, the OP decreases as the SNR increases. In contrast, an error floor occurs when dB, since the first link becomes dominant in this SNR regime.
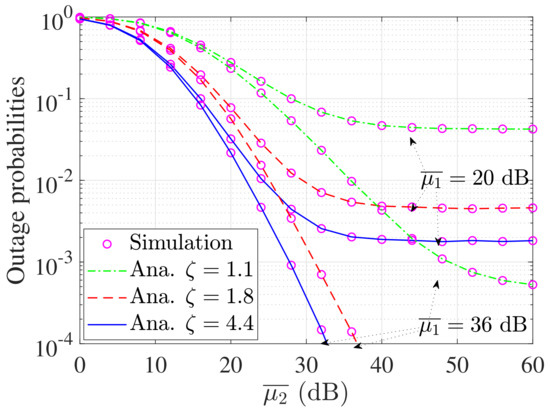
Figure 4.
OP versus for fixed values of .
Figure 5 shows the EC performance for both detection modes in the cases of low, moderate, and high turbulence. As can be seen, strong turbulence conditions result in a lower EC value than those obtained under moderate and and weak turbulence conditions. In addition, the HD outperforms the IM/DD under the same channel conditions, and the degree of performance degradation under different channel conditions with the IM/DD is more distinguishable than for the HD.
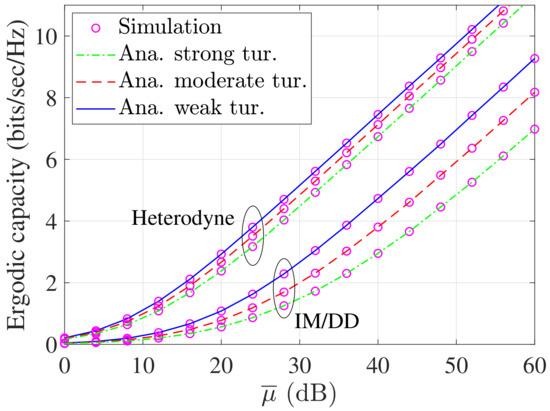
Figure 5.
EC versus with different turbulence conditions.
The BER of the proposed system is given in Figure 6 with different turbulence conditions and two modulation schemes OOK and BPSK. Similarly to the OP and EC performances, various atmospheric turbulences affect the BER performance significantly. It is also clear that the system with BPSK modulation can maintain a better performance than the OOK modulation.
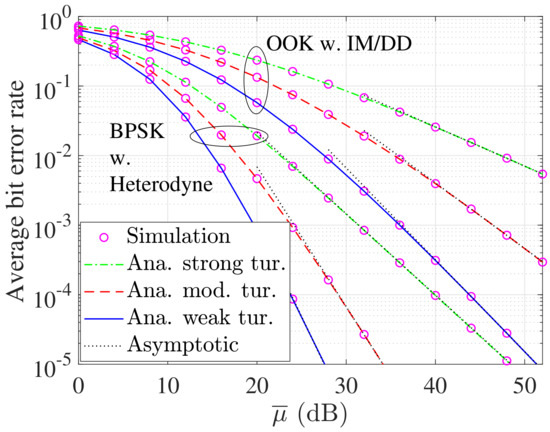
Figure 6.
Average BER versus with different turbulence conditions.
Finally, Figure 7 shows a Monte Carlo simulation of the BER performance of the proposed system under both and GG turbulence distributions with the impact of pointing errors. More specifically, we set and for the case of turbulence, while and for the case of GG turbulence for a fair comparison [6]. In addition, the varying pointing error level is set, with the values of z being 1.1, 1.8, and 4.4 when and are the same and the value is z. As can be seen, the performance of the proposed system with both distributions are the same, which means that the system performance is independent of the turbulence channel models. Moreover, as the pointing error level increases, the BER performance is degraded, as expected.
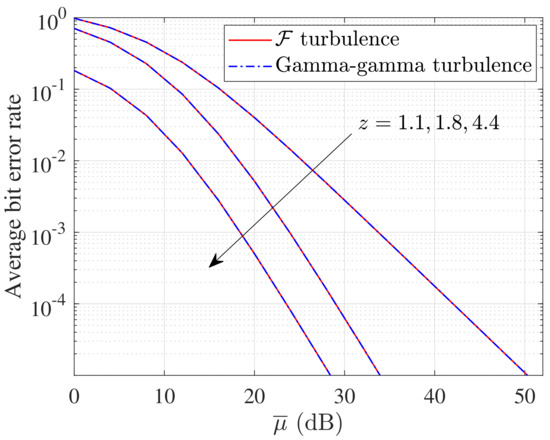
Figure 7.
Average BER versus of and GG turbulence channel models under varying effects of pointing errors.
6. Conclusions
In this letter, we analyze the OP performance, EC, and average BER of a dual-hop FSO transmission system with fixed-gain AF relay over turbulence. Additionally, we present a tight asymptotic derivation in terms of elementary functions to obtain additional insights into the performance of the proposed system at high SNR. As a result, the simulation results match with the analytical ones for various SNR ranges. Consequently, when the effects of the pointing error and turbulence decrease, the performance can be significantly improved. Moreover, the diversity order is impacted by the pointing error parameter z and one turbulence parameter a, but not by b. The results also reveal that the Monte Carlo simulation of the analysis results is independent of the channel model for a dual-hop system when the parameters of the model are properly determined.
Author Contributions
All authors discussed the contents of the manuscript and contributed to its presentation. M.L.-T. designed and implemented the proposed scheme, analyzed the simulation results, and wrote the paper under the supervision of S.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Research Program through the National Research Foundation of Korea (NRF-2019R1A2C1005920).
Institutional Review Board Statement
The study did not involve humans or animal studies.
Informed Consent Statement
The study did not involve humans or animal studies.
Data Availability Statement
The study did not report any data.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AWGN | Additive white Gaussian noise |
| FSO | Free-space optical |
| CDF | Cumulative distribution function |
| OOK | On–off keying |
| Probability density function | |
| SNR | Signal-to-noise ratio |
| AF | Amplify-and-forward |
| BPSK | Binary phase-shift keying |
| QPSK | Quadrature phase-shift keying |
| BER | Bit error rate |
References
- Ghassemlooy, Z.; Popoola, W.; Rajbhandari, S. Optical Wireless Communications: System and Channel Modelling with MATLAB, 2nd ed.; CRC Press/Taylor & Francis Group: Boca Raton, FL, USA, 2018. [Google Scholar]
- Gupta, A.; Sharma, N.; Garg, P.; Alouini, M. Cascaded FSO-VLC Communication System. IEEE Wirel. Commun. Lett. 2017, 6, 810–813. [Google Scholar] [CrossRef] [Green Version]
- Ansari, I.S.; Yilmaz, F.; Alouini, M. Impact of Pointing Errors on the Performance of Mixed RF/FSO Dual-Hop Transmission Systems. IEEE Wirel. Commun. Lett. 2013, 2, 351–354. [Google Scholar] [CrossRef] [Green Version]
- Le-Tran, M.; Vu, T.H.; Kim, S. Performance Analysis of Optical Backhauled Cooperative Noma Visible Light Communication. IEEE Trans. Veh. Technol. 2021, 70, 12932–12945. [Google Scholar] [CrossRef]
- Ansari, I.S.; Yilmaz, F.; Alouini, M. Performance Analysis of Free-Space Optical Links over Málaga (M) Turbulence Channels with Pointing Errors. IEEE Trans. Wirel. Commun. 2016, 15, 91–102. [Google Scholar] [CrossRef] [Green Version]
- Peppas, K.P.; Alexandropoulos, G.C.; Xenos, E.D.; Maras, A. The Fischer–Snedecor F-Distribution Model for Turbulence-Induced Fading in Free-Space Optical Systems. J. Light. Technol. 2020, 38, 1286–1295. [Google Scholar] [CrossRef]
- Badarneh, O.S.; Derbas, R.; Almehmadi, F.S.; Bouanani, F.E.; Muhaidat, S. Performance Analysis of FSO Communications over F Turbulence Channels with Pointing Errors. IEEE Commun. Lett. 2021, 25, 926–930. [Google Scholar] [CrossRef]
- Sharda, P.; Jaiswal, A.; Bhatnagar, M.R.; Garg, A.; Song, L. Clustering Based Diversity Improving Transmit Laser Selection Schemes Using Quantized Feedback for FSO System. IEEE Trans. Veh. Technol. 2021, 70, 6855–6868. [Google Scholar] [CrossRef]
- Ashrafzadeh, B.; Soleimani-Nasab, E.; Zaimbashi, A.; Uysal, M. Outage Performance of Mixed RF-FSO Systems over DGG and Nakagami-m Channels. IEEE Wirel. Commun. Lett. 2020, 4, 245–249. [Google Scholar] [CrossRef]
- Le-Tran, M.; Kim, S. Performance Analysis of Dual-Hop Mixed Power Line Communication/Free-Space Optical Cooperative Systems. Photonics 2021, 8, 230. [Google Scholar] [CrossRef]
- Cheng, M.; Guo, Y.; Li, J.; Zheng, X.; Guo, L. Inverse Gaussian Gamma Distribution Model for Turbulence-Induced Fading in Free-Space Optical Communication. Appl. Opt. 2018, 57, 3031–3037. [Google Scholar] [CrossRef] [PubMed]
- Mathai, A.M.; Saxena, R.K.; Haubold, H.J. The H-Function: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Chergui, H.; Benjillali, M.; Saoudi, S. Performance Analysis of Project-and-Forward Relaying in Mixed MIMO-Pinhole and Rayleigh Dual-Hop Channel. IEEE Commun. Lett. 2016, 20, 610–613. [Google Scholar] [CrossRef] [Green Version]
- Saigō, M.; Kilbas, A.A. H-Transforms: Theory and Applications; Analytical Methods and Special Functions; Chapman & Hall/CRC: Boca Raton, FL, USA, 2004. [Google Scholar]
- Peppas, K.P.; Mansour, A.; Tombras, G.S. Dual-Hop Transmissions with Fixed-Gain Relays over Generalized-Gamma Fading Channels. arXiv 2010, arXiv:1003.1910. [Google Scholar]
- Gradshteĭn, I.S.; Zwillinger, D. Table of Integrals, Series, and Products, 8th ed.; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).