Abstract
External environment disturbances in open space cause scintillation noise in tunable diode laser absorption spectroscopy (TDLAS), which is used to detect the concentration of gases in air. However, most gases analyzed by TDLAS are present in trace amounts in air. Thus, useful information is typically submerged in strong noise, thereby reducing the detection accuracy. Herein, a method is proposed to eliminate the scintillation noise caused by external environment disturbances in open space. First, the submerged signal is detected via fast coarse-tuning filtering. Then, scintillation noise is eliminated through the extraction and reconstruction of the main feature information. Thereafter, the background signal is obtained by unequal precision. Furthermore, adaptive iterative fitting is performed. Finally, an experimental setup is established for atmospheric detection in an open optical path. The experimental results show that the COD and RSS fitted using the traditional method are 0.87859 and 1.5772 × 10−5, respectively, and those fitted using the proposed method are 0.91448 and 8.81639 × 10−6, respectively. The field results imply that the proposed method has improved accuracy for detecting trace gases in open space and can be employed for practical engineering applications.
1. Introduction
Tunable diode laser absorption spectroscopy (TDLAS) [1,2,3,4,5,6] has the advantages of a high spectral resolution, sensitivity, and selectivity. Thus, it is an effective method for the rapid analysis of gas concentrations in air. However, external environment disturbances in open space cause scintillation noise in TDLAS. External environment disturbances include weather effects [7,8], dust particle scattering, atmospheric turbulence [9,10,11], and atmospheric scintillation [12]. Typically, the gases analyzed by TDLAS are present in trace amounts in air. Thus, external environment disturbances may cause useful information to be submerged in strong noise and thus inaccurate detection of the concentration of gases in the air. Therefore, the effective extraction of useful information regarding spectral absorption is necessary for ensuring accurate detection.
Digital filtering [13] is a convenient and flexible method as it does not require additional hardware, components, or detection steps. Based on wavelet denoising (WD), which is a digital filtering technique that effectively suppresses noise, a novel WD-assisted wavelength modulation technique was proposed [14]. In addition, to improve the signal-to-noise ratio (SNR) of TDLAS detection systems, a Gabor transform-based denoising method was proposed [15] for second harmonic signal noise reduction. Furthermore, to suppress the scintillation noise in the detection systems, a WD method was used to perform experiments with different parameters [16]. An adaptive Savitzky−Golay (S-G) filtering algorithm with a χ2 statistical criterion for the LITES technique was introduced [17].
Several studies, including the ones mentioned above, have utilized the time domain angle to analyze and apply digital filtering methods. Furthermore, signal processing in most studies has been performed using second harmonic signals [18], which have high SNRs, and their processing is complex and time-consuming when applied to open optical path for demodulation. In contrast, the SNR afforded by the direct absorption method is low; however, the method is simple because it does not require modulation and demodulation. In order to eliminate scintillation noise caused by external environment disturbances in open space, simple methods without increasing hardware need to be investigated.
In this paper, a method is proposed for eliminating the scintillation noise caused by external environment disturbances in open space. An experimental setup is established for atmospheric detection in an open optical path. The effectiveness and applicability of the proposed method are verified experimentally.
2. Measurement Principle
According to Beer-Lambert’s law:
where I0 is the incident light intensity, I is the transmitted light intensity, S* is the absorption line strength, Φ is the normalized line shape function, P is the pressure, c is the component concentration of the absorbed gas, and L is the optical path length, and so:
where A is the integral absorbance.
3. Method for Eliminating Scintillation Noise Caused by External Environment Disturbances
The reference optical path signal y(m) is defined as follows:
where c(m) is the “pure signal” and n(m) is random noise.
The detection optical path signal d(m) is expressed as follows:
where d(m) is the “target signal” used for detecting the optical path signal, n’(m) is random noise, and ru(m) denotes various disturbance signals (assuming U).
Through fast coarse-tuning filtering, the signal submerged in the noise can be detected. First, the frequency spectrum of d(m) is obtained quickly. According to the previous cycle signal, N points (number of samples in a time period) are used as a window. The FFT [19] of d(m) is quickly calculated using the sliding FFT algorithm.
where Dk(n) represents the N-point FFT of the signal in the current cycle; i represents the starting position of the window; and Dk+1(n) represents the signal in the next cycle, whose FFT can be quickly obtained using the difference between the values.
By passing d(m) through a filter w(m), then Dk(n) becomes:
After IFFT:
d′(m) is made up of the target signal and the interference signal . Assuming that the spectra of the target signal and the interference signal do not overlap, the bandwidth w(m) of the filter is adjusted. Finally, the d’(m) signal that mainly contains the target signal is obtained.
The d’(m) signal still contains a significant amount of noise and thus requires further processing, which is performed by constructing a matrix H with d’(m).
The matrix H can be expressed as follows:
where q = N − i + 1, Uq×i and Vi×i are orthogonal matrices, respectively, and Λ is a diagonal matrix.
The eigenvalues lie on the main diagonal, and the main eigenvalues can be quickly selected. Then, the matrix is reconstructed to obtain a signal d’(m).
According to the absorption position of the reference optical path signal y(m), the line is locked, and a signal without an absorption region is selected for two-step fitting. The background signal is obtained through unequal precision. Then, adaptive iterative fitting is performed and y(m) is processed. The concentration is detected by inversion.
4. Experimental Setup for Atmospheric Detection in Open Optical Path
The experimental setup is shown in Figure 1. Methane gas [20,21,22] is considered as the target gas. A methane laser with a central wavelength of 1653 nm (model: NLK1U5EAAA, NTT Corp., Tokyo, Japan) is employed as the light source. According to the input signal of the signal generator, the laser controller modulates the output wavelength of the laser. The laser control module and the function generator are separately developed in the laboratory. The signal generator generates a sawtooth signal with a frequency of 170 Hz and a duty ratio of 90% to scan the selected absorption line. The laser beam is split into two beams: a reference beam and a detection beam. The reference beam is collimated using collimator 1 and is passed through a 20 cm standard cell with 5% concentration and is focused on a photodetector. The detection beam is collimated by collimator 2, is emitted through the telescope, and is reflected along the same path by a corner reflector. The reflected beam is then focused on the photodetector in the telescope through a Fresnel lens. The signals are applied as inputs to the signal processing and acquisition module for the analysis and inversion.
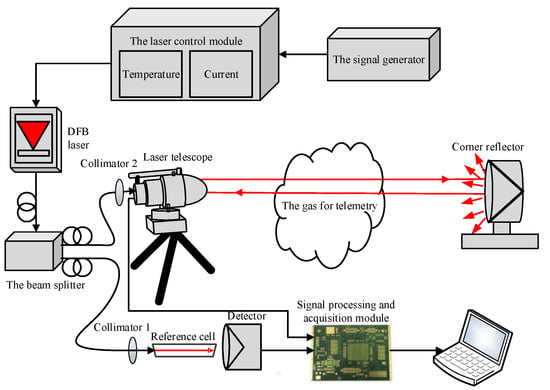
Figure 1.
System construction.
5. Results
The experiment was conducted using the established experimental setup. Before spectral data processing, the signals of the reference and detection optical path were collected simultaneously, as shown in Figure 2. As can be seen from Figure 2b, it is a continuously measured 14-cycle detection signal. In open space detection, the signal of the detection optical path was submerged in noise caused by external environment disturbances, which caused the wavefront distortion of the signal.
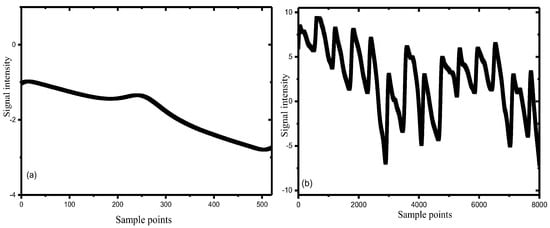
Figure 2.
Spectral signals. (a) Signal of the reference optical path, (b) Signal of the detection optical path (multiple periodic signals).
First, fast coarse-tuning filtering was used to coarse-tune the signal, as shown in Figure 3. It can be seen from the signal (black curve) that the absorption position was between approximately 150–300 sample points. However, the signal was greatly interfered by the external environment, so the position of the absorption signal could not be determined accurately. Apparently, the useful signal was effectively detected with a considerably high signal-to-noise ratio. After fast coarse-tuning filtering, the signal (red curve) could be used to quickly determine the approximate position of absorption at 180–250 sample points. The maximum residual was 0.02572; however, a significant amount of noise was present.
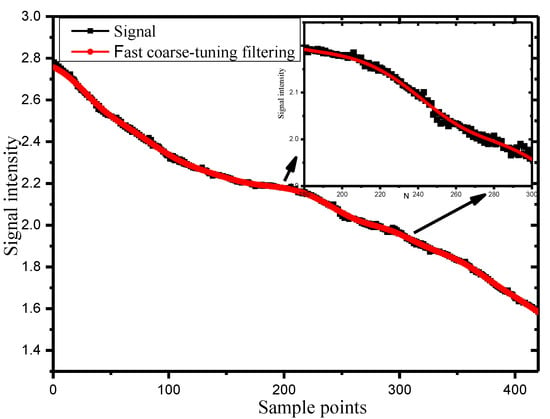
Figure 3.
Fast coarse-tuning filtering.
Figure 4 illustrates that scintillation noise caused by external environment disturbances could be effectively eliminated through the extraction and reconstruction of the main feature information. Figure 4a shows the signals before and after the extraction and reconstruction of the main feature information. The correlation coefficient between the signals before (red curve) and after (blue curve) processing was 0.999. Note that after the extraction and reconstruction of the main feature information, the useful signals submerged in the noise could be effectively extracted. Figure 4b shows the residuals, where the maximum residual and the sum of the residuals were 0.0128 and 0.125, respectively.
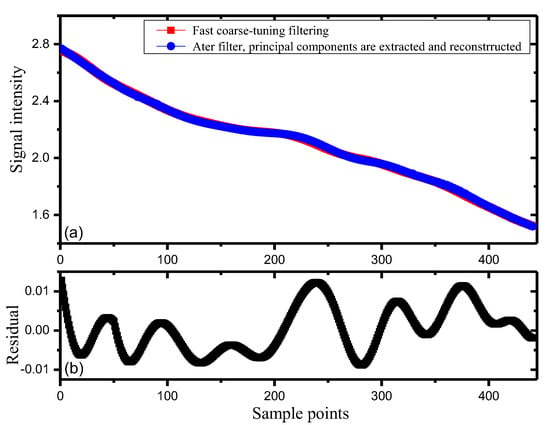
Figure 4.
Extraction and reconstruction of the main feature information. (a) Signals before and after the extraction and reconstruction of the main feature information; (b) Residual.
According to the absorption position of the reference optical path signal, the line was locked. The main feature information was extracted and the non-absorption part of the reconstructed signal was selected for two-step fitting. The background signal was obtained through unequal precision, as shown in Figure 5. Notably, the background signal obtained herein was more significant than that obtained via the traditional method [23,24]. Figure 5b shows that the maximum residual via the traditional method was 0.037, and the sum of the residuals was 0.0.88. The maximum residual and the sum of the residuals via the proposed method were 0.029 and −0.16, respectively.
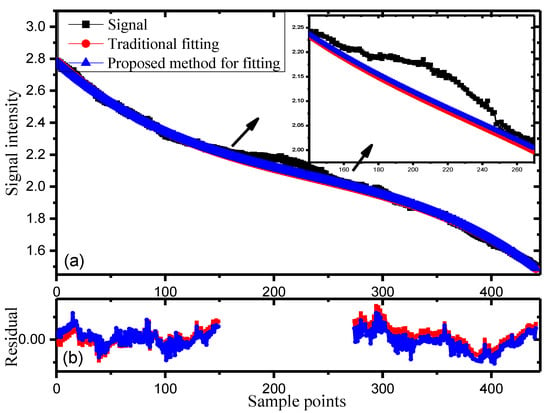
Figure 5.
Background signal fitting: (a) background signal fitting and (b) residual signals in the non-absorbed part.
The proposed method and the traditional method [25] were used to remove the background noise, as shown in Figure 6. Apparently, the proposed method (blue curve) significantly improved the signal quality after removing the background noise compared with the traditional method (red curve). In Figure 6, the red curve was obtained using the traditional method after background noise removal of the signal of the detection optical path. The blue curve shows the eliminated scintillation noise caused by the external environment disturbances and has a higher fitting degree.
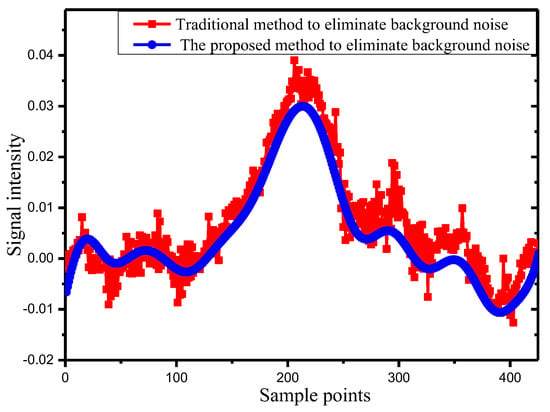
Figure 6.
Signal obtained after background noise removal.
Subsequently, adaptive iterative fitting was performed, and the obtained signal is shown in Figure 7. Figure 7a shows that R-Square (COD) and Reduced Chi-Sqr (RSS) fitted via the traditional method were 0.87859 and 1.5772 × 10−5, respectively. Figure 7b shows that COD and RSS fitted via the proposed method were 0.91448 and 8.81639 × 10−6, respectively.
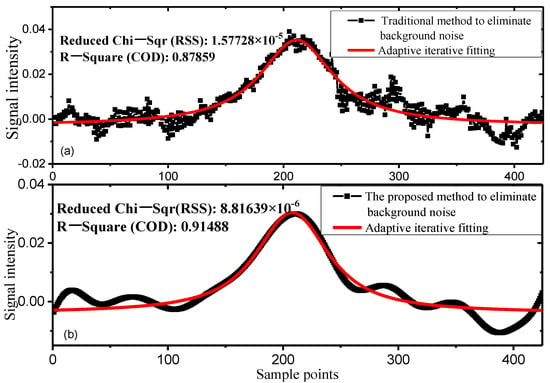
Figure 7.
Adaptive iterative fitting.
Finally, a practical application of the proposed method was demonstrated. CH4 emission from wheat in a farmland was recorded continuously for 72 h using the established experimental setup and L = 196 m. Two days before the experiment, it rained. The recorded values, as shown in Figure 8, indicated diurnal variations in CH4 emissions. Peak concentrations were observed within intervals of 9–13, 33–35, and 60–62 h for the duration of detection. Valley concentrations were observed approximately 24, 46, and 69 h after the start of the detection period. The daily average of the intervals for 0–24, 24–48, and 48–72 h were 2.716, 2.5521, and 2.432 ppm, respectively. For a period of time after the rain, the rain may have affected the emission of CH4. Therefore, the proposed method could be employed for practical engineering applications, such as detecting environmental gas in the hazard zone, monitoring agricultural and animal husbandry gas emissions, and detecting the leakage of natural gas pipelines.
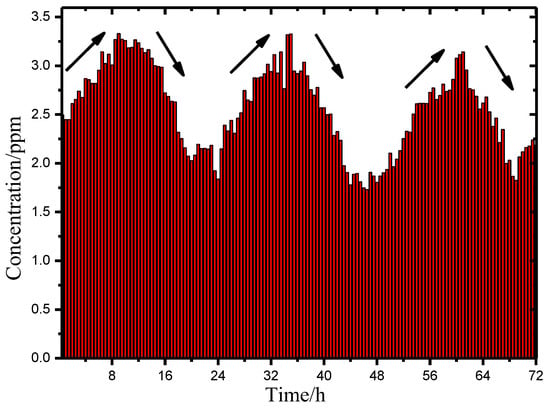
Figure 8.
Recorded values for the CH4 concentrations.
6. Conclusions
A method is proposed in this study for eliminating scintillation noise caused by external environment disturbances in open space. An experimental setup is established for open optical path atmospheric detection. The proposed method has the following features:
- Signals submerged in noise are detected via fast coarse-tuning filtering.
- Scintillation noise caused by external environment disturbances are eliminated through the extraction and reconstruction of the main feature information.
- Background signal is obtained via unequal precision, background noise is eliminated, and adaptive iterative fitting is performed. COD and RSS fitted via the traditional method are 0.87859 and 1.5772 × 10−5, respectively, and those fitted via the proposed method are 0.91448 and 8.81639 × 10−6, respectively.
- A field experiment is carried out, and diurnal variations in CH4 emissions are observed. The daily average for the intervals 0–24, 24–48, and 48–72 h are 2.716, 2.5521, and 2.432 ppm, respectively. For a period of time after rain, the rain may affect the emission of CH4. Thus, the accuracy of detection of trace gases in open space is improved using the proposed method.
- It is proven that there is a good engineering practical value in the proposed method, such as detecting environmental gas in the hazard zone, monitoring agricultural and animal husbandry gas emissions, and detecting leakage of the natural gas pipeline.
Author Contributions
Q.-X.T., methodology, data curation and formal analysis, and writing—original draft; H.G., formal analysis and supervision; Y.-J.Z., methodology and writing—review and editing; D.C., software and validation. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (52105539), the Anhui Natural Science Foundation (2108085QD179), the National Engineering Laboratory of Advanced Technology and Equipment for Atmospheric Pollution Monitoring (2005DP173065-2021-04), and the Natural Science Research for Universities in Anhui Province (KJ2020A0104).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interests.
References
- Wang, Z.; Fu, P.; Chao, X. Laser absorption sensing systems: Challenges, modeling, and design optimization. Appl. Sci. 2019, 9, 2723. [Google Scholar] [CrossRef] [Green Version]
- Deng, B.; Sima, C.; Xiao, Y.; Wang, X.; Ai, Y.; Li, T.; Lu, P.; Liu, D. Modified laser scanning technique in wavelength modulation spectroscopy for advanced TDLAS gas sensing. Opt. Lasers Eng. 2022, 151, 106906. [Google Scholar] [CrossRef]
- Ruxton, K.; Chakraborty, A.L.; Johnstone, W.; Lengden, M.; Stewart, G.; Duffin, K. Tunable diode laser spectroscopy with wavelength modulation: Elimination of residual amplitude modulation in a phasor decomposition approach. Sens. Actuators B Chem. 2010, 150, 367–375. [Google Scholar] [CrossRef]
- Xia, J.; Feng, C.; Zhu, F.; Ye, S.; Zhang, S.; Kolomenskii, A.; Wang, Q.; Dong, J.; Wang, Z.; Jin, W. A sensitive methane sensor of a ppt detection level using a mid-infrared interband cascade laser and a long-path multipass cell. Sens. Actuators B Chem. 2021, 334, 129641. [Google Scholar] [CrossRef]
- Yuan, W.; Zhang, D.; Lu, S.; Zhang, H.P.; Guan, Y. Fast-response concentration measurement of bromotrifluoromethane using a quantum cascade laser (QCL) at 8.280 μm. Opt. Express 2019, 27, 8838–8847. [Google Scholar] [CrossRef] [PubMed]
- Behera, A.; Wang, A. Calibration-free wavelength modulation spectroscopy: Symmetry approach and residual amplitude modulation normalization. Appl. Opt. 2016, 55, 4446–4455. [Google Scholar] [CrossRef]
- Craig, I.M.; Taubman, M.S.; Bernacki, B.E.; Stahl, R.D.; Schiffern, J.T.; Myers, T.L.; Cannon, B.D.; Phillips, M.C. Tunable diode laser absorption spectrometer for detection of hydrogen fluoride gas at ambient pressure. In Proceedings of the (CLEO)—Science and Innovations, San Jose, CA, USA, 8–13 June 2014. [Google Scholar]
- Kuehnreich, B.; Wagner, S.; Habig, J.C.; Saathoff, H.; Moyer, E.J.; Ebert, V. Open-path TDLAS for in-situ detection of water isotopes in ice clouds down to 190 K. In Proceedings of the Laser Applications to Chemical, Security and Environmental Analysis 2014, Seattle, WA, USA, 13–17 July 2014. [Google Scholar]
- Rao, R.Z. Light Propagation in the Turbulent Atmosphere; Anhui Science and Technology Press: Hefei City, China, 2005. [Google Scholar]
- Wyngaard, J.C. Turbulence in the Atmosphere; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Kulikov, V.A.; Vorontsov, M.A. Analysis of the joint impact of atmospheric turbulence and refractivity on laser beam propagation. Opt. Express 2017, 25, 28524–28535. [Google Scholar] [CrossRef]
- Witzel, O.; Klein, A.; Meffert, C.; Wagner, S.; Kaiser, S.; Schulz, C.; Ebert, V. VCSEL-based, high-speed, in situ TDLAS for in-cylinder water vapor measurements in IC engines. Opt. Express 2013, 21, 19951–19965. [Google Scholar] [CrossRef]
- Zhang, D.; Guo, J.; Jin, Y. Efficient subtle motion detection from high-speed video for sound recovery and vibration analysis using singular value decomposition-based approach. Opt. Eng. 2017, 56, 094105. [Google Scholar] [CrossRef]
- Gao, Z.L.; Ye, W.L.; Zheng, C.T.; Wang, Y.-D. Wavelet-denoising technique in near-infrared methane detection based on tunable diode laser absorption spectroscopy. Optoelectron. Lett. 2014, 10, 299–303. [Google Scholar] [CrossRef]
- Chui, H.; Yang, K.; Zhang, L.; Wu, X.; Liu, Y.; Wang, A.; Li, H.; Ji, M. Tunable diode laser absorption spectroscopy (TDLAS) detection signal denoising based on gabor transform. Guang Pu Xue Yu Guang Pu Fen Xi Guang Pu 2016, 36, 2997–3002. [Google Scholar] [PubMed]
- Ye, W.; Xu, X.; Peng, C.; Xiao, X.; Xia, Z.; Liu, W.; Luo, W.; Wu, F.; Wu, T. A LabVIEW-based TDLAS methane detection system using a wavelet denoising method. Microw. Opt. Technol. Lett. 2021, 1–6. [Google Scholar] [CrossRef]
- Liu, X.; Qiao, S.; Ma, Y. Highly sensitive methane detection based on light-induced thermoelastic spectroscopy with a 2.33 µm diode laser and adaptive Savitzky-Golay filtering. Opt. Express 2022, 30, 1304–1313. [Google Scholar] [CrossRef]
- Zhao, G.; Tan, W.; Hou, J.; Qiu, X.; Ma, W.; Li, Z.; Dong, L.; Zhang, L.; Yin, W.; Xiao, L.; et al. Calibration-free wavelength-modulation spectroscopy based on a swiftly determined wavelength-modulation frequency response function of a DFB laser. Opt. Express 2016, 24, 1723–1733. [Google Scholar] [CrossRef]
- Chen, X.; Fan, R.; Wu, J.; Song, X.; Liu, Q.; Wang, Y.; Wang, Y.; Tao, B. Fourier-transform-based two-stage camera calibration method with simple periodical pattern. Opt. Lasers Eng. 2020, 133, 106121. [Google Scholar] [CrossRef]
- Wang, R.; Yang, Z.N.; Wang, H.Y.; Xu, X.J. Methane-based in situ temperature rise measurement in a diode-pumped rubidium laser. Opt. Lett. 2017, 42, 667–670. [Google Scholar] [CrossRef]
- Brandt, A.R.; Heath, G.A.; Kort, E.A.; O’sullivan, F.; Pétron, G.; Jordaan, S.M.; Tans, P.; Wilcox, J.; Gopstein, A.M.; Arent, D.; et al. Methane leaks from North American natural gas systems. Science 2014, 343, 733–735. [Google Scholar] [CrossRef] [Green Version]
- Wang, M.; Zhang, Y.J.; Liu, J.G.; Liu, W.Q.; Kan, R.F.; Wang, T.D.; Chen, D.; Chen, J.Y.; Wang, X.M.; Xia, H.; et al. Applications of a tunable diode laser absorption spectrometer in monitoring greenhouse gases. Chin. Opt. Lett. 2006, 4, 363–365. [Google Scholar]
- Xu, L.; Hou, G.; Qiu, S.; Huang, A.; Zhang, H.; Cao, Z. Noise immune TDLAS temperature measurement through spectrum shifting by using a Mach–Zehnder interferometer. IEEE Trans. Instrum. Meas. 2021, 70, 1–9. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, J.; Xu, Z.; He, Y.; Kan, R. Characterization of temperature non-uniformity over a premixed CH4–air flame based on line-of-sight TDLAS. Appl. Phys. B 2016, 122, 1–9. [Google Scholar] [CrossRef]
- Wang, F.; Wu, Q.; Huang, Q.; Zhang, H.; Yan, J.; Cen, K. Simultaneous measurement of 2-dimensional H2O concentration and temperature distribution in premixed methane/air flame using TDLAS-based tomography technology. Opt. Commun. 2015, 346, 53–63. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).