First-Principles Study of the Optical Properties of TMDC/Graphene Heterostructures
Abstract
1. Introduction
2. Materials and Methods
3. Results
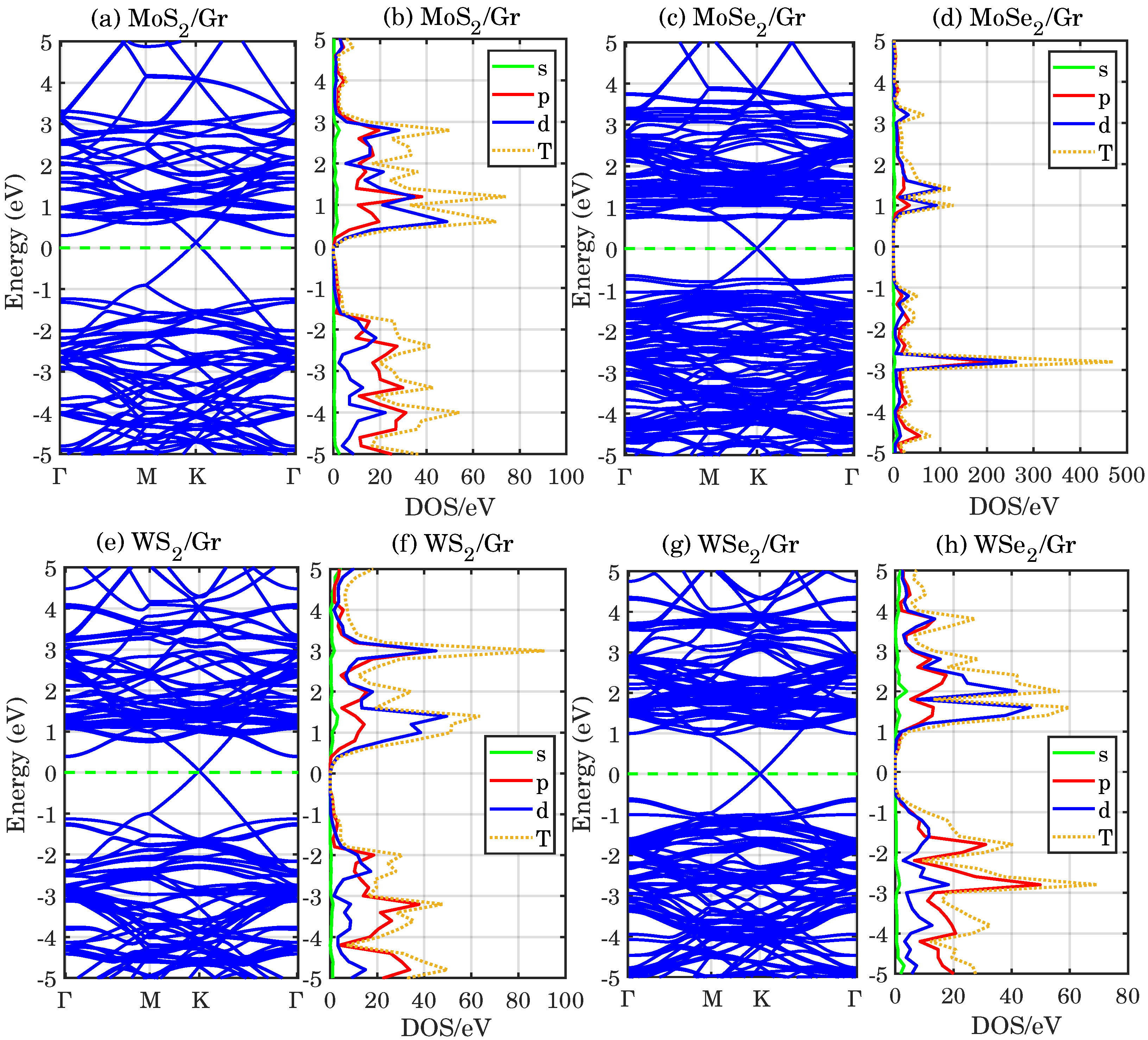
3.1. Band Structures
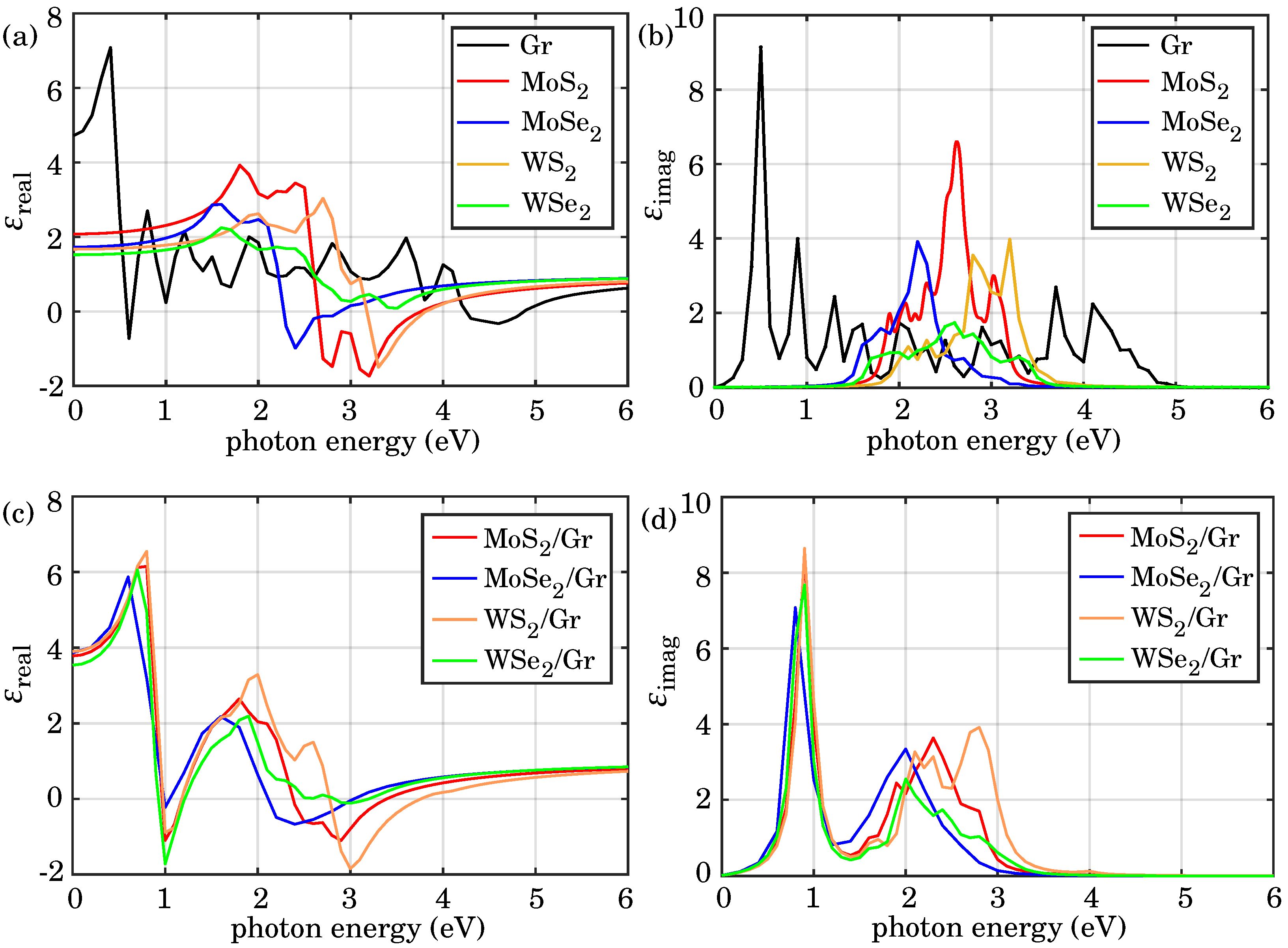
3.2. Optical Properties
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| TMDC | Transition metal dichalcogenide |
| Gr | Graphene |
| SBH | Schottky barrier height |
| DFT | Density functional theory |
| DOS | Density of states |
| CBM | Conduction band minimum |
| VBM | Valence band maximum |
References
- Su, W.P.; Schrieffer, J.R.; Heeger, A.J. Solitons in Polyacetylene. Phys. Rev. Lett. 1979, 42, 1698–1701. [Google Scholar] [CrossRef]
- Haldane, F.D.M. Nonlinear Field Theory of Large-Spin Heisenberg Antiferromagnets: Semiclassically Quantized Solitons of the One-Dimensional Easy-Axis Néel State. Phys. Rev. Lett. 1983, 50, 1153–1156. [Google Scholar] [CrossRef]
- Xu, G.; DiTusa, J.F.; Ito, T.; Oka, K.; Takagi, H.; Broholm, C.; Aeppli, G. Y2BaNiO5: A nearly ideal realization of the S = 1 Heisenberg chain with antiferromagnetic interactions. Phys. Rev. B 1996, 54, R6827–R6830. [Google Scholar] [CrossRef]
- Buyers, W.J.L.; Morra, R.M.; Armstrong, R.L.; Hogan, M.J.; Gerlach, P.; Hirakawa, K. Experimental evidence for the Haldane gap in a spin-1 nearly isotropic, antiferromagnetic chain. Phys. Rev. Lett. 1986, 56, 371–374. [Google Scholar] [CrossRef] [PubMed]
- Renard, J.P.; Verdaguer, M.; Regnault, L.P.; Erkelens, W.A.C.; Rossat-Mignod, J.; Stirling, W.G. Presumption for a Quantum Energy Gap in the Quasi-One-Dimensional S = 1 Heisenberg Antiferromagnet Ni(C2H8N2)2NO2(ClO4). Europhys. Lett. 1987, 3, 945–952. [Google Scholar] [CrossRef]
- Tzeng, Y.C. Parity quantum numbers in the density matrix renormalization group. Phys. Rev. B 2012, 86, 024403. [Google Scholar] [CrossRef]
- Tzeng, Y.C.; Onishi, H.; Okubo, T.; Kao, Y.J. Quantum phase transitions driven by rhombic-type single-ion anisotropy in the S = 1 Haldane chain. Phys. Rev. B 2017, 96, 060404. [Google Scholar] [CrossRef]
- Pajerowski, D.M.; Podlesnyak, A.P.; Herbrych, J.; Manson, J. High-pressure inelastic neutron scattering study of the anisotropic S = 1 spin chain [Ni(HF2)(3-Clpyradine)4]BF4. Phys. Rev. B 2022, 105, 134420. [Google Scholar] [CrossRef]
- Tzeng, Y.C.; Dai, L.; Chung, M.; Amico, L.; Kwek, L.C. Entanglement convertibility by sweeping through the quantum phases of the alternating bonds XXZ chain. Sci. Rep. 2016, 6, 26453. [Google Scholar] [CrossRef]
- Tu, Y.T.; Tzeng, Y.C.; Chang, P.Y. Rényi entropies and negative central charges in non-Hermitian quantum systems. arXiv 2022, arXiv:2107.13006. [Google Scholar]
- Klitzing, K.v.; Dorda, G.; Pepper, M. New Method for High-Accuracy Determination of the Fine-Structure Constant Based on Quantized Hall Resistance. Phys. Rev. Lett. 1980, 45, 494–497. [Google Scholar] [CrossRef]
- Ng, K.K.; Chen, Y.C.; Tzeng, Y.C. Quarter-filled supersolid and solid phases in the extended Bose-Hubbard model. J. Phys. Cond. Mat. 2010, 22, 185601. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Chen, Y.C.; Yang, M.F. Two supersolid phases in hard-core extended Bose-Hubbard model. J. Phys. Commun. 2017, 1, 035009. [Google Scholar] [CrossRef]
- Geim, A.K. Graphene: Status and prospects. Science 2009, 324, 1530–1534. [Google Scholar] [CrossRef] [PubMed]
- Bolotin, K.I.; Sikes, K.J.; Jiang, Z.; Klima, M.; Fudenberg, G.; Hone, J.; Kim, P.; Stormer, H.L. Ultrahigh electron mobility in suspended graphene. Solid State Commun. 2008, 146, 351–355. [Google Scholar] [CrossRef]
- Chan, K.T.; Neaton, J.B.; Cohen, M.L. First-principles study of metal adatom adsorption on graphene. Phys. Rev. B 2008, 77, 235430. [Google Scholar] [CrossRef]
- Torbatian, Z.; Asgari, R. Plasmonic physics of 2D crystalline materials. Appl. Sci. 2018, 8, 238. [Google Scholar] [CrossRef]
- Koukaras, E.N.; Kalosakas, G.; Galiotis, C.; Papagelis, K. Phonon properties of graphene derived from molecular dynamics simulations. Sci. Rep. 2015, 5, 12923. [Google Scholar] [CrossRef]
- Wendler, F.; Knorr, A.; Malic, E. Ultrafast carrier dynamics in Landau-quantized graphene. Nanophotonics 2015, 4, 224–249. [Google Scholar] [CrossRef]
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef]
- Fan, Q.; Yan, L.; Tripp, M.W.; Krejčí, O.; Dimosthenous, S.; Kachel, S.R.; Chen, M.; Foster, A.S.; Koert, U.; Liljeroth, P.; et al. Biphenylene network: A nonbenzenoid carbon allotrope. Science 2021, 372, 852–856. [Google Scholar] [CrossRef] [PubMed]
- Al-Jayyousi, H.K.; Sajjad, M.; Liao, K.; Singh, N. Two-dimensional biphenylene: A promising anchoring material for lithium-sulfur batteries. Sci. Rep. 2022, 12, 4653. [Google Scholar] [CrossRef] [PubMed]
- Bafekry, A.; Faraji, M.; Fadlallah, M.M.; Jappor, H.R.; Karbasizadeh, S.; Ghergherehchi, M.; Gogova, D. Biphenylene monolayer as a two-dimensional nonbenzenoid carbon allotrope: A first-principles study. J. Phys. Cond. Mat. 2021, 34, 015001. [Google Scholar] [CrossRef] [PubMed]
- Ren, K.; Shu, H.; Huo, W.; Cui, Z.; Xu, Y. Tuning electronic, magnetic and catalytic behaviors of biphenylene network by atomic doping. Nanotechnology 2022. [Google Scholar] [CrossRef]
- Bernevig, B.A.; Hughes, T.L.; Zhang, S.C. Quantum Spin Hall Effect and Topological Phase Transition in HgTe Quantum Wells. Science 2006, 314, 1757–1761. [Google Scholar] [CrossRef]
- König, M.; Wiedmann, S.; Brüne, C.; Roth, A.; Buhmann, H.; Molenkamp, L.W.; Qi, X.L.; Zhang, S.C. Quantum Spin Hall Insulator State in HgTe Quantum Wells. Science 2007, 318, 766–770. [Google Scholar] [CrossRef]
- Vogt, P.; De Padova, P.; Quaresima, C.; Avila, J.; Frantzeskakis, E.; Asensio, M.C.; Resta, A.; Ealet, B.; Le Lay, G. Silicene: Compelling Experimental Evidence for Graphenelike Two-Dimensional Silicon. Phys. Rev. Lett. 2012, 108, 155501. [Google Scholar] [CrossRef]
- Coleman, J.N.; Lotya, M.; O’Neill, A.; Bergin, S.D.; King, P.J.; Khan, U.; Young, K.; Gaucher, A.; De, S.; Smith, R.J.; et al. Two-Dimensional Nanosheets Produced by Liquid Exfoliation of Layered Materials. Science 2011, 331, 568–571. [Google Scholar] [CrossRef]
- Latzke, D.W.; Zhang, W.; Suslu, A.; Chang, T.R.; Lin, H.; Jeng, H.T.; Tongay, S.; Wu, J.; Bansil, A.; Lanzara, A. Electronic structure, spin–orbit coupling, and interlayer interaction in bulk MoS2 and WS2. Phys. Rev. B 2015, 91, 235202. [Google Scholar] [CrossRef]
- Hsu, W.T.; Lu, L.S.; Wang, D.; Huang, J.K.; Li, M.Y.; Chang, T.R.; Chou, Y.C.; Juang, Z.Y.; Jeng, H.T.; Li, L.J.; et al. Evidence of indirect gap in monolayer WSe2. Nat. Commun. 2017, 8, 929. [Google Scholar] [CrossRef]
- Zhang, Y.; Chang, T.R.; Zhou, B.; Cui, Y.T.; Yan, H.; Liu, Z.; Schmitt, F.; Lee, J.; Moore, R.; Chen, Y.; et al. Direct observation of the transition from indirect to direct bandgap in atomically thin epitaxial MoSe2. Nat. Nanotechnol. 2014, 9, 111–115. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.H.; Chung, Y.F.; Su, Y.S.; Chen, K.T.; Huang, Y.S.; Chang, S.T. Band structure of molybdenum disulfide: From first principle to analytical band model. J. Comput. Electron. 2022, 21, 571–581. [Google Scholar] [CrossRef]
- Kumar, S.; Schwingenschlogl, U. Thermoelectric response of bulk and monolayer MoSe2 and WSe2. Chem. Mater. 2015, 27, 1278–1284. [Google Scholar] [CrossRef]
- Kormányos, A.; Burkard, G.; Gmitra, M.; Fabian, J.; Zólyomi, V.; Drummond, N.D.; Fal’ko, V. k·p theory for two-dimensional transition metal dichalcogenide semiconductors. 2D Mater. 2015, 2, 022001. [Google Scholar] [CrossRef]
- Cheiwchanchamnangij, T.; Lambrecht, W.R.L. Quasiparticle band structure calculation of monolayer, bilayer, and bulk MoS2. Phys. Rev. B 2012, 85, 205302. [Google Scholar] [CrossRef]
- Haldar, S.; Vovusha, H.; Yadav, M.K.; Eriksson, O.; Sanyal, B. Systematic study of structural, electronic, and optical properties of atomic-scale defects in the two-dimensional transition metal dichalcogenides MX2 (M = Mo,W; X = S, Se, Te). Phys. Rev. B 2015, 92, 235408. [Google Scholar] [CrossRef]
- Gusakova, J.; Wang, X.; Shiau, L.L.; Krivosheeva, A.; Shaposhnikov, V.; Borisenko, V.; Gusakov, V.; Tay, B.K. Electronic properties of bulk and monolayer TMDs: Theoretical study within DFT framework (GVJ-2e method). Phys. Status Solidi A 2017, 214, 1700218. [Google Scholar] [CrossRef]
- Molina-Sánchez, A.; Wirtz, L. Phonons in single-layer and few-layer MoS2 and WS2. Phys. Rev. B 2011, 84, 155413. [Google Scholar] [CrossRef]
- Gu, X.; Yang, R. Phonon transport in single-layer transition metal dichalcogenides: A first-principles study. Appl. Phys. Lett. 2014, 105, 131903. [Google Scholar] [CrossRef]
- Chang, T.R.; Lin, H.; Jeng, H.T.; Bansil, A. Thickness dependence of spin polarization and electronic structure of ultra-thin films of MoS2 and related transition-metal dichalcogenides. Sci. Rep. 2014, 4, 6270. [Google Scholar] [CrossRef]
- Splendiani, A.; Sun, L.; Zhang, Y.; Li, T.; Kim, J.; Chim, C.Y.; Galli, G.; Wang, F. Emerging photoluminescence in monolayer MoS2. Nano Lett. 2010, 10, 1271–1275. [Google Scholar] [CrossRef] [PubMed]
- Helmrich, S.; Sampson, K.; Huang, D.; Selig, M.; Hao, K.; Tran, K.; Achstein, A.; Young, C.; Knorr, A.; Malic, E.; et al. Phonon-Assisted Intervalley Scattering Determines Ultrafast Exciton Dynamics in MoSe2 Bilayers. Phys. Rev. Lett. 2021, 127, 157403. [Google Scholar] [CrossRef] [PubMed]
- Gutiérrez, H.R.; Perea-López, N.; Elías, A.L.; Berkdemir, A.; Wang, B.; Lv, R.; López-Urías, F.; Crespi, V.H.; Terrones, H.; Terrones, M. Extraordinary Room-Temperature Photoluminescence in Triangular WS2 Monolayers. Nano Lett. 2013, 13, 3447–3454. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Wang, C.; Shaw, J.C.; Cheng, R.; Chen, Y.; Huang, X.; Liu, Y.; Weiss, N.O.; Lin, Z.; Huang, Y.; et al. Large area growth and electrical properties of p-type WSe2 atomic layers. Nano Lett. 2015, 15, 709–713. [Google Scholar] [CrossRef]
- Liu, R.Y.; Lin, M.K.; Chen, P.; Suzuki, T.; Clark, P.C.J.; Lewis, N.K.; Cacho, C.; Springate, E.; Chang, C.S.; Okazaki, K.; et al. Symmetry-breaking and spin-blockage effects on carrier dynamics in single-layer tungsten diselenide. Phys. Rev. B 2019, 100, 214309. [Google Scholar] [CrossRef]
- Mak, K.F.; Lee, C.; Hone, J.; Shan, J.; Heinz, T.F. Atomically Thin MoS2: A New Direct-Gap Semiconductor. Phys. Rev. Lett. 2010, 105, 136805. [Google Scholar] [CrossRef]
- Yoon, Y.; Ganapathi, K.; Salahuddin, S. How Good Can Monolayer MoS2 Transistors Be? Nano Lett. 2011, 11, 3768–3773. [Google Scholar] [CrossRef]
- Lee, C.; Li, Q.; Kalb, W.; Liu, X.Z.; Berger, H.; Carpick, R.W.; Hone, J. Frictional Characteristics of Atomically Thin Sheets. Science 2010, 328, 76–80. [Google Scholar] [CrossRef]
- Chang, K.; Chen, W. In situ synthesis of MoS2/graphene nanosheet composites with extraordinarily high electrochemical performance for lithium ion batteries. Chem. Commun. 2011, 47, 4252–4254. [Google Scholar] [CrossRef]
- Jobayr, M.R.; Salman, E.M.T. Investigation of the thermoelectric properties of one-layer transition metal dichalcogenides. Chin. J. Phys. 2021, 74, 270–278. [Google Scholar] [CrossRef]
- Chang, T.R.; Chen, P.J.; Bian, G.; Huang, S.M.; Zheng, H.; Neupert, T.; Sankar, R.; Xu, S.Y.; Belopolski, I.; Chang, G.; et al. Topological Dirac surface states and superconducting pairing correlations in PbTaSe2. Phys. Rev. B 2016, 93, 245130. [Google Scholar] [CrossRef]
- Bian, G.; Chang, T.R.; Sankar, R.; Xu, S.Y.; Zheng, H.; Neupert, T.; Chiu, C.K.; Huang, S.M.; Chang, G.; Belopolski, I.; et al. Topological nodal-line fermions in spin–orbit metal PbTaSe2. Nat. Commun. 2016, 7, 10556. [Google Scholar] [CrossRef] [PubMed]
- Chang, T.R.; Xu, S.Y.; Chang, G.; Lee, C.C.; Huang, S.M.; Wang, B.; Bian, G.; Zheng, H.; Sanchez, D.S.; Belopolski, I.; et al. Prediction of an arc-tunable Weyl Fermion metallic state in MoxW1−xTe2. Nat. Commun. 2016, 7, 10639. [Google Scholar] [CrossRef] [PubMed]
- Tzeng, Y.C.; Yang, M.F. Fate of Fermi-arc states in gapped Weyl semimetals under long-range interactions. Phys. Rev. B 2020, 102, 035148. [Google Scholar] [CrossRef]
- Sufyan, A.; Macam, G.; Hsu, C.H.; Huang, Z.Q.; Huang, S.M.; Lin, H.; Chuang, F.C. Theoretical prediction of topological insulators in two-dimensional ternary transition metal chalcogenides (MM’X4, M = Ta, Nb, or V; M’ = Ir, Rh, or Co; X = Se or Te). Chin. J. Phys. 2021, 73, 95–102. [Google Scholar] [CrossRef]
- Hlevyack, J.A.; Feng, L.Y.; Lin, M.K.; Villaos, R.A.B.; Liu, R.Y.; Chen, P.; Li, Y.; Mo, S.K.; Chuang, F.C.; Chiang, T.C. Dimensional crossover and band topology evolution in ultrathin semimetallic NiTe2 films. npj 2D Mater. Appl. 2021, 5, 40. [Google Scholar] [CrossRef]
- Feng, L.Y.; Villaos, R.A.B.; Cruzado, H.N.; Huang, Z.Q.; Hsu, C.H.; Hsueh, H.C.; Lin, H.; Chuang, F.C. Magnetic and topological properties in hydrogenated transition metal dichalcogenide monolayers. Chin. J. Phys. 2020, 66, 15–23. [Google Scholar] [CrossRef]
- Yelgel, C.; Yelgel, Ö.C.; Gülseren, O. Structural and electronic properties of MoS2, WS2, and WS2/MoS2 heterostructures encapsulated with hexagonal boron nitride monolayers. J. Appl. Phys. 2017, 122, 065303. [Google Scholar] [CrossRef]
- Ren, K.; Sun, M.; Luo, Y.; Wang, S.; Yu, J.; Tang, W. First-principle study of electronic and optical properties of two-dimensional materials-based heterostructures based on transition metal dichalcogenides and boron phosphide. Appl. Surf. Sci. 2019, 476, 70–75. [Google Scholar] [CrossRef]
- Phuc, H.V.; Hieu, N.N.; Hoi, B.D.; Phuong, L.T.T.; Nguyen, C.V. First principle study on the electronic properties and Schottky contact of graphene adsorbed on MoS2 monolayer under applied out-plane strain. Surf. Sci. 2018, 668, 23–28. [Google Scholar] [CrossRef]
- Nguyen, C.V. Tuning the electronic properties and Schottky barrier height of the vertical graphene/MoS2 heterostructure by an electric gating. Superlattices Microstruct. 2018, 116, 79–87. [Google Scholar] [CrossRef]
- Ma, Y.; Dai, Y.; Guo, M.; Niu, C.; Huang, B. Graphene adhesion on MoS2 monolayer: An ab initio study. Nanoscale 2011, 3, 3883–3887. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Dai, Y.; Wei, W.; Niu, C.; Yu, L.; Huang, B. First-principles study of the graphene@MoSe2 heterobilayers. J. Phys. Chem. C 2011, 115, 20237–20241. [Google Scholar] [CrossRef]
- Zhang, W.; Hao, G.; Zhang, R.; Xu, J.; Ye, X.; Li, H. Effects of vertical strain and electrical field on electronic properties and Schottky contact of graphene/MoSe2 heterojunction. J. Phys. Chem. Solids 2021, 157, 110189. [Google Scholar] [CrossRef]
- Hao, G.-Q.; Zhang, R.; Zhang, W.-J.; Chen, N.; Ye, X.-J.; Li, H.-B. Regulation and control of Schottky barrier in graphene/MoSe2 heteojuinction by asymmetric oxygen doping. Acta Phys. Sin. 2022, 71, 017104. [Google Scholar] [CrossRef]
- Zheng, J.; Li, E.; Ma, D.; Cui, Z.; Peng, T.; Wang, X. Effect on Schottky barrier of graphene/WS2 heterostructure with vertical electric field and biaxial strain. Phys. Status Solidi B 2019, 256, 1900161. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, Y.; Gao, W.; Lin, Y.; Zhao, X.; Wang, Q.; Yao, X.; He, M.; Ye, X.; Liu, Y. Sizable bandgaps of graphene in 3d transition metal intercalated defective graphene/WSe2 heterostructures. RSC Adv. 2019, 9, 18157–18164. [Google Scholar] [CrossRef]
- Ma, H.-H.; Zhang, X.-B.; Wei, X.-Y.; Cao, J.-M. Theoretical study on Schottky regulation of WSe2/graphene heterostructure doped with nonmetallic elements. Acta Phys. Sin. 2020, 69, 20200080. [Google Scholar] [CrossRef]
- Qiu, B.; Zhao, X.; Hu, G.; Yue, W.; Ren, J.; Yuan, X. Optical Properties of Graphene/MoS2 Heterostructure: First Principles Calculations. Nanomaterials 2018, 8, 962. [Google Scholar] [CrossRef]
- Qiu, B.; Zhao, X.; Hu, G.; Yue, W.; Yuan, X.; Ren, J. Tuning optical properties of Graphene/WSe2 heterostructure by introducing vacancy: First principles calculations. Physica E 2020, 116, 113729. [Google Scholar] [CrossRef]
- Sun, Z.; Chu, H.; Li, Y.; Zhao, S.; Li, G.; Li, D. Theoretical investigation on electronic and optical properties of the graphene-MoSe2-graphene sandwich heterostructure. Mater. Des. 2019, 183, 108129. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Taylor, J.; Guo, H.; Wang, J. Ab initio modeling of quantum transport properties of molecular electronic devices. Phys. Rev. B 2001, 63, 245407. [Google Scholar] [CrossRef]
- Taylor, J.; Guo, H.; Wang, J. Ab initio modeling of open systems: Charge transfer, electron conduction, and molecular switching of a C60 device. Phys. Rev. B 2001, 63, 121104. [Google Scholar] [CrossRef]
- Bardeen, J. Surface States and Rectification at a Metal Semi-Conductor Contact. Phys. Rev. 1947, 71, 717–727. [Google Scholar] [CrossRef]
- Tung, R.T. Recent advances in Schottky barrier concepts. Mater. Sci. Eng. R Rep. 2001, 35, 1–138. [Google Scholar] [CrossRef]
- Spicer, W.E.; Chye, P.W.; Skeath, P.R.; Su, C.Y.; Lindau, I. New and unified model for Schottky barrier and III–V insulator interface states formation. J. Vac. Sci. Technol. 1979, 16, 1422–1433. [Google Scholar] [CrossRef]
- Grosso, G.; Parravicini, G.P. Solid State Physics; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
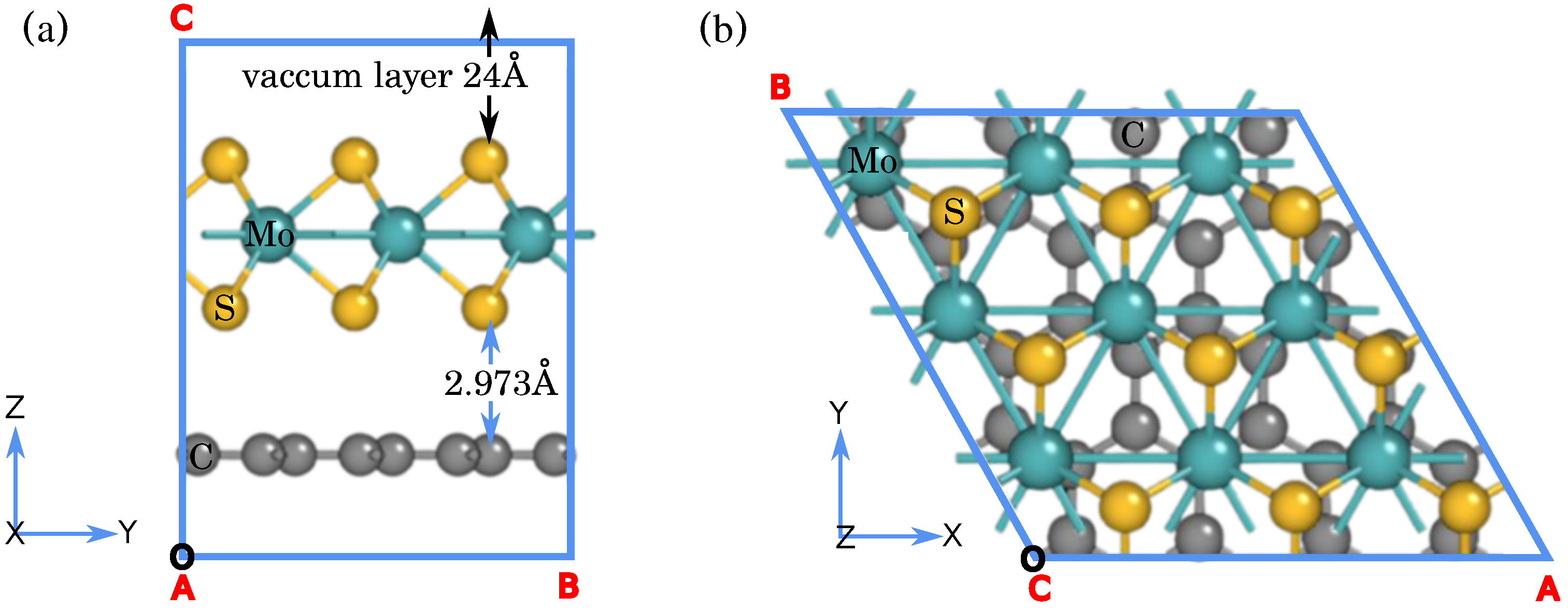

| /Gr | /Gr | /Gr | /Gr | /Gr |
|---|---|---|---|---|
| mismatch ratio | 1.83% | 0.10% | 2.04% | 0.01% |
| meV | meV | meV | meV |
| /Gr | Mo-S | Mo-C | S-C | C-C | -Gr |
|---|---|---|---|---|---|
| 2.404 Å | 4.826 Å | 3.089 Å | 1.600 Å | 2.973 Å | |
| /Gr | Mo-Se | Mo-C | Se-C | C-C | -Gr |
| 2.349 Å | 4.920 Å | 3.270 Å | 1.626 Å | 3.161 Å | |
| /Gr | W-S | W-C | S-C | C-C | -Gr |
| 2.379 Å | 4.774 Å | 3.078 Å | 1.596 Å | 2.954 Å | |
| /Gr | W-Se | W-C | Se-C | C-C | -Gr |
| 2.354 Å | 4.940 Å | 3.286 Å | 1.625 Å | 3.178 Å |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.-H.; Chang, S.-T. First-Principles Study of the Optical Properties of TMDC/Graphene Heterostructures. Photonics 2022, 9, 387. https://doi.org/10.3390/photonics9060387
Yang C-H, Chang S-T. First-Principles Study of the Optical Properties of TMDC/Graphene Heterostructures. Photonics. 2022; 9(6):387. https://doi.org/10.3390/photonics9060387
Chicago/Turabian StyleYang, Cheng-Hsien, and Shu-Tong Chang. 2022. "First-Principles Study of the Optical Properties of TMDC/Graphene Heterostructures" Photonics 9, no. 6: 387. https://doi.org/10.3390/photonics9060387
APA StyleYang, C.-H., & Chang, S.-T. (2022). First-Principles Study of the Optical Properties of TMDC/Graphene Heterostructures. Photonics, 9(6), 387. https://doi.org/10.3390/photonics9060387




