All Optical Stabilizations of Nano-Structure-Based QDash Semiconductor Mode-Locked Lasers Based on Asymmetric Dual-Loop Optical Feedback Configurations

Abstract

We report feedback-induced frequency oscillations using a power-split-ratio through asymmetric dual-loop optical feedback (Loop I: ~2.2 km and Loop II: ~20 m) subject to a self-mode-locked two-section QDash laser emitting at 1550 nm and operating at 21 GHz repetition rate. To assess the suppression of frequency resonances, three chosen combinations of feedback power (Loop I: −27.27 dB and Loop II: −19.74 dB, Loop I: −22 dB and Loop II: −22 dB, and Loop I: −19.74 dB and Loop II: −27.27 dB) through asymmetric dual-loop optical feedback have been studied. Based on the chosen coupling strength, an optimum feedback ratio that yields better side-mode suppression has been identified. Our results demonstrate that side-mode suppression can be achieved by the fine adjustment of coupling power through either cavity of dual-loop feedback configurations. Furthermore, we have further demonstrated that frequency fluctuations from the RF spectra can be filtered by carefully selecting the delay phase of the second cavity. Our experimental findings suggest that semiconductor mode-locked lasers based on dual-loop feedback configurations can be used to develop noise oscillations free from integrated photonic oscillators for potential applications in telecommunications, multiplexing, and frequency-comb generation.

1. Introduction

Mode-locked lasers (SMLLs) are potential candidates for key applications in many fields of optical sampling [1], frequency comb generation [2,3,4], data center networks [5], clock recovery [6,7], telecommunications [8,9,10,11,12,13,14,15], and spectroscopy [16]. Some ideal features of SMLLs include compactness, low fabrication costs, low threshold current, low amplified spontaneous emission fast carrier dynamics, and an inhomogeneous wide spectrum [17]. To enhance the improvement and for better applications of SMLLs in telecommunications, high timing stability is paramount. The timing stability of SMLLs can be improved using the optical fiber cavity [18], which reduces the RF linewidth and corresponding integrated timing jitter of the optical pulse train. The optical fiber loop in the feedback cavity can be considered as the energy storage component, with Q-factor being determined by the length of the resonator [19]. For single-loop optical feedback, there is an increase in the system memory, which directly corresponds with the reduction in the timing jitter [20,21,22,23,24,25,26]. With improved timing jitter, single-loop optical feedback produces additional cavity sidebands around the main frequency in the power spectrum [20,21,22,23,24,25,26,27]. Recently, we have proposed the asymmetric dual-loop optical feedback scheme with equal feedback ratio through each loop, to suppress the first sideband around the fundamental frequency; however, the second appears unsuppressed (modal overlap) [22]. To eliminate these cavity sidebands and modal overlap, we reported how to optimize balanced asymmetric dual-loop optical feedback by varying the second feedback cavity length [23].

In this paper, we report the effect of unequal coupling power through asymmetric dual-loop optical feedback on the adverse dynamical effects induced due to longer feedback cavities. We identify the optimum conditions for coupling power and the second feedback loop length, which yields much better suppression in external cavity side modes. These findings reveal that optimized asymmetric dual-loop feedback is a robust and potential source for overcoming the disadvantages of frequency fluctuations in mode-locked QDash lasers, which limits the applications of semiconductor MLLs.

2. Experimental Setup

The device under test is an InAs/InP SML QDash laser, and details about the device are given in [24]. The schematic of the experimental setup is depicted in Figure 1. The emission from the device under test (QDash MLL) was collected using lensed fiber and then fed into an optical circulator through Port 2. Port 3 collects light, and then the semiconductor optical amplifier amplifies the optical signal. The amplified light was then equally divided into two parts through a 3-dB coupler. One part of optical light is used to analyze the optical spectra and the other part for electrical spectra. The other part of the light was fed into the experimental arrangements. Each feedback loop consisted of a variable optical attenuator, a polarization controller, and an optical delay line. Loop I and Loop II consisted of fiber spool of length ~2.2 km and ~20 m, respectively. The optical strength in each feedback loop was fixed through an optical attenuator. The overall feedback ratio was fixed to be −22 dB and was again injected into the gain section of the laser from Port 1 of an optical circulator.

3. Results and Discussions

In the present work, an asymmetric dual-loop optical feedback configuration has been adopted to prevent unwanted spurious sidebands from appearing due to the length of the feedback cavity. For that purpose, two approaches have been proposed: an asymmetric dual-loop feedback with various couplings of power-split-ratio via each optical feedback loop and the effect of the second feedback loop length on the cavity side modes.

3.1. Effect of Power-Split-Ratio Controlled Asymmetric Dual-Loop Feedback Scheme on RF Linewidth and Integrated Timing Jitter

In this section, we have investigated the effect of power split-ratio through an asymmetric dual-loop optical feedback scheme on the integrated timing jitter and RF linewidth of an SML QDash laser. A ~2.2 km fiber span was used in a single-loop optical feedback scheme, and the cavity length was varied by using an optical delay line, which was optimized in steps of 1.67 ps from 0 to 84 ps. Under integer resonance, external cavity side modes with a frequency spacing of ~95 kHz appear in the RF spectrum, and they are depicted in Figure 2a. The frequency fluctuations that appear in the RF spectra limit the practical applications of QDash MLLs. To eliminate these resonance frequencies, an additional cavity loop with a delay time of more than ~100× smaller than the period of the frequency oscillations of the first loop was demonstrated. For this dual-loop scheme, the polarization controllers (PC-I and PC-II) and optical delay lines (ODL-I and ODL-II) attached with both loops were fine-tuned. The light signal was further split in different percentages into both cavities by using optical-attenuators (Att-I and Att-II). Three different combinations of feedback strength fed through each feedback loop of asymmetric dual-loop feedback scheme are listed in

Table 1. Three different combinations of feedback strength through each feedback loop with resulting overall coupling strength of −22 dB into the gain section of QDash laser.

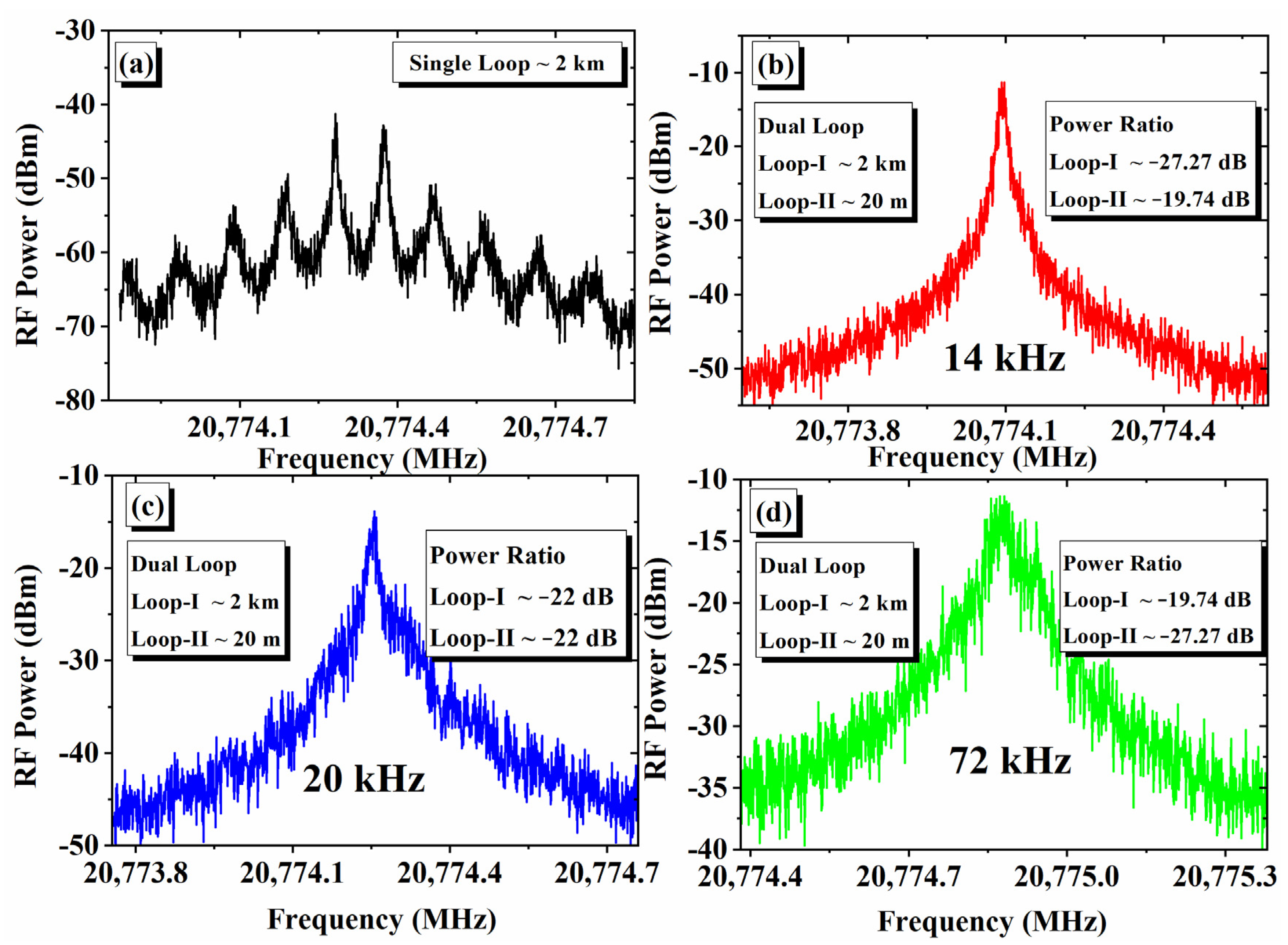
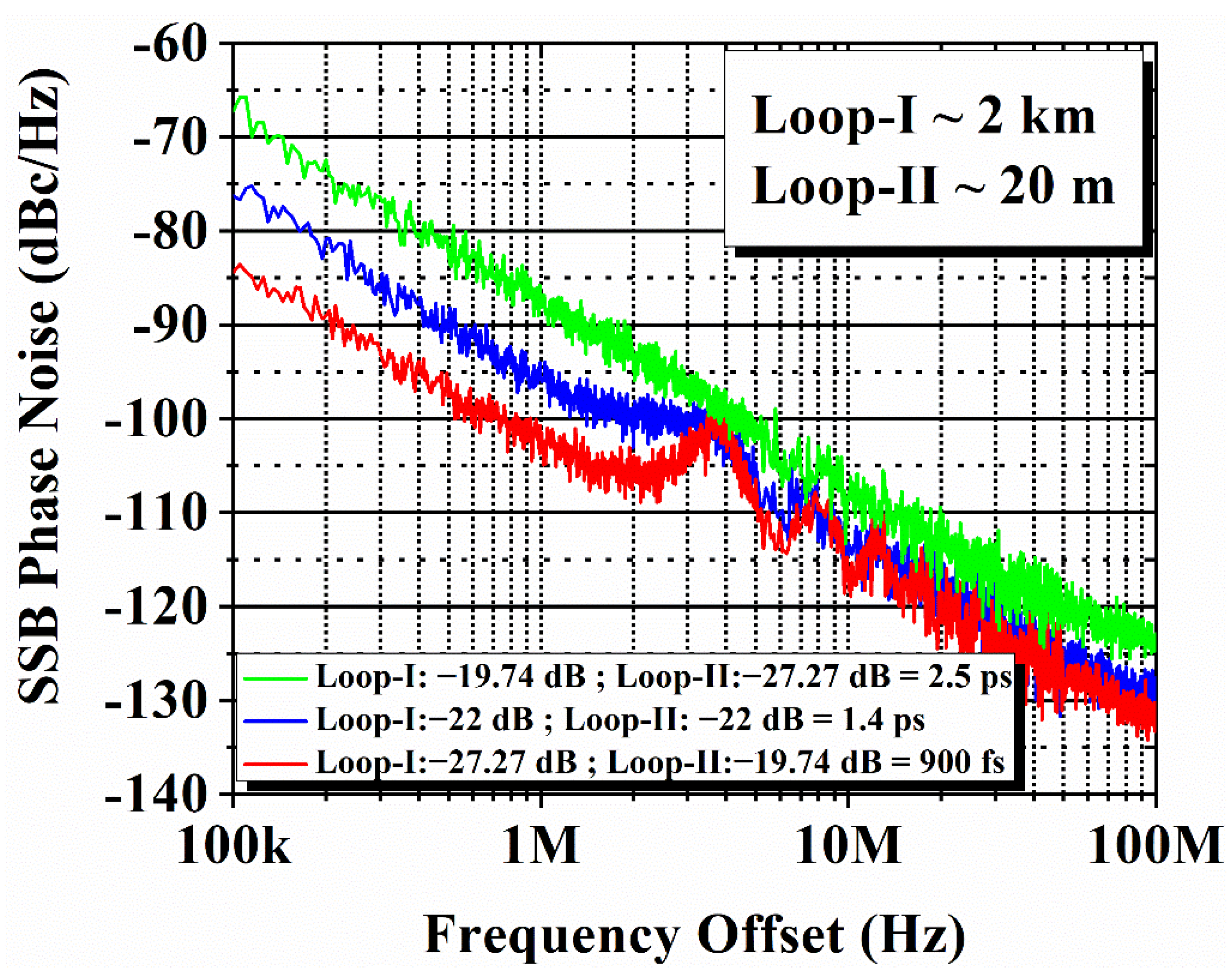
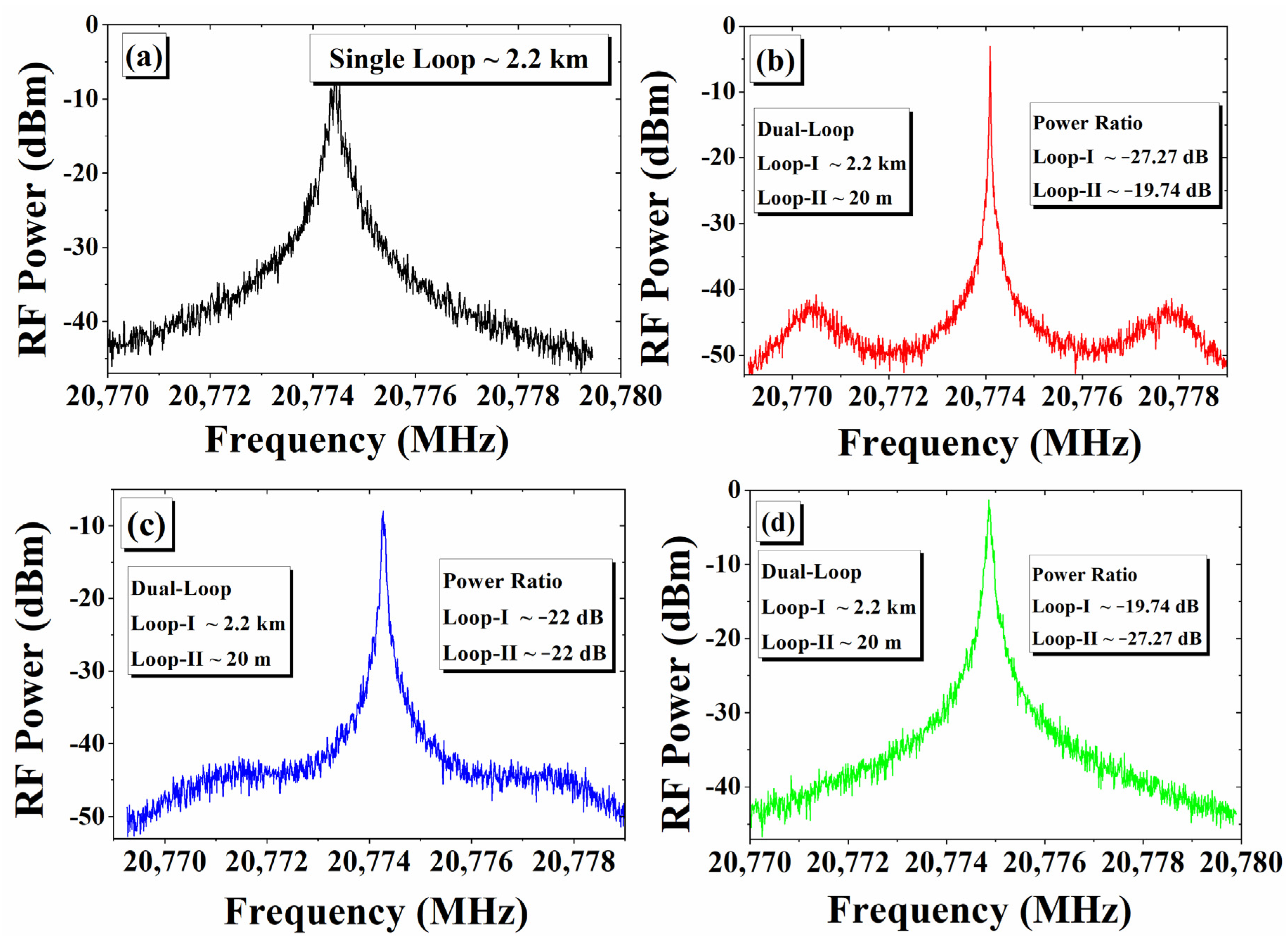
Loop I	Loop II	Feedback Ration into Gain Section
−27.27 dB	−19.74 dB	−22 dB
−22 dB	−22 dB	−22 dB
−19.74 dB	−27.27 dB	−22 dB

.

First, a −27.27 dB feedback strength via Loop I and a −19.74 dB via Loop II was fixed using variable optical attenuators. It should be noted that ODL-I was retuned such that Loop I modes precisely overlap with that of Loop II. Under such a situation, strong side-band elimination occurs, and all feedback-induced frequency fluctuations disappeared, as shown in Figure 2b. Our results demonstrate that the RF linewidth narrows down to 14 kHz from a 100 kHz free-running case when both feedback loops were integer resonant. The spectra were measured under a frequency span of 1 MHz, with a video-bandwidth (VBW) of 100 Hz and resolution-bandwidth (RBW) of 1 kHz. Similarly, when a balanced feedback strength (Loop I: −22 dB and Loop II: −22 dB) was passed via each external feedback cavity, then RF linewidth to as low as 20 kHz was noticed. The measured RF spectra is shown in Figure 2c under a span of 1 MHz (RBW 1 kHz and VBW 100 Hz). Furthermore, asymmetric-dual-loop feedback was further implemented such that a −19.74 dB feedback strength was fed through Loop I, and −27.27 dB was fed via Loop II. Under this chosen combination of feedback ratios, the RF linewidth reduces to 72 kHz. The measured RF spectra is shown in Figure 2d under a span of 1 MHz (RBW 1 kHz and VBW 100 Hz).

The experimentally measured phase noise traces of asymmetric dual-loop versus frequency-offset from the mode-locked frequency are shown in Figure 3.

When each feedback loop was fully resonant, the timing jitter reduces to 2.5 ps from 3.9 ps (integrated from 10 kHz to 100 MHz) for a dual-loop feedback configuration with feedback ratio (Loop I: −19.74 dB and Loop II: −27.27 dB), 1.4 ps for dual-loop feedback configuration with coupling ratio (Loop I: −22 dB and Loop II: −22 dB), and 0.9 ps for dual-loop feedback with feedback ratio (Loop I: −27.27 dB and Loop II: −19.74 dB).

The calculated RF linewidth is directly proportional to the root-mean-square (RMS) timing jitter [28]. Hence, the integrated timing jitter under feedback strength (Loop I: −19.74 dB and Loop II: −27.27 dB) was higher, as RF linewidth with such combinations of feedback ratio was 72 kHz. Similarly, the integrated timing jitter under feedback strength (Loop I: −27.27 dB and Loop II: −19.74 dB) was lower, because RF linewidth with this coupling strength was 14 kHz.

A comparison of the RF linewidth and integrated timing-jitter under the stable resonance condition as functions of three combinations of feedback ratios is shown in Figure 4. These results indicate that optimum stabilization (lowest timing jitter) in an SML QDash laser was achieved for the asymmetric dual-loop with a feedback ratio of −27.27 dB through Loop I and −19.74 dB through Loop II. On the other hand, better side-mode suppression was achieved for the dual-loop with a feedback strength of −19.74 dB from Loop I and −27.27 dB via Loop II.

3.2. Effect of Power-Split-Ratio Controlled Asymmetric Dual-Loop Feedback Scheme on Suppression of Frequency Fluctuations

In the following, we discuss the suppression of feedback-induced frequency fluctuations at various combinations of feedback ratios. The measured RF spectra for single loop feedback with a fiber spool of 2.2 km is shown in Figure 5a under frequency spans of 10 MHz, RBW 10 kHz, and VBW 1 kHz. However, for dual-loop optical feedback configurations, the feedback strength in Loop I was fixed to −27.27 dB and that in Loop II to −19.74 dB. The measured RF spectra for single loop feedback with a fiber spool of 2.2 km is shown in Figure 5b under frequency spans of 10 MHz, RBW 10 kHz, and VBW 1 kHz. It was observed from measured spectra that modal overlap appears at a particular frequency offset, corresponding to the length of the second feedback loop. These results indicate that this chosen combination of feedback strength (Loop I: −27.27 dB; Loop II: −19.74 dB) is not suitable for better suppression of feedback-induced cavity sidebands. However, for a balanced feedback ratio (Loop I: −22 dB; Loop II: −22 dB) on a larger frequency span (10 MHz), weak side modes were observed. The RF spectra were measured under span 10 MHz (RBW 10 kHz and VBW 1 kHz) and are shown in Figure 5c. The measured experimental results show that cavity sidebands cannot effectively be suppressed by considering a balanced feedback ratio through an asymmetric dual-loop feedback scheme. In order to acquire stable and flat RF spectra, we demonstrated an unbalanced-asymmetric dual-loop feedback scheme for better external cavity sideband suppression, which yields fluctuation-free RF-spectra compared to single and dual-loop feedback schemes. With feedback ratio Loop I: −27.27 dB and Loop II: −19.74 dB, fine-tuning of both external feedback cavities was carried out such that precise coincidence of the modes of Loop I with a mode of Loop II occurs. When the optical delay lines connected to each feedback loop are fully resonant, a strong side-mode suppression was noticed. A flat RF spectra can be seen in Figure 5d under a span of 10 MHz (RBW 10 kHz and VBW 1 kHz). In this feedback configurations, the RF linewidth is 5× higher than the dual-loop configuration with feedback ratio (Loop I: −27.27 dB and Loop II: −19.74 dB), but the side modes are eliminated. These results agree well with our recently published data [23]. These finding further suggests that better suppression in external cavity sidebands can be achieved by precisely controlling the percentage of feedback ratio through either external feedback loop. Furthermore, the resulting setup can be implemented for applications where less noise and a stable RF spectrum are desired, as in frequency-comb-generation. Most recently, it was theoretically predicted that dual-loop optoelectronic oscillators could be optimized by controlling the phase delay and power split ratio [29], which agrees with our experimental measurements.

3.3. Effect of the Length of Second Cavity on Suppression of Frequency Resonances

In this section, we further studied the effect of the length of the second feedback cavity on the suppression of laser-induced frequency resonances. Similar to the above experimental arrangement, a fiber length of ~2.2 km was fixed in Loop I, and a ~220 m fiber length was used in the second loop, with equal feedback strength through each external feedback loop. The signals of a few gigahertz repetition rate were generated with a mode spacing of 95 kHz away from the main mode-locked frequency, as shown in Figure 6. Upon fine tuning of both external feedback loops, the asymmetric dual-loop configuration suggested here (Loop I = ~2.2 km and Loop II = ~220 m) is a promising approach that leads towards significant suppression in external cavity sidebands closer to the main peak. Furthermore, when ODL-I, attached for the first feedback loop, was tuned to 24 ps and ODL II, connected to the second feedback cavity, was varied to 13 ps, the modes of Loop I overlap with the modes of Loop II. Consequently, a maximum of 30 dB sideband compression in the first frequency harmonic occurs. The measured RF spectrum is shown in Figure 5 using single-loop feedback with a fiber length of ~2.2 km (black line), ~220 m (red line), and dual-loop (blue line) feedback.

The asymmetric dual-loop feedback scheme demonstrated here is a better technique that effectively suppresses unwanted noise-induced oscillations and yields side-band free RF spectra when an equal percentags of feedback ratio was used. Furthermore, this behavior shows that better suppression in cavity sidebands can be obtained by varying the second feedback loop length using ODL.

4. Conclusions

In the present work, we experimentally demonstrate how to suppress the feedback-induced frequency fluctuations from conventional single and dual-loop feedback schemes, with feedback ratio controlled for short as well as long optical cavities. The device under test was a two-section InAs/InP QDash MLLs operating at 21 GHz and emitting at 1550 nm. These results reveal that dual-loop feedback with precise alignment of the loop lengths and fine-tuning of feedback ratio through external feedback cavities effectively suppresses external cavity sidebands. The proposed asymmetric dual-loop feedback configuration makes semiconductor mode-locked lasers promising for the development of compact and cost-effective optoelectronic oscillators with low timing jitter. The resulting setup using this method is also integrable in a hybrid integrated optics, compact fiber loops and stable OEOs.