Resolution and Contrast Enhancement for Lensless Digital Holographic Microscopy and Its Application in Biomedicine
Abstract
1. Introduction
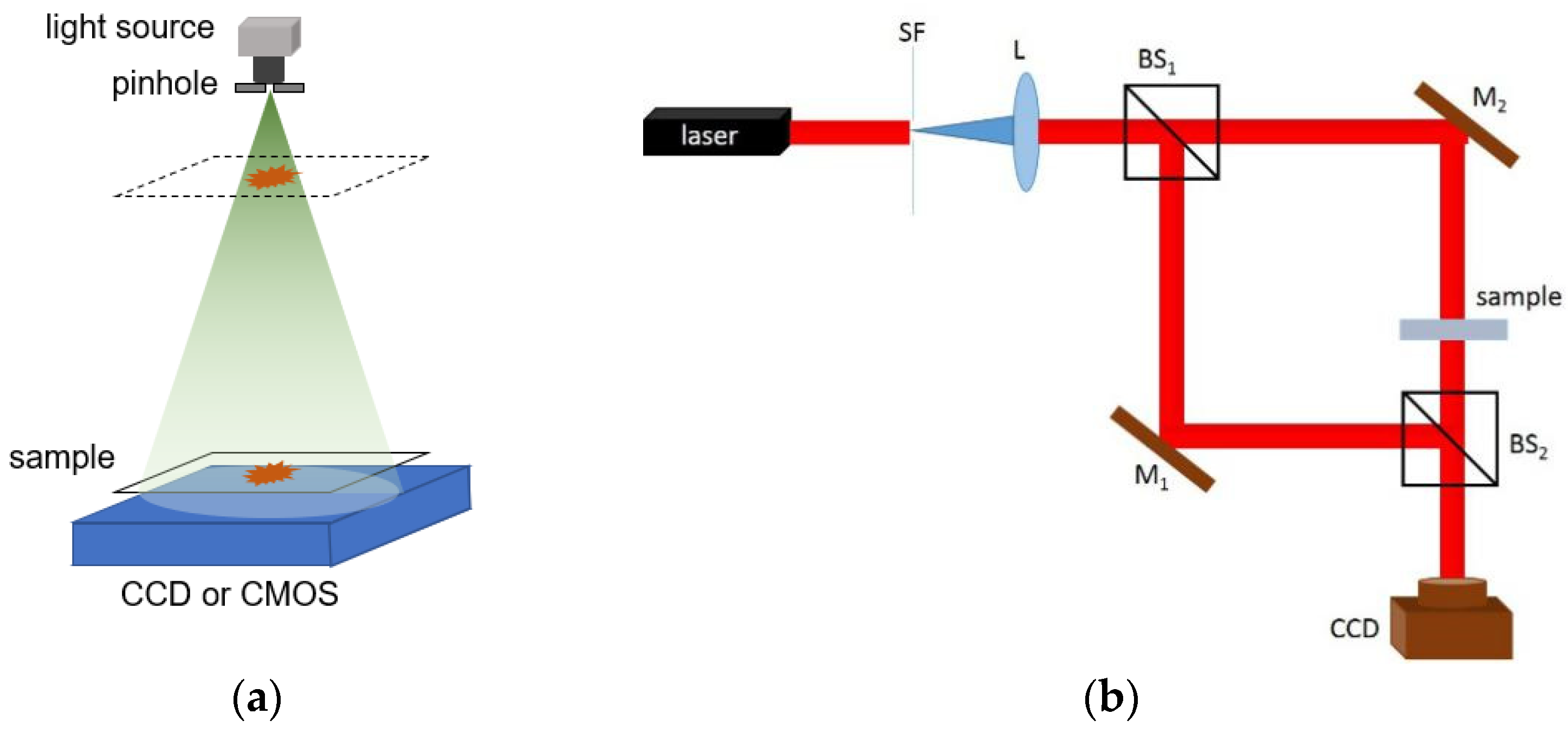
2. Principles of Lensless Digital Holographic Microscopy
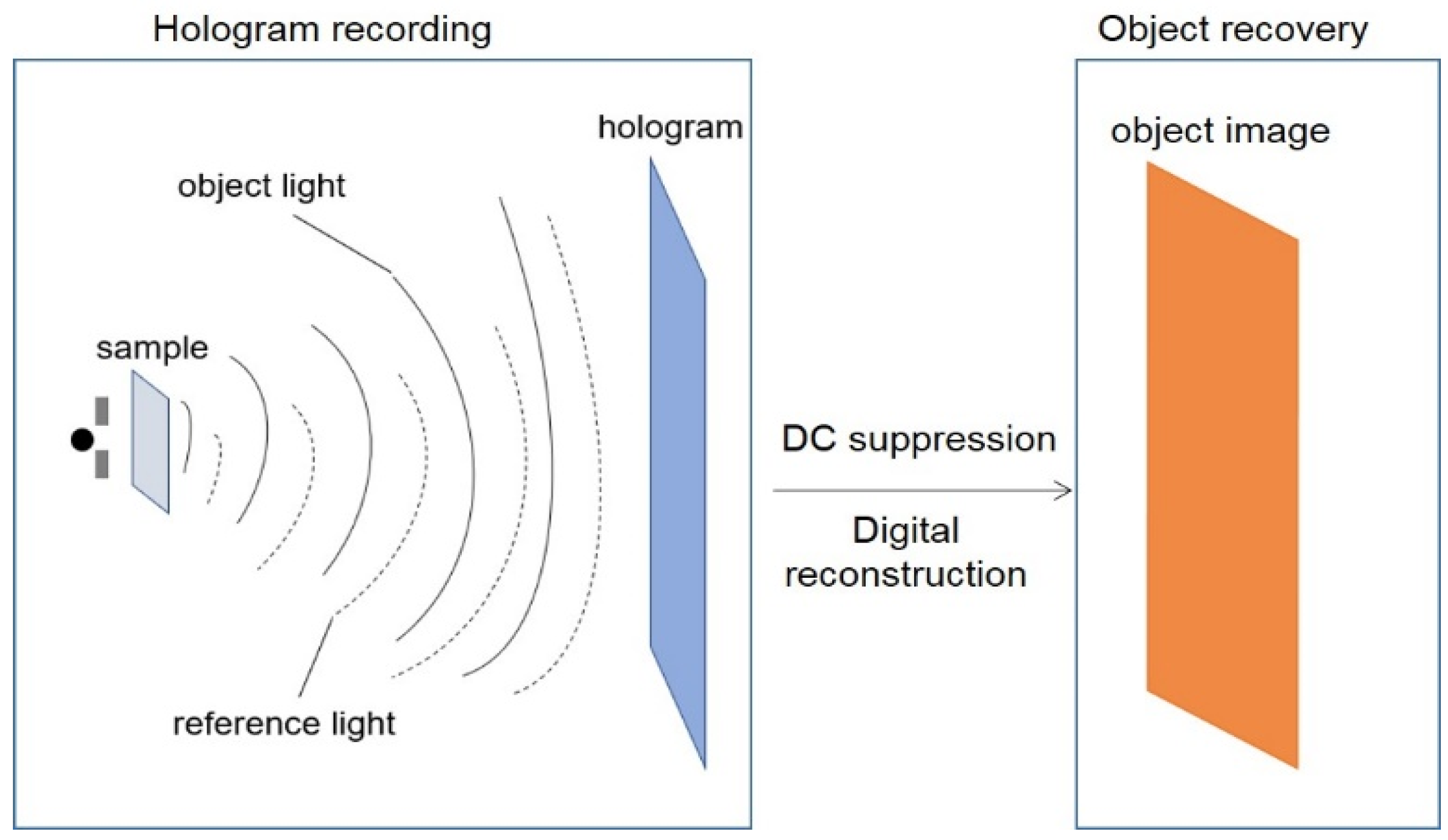
2.1. Hologram Recording
2.2. Digital Reconstruction
3. Contrast and Resolution Enhancement
3.1. Contrast Improvement
3.1.1. HRO and Hologram Normalization
3.1.2. Gerchberg–Saxton Iterative Algorithm
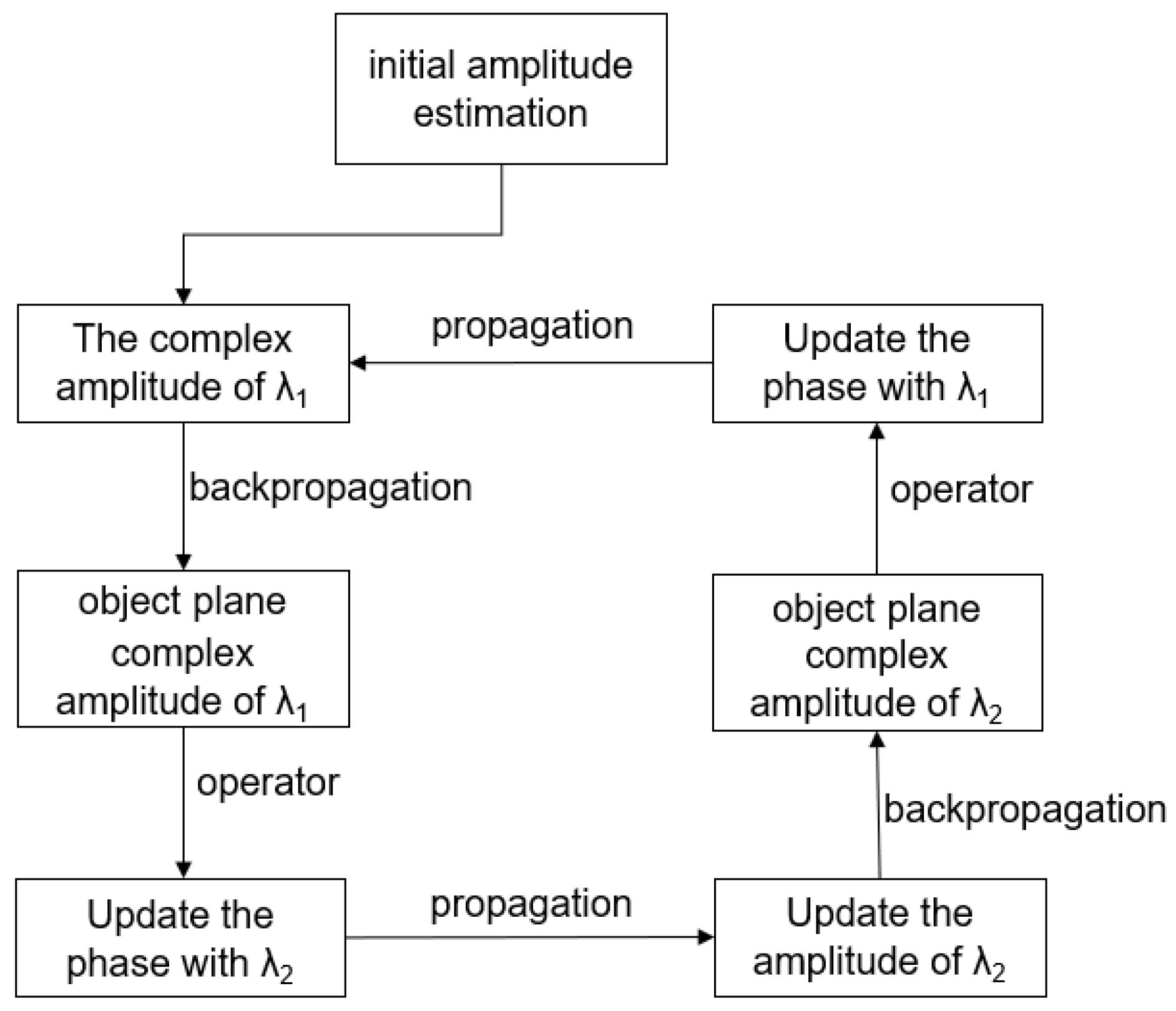
3.1.3. Multiwavelength Phase Retrieval
3.1.4. Phase Retrieval Based on Compressive Sensing
3.2. Resolution Enhancement
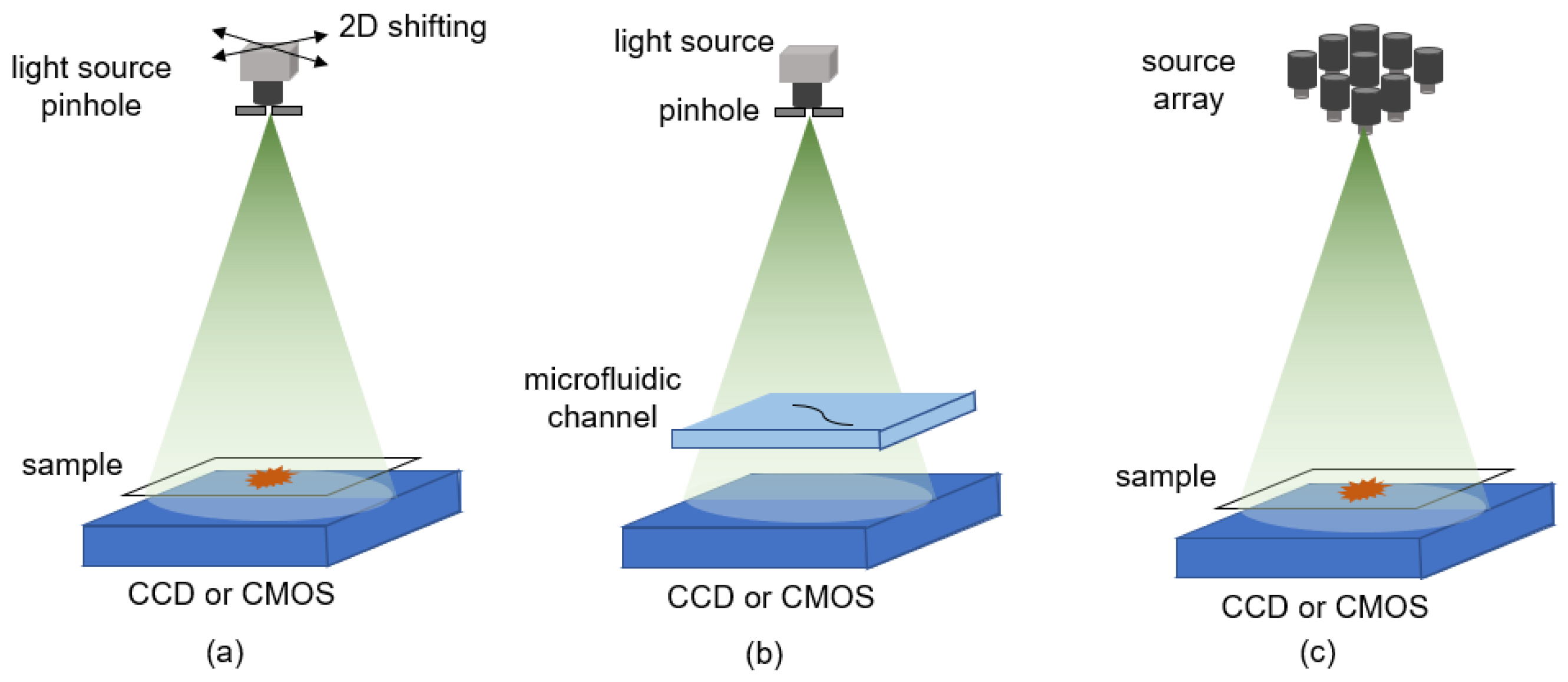
3.2.1. Pixel Super-Resolution Strategy
3.2.2. Synthetic Aperture Technology
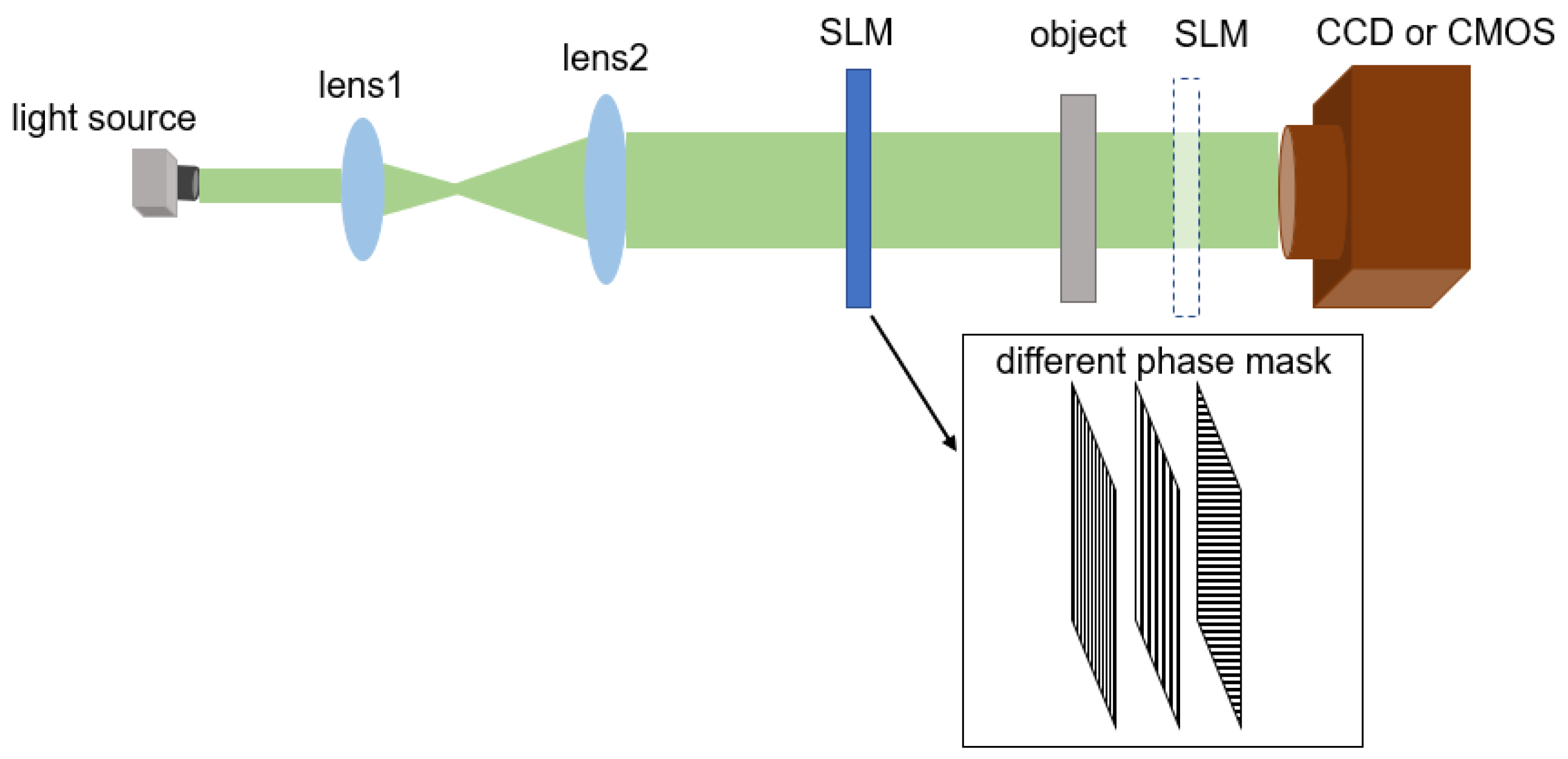
3.2.3. Use of SLM
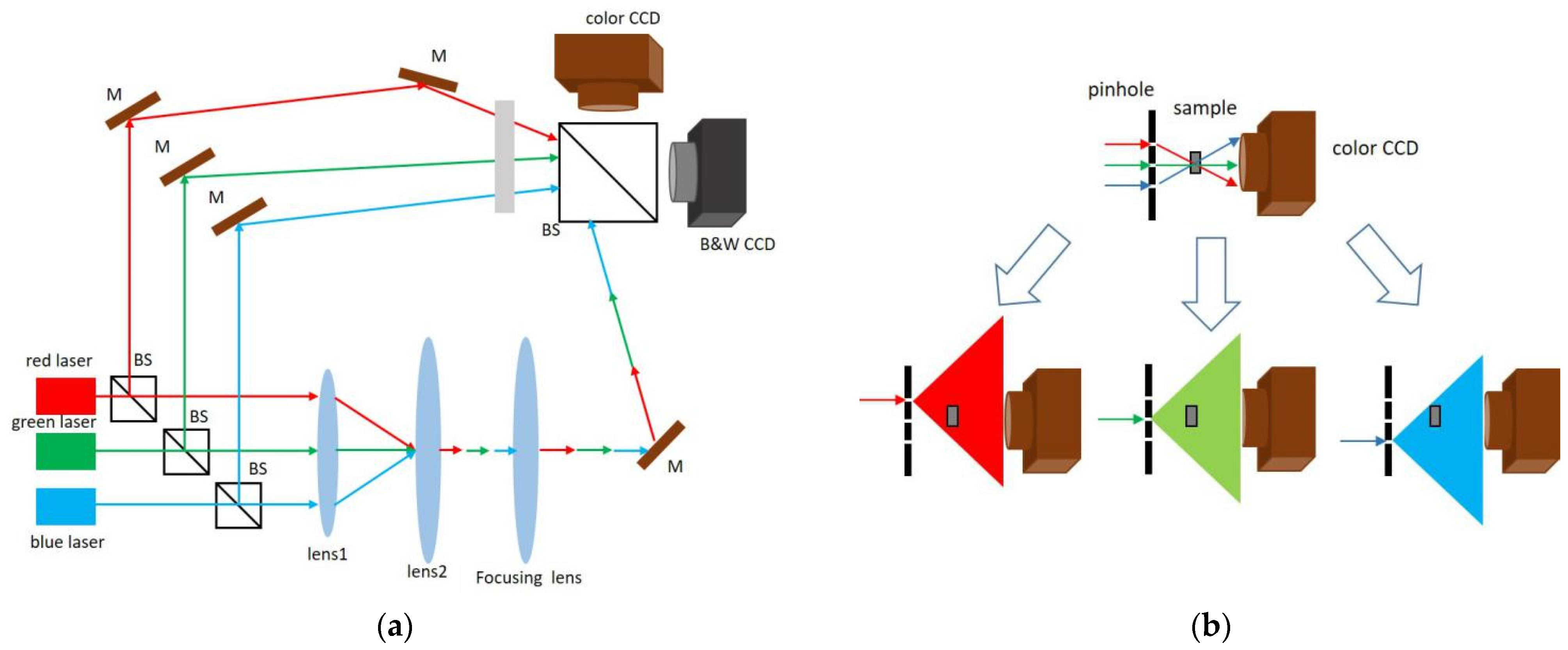
3.2.4. RGB Multiplexing
3.2.5. Data Interpolation
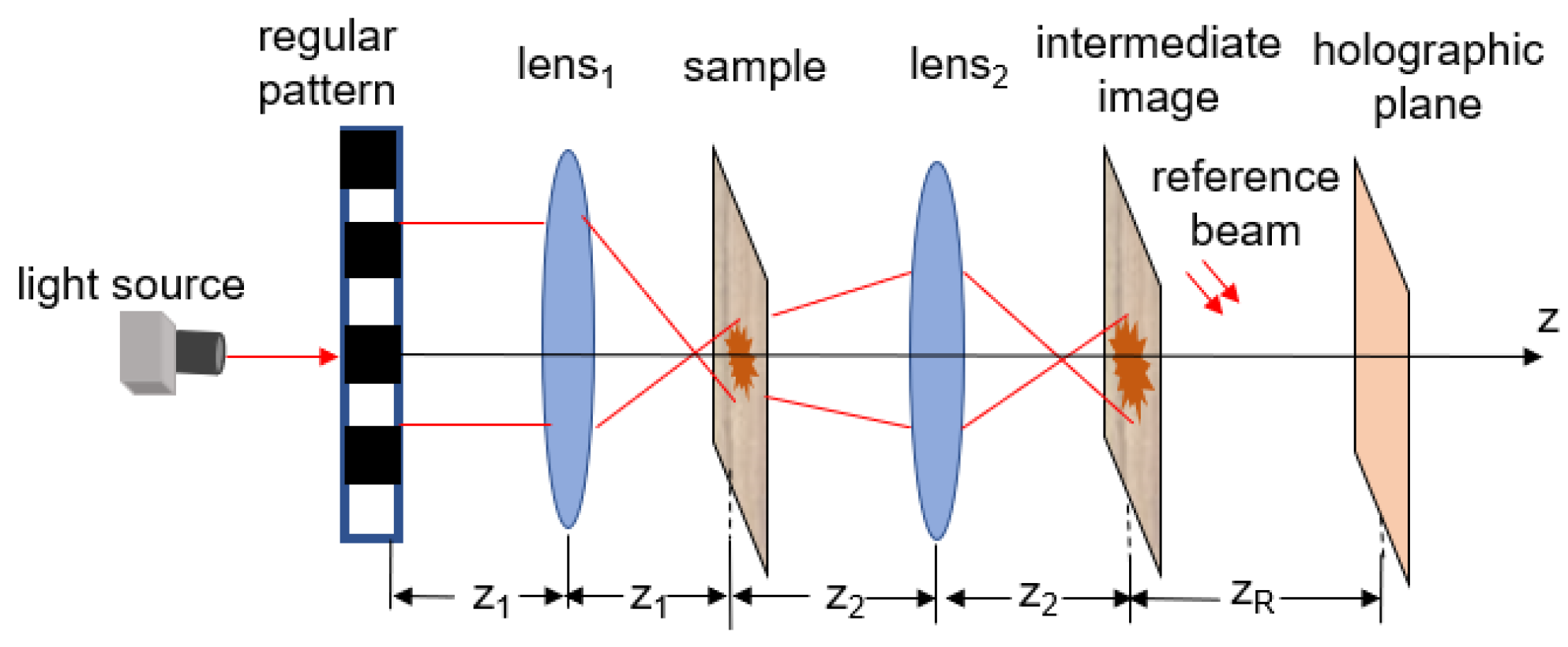
3.2.6. Different Illumination Strategies
3.2.7. Deep Learning
4. Application of Lensless High-Resolution Holographic Microscopy in Biomedicine
4.1. Molecular Quantitative Analysis
4.2. Flow Cytometry
4.3. Biomolecular Classification
5. Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Bardell, D. The Biologists’ Forum: The Invention of the Microscopy. Bios 2004, 75, 18–20. [Google Scholar] [CrossRef]
- Huang, T.S. Digital holography. Proc. IEEE 1971, 59, 1335–1346. [Google Scholar] [CrossRef]
- Pavillon, N.; Kühn, J.; Moratal, C.; Jourdain, P.; Depeursinge, C.; Magistretti, P.J.; Marquet, P. Early Cell Death Detection with Digital Holographic Microscopy. PLoS ONE 2012, 7, e30912. [Google Scholar] [CrossRef]
- Pavillon, N.; Kühn, J.; PJourdain Depeursinge, C.; Magistretti, P.J.; Marquet, P. Cell Death and Ionic Regulation Detection with Digital Holographic Microscopy. In Digital Holography and Three-Dimensional Imaging; Optical Society of America: Washington, DC, USA, 2011; p. DTuC25. [Google Scholar]
- Zeng, Y.; Lu, J.; Hu, X.; Chang, X.; Sun, Q. Axial displacement measurement with high resolution of particle movement based on compound digital holographic microscopy. Opt. Commun. 2020, 475, 126300. [Google Scholar] [CrossRef]
- El-Schich, Z.; Leida Mölder, A.; Gjörloff Wingren, A. Quantitative Phase Imaging for Label-Free Analysis of Cancer Cells—Focus on Digital Holographic Microscopy. Appl. Sci. 2018, 8, 1027. [Google Scholar] [CrossRef]
- Wu, Y.; Luo, Y.; Chaudhari, G.; Rivenson, Y.; Calis, A.; de Haan, K.; Ozcan, A.A. Bright-field holography: Cross-modality deep learning enables snapshot 3D imaging with bright-field contrast using a single hologram. Light Sci. Appl. 2019, 8, 25. [Google Scholar] [CrossRef]
- Pedrini, G.; Fröning, P.; Fessler, H.; Tiziani, H.J. In-line digital holographic interferometry. Appl. Opt. 1998, 37, 6262–6269. [Google Scholar] [CrossRef] [PubMed]
- Mudanyali, O.; Oztoprak, C.; Tseng, D.; Erlinger, A.; Ozcan, A. Detection of waterborne parasites using field-portable and cost-effective lensfree microscopy. Lab Chip 2010, 10, 2419–2423. [Google Scholar] [CrossRef]
- Cuche, E.; Marquet, P.; Depeursinge, C. Spatial filtering for zero-order and twin-image elimination in digital off-axis holography. Appl. Opt. 2000, 39, 4070–4075. [Google Scholar] [CrossRef]
- Liebling, M.; Blu, T.; Unser, M. Complex-wave retrieval from a single off-axis hologram. JOSA A 2004, 21, 367–377. [Google Scholar] [CrossRef]
- Sencan, I.; Coskun, A.F.; Sikora, U.; Ozcan, A. Spectral demultiplexing in holographic and fluorescent on-chip microscopy. Sci. Rep. 2014, 4, 3760. [Google Scholar] [CrossRef]
- Latychevskaia, T.; Fink, H. Solution to the twin image problem in holography. Phys. Rev. Lett. 2007, 98, 233901. [Google Scholar] [CrossRef] [PubMed]
- Greenbaum, A.; Luo, W.; Su, T.W.; Gorocs, Z.; Xue, L.; Isikman, S.O.; Coskun, A.F.; Mudanyali, O.; Ozcan, A. Imaging without lenses: Achievements and remaining challenges of wide-field on-chip microscopy. Nat. Methods 2012, 9, 889–895. [Google Scholar] [CrossRef] [PubMed]
- Mudanyali, O.; Tseng, D.; Oh, C.; Isikman, S.O.; Sencan, I.; Bishara, W.; Oztoprak, C.; Seo, S.K.; Khademhosseini, B.; Ozcan, A. Compact, light-weight and cost-effective microscopy based on lensless incoherent holography for telemedicine applications. Lab Chip 2010, 10, 1417–1428. [Google Scholar] [CrossRef] [PubMed]
- Luo, W.; Shabbir, F.; Gong, C.; Gulec, C.; Pigeon, J.; Shaw, J.; Greenbaum, A.; Tochitsky, S.; Joshi, C.; Ozcan, A. High throughput on-chip analysis of high-energy charged particle tracks using lensfree imaging. Appl. Phys. Lett. 2015, 106, 151107. [Google Scholar] [CrossRef]
- Wu, Y.; Ozcan, A. Lensless digital holographic microscopy and its applications in biomedicine and environmental monitoring. Methods 2018, 136, 4–16. [Google Scholar] [CrossRef]
- Garcia-Sucerquia, J.; Xu, W.; Jericho, S.K.; Klages, P.; Jericho, M.H.; Kreuzer, H.J. Digital in-line holographic microscopy. Opt. Lett. 2006, 45, 836–850. [Google Scholar] [CrossRef]
- Carlos, T.; Jorge, G.S. Numerical dark field illumination applied to experimental digital lensless holographic microscopy for reconstructions with enhanced contrast. Opt. Lett. 2018, 43, 4096–4099. [Google Scholar]
- Mendoza-Yero, O.; Tajahuerce, E.; Lancis, J.; Garcia-Sucerquia, J. Diffractive digital lensless holographic microscopy with fine spectral tuning. Opt. Lett. 2013, 38, 2107–2109. [Google Scholar] [CrossRef]
- Nicola, S.D.; Ferraro, P.; Finizio, A.; Pierattini, G. Wave front reconstruction of Fresnel off-axis holograms with compensation of aberrations by means of phase-shifting digital holography. Opt. Lasers Eng. 2002, 37, 331–340. [Google Scholar] [CrossRef]
- Schnars, U.; Jüptner, W.P.O. Digital recording and numerical reconstruction of holograms. Meas. Sci. Technol. 2002, 13, R85–R101. [Google Scholar] [CrossRef]
- Mann, C.J.; Kim, M.K. Quantitative phase-contrast microscopy by angular spectrum digital holography. SPIE 2006, 6090, 60900B. [Google Scholar]
- Loïc, D.; Fournier, C.; Fournel, T.; Ducottet, C. Twin-image noise reduction by phase retrieval in in-line digital holography. SPIE 2005, 5914, 59140J. [Google Scholar]
- Menesesfabian, C.; Rodriguezzurita, G.; Víctor, A. Optical tomography of transparent objects with phase-shifting interferometry and stepwise-shifted ronchi ruling. JOSA A 2006, 23, 298–305. [Google Scholar] [CrossRef] [PubMed]
- Arapov, Y.D.; Dvornichenko, M.E.; Kamenev, V.G.; Turkin, V.N. Reconstruction of Digital in-line Holograms and Suppression of the Twin-image in Gabor Holography. Sens. Transducers 2019, 233, 40–45. [Google Scholar]
- Fienup, J.R. Phase retrieval algorithms: A comparison. Appl. Opt. 1982, 21, 2758–2769. [Google Scholar] [CrossRef]
- Greenbaum, A.; Ozcan, A. Maskless imaging of dense samples using pixel super-resolution based multi-height lensfree on-chip microscopy. Opt. Express. 2012, 20, 3129–3143. [Google Scholar] [CrossRef]
- Greenbaum, A.; Zhang, Y.; Feizi, A.; Chung, P.; Luo, W.; Kandukuri, S.R.; Ozcan, A. Wide-field computational imaging of pathology slides using lens-free on-chip microscopy. Sci. Transl. Med. 2014, 6, 267ra175. [Google Scholar] [CrossRef]
- Guo, Y.; Fang, Z.; Qiang, S.; Jing, Z. Application of hybrid iterative algorithm in tie phase retrieval with large defocusing distance. Acta Opt. Sin. 2016, 36, 0912001. [Google Scholar]
- Zhou, W.; Guan, X.; Liu, F.; Yu, Y.; Zhang, H.; Poon, T.C.; Banerjee, P.P. Phase retrieval based on transport of intensity and digital holography. Appl. Opt. 2018, 57, A229–A234. [Google Scholar] [CrossRef]
- Lu, R.; Feng, P.; Wen, X.; Li, Y.; Wang, F. Twin image elimination from two in-line holograms via phase retrieval. Chin. Opt. Lett. 2012, 10, 0902. [Google Scholar]
- Barton, J.J. Removing multiple scattering and twin images from holographic images. Phys. Rev. Lett. 1991, 67, 3106–3109. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Stangner, T.; Wiklund, K.; Andersson, M. Object plane detection and phase retrieval from single-shot holograms using multi-wavelength in-line holography. Appl. Opt. 2018, 57, 9855–9862. [Google Scholar] [CrossRef] [PubMed]
- Emmanuel, J.; Candès Romberg, J.K.; Tao, T. Stable Signal Recovery from Incomplete and Inaccurate Measurements. Commun. Pure Appl. Math. 2006, 59, 1207–1223. [Google Scholar]
- Candes, E.J.; Tao, T. Near-Optimal Signal Recovery from Random Projections: Universal Encoding Strategies? IEEE Trans. Inf. Theory 2006, 52, 5406–5425. [Google Scholar] [CrossRef]
- Boyd, V.; Vandenberghe, L. Faybusovich, “Convex optimization”. IEEE Trans. Automat. Contr. 2006, 51, 1859. [Google Scholar]
- Weng, J.; Yang, C.; Qin, Y.; Hai, L. LED-based digital hologram reconstruction by compressive sensing. SPIE 2015, 9675, 967505. [Google Scholar]
- Zhang, W.; Cao, L.; Brady, D.J.; Zhang, H.; Cang, J.; Zhang, H.; Jin, G. Twin-Image-Free Holography: A Compressive Sensing Approach. Phys. Rev. Lett. 2018, 121, 093902. [Google Scholar] [CrossRef] [PubMed]
- Souza, J.C.; Freire, R.B.R.; Santos, P.A.M. Compressive holography with resolution improvement and lensless adjustable magnification. Opt. Commun. 2019, 437, 337–341. [Google Scholar] [CrossRef]
- Hua, L.; Xie, G.; Shaw, D.T.; Scott, P.D. Resolution enhancement in digital in-line holography. SPIE 1991, 1385, 142–151. [Google Scholar]
- Zhang, W.; Zhang, H.; David, J.; Jin, G.; Cao, L. Compressive depth-resolved holographic microscopy. In Digital Holography and Three-Dimensional Imaging; Optical Society of America: Washington, DC, USA, 2019; p. Th3A.8. [Google Scholar]
- Rivenson, Y.; Wu, Y.; Wang, H.; Zhang, Y.; Feizi, A.; Ozcan, A. Sparsity-based multi-height phase recovery in holographic microscopy. Sci. Rep. 2018, 6, 37862. [Google Scholar] [CrossRef] [PubMed]
- Ozcan, A.; McLeod, E. Lensless imaging and sensing. Annu. Rev. Biomed. Eng. 2016, 18, 77–102. [Google Scholar] [CrossRef] [PubMed]
- Farsiu, S.; Robinson, M.D.; Elad, M.; Milanfar, P. Fast and robust multiframe super resolution. IEEE Trans. Image. Process. 2004, 13, 1327–1344. [Google Scholar] [CrossRef]
- Greenbaum, A.; Luo, W.; Khademhosseinieh, B.; Su, T.W.; Coskun, A.F.; Ozcan, A. Increased space-bandwidth product in pixel super-resolved lensfree on-chip microscopy. Sci. Rep. 2013, 3, 1717. [Google Scholar] [CrossRef]
- Bishara, W.; Zhu, H.; Ozcan, A. Holographic opto-fluidic microscopy. Opt. Express. 2010, 18, 27499–27510. [Google Scholar] [CrossRef] [PubMed]
- Bishara, W.; Sikora, U.; Mudanyali, O.; Su, T.; Yaglidere, O.; Luckhart, S.; Ozcan, A. Holographic pixel super-resolution in portable lensless on-chip microscopy using a fiber-optic array. Lab Chip 2010, 11, 1276–1279. [Google Scholar] [CrossRef]
- Gao, Y.; Cao, L. Generalized optimization framework for pixel super-resolution imaging in digital holography. Opt. Express 2021, 29, 28805–28823. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Kim, J.; Kim, J.; Jeon, P.; Lee, S.A.; Kim, D. Noniterative sub-pixel shifting super-resolution lensless digital holography. Opt. Express 2021, 29, 29996–30006. [Google Scholar] [CrossRef]
- Curlander, J.C.; McDonough, R.N. Synthetic Aperture Radar; John Wiley and Sons: New York, NY, USA, 1991. [Google Scholar]
- Vicente, M.; Zalevsky, Z. Superresolved digital in-line holographic microscopy for high-resolution lensless biological imaging. J. Biomed. Opt. 2010, 15, 046027. [Google Scholar]
- Barak, K.; Joseph, R. Super-resolution in incoherent optical imaging using synthetic aperture with Fresnel elements. Opt. Express 2010, 18, 962–972. [Google Scholar]
- Ferreira, C.; García, J.; Micó, V. Surpassing digital holography limits by lensless object scanning holography. Opt. Express 2012, 20, 9382. [Google Scholar]
- Lai, X.; Tu, H.; Wu, H.; Lin, Y.; Cheng, J. Resolution enhancement of spectrum normalization in synthetic aperture digital holographic microscopy. Appl. Opt. 2015, 54, 51–58. [Google Scholar] [CrossRef]
- Huang, H.; Rong, L.; Wang, D.; Li, W.; Deng, Q.; Li, B.; Wang, Y.; Zhan, Z.; Wang, X.; Wu, D. Synthetic aperture in terahertz in-line digital holography for resolution enhancement. Appl. Opt. 2016, 55, A43–A48. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.; Tu, H.; Wu, X.; Lai, X.; Cheng, C. One-shot synthetic aperture digital holographic microscopy with non-coplanar angular-multiplexing and coherence gating. Opt. Express 2018, 26, 12620–12631. [Google Scholar] [CrossRef] [PubMed]
- Bernet, S.; Harm, W.; Jesacher, A.; Ritsch-Marte, M. Lensless digital holography with diffuse illumination through a pseudo-random phase mask. Opt. Express 2011, 19, 25113–25124. [Google Scholar] [CrossRef] [PubMed]
- Hussain, A.; Li, Y.; Liu, D.; Kuang, C.; Xu, L. Lensless imaging through multiple phase patterns illumination. J. Biomed. Opt. 2017, 22, 110502. [Google Scholar] [CrossRef] [PubMed]
- Katkovnik, V.; Shevkunov, I.; Petrov, N.V.; Egiazarian, K. Computational wavelength resolution for in-line lensless holography: Phase-coded diffraction patterns and wavefront group-sparsity. SPIE 2017, 10335, 033509. [Google Scholar]
- Li, B.; Wang, D.; Wang, Y.; Rong, L. High-resolution digital holographic imaging by using a spatial light modulator. SPIE 2017, 9282, 92820N. [Google Scholar]
- Lin, Q.; Wang, D.; Wang, Y.; Rong, L.; Chang, S. Super-resolution imaging in digital holography by using dynamic grating with a spatial light modulator. Opt. Lasers Eng. 2015, 66, 279–284. [Google Scholar] [CrossRef]
- Calabuig, A.; Ferreira, C.; Garcia, J.; Zalevsky, Z.; Mico, V. Resolution improvement by single-exposure superresolved interferometric microscopy with a monochrome sensor. JOSA A 2011, 28, 2346–2358. [Google Scholar] [CrossRef]
- Ferraro, P.; Grilli, S.; Ritsch-Marte, M.; Stifter, D.; Sanz, M.; Picazo-Bueno, J.A.; Garcia, J.; Mico, V. Multi-illumination Gabor holography recorded in a single camera snap-shot for high-resolution phase retrieval in digital in-line holographic microscopy. SPIE 2015, 9529, 95290B. [Google Scholar]
- Calabuig, A.; Micó, V.; Garcia, J.; Zalevsky, Z.; Ferreira, C. Single-exposure super-resolved interferometric microscopy by red-green-blue multiplexing. Opt. Lett. 2011, 36, 885–887. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Granero, L.; Ferreira, C.; Zalevsky, Z.; Garcia, J.; Mico, V. Single-exposure super-resolved interferometric microscopy by RGB multiplexing in lensless configuration. Opt. Lasers Eng. 2016, 82, 104–112. [Google Scholar] [CrossRef]
- Granero, L.; Ferreira, C.; Garcia, J. Lensless single-exposure super-resolved interferometric microscopy. SPIE 2013, 8788, 878808. [Google Scholar]
- Podorov, S.G.; Bishop, A.I.; Paganin, D.M.; Pavlov, K.M. Re-sampling of inline holographic images for improved reconstruction resolution. arXiv 2009, arXiv:0911. 0520. [Google Scholar]
- Tahara, T.; Awatsuji, Y.; Kaneko, A.; Koyama, T.; Nishio, K.; Ura, S.; Matoba, K. Parallel two-step phase-shifting digital holography using polarization. Opt. Rev. 2010, 17, 108–113. [Google Scholar] [CrossRef]
- Wang, M.; Wu, J. Iterative digital in-line holographic reconstruction with improved resolution by data interpolation. SPIE 2014, 9271, 927110. [Google Scholar]
- Neil, M.A.A.; Juškaitis, R.; Wilson, T. Method of obtaining optical sectioning by using structured light in a conventional microscopy. Opt. Lett. 1997, 22, 1905–1907. [Google Scholar] [CrossRef]
- Lai, X.; Tu, H.; Lin, Y.; Cheng, C. Structured illumination induced moiré fringes for resolution enhancement in digital holographic microscopy. In Digital Holography and Three-Dimensional Imaging; Optical Society of America: Washington, DC, USA, 2016; p. DT4G.4. [Google Scholar]
- Ma, J.; Yuan, C.; Situ, G.; Pedrini, G.; Osten, W. Resolution enhancement in digital holographic microscopy with structured illumination. Chin. Opt. Lett. 2013, 11, 090901. [Google Scholar]
- Feng, S.; Wang, M.; Wu, J. Enhanced resolution for amplitude object in lensless inline holographic microscopy with grating illumination. Opt. Eng. 2017, 56, 093107. [Google Scholar] [CrossRef]
- Gao, P.; Pedrini, G.; Osten, W. Structured illumination for resolution enhancement and autofocusing in digital holographic microscopy. Opt. Lett. 2013, 38, 1328–1330. [Google Scholar] [CrossRef] [PubMed]
- Ganjkhani, Y.; Charsooghi, M.A.; Akhlaghi, E.A.; Moradi, A. Super-resolved Mirau digital holography by structured illumination. Opt. Commun. 2017, 404, 110–117. [Google Scholar] [CrossRef]
- Ma, J.; Yin, Y.; Su, P. Radial super-resolution in digital holographic microscopy using structured illumination with circular symmetry. SPIE 2018, 10616, 1061603. [Google Scholar]
- Greenbaum, A.; Akbari, N.; Feizi, A.; Wei, L.; Ozcan, A. Field-Portable Pixel Super-Resolution Color Microscopy. PLoS ONE 2013, 8, e76475. [Google Scholar] [CrossRef]
- Feng, S.; Wu, J. Resolution enhancement method for lensless in-line holographic microscopy with spatially-extended light source. Opt. Express 2017, 25, 24735–24744. [Google Scholar] [CrossRef] [PubMed]
- Shaodong, F.; Jigang, W. Differential holographic reconstruction for lensless in-line holographic microscopy with ultra-broadband light source illumination. Opt. Commun. 2019, 430, 9–13. [Google Scholar]
- Wagner, K.H. Deep optical learning devices and architectures. In Proceedings of the IEEE Photonics Society Summer Topical Meeting Series (SUM), Newport Beach, CA, USA, 11–13 July 2016; p. 16263439. [Google Scholar]
- Rivenson, Y.; Zhang, Y.; Gunaydin, H.; Da, T.; Ozcan, A. Phase recovery and holographic image reconstruction using deep learning in neural networks. Light Sci. Appl. 2017, 7, 17141. [Google Scholar] [CrossRef]
- Wu, Y.; Rivenson, Y.; Zhang, Y.; Wei, Z.; Gunaydin, H.; Lin, X.; Ozcan, A. Extended depth-of-field in holographic image reconstruction using deep learning based auto-focusing and phase-recovery. Optica 2018, 6, 704–710. [Google Scholar] [CrossRef]
- Gong, Z.; Tian, G.; Shen, Z.; Wang, X.; Hu, T.; Wang, D.; He, Y.; Xie, N. Fast phase retrieval in off-axis digital holographic microscopy through deep learning. Opt. Express 2018, 26, 19388–19405. [Google Scholar]
- Ren, Z.; Xu, Z.; Edmund, Y.M. End-to-end deep learning framework for digital holographic reconstruction. SPIE 2019, 1, 016004. [Google Scholar] [CrossRef]
- Liu, T.; De Haan, K.; Rivenson, Y.; Wei, Z.; Zeng, X.; Zhang, Y.; Ozcan, A. Deep learning-based super-resolution in coherent imaging systems. Sci. Rep. 2019, 9, 3926. [Google Scholar] [CrossRef]
- Seo, S.; Isikman, S.O.; Sencan, I.; Mudanyali, O.; Su, T.; Bishara, W.; Erlinger, A.; Ozcan, A. High-Throughput Lens-Free Blood Analysis on a Chip. Anal. Chem. 2010, 82, 4621–4627. [Google Scholar] [CrossRef] [PubMed]
- Yi, F.; Moon, I.; Javidi, B. Automated red blood cells extraction from holographic images using fully convolutional neural networks. Biomed. Opt. Express 2017, 8, 4466–4479. [Google Scholar] [CrossRef]
- Jo, Y.J.; Park, S.; Jung, J.H.; Yoon, J.; Park, Y.K. Holographic deep learning for rapid optical screening of anthrax spores. Sci. Adv. 2017, 3, e1700606. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.B.; Koydemir, H.C.; Shimogawa, M.M.; Yalcin, S.; Guziak, A.; Liu, T.; Oguz, I.; Huang, Y.; Bai, B.; Luo, Y.; et al. Motility-based label-free detection of parasites in bodily fluids using holographic speckle analysis and deep learning. Light Sci. Appl. 2018, 7, 108. [Google Scholar] [CrossRef]
- Mangal, J.; Monga, R.; Mathur, S.R.; Dinda, A.K.; Khare, K. Unsupervised organization of cervical cells using high resolution digital holographic microscopy. arXiv 2018, arXiv:1811.05214. [Google Scholar]
- Zikmund, T.; Kvasnica, L.; Tyc, M.; Krizova, A.; Collakova, J.; Chmelik, R. Sequential processing of quantitative phase images for the study of cell behaviour in real-time digital holographic microscopy. J. Microsc. 2014, 256, 117–125. [Google Scholar] [CrossRef]
- Hannel, M.D.; Abdulali, A.; O’Brien, M.; Grier, D.G. Machine-learning techniques for fast and accurate feature localization in holograms of colloidal particles. Opt. Express 2018, 26, 15221–15231. [Google Scholar] [CrossRef] [PubMed]
- Serabyn, E.; Liewer, K.; Lindensmith, C.; Kent, W.; Jay, N. Compact, lensless digital holographic microscopy for remote microbiology. Opt. Express 2016, 24, 28540–28548. [Google Scholar] [CrossRef] [PubMed]
- Langehanenberg, P.; Ivanova, L.; Bernhardt, I.; Ketelhut, S.; Vollmer, A.; Dirksen, D. Automated three-dimensional tracking of living cells by digital holographic microscopy. J. Biomed. Opt. 2009, 14, 014018. [Google Scholar] [CrossRef]
- Xiao, W.; Wang, O.; Pan, F.; Cao, R.; Yi, X. Unlabeled flow cellular deformation measurement based on digital holographic microscopy. SPIE 2018, 10749, 107490L. [Google Scholar]
- Langehanenberg, P.; Bally, G.V.; Kemper, B. Autofocusing in digital holographic microscopy. 3D Res. 2011, 2, 4. [Google Scholar] [CrossRef]
- Boudejltia, K.Z.; Daniel, R.D.S.; Uzureau, P.; Yourassowsky, C.; David, P.M.; Guy, C.; Chopard, B.; Frank, D. Quantitative analysis of platelets aggregates in 3D by digital holographic microscopy. Biomed. Opt. Express 2015, 6, 3556–3563. [Google Scholar] [CrossRef] [PubMed]
- Jolivet, F.; Momey, F.; Denis, L.; Méès, L.; Faure, N.; Grosjean, N.; Pinston, F.; Marié, J.L.; Fournier, C. Regularized reconstruction of absorbing and phase objects from a single in-line hologram, application to fluid mechanics and micro-biology. Opt. Express 2018, 26, 8923–8940. [Google Scholar] [CrossRef] [PubMed]
- Barbastathis, G.; José, A.; Domínguez-Caballero, J.A.; Barbastathis, G. Quantitative measurement of size and three-dimensional position of fast-moving bubbles in air-water mixture flows using digital holography. Appl. Opt. 2010, 49, 1549. [Google Scholar]
- Loïc, D.; Fournier, C.; Fournel, T.; Ducottet, C.; Jeulin, D. Direct extraction of the mean particle size from a digital hologram. Appl. Opt. 2008, 45, 944–952. [Google Scholar]
- Dubois, F.; Callens, N.; Yourassowsky, C.; Hoyos, M.; Kurowski, P.; Monnom, O. Digital holographic microscopy with reduced spatial coherence for three-dimensional particle flow analysis. Appl. Opt. 2006, 45, 864–871. [Google Scholar] [CrossRef]
- Ray, A.; Li, S.; Segura, T.; Ozcan, A. High-throughput quantification of nanoparticle degradation using computational microscopy and itsapplication to drug delivery nanocapsules. ACS Photonics 2017, 4, 1216–1224. [Google Scholar] [CrossRef]
- Wu, Y.; Shiledar, A.; Li, Y.; Wong, J.; Feng, S.; Chen, X.; Chen, C.; Jin, K.; Janamian, S.; Yang, Z.; et al. Air quality monitoring using mobile microscopy and machine learning. Light Sci. Appl. 2017, 6, e17046. [Google Scholar] [CrossRef]
- Isikman, S.O.; Bishara, W.; Sikora, U.; Yaglidere, O.; Yeah, J.; Ozcan, A. Field-portable lensfree tomographic microscope. Lab Chip 2011, 11, 2222–2230. [Google Scholar] [CrossRef]
- Isikman, S.O.; Bishara, W.; Zhu, H.; Ozcan, A. Optofluidic tomography on a chip. Appl. Phys. Lett. 2011, 98, 161109. [Google Scholar] [CrossRef] [PubMed]
- Bian, Y.; Zhang, Y.; Yin, P.; Li, H.; Ozcan, A. Optical refractometry using lensless holography and autofocusing. Opt. Express 2018, 26, 29614–29628. [Google Scholar] [CrossRef] [PubMed]
- Trask, B.J.; Engh, G.J.V.D.; Elgershuizen, J.H.B.W. Analysis of phytoplankton by flow cytometry. Cytom. A 1982, 2, 258–264. [Google Scholar] [CrossRef] [PubMed]
- Dominguez-Caballero, J.A.; Loomis, N.; Li, W. Advances in Plankton Imaging Using Digital Holography. In Digital Holography and Three-Dimensional Imaging; Optical Society of America: Washington, DC, USA, 2007; p. DMB5. [Google Scholar]
- Merola, F.; Memmolo, P.; Miccio, L.; Savoia, R.; Mugnano, M.; Fontana, A.; D’Ippolito, G.; Sardo, A.; Iolascon, A.; Gambale, A.; et al. Tomographic flow cytometry by digital holography. Light Sci. Appl. 2016, 6, e16241. [Google Scholar] [CrossRef] [PubMed]
- Gorocs, Z.; Tamamitsu, M.; Bianco, V.; Wolf, P.; Roy, S.; Shindo, K.; Yanny, K.; Wu, Y.; Koydemir, H.C.; Rivenson, Y.; et al. A deep learning-enabled portable imaging flow cytometer for cost-effective, high-throughput, and label-free analysis of natural water samples. Light Sci. Appl. 2018, 7, 66. [Google Scholar] [CrossRef]
- Delikoyun, K.; Cine, E.; Anil-Inevi, M.; Ozuysal, M.; Tekin, H.C. Lensless Digital in-Line Holographic Microscopy for Space Biotechnology Applications. In Proceedings of the IEEE 9th International Conference on Recent Advances in Space Technologies, Istanbul, Turkey, 11–14 June 2019. [Google Scholar]
- Wu, Y.C.; Ayfer, C.; Yi, L.; Chen, C.; Lutton, M.; Rivenson, Y.; Lin, X.; Koydemir, H.C.; Zhang, Y.; Wang, H.; et al. Label-free bio-aerosol sensing using mobile microscopy and deep learning. Rights Permis. 2018, 5, 4617–4627. [Google Scholar]
- Holmes, D.; Whyte, G.; Bailey, J.; Vergara-Irigaray, N.; Ekpenyong, A.; Guck, J.; Duke, T. Separation of blood cells with differing deformability using deterministic lateral displacement. Interface Focus 2014, 4, 20140011. [Google Scholar] [CrossRef]
- Schneider, B.; Vanmeerbeeck, G.; Stahl, R.; Lagae, L.; Dambre, J.; Bienstman, P. Neural network for blood cell classification in a holographic microscopy system. In Proceedings of the IEEE 17th International Conference on Transparent Optical Networks, Budapest, Hungary, 5–9 July 2015; pp. 1–4. [Google Scholar]
- Schneider, B.; Vanmeerbeeck, G.; Stahl, R.; Lagae, L.; Bienstman, P. Using neural networks for high-speed blood cell classification in a holographic-microscopy flow-cytometry system. SPIE 2015, 9328, 93281F. [Google Scholar]
- Lugnan, A.; Dambre, J.; Bienstman, P. Integrated pillar scatterers for speeding up classification of cell holograms. Opt. Express 2017, 25, 30526–30538. [Google Scholar] [CrossRef]
- Lugnan, A.; Dambre, J.; Bienstman, P. Integrated dielectric scatterers for fast optical classification of biological cells. Neuro-Inspir. Photonic Comput. Workshop 2018, 10689, 1068907. [Google Scholar]
- Chen, D.; Wang, Z.; Chen, K.; Zeng, Q.; Wang, L.; Xu, X.; Liang, J.; Chen, X. Classification of unlabelled cells using lensless digital holographic images and deep neural networks. Quant. Imaging Med. Surg. 2021, 11, 4137–4148. [Google Scholar] [CrossRef] [PubMed]
- Buzalewicz, I.; Kujawińska, M.; Krauze, W.; Podbielska, H. Novel Perspectives on the Characterization of Species-Dependent Optical Signatures of Bacterial Colonies by Digital Holography. PLoS ONE 2016, 11, e0150449. [Google Scholar] [CrossRef] [PubMed]
- Ling, H.; Sridhar, K.; Gollapudi, S.; Kumar, J.; Kumar, J.; Ohgami, R.S. Measurement of cell volume using in-line digital holography. Microscopy 2021, 70, 333–339. [Google Scholar] [CrossRef] [PubMed]
- Eder, K.M.; Marzi, A.; Barroso, Á.; Ketelhut, S.; Kemper, B.; Schnekenburger, J. Label-Free Digital Holographic Microscopy for In Vitro Cytotoxic Effect Quantification of Organic Nanoparticles. Cells 2022, 11, 644. [Google Scholar] [CrossRef]
- Vom Werth, K.L.; Wörmann, T.; Kemper, B.; Kümpers, P.; Kampmeier, S.; Mellmann, A. Investigating Morphological Changes of T-lymphocytes after Exposure with Bacterial Determinants for Early Detection of Septic Conditions. Microorganisms 2022, 10, 391. [Google Scholar] [CrossRef]
- Steike, D.R.; Hessler, M.; Korsching, E.; Lehmann, F.; Schmidt, C.; Ertmer, C.; Schnekenburger, J.; Eich, H.T.; Kemper, B.; Greve, B. Digital holographic microscopy for label-free detection of leukocyte alternations associated with perioperative inflammation after cardiac surgery. Cells 2022, 11, 755. [Google Scholar] [CrossRef]




| Technique | Configuration | Phase | Improvement (Times) |
|---|---|---|---|
| Pixel super-resolution [46,47,48,49,50] | Single light source or source array | Not required | 6 |
| Synthetic aperture [52,53,54,55,56,57] | Single channel or three channels | Required, by SLM | ~1.5 |
| SLM-based [58,59,60,61,62] | Single channel | Required, by SLM | ~2 |
| RGB multiplexing [63,64,65,66,67] | Three channels | Not required | 2.5 |
| Data interpolation [68,69,70] | None | Not required | ~1.26 |
| Structured light [71,72,73,74,75,76,77] | Single channel | Required, by SLM | ~1.5 |
| Spatially-extended light [79] | Single channel | Not required | Not given |
| Deep learning [7,82,83,84,85,86] | None | Not required | Diffraction limited |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, D.; Wang, L.; Luo, X.; Xie, H.; Chen, X. Resolution and Contrast Enhancement for Lensless Digital Holographic Microscopy and Its Application in Biomedicine. Photonics 2022, 9, 358. https://doi.org/10.3390/photonics9050358
Chen D, Wang L, Luo X, Xie H, Chen X. Resolution and Contrast Enhancement for Lensless Digital Holographic Microscopy and Its Application in Biomedicine. Photonics. 2022; 9(5):358. https://doi.org/10.3390/photonics9050358
Chicago/Turabian StyleChen, Duofang, Lin Wang, Xixin Luo, Hui Xie, and Xueli Chen. 2022. "Resolution and Contrast Enhancement for Lensless Digital Holographic Microscopy and Its Application in Biomedicine" Photonics 9, no. 5: 358. https://doi.org/10.3390/photonics9050358
APA StyleChen, D., Wang, L., Luo, X., Xie, H., & Chen, X. (2022). Resolution and Contrast Enhancement for Lensless Digital Holographic Microscopy and Its Application in Biomedicine. Photonics, 9(5), 358. https://doi.org/10.3390/photonics9050358






