The Optimization of Metal Nitride Coupled Plasmon Waveguide Resonance Sensors Using a Genetic Algorithm for Sensing the Thickness and Refractive Index of Diamond-like Carbon Thin Films
Abstract
1. Introduction
2. Materials and Methods
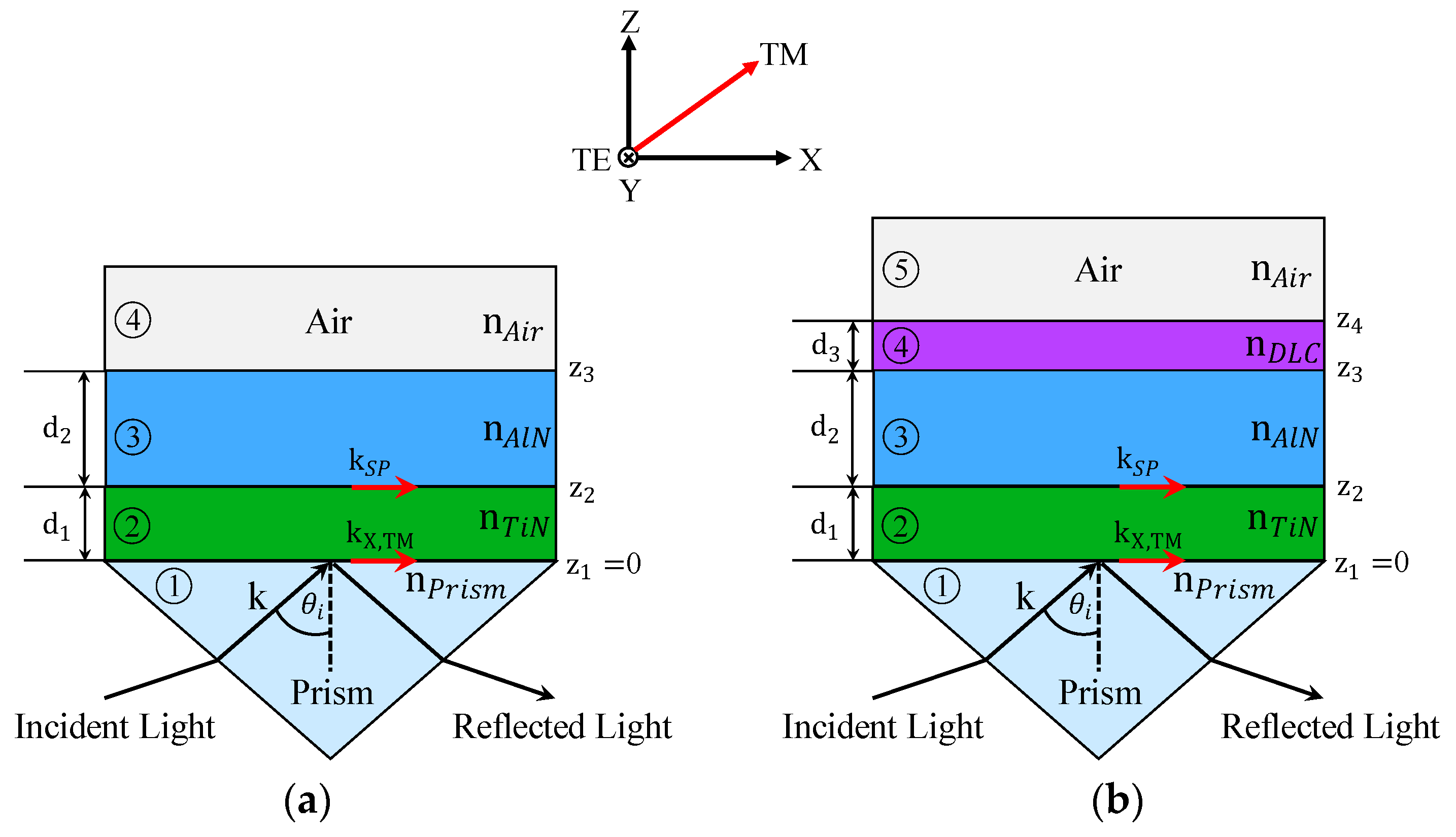
2.1. Selection of Materials for CPWR Sensor
2.2. Theoretical Modeling
2.2.1. Transfer Matrix Method (TMM)
2.2.2. Drude–Lorentz Model
2.3. The Finite-Difference Time-Domain (FDTD) Method
2.4. Genetic Algorithm Optimization
3. Results
3.1. The Results from the GA Approach
3.2. Theoretical CPWR Spectra
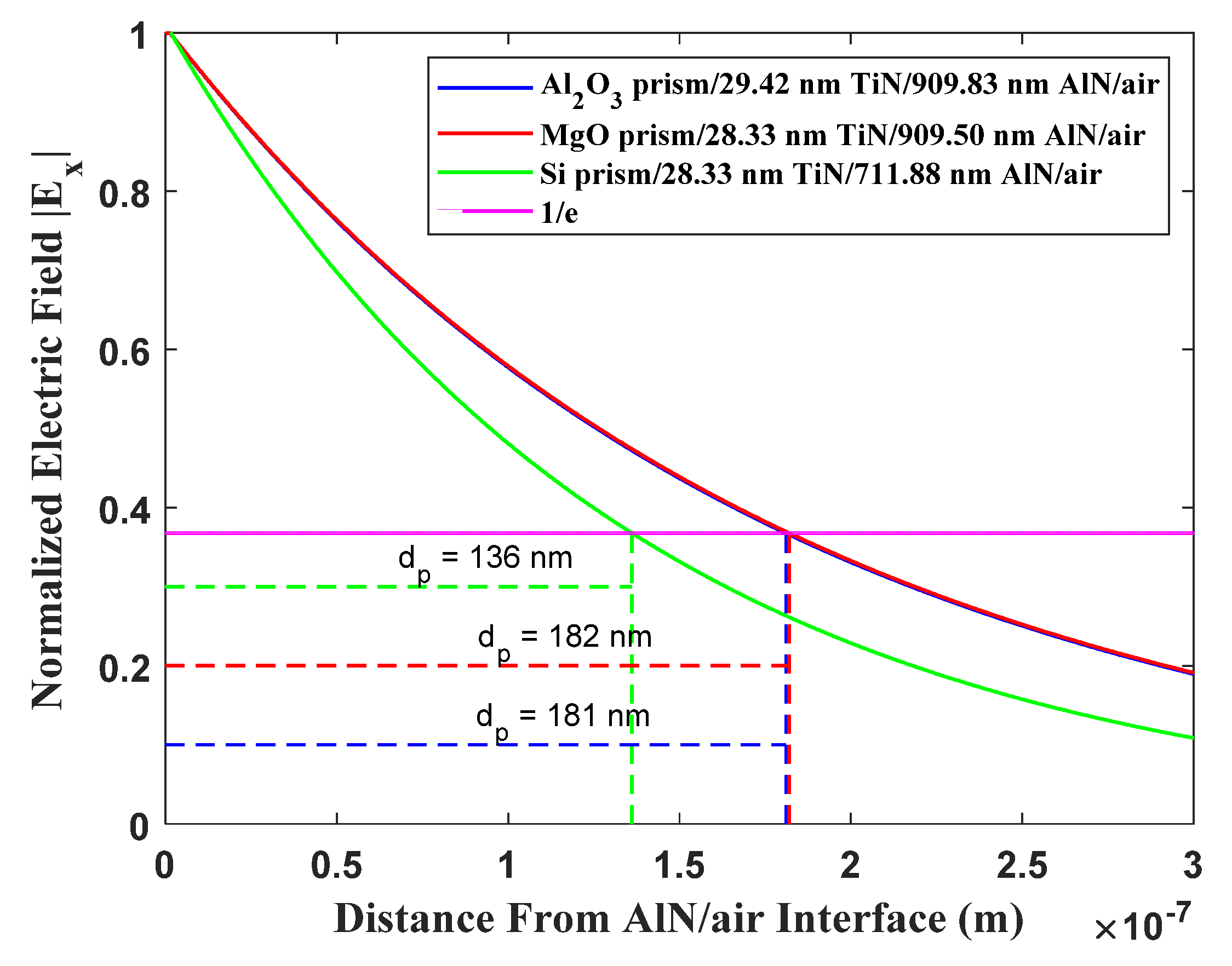
3.3. Field Distribution for TM Polarized Light and Penetration Depth
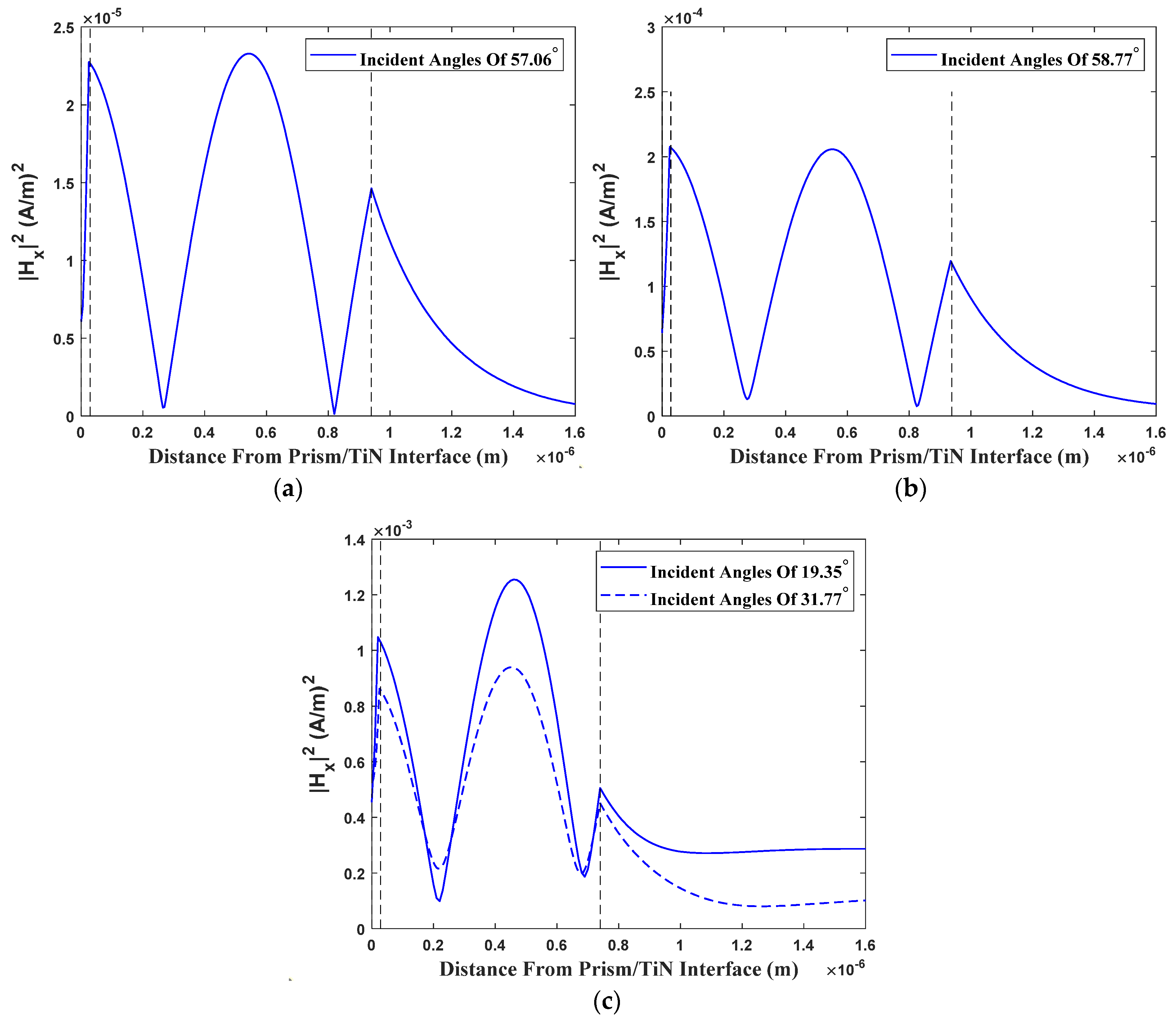
3.4. Field Distribution for TE Polarized Light
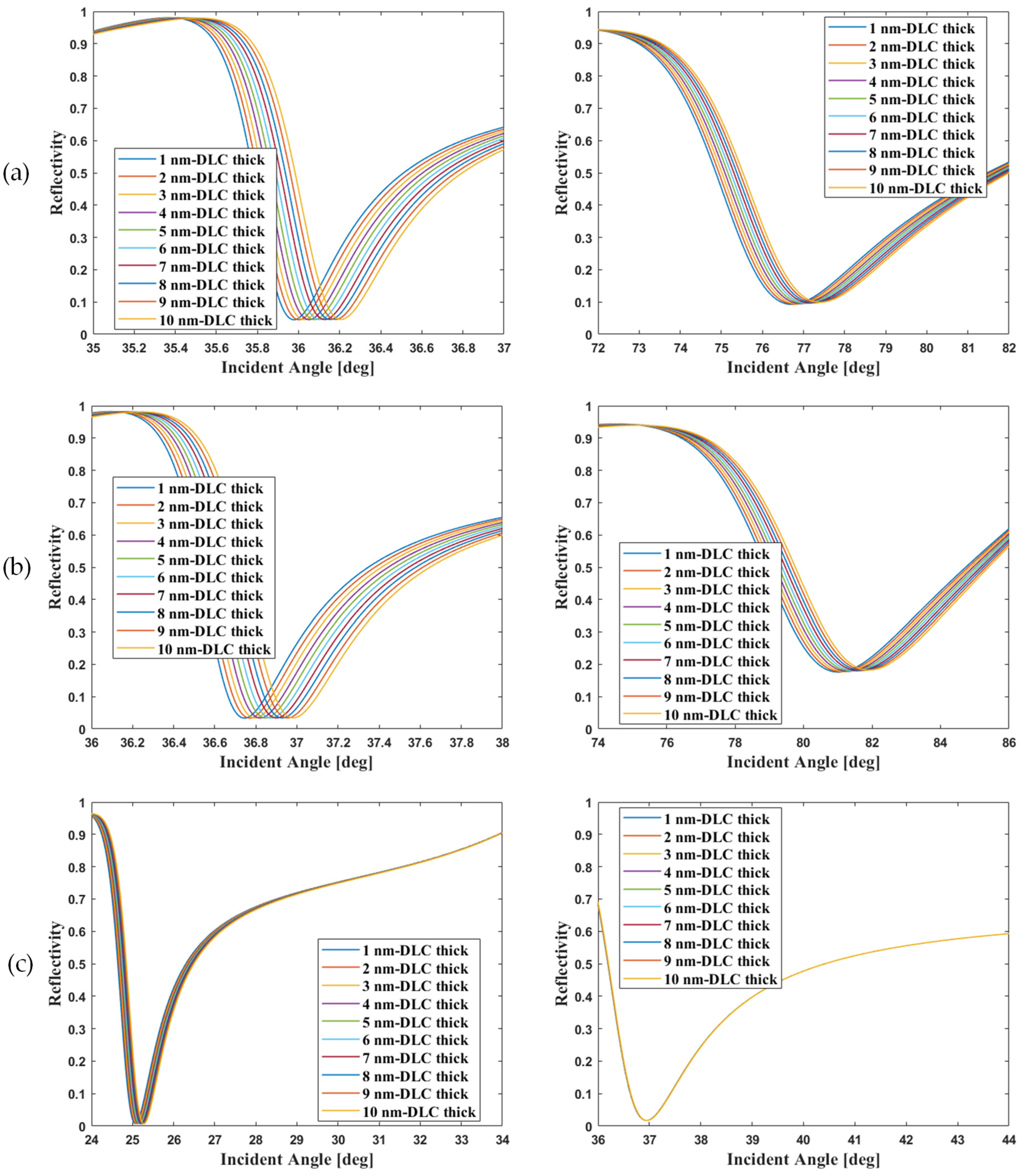
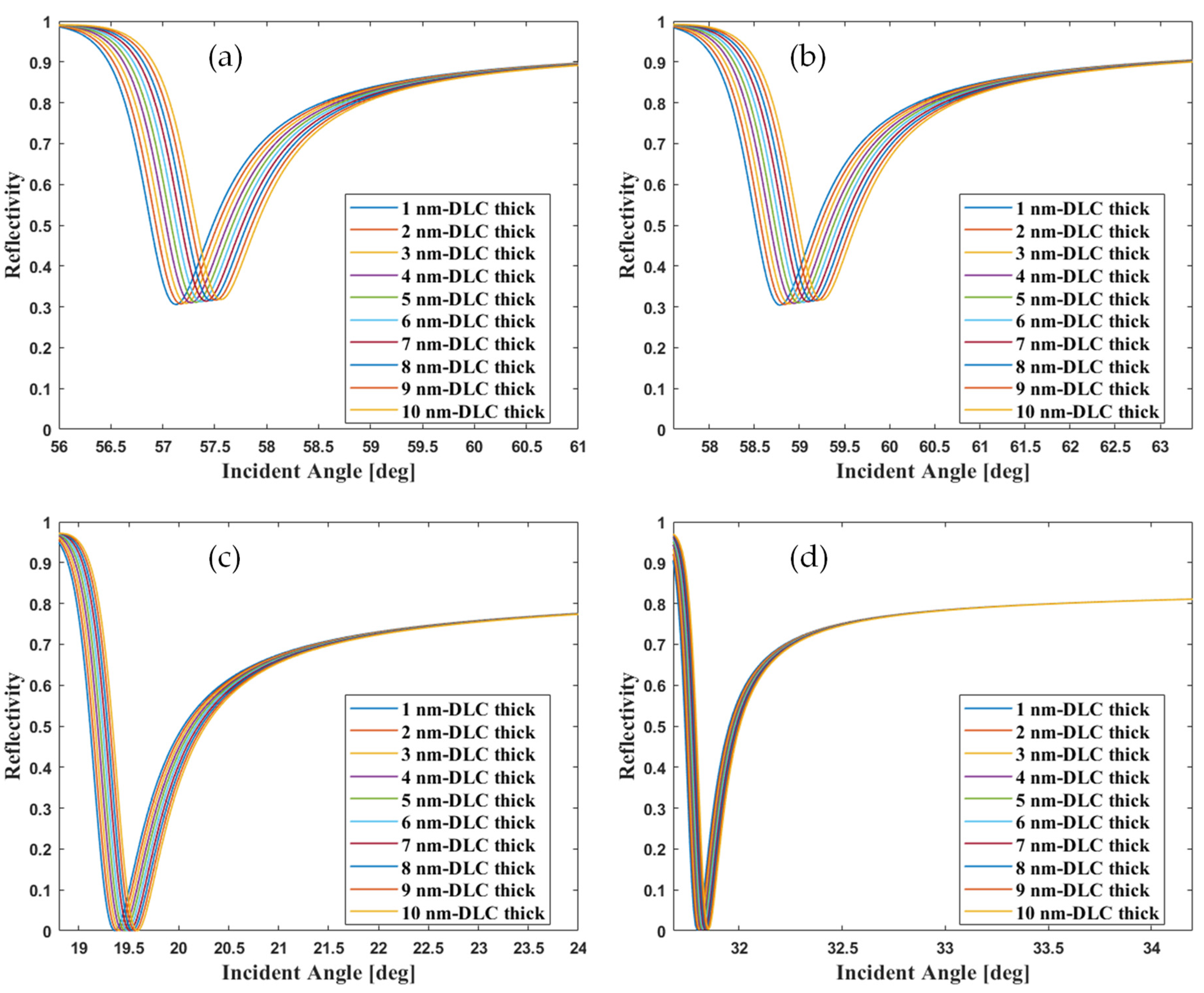
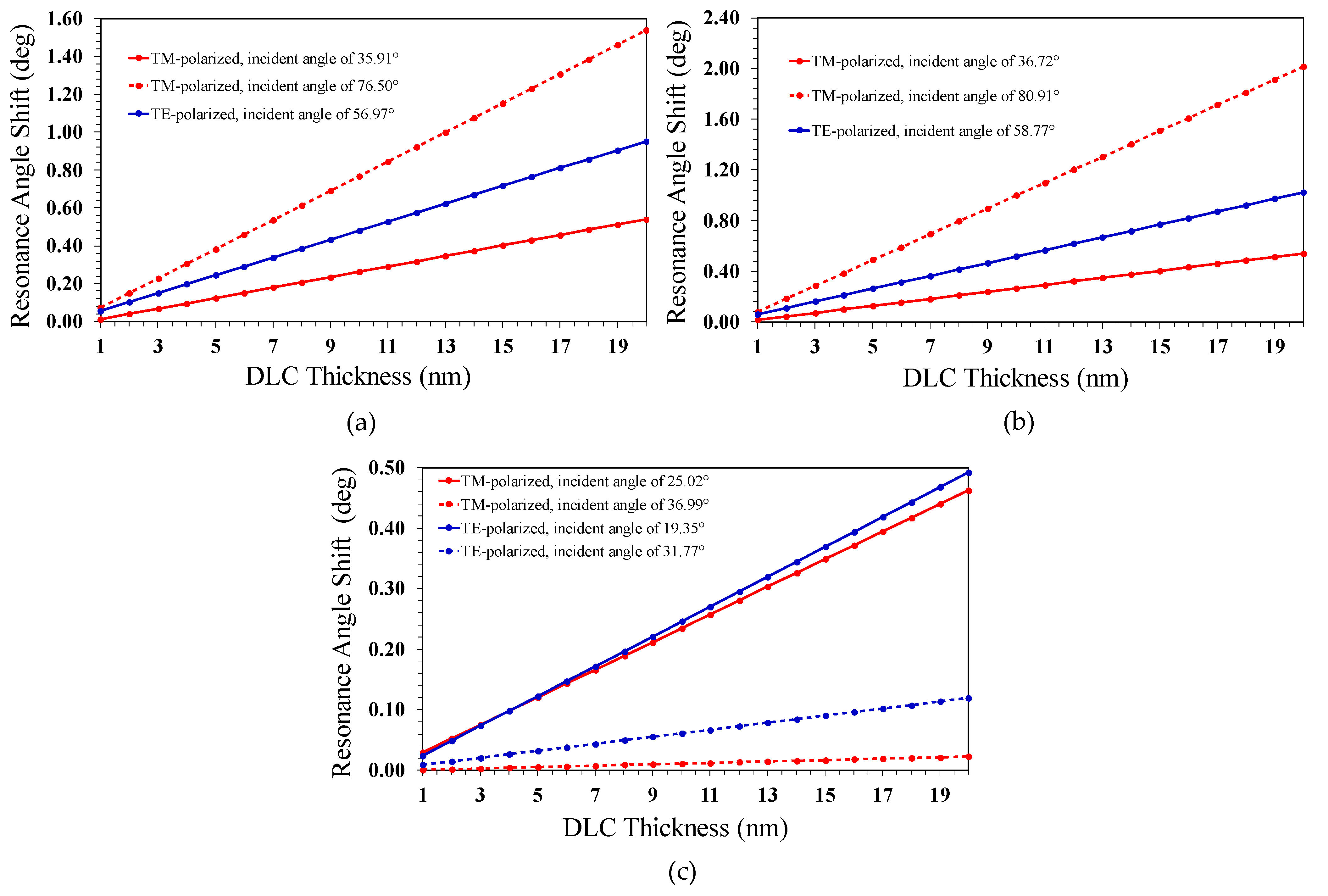
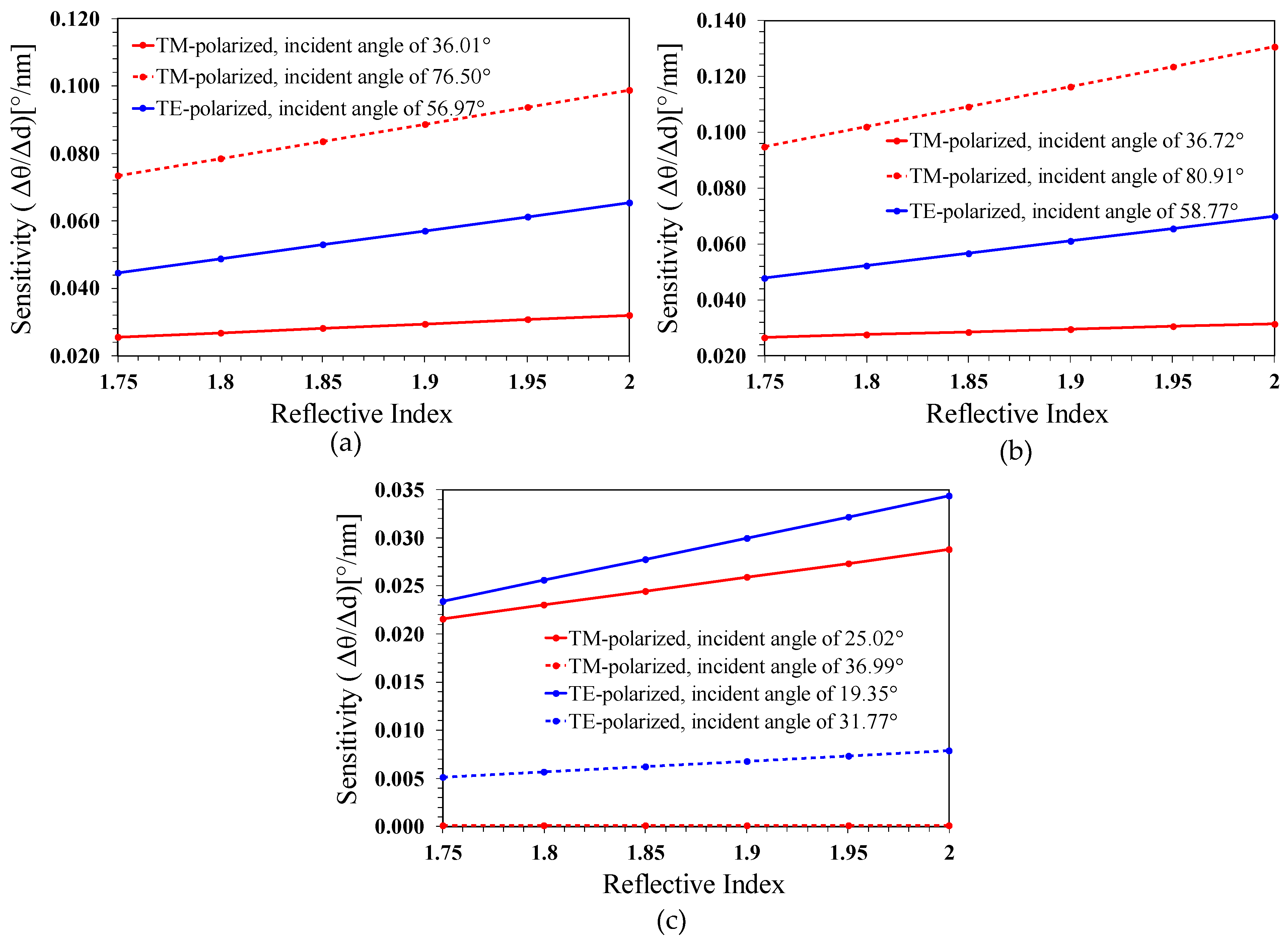
3.5. The Optimized CPWR Sensors Responds to the DLC Film Thicknesses
3.6. Example for Simultaneous Measuring the Thickness and Refractive Index of the DLC Film Using the GA Optimized Sapphire Prism/TiN/AlN/Air Sensor
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Raether, H. Surface Plasmons on Smooth and Rough Surfaces and on Gratings; Springer: New York, NY, USA, 2014; ISBN 9783662151235. [Google Scholar]
- Kravets, V.G.; Kabashin, A.V.; Barnes, W.L.; Grigorenko, A.N. Plasmonic Surface Lattice Resonances: A Review of Properties and Applications. Chem. Rev. 2018, 118, 5912–5951. [Google Scholar] [CrossRef] [PubMed]
- Yesudasu, V.; Pradhan, H.S.; Pandya, R.J. Recent Progress in Surface Plasmon Resonance Based Sensors: A Comprehensive Review. Heliyon 2021, 7, e06321. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Zheng, Y.; Luo, Y.; Zhang, J.; Yi, Z.; Wu, X.; Cheng, S.; Yang, W.; Yu, Y.; Wu, P. A Four-Band and Polarization-Independent BDS-Based Tunable Absorber with High Refractive Index Sensitivity. Phys. Chem. Chem. Phys. 2021, 23, 26864–26873. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Chen, Z.; Yang, H.; Wen, L.; Yi, Z.; Zhou, Z.; Dai, B.; Zhang, J.; Wu, X.; Wu, P. Multi-mode surface plasmon resonance absorber based on dart-type single-layer graphene. RSC Adv. 2022, 12, 7821–7829. [Google Scholar] [CrossRef]
- Yin, H.; Chen, S.; Huang, R.; Chang, H.; Liu, J.; Qi, W.; He, Z.; Su, R. Real-Time Thickness Measurement of Marine Oil Spill by Fiber-Optic Surface Plasmon Resonance Sensors. Front. Mar. Sci. 2022, 8, 764970. [Google Scholar] [CrossRef]
- Andam, N.; Refki, S.; Hayashi, S.; Sekkat, Z. Plasmonic mode coupling and thin film sensing in metal–insulator–metal structures. Sci. Rep. 2021, 11, 15093. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, X.; Tian, J.; Zhu, W.; Song, J.; Xiao, H. Evaluating the Refractive Index, Thickness and Porosity of Ultrathin Cellulose Nanocrystal Films with Different Polymorphs by SPR Technique. Int. J. Biol. Macromol. 2021, 193, 1209–1214. [Google Scholar] [CrossRef]
- Salamon, Z.; Macleod, H.A.; Tollin, G. Coupled Plasmon-Waveguide Resonators: A New Spectroscopic Tool for Probing Proteolipid Film Structure and Properties. Biophys. J. 1997, 73, 2791–2797. [Google Scholar] [CrossRef]
- Hayashi, S.; Nesterenko, D.V.; Sekkat, Z.; Inoue, Y.; Kawata, S. Sharp Resonances in Waveguide-Coupled Surface Plasmon Sensors for Super-Resolution Sensing. In Proceedings of the JSAP-OSA Joint Symposia 2014 Abstracts; OSA: Washington, DC, USA, 2014. [Google Scholar]
- Jiang, X.D.; Xu, W.R.; Ilyas, N.; Li, M.C.; Guo, R.K.; Khan, R.; Li, W.; Wang, J.M. High-performance coupled plasmon waveguide resonance optical sensor based on SiO2:Ag film. Results Phys. 2021, 26, 104308. [Google Scholar] [CrossRef]
- Convert, L.; Chabot, V.; Zermatten, P.-J.; Hamel, R., Jr.; Cloarec, J.-P.; Lecomte, R.; Aimez, V.; Charette, P.G. Passivation of KMPR Microfluidic Channels with Bovine Serum Albumin (BSA) for Improved Hemocompatibility Characterized with Metal-Clad Waveguides. Sens. Actuators B Chem. 2012, 173, 447–454. [Google Scholar] [CrossRef][Green Version]
- Zourob, M.; Goddard, N.J. Metal Clad Leaky Waveguides for Chemical and Biosensing Applications. Biosens. Bioelectron. 2005, 20, 1718–1727. [Google Scholar] [CrossRef] [PubMed]
- Gupta, R.; Goddard, N.J. Leaky Waveguides (LWs) for Chemical and Biological Sensing−A Review and Future Perspective. Sens. Actuators B Chem. 2020, 322, 128628. [Google Scholar] [CrossRef]
- Harte, E.; Alves, I.D.; Ihrke, I.; Elezgaray, J. Thickness determination in anisotropic media with plasmon waveguide resonance imaging. Opt. Express 2019, 27, 3264–3275. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.; Gao, L.; Zou, C.; Xie, W.; Tian, C.; Wang, Z.; Liang, F.; Ke, Y.; Zhou, X.; Li, S. Differential Refractive Index Sensor Based on Coupled Plasmon Waveguide Resonance in the C-Band. Sensors 2021, 21, 7984. [Google Scholar] [CrossRef]
- Chien, F.C.; Chen, S.J. Direct Determination of the Refractive Index and Thickness of a Biolayer Based on Coupled Waveguide Surface Plasmon Resonance Mode. Opt. Lett. 2006, 31, 187–189. [Google Scholar] [CrossRef]
- Zaman, Q.; Costa, J.S.; Tahir; Barreto, A.R.J.; Araujo, J.F.D.F.; Carlos, L.D.; Carneiro Neto, A.N.; Cremona, M.; Ahmed, Z.; Cruz, A.F.S.; et al. Dielectric-Loaded Waveguides as Advanced Platforms for Diagnostics and Application of Transparent Thin Films. Langmuir 2021, 37, 3248–3260. [Google Scholar] [CrossRef]
- West, P.R.; Ishii, S.; Naik, G.V.; Emani, N.K.; Shalaev, V.M.; Boltasseva, A. Searching for Better Plasmonic Materials. Laser Photon. Rev. 2010, 4, 795–808. [Google Scholar] [CrossRef]
- Khurgin, J.B. Replacing Noble Metals with Alternative Materials in Plasmonics and Metamaterials: How Good an Idea? Philos. Trans. A Math. Phys. Eng. Sci. 2017, 375, 20160068. [Google Scholar]
- Boltasseva, A.; Atwater, H.A. Materials Science. Low-Loss Plasmonic Metamaterials. Science 2011, 331, 290–291. [Google Scholar] [CrossRef]
- Bobb, D.A.; Zhu, G.; Mayy, M.; Gavrilenko, A.V.; Mead, P.; Gavrilenko, V.I.; Noginov, M.A. Engineering of Low-Loss Metal for Nanoplasmonic and Metamaterials Applications. Appl. Phys. Lett. 2009, 95, 151102. [Google Scholar] [CrossRef]
- Jablan, M.; Buljan, H.; Soljačić, M. Plasmonics in Graphene at Infrared Frequencies. Phys. Rev. B Condens. Matter Mater. Phys. 2009, 80, 245435. [Google Scholar] [CrossRef]
- Chen, N.C.; Lien, W.C.; Liu, C.R.; Huang, Y.L.; Lin, Y.R.; Chou, C.; Chang, S.Y.; Ho, C.W. Excitation of Surface Plasma Wave at TiN/Air Interface in the Kretschmann Geometry. J. Appl. Phys. 2011, 109, 043104. [Google Scholar] [CrossRef]
- Gioti, M.; Arvanitidis, J.; Christofilos, D.; Chaudhuri, K.; Zorba, T.; Abadias, G.; Gall, D.; Shalaev, V.M.; Boltasseva, A.; Patsalas, P. Plasmonic and phononic properties of epitaxial conductive transition metal nitrides. J. Opt. 2020, 22, 084001. [Google Scholar] [CrossRef]
- Catellani, A.; Calzolari, A. Plasmonic Properties of Refractory Titanium Nitride. Phys. Rev. B. 2017, 95, 115145. [Google Scholar] [CrossRef]
- Banerjee, A.; Heath, R.M.; Morozov, D.; Hemakumara, D.; Nasti, U.; Thayne, I.; Hadfield, R.H. Optical Properties of Refractory Metal Based Thin Films. Opt. Mater. Express 2018, 8, 2072. [Google Scholar] [CrossRef]
- Gosciniak, J.; Atar, F.B.; Corbett, B.; Rasras, M. Plasmonic Schottky Photodetector with Metal Stripe Embedded into Semiconductor and with a CMOS-Compatible Titanium Nitride. Sci. Rep. 2019, 9, 6048. [Google Scholar] [CrossRef]
- Guo, W.-P.; Mishra, R.; Cheng, C.-W.; Wu, B.-H.; Chen, L.-J.; Lin, M.-T.; Gwo, S. Titanium Nitride Epitaxial Films as a Plasmonic Material Platform: Alternative to Gold. ACS Photonics 2019, 6, 1848–1854. [Google Scholar] [CrossRef]
- Maurya, K.C.; Shalaev, V.M.; Boltasseva, A.; Saha, B. Reduced Optical Losses in Refractory Plasmonic Titanium Nitride Thin Films Deposited with Molecular Beam Epitaxy. Opt. Mater. Express 2020, 10, 2679. [Google Scholar] [CrossRef]
- Surre, F.; Bernal, O.D.; Seat, H.-C.; Sharp, J.H. Estimation of Transition Metal Nitride Surface Plasmon Refractometer Sensitivity. In Proceedings of the 2019 IEEE SENSORS, Montreal, QC, Canada, 27–30 October 2019. [Google Scholar]
- Esfahani Monfared, Y. Refractive Index Sensor Based on Surface Plasmon Resonance Excitation in a D-Shaped Photonic Crystal Fiber Coated by Titanium Nitride. Plasmonics 2020, 15, 535–542. [Google Scholar] [CrossRef]
- Asencios, J.; Moro, R.; Luyo, C.; Talledo, A. High Sensitive Biosensors Based on the Coupling between Surface Plasmon Polaritons on Titanium Nitride and a Planar Waveguide Mode. Sensors 2020, 20, 1784. [Google Scholar] [CrossRef]
- Mishra, P.; Debnath, A.K.; Choudhury, S.D. Titanium nitride as an alternative and reusable plasmonic substrate for fluorescence coupling. Phys. Chem. Chem. Physics. 2022, 24, 6256–6265. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Cai, H.; Wang, X.; Zhan, S. Optimization methodology for structural multiparameter surface plasmon resonance sensors in different modulation modes based on particle swarm optimization. Opt. Commun. 2019, 431, 142–150. [Google Scholar] [CrossRef]
- Han, L.; Xu, C.; Huang, T.; Dang, X. Improved particle swarm optimization algorithm for high performance SPR sensor design. Appl. Opt. 2021, 60, 1753–1760. [Google Scholar] [CrossRef] [PubMed]
- Bahrami, F.; Maisonneuve, M.; Meunier, M.; Aitchison, J.S.; Mojahedi, M. An improved refractive index sensor based on genetic optimization of plasmon waveguide resonance. Opt. Express 2013, 21, 20863–20872. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.; Chen, S. Design of high-performance Au-Ag-dielectric-graphene based surface plasmon resonance biosensors using genetic algorithm. J. Appl. Phys. 2019, 125, 113101. [Google Scholar] [CrossRef]
- Cai, H.; Shan, S.; Wang, X. High Sensitivity Surface Plasmon Resonance Sensor Based on Periodic Multilayer Thin Films. Nanomaterials 2021, 11, 3399. [Google Scholar] [CrossRef]
- Robertson, J. Diamond-like Amorphous Carbon. Mater. Sci. Eng. R Rep. 2002, 37, 129–281. [Google Scholar] [CrossRef]
- Nakamura, M.; Kubota, S.; Suzuki, H.; Haraguchi, T. Wear and Friction Characteristics of AlN/Diamond-like Carbon Hybrid Coatings on Aluminum Alloy. J. Mater. Eng. Perform. 2015, 24, 3789–3797. [Google Scholar] [CrossRef]
- Deng, Y.; Cao, G.; Wu, Y.; Zhou, X.; Liao, W. Theoretical Description of Dynamic Transmission Characteristics in MDM Waveguide Aperture-Side-Coupled with Ring Cavity. Plasmonics 2015, 10, 1537–1543. [Google Scholar] [CrossRef]
- Deng, Y.; Cao, G.; Yang, H.; Zhou, X.; Wu, Y. Dynamic Control of Double Plasmon-Induced Transparencies in Aperture-Coupled Waveguide-Cavity System. Plasmonics 2018, 13, 345–352. [Google Scholar] [CrossRef]
- Naik, G.V.; Schroeder, J.L.; Ni, X.; Kildishev, A.V.; Sands, T.D.; Boltasseva, A. Titanium Nitride as a Plasmonic Material for Visible and Near-Infrared Wavelengths. Opt. Mater. Express 2012, 2, 478. [Google Scholar] [CrossRef]
- Moatti, A.; Narayan, J. High-Quality TiN/AlN Thin Film Heterostructures on c-Sapphire. Acta Mater. 2018, 145, 134–141. [Google Scholar] [CrossRef]
- Madan, A.; Kim, I.W.; Cheng, S.C.; Yashar, P.; Dravid, V.P.; Barnett, S.A. Stabilization of Cubic AlN in Epitaxial AlN/TiN Superlattices. Phys. Rev. Lett. 1997, 78, 1743–1746. [Google Scholar] [CrossRef]
- Auger, M.A.; Gago, R.; Fernández, M.; Sánchez, O.; Albella, J.M. Deposition of TiN/AlN Bilayers on a Rotating Substrate by Reactive Sputtering. Surf. Coat. Technol. 2002, 157, 26–33. [Google Scholar] [CrossRef]
- Oila, A.; Bull, S.J. Experimental Assessment of the Elastic Properties of Thin TiN/AlN Superlattice and Nano-Multilayer Coatings. Surf. Coat. Technol. 2014, 257, 87–94. [Google Scholar] [CrossRef]
- Shalabney, A.; Abdulhalim, I. Electromagnetic fields distribution in multilayer thin film structures and the origin of sensitivity enhancement in surface plasmon resonance sensors. Sens. Actuators B Chem. 2010, 159, 24–32. [Google Scholar] [CrossRef]
- OptiFDTD: Technical Background and Tutorials, 12th ed.; Optiwave Systems Inc.: Ottawa, ON, Canada, 2014.
- Dodge, M.J. “Refractive Index” in Handbook of Laser Science and Technology; Optical Materials: Part 2; CRC Press: Boca Raton, FL, USA, 1986; Volume IV, p. 30. [Google Scholar]
- RStephens, E.; Malitson, I.H. Index of refraction of magnesium oxide. J. Res. Natl. Bur. Stand. 1952, 49, 249–252. [Google Scholar] [CrossRef]
- Kischkat, J.; Peters, S.; Gruska, B.; Semtsiv, M.; Chashnikova, M.; Klinkmüller, M.; Fedosenko, O.; Machulik, S.; Aleksandrova, A.; Monastyrskyi, G.; et al. Mid-Infrared Optical Properties of Thin Films of Aluminum Oxide, Titanium Dioxide, Silicon Dioxide, Aluminum Nitride, and Silicon Nitride. Appl. Opt. 2012, 51, 6789–6798. [Google Scholar] [CrossRef]
- Smietana, M.; Bock, W.J.; Szmidt, J.; Grabarczyk, J. Substrate Effect on the Optical Properties and Thickness of Diamond-like Carbon Films Deposited by the RF PACVD Method. Diam. Relat. Mater. 2010, 19, 1461–1465. [Google Scholar] [CrossRef]
- Shalabney, A.; Abdulhalim, I. Sensitivity Enhancement Methods for Surface Plasmon Sensors. Laser Photonics Rev 2011, 5, 571–606. [Google Scholar] [CrossRef]
- Shrivastav, A.M.; Satish, L.; Kushmaro, A.; Shvalya, V.; Cvelbar, U.; Abdulhalim, I. Engineering the Penetration Depth of Nearly Guided Wave Surface Plasmon Resonance towards Application in Bacterial Cells Monitoring. Sens. Actuators B. Chem. 2021, 345, 130338. [Google Scholar] [CrossRef]
- Isaacs, S.; Harté, E.; Alves, I.D.; Abdulhalim, I. Improved Detection of Plasmon Waveguide Resonance Using Diverging Beam, Liquid Crystal Retarder, and Application to Lipid Orientation Determination. Sensors 2019, 19, 1402. [Google Scholar] [CrossRef] [PubMed]
- Peterlinz, K.A.; Georgiadis, R.M.; Herne, T.M.; Tarlov, M.J. Observation of Hybridization and Dehybridization of Thiol-Tethered DNA Using Two-Color Surface Plasmon Resonance Spectroscopy. J. Am. Chem. Soc. 1997, 119, 3401–3402. [Google Scholar] [CrossRef]
- Bahrami, F.; Aitchison, J.S.; Mojahedi, M. Multimode Spectroscopy Using Dielectric Grating Coupled to a Surface Plasmon Resonance Sensor. Opt. Lett. 2014, 39, 3946–3949. [Google Scholar] [CrossRef] [PubMed]
- de Bruijn, H.E.; Altenburg, B.S.F.; Kooyman, R.P.H.; Greve, J. Determination of Thickness and Dielectric Constant of Thin Transparent Dielectric Layers Using Surface Plasmon Resonance. Opt. Commun. 1991, 82, 425–432. [Google Scholar] [CrossRef]
- Del Rosso, T.; Sánchez, J.E.H.; Carvalho, R.S.; Pandoli, O.; Cremona, M. Accurate and Simultaneous Measurement of Thickness and Refractive Index of Thermally Evaporated Thin Organic Films by Surface Plasmon Resonance Spectroscopy. Opt. Express 2014, 22, 18914–18923. [Google Scholar] [CrossRef]
- Li, L.; Lei, J.; Wu, L.; Pan, F.; Aliofkhazraei, M.; Ali, N.; Chipara, M.; Laidani, N.B. Spectroscopic Ellipsometry. Handb. Mod. Coat. Technologies. 2021, 45–83. [Google Scholar] [CrossRef]
- Nestler, P.; Helm, C.A. Determination of Refractive Index and Layer Thickness of nm-Thin Films via Ellipsometry. Opt. Express 2017, 25, 27077. [Google Scholar] [CrossRef]
- Akasaka, H.; Gawazawa, N.; Kishimoto, S.-I.; Ohshio, S.; Saitoh, H. Surface Plasmon Resonance Detection Using Amorphous Carbon/Au Multilayer Structure. Appl. Surf. Sci. 2009, 256, 1236–1239. [Google Scholar] [CrossRef]
- Takarada, A.; Suzuki, T.; Kanda, K.; Niibe, M.; Nakano, M.; Ohtake, N.; Akasaka, H. Structural Dependence of Corrosion Resistance of Amorphous Carbon Films against Nitric Acid. Diam. Relat. Mater. 2015, 51, 49–54. [Google Scholar] [CrossRef]
- Peterlinz, K.A.; Georgiadis, R. Two-Color Approach for Determination of Thickness and Dielectric Constant of Thin Films Using Surface Plasmon Resonance Spectroscopy. Opt. Commun. 1996, 130, 260–266. [Google Scholar] [CrossRef]
- Granqvist, N.; Liang, H.; Laurila, T.; Sadowski, J.; Yliperttula, M.; Viitala, T. Characterizing Ultrathin and Thick Organic Layers by Surface Plasmon Resonance Three-Wavelength and Waveguide Mode Analysis. Langmuir 2013, 29, 8561–8571. [Google Scholar] [CrossRef] [PubMed]
- Francis, D.; Ford, H.D.; Tatam, R.P. Spectrometer-Based Refractive Index and Dispersion Measurement Using Low-Coherence Interferometry with Confocal Scanning. Opt. Express 2018, 26, 3604. [Google Scholar] [CrossRef] [PubMed]
- Sun, P.; Zhou, C.; Jia, W.; Wang, J.; Xiang, C.; Xie, Y.; Zhao, D. Self-Referenced Refractive Index Sensor Based on Hybrid Mode Resonances in 2D Metal-Dielectric Grating. J. Phys. D Appl. Phys. 2020, 53, 145101. [Google Scholar] [CrossRef]



| Layer | Material | Refractive Index |
|---|---|---|
| Prism | Sapphire | 1.746 [51] |
| Silicon | 3.48 [28] | |
| Magnesium oxide | 1.715 [52] | |
| Plasmon active | Titanium nitride | 0.9857 + 9.1899i [29] |
| Waveguide | Aluminum nitride | 2.0293 + 0.0001i [53] |
| Sensing | Dimond-like carbon | 1.79 + 0.0099i [54] |
| Surrounding | Air | 1.00002 [54] |
| Structure | Thickness | |
|---|---|---|
| TiN Layer | AlN Layer | |
| sapphire prism/TiN/AlN/air | 29.42 nm | 909.83 nm |
| magnesium oxide-prism/TiN/AlN/air | 28.33 nm | 909.50 nm |
| silicon prism/TiN/AlN/air | 28.33 nm | 771.88 nm |
| Method | Advantage | Disadvantage | |
|---|---|---|---|
| Conventional SPR: prism/metal/air | One wavelength [64,65] |
|
|
| Two-color [66] Three-wavelength [67] |
|
| |
| Two-medium [60] |
| ||
| Optical fiber SPR: SiO2/Au/water | One wavelength [6] |
|
|
| Conventional CPWR: prism/Au/SiO2/air | One wavelength [15,16,17,18] |
|
|
| Proposed CPWR: prism/TiN/AlN/air | One wavelength |
|
|
| Ellipsometry [62,63] | Multi wavelength |
|
|
| Interferometry [68] | One wavelength |
|
|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Junrear, J.; Sakunasinha, P.; Chiangga, S. The Optimization of Metal Nitride Coupled Plasmon Waveguide Resonance Sensors Using a Genetic Algorithm for Sensing the Thickness and Refractive Index of Diamond-like Carbon Thin Films. Photonics 2022, 9, 332. https://doi.org/10.3390/photonics9050332
Junrear J, Sakunasinha P, Chiangga S. The Optimization of Metal Nitride Coupled Plasmon Waveguide Resonance Sensors Using a Genetic Algorithm for Sensing the Thickness and Refractive Index of Diamond-like Carbon Thin Films. Photonics. 2022; 9(5):332. https://doi.org/10.3390/photonics9050332
Chicago/Turabian StyleJunrear, Jaturong, Panarit Sakunasinha, and Surasak Chiangga. 2022. "The Optimization of Metal Nitride Coupled Plasmon Waveguide Resonance Sensors Using a Genetic Algorithm for Sensing the Thickness and Refractive Index of Diamond-like Carbon Thin Films" Photonics 9, no. 5: 332. https://doi.org/10.3390/photonics9050332
APA StyleJunrear, J., Sakunasinha, P., & Chiangga, S. (2022). The Optimization of Metal Nitride Coupled Plasmon Waveguide Resonance Sensors Using a Genetic Algorithm for Sensing the Thickness and Refractive Index of Diamond-like Carbon Thin Films. Photonics, 9(5), 332. https://doi.org/10.3390/photonics9050332






