Thermal Stability Analysis of Surface Wave Assisted Bio-Photonic Sensor
Abstract
:1. Introduction
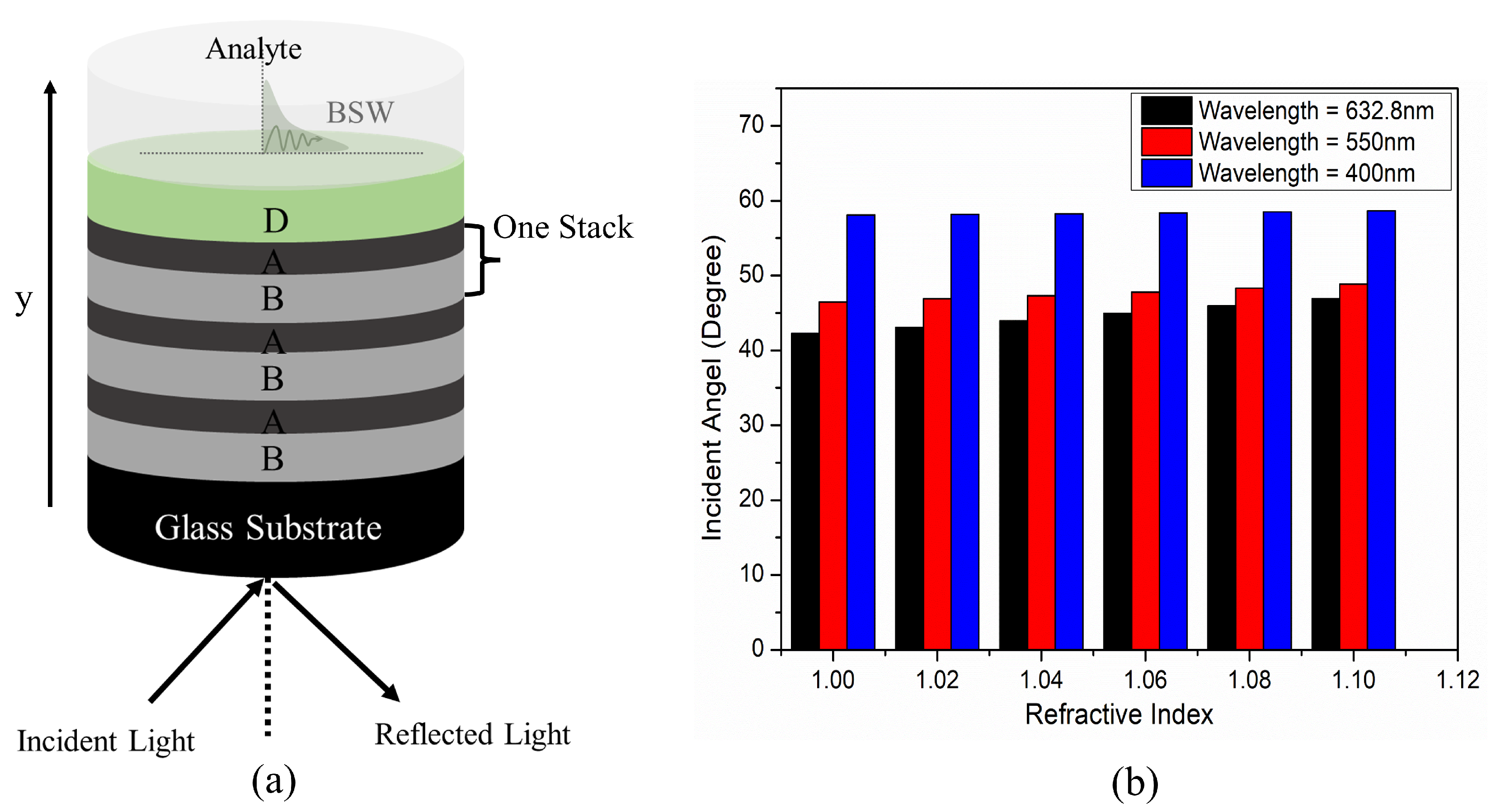
2. Structure Design and Methods
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ciminelli, C.; Campanella, C.M.; Dell’Olio, F.; Campanella, C.E.; Armenise, M.N. Label free optical resonant sensors for biochemical applications. Prog. Quant. Electron. 2013, 37, 51–107. [Google Scholar] [CrossRef]
- Goyal, A.K. Design Analysis of One-Dimensional Photonic Crystal Based Structure for Hemoglobin Concentration Measurement. Prog. Electromagn. Res. M 2020, 97, 77–86. [Google Scholar] [CrossRef]
- Homola, J.; Yee, J.J.; Gauglitz, G. Surface plasmon resonance sensors review. Sens. Actuators B 1999, 54, 3–15. [Google Scholar] [CrossRef]
- Zaky, Z.A.; Ahmed, A.M.; Shalaby, A.S.; Aly, A.H. Refractive index gas sensor based on the Tamm state in a one-dimensional photonic crystal: Theoretical optimisation. Sci. Rep. 2020, 10, 9736. [Google Scholar] [CrossRef]
- Seitz, W.R. Chemical sensors based on fiber optics. Anal. Chem. 1984, 56, 16A. [Google Scholar] [CrossRef]
- Choi, C.J.; Belobraydich, A.R.; Chan, L.L.; Mathias, P.C.; Cunningham, B.T. Comparison of label-free biosensing in microplate, microfluidic, and spot-based affinity capture assays. Anal. Biochem. 2010, 405, 1–10. [Google Scholar] [CrossRef]
- Karlsson, R.; Stahlebrg, R. Surface plasmon resonance detection and multispot sensing for direct monitoring of interactions involving low-molecular-weight analytes and for determination of low affinities. Anal. Biochem. 1995, 228, 274–280. [Google Scholar] [CrossRef]
- Saleh, E.A.; Teich, M.C. Fundamentals of Photonics; Wiley-Interscience: Hoboken, NJ, USA, 2007. [Google Scholar]
- Goyal, A.K.; Saini, J. Performance analysis of Bloch surface wave-based sensor using transition metal dichalcogenides. Appl. Nanosci. 2020, 10, 4307. [Google Scholar] [CrossRef]
- Zaky, Z.A.; Aly, A.H. Modeling of a biosensor using Tamm resonance excited by graphene. Appl. Opt. 2021, 60, 1411–1419. [Google Scholar] [CrossRef]
- Yeh, P.; Yariv, A.; Hong, C. Electromagnetic propagation in periodic stratified media. I. General theory. J. Opt. Soc. Am. 1977, 67, 423–438. [Google Scholar] [CrossRef] [Green Version]
- Yeh, P.; Yariv, A.; Cho, A.Y. Optical surface waves in periodic layered media. Appl. Phys. Lett. 1978, 32, 104–105. [Google Scholar] [CrossRef] [Green Version]
- Goyal, A.K.; Dutta, H.S.; Pal, S. Porous photonic crystal structure for sensing applications. J. Nanophotonics 2018, 12, 040501. [Google Scholar] [CrossRef]
- Baghbadorani, H.K.; Barvestani, J.; Entezar, S.R. Biosensors based on Bloch surface waves in one-dimensional photonic crystal with graphene nanolayers. Appl. Opt. 2017, 56, 462–469. [Google Scholar] [CrossRef] [PubMed]
- Baghbadorani, H.K.; Aurelio, D.; Barvestani, J.; Liscidini, M. Guided modes in photonic crystal slabs supporting Bloch surface waves. J. Opt. Soc. Am. B 2018, 35, 805–810. [Google Scholar] [CrossRef]
- Vinogradov, A.P.; Dorofeenko, A.V.; Merzlikin, A.M.; Lisyansky, A.A. Surface states in photonic crystals. Physics-Uspekhi 2010, 53, 243. [Google Scholar] [CrossRef]
- Abouti, O.E.; Boudouti, E.H.E.; Hassouani, Y.E.; Noual, A.; Djafari-Rouhani, B. Optical Tamm states in one-dimensional superconducting photonic crystal. Physics-Uspekhi 2016, 23, 082115. [Google Scholar] [CrossRef]
- Bijalwan, A.; Singh, B.K.; Rastogi, V. Surface Plasmon Resonance-Based Sensors Using Nano-Ribbons of Graphene and WSe2. Plasmonics 2020, 15, 1015–1023. [Google Scholar] [CrossRef]
- Jia, Y.; Li, Z.; Wang, H.; Saeed, M.; Cai, H. Sensitivity Enhancement of a Surface Plasmon Resonance Sensor with Platinum Diselenide. Sensors 2020, 20, 131. [Google Scholar] [CrossRef] [Green Version]
- Goyal, A.K.; Pal, S. Design analysis of Bloch surface wave based sensor for haemoglobin concentration measurement. Appl. Nanosci. 2020, 10, 3639–3647. [Google Scholar] [CrossRef]
- Gryga, M.; Ciprian, D.; Gembalova, L.; Hlubina, P. Sensing based on Bloch surface wave and self-referenced guided mode resonances employing a one-dimensional photonic crystal. Opt. Express 2021, 29, 12996. [Google Scholar] [CrossRef]
- Luo, H.; Tang, X.; Lu, Y.; Wang, P. Low-Loss Photonic Integrated Elements Based on Bound Bloch Surface Wave in the Continuum. Phys. Rev. Appl. 2021, 16, 014064. [Google Scholar] [CrossRef]
- Sfez, T.; Descrovi, E.; Yu, L.; Brunazzo, D.; Quaglio, M.; Dominici, L.; Nakagawa, W.; Michelotti, F.; Giorgis, F.; Martin, O.J.F.; et al. Bloch surface waves in ultrathin waveguides: Near-field investigation of mode polarization and propagation. J. Opt. Soc. Am. B 2010, 27, 1617–1625. [Google Scholar] [CrossRef]
- Yu, L.; Barakat, E.; Sfez, T.; Hvozdara, L.; Francesco, J.; Herzig, H.P. Manipulating Bloch surface waves in 2D: A platform concept-based flat lens. Light Sci. Appl. 2014, 3, e124. [Google Scholar] [CrossRef]
- Augenstein, Y.; Vetter, A.; Lahijani, B.V.; Herzig, H.P.; Rockstuhl, C.; Kim, M.S. Inverse photonic design of functional elements that focus Bloch surface waves. Light Sci. Appl. 2018, 7, 104. [Google Scholar] [CrossRef] [PubMed]
- Dubey, R.; Lahijani, B.V.; Barakat, E. Near-field characterization of a Bloch-surface-wave-based 2D disk resonator. Opt. Lett. 2016, 41, 4867–4870. [Google Scholar] [CrossRef]
- Rodriguez, G.; Aurelio, D.; Liscidini, M.; Weiss, S. Bloch surface wave ring resonator based on porous silicon. Appl. Phys. Lett. 2019, 115, 0111019. [Google Scholar] [CrossRef]
- Safronov, K.R.; Gulkin, D.N.; Antropov, I.M.; Abrashitova, K.A.; Bessonov, V.O.; Fedyanin, A.A. Multimode interference of Bloch surface electromagnetic waves. ACS Nano 2020, 14, 10428–10437. [Google Scholar] [CrossRef]
- Moreira, C.S.; Lima, A.M.N.; Neff, H.; Thirstrup, C. Temperature-dependent sensitivity of surface plasmon resonance sensors at the gold–water interface. Sens. Actuators B Chem. 2008, 134, 854–862. [Google Scholar] [CrossRef]
- Yaremchuk, I.; Fitio, V.; Petrovska, H.; Bobitski, Y. The temperature impact on the characteristics of the surface plasmon resonance sensors element. Optik 2019, 192, 162969. [Google Scholar] [CrossRef]
- Dhibi, A. Temperature effect on the performance of a 1D grating-based surface-plasmon resonance sensors. Opt. Quant. Electron. 2019, 51, 78. [Google Scholar] [CrossRef]
- Chen, Y.; Shi, W.; Feng, L.; Xu, X.; Shang-Guan, M. Study on simultaneous sensing of gas concentration and temperature in one-dimensional photonic crystal. Superlattices Microstruct. 2019, 131, 53–58. [Google Scholar] [CrossRef]
- Ratra, K.; Singh, M.; Goyal, A.K. Design and Analysis of Omni-directional Solar Spectrum Reflector using One-dimensional Photonic Crystal. J. Nanophoton. 2020, 14, 026005. [Google Scholar] [CrossRef]
- Ratra, K.; Singh, M.; Goyal, A.K.; Kaushik, R. Design and Analysis of Broadband Reflector for Passive Radiative Cooling. In Proceedings of the 5th International Conference on Signal Processing and Communication (ICSC), Noida, India, 7–9 March 2019. [Google Scholar] [CrossRef]
- Goyal, A.K.; Dutta, H.S.; Pal, S. Development of uniform porous one-dimensional photonic crystal based sensor. Optik 2020, 223, 165597. [Google Scholar] [CrossRef]
- Goyal, A.K.; Dutta, H.S.; Pal, S. Porous Multilayer Photonic Band Gap Structure For Optical Sensing. In Proceedings of the 13th International Conference on Fiber Optics and Photonic, Kanpur, India, 4–8 December 2016. [Google Scholar] [CrossRef]
- Zaky, Z.A.; Panda, A.; Pukhrambam, P.D.; Aly, A.H. The impact of magnetized cold plasma and its various properties in sensing applications. Sci. Rep. 2022, 12, 3754. [Google Scholar] [CrossRef] [PubMed]
- Aly, A.H.; Zaky, Z.A.; Shalaby, A.S.; Ahmed, A.M.; Vigneswaran, D. Theoretical study of hybrid multifunctional one-dimensional photonic crystal as a flexible blood sugar sensor. Phys. Scr. 2020, 95, 035510. [Google Scholar] [CrossRef]
- Goyal, A.K.; Kumar, A. Recent advances and progresses in photonic devices for passive radiative cooling application: A review. J. Nanophoton. 2020, 14, 030901. [Google Scholar] [CrossRef]
- Lourtioz, J.M.; Benisty, H.; Berger, V.; Gerard, J.M.; Maystre, D.; Tchelnokov, A. Optical Properties of Photonic Crystals. In Photonic Crystals: Towards Nanoscale Photonic Devices, 2nd ed.; Springer: New York, NY, USA, 2008. [Google Scholar]
- Gulsen, G.; Inci, M.N. Thermal optical properties of TiO2 films. Opt. Mater. 2002, 18, 373–381. [Google Scholar] [CrossRef]
- Ghosh, G. Model for the thermo-optic coefficients of some standard optical glasses. J. Non-Cryst. Solids 1995, 189, 191–196. [Google Scholar] [CrossRef]
- Aly, A.H.; Mohamed, D.; Mohaseb, M.A.; El-Gawaad, N.; Trabelsi, Y. Biophotonic sensor for the detection of creatinine concentration in blood serum based on 1D photonic crystal. RSC Adv. 2020, 10, 31765. [Google Scholar] [CrossRef]
- Dutta, H.S.; Goyal, A.K.; Pal, S. Analysis of Dispersion Diagram for High Performance Refractive Index Sensor based on Photonic Crystal Waveguides. Photonics Nanostruct. Appl. 2017, 23, 21–27. [Google Scholar] [CrossRef]


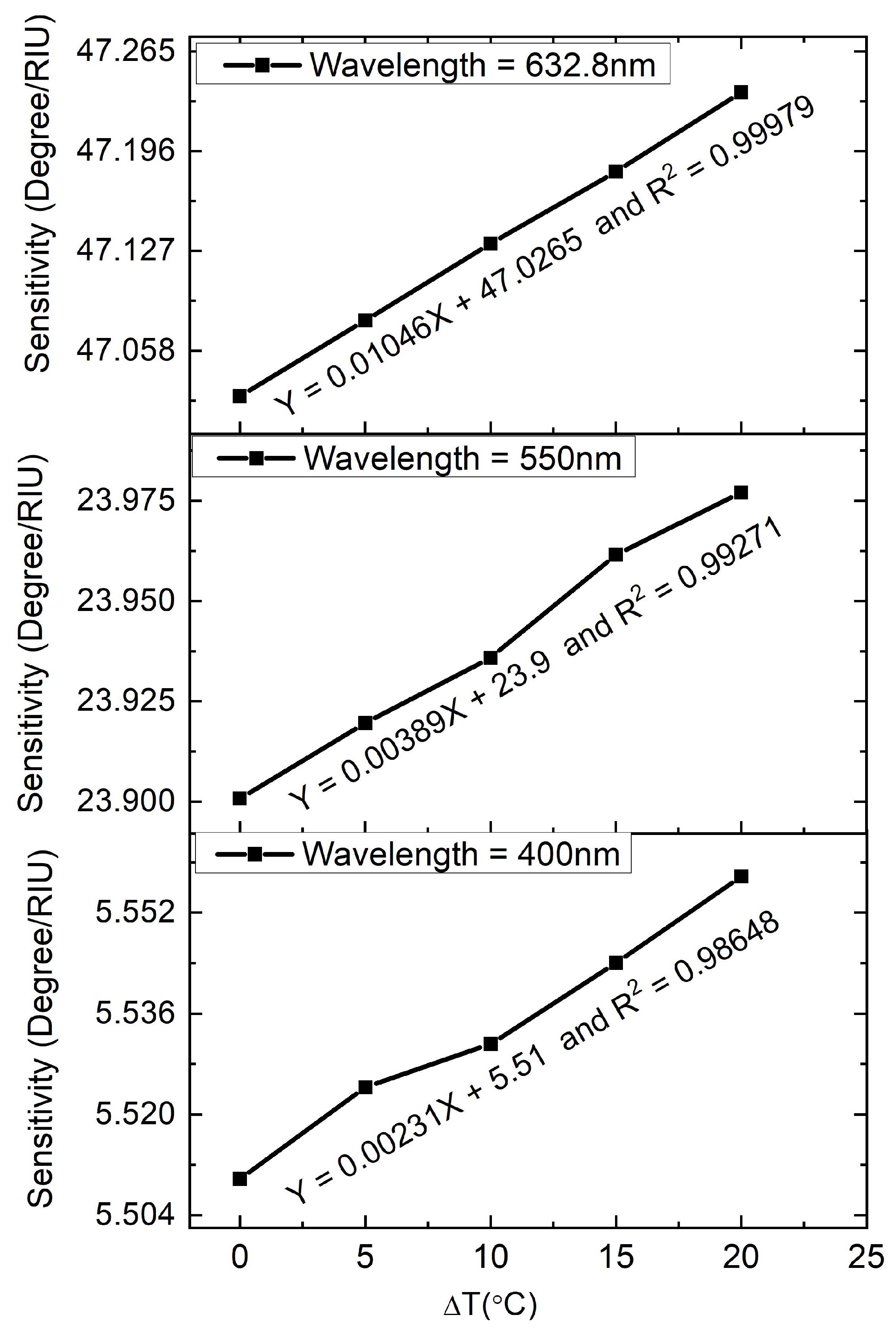
| Incident Wavelength | Temperature Variations () | Effective Refractive Index | Excitation Angle (Degree) | Sensitivity (Degree/RIU) | Excitation Angle Variations | Sensitivity Variation |
|---|---|---|---|---|---|---|
| 400 nm | 0 | 1.89546 | 58.08219 | 5.50975 | −0.0027 (Degree/) | 0.00231 ((Degree/RIU)/) |
| 5 | 1.89122 | 58.06899 | 5.52432 | |||
| 10 | 1.89051 | 58.05579 | 5.53118 | |||
| 15 | 1.88978 | 58.04199 | 5.54404 | |||
| 20 | 1.88907 | 58.02819 | 5.55775 | |||
| 550 nm | 0 | 1.84284 | 46.48411 | 23.90073 | −0.0016 (Degree/) | 0.00389 ((Degree/RIU)/) |
| 5 | 1.83921 | 46.47631 | 23.91959 | |||
| 10 | 1.83861 | 46.46851 | 23.93587 | |||
| 15 | 1.83798 | 46.46011 | 23.96159 | |||
| 20 | 1.83738 | 46.45231 | 23.97702 | |||
| 632.8 nm | 0 | 1.82569 | 42.24868 | 47.0266 | −0.00096 (Degree/) | 0.01046 ((Degree/RIU)/) |
| 5 | 1.82227 | 42.24388 | 47.0788 | |||
| 10 | 1.82171 | 42.23908 | 47.132 | |||
| 15 | 1.82111 | 42.23428 | 47.18174 | |||
| 20 | 1.82055 | 42.22948 | 47.2366 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goyal, A.K.; Kumar, A.; Massoud, Y. Thermal Stability Analysis of Surface Wave Assisted Bio-Photonic Sensor. Photonics 2022, 9, 324. https://doi.org/10.3390/photonics9050324
Goyal AK, Kumar A, Massoud Y. Thermal Stability Analysis of Surface Wave Assisted Bio-Photonic Sensor. Photonics. 2022; 9(5):324. https://doi.org/10.3390/photonics9050324
Chicago/Turabian StyleGoyal, Amit Kumar, Ajay Kumar, and Yehia Massoud. 2022. "Thermal Stability Analysis of Surface Wave Assisted Bio-Photonic Sensor" Photonics 9, no. 5: 324. https://doi.org/10.3390/photonics9050324
APA StyleGoyal, A. K., Kumar, A., & Massoud, Y. (2022). Thermal Stability Analysis of Surface Wave Assisted Bio-Photonic Sensor. Photonics, 9(5), 324. https://doi.org/10.3390/photonics9050324







